0 引　言

船舶凝给水系统作为船用蒸汽动力系统中连接除氧器、冷凝器以及汽轮给水机组等设备的关键纽带^[1]，其运行正常与否关系着整条船舶的健康命脉。在实际运行中，船舶凝给水系统结构复杂，子系统及设备零件众多，当出现故障时仅靠操作人员过往的经验难以快速准确地找出故障源头，从而会导致故障程度的加深，造成船舶的安全性和机动性受损，严重影响船舶的正常航行。因此，为了能够更加准确高效地找出故障原因，基于机器学习的智能故障监测方法应运而生。在过去的近20多年里，国内外学者对其进行了大量研究。

刘锐等^[2]在传统遗传算法的基础上，引入信息熵对其进行优化，并以核动力船舶设备为研究对象，结果表明，信息熵免疫遗传算法相比优化前的遗传算法具有更好的通用性，寻优速度以及故障诊断精度。许伟等^[3]以舰船主冷凝器为研究对象，建立具有时间序列特性的贝叶斯网络故障诊断模型，并通过实验验证了该模型的准确可靠性。李成钿等^[4]在结合实际情况和专家经验的基础上，建立完整的凝给水系统故障知识库，并引入深度置信神经网络诊断模型，结果表明该模型的故障诊断准确率高达98%。在过往有关船舶凝给水系统的故障诊断研究中，或者需要结合专家的经验判断，或者所需的故障诊断模型过于复杂，没有较好的实用性。在常见的机器学习算法中，BP神经网络因其具有简单易行、并行性好以及计算量小等特性，已成为目前最为成熟的神经网络之一，并且在故障诊断、趋势预测等领域获得广泛应用^[5]。但是，BP神经网络存在易陷入局部极小值，收敛速度慢等缺点。为了弥补这些不足，研究人员尝试了多种方法对BP神经网络进行优化。

朱馨渝等^[6]提出BP神经网络PID控制器算法，并利用优化后的粒子群算法优化BP神经网络的权值矩阵，结果显示优化后的粒子群算法具有更好的适应度函数曲线，其超调量以及调节时间也有明显改善。赵侃等^[7]采用分段线性混沌映射(PWLCM)和萤火虫算法(FA)改进麻雀搜索算法(SSA)，并用改进后的麻雀搜索算法优化BP神经网络模型的权值和阈值。结果显示改进后的麻雀搜索算法具有高效的全局最优搜索能力，优化后的ISSA-BP 神经网络精度优于BP、SSA-BP神经网络模型，具有更高的预测稳定性。徐猛等^[8]利用鲸鱼算法(WOA)对BP神经网络的初始权值和阈值进行优化，并用优化后的模型对结晶器液面波动进行预测，结果显示经过WOA优化后的BP神经网络有更好的预测效果。

在众多优化BP的算法中，利用鲸鱼算法对BP进行优化在近几年得到了许多学者的青睐，鲸鱼优化算法（WOA）通常用于复杂工程的优化，其目标是调整重要参数以满足约束和优化目标。WOA结构简单，参数少，搜索能力强，易于实现。然而，同其他元启发式算法一样，容易出现局部最优和收敛速度慢的问题。吕昊等^[9]提出了一种结合了非线性收敛因子、自适应权重以及模拟退火策略的混合鲸鱼退火算法（HWSA），并且通过不同损伤工况下ASCE Benchmark 结构模型的损伤识别数值模拟验证了改进方法的有效性。结果表明，混合鲸鱼退火算法能有效识别损伤位置及程度，其收敛精度和寻优性能有了明显提升，且在噪声环境下性能稳定，具有一定的抗噪鲁棒性。Deepa等^[10] 提出一种 Lévy 飞行鲸鱼优化算法(LWOA)，利用Lévy飞行策略调整位置更新后的座头鲸位置。实验结果表明，Levy WOA（LWOA）的性能显著提高了全局搜索能力，提高了收敛效率，大大提高了节点的覆盖效率，从而放大了网络的整体性能。

本文以船舶凝给水系统为研究对象，以BP神经网络为基础，首先，利用高度随机混沌Cubic map映射生成高质量的鲸鱼初始种群，然后利用自适应权重调整来帮助鲸鱼算法越过局部极小值，接着利用优化后的鲸鱼算法优化BP神经网络的权值和阈值矩阵，帮助BP神经网络克服容易陷入局部极小值，收敛速度慢等缺陷。最后利用Gensystem仿真平台生成的正常及故障数据给CAWOA-BP神经网络提供学习样本，并针对5种常见的凝给水系统故障进行实例演示，以此验证改进后模型的优越性。

1 故障监测方法描述 1.1 鲸鱼算法

鲸鱼算法^[11] (whale optimization algorithm,WOA)是一种类似于蚁群算法、灰狼算法的新型群体智能优化算法，其优点在于操作步骤简单、不需要过多参数以及容易越过局部极值。鲸鱼算法模拟了座头鲸的捕食猎物的整个过程，称为气泡网攻击。这种攻击是座头鲸包围猎物时，沿着螺旋路径形成独特气泡完成的，如图1所示。该算法总体包含包围猎物、气泡袭击(开发)、搜索猎物(探索) 3个阶段。

1.1.1 包围猎物

在该阶段中，每条鲸鱼的空间位置向量代表一个解，由于猎物目标在搜索空间中的位置未知，于是在鲸鱼算法中，假设距离目标猎物最近的鲸鱼就相当于当前的最优解，其他鲸鱼均向最优解的位置收缩包围来更新自身位置。鲸鱼包围猎物的数学模型如下：

$ \overrightarrow X (t + 1) = {\overrightarrow X _{gbest}}(t) - \overrightarrow A \cdot {D_1}\text{，} $

(1)

$ {D_1} = |\overrightarrow {C \cdot } {\overrightarrow X _{gbest}}(t) - \overrightarrow X (t)| 。$

(2)

其中： $ t $ 为当前迭代次数； $ {\overrightarrow X _{gbest}}(t) $ 为当前最优解的位置向量； $ \overrightarrow X (t) $ 为鲸鱼个体当前的位置向量； $ {D_1} $ 为鲸鱼个体与猎物之间的距离； $ \overrightarrow A $ 和 $ \overrightarrow C $ 为系数向量，用于控制鲸鱼的移动方式，定义如下：

$ \overrightarrow A = 2a \cdot \overrightarrow {{r_1}} - a \text{，}$

(3)

$ \overrightarrow C = 2 \cdot \overrightarrow {{r_2}}\text{，} $

(4)

$ a=2-2 t / t_{\max}\text{。} $

(5)

其中： $ \overrightarrow {{r_1}} $ ， $ \overrightarrow {{r_2}} $ 为 $ \left[0，1\right] $ 之间均匀分布产生的随机数； $ a $ 为收敛因子，随着迭代次数 $ t $ 的增加， $ a $ 从2线性减小到0； $ {t_{\max }} $ 为最大迭代次数。

1.1.2 气泡袭击

鲸鱼在气泡袭击阶段主要通过收缩包围机制和螺旋更新位置2种方式实现鲸鱼的局部寻优。

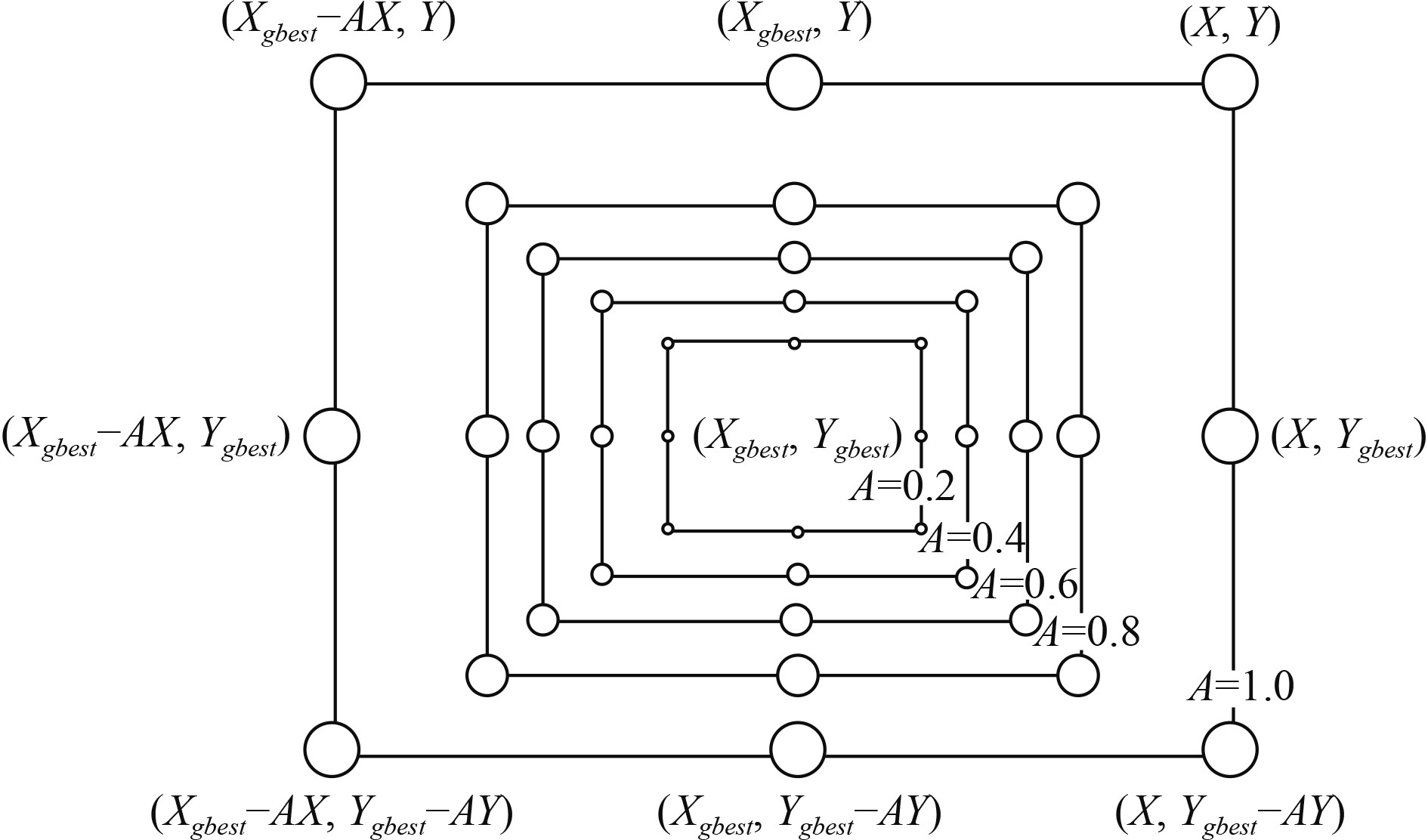
收缩包围机制：当收敛因子 $ a $ 的大小发生变化时，收缩包围机制得以实现。 $ a $ 的值从2减小到0时，系数向量 $ \overrightarrow A $ 在 $ [ - a,a] $ 范围内波动。当系数向量 $ \overrightarrow A $ 为[−1,1]内的随机值时，鲸鱼处于初始位置与当前最优位置之间的任意位置，说明鲸鱼的游动范围始终在收缩包围圈内。图2为二维空间中， $ 0 \leqslant \overrightarrow A \leqslant 1 $ 时鲸鱼在 $ (X,Y) $ 与 $ ({X_{{\text{g}}best}},{Y_{gbest}}) $ 之间能够去到的位置。

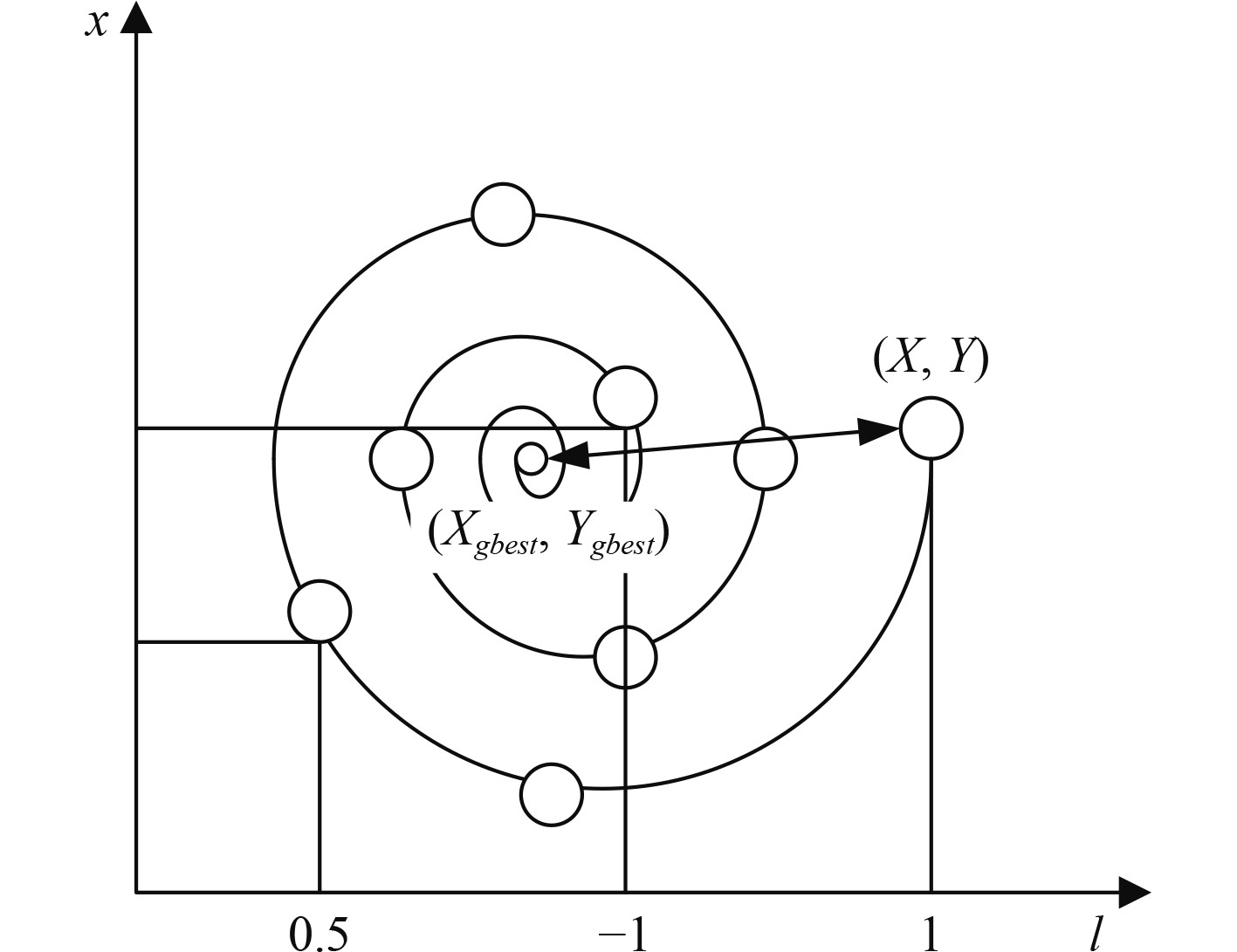
螺旋更新位置机制：如图3所示，首先计算鲸鱼个体 $ (X,Y) $ 到当前目标猎物 $ ({X_{{\text{g}}best}},{Y_{gbest}}) $ 之间的空间距离，然后建立一个螺旋方程来模拟鲸鱼的螺旋运动，数学模型如下：

$ \overrightarrow X (t + 1) = {\overrightarrow X _{gbest}}(t) + {D_2} \cdot {e^{bl}} \cdot \cos (2 \text{π} l)\text{，} $

(6)

$ {D_2} = |{\overrightarrow X _{gbest}}(t) - \overrightarrow X (t)| 。$

(7)

其中： $ {D_2} $ 为鲸鱼个体到猎物的距离； $ b $ 为限定对数螺旋形状的常数； $ l $ 为[-1,1]间的随机数。

鲸鱼在靠近猎物时，会同步展开收缩包围机制和螺旋更新位置2种方式。为了模拟该行为，假设鲸鱼采用收缩包围机制或螺旋更新位置的概率均为0.5，其数学模型描述如下：

$ \begin{aligned} & \overrightarrow{X}(t+1)=\\ & \left\{\begin{array}{l}{\overrightarrow{X}}_{gbest}(t)-\overrightarrow{A}\cdot {D}_{1}\\ \overrightarrow{X}(t+1)={\overrightarrow{X}}_{gbest}(t)+{D}_{2}\cdot {e}^{bl}\cdot \mathrm{cos}(2\pi l)\end{array} \;\; \begin{gathered} p \lt 0.5 \text{，} \\ p \geqslant 0.5 \text{。} \\ \end{gathered}\right. \end{aligned}$

(8)

其中， $ p $ 表示[0,1]间的随机数。

1.1.3 搜索猎物

在此阶段，鲸鱼种群进行全局探索。此时， $ |\overrightarrow A | \geqslant 1 $ ，为了增加搜索范围，鲸鱼种群位置不再根据当前最优解进行位置更新，而是根据随机选择的一条鲸鱼，其他鲸鱼以此鲸鱼位置为目标位置进行更新。此阶段的数学模型如下：

$ \overrightarrow X (t + 1) = {\overrightarrow X _{{\rm{rand}}}} - \overrightarrow A \cdot {D_{{\rm{rand}}}} \text{，} $

(9)

$ {D_{{\rm{rand}}}} = |\overrightarrow C \cdot {\overrightarrow X _{{\rm{rand}}}} - \overrightarrow X (t)|\text{。} $

(10)

式中： $ {\overrightarrow X _{{\rm{rand}}}} $ 表示随机选取的鲸鱼个体的位置向量； $ {D_{{\rm{rand}}}} $ 表示随机选取的鲸鱼个体到其他鲸鱼之间的距离。

1.2 鲸鱼算法的优化 1.2.1 混沌映射

研究表明, 初始种群的好坏影响着算法的求解精度和收敛速度，多样性较好初始种群能很好提高算法性能^[12]。然而，WOA算法通常采取的是随机初始化种群，这使得初始种群会存在分布不均，多样性较差的风险。因此，采用混沌系统中较为典型的cubic map混沌映射，利用混沌变量的随机性、遍历性和规律性等优点，以此提高混沌初始种群的多样性。此过程的表达式为：

$ {\overrightarrow X _{gbest}}({\text{t}}) = \rho (1 - {\overrightarrow X ^2}(t)) 。$

(11)

其中： $ \rho $ 为控制参数，取值为1； $ \overrightarrow X (t) $ 为所有初始化鲸鱼位置向量中随机所取的一个随机向量。

1.2.2 自适应惯性权重调整策略

惯性权重值对鲸鱼算法的目标寻优有重要作用，当惯性权重较大时，算法搜索能力较强，可以搜索较大的区域，当惯性权重较小时，算法后期搜索能力较强，可以在最优解周围精细搜索^[13]。传统的鲸鱼算法采取的是线性惯性权重调整策略，经常出现惯性权重值不合适导致算法收敛速度变慢的情况。因此本文提出一种根据当前鲸鱼种群分布情况自适应改变权值的方法，公式如下:

$ \omega = {e^{\tfrac{{ - t}}{{{t_{\max }}}}}} 。$

(12)

可以看出，在算法迭代初期，自适应权重较大且较快减小，可以较大范围内搜索最优值，避免算法过早陷入局部最优，后期自适应权重较小且下降缓慢,能够在局部范围内进行精确搜索。引入自适应权重后的鲸鱼位置更新计算公式为：

$ \overrightarrow X (t + 1) = \left\{ \begin{gathered} w{\overrightarrow X _{gbest}}(t) - \overrightarrow A \cdot {D_1} \\ w{\overrightarrow X _{gbest}}(t) + {D_2} \cdot {e^{bl}} \cdot \cos (2 \text{π} l) \\ w{\overrightarrow X _{{\rm{rand}}}} - \overrightarrow A \cdot {D_{{\rm{rand}}}} \\ \end{gathered} \right.\quad \begin{gathered} p \lt 0.5,|\overrightarrow A | \leqslant 1 \text{，} \\ p \geqslant 0.5 \text{，} \\ p \lt 0.5,|\overrightarrow A | \gt 1 \text{。} \\ \end{gathered} $

(13)

1.3 BP神经网络

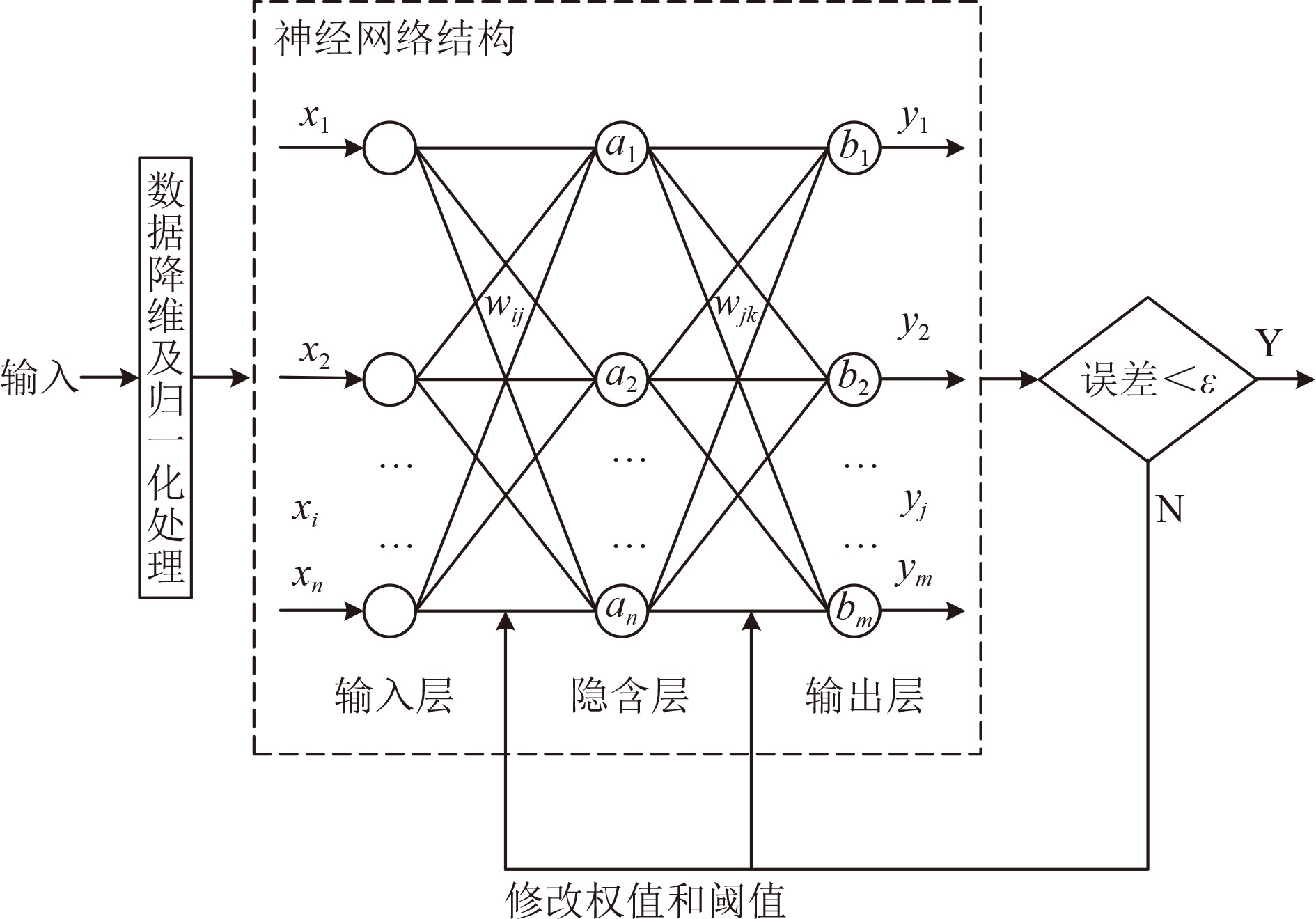
BP 神经网络是一种典型的基于误差反向传播训练的多层前馈型（输入、隐含和输出层）人工神经网络，其理论基础为梯度下降法，通过梯度搜索技术达到真实输出值与期望输出值的误差均方差最小的目标。标准BP算法主要包括信号的正向传播和误差的反向传播2个过程。在信号的正向传播阶段，初始信号先从输入层进入模型，并在经过隐含层后最终到达输出层，每一层神经元的状态只会影响到下一层神经元状态。如果输出层没有获得预期输出，则开始误差反向传播阶段。在该阶段，不满足精度要求的误差信号沿着原来的连接路径返回，并调整各层的连接权值及阈值，使得误差沿着梯度方向下降。通过多次调节和训练，神经网络中的阈值和权值不断修正，最终得到期望输出信号，BP神经网络的学习过程结束。其故障诊断模型如图4所示。

1.4 故障诊断流程

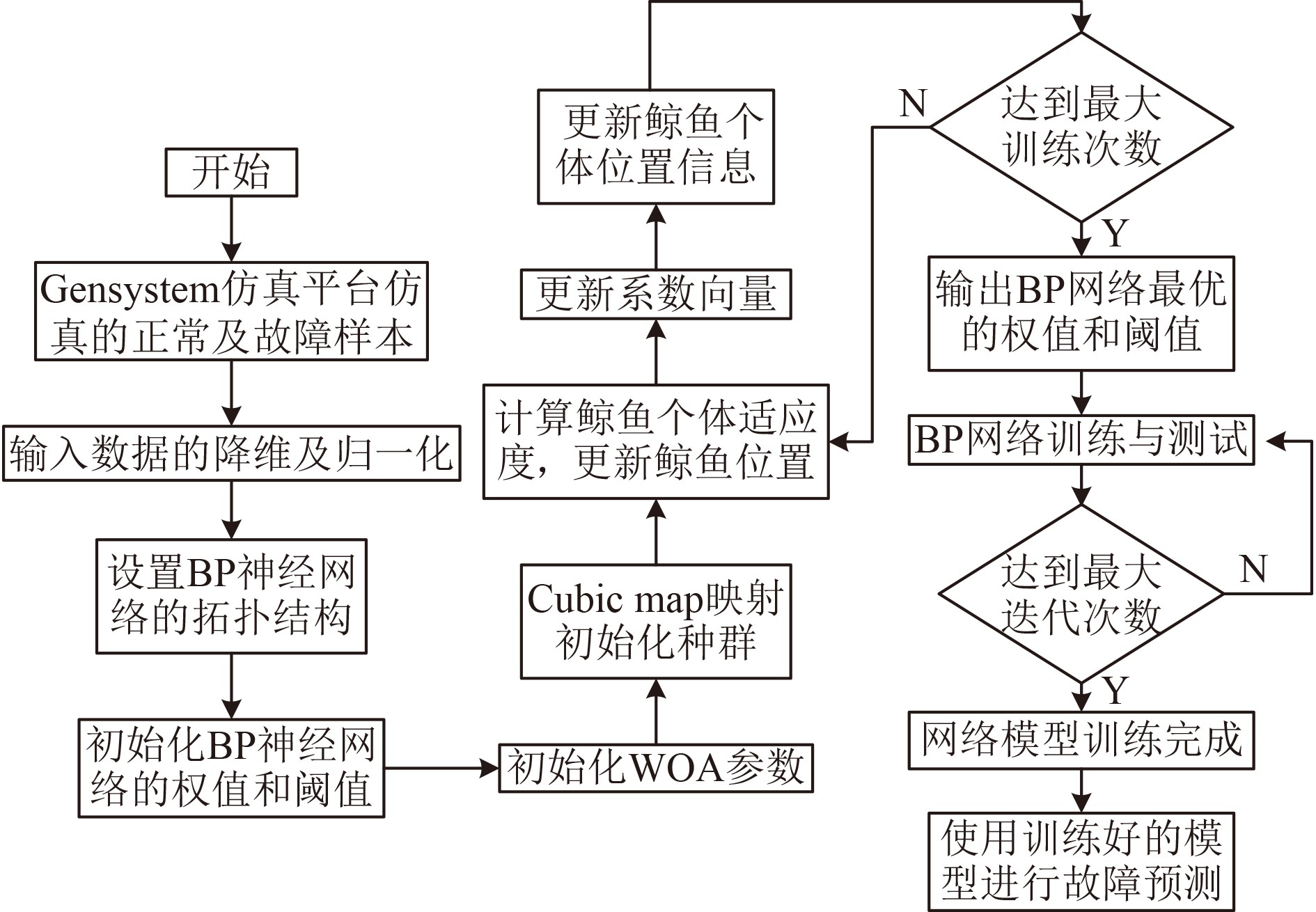
由于BP神经网络存在容易陷入局部极小值以及收敛速度慢的缺点，因此本文提出利用优化后的WOA更新BP神经网络的权值和阈值，以帮助它越过局部极小值，提高模型的预测准确率。基于CAWOA-BP神经网络的舰船凝给水系统故障预测模型流程如图5所示。

2 基于舰船凝给水系统仿真模型的故障监测研究 2.1 数据描述

利用Gensystem模型开发平台对舰船蒸汽动力系统的设计计算模型进行建立，并对汽轮机组转速稳定在低工况108 r/min附近的仿真模型进行研究。通过改变除氧器压力、给水泵转速、冷凝器压力、凝水泵压力和增压泵转速来模拟舰船凝给水系统的故障工况。其中每种工况由15个特征进行描述，其特征为过热蒸汽压力、微过热蒸汽压力、废汽压力、汽包压力、汽包水位、除氧器压力、除氧器水位、冷凝器压力、冷凝器水位、给水泵出口压力、给水泵转速、凝水泵出口压力、凝水泵转速、增压泵出口压力、增压泵转速。该蒸汽动力系统仿真模型运行大约45 min 后进入稳定期，在模型运行平稳后，开始进行故障工况模拟以及数据的采集，从中获得1400个正常与故障工况样本。数据描述如表1所示。

在本文研究中，将训练数据集和测试数据集按照7∶3的比例随机划分，其中训练数据集共计980个，包括正常工况数据280个以及5种故障工况各140个，该数据集用于建立CAWOA-BP故障监测模型。测试数据集共计420个，包括正常工况数据120个以及5种故障工况各60个,测试数据集用于评估故障监测方案的性能。

2.2 数据预处理

1）数据归一化处理

为了更好地训练CAWOA-BP网络模型，对每个数据样本进行把归一化处理，其数学表达式为：

$ X = \left\{ {{x_i}} \right\} = \frac{{{x_i} - {x_{_{\min }}}}}{{{x_{\max }} - {x_{\min }}}}\text{。} $

(14)

2）数据降维

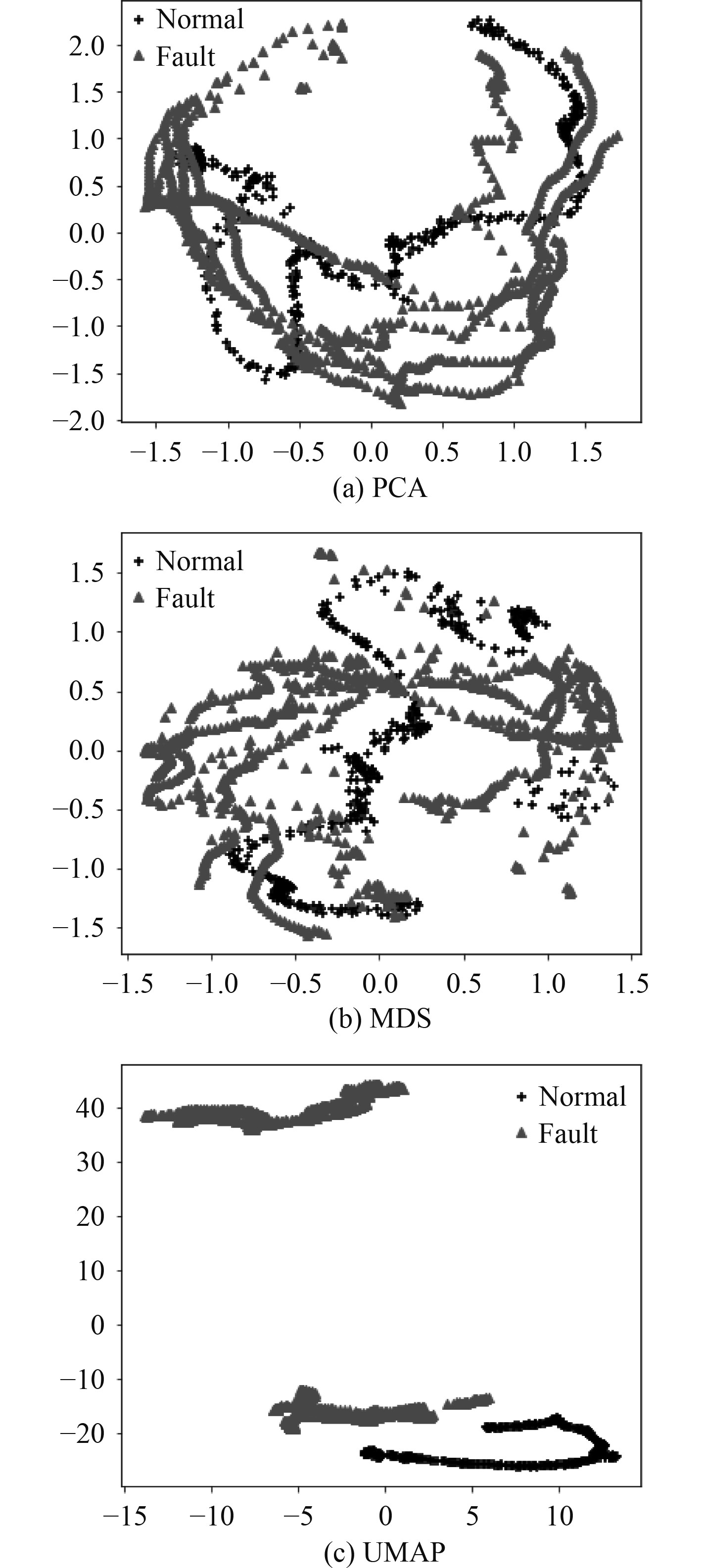
由于原始数据有着高维度的特征，其较高的复杂度会给训练模型带来较大的负担，因此为了后期数据能够进行高效处理和分类，将原始数据的15维特征通过常见的几种降维方法降至2维特征。采用的降维算法包括PCA，MDS，以及UMAP。经过数据的可视化处理后，图6为不同降维算法对相同数据降维的处理效果。降维后的数据被输入到最终的CAWOA-BP故障诊断模型，实现对舰船凝给水系统的故障诊断。

针对降维效果图展开分析。从图6(a)可以看出，经过PCA降维后的正常及故障数据相互交叉重叠，效果不佳。从图6(b)可以看出，经过MDS降维后的数据有部分类别能够区分开来，相比PCA效果有了较为明显的进步，但是仍然有明显的交叉重叠现象。从图6(c)可以看出，UMAP具有最好的降维效果，筛选后的数据分类清晰。因为同一类的数据都聚集在了一块，不同类别的数据则在低维空间距离有着明显的区分。因此本文采用降维效果最好的UMAP算法处理原始的高维数据，为优化后的模型提供有效数据。

3 结果分析和对比验证 3.1 CAWOA-BP的结果评估

为了更好地评估 CAWOA-BP 算法，引用精确率、召回率以及F1调和均值对CAWOA-BP算法进行评估。表2为CAWOA-BP的诊断结果。

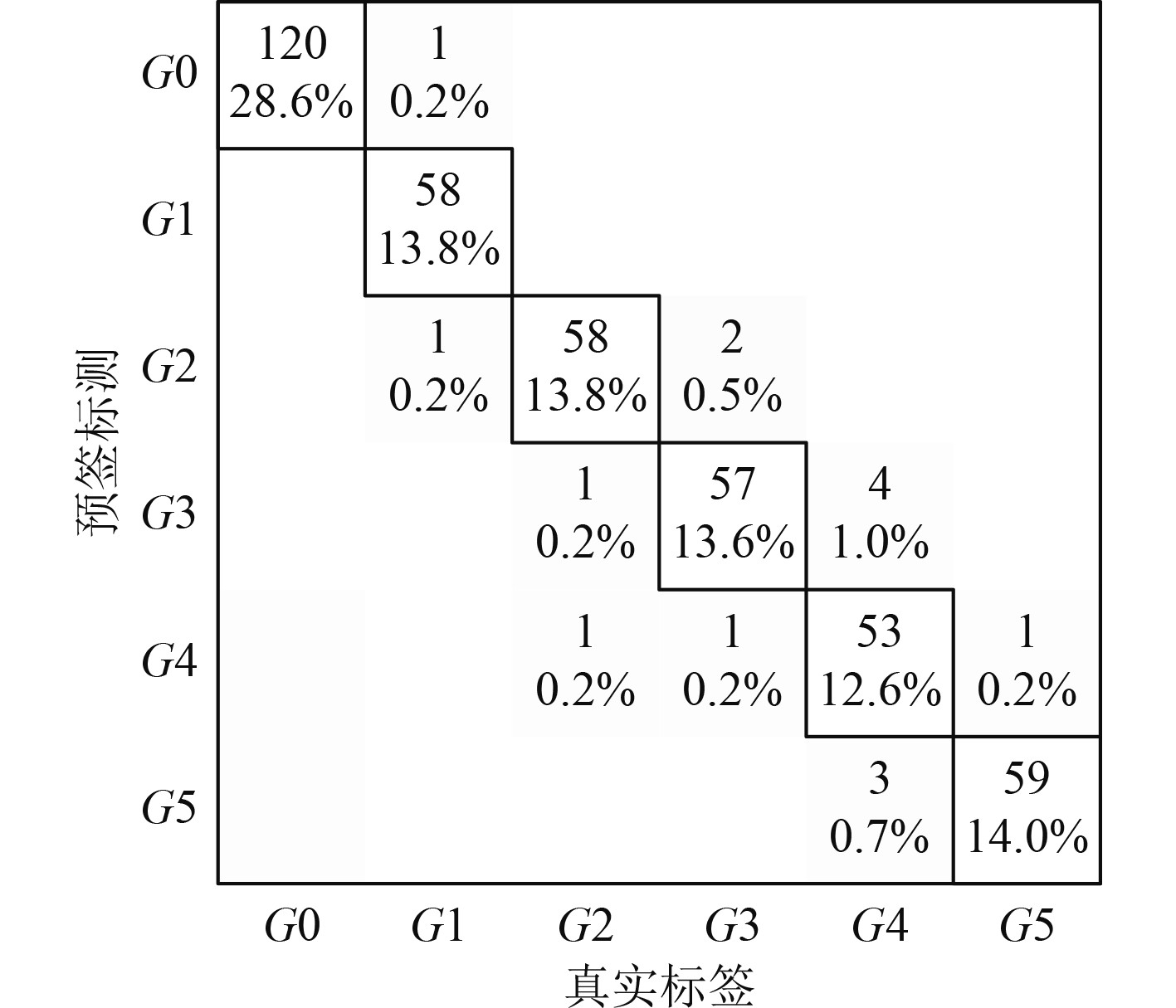
引入多分类混淆矩阵对诊断结果展开更具体的分析。

由图7可知，在测试集上的420个样本中只有少数样本被预测错误，模型对正常样本G0的预测全部正确，对故障类型G3（冷凝器失真空）、G4（凝水泵汽蚀）的预测精确度稍低，但是对其余几种故障类型也只出现了极少数的预测错误。由此可见CAWOA-BP算法对舰船凝给水系统的常见故障类型有着很好的识别能力以及极高的准确率。

3.2 与其他算法对比分析

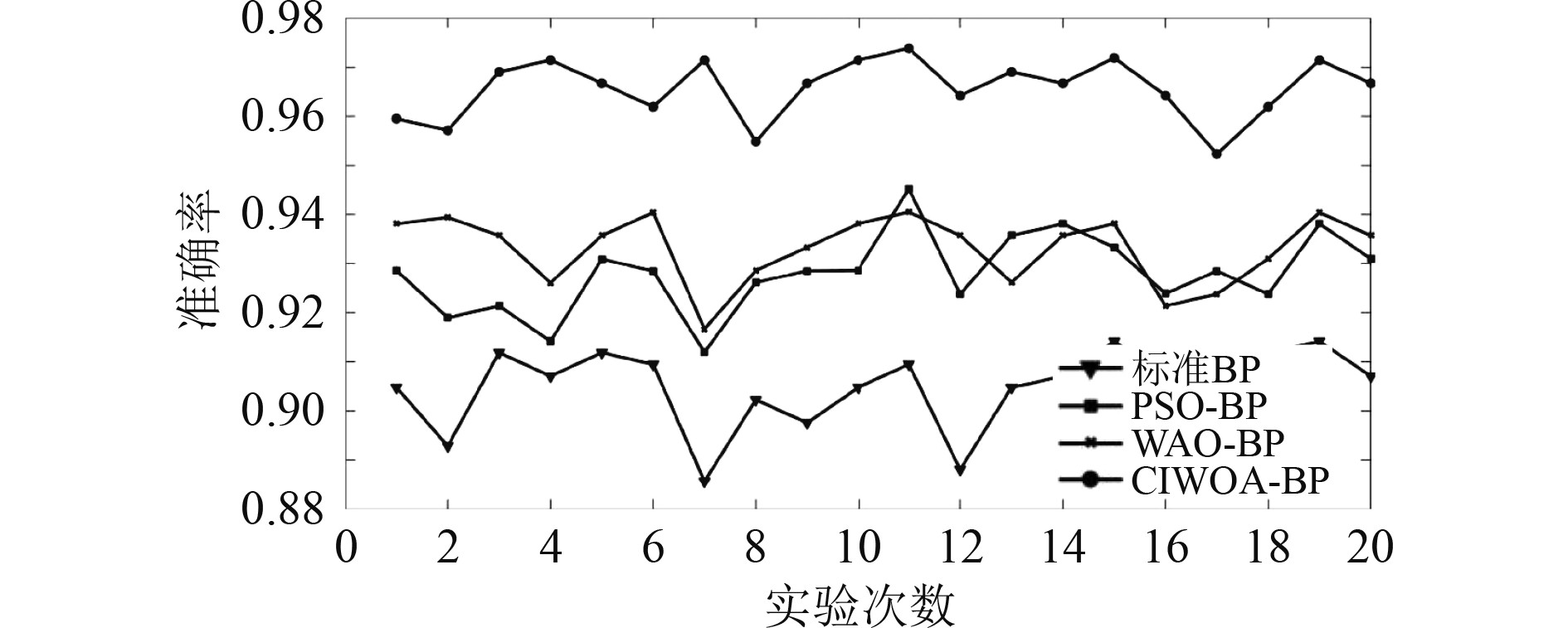
为验证本文提出的方法相比优化前的BP算法在故障诊断及预测方面的有效性，将CAWOA-BP诊断结果与BP，PSO-BP，WOA-BP 进行对比验证，比较每种算法故障预测的准确率。为了减少数据随机分类的偶然性对模型产生的干扰，利用原始数据集重复实验 20 次，并以平均准确率作为诊断方案性能指标。各类算法每次实验的准确率对比图如图8所示，平均准确率如表3所示。

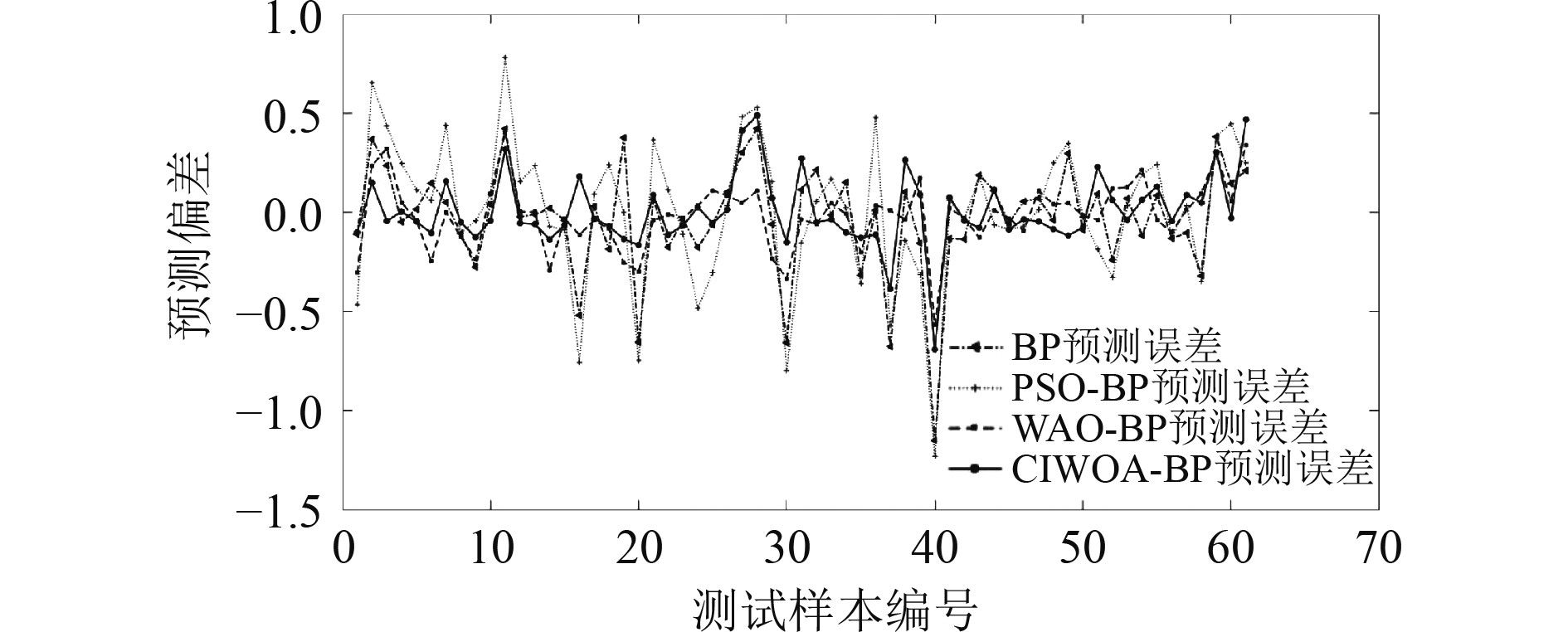
另外将正常以及各类故障定义为0～5的数值作为模型的预测值，并将预测值和真实值作差，将误差值进行对比，结果如图9所示。以平均绝对误差mae、均方误差mse、均方误差根rmse为对各类算法进行评估，结果如表4所示。

从图9和表4可知，CAWOA-BP算法诊断出来的结果相比其他优化算法对真实值的预测具有更小的误差值，CAWOA-BP可以克服随机初始化种群带来的初始种群分布不均，并且能够很好越过局部极小值，因此在对舰船凝给水系统的故障诊断中取得了较高的故障识别率并可对故障进行较为准确的定位，这对舰船凝给水系统在实际工作中故障的快速诊断定位及维护有着重要意义。

4 结　语

针对船舶凝给水系统故障定位难度较大、发现时间较长问题，本文提出一种利用优化后的鲸鱼算法对BP神经网络进行改进的CAWOA-BP故障诊断模型，用于船舶凝给水系统故障诊断。通过Gensystem仿真平台生成的船舶凝给水系统运行数据，对该故障诊断模型进行了验证。分析结果表明：

1）相比于典型的降维算法PCA及MDS，UMAP对于原始高维数据集具有更好的降维效果。利用UMAP将原本复杂高维度的数据降至2维，显著改善了原始数据的复杂程度，提高后续故障诊断模型的性能。

2）与未经优化的标准BP神经网络模型相比，WOA-BP、PSO-BP、CAWOA-BP等优化后的模型具有更高的准确率、精确率及召回率。其中CAWOA-BP的诊断效果最好。

3）通过将预测目标数字化，对比各类算法的预测值与目标值之间的误差，发现CAWOA-BP故障诊断模型具有最小的预测误差。

基于优化后的CAWOA-BP神经网络船舶凝给水系统故障诊断模型能够有效提高故障识别的准确率和可靠性，具有一定的理论参考意义和应用价值。