2. 船舶与海洋工程特种装备和动力系统国家工程研究中心,上海200090
2. National Engineering Research Center of Special Equipment and Power System for Ship and Marine Engineering, Shanghai 201108, China
水文条件随季节、天气、水域变化可能呈现出复杂多变的特点,相较传统柴油机船舶,混合动力船舶可以根据实时航况及时切换动力设备、改变能量流向,使船舶运行于最佳工作模式,从而在动力性、经济性、排放性等方面占据优势。但现有模式切换时,由于工况突变、负载冲击等情况,有时会出现排放恶化、设备熄火等问题,影响切换过程的排放性和动力性。为满足我国船舶排放法规和船用动力需求,须提升模式切换过程的平稳性,避免排放恶化或设备熄火问题。
近年来国内外针对混合动力系统的模式切换技术已开展广泛研究,对发动机转矩进行估计或监测并利用电机进行转矩补偿、借鉴成熟的控制算法设计模式切换策略、针对关键参数进行协调控制是重要的研究方法。崔宇轩[1]根据发动机图谱、王卉[2]建立BP神经网络模型、Hyunsup[3]设计状态监测器估计发动机转矩,利用电机对发动机转矩与目标转矩间差值进行补偿。赵冶国等[6]针对串联式混合动力系统,设计基于电机的辅助接排策略,实现模式切换中平稳接排。朱剑昀等[7-9]建立传动系统的动力模型,采用模型参考控制及预测控制,设计稳定切换的力矩协调方案。但以上研究对象多为车用混合动力系统,船舶领域研究成果相对较少。针对混合动力船舶开展模式切换优化技术研究符合未来推广船用混合动力系统的需要。
本文以某型柴-电混合动力散货船(以下简称“目标船舶”)为研究对象。通过切换主机侧离合器状态和轴带电机工作模式,可使目标船舶在多种模式下航行,包括主机模式、电机推进(PTH)模式、轴带发电(PTO)模式和并车推进(PTI)模式,各模式功能说明如表1所示。
|
|
表 1 多航行模式功能说明表 Tab.1 Multi navigation mode function description table |
通过模式切换控制装置可以操控目标船舶按照图1所示规则自由进行模式切换。
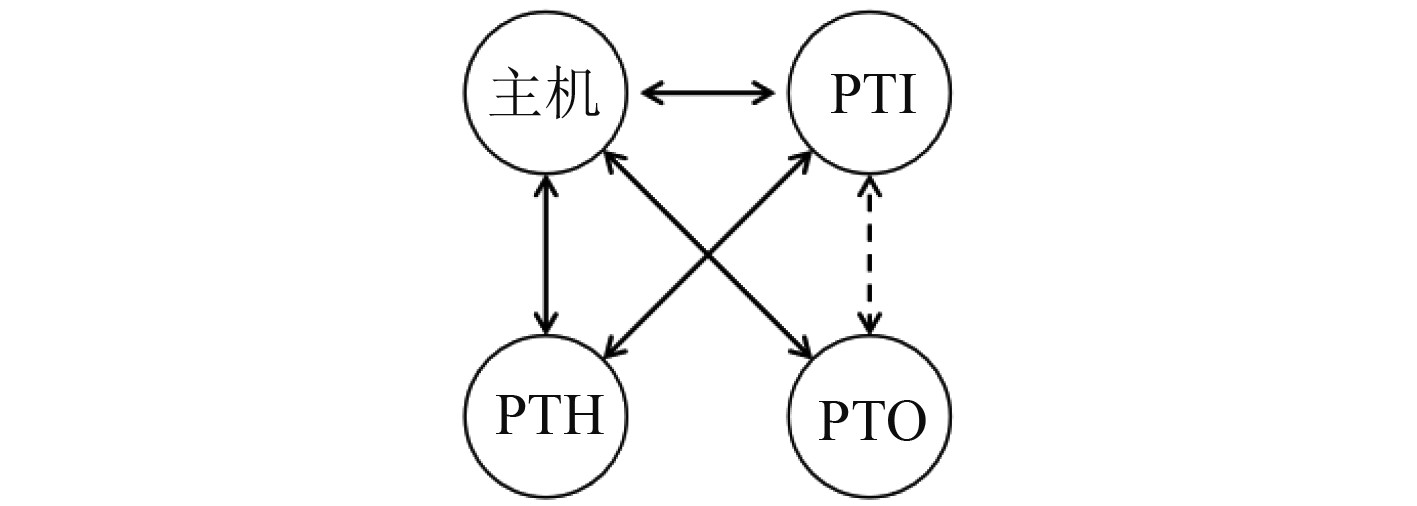
|
图 1 模式切换说明图 Fig. 1 Mode switching diagram |
可知,主机模式切换至PTO模式、PTO模式切换至主机模式、主机模式切换至PTI模式与PTI模式切换至主机模式共4个模式切换过程中主机侧离合器始终保持接合状态,切换时仅涉及轴带电机与配电板的状态调整,不存在主机与轴带电机间的负载转移。而PTH模式切换至主机模式、PTH模式切换至PTI模式时,在主机侧离合器接排阶段存在主机与轴带电机间的负载转移,易造成主机排放恶化、甚至熄火等问题。本文针对该问题,以PTH模式切换至主机模式为例,借助建模仿真软件,对模式切换过程中主机侧离合器接排阶段进行仿真及优化分析。对比基于电机补偿的多种平稳接排策略的改善效果,为后续混合动力系统的设计优化提供参考与借鉴。
1 仿真模型建立目标船舶采用柴-电混合动力系统,动力系统整体架构如图2所示,动力设备主要参数如表2所示。该动力系统由柴油主机、齿轮箱、轴带电机、LNG气体机组和配电板组成,混合度高达33%,是典型的高混合度动力系统,模式切换过程中更容易出现由大功率推进负载转移导致的主机转速骤降等动态性能恶化问题。
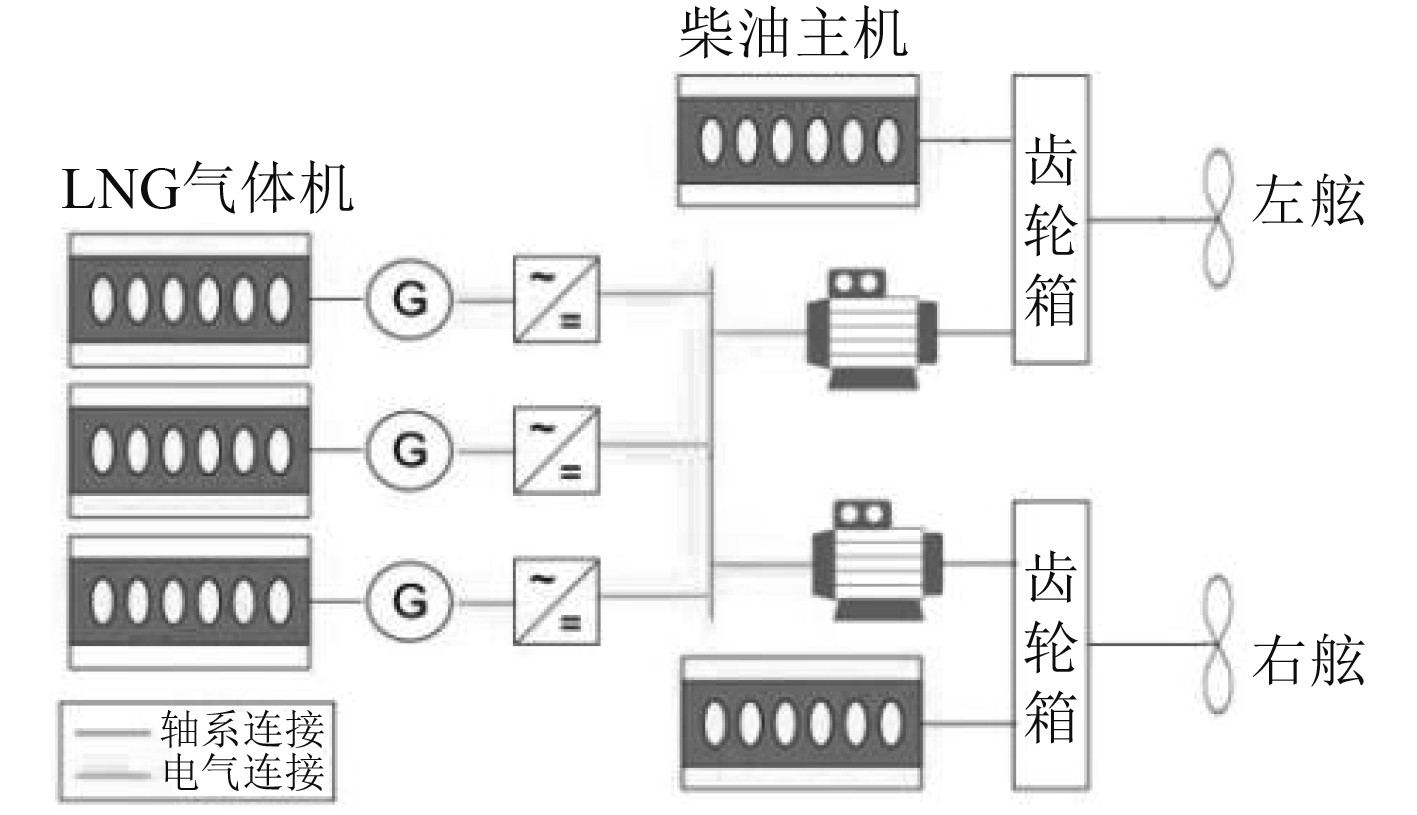
|
图 2 动力系统整体架构图 Fig. 2 Overall structure diagram of power system |
|
|
表 2 动力系统主要设备关键参数表 Tab.2 Key parameters of main equipment of power system |
为在满足仿真需求的同时降低模型复杂度,将动力系统组成简化为柴油主机、轴带电机、齿轮箱和螺旋桨。目标船舶整体仿真模型如图3所示。

|
图 3 目标船舶整体仿真模型图 Fig. 3 Overall simulation model diagram of target ship |
仿真模型主要包括柴油机模型、轴带电机模型、螺旋桨模型和船舶阻力模型。柴油机模型采用平均值模型(MVEM),利用经验指示热效率描述缸内燃烧热向指示功转化的过程,通过时间平均值宏观、准确地描述发动机运行的综合结果;轴带电机采用交流电机模型,根据目标转矩进行电压控制、调节输出转矩;螺旋桨模型根据螺旋桨进速和船舶航速计算螺旋桨转矩和推力;船舶阻力模型根据国际拖曳水池会议(ITTC)提出的船舶阻力预测方法搭建,根据船模试验和经验信息估算行波阻力、根据实船参数和水域条件计算粘性阻力和空气阻力,由兴波阻力、粘性阻力和空气阻力共同组成船舶总阻力,模型中所用公式参见ITTC1978船舶阻力计算方法[10]。
1.2 模型验证分别验证以上模型,将仿真结果与性能参数和试验数据进行对比,结果如图4所示。
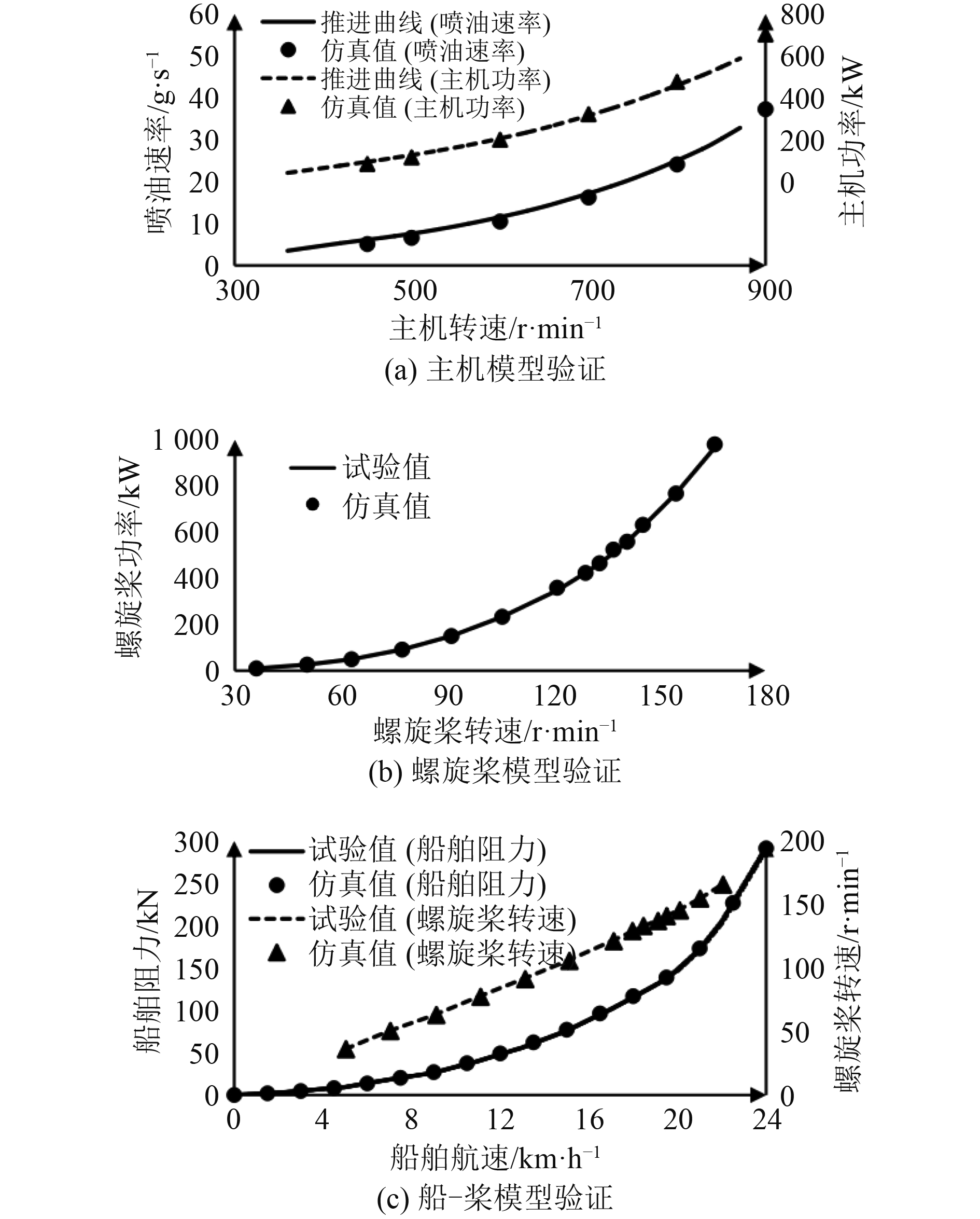
|
图 4 稳态特性验证结果图 Fig. 4 Steady state characteristic verification result diagram |
可知,船舶与螺旋桨模型仿真结果与试验数据间误差在1.5%以内,柴油机模型仿真结果与推进特性间平均误差在2%以内,具有较高的仿真精度。
2 原模式切换策略分析PTH模式向主机模式切换的基本流程为:在PTH模式下,轴带电机将螺旋桨转速调整至稳定转速,同时主机起动并加速至怠速;在动力系统稳定后轴带电机停机,螺旋桨在水流作用下自由降速;随后离合器接排,系统切换至主机模式。
本文选取PTH模式下螺旋桨稳定转速与主机接排怠速相当,主机怠速为450 r/min,相应的轴带电机和螺旋桨转速分别为750 r/min和75 r/min。起初动力系统处于PTH模式,同时主机保持怠速空载运行;第200 s时开始模式切换,轴带电机停机,螺旋桨自由降速;第205 s时主机侧离合器接排,历时5 s完全接排;完全接排后主机转速重新趋于怠速,并最终达到稳定。上述过程中离合器接排阶段的仿真结果如图5所示。
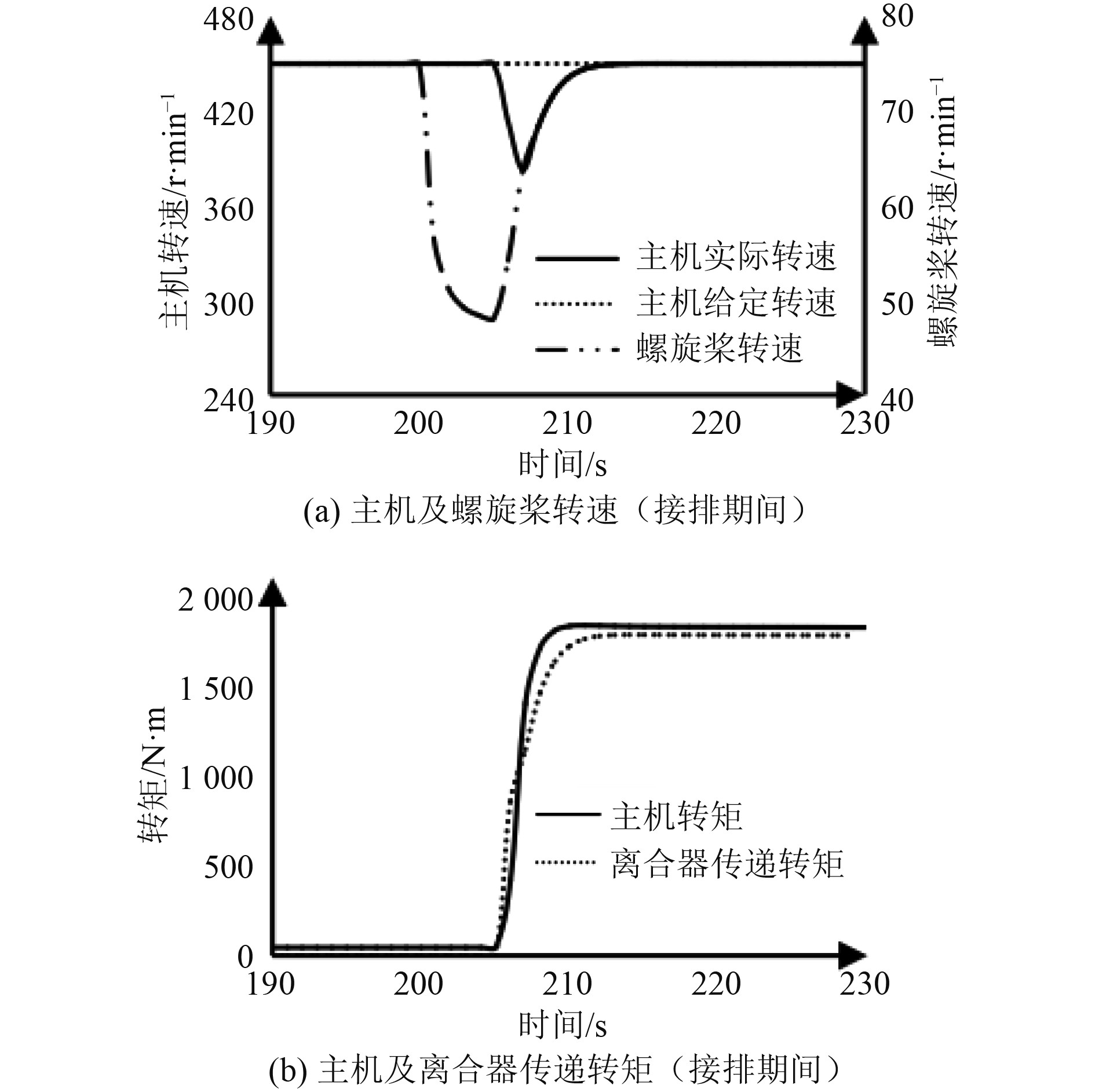
|
图 5 原切换策略下仿真结果图 Fig. 5 Simulation results of the original switching strategy |
可知,轴带电机停机后螺旋桨转速快速下降,离合器接排后,主机转速降低,螺旋桨转速回升,离合器两端转速差逐渐降低至0。在此过程中,主机转速的最低值为376.2 r/min,转速超调率达到了16.40%。图5表明,原切换策略下切换过程中会出现较为严重的主机转速骤降问题,将直接影响动力系统的稳定性和动力性。
以接排时间为5 s、接排怠速为450 r/min的原模式切换策略为基准,采用多种方式降低接排过程中的主机转速超调率,改进目标船舶动力系统的模式切换稳定性。
3 模式切换优化策略研究
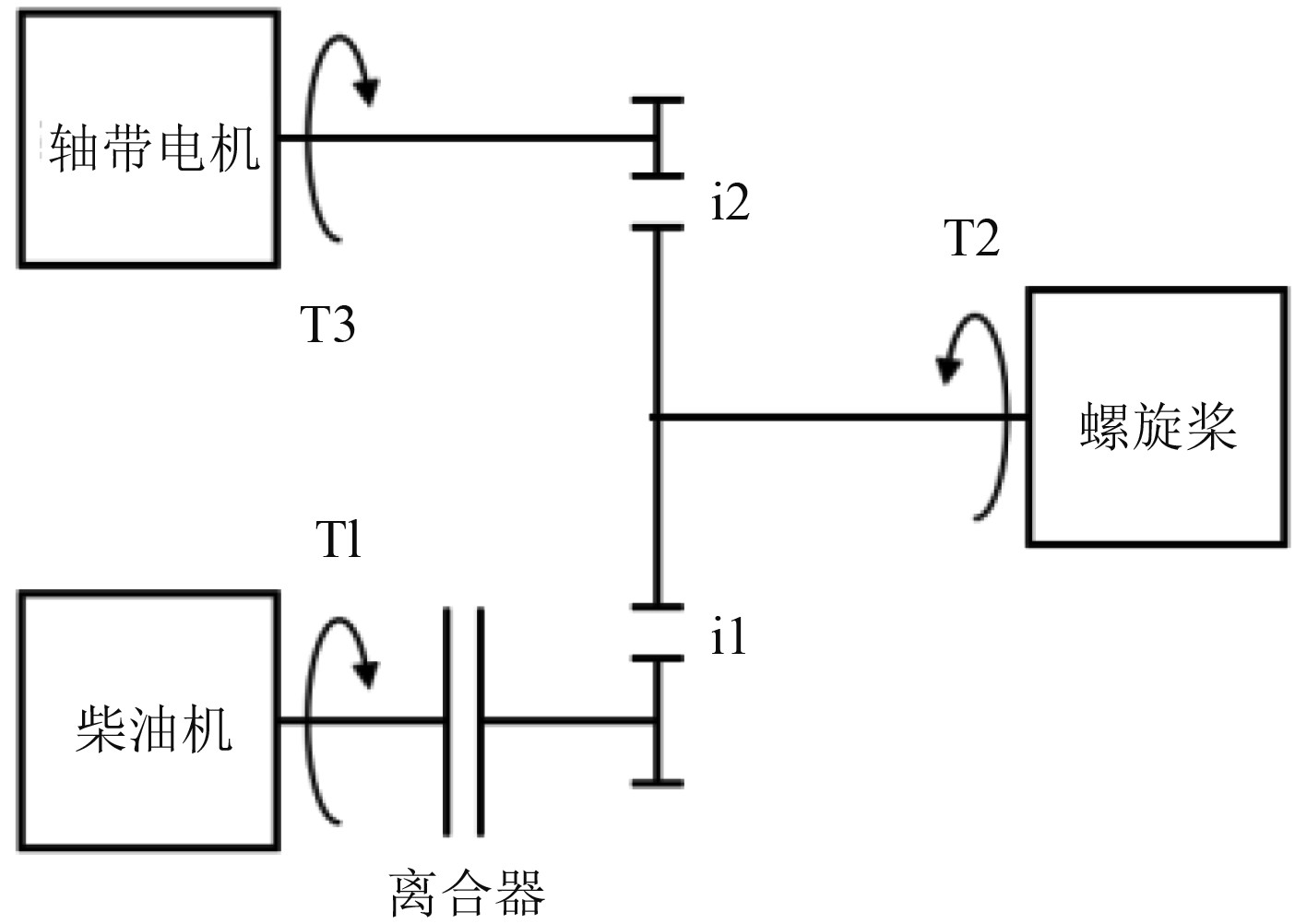
|
图 6 动力系统简化模型 Fig. 6 Simplified model of power system |
据此可得到动力系统动力学方程:
| $ {T_1} - {J_1}\left( {{{{{\dot \omega }_1}} \mathord{\left/ {\vphantom {{{{\dot \omega }_1}} {60}}} \right. } {60}}} \right) = {T_e}, $ | (1) |
| $ \left( {{T_3} - {J_3}\left( {{{{{\dot \omega }_3}} \mathord{\left/ {\vphantom {{{{\dot \omega }_3}} {60}}} \right. } {60}}} \right)} \right) \cdot {i_2} + T_c'{i_1} - {J_2}\left( {{{{{\dot \omega }_2}} \mathord{\left/ {\vphantom {{{{\dot \omega }_2}} {60}}} \right. } {60}}} \right) = {T_2}。$ | (2) |
式中:
根据离合器两端转速差,可以将离合器的接排过程分为分离、滑摩和锁止阶段。分离阶段,离合器传递转矩为0;滑摩阶段,离合器传递滑摩转矩;锁止阶段,离合器两端转速差为0。各阶段主机转速变化率如下:
| $ 分离阶段\;\;\; \dot{{\omega }_{1}}={T}_{1}/{J}_{1} ,$ | (3) |
| $ 滑摩阶段\;\;\; \dot{{\omega }_{1}}=({T}_{1}-{T}_{c})/{J}_{1} ,$ | (4) |
| $ 锁止阶段 \;\;\; \dot{{\omega }_{1}}=({T}_{1}{i}_{1}-{T}_{2}+{T}_{3}{i}_{2})/({J}_{1}{i}_{1}+{J}_{2}+{J}_{3}{i}_{2}) 。$ | (5) |
其中滑摩阶段离合器传递转矩为离合器滑摩转矩,相关计算式为:
| $ {T_c} = {\rm{sign}} \left( {\Delta \omega } \right){\mu _d}S{P_n}Z\frac{2}{3}\left( {\frac{{R_0^3 - R_1^3}}{{R_0^2 - R_1^2}}} \right)\text{。} $ | (6) |
式中:
根据式
根据式(3)~式(5),离合器将主要通过滑摩转矩影响滑摩阶段的主机转速变化,可通过调节离合器油压控制滑摩转矩,从而改善主机转速骤降问题。工程中离合器控制指令通常为接排时间,即离合器由开始至完全接排的时间间隔。延长接排时间可以使离合器油压缓慢上升,避免接排瞬间对主机造成过大的负载冲击,进而避免主机的转速骤降和熄火。
在原切换策略的基础上,将接排时间由5
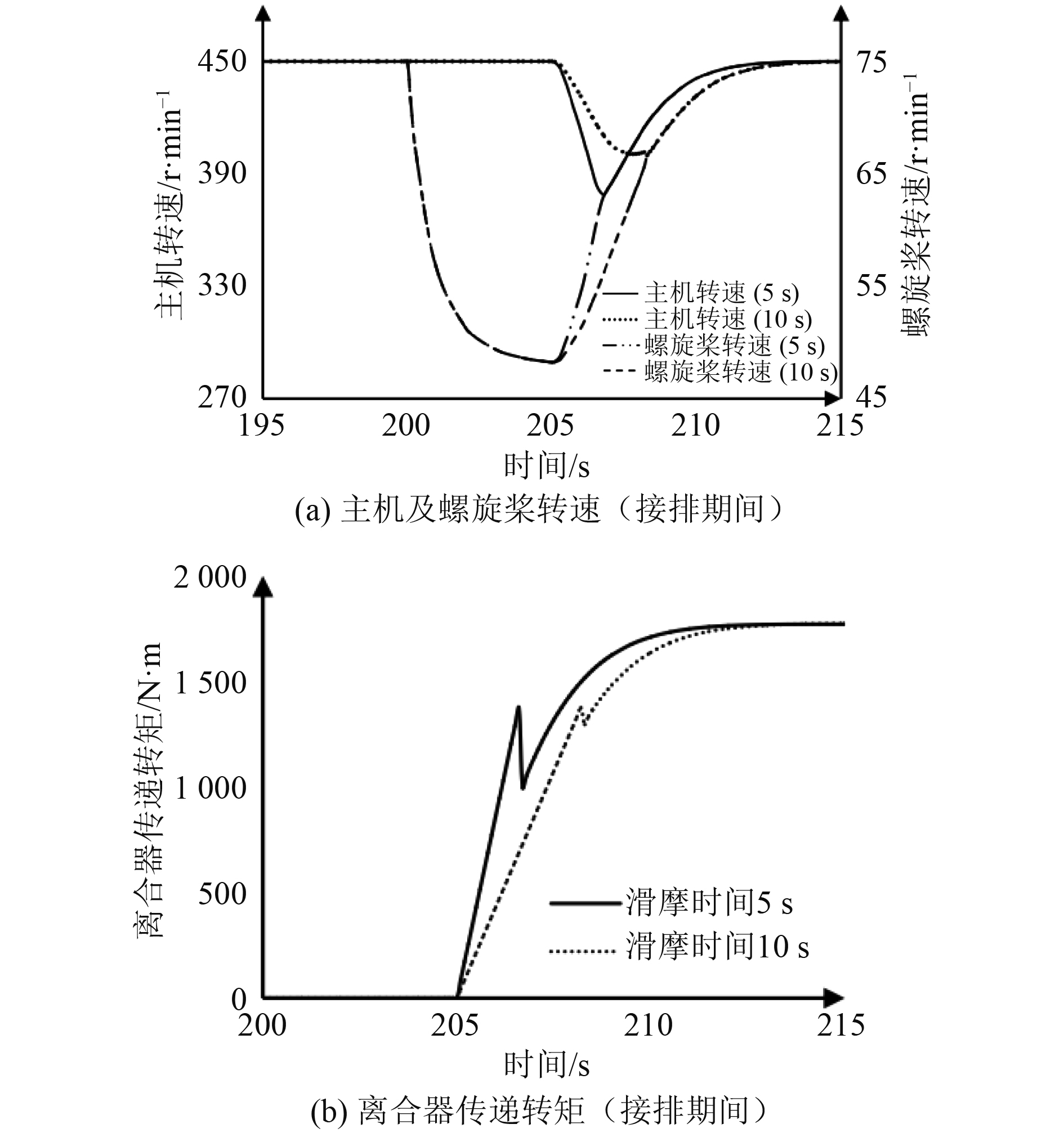
|
图 7 采用长延时滑摩策略时仿真结果 Fig. 7 Simulation results with time extension strategy of clutch connection |
|
|
表 3 不同接排转速下仿真结果统计表 Tab.3 Simulation results of different connection speeds |
由图7可知,开始接排后,离合器传递转矩快速上升,短时间内达到峰值后突然降低,该部分转矩突增量即为离合器滑摩转矩。延长接排时间后,离合器传递转矩的峰值未发生明显变化,但达到峰值的时间稍微延后。由于接排后离合器传递转矩的增长变慢,主机转速和螺旋桨转速的变化同样放缓,同时螺旋桨轴系的转动惯量大于主机曲轴的转速惯量,离合器传递转矩的变化对主机转速的影响更加明显,所以主机最低转速,即离合器两端转速差降低至0时的主机转速随接排时间延长而升高。
由表3可知,主机转速超调率随接排时间的延长而降低,但降低效果有限,接排时间由5
因此延长接排时间可以一定程度解决主机转速骤降问题,但其应用受到实际工程要求的限制。
3.2 接排转速优化策略研究原模式切换策略下仿真结果表明,主机转速骤降主要发生在开始接排至离合器两端转速差降低至0的过程中,即离合器接排的滑摩阶段。根据式
在原切换策略基础上,在PTH模式阶段,令电机以高于主机怠速的转速运行,分别设置电机转速为800 r/min,850 r/min和900 r/min,使螺旋桨转速分别升高至80 r/min,85 r/min和90 r/min。不同电机转速下各参数变化趋势与原切换策略下相似,以电机转速为900 r/min为例,与原切换策略下的仿真结果对比如图8所示,不同电机转速下仿真统计结果如表4所示。
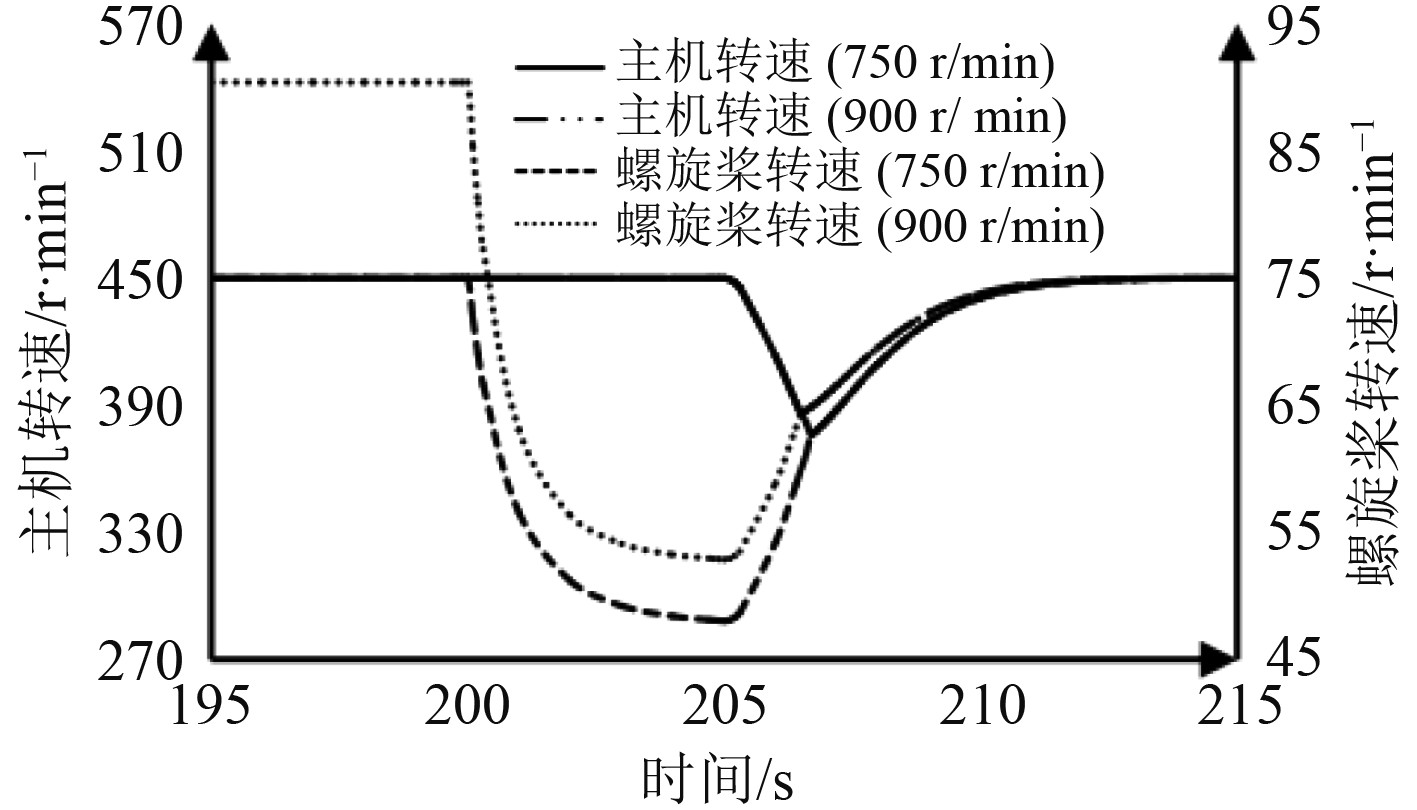
|
图 8 采用接排转速优化策略时仿真结果 Fig. 8 Simulation results with speed optimization strategy |
|
|
表 4 不同接排转速下仿真结果统计表 Tab.4 Simulation results of different connection speeds |
由图8可知:切换前电机转速升高后,主机转速没有明显变化;不同策略下接排时电机转速差远小于切换时电机转速差,接排后已无明显区别。由表4可知,主机最低转速随切换前电机转速升高而升高,但升高幅度极小,切换前电机转速由750 r/min升至900 r/min,主机转速超调率仅降低2.26%。原因在于切换开始时电机即刻停机,螺旋桨失去动力在水流阻力作用下自由降速,切换前电机转速越高,切换时船舶航速越高,相应的水流阻力越大,螺旋桨降速速率也越大,切换开始后不同策略下的螺旋桨转速差距逐渐减小;接排后离合器处于滑摩阶段,此时离合器传递转矩主要为滑摩转矩,该转矩主要与离合器接合程度有关,受转速差影响较小,因此不同策略下接排初期的主机转速降速率和螺旋桨转速加速率没有明显区别。
不同策略下主机和螺旋桨接排时的转速差距较小、接排后转速变化速率基本一致,主机的最低转速也就没有明显区别。因此调节接排转速可以一定程度、但无法有效改善主机转速骤降问题。
3.3 转矩补偿策略研究利用混合动力系统多动力源的优势,在接排期间启动轴带电机并输出一定转矩,即令动力系统以PTI模式,在开始接排至完全接排的过程中,即在仿真中第205~210 s内向主机提供补偿转矩,可以减轻离合器接排对主机造成的负载冲击,达到提升模式切换过程稳定性的目的。
根据式
| $ {T_3} = \frac{{{T_2} - {T_1} \cdot {i_1}}}{{{i_2}}}。$ | (7) |
但根据原切换策略下仿真结果,主机转速骤降主要发生在滑摩阶段,此时主机的主要阻力为滑摩转矩;离合器进入锁止阶段后,主机转矩高于螺旋桨等效转矩、主机转速处于上升阶段。若采用式
可通过以下2种方法调整转矩补偿策略:1)根据主机和螺旋桨间转速差估算滑摩转矩并补偿;2)根据螺旋桨当前转速、目标转速和轴系转动惯量,设计加速时间,计算相应的加速转矩并补偿。针对滑摩转矩和加速转矩的补偿转矩按下式计算:
| $ {T_f} = {k_f} \cdot {T_{c\max }} \cdot \tanh \left( {{\omega _1} - {\omega _2} \cdot {i_1}} \right) ,$ | (8) |
| $ {T_a} = {k_a} \cdot {J_2} \cdot \frac{{{{{\omega _{1,0}}} \mathord{\left/ {\vphantom {{{\omega _{1,0}}} {{i_1}}}} \right. } {{i_1}}} - {\omega _2}}}{t}。$ | (9) |
式中:
即轴带电机的总补偿转矩为:
| $ T_3' = {T_3} + {T_f} + {T_a} 。$ | (10) |
仿真时滑摩转矩补偿系数
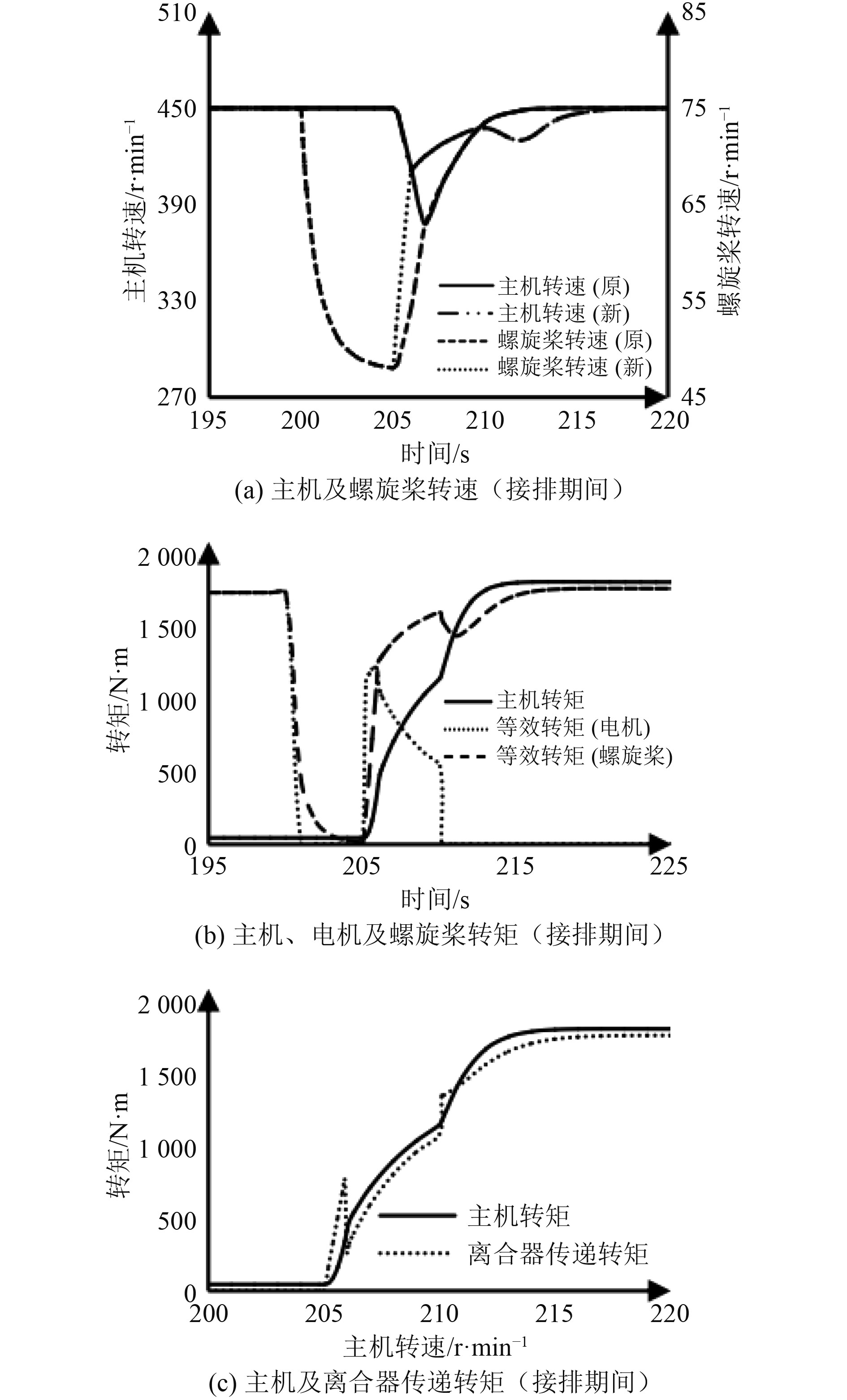
|
图 9 采用转矩补偿策略时仿真结果 Fig. 9 Simulation results with torque compensation strategy |
可知,采用基于滑摩和加速转矩的转矩补偿策略后,相较原模式切换策略,接排时离合器两端转速差、接排后主机转速降低速率没有明显差别,但接排后螺旋桨转速升高速率明显加快,离合器两端转速差降低至0的时间点提前,主机的最低转速相应增大;在离合器完全接排时再次出现主机转速下降,但降低幅度与降低后的最低转速分别小于和高于第一次转速下降。原因在于轴带电机分担了部分阻力转矩,接排后离合器传递转矩小于螺旋桨等效转矩,且电机加快了螺旋桨的加速过程,缩短了离合器滑摩阶段的持续时间,限制了滑摩转矩的最大值,降低了接排对主机产生的负载冲击,主机转速骤降问题得到改善;但在离合器完全接排,即转矩补偿结束时主机转速仍未达到目标转速,此时轴带电机即刻停机,螺旋桨由于失去部分动力转速下降,同时螺旋桨负载全部转移至主机,离合器传递转矩再次突然上升造成二次负载冲击,主机转速出现二次下降。
该策略下主机转速最低值为411.2
高混合度动力系统模式切换过程中(主要是PTH模式向主机模式切换),由于存在大功率推进负载转移,容易引起主机转速骤降等动态性能恶化问题。本文针对目标船舶开展模式切换性能优化控制技术研究,提出了长延时滑摩策略、接排转速优化策略和转矩补偿策略。各模式切换接排策略仿真结果如表5所示。
|
|
表 5 不同模式切换策略下仿真结果统计表 Tab.5 Simulation results of different mode switching strategies |
主要结论如下:
1)采用长延时滑摩策略可以有效解决主机转速骤降问题。相较原模式切换策略,延长接排时间至10
2)采用接排转速优化策略可以一定程度、但无法有效改善主机转速骤降问题。相较原模式切换策略,接排转速升高至900 r/min时,主机转速超调率仅降低2.16%。
3)采用转矩补偿策略可以有效改善主机转速骤降问题。相较原模式切换策略,主机转速超调率降低7.78%。补偿期间轴带电机需求功率远低于其额定功率,具备较高的适用性和可行性。
本文仅针对长延时滑摩策略、接排转速优化策略和转矩补偿策略的单独使用展开研究,部分策略单独应用时无法充分发挥效果,更适合作为辅助策略改进模式切换性能。后续可针对多模式切换优化策略的综合使用展开深入研究。
| [1] |
崔宇轩. 混联式混合动力汽车模式切换控制策略研究[D]. 北京: 北京交通大学, 2021.
|
| [2] |
王卉. 混合动力汽车模式切换动态协调控制研究[D]. 镇江: 江苏大学, 2020.
|
| [3] |
HYUNSUP K, KIM J, HYEONGCHEOL L. Mode transition control using disturbance compensation for a parallel hybrid electric vehicle[J]. Proceedings of the Institution of Mechanical Engineers, Part D:Journal of Automobile Engineering, 2011, 225(2): 150-166. DOI:10.1243/09544070JAUTO1523 |
| [4] |
赵冶国. 四轮驱动混合动力轿车驱动模式切换控制[J]. 机械工程学报, 2011, 47(4): 100-109. |
| [5] |
赵晨. 基于P2构型的混合动力汽车模式切换协调控制策略的研究[D]. 天津: 天津大学, 2020.
|
| [6] |
BECK R, et al. Model predictive control of a parallel hybrid vehicle drivetrain, [C]// Proceedings of the 44th IEEE Conference on Decision and Control, 2005:2670−2675.
|
| [7] |
朱剑昀. 混合动力船舶模式切换过程力矩协调控制[J]. 中国机械工程, 2017, 28(23): 2859-2867. DOI:10.3969/j.issn.1004-132X.2017.23.013 |
| [8] |
张益敏. 基于某内河公务船的柴电混合动力模式切换研究[D]. 上海: 上海交通大学, 2018.
|
| [9] |
贺春荣. 混合动力系统模式切换平顺性优化控制[D]. 镇江: 江苏大学, 2017.
|
| [10] |
GERHARD S. 1978 ITTC Performance Prediction Method [J/OL]. https://www.ittc.info/media/8017/75−02−03−0 14
|
 2023, Vol. 45
2023, Vol. 45
