0 引　言

21世纪是海洋的世纪，世界各国之间展开了海洋竞赛^[1]。自主式无人水下航行器（autonomous underwater vehicle，AUV）因其在海洋开发研究与水下作战中的重要作用，而成为海洋研究的重要工具，受到世界各海洋大国和军事强国的重视^[2]。

控制问题是AUV的关键技术之一，AUV系统具有高度非线性、时变性和强耦合性，水动力参数不确定，水下航行环境复杂多变受海流、海浪干扰等^[3]，给AUV运动控制带来极大的挑战，要求控制算法具有足够的鲁棒性和自适应性。目前，已有许多控制方法已经运用在AUV运动控制上。传统PID控制是主流的控制方法之一，其基于误差信号的反馈控制，不依赖于具体对象模型。刘学敏等^[4]从模糊逻辑控制出发，借鉴PID控制结构形式推导出S面控制方法，效果好于PID控制器，结构简单且实用。此外，还有一些PID及S面控制的改进算法大多是引入智能算法对其进行参数优化以提高控制效果。韩京清^[5-6]提出了自抗扰控制（active disturbance rejection control，ADRC）理论，将被控对象中的不确定因素归为总扰动，利用扩张状态观测器（extended state observer, ESO）观测总扰动，并将系统补偿为积分串联型，再辅以一定的控制律就可以实现误差控制。但由于非线性自抗扰控制（nonlinear active disturbance rejection control, NLADRC）参数较多，参数整定较为困难。高志强^[7]在此基础上提出了线性自抗扰控制（linear active disturbance rejection control, LADRC），并以带宽的概念整定控制器和观测器参数，大幅缩减了参数的数量，提高了工程实用性。目前ADRC在水平面、垂直面以及解耦控制方面都取得了不错的效果^[8-9]。

然而，大多数AUV控制算法的研究多基于简化模型，忽略了执行机构的响应特性对控制的影响，以及控制算法的节能特性。因此，本文在AUV六自由度空间运动模型的基础上考虑AUV执行机构响应特性的影响，并采用基于正切Sigmoid函数的跟踪微分器 (tangent sigmoid tracking differentiator, TSTD)^[10]优化LADRC，最终通过与传统LADRC和S面控制方法在有无干扰条件下进行仿真对比，从控制精度和操舵引起的航行能耗2个方面反映其控制性能。

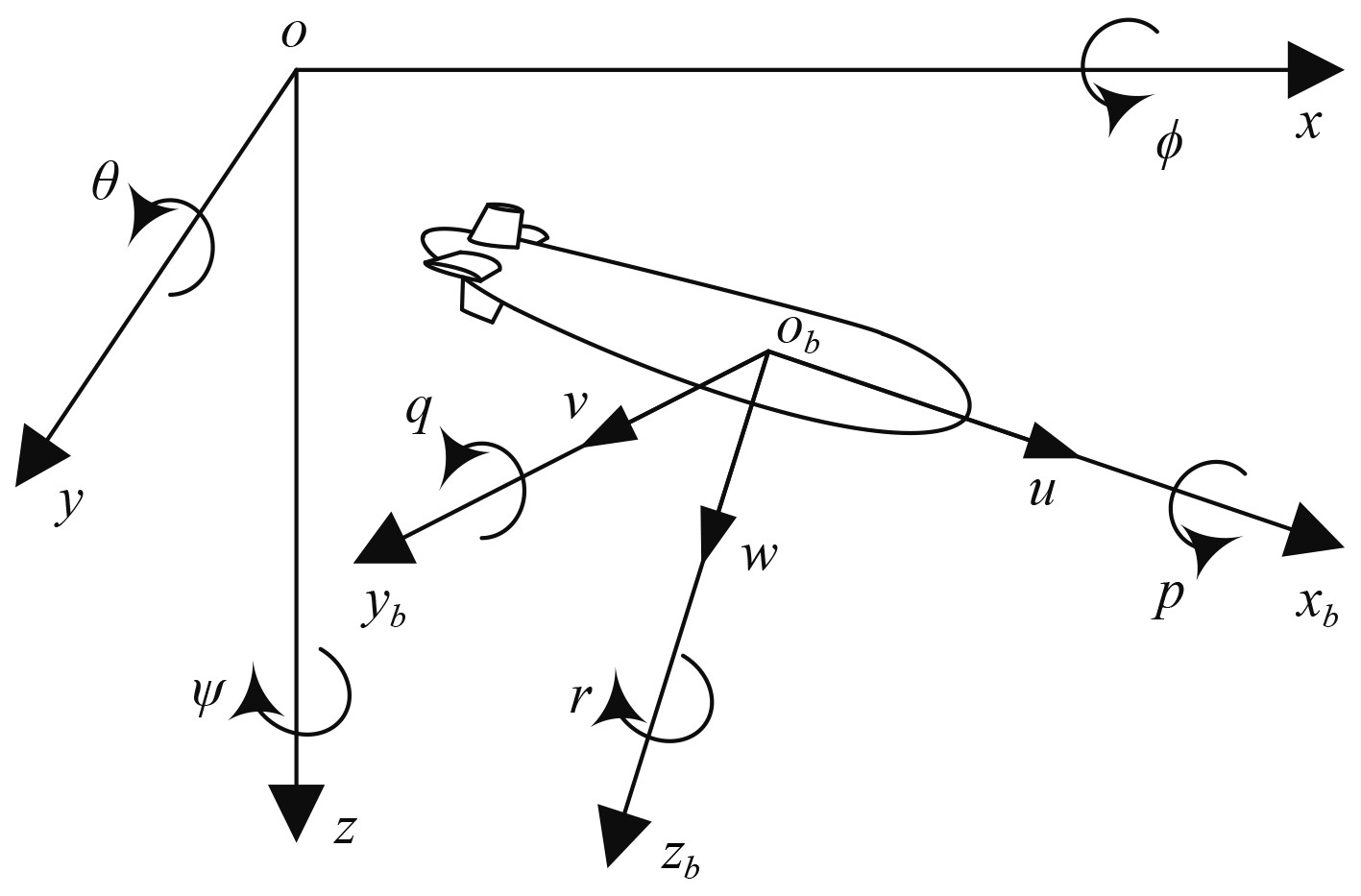
1 模型建立 1.1 AUV空间运动模型 1.1.1 AUV动力学方程

AUV作空间六自由度运动，通过图1所示的固定坐标系（记为f系）和载体坐标系（记为b系）。设位置姿态矢量为 $ \eta = {\left[ {p,\Theta } \right]^{\rm{T}}} $ ，其中位置 $ p = {[x,y,z]^{\rm{T}}} $ ，姿态 $ \Theta = {[\phi ,\theta ,\psi ]^{\rm{T}}} $ 。设速度矢量 $ \nu = {\left[ {v_{nb}^b,\omega _{nb}^b} \right]^{\rm{T}}} $ ，其中线速度 $ v_{nb}^b = {[u,v,w]^{\rm{T}}} $ ，角速度 $ \omega _{nb}^b = {[p,q,r]^{\rm{T}}} $ 。各自由度上的受力及运动参数如表1所示。

根据刚体动力学方程和流体力学原理，考虑非旋转定常海流时AUV动力学方程为：

$ M{\dot \nu _r} + \left[ {C\left( {{\nu _r}} \right) + D\left( {{\nu _r}} \right)} \right]{\nu _r} + g\left( \eta \right) + {g_0} = \tau 。$

(1)

式中： $ {\nu _r} $ 为AUV对水速度， $ {\nu _r} = \nu - {\nu _c} $ ，海流速度 $ {\nu _c}{\text{ = [}}{u_c},{\upsilon _c},{w_c},0,0,0{]^{\text{T}}} $ ； $ M $ 为系统惯性矩阵； $ C({\nu _r}) $ 为科氏-向心力矩阵； $ D({\nu _r}) $ 为阻力阵； $ g\left( \eta \right) $ 为恢复力； $ {g_0} $ 为压载控制力； $ \tau $ 为控制输入的力和力矩。

其中，系统惯性矩阵 $ M $ 可展开为 $ M{\text{ = }}{M_{RB}} + {M_A} $ ，科氏-向心力阵 $ C({\nu _r}) $ 可展开为 $ C\left( {{\nu _r}} \right) = {C_{RB}}\left( {{\nu _r}} \right) + {C_A}\left( {{\nu _r}} \right) $ 。则AUV动力学方程可展开为如下形式：

$ ({M_{RB}} + {M_A}){\dot \nu _r} + \left[ {{C_{RB}}\left( {{\nu _r}} \right) + {C_A}\left( {{\nu _r}} \right) + D\left( {{\nu _r}} \right)} \right]{\nu _r} + g\left( \eta \right) + {g_0} = \tau。$

(2)

1.1.2 AUV运动学模型

AUV运动学方程本质上是载体坐标系到固定坐标系的速度和角速度转换方程，有欧拉角法和四元数法两种方法。四元数法计算量小、不存在奇异值问题，应用更为广泛。令转动四元数 $q = {[{q_0},{q_1},{q_2},{q_3}]^{\rm{T}}}$ ，广义位置矢量 $ {\eta _q} = {[p,q]^{\rm{T}}} $ ，则运动学方程为：

$ {\dot \eta _q}{\text{ = }}{J_q}\left( {{\eta _q}} \right)\nu \Leftrightarrow \left[ \begin{gathered} {\dot p} \\ {\dot q} \\ \end{gathered} \right] = \left[ \begin{gathered} R\left( q \right){\text{ }}{{\text{0}}_{3 \times 3}} \\ {\text{ }}{0_{4 \times 3}}{\text{ }}T\left( q \right) \\ \end{gathered} \right]\left[ \begin{gathered} \upsilon _{nb}^b \\ \omega _{nb}^b \\ \end{gathered} \right]，$

(3)

其中， $ R\left( q \right) $ 和 $ T\left( q \right) $ 为转换矩阵。

$\begin{aligned} & R\left( q \right) = \\ & \left[ {\begin{array}{*{20}{c}} {1 - 2\left( {q_2^2 + q_3^2} \right)}&{{\text{2}}\left( {{q_1}{q_2} - {q_0}{q_3}} \right)}&{2\left( {{q_1}{q_3} + {q_0}{q_2}} \right)} \\ {2\left( {{q_1}{q_2} + {q_0}{q_3}} \right)}&{1 - 2\left( {q_1^2 + q_3^2} \right)}&{{\text{2}}\left( {{q_2}{q_3} - {q_0}{q_1}} \right)} \\ {2\left( {{q_1}{q_3} - {q_0}{q_2}} \right)}&{{\text{2}}\left( {{q_2}{q_3}{\text{ + }}{q_0}{q_1}} \right)}&{1 - 2\left( {q_1^2 + q_2^2} \right)} \end{array}} \right] ，\end{aligned} $

(4)

$ T\left( q \right) = \frac{1}{2}\left[ {\begin{array}{*{20}{c}} { - {q_1}}&{ - {q_2}}&{ - {q_3}} \\ {{q_0}}&{ - {q_3}}&{{q_2}} \\ {{q_3}}&{{q_0}}&{ - {q_1}} \\ { - {q_2}}&{{q_1}}&{{q_0}} \end{array}} \right]，$

(5)

四元数与欧拉角之间可由如下公式进行转换：

$ \left\{\begin{gathered} \phi = \arctan \left(\frac{{2({q_0}{q_1} + {q_2}{q_3})}}{{1 - 2(q_1^2 + q_2^2)}}\right)，\\ \theta = - \arcsin (2({q_1}{q_3} - {q_0}{q_2})) ，\\ \psi = \arctan \left(\frac{{2({q_0}{q_3} + {q_1}{q_2})}}{{1 - 2(q_2^2 + q_3^2)}}\right)。\\ \end{gathered} \right.$

(6)

1.2 执行机构模型 1.2.1 舵机模型

舵机驱动舵翼实现AUV的转向和变深，舵机一般采用电动舵机，舵机系统通常具有延迟、死区、饱和等非线性，舵机响应特性可用一阶惯性环节近似表示：

$ \frac{\delta }{{{\delta _c}}} = \frac{{{K_R}}}{{{T_R}s + 1}} 。$

(7)

其中， $ {\delta _c} $ 为输入指令舵角； $ \delta $ 为输出舵角； $ {T_R} $ 为时间常数； $ {K_R} $ 为增益系数。此外，舵角和舵速还具有如下饱和特性：

$ \begin{gathered}\delta (t) = \left\{ \begin{array}{*{20}{c}} {\displaystyle\int_{{t_1}}^{{t_2}} {\dot \delta {\rm{d}}t} }，&{\delta {\text{(}}t{\text{)}} < {\delta _{{\text{max}}}}}，\\ {\delta _{\max }}，&\delta {\text{(}}t{\text{)}} \geqslant {\delta _{{\text{max}}}} ，\end{array} \right. \\ \dot \delta (t) = \left\{ \begin{array}{*{20}{c}} {\displaystyle\int_{{t_1}}^{{t_2}} {\ddot \delta {\rm{d}}t} }，&{\dot \delta {\text{(}}t{\text{)}} < {{\dot \delta }_{{\text{max}}}}} ，\\ {{\dot \delta }_{\max }}，& \dot \delta {\text{(}}t{\text{)}} \geqslant {{\dot \delta }_{{\text{max}}}}。\end{array} \right. \end{gathered} $

(8)

1.2.2 推进电机模型

推进电机实现转速的闭环控制，与舵机模型类似，推进电机响应特性可近似用一阶惯性环节描述：

$ \frac{n}{{{n_c}}} = \frac{1}{{{T_M}s + 1}} 。$

(9)

式中， $ {n_c} $ 和 $ n $ 分别为指令转速和实际转速， $ {T_M} $ 为时间常数。同时具有转速和加速度饱和特性如下：

$ \begin{gathered}n(t) = \left\{ \begin{array}{*{20}{c}} {\displaystyle\int_{{t_1}}^{{t_2}} {\dot n{\rm{d}}t} }，&{n{\text{(t)}} < {n_{{\text{max}}}}} ，\\ {n_{\max }}，& n{\text{(t)}} \geqslant {n_{{\text{max}}}}，\end{array} \right. \\ \dot n(t) = \left\{ \begin{array}{*{20}{c}} {\displaystyle\int_{{t_1}}^{{t_2}} {\ddot n{\rm{d}}t} }，&{\dot n{\text{(}}t{\text{)}} < {{\dot n}_{{\text{max}}}}} ，\\ {{\dot n}_{\max }}，& \dot n{\text{(}}t{\text{)}} \geqslant {{\dot n}_{{\text{max}}}} 。\end{array} \right. \end{gathered}$

(10)

1.3 AUV系统模型

由图2可知，AUV运动控制器输出控制信号为指令舵角 $ {\delta _{sc}},{\delta _{rc}} $ 和指令转速 $ {n_c} $ ，经过执行机构响应模型后输出为实际舵角 $ {\delta _s},{\delta _r} $ 和实际转速 $ n $ 。实际舵角和转速输入六自由度空间动力学方程后转换为相应的力和力矩，经六自由度空间动力学方程得到对应的速度 $ v_{nb}^b $ 和角速度 $ \omega _{nb}^b $ 后经过坐标转换得到姿态角 $ \Theta $ 和位置 $ p $ 。

1.4 平均操舵能耗指标

舵的转动不仅引起纵倾力矩和垂向力的改变，还会产生纵向阻力^[11]。由舵产生的纵向阻力与舵角的平方成正比，则可定义平均操舵能耗指标：

$ W = \frac{1}{T}\int_0^T {{\delta ^2}{\rm{d}}t}。$

(11)

2 控制系统设计 2.1 ADRC概述

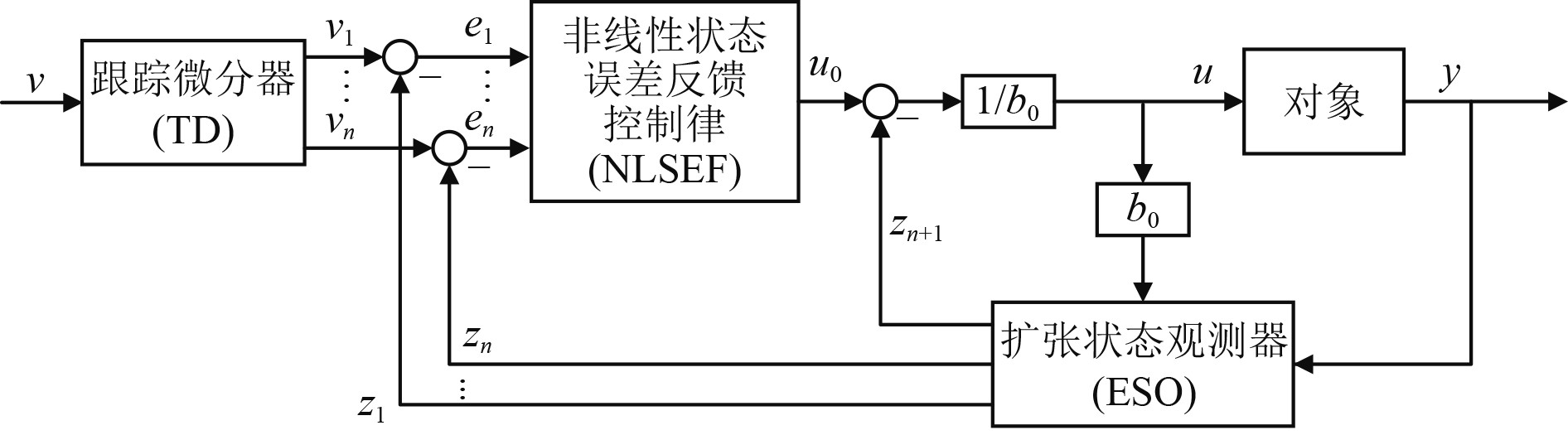
韩京清提出的非线性自抗扰控制主要由跟踪微分器（tracking differentiator, TD）、扩张状态观测器(extended state observer, ESO)以及非线性状态误差反馈（nonlinear state error feedback, NLSEF）控制律组成，其基本结构如图3所示。ADRC的基本思想要点包括：标准型与总扰动、扩张状态与扰动整体辨识、微分信号生成与安排过渡过程以及扰动的消减与控制量产生^[12]。

但是二阶系统的非线性自抗扰控制器(NLADRC)一般形式需整定的参数多达12个，调参难度较高。高志强^[7]提出的LADRC将ESO和NLSEF改用线性化的LESO和LSEF，需整定的参数大幅缩减，极大促进了工程应用。

2.1.1 线性扩张状态观测器

线性扩张状态观测器（LESO）是LADRC的核心，将总扰动扩张为系统的一个状态变量，利用状态观测器观测出扰动在控制输入前补偿。以二阶系统为例，假设对象为：

$ \ddot y = f(y,\dot y,w,t) + bu。$

(12)

其中： $ w $ 为外部扰动； $ f(y,\dot y,w,t) $ 为综合内外扰动的总扰动。将 $ f(y,\dot y,w,t) $ 扩张为状态变量 $ {x_3} $ ，令 $ {x_1} = y $ ， $ {x_2} = \dot y $ ， $ {x_3} = f(y,\dot y,w,t) $ ， $ {b_0} $ 为控制器增益 $ b $ 的已知部分，则式（12）可整理为状态空间方程形式：

$ \left\{ \begin{gathered} \dot x = Ax + Bu + E\dot f，\\ y = Cx + Du。\\ \end{gathered} \right. $

(13)

其中： ${\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&1&0 \\ 0&0&1 \\ 0&0&0 \end{array}} \right], {\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{b_0}} \\ 0 \end{array}} \right]，{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} 0 \\ 0 \\ 1 \end{array}} \right]，$ ${\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]，{\boldsymbol{D}} = [0]$ 。

采用零阶保持（ZOH）法得到LESO离散形式为^[12]：

$ \left\{ \begin{gathered} x(k + 1) = \varPhi x(k) + \varGamma u(k)，\\ y(k) = Hx(k) + Ju(k)。\\ \end{gathered} \right. $

(14)

其中： $\varPhi = \left[ {\begin{array}{*{20}{c}} 1&h&{{h^2}/2} \\ 0&1&h \\ 0&0&1 \end{array}} \right]，\varGamma = \left[ {\begin{array}{*{20}{c}} {{b_0}{h^2}/2} \\ {{b_0}h} \\ 0 \end{array}} \right]，{H} = \left[ {\begin{array}{*{20}{c}} 1&0&0 \end{array}} \right]，$ $J = \left[ 0 \right] $ ， $ h $ 为采样周期。

构造离散观测器方程为：

$ \left\{ \begin{gathered} z(k + 1) = [\varPhi - \varPhi {L_c}H]z(k) + [\varGamma \;\;{\varPhi {L_c}} ]{u_d}(k) ，\\ {y_d}(k) = [I - {L_c}H]z(k) + [0\;\;{{L_c}} ]{u_d}(k) 。\\ \end{gathered} \right. $

(15)

其中： $ {y_d}(k) $ 为观测器输出； $ {u_d}(k) = {[u(k),y(k)]^{\rm{T}}} $ 为观测器的输入组合； $ {L_c} $ 为误差反馈增益矩阵，令特征方程满足 $ \lambda (z) = \left| {zI - (\varPhi - \varPhi {L_c}H)} \right| = {(z - \beta )^3} $ （此处z为离散化变换算子），可使增益矩阵与离散观测器带宽 $ \beta $ 唯一相关。离散观测器带宽与连续观测器带宽 $ {\omega _0} $ 之间的关系为 $ \beta = {e^{ - {\omega _0}h}} $ 。

2.1.2 跟踪微分器

跟踪微分器(TD)的目的，是根据设定值v安排过渡过程v₁并提取其微分信号v₂，安排过渡过程是实现无超调快速跟踪的有效方法^[13]，且基于正切Sigmoid函数优化的跟踪微分器(TSTD)具有响应速度快、精度高，具有较强噪声抑制的能力^[10]，因此采用TSTD优化LADRC控制效果，其离散形式为：

$ \left\{ \begin{gathered} {a_1} = - {l_1}{\left| {{v_1}(k) - v(k)} \right|^p}{\rm{tansig}}[{\beta _0}({v_1}(k) - v(k))] ，\\ {a_2} = - {l_2}{\rm{tansig}}\left[\frac{{{v_2}(k)}}{{{k_0}}}\right]，\\ {v_1}(k + 1) = {v_1}(k) + h{v_2}(k)，\\ {v_2}(k + 1) = {v_2}(k) + hk_0^2({a_1} + {a_2}) 。\\ \end{gathered} \right. $

(16)

式中： $ h $ 为对象采样周期； $ {k_0},{l_1},{l_2},p,{\beta _0} $ 为TSTD需要调节的参数， $ {\rm{tansig}}(x) $ 为正切Sigmoid函数

$ {\rm{tansig}}(x) = \frac{2}{{1 + {e^{( - 2x)}}}} - 1。$

(17)

2.1.3 线性误差状态反馈控制律

状态误差反馈控制律将过渡过程的误差信号、误差微分信号等进行组合形成控制律。由于系统输出 $ y $ 可测量得到，则可采用PD形式LSEF控制律。

$ {u_0} = {k_p}({v_1} - y) - {k_d}{z_2}。$

(18)

由于LSEF只是误差信号、误差微分信号按增益 $ {k_p},{k_d} $ 放大后线性组合，无需离散化。经参数化，令 $ {k_p} = \omega _c^2,{k_d} = 2{\omega _c} $ ，PD控制器参数可与控制器带宽 $ {\omega _c} $ 唯一相关^[7]。

最后取相应控制量为：

$ u = \frac{{{u_0} - {z_3}}}{{{b_0}}}。$

(19)

2.2 参数整定

TSTD，LESO，LSEF的参数整定可以分开进行，先整定TSTD和LESO的参数，取得满意效果后结合LSEF的参数进行整体调整。TSTD的参数 $ {k_0},{l_1},{l_2}, p,{\beta _0} $ 意义明确，参数整定较为简单。此外，对于大部分工程对象 $ {\omega _o} $ 和 $ {\omega _c} $ 可先按照 $ {\omega _o} = (3\sim 5){\omega _c} $ 关系选择^[12]，然后根据具体情况调整 $ {k_p},{k_d} $ 。

3 仿真与分析

深度控制是AUV进行其他复杂空间运动的基础，因此本文以深度控制为例，将传统LADRC方法（LADRC）、采用TSTD优化的LADRC（TSTD-LADRC）方法以及S面（S Plane）控制进行对比，验证TSTD-LADRC的控制效果。以REMUS AUV为研究对象，直径D=0.19 m，长度L=1.5 m，其他相关水动力参数可参考文献[14]。初始值：深度20 m，纵摇角0°，航速1.54 m/s。目标值：深度30 m。仿真步长为0.01 s，其他控制器参数如表2所示。

图4为LADRC，TSTD-LADRC以及S面控制3种方法在无干扰情况下深度控制的深度和纵摇曲线。LADRC方法超调量最大，为0.2 m；TSTD-LADRC和S面控制方法超调较小，分别为0.008 m和0.007 m。LADRC，TSTD-LADRC以及S面控制方法在到达目标深度后误差分别为0.03 m，0.005 m和0.003 m。从图4（a）可以看出，3种控制方法响应速度非常接近，LADRC和TSTD-LADRC方法响应速度略快。进入稳态前LADRC和S面控制方法深度控制有振荡而TSTD-LADRC方法几乎没有振荡，这一点也体现在图4（b）的纵摇角振荡中。在控制精度上3种控制方法相近，且相对于AUV直径而言差距很小。图5为3种控制方法的升降舵角响应，可知S面控制方法操舵次数最多，LADRC方法次之，TSTD-LADRC方法最少，对应3种方法的平均操舵能耗指标如表3所示。LADRC和TSTD-LADRC方法相对S面控制平均操舵能耗指标分别降低了41.2%和55.9%。

综上所述，在无干扰情况下TSTD-LADRC方法的控制精度和平均操舵能耗指标均优于LADRC方法，S面控制方法控制精度最高，但操舵次数和操舵能耗最多。因此，选择精度最高的S面控制方法和操舵能耗最少的TSTD-LADRC方法进一步仿真对比。

为了验证TSTD-LADRC方法的抗扰动能力，在原有基础上添加流速0.5sin(t/10) m/s，迹向角30°，潜伏角15°的非旋转干扰海流，均值为0方差为1°的等效舵角干扰，40 s后模型主要参数 $ M $ 矩阵增大30%。

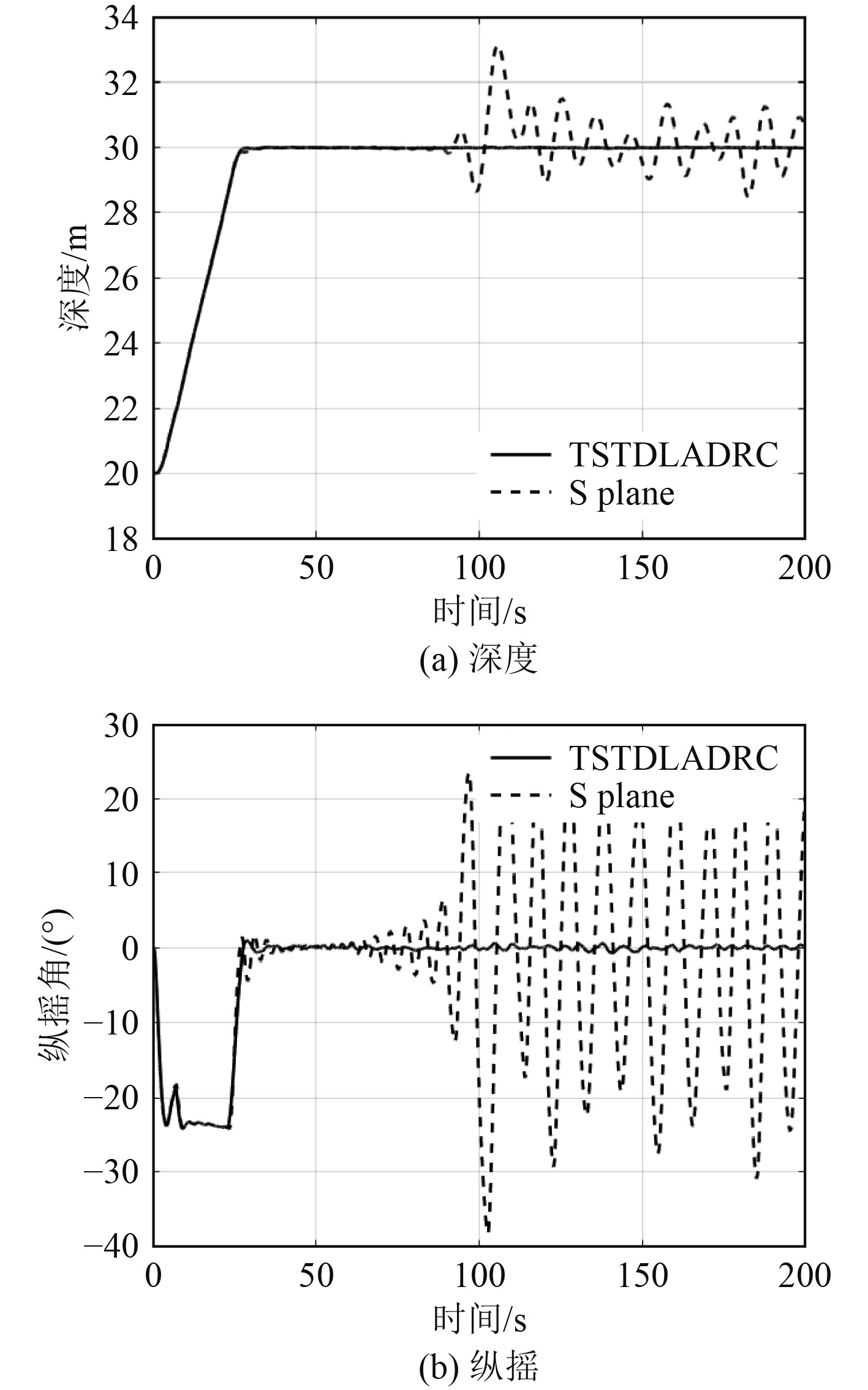
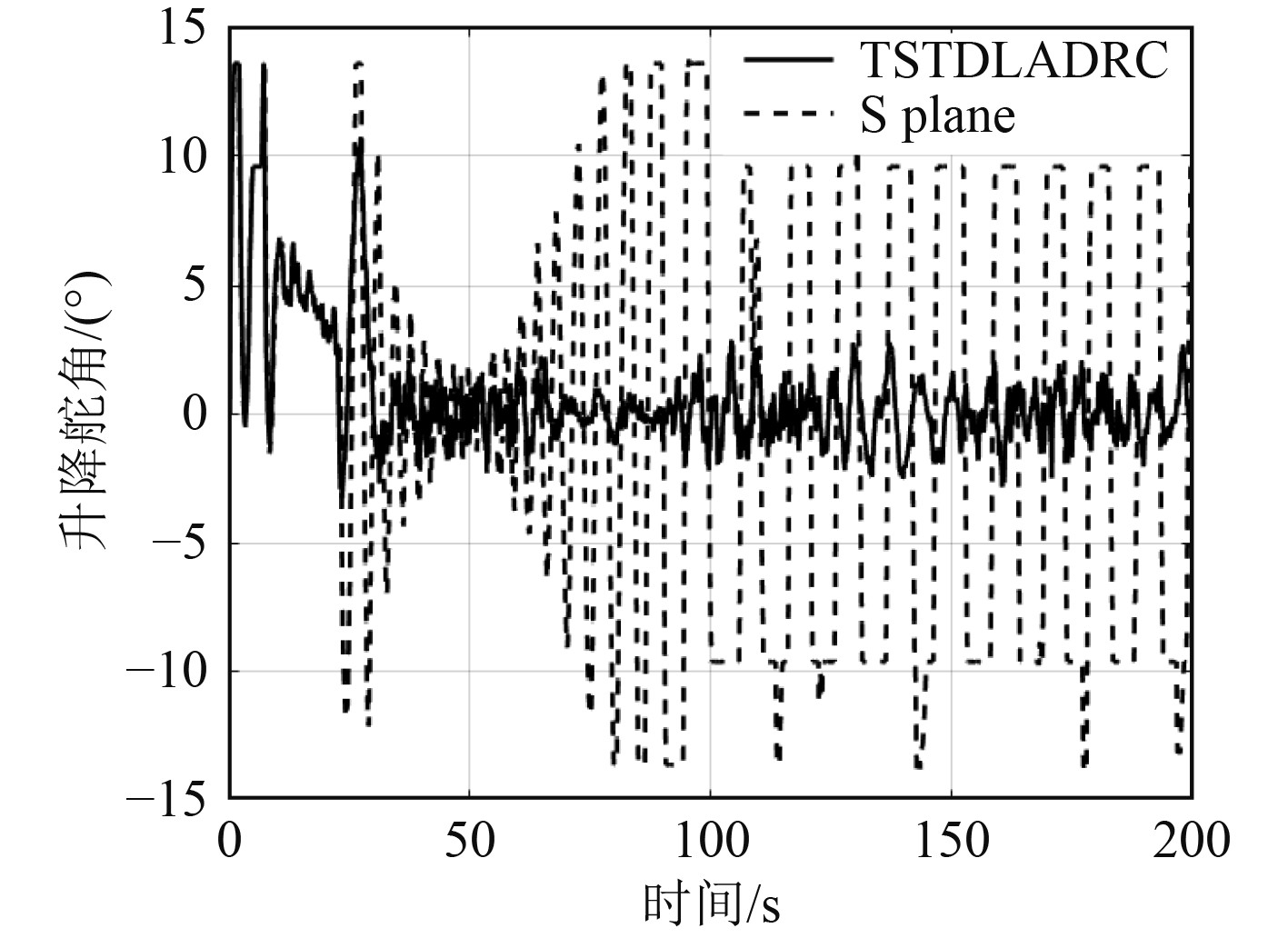
2种控制方法的深度和纵摇曲线以及舵角响应曲线如图6和图7所示。由图6可知，模型参数变化后S面控制方法出现了较大幅度的振荡，深度控制最大误差为3.2m，而TSTD-LADRC方法为0.02 m。由图7和表3可知，TSTD-LADRC方法的操舵幅度更小，且平均操舵能耗指标小于S面控制方法，相对S面控制平均操舵能耗指标大幅降低。综合来看，TSTD-LADRC方法的控制精度更高且操舵次数和耗能更少，其深度控制效果优于S面控制。

4 结　语

LADRC方法在AUV深度控制上是有效的，采用TSTD优化的LADRC方法相比传统LADRC可获得更好的控制效果，但在一定程度上增加了参数整定的复杂度。在内外界干扰作用下，S面控制方法控制精度大幅下滑，而采用TSTD优化的LADRC方法依然具有较好控制精度，说明LESO可以实时有效地估计总扰动并加以补偿。此外，LADRC方法还在节能和减少机械损耗体现出了优越性，采用TSTD优化的LADRC方法在保持较高控制精度的同时操舵次数和能耗更少，有助于提升AUV续航能力和减少机械损耗。