2. 中国船舶及海洋工程设计研究院,上海 200011
2. China Ship and Ocean Engineering Design and Research Institute, Shanghai 200011, China
船舶码头系泊是一个较为复杂、没有线性规律的系统,并且船体与码头之间存在耦合作用,倘若系泊布置不合理,在风浪流环境载荷联合作用下,船舶或与码头发生碰撞,甚至倾覆,造成不可挽回的巨大损失。因此,保证码头系泊船舶在风浪流环境载荷共同作用下的安全一直是行业内研究的重点,而减小船体运动响应以及系泊缆绳的张力是分析码头系泊系统可靠性的关键因素。
刘必劲[1]采用试验分析与理论对比的方法,分析码头系泊船舶系泊缆受力情况的变化规律,并提出了系泊缆张力计算公式。基于三维势流理论,马小剑[2]建立了码头系泊船在风浪流载荷联合作用下的数值模型,将系泊缆非线性变形因素作为影响因子,并提出泊位长度及横缆优化方案。刘宇[3]比较系泊船在多种工况下的时域响应,通过控制变量法分析了系泊缆属性对船舶系泊张力的影响。郭建廷[4]对码头系泊船舶进行水动力耦合分析,比较沿型深方向不同首尾缆和尾横缆效果,发现增大首尾系泊缆与码头轴线的夹角,系泊缆的受力更加均匀。卫欣等[5]设计了海洋工程船PSV不同形式的系泊方案,并利用Ariane软件对方案的可行性进行了数值验证。常纪磊等[6]提出了台风期采用纯锚系泊泵船、泵船下沉减小波浪力作用面积等可行性方案及其对应适用性条件。卢西伟等[7]通过对20万吨邮轮系泊船舶得模型试验,提出蝶形泊位长度对船舶运动响应有一定影响。
相关学者对于船舶码头系泊方案的设计研究较少,采用不同材质的缆绳对系泊船运动响应的影响尚不明确。因此,本文选取舟山港某码头,针对一典型船舶提出了一种系泊方案,对比首尾缆采用不同材质在风浪流联合作用及多种工况下的水动力性能。首先在经典Ansys中对船体进行建模和有限元网格划分,调用Aqwa软件采用耦合计算方法,分析首尾缆材质对船舶运动和系泊缆张力时域响应的影响。最后通过进一步对比,选出系泊方案中最优的首尾缆形式,为码头系泊布置提供参考。
1 船舶码头系泊水动力分析方法 1.1 运动方程基于三维势流理论建立船体在时域内的运动方程[8]为:
| $ \left( {M + {{m}}} \right)\ddot x + \int_{ - \infty }^t {K(t - \tau )} \dot x(t){\rm{d}}\tau + Cx(t) = F(t) 。$ | (1) |
式中:
船体在环境载荷的作用下,除受到一阶波浪力以外,还受到二阶漂移力[9]。一阶波浪力与波高存在线性关系,能够使船体跟随波浪发生周期性的摇荡运动;二阶漂移力则与波高的平方成正比,其中,在不规则波的作用下,二阶低频漂移力可以使船体发生较大幅度的漂移运动。对于一阶波浪力,可以利用脉冲响应方法将规则波上的波浪力,通过Fourier变换,得到:
| $ \left\{ \begin{aligned} & {{f_{wi}}\left( \omega \right) = \int_{ - \infty }^\infty {{h_i}\left( t \right){e^{ - i\omega t}}{\rm{d}}t} },\\ & {{h_i}\left( t \right) = \dfrac{1}{{2\text{π} }}\int_{ - \infty }^\infty {{f_{wi}}\left( \omega \right){e^{ - i\omega t}}{\rm{d}}t} } 。\end{aligned} \right. $ | (2) |
式中:
对于二阶波浪力,由波浪在不同频率和不同浪向下的传递函数,通过Fourier变换可以得到二次脉冲响应函数:
| $\begin{split} {g_i}\left( {{\tau _1},{\tau _2}} \right) = &{\left( {\dfrac{1}{{2\text{π} }}} \right)^2}\int_{ - \infty }^{ + \infty } \int_{ - \infty }^{ + \infty } G_i^{\left( 2 \right)}\left( {{\omega _1},{\omega _2}} \right)\times \\ &{e^{\left( {i{\omega _1}{\tau _1} - i{\omega _2}{\tau _2}} \right)}}{\rm{d}}{\omega _1}{{\rm{d}}\omega _2} ,\end{split} $ | (3) |
| $ G_i^{\left( 2 \right)}\left( {{\omega _1},{\omega _2}} \right) = P\left( {{\omega _1},{\omega _2}} \right) + iQ\left( {{\omega _1},{\omega _2}} \right)。$ | (4) |
式中:
给定波高及波浪周期后,时域二阶漂移力可以表示为:
| $ {F_i}^{wave\left( 2 \right)}\left( t \right) = \int_0^{ + \infty } {{\int}_0^{ + \infty }{{g_i}\left( {{\tau _1},{\tau _2}} \right)\zeta \left( {t - {\tau _1}} \right)\zeta \left( {t - {\tau _2}} \right){\rm{d}}{\tau _1}{\rm{d}}{\tau _2}} },$ | (5) |
式中,
在AQWA中对船体进行运动响应和系泊缆张力分析时,采用波浪谱来描述波浪载荷,本文在计算过程中采用的是JONSWAP谱。JONSWAP谱的公式如下:
| $ {S_\zeta }\left( \omega \right) = \alpha {g^2}\dfrac{1}{{{\omega ^5}}}\exp \left\{ { - \dfrac{5}{4}{{\left( {\dfrac{{{\omega _0}}}{\omega }} \right)}^4}} \right\}{\gamma ^{\exp \left\{ { - \dfrac{1}{{2{\sigma ^2}}}{{\left( {\dfrac{{\omega - {\omega _0}}}{\omega }} \right)}^2}} \right\}}}。$ | (6) |
式中:
根据OCIMF规范的有关规定[10],船体受到的纵荡方向风力
| $ {F_{xw}} = \dfrac{1}{2}{C_{xw}}{\rho _w}V_w^2{A_T},$ | (7) |
| $ {F_{yw}} = \dfrac{1}{2}{C_{yw}}{\rho _w}V_w^2{A_L},$ | (8) |
| $ {M_{xyw}} = \dfrac{1}{2}{C_{xyw}}{\rho _w}V_w^2{A_L}{L_{BP}}。$ | (9) |
式中:
定常流作用下的船体会有沿着流速方向的平面力以及绕Z轴方向的首摇力矩[10],船体受到的纵荡方向流力
| $ {F_{xc}} = \dfrac{1}{2}{C_{xc}}{\rho _c}V_c^2{L_{BP}}T,$ | (10) |
| $ {F_{yc}} = \dfrac{1}{2}{C_{yc}}{\rho _c}V_c^2{L_{BP}}T,$ | (11) |
| $ {M_{xyc}} = \dfrac{1}{2}{C_{xyc}}{\rho _c}V_c^2L_{BP}^2T。$ | (12) |
式中:
一般系泊缆绳的弹性拉伸具有非线性规律,威尔逊提出系泊缆拉伸应力与变形间的关系式[11],如下式:
| $ {F_R} = {K_c}{d^2}{\left( {\dfrac{{\Delta S}}{S}} \right)^n}。$ | (13) |
式中:
若码头上带缆桩的坐标为
| $ S = \sqrt {{{\left( {{X_2} - {X_1}} \right)}^2} + {{\left( {{Y_2} - {Y_1}} \right)}^2} + {{\left( {{Z_2} - {Z_1}} \right)}^2}}。$ | (14) |
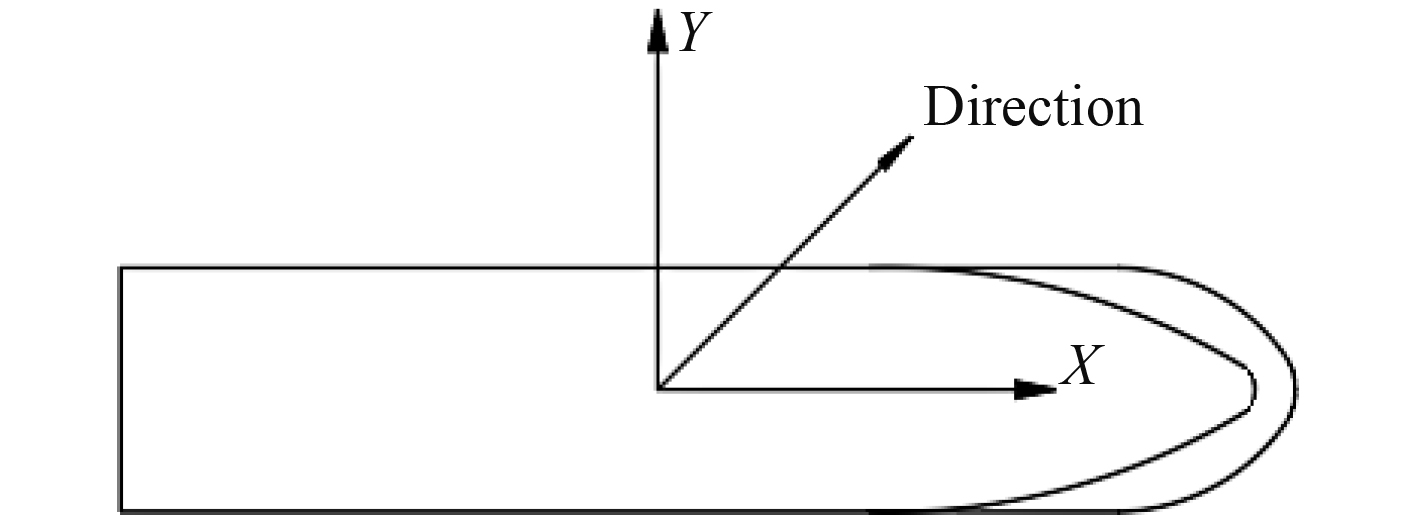
船体坐标系及环境坐标系的定义,如图1所示。X轴位于船体中心线,由船尾指向船首,Y轴遵循左手定则,由右舷指向左舷,Z轴垂直水平面,沿船舶型深方向向上。风浪流环境载荷的方向以逆时针旋转为正,从船尾指向船首为0°,首摇以X正轴向Y正轴转动的右手坐标系为正。
|
图 1 坐标系定义 Fig. 1 Definition of coordinate system |
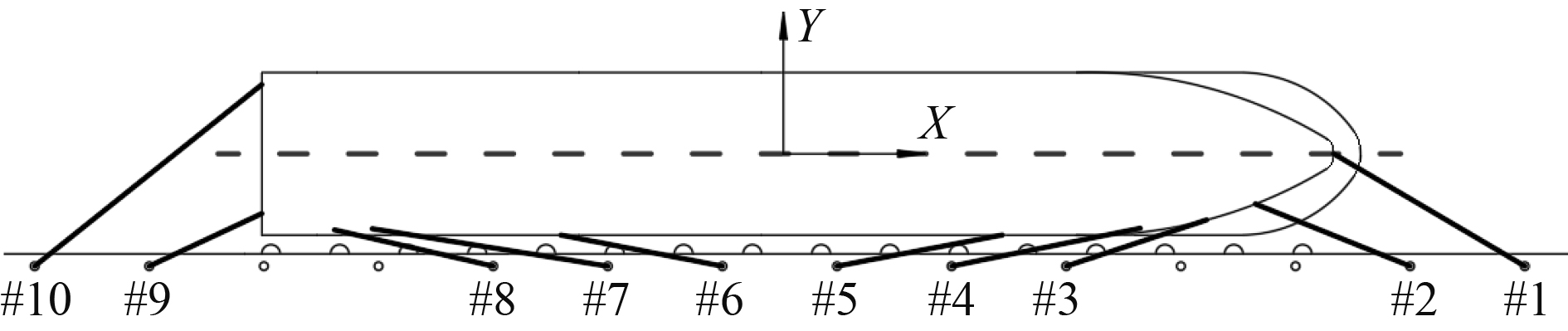
针对典型船舶提出一种系泊方案,如图2所示。采用10根系泊缆绳进行码头系泊,方案中首缆#1、#2与码头夹角范围为20°~30°,尾缆#9、#10与码头夹角范围为20°~50°;首尾倒缆#3~#8关于Y轴对称,各倒缆与码头夹角在10°左右;系缆桩间距25 m,护舷采用的是SUC2250H 标准鼓型橡胶护舷,间距15 m,最大压缩变形量是55%,最大反力为2659 kN。
|
图 2 系泊方案布置示意图 Fig. 2 Schematic diagram of mooring scheme layout |
选取一型散货船为例,进行风浪流载荷联合作用及多种工况下的数值分析,船舶排水量为39700 t,吃水7.0 m;码头长400 m,宽30 m。根据舟山海域的水文气象资料[12],港域内四周岛屿环抱,波浪变化较小,波浪平均周期在4~8 s,
|
|
表 1 计算工况参数 Tab.1 Calculation condition parameters |
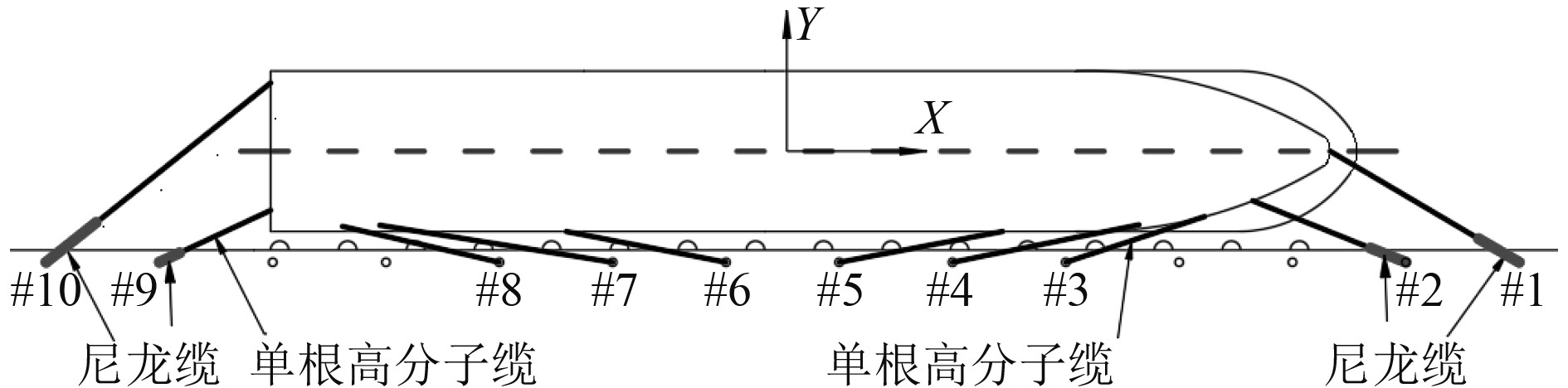
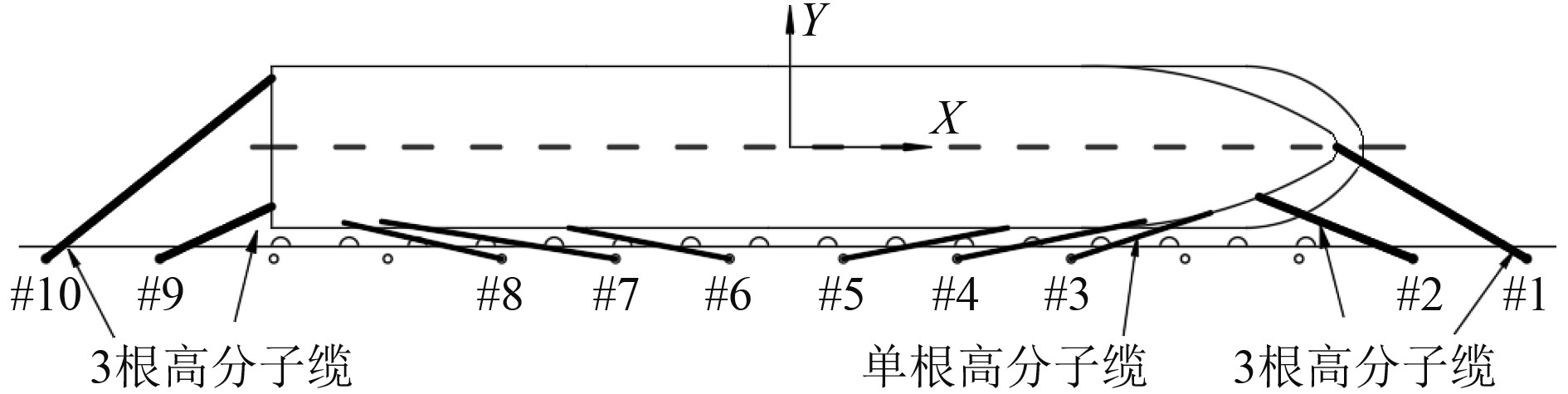
基于本文提出的系泊方案,设计3种首尾缆系泊形式,分析缆绳材质对船舶水动力性能的影响。形式1中3根系泊缆全部采用单根高分子缆绳,如图3所示;形式2中#1,#2,#9,#10缆绳尾部采用尼龙缆绳,占所在缆绳总长度1/5,如图4所示;形式3中#1,#2,#9,#10采用3根高分子缆绳,如图5所示。高分子系泊缆绳采用的直径为40 mm,破断载荷为1172 kN,3根高分子缆绳破断载荷为单根的3倍,尼龙尾缆的直径为104 mm,破断载荷为1650 kN。

|
图 3 形式1系泊示意图 Fig. 3 Schematic diagram of form 1 mooring |
|
图 4 形式2系泊示意图 Fig. 4 Schematic diagram of form 2 mooring |
|
图 5 形式3系泊示意图 Fig. 5 Schematic diagram of form 3 mooring |
1)运动响应
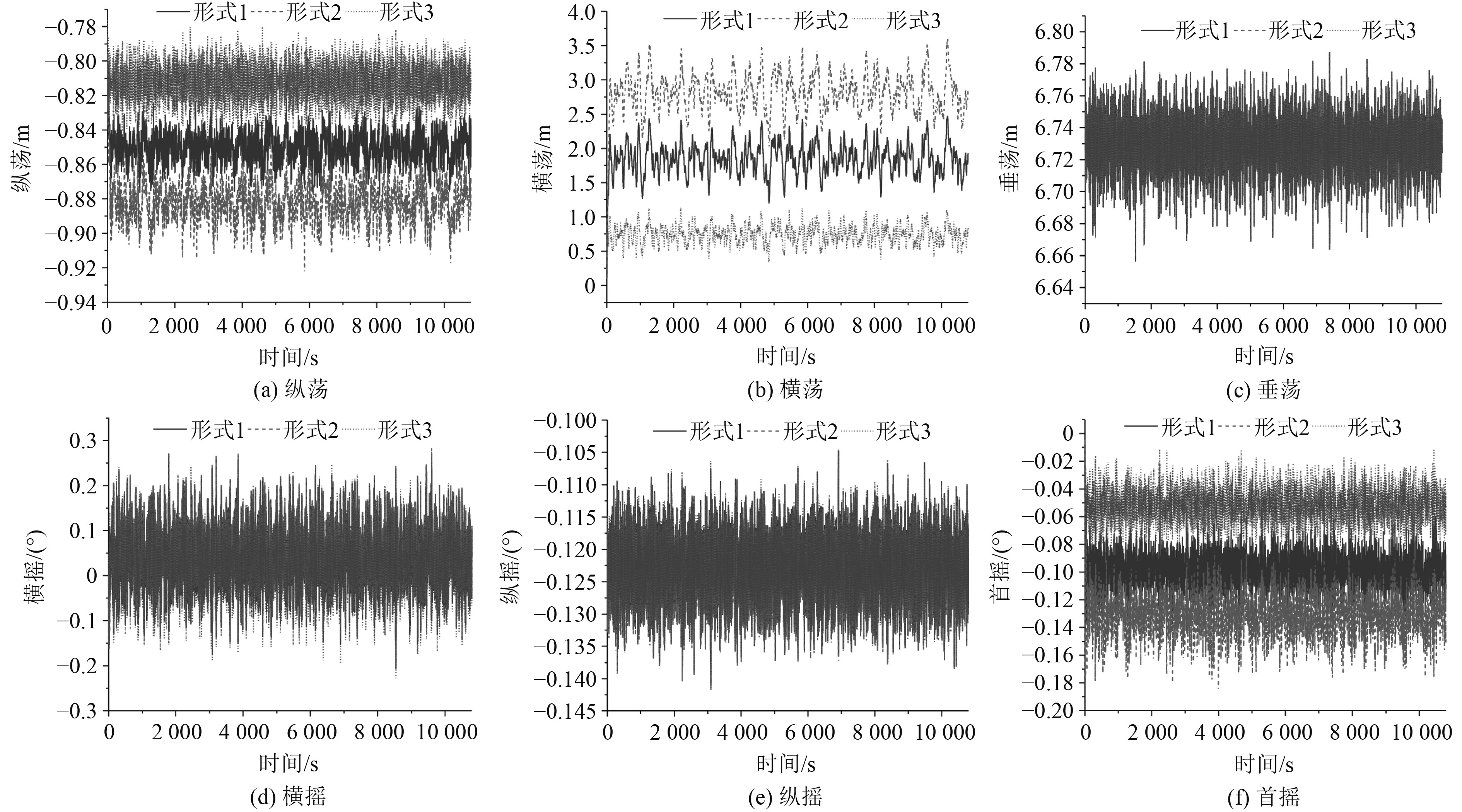
对3种首尾缆系泊形式下的船舶进行仿真,船体在工况1~工况4下的六自由度运动响应幅值时间历程曲线如图6所示。
|
图 6 工况1下3种系泊形式的运动响应时历曲线 Fig. 6 Time history curves of motion response of three mooring forms under condition 1 |
可知,风速与风向是影响船舶码头安全系泊的重要因素。在工况1下,形式3中船舶纵荡、横荡、横摇和首摇的运动幅值小于形式1、形式2,其中横荡运动幅值为0.74 m,较形式1小59.8%,较形式2小73.7%;首摇运动幅值为−0.05°,较形式1小50%,较形式2小61.5%。在工况2~工况4下,首尾缆3种系泊形式的运动响应结果差异较小;4种工况下,首尾缆采用不同材质对船舶垂荡和纵摇运动无明显影响;随负向角增大,形式1和形式2的纵荡运动幅值随之增大,形式1和形式3的横摇运动幅值随之增大,其中形式1的横摇增加了6倍,形式3增加了10倍。
2)系泊缆张力
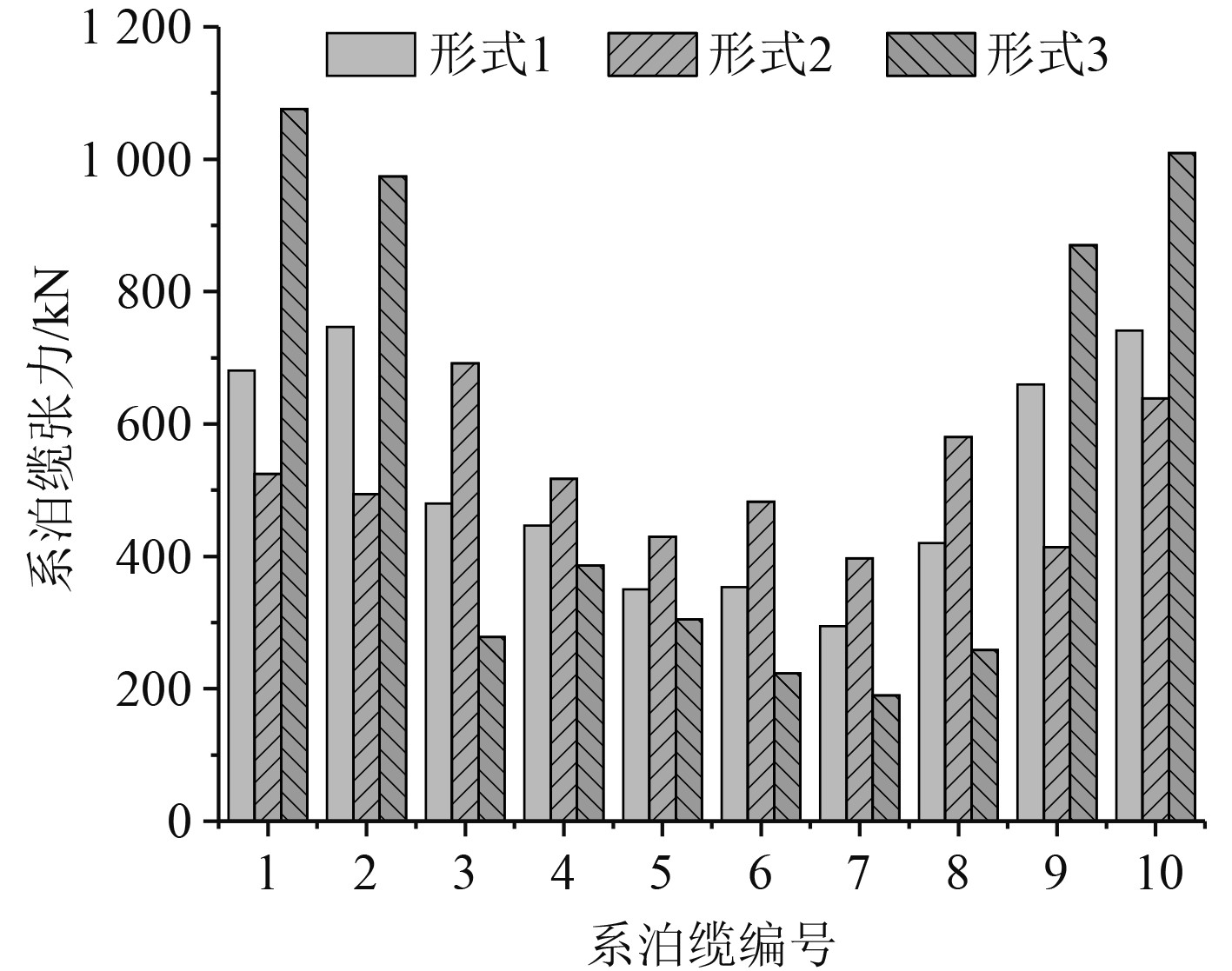
预张力是指在无环境载荷的条件下,通过绞车绞紧提供给系泊缆的初始张力。基于缆绳受力分配和最小安全系数的考虑,本文选取的预张力为单根高分子缆绳破断载荷的10%,即117.2 kN。首尾缆3种形式下的船体在工况1~工况4的系泊缆最大张力如图7~图10所示。
|
图 7 工况1系泊缆最大张力 Fig. 7 Maximum tension diagram of mooring line under condition 1 |
在工况1下,首尾缆3种形式所有系泊缆张力均满足破断载荷,其中形式1的最大张力为746.7 kN,发生在#2号系泊缆,小于破断载荷36%,形式1、形式3中#1,#2,#9和#10为主要受力缆;形式2中#3~#8系泊缆受力大于形式1和形式3,各系泊缆绳受力相对均匀;形式3各系泊缆张力均小于破断载荷的30%。对于工况2~工况4,各系泊缆受力情况良好,均满足破断载荷,#1~#10缆绳不同方案下的受力情况相似。可见,提出的船舶码头系泊方案均能防御28 m/s的台风。

|
图 8 工况2系泊缆最大张力 Fig. 8 Maximum tension diagram of mooring line under condition 2 |
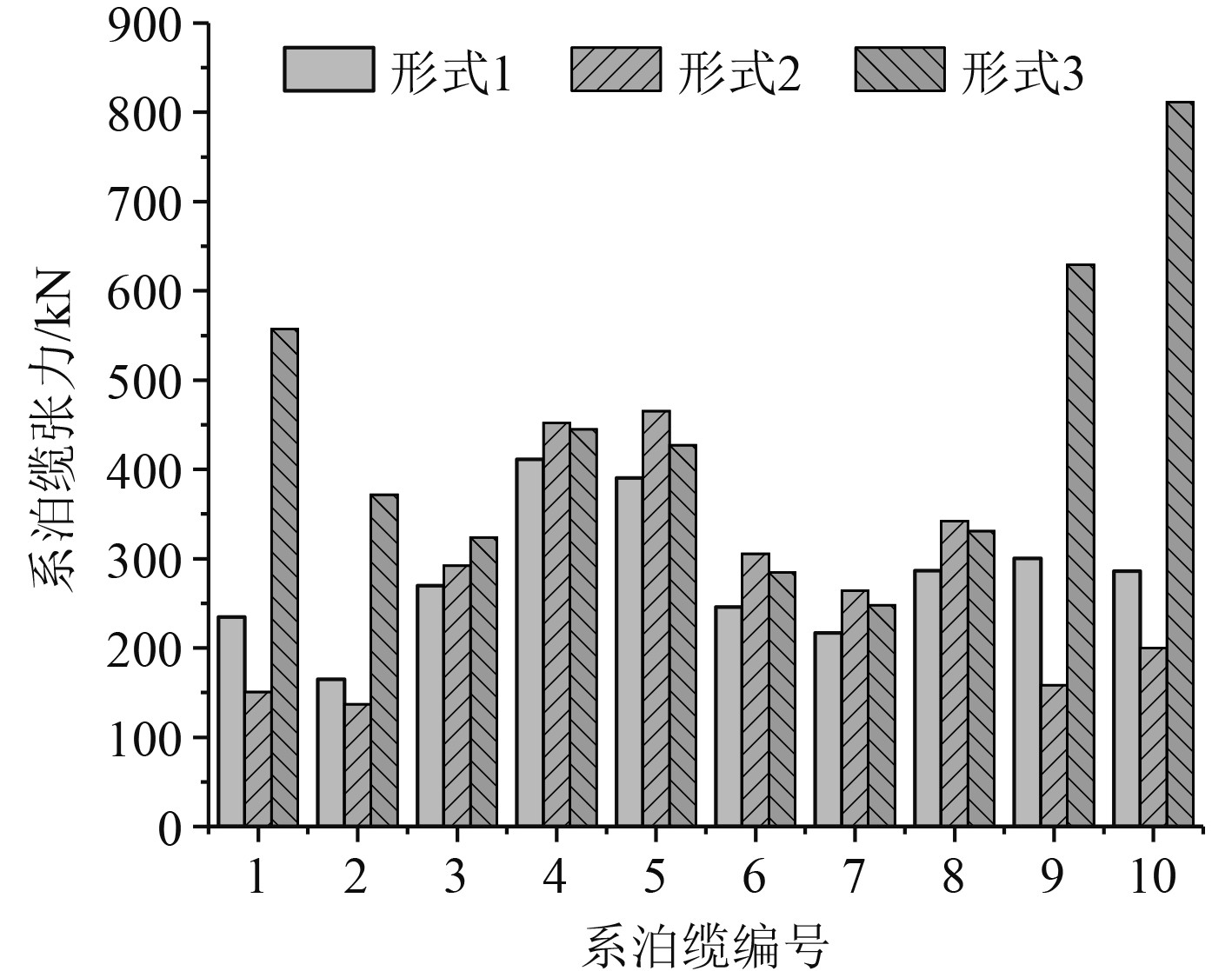
|
图 9 工况3系泊缆最大张力 Fig. 9 Maximum tension diagram of mooring line under condition 3 |
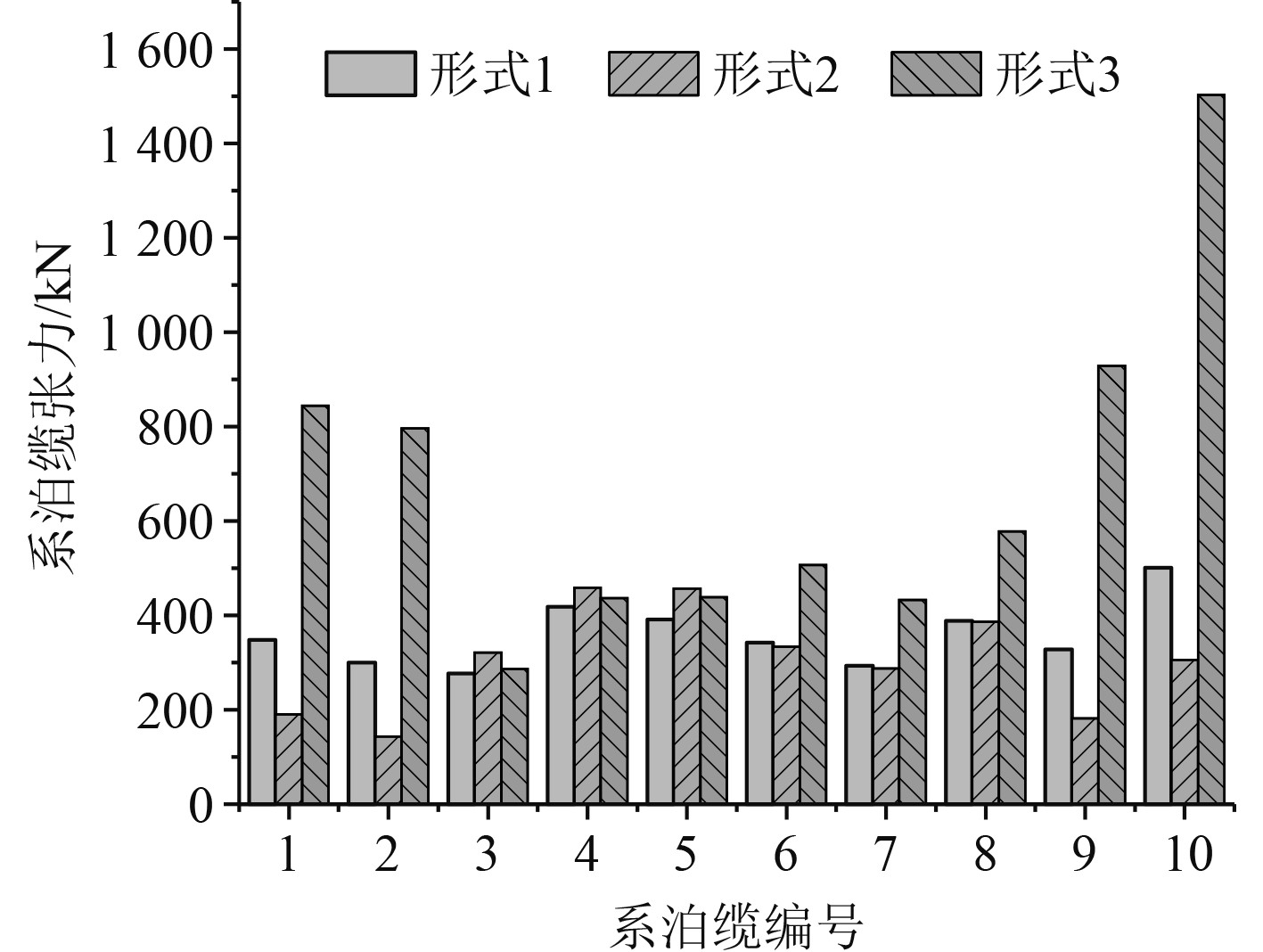
|
图 10 工况4系泊缆最大张力 Fig. 10 Maximum tension diagram of mooring line under condition 4 |
风浪方向为90°是系泊方案中的最危险工况,选取12级台风,极大风速为36.9 m/s,其他环境参数不变,进一步探究方案中最优的首尾缆形式。仿真结果为:形式1不满足破断要求,形式2和形式3满足破断要求。形式2和形式3的船体系泊缆最大张力和六自由度结果如图11所示。

|
图 11 2种形式的运动响应时历曲线 Fig. 11 Time history curves of motion response in two forms |
可知,首尾缆2种系泊形式的垂荡和纵摇相同,形式3纵荡、横荡、横摇和首摇的运动响应幅值均小于形式2,纵荡幅值比形式2小11%,横荡幅值比形式2小70%,横摇幅值比形式2小20%,首摇幅值比形式2小76%。
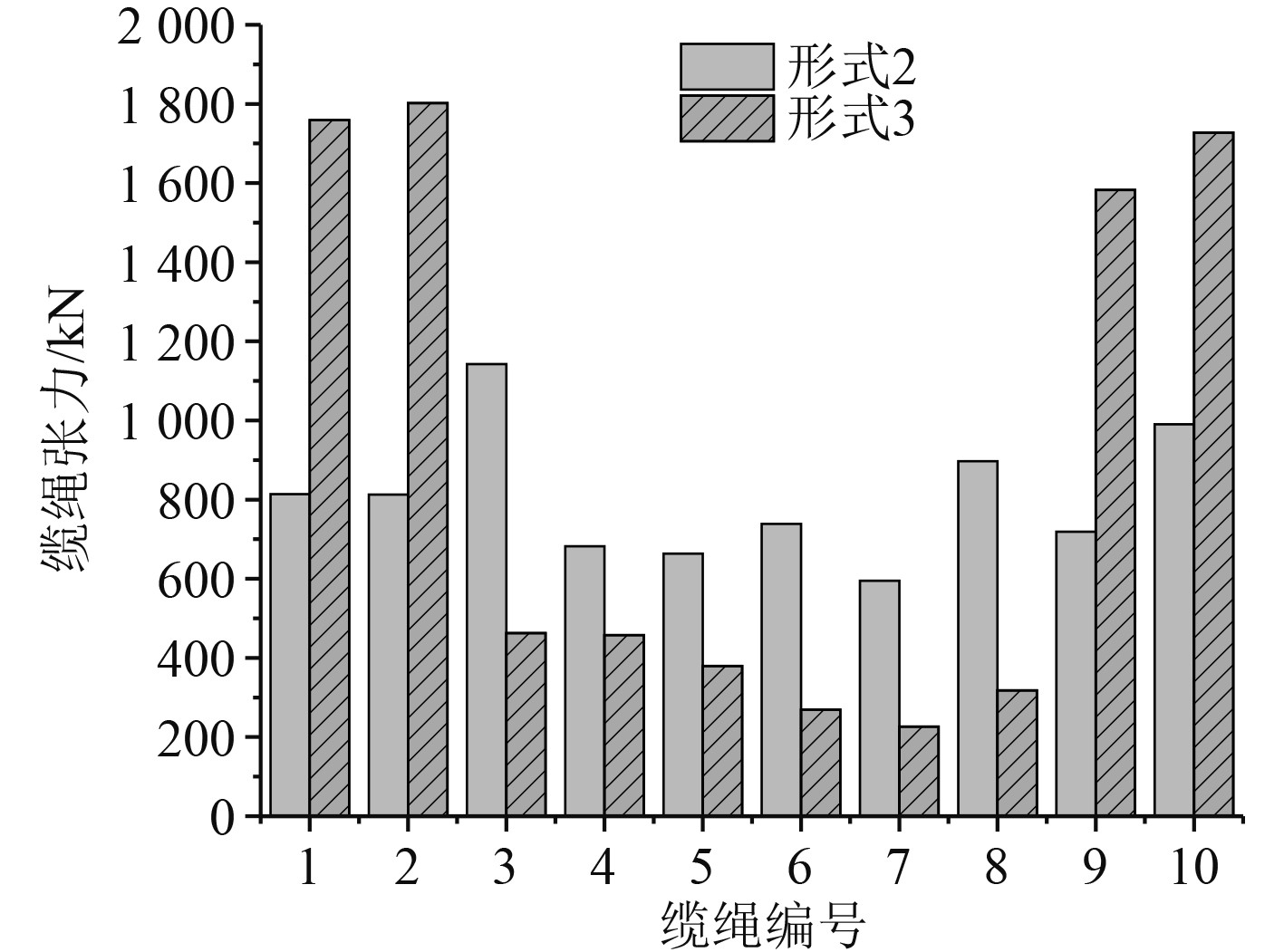
由图12可知,形式3#3~#8系泊缆受力均小于形式2,#1,#2,#9和#10为主要受力缆,对比工况1,#3~#8系泊缆绳总张力增加29%,#1,#2,#9和#10系泊缆绳总张力增加71%。形式2#3系泊缆张力接近破断值,对比工况1,形式2所有系泊缆绳都为主要受力缆,系泊张力均匀变化。可见,首尾缆采用3根高分子缆的系泊形式最优。
|
图 12 系泊缆最大张力 Fig. 12 Maximum mooring line tension |
本文设计一种码头系泊方案,并对首尾缆提出3种系泊形式,在数值模拟中得到了船体在风浪流载荷联合作用及多种工况下的时域响应,并求得了系泊缆张力,进一步对比分析首尾缆3种系泊形式的运动响应和系泊缆张力,得到以下结论:
1)本文设计的码头系泊方案能抵御28 m/s台风,首尾缆材质形式不同对方案的时域响应有显著影响。首尾缆为单根高分子缆形式的时域响应最差;采用单根高分子缆与尼龙绳组合形式的时域响应次之;采用3根高分子缆的形式在风浪流联合作用下的运动响应和系泊缆张力最优,可抵御12级台风。
2)在90°风浪方向下,首尾缆尾接尼龙绳可使系泊系统受力更加均匀,采用3根高分子缆对于降低船体运动响应效果最好,可有效降低船舶横荡和首摇运动,其中横荡运动幅值为0.74 m,比采用尼龙绳组合形式的横荡运动幅值小74%。
3)在斜风浪方向下,系泊方案中首尾缆材质对船体运动响应差异较小。同一系泊形式中,风浪方向的变化对横摇影响最为明显,随着负向角由−30°~−60°,首尾缆采用单根高分子缆的横摇增加了6倍。
| [1] |
刘必劲, 张亦飞, 徐伟. 波浪作用下大型开敞式码头系泊船舶系缆力研究[J]. 中国水运:下半月, 2010, 10(11): 5-7. |
| [2] |
马小剑. 开敞式码头系泊船运动响应及缆绳张力研究[D]. 大连: 大连理工大学, 2012.
|
| [3] |
刘宇. 开敞式油品码头系泊安全及泊位长度优化研究[D]. 大连: 大连理工大学, 2010.
|
| [4] |
郭建廷. 船舶码头系泊形式及水动力性能分析[D]. 镇江: 江苏科技大学, 2016.
|
| [5] |
卫欣, 吴恭兴, 史旦达, 等. 海洋工程船舶码头防台系泊方案设计及计算分析[J]. 船舶标准化工程师, 2017, 50(6): 42-47. DOI:10.14141/j.31-1981.2017.06.008 |
| [6] |
常纪磊, 雷明月. 半开敞水域浮码头防台设计研究[J]. 中国水运:下半月, 2019, 19(8): 168-169. |
| [7] |
卢西伟, 孙昭晨, 张志明, 等. 开敞水域蝶形码头泊位长度优化试验研究[J]. 水运工程, 2009(12): 82-86. DOI:10.3969/j.issn.1002-4972.2009.12.019 |
| [8] |
张炳夫, 钱昆. 系泊浮体在浅水波浪中运动响应的计算研究[J]. 船海工程, 2010, 39(5): 32-35+39. DOI:10.3963/j.issn.1671-7953.2010.05.010 |
| [9] |
LOW Y M, LANGLEY R S. A hybrid time/frequency domain approach for efficient coupled analysis of vessel/mooring/riser dynamics[J]. Ocean Engineering, 2008, 35(5-6): 433-446. DOI:10.1016/j.oceaneng.2008.01.001 |
| [10] |
Oil Companies International Marine Forum (OCIMF). Prediction of Wind and Current Loads on VLCCs, 2nd edition[S]. 1994.
|
| [11] |
王金光, 丁朝蓬, 韩荣贵. 半潜式平台码头系泊系统设计[J]. 船舶工程, 2013, 35(4): 99-102. DOI:10.13788/j.cnki.cbgc.2013.04.013 |
| [12] |
孙伟铭. 舟山港鼠浪湖矿石码头大型船舶组合靠泊研究[D]. 大连: 大连海事大学, 2019.
|
 2023, Vol. 45
2023, Vol. 45
