2. 江苏大学 土木工程与力学学院,江苏 镇江212013
2. Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China
钢夹层板以良好的性能已广泛应用于航空航天、船舶、汽车、桥梁和医疗等领域[1-4]。钢夹层板由于制造简单、重量轻、抗疲劳、耐腐蚀、减振、隔声降噪、成本低等性能,在船舶结构中的应用备受关注[5-6]。美国海军已开展许多研究工作[7-9],解决夹层板的制造、设计和应用等方面的关键技术,为现代化的舰船结构提供技术支持。
学者们研究夹层板的声学特性建立了解析和半解析模型。Moore等[10]开发了具有各向同性和各向异性芯材的夹层结构声传输解析模型。Liu等[11]利用Biot理论描述了声波在多孔弹性材料双层夹层板中通过孔隙弹性介质的传播。Guenfoud等[12]通过修改多层板芯的几何特性控制其传声损失。Errico等[13]利用周期结构理论研究了夹层复合板的振动声学行为。
在分析方法中,一般使用统计能量法、解析法、实验研究和数值计算这4种方法研究夹层板的传声损失[14]。Renji等[15]利用Mindlin的理论,考虑夹层板芯的横向剪切柔度,得到模态密度的解析表达式。统计能量分析(SEA)是预测面板传输损耗(STL)的有效方法。Zhou等[16]基于六阶控制方程给出了计算泡沫填充夹层板模态密度的封闭式表达式,并发现在临界频率区域使用实验值代替解析值,可以更准确地预测传输损耗。Dickow[17]等利用单柱双板结构的有限元模型,研究了板与框架结构之间的不同耦合对直接声传播的影响。考虑了4种不同的耦合配置得出耦合条件是求解双层夹层板板结构声辐射的一个重要参数。王金友[18]利用有限元验证了理论与仿真的吻合,继而研究了聚氨酯蜂窝板的隔声性能及面板厚度、芯层厚度对隔声量的影响。
由于夹层板结构的复杂性,很难求出其隔声量的理论解,数值仿真方法能模拟较复杂过程且可以施加各种方向的荷载,求解速度快、成本低廉等优点被广泛应用于求解复杂的声振响应问题。因此本文在利用LMS Virtual.Lab软件的基础上研究影响V性钢夹层板的隔声因素,通过理论与仿真的对比验证数值模拟的真实性,对设计钢夹层板提供帮助。
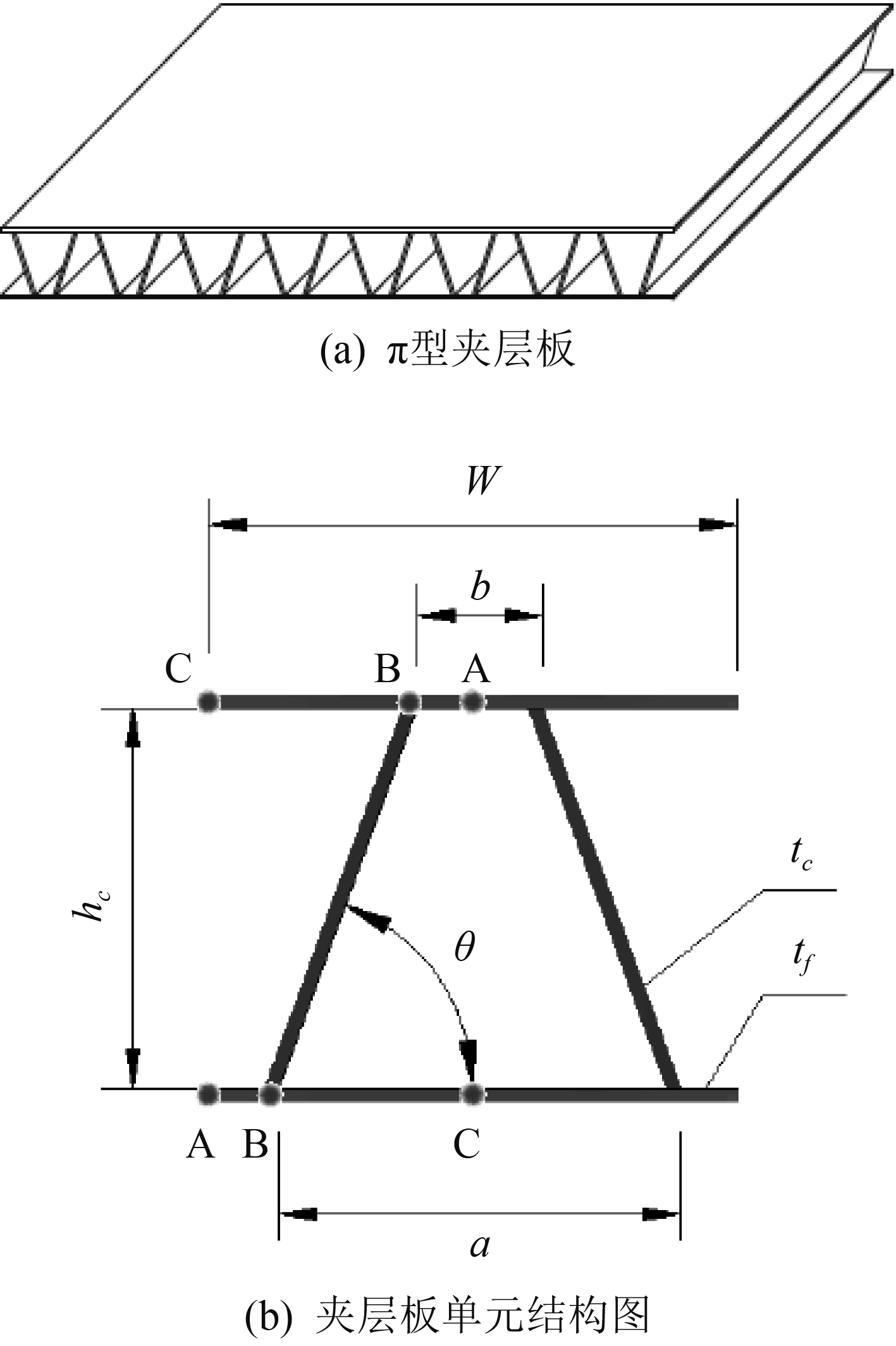
1 结构设计π型夹层板立体图如图1所示。其中夹层板尺寸为1.2 m×1.2 m,上下面板厚度tf =4 mm,单元宽度W=172 mm,夹芯层高度hc=120 mm,夹芯层厚度tc=2.5 mm,夹芯层间距a=132 mm,b=42 mm,夹芯层与面板夹角θ=70o。
|
图 1 夹层板立体图 Fig. 1 Space diagrams of sandwich panel |
基于有限元软件Ansys,建立有限元模型及固支边界条件。其中材料密度ρ=7850 kg/m3,泊松比γ=0.3,弹性模量E=200 GPa。表1为π型夹层板的前6阶固有频率。
|
|
表 1 夹层板的固有频率 Tab.1 Natural frequencies of sandwich panel |
由于折叠式夹层板的近似理论解求解困难,以两端固支钢梁为例,说明模态数值仿真方法的正确性,其模型如图2所示,尺寸为300 mm×10 mm×0.5 mm。

|
图 2 两端固支梁模型 Fig. 2 Model of a beam fixed at both ends |
根据文献[19]的结论,求得两端固支梁的理论固有频率,如表2所示。计算表明,利用有限元数值仿真求得的固有频率和理论计算的固有频率值非常接近,绝对误差和相对误差都比较理想,验证了有限元仿真的正确性。
|
|
表 2 数值仿真与理论计算的固有频率对比 Tab.2 Comparisons of analytical and numerical results on the natural frequencies |
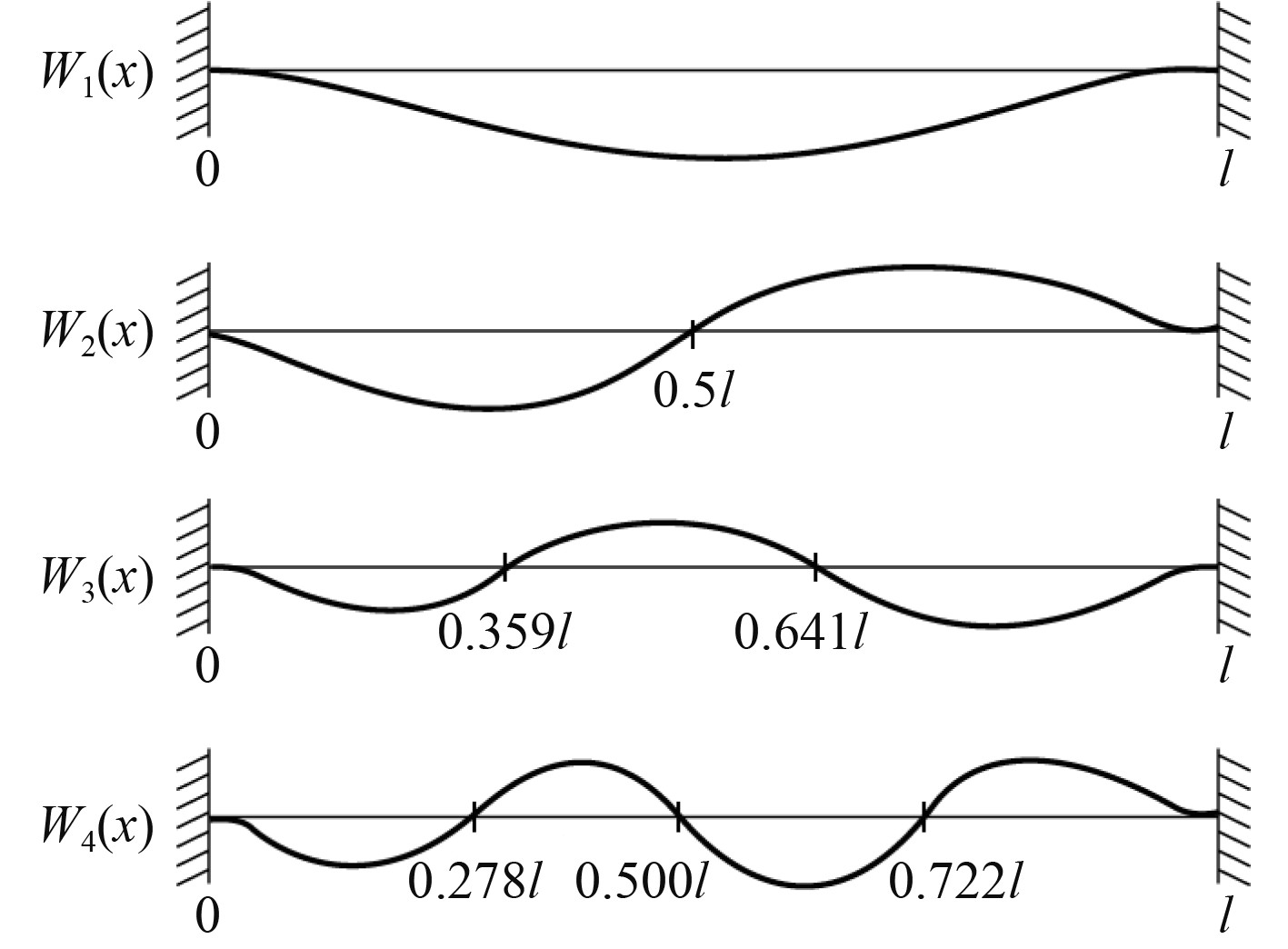
根据Singiresu的连续系统振动[19]理论计算的模态函数如图3所示,有限元仿真计算结果如图4所示。可知,有限元仿真计算的模态函数与理论计算的模态函数比较吻合,进一步证明有限元仿真计算的有效性。
|
图 3 理论计算的模态 Fig. 3 Theoretical mode shapes of a beam fixed at both ends |

|
图 4 数值仿真的模态 Fig. 4 Numerical mode shapes of a beam fixed at both ends |
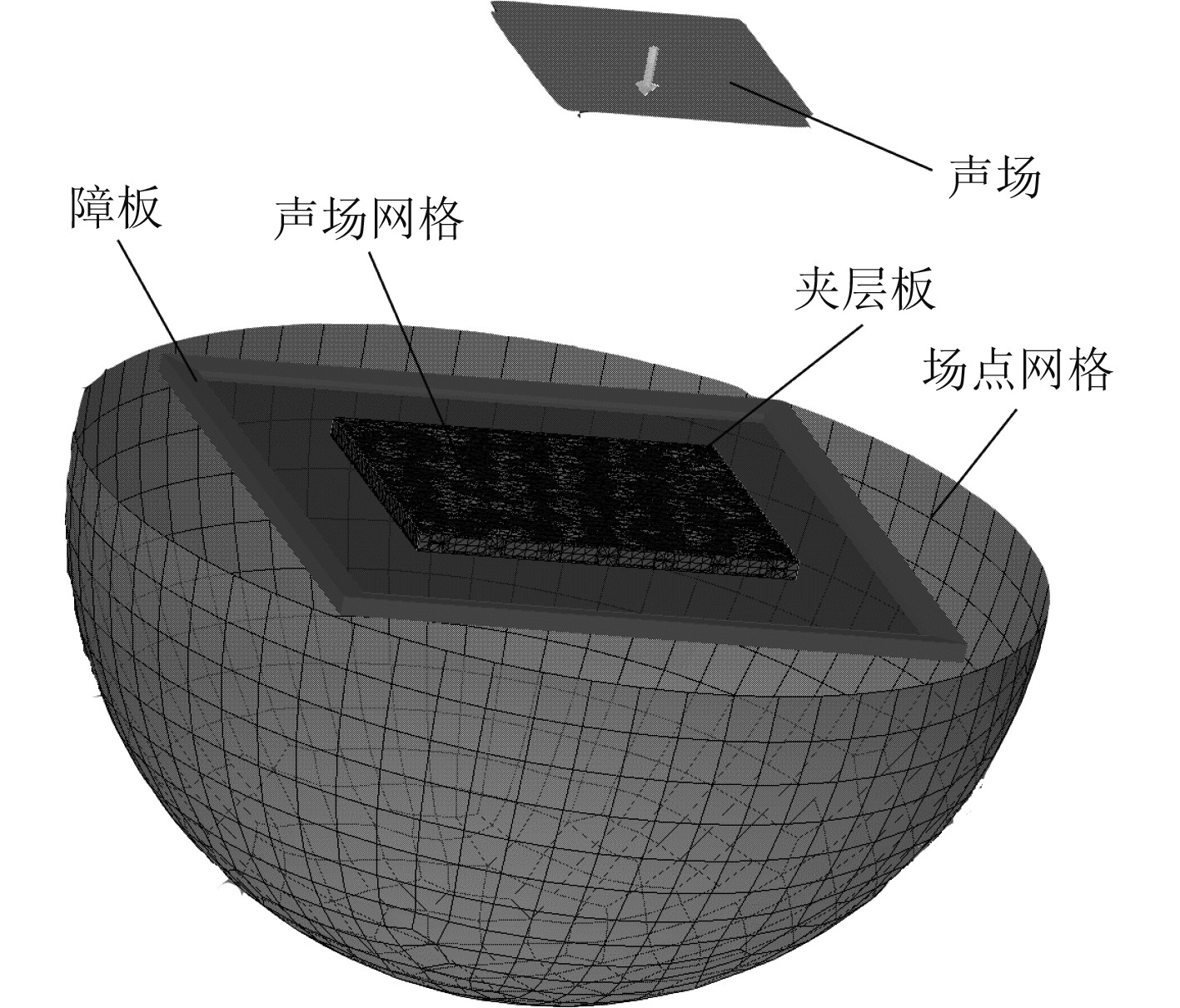
基于声学有限元软件LMS Virtual.Lab Acoustics计算隔声量,在模态分析的基础上计算结构的固有频率,将结果文件导入软件中的Acoustic Harmonic BEM模块进行计算。数值模拟如图5所示。π型钢夹层板结构设置四边固支约束,采用1 Pa的平面波辐射垂直入射到夹层板上面板,隔声量公式定义为:
|
图 5 LMS Virtual.Lab Acoustics声学仿真 Fig. 5 LMS Virtual. Lab Acoustics acoustic simulation |
| $ {\rm{STL}} = 10\lg10 \Bigg(\frac{{{W_i}}}{{{W_t}}}\Bigg)。$ | (1) |
式中:
| $ W = \frac{{{p^2}}}{{2\rho _0^2{c_0}}}S 。$ | (2) |
其中,
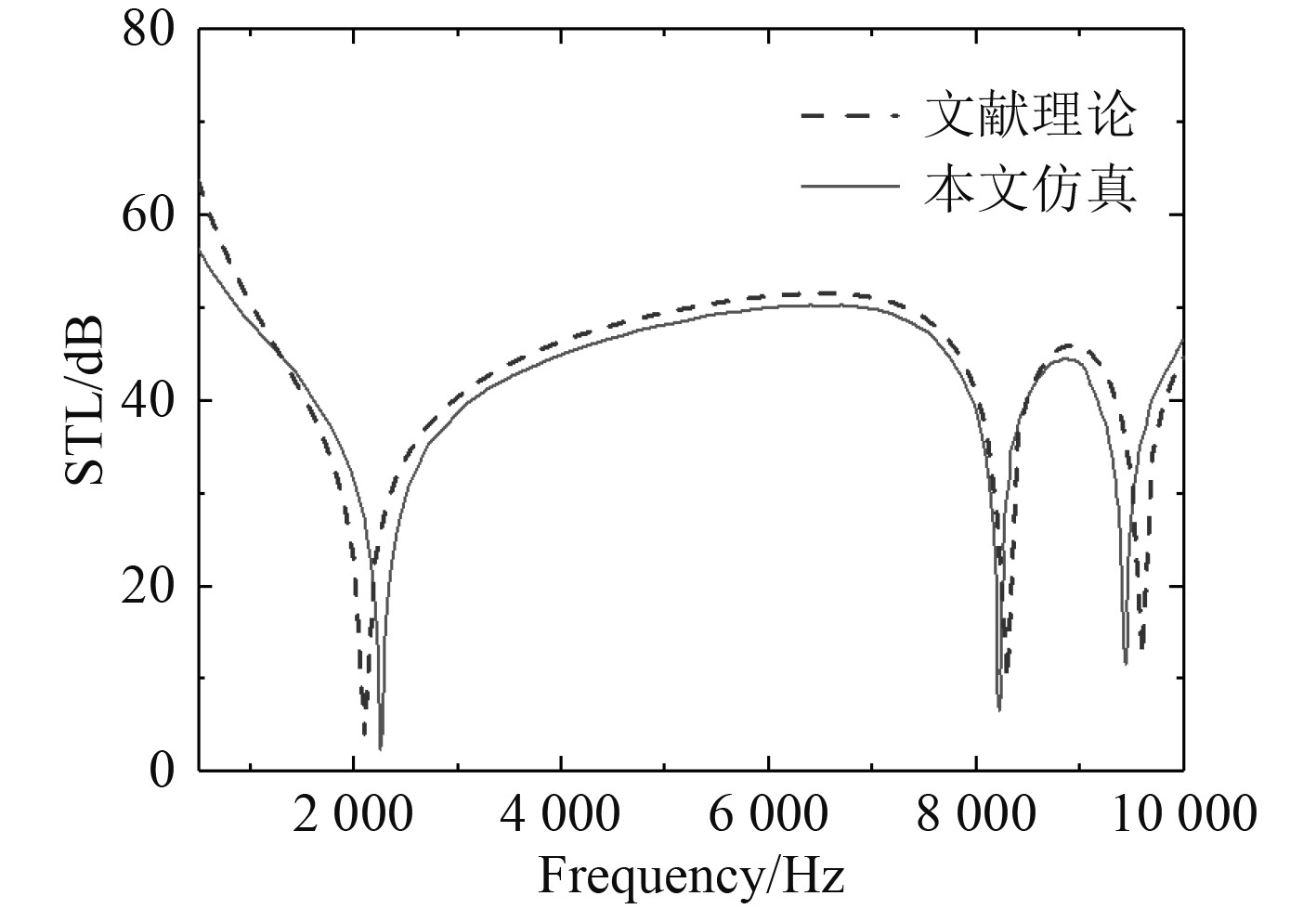
为了验证方法的正确性,根据文献[20]所给结构按照上述方法进行隔声量仿真计算,得到的结果与文献理论值进行比较,如图6所示。可知,本文计算结果与理论值趋势基本一致,可以有效地反映夹层板结构仿真结果的正确性。
|
图 6 理论与仿真计算比较 Fig. 6 Comparison between theory and simulation |
船舶动力机械噪声主要来自主机[21],常用主机为柴油机。其中低速柴油机(转速低于200 r/min)与中速柴油机(转速为300~750 r/min)的噪声频率主要出现在中低频段(0~1000 Hz),且振动性能主要受结构前几阶固有频率影响。
基于以上分析,振动性能讨论前6阶频率范围下的影响,隔声效果在0~800 Hz频率范围内的影响,分析单元结构参数对系统固有频率、幅频响应以及隔声的影响。其中振动部分载荷为谐和激励,激励幅值为1000 N的上面板面内分布力,频率范围为0~800 Hz,扫频步长为5 Hz。
3.1 面板厚度不同上下面板厚度固有频率计算结果如表3所示,幅频响应曲线如图7(a)所示。计算表明,随着面板厚度增加,固有频率有上升趋势,面板厚度越大减振效果越优越。
|
|
表 3 面板厚度对固有频率的影响 Tab.3 Influence of the thickness of face plate on the natural frequencies |
|
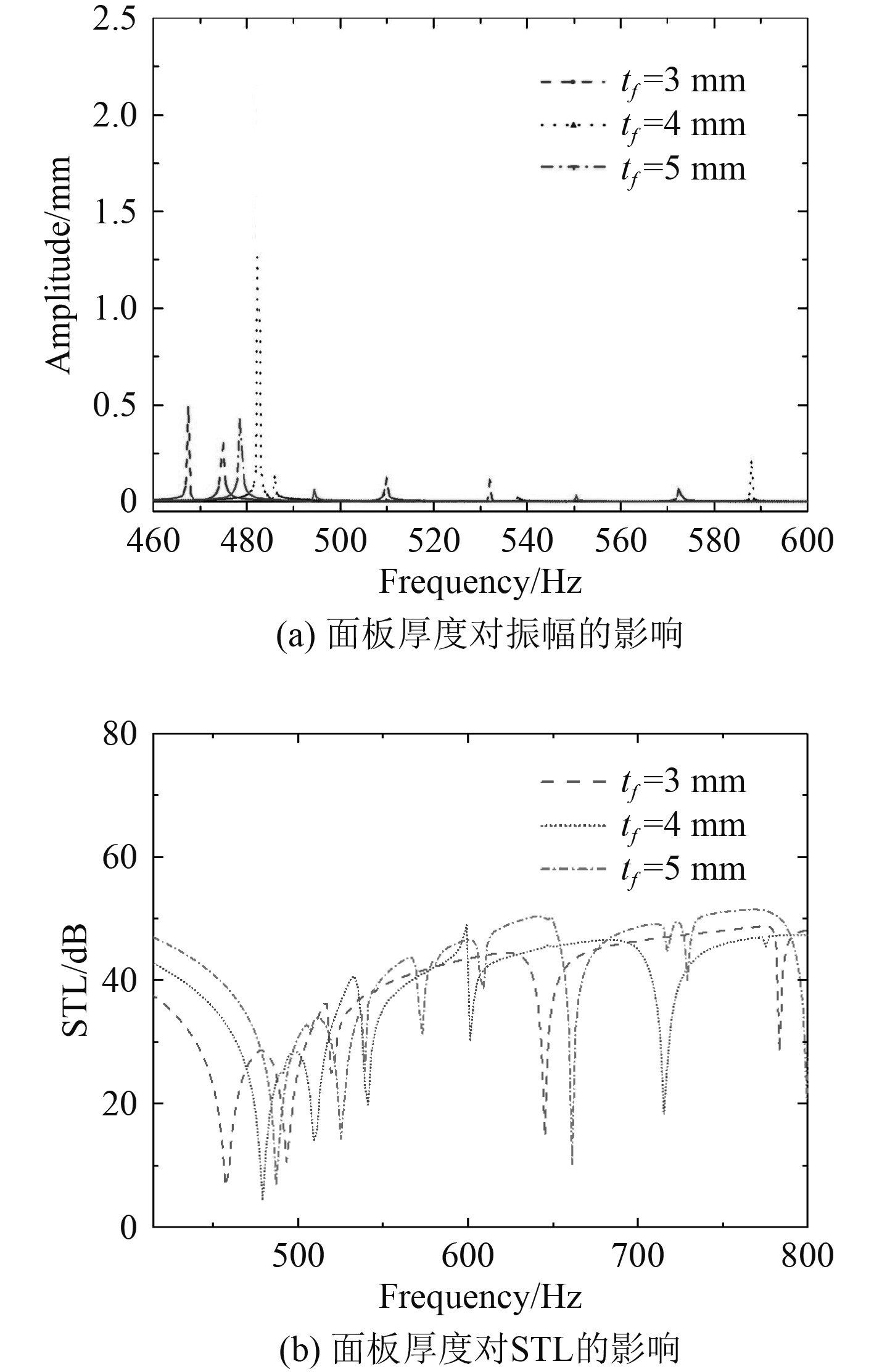
图 7 面板厚度对振幅和STL影响 Fig. 7 Influence of the thickness of face plate on amplitude and STL |
由图7(b)可知,改变面板厚度导致固有频率波动。在整个频率范围内,随着面板厚度的增加,STL值增加。此外,面板厚度的变化导致传输损耗曲线的整体偏移,这是由结构共振引起的。在400~800 Hz范围内的平均隔声量依次为38.55 dB,40.16 dB,41.32 dB,厚度的增加整体上提高了减振和隔声效果。
3.2 夹芯板厚不同夹芯板厚固有频率计算结果如表4所示,幅频响应曲线如图8(a)所示。可知,随着夹芯板厚的增加,前6阶固有频率都相应地依次增加,随着芯层厚度增加减振效果更好。
|
|
表 4 夹芯厚度对固有频率的影响 Tab.4 Influence of the thickness of core plate on the natural frequencies |
|
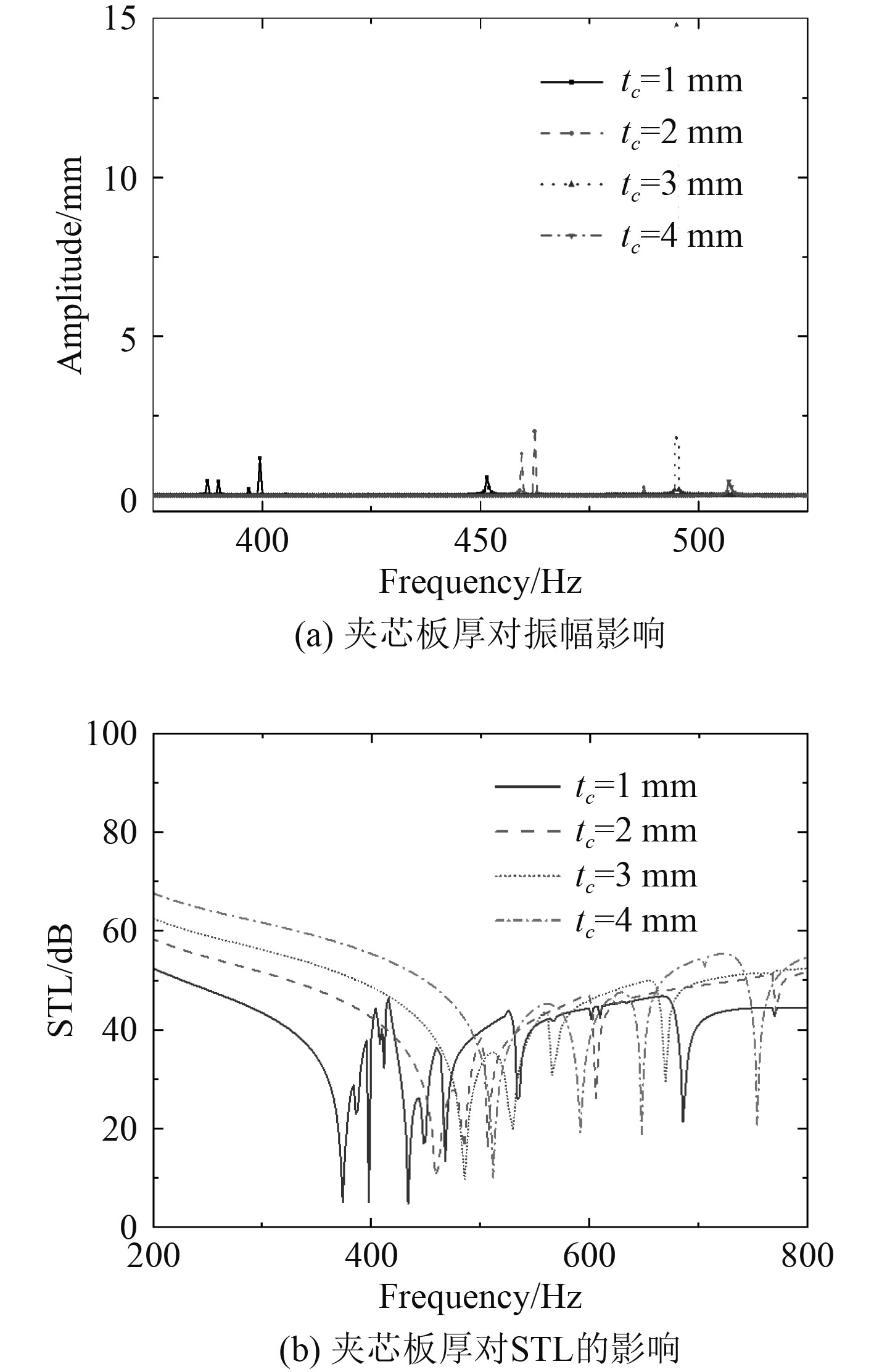
图 8 夹芯板厚对振幅和STL影响 Fig. 8 Influence of the thickness of core plate on the amplitude and STL |
由图8(b)可知,芯层板厚其波谷和波峰向高频移动明显。芯层板厚增加其对应的平均隔声量分别是44.4 dB,49.3 dB,51.1 dB,52.2 dB,仅增加芯层板厚可以增加π型钢夹层板的隔声性能。这是由于芯层板厚的改变增加了π型钢夹层板的夹芯剪切刚度和夹层板的抗弯刚度,从而改变π型钢夹层板的振动特性,提高了π型钢夹层板的隔声性能,且隔声波谷出现在振幅较大处,与图中共振效应相吻合。产生共振时,透射声功率上升,隔声效果下降,可根据实际应用需求对其进行适当调整,以获得最佳的声学性能。随着厚度的增加隔声波谷增多且波谷间距在减小。
3.3 夹芯高度不同夹芯高度固有频率计算结果如表5所示,幅频响应曲线如图9(a)所示。可知,随着夹芯高度的增加,前6阶固有频率依次大幅增加,可见固有频率对夹芯高度非常敏感。此外,在前6阶固有频率范围内,夹芯高度为120 mm时的响应幅值最大,夹芯高度为60 mm时的响应幅值最小,可知夹芯高度在60 mm时的减振性能更优越。
|
|
表 5 夹芯高度对固有频率的影响 Tab.5 Influence of the height of core plate on the natural frequencies |
|
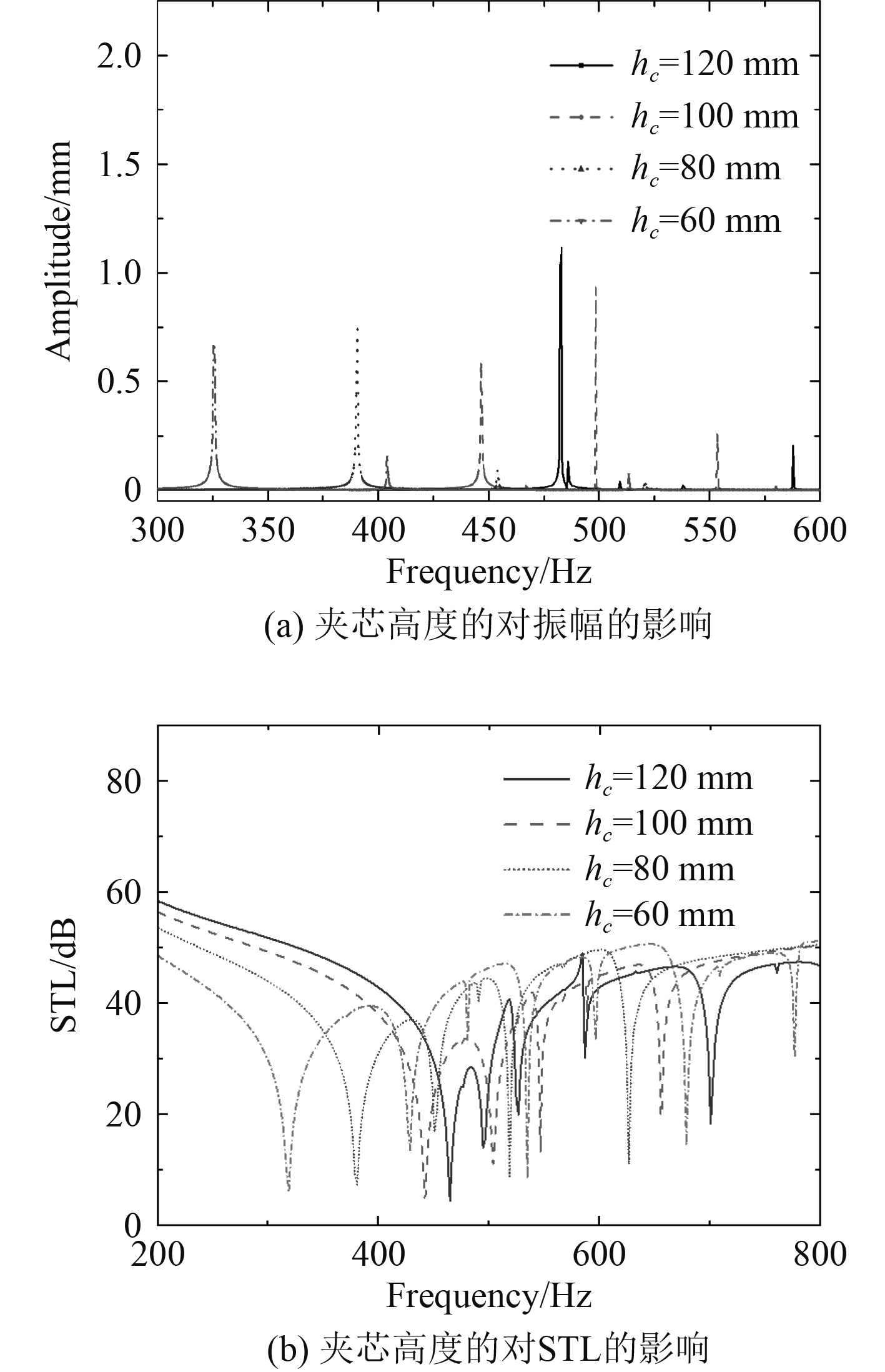
图 9 夹芯高度的对振幅和STL影响 Fig. 9 Influence of the height of core plate on amplitude and STL |
由图9(b)可知,夹层板芯层高度改变导致第一阶共振波谷频率改变,随着夹芯高度的增加每一阶对应的共振波谷和波峰都向高频移动。4种不同夹芯高度的π型钢夹层板平均隔声量分别为40.16 dB,41.12 dB,43.48 dB,43.97 dB,随着夹芯高度递减,结构刚度上升,根据4个阶段[22]隔声特性曲线可知,在低频处先是结构刚度控制,在这一隔声曲线区域结构的隔声性能由结构刚度占主导地位来决定隔声量的大小,结构刚度与隔声量大小成正比。同时共振效应导致夹层板振动明显,出现隔声波谷,隔声曲线与幅频响应曲线有较好的契合。在设计时可以针对性考虑芯层高度影响,达到较好的效果。
3.4 夹芯与面板夹角不同夹芯与面板夹角固有频率计算结果如表6所示,幅频响应曲线如图10(a)所示。可知,随着夹芯与面板夹角的增加,一阶、四阶、五阶和六阶固有频率增加,二阶和三阶固有频率略有波动。此外,夹芯与面板夹角为70°和80°时的响应幅值最大,且非常接近,夹角为60°时的响应幅值最小。
|
|
表 6 夹芯与面板夹角对固有频率的影响 Tab.6 Influence of the angle on the natural frequencies |
|
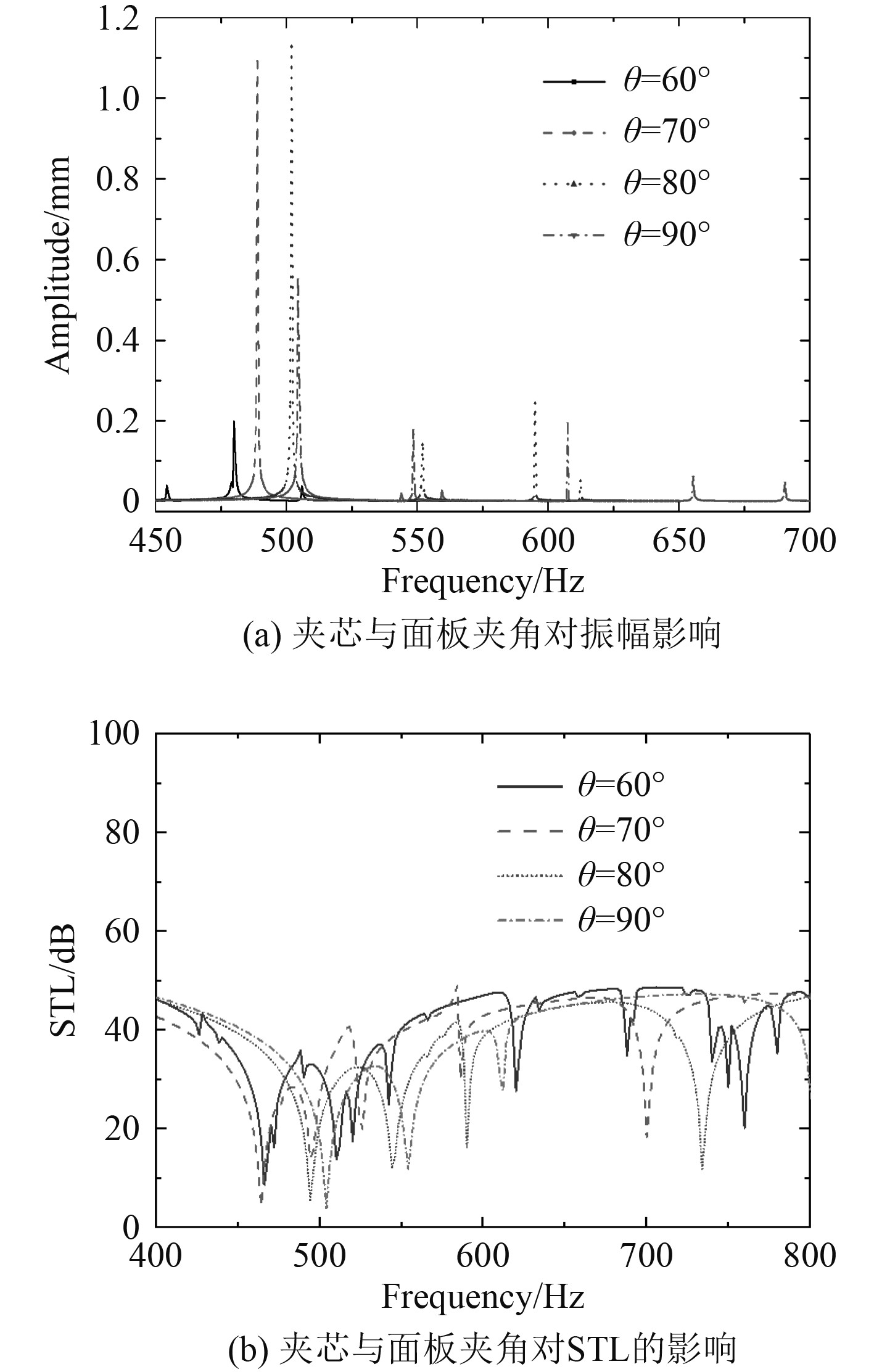
图 10 夹芯与面板夹角对振幅和STL影响 Fig. 10 Influence of angle between sandwich and panel on amplitude and STL |
为了量化波形铁芯倾角对声传输的影响,绘制了所选倾角STL与频率的预测曲线,如图10(b)所示。波纹芯的倾角直接关系到其刚度,对夹层结构的隔声性能影响很大。随着倾角的增大,核心层刚度增大,由结构共振引起的第一隔声波谷向更高的频率移动。与之相对应的是,夹角越大的夹层在高频范围的隔声性能越差,但在低频范围的隔声性能略好。4种不同夹芯与面板夹角夹层板平均隔声量分别为42.45 dB,40.16 dB,39.42 dB,41.3 dB。结合幅频响应曲线可知,在前6阶固有频率下,60°振幅最小,能量传递最少,隔声和减振效果较优。
4 结 语本文利用有限元软件,基于等质量控制条件研究船用π型钢夹层板隔声性能,分析了夹层板结构参数对固有频率和隔声性能的影响,得出以下结论:
1)随着面板厚度、夹芯厚度、夹芯高度、夹芯与面板夹角的增大,固有频率呈上升趋势。
2)结构的减振效应与隔声有较好的契合,在共振处出现振动峰值和隔声波谷,减振效果越好,同时隔声效果越优。
3)在0~800 Hz范围内增加上下面板厚度和夹芯厚度对减振隔声性能的提升有较好效果;夹芯高度和面板夹角在给定频率范围内较小时有利于振动和整体隔声效果。
| [1] |
KUJALA P, KLANAC A. Steel sandwich panels in marine applications[J]. Brodogradnja, 2005, 56(4): 305-314. |
| [2] |
MOURITZ A P, GELLERT E, BURCHILL P, et al. Review of advanced composite structures for naval ships and submarines[J]. Composite Structures, 2001, 53: 21-41. DOI:10.1016/S0263-8223(00)00175-6 |
| [3] |
俞程亮, 赵洪伦, 蒋伟明. 夹层板结构的特性及其在轨道车辆中的应用[J]. 铁道车辆, 2005, 43(10): 29-31. DOI:10.3969/j.issn.1002-7602.2005.10.007 |
| [4] |
杜善义. 先进复合材料与航空航天[J]. 复合材料学报, 2007, 24(1): 1-12. DOI:10.3321/j.issn:1000-3851.2007.01.001 |
| [5] |
王自力, 张延昌. 基于夹层板的单壳船体结构耐撞性设计[J]. 中国造船, 2008, 49(1): 60-65. DOI:10.3969/j.issn.1000-4882.2008.01.009 |
| [6] |
卢天健, 刘涛, 邓子辰. 多孔金属材料多功能化设计的若干进展[J]. 力学与实践, 2008, 30(1): 1-9. |
| [7] |
RAJAPAKSE Y D H. Marine composites and sandwich structures[J]. Composites Part B Engineering, 2008, 39(1): 1-4. DOI:10.1016/j.compositesb.2007.02.003 |
| [8] |
WADLEY H, DHARMASENA K, CHEN Yungchia, et al. Compressive response of multilayered pyramidal lattices during underwater shock loading[J]. International Journal of Impact Engineering, 2008, 35: 1102-1114. DOI:10.1016/j.ijimpeng.2007.06.009 |
| [9] |
XUE ZHENYU, HUTCHINSON J W. A comparative study of impulse-resistant metal sandwich panels[J]. International Journal of Impact Engineering, 2004, 30: 1283-1305. DOI:10.1016/j.ijimpeng.2003.08.007 |
| [10] |
MOORE JA. Sound transmission loss characteristics of sandwich panel constructions[J]. Journal of the Acoustical Society of America, 1991, 89(2): 777-791. DOI:10.1121/1.1894638 |
| [11] |
LIU Y, DAUDIN C. Analytical modelling of sound transmission through finite clamped double-wall sandwich panels lined with poroelastic materials[J]. Composite Structures, 2017, 172(JT.): 359-373. |
| [12] |
GUENFOUD N, DROZ C, ICHCHOU MN, et al. On the multi- scale vibroacoustic behavior of multi-layer rectangular core topology systems[J]. Mech Syst Sig Process, 2020, 143: 106629.
|
| [13] |
ERRICO F , ICHCHOU M , ROSA S D , et al. Investigations about periodic design for broadband increased sound transmission loss of sandwich panels using 3D-printed models[J]. Mechanical Systems and Signal Processing, 2019, 136(6).
|
| [14] |
王盛春. 蜂窝夹层结构复合材料的声振特性研究[D]. 重庆: 重庆大学, 2011.
|
| [15] |
RENI K, NAIR PS, NARAYANAN S. Modal density of composite honeycomb panels[J]. Journal of Sound and Vibration, 1996, 195: 687−99.
|
| [16] |
ZHOU R, CROCKER MJ. Sound transmission loss of foam-filled honeycomb sandwich panels using statistical energy analysis and theoretical and measured dynamic properties[J]. Journal of Sound and Vibration, 2010, 329(6): 673−86.
|
| [17] |
DICKOW K A , DOMADIYA P G , ANDERSEN L , et al. A parameter study of coupling properties in finite element models of single-stud double-plate panels[C]// INTER-NOISE and NOISE-CON Congress and Conference Proceedings. 2011.
|
| [18] |
王金友. 船用聚氨酯蜂窝板的隔声特性研究[D]. 镇江: 江苏科技大学, 2020.
|
| [19] |
RAO S S. Vibration of continuous systems[M]. John Wiley and Sons, New Jersey, 2007.
|
| [20] |
任树伟, 辛锋先, 卢天健. 蜂窝层芯夹层板结构振动与传声特性研究[J]. 力学学报, 2013, 45(3): 349-358. DOI:10.6052/0459-1879-12-280 |
| [21] |
武国启, 林劲. 船舶舱室空气噪声激励引起水下辐射噪声传递特性试验研究[J]. 振动与冲击, 2020, 39(21): 42-46,78. DOI:10.13465/j.cnki.jvs.2020.21.006 |
| [22] |
王笃勇. 板结构隔声性能数值仿真与实验验证[D]. 哈尔滨: 哈尔滨工程大学, 2012.
|
 2023, Vol. 45
2023, Vol. 45
