2. 武汉第二船舶设计研究所,湖北 武汉430064
2. Wuhan Second Ship Design and Research Institute, Wuhan 430064, China
板类结构广泛应用于汽车、船舶、航天和土木等诸多民用和军用领域,因此对其振动特性和结构振动噪声抑制方法的研究备受海内外专家学者的关注。随着减振降噪技术的发展,目前对板类结构振动噪声的抑制有以下常用方案:增加板厚、贴覆阻尼层、安装吸振器、优化结构形式和使用复合材料等[1]。夹层板也是近些年来板类结构的研究重点之一,它是由2层面板和中间夹芯共同组成的复合材料结构。其中聚氨酯弹性体钢夹层板[2]是一种新型夹层结构,使用钢板作为面板,聚氨酯弹性体作为中间夹芯。聚氨酯弹性体具有材料属性可调节的性质,材料的杨氏模量、密度和阻尼系数均可以根据要求在一定范围内进行调整,同时具有良好的减振吸能性能,在减振降噪领域有广阔的应用前景,所以有必要对聚氨酯弹性体钢夹层板等复合材料结构的振动特性进行研究。
20世纪以来,学者们已经对复合材料结构的力学和声振特性进行了大量研究。针对夹层板结构的早期研究主要有Reissner理论、Hoff理论和普鲁沙柯夫-杜庆华理论[3],后续又发展建立出无限大正交异性夹层板的振动控制方程[4]和有限大双层隔板结构的理论模型[5]等。薛启超[6]基于经典夹层板的弯曲理论,提出了一种隔板加筋夹层复合结构的等效计算方法。仝博等[7]通过试验手段,研究了以聚氨酯作为夹芯的复合材料圆柱壳的水下声振性能,结果表明该复合材料结构具有良好的减振效果。任树伟等[8-10]研究了其他不同形式复合材料结构在隔声减振、振动传声和抗爆炸等方面的特性。
本文以双层加筋板为研究对象。双层加筋板在填充聚氨酯作为芯材之后,可以近似成聚氨酯弹性体钢夹层板的改进形式。通过振动试验研究填充芯材前后该结构的模态和均方振速,进而评估该复合结构的减振性能。同时辅以有限元仿真,与试验结果进行对比,在验证仿真计算结果的准确性后,还通过有限元方法研究了芯材阻尼系数的变化对该复合结构振动特性影响的规律。
1 试验模型 1.1 几何模型首先制作2个双层加筋板(见图1),模型主体由双层方形面板和25根单向C形加筋组成,为了模拟实际工作中的约束条件,又在主体的下方设置了一周工字钢。方形面板边长L1=690 mm,厚度t1=3 mm,2层面板间距h1=20 mm;C形加筋长度L1=690 mm,厚度t2=2 mm,高度h2=20 mm,翼板宽度W=10 mm。选取其中一个加筋板模型,在其层间填充芯材,构成复合材料结构对比模型。为了减少试验误差的影响因素,采用浇筑的方式来填充聚氨酯,保证芯材能与结构紧密贴合。图2为2个模型部分截面的示意图。

|
图 1 双层加筋板模型 Fig. 1 The model of double-layer stiffened plate |

|
图 2 双层加筋板截面示意图 Fig. 2 The section of double-layer stiffened plate |
模型的面板和C形加筋使用不锈钢材料,芯材为聚氨酯弹性体材料,工字钢为普通钢材。各项材料参数如表1所示。
|
|
表 1 材料参数 Tab.1 Material parameters |
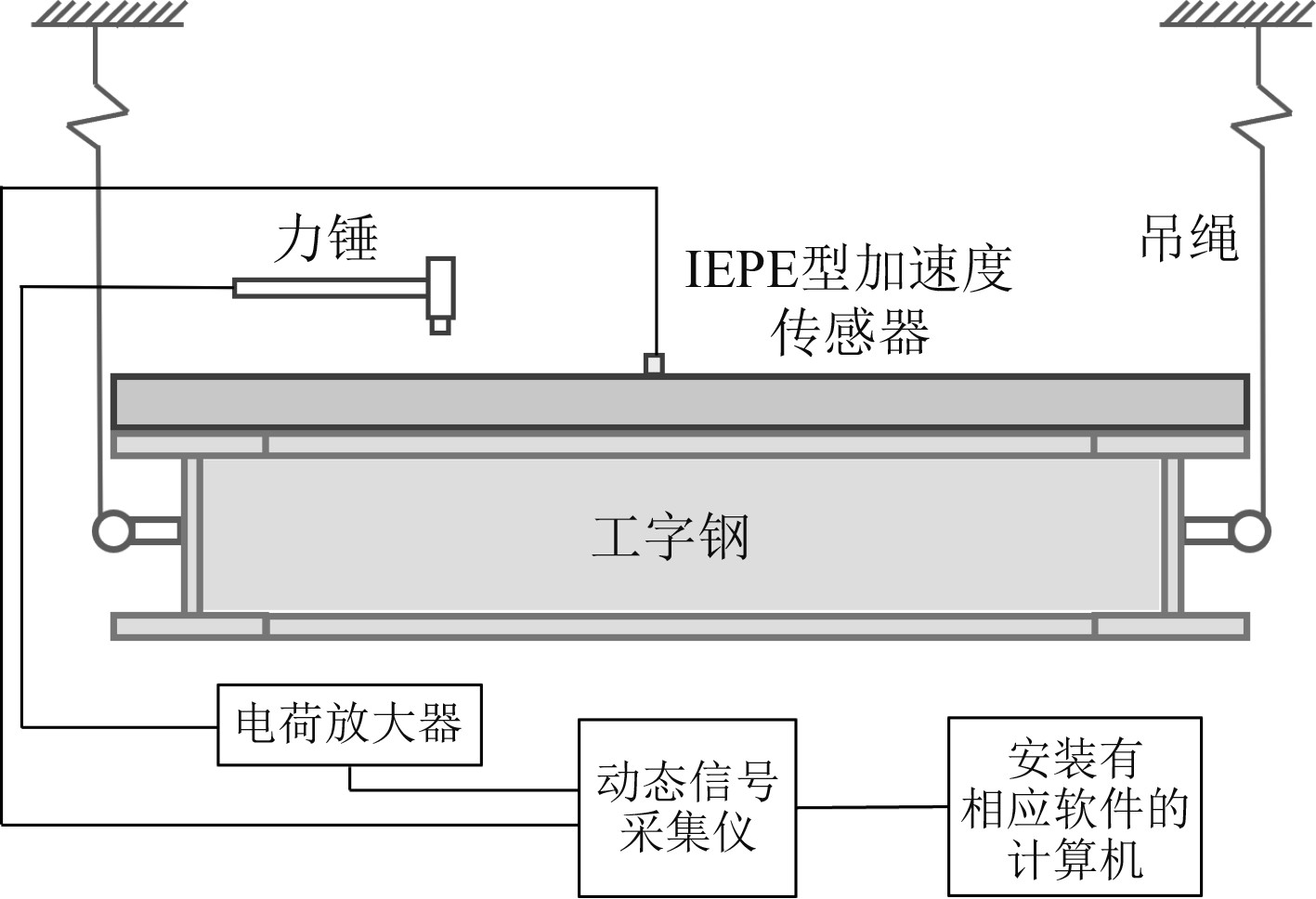
试验在空气中进行,主要针对试验对象的模态和表面均方振速进行研究。考虑到试验环境、试验对象等因素,主要采用锤击法,以多点激励单点测量的方式进行试验。该方法采用力锤施加激励,操作便捷,且需要的传感器数量不多,适合于中小型结构的模态试验。根据模型在测试中的实际情况,将采样频率设置为5.12 kHz,采样时长设置为1.6 s。为了减少试验结果的误差,需要合理布置激励点和测点的位置,选择能反映系统最多固有频率成分的点作为激励点或测点,并且尽可能在面板上均匀密布激励点。激励点和测点布置如图3所示。在模型上层面板上的横纵方向分别布置13行激励点,共计169个激励点(图3中直线交点处),试验中使用力锤依次在激励点处输入脉冲激励;在模型上下2层面板外表面分别布置4个测点,共计8个测点(图3中圆点及箭头标记处),并在测点处安装加速度传感器。为了模拟该模型的自由边界条件,使用吊绳将模型悬挂在空气中。由于模型尺寸较大,吊绳较长,模型刚体运动频率较低,对试验测试内容的影响较小。试验装置如图4所示。

|
图 3 激励点和测点布置图 Fig. 3 The distribute of motivation point and measuring point |
|
图 4 试验装置示意图 Fig. 4 The diagram of experimental apparatus |
使用相关测试软件识别出试验对象的前4阶模态,并与有限元仿真结果进行对比分析,结果如图5、表2和表3所示。由图5可知,相较于普通双层板,填芯双层板固有频率的试验结果平均低6.9%、仿真结果平均低5.6%,而振型未发生明显变化。由表2和表3可知,两类加筋板通过试验和仿真获取的固有频率非常接近,最大误差为–4.9%,说明了有限元方法的准确性。

|
图 5 模态振型对比图 Fig. 5 Vibration modes contrast |
|
|
表 2 普通双层加筋板固有频率 Tab.2 The natural frequency of double-layer stiffened plate |
|
|
表 3 填充芯材的双层加筋板固有频率 Tab.3 The natural frequency of double-layer stiffened plate filled with core material |
根据互易性原理,可以对每个测点的传感器采集数据进行归一化频谱分析,进而获取模型面板表面的均方振速及其总级。均方振速和均方振速级计算公式如下[11]:
| $ {v^2} = \frac{1}{S}{\iint\limits_S {\left| V \right|}^2}{\rm{d}}s,$ | (1) |
| $ l = 10{\log _{10}}\left( {{{{v^2}} \mathord{\left/ {\vphantom {{{v^2}} {v_0^2}}} \right. } {v_0^2}}} \right)。$ | (2) |
式中:
根据生产厂家提供的资料,该聚氨酯材料的阻尼系数在低频段内随频率变化较为剧烈,在200 Hz以后稳定在0.8左右,因此在计算振速的总级时只选取200 Hz频段以后的数据。均方振速总级通过能量叠加的方式计算:
| $ L = 10{\log _{10}}\sum\limits_{i = 200}^n {{{10}^{\left( {{{{l_i}} \mathord{\left/ {\vphantom {{{l_i}} {10}}} \right. } {10}}} \right)}}} 。$ | (3) |
式中:
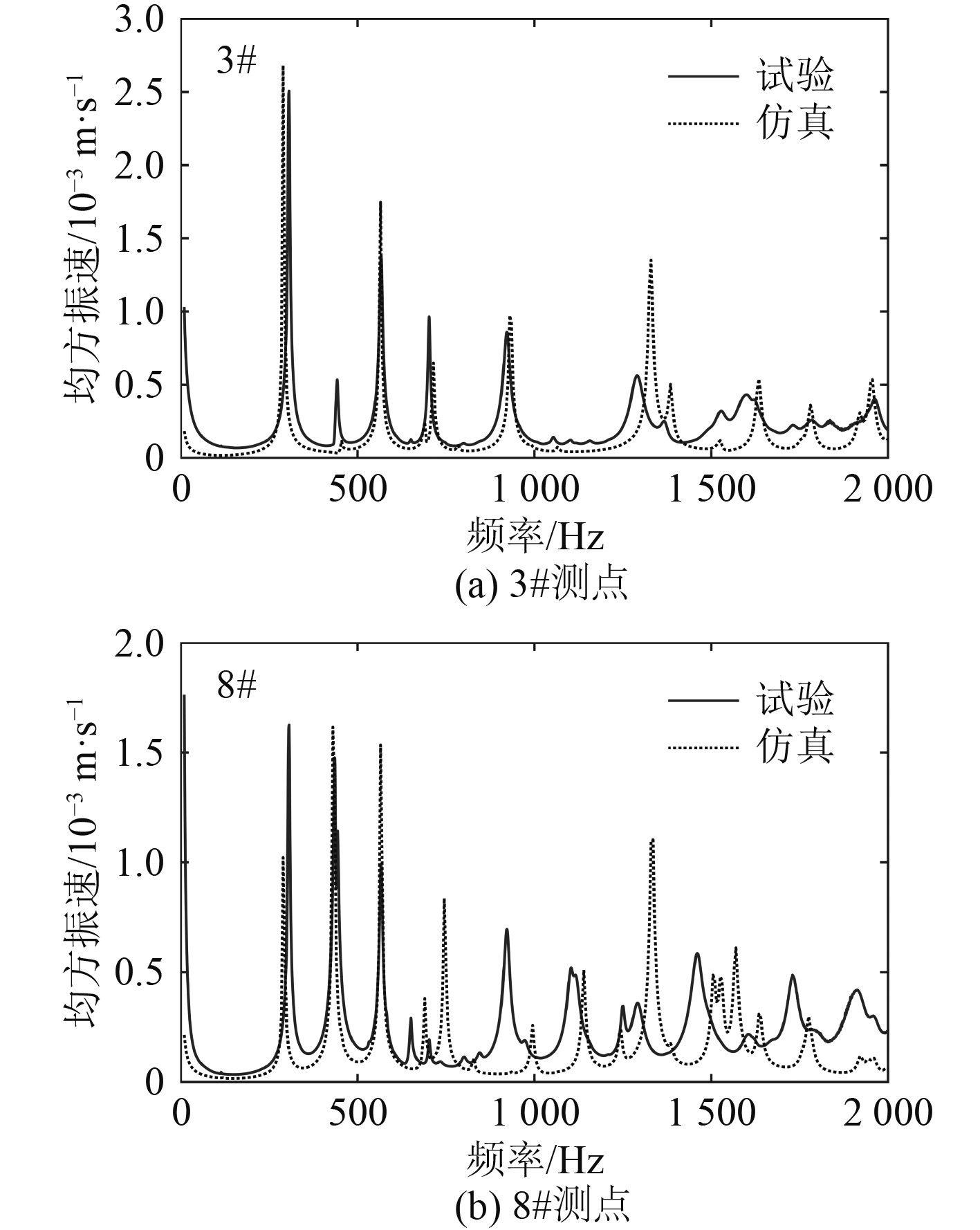
同时采用有限元方法计算均方振速,并与试验结果进行对比分析。以3#测点和8#测点为例,对比结果如图6和图7所示。
|
图 6 普通双层加筋板均方振速曲线 Fig. 6 Mean square vibration velocity curves of double-layer stiffened plate |

|
图 7 填充芯材的双层加筋板均方振速曲线 Fig. 7 Mean square vibration velocity curves of double-layer stiffened plate with core material |
由图6可知,对于普通双层加筋板,试验和仿真获取的均方振速曲线在幅值和总体走势上一致性较高,且1000 Hz以下吻合程度更好。由图7可知,在填充聚氨酯后,双层加筋板均方振速曲线的幅值有较大程度的下降,最大峰值约为3×104 m/s。从试验和仿真对比验证的角度看,两者均方振速曲线幅值大致接近,曲线变化趋势较为吻合。总体来说,有限元方法对两类加筋板的计算结果是准确的。
对两类加筋板均方振速总级进行对比分析,可以从整体上反映填充芯材对双层加筋板结构的减振效果,结果如表4所示。可知,填充聚氨酯芯材之后,试验结果平均减振11.73 dB,仿真结果平均减振10.89 dB,说明该复合材料结构具有良好的减振效果。
|
|
表 4 总级对比表 Tab.4 The contrast of overall |
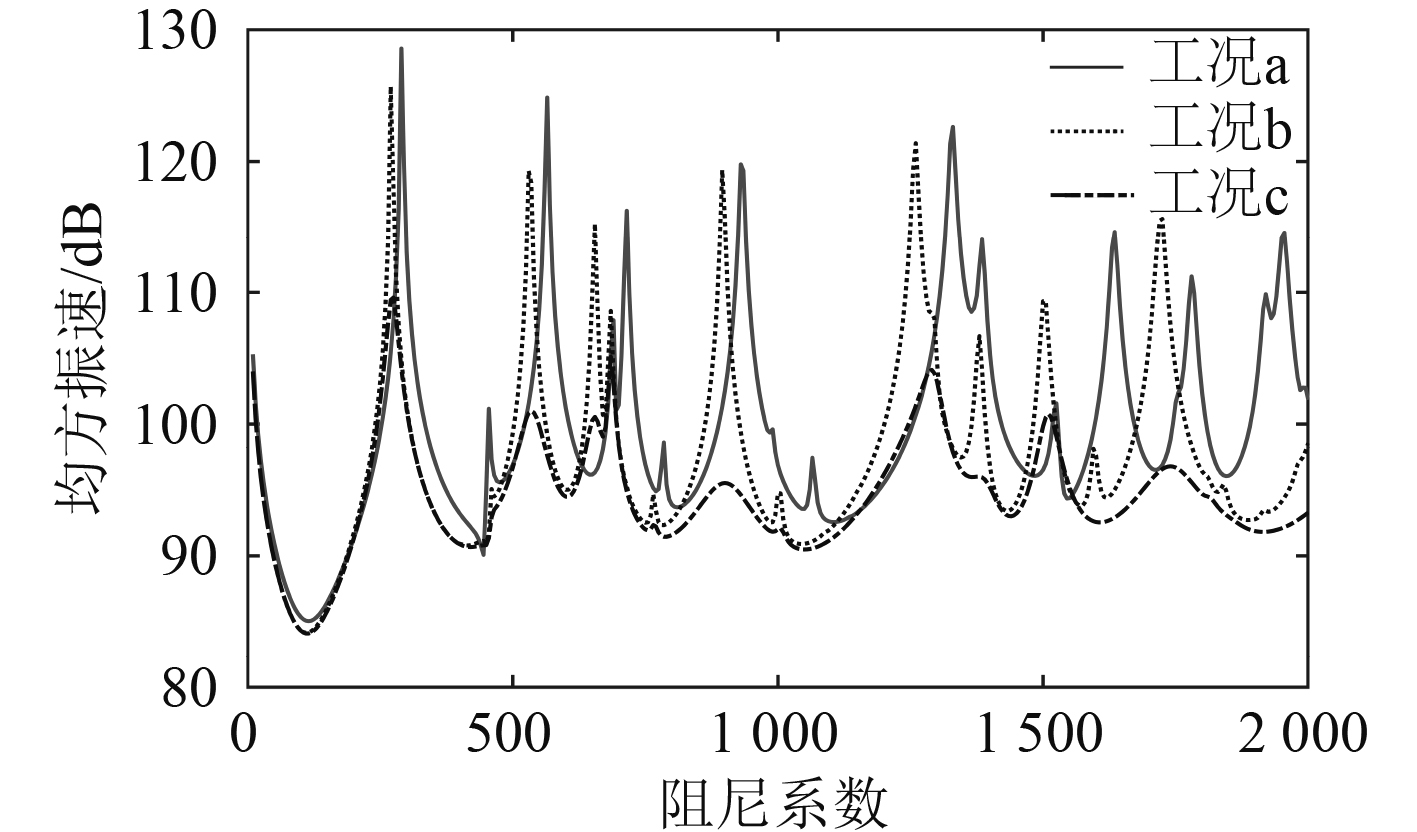
在填充聚氨酯芯材之后,双层加筋板受到芯材的附加刚度、附加质量和高阻尼特性的共同影响,实现了优异的减振效果。为了针对性地分析其影响因素,可以更换具有不同材料属性的芯材,研究双层加筋板在不同工况下的振动特性。由于难以在实际中控制聚氨酯材料属性的单一变化,在前文已经验证有限元方法足够准确的情况下,采取仿真计算的方法进行研究。图8为在3种不同工况下仿真计算出的均方振速级曲线。工况a代表未填充芯材,与普通双层加筋板相同;工况b代表填充了芯材,材料的杨氏模量、密度和泊松比均与表1中的聚氨酯相同,但是其阻尼系数设置为0;工况c代表填充芯材各项材料属性(包括阻尼系数)与上述的聚氨酯完全相同。对比研究工况a和工况b,可以单独研究芯材的附加刚度、附加质量对结构振动特性的影响。分析图8可知,填充芯材的附加刚度和附加质量对双层加筋板有一定影响,主要作用是降低该结构的固有频率,同时也在一定程度上起到了削弱峰值高度的作用。对比研究工况b和工况c,可以单独研究芯材的阻尼系数对结构振动特性的影响。分析图8可知,芯材的高阻尼特性在该复合材料结构的减振中起主要作用。
|
图 8 不同工况下均方振速级对比图 Fig. 8 Comparison chart of mean square vibration velocity under different conditions |
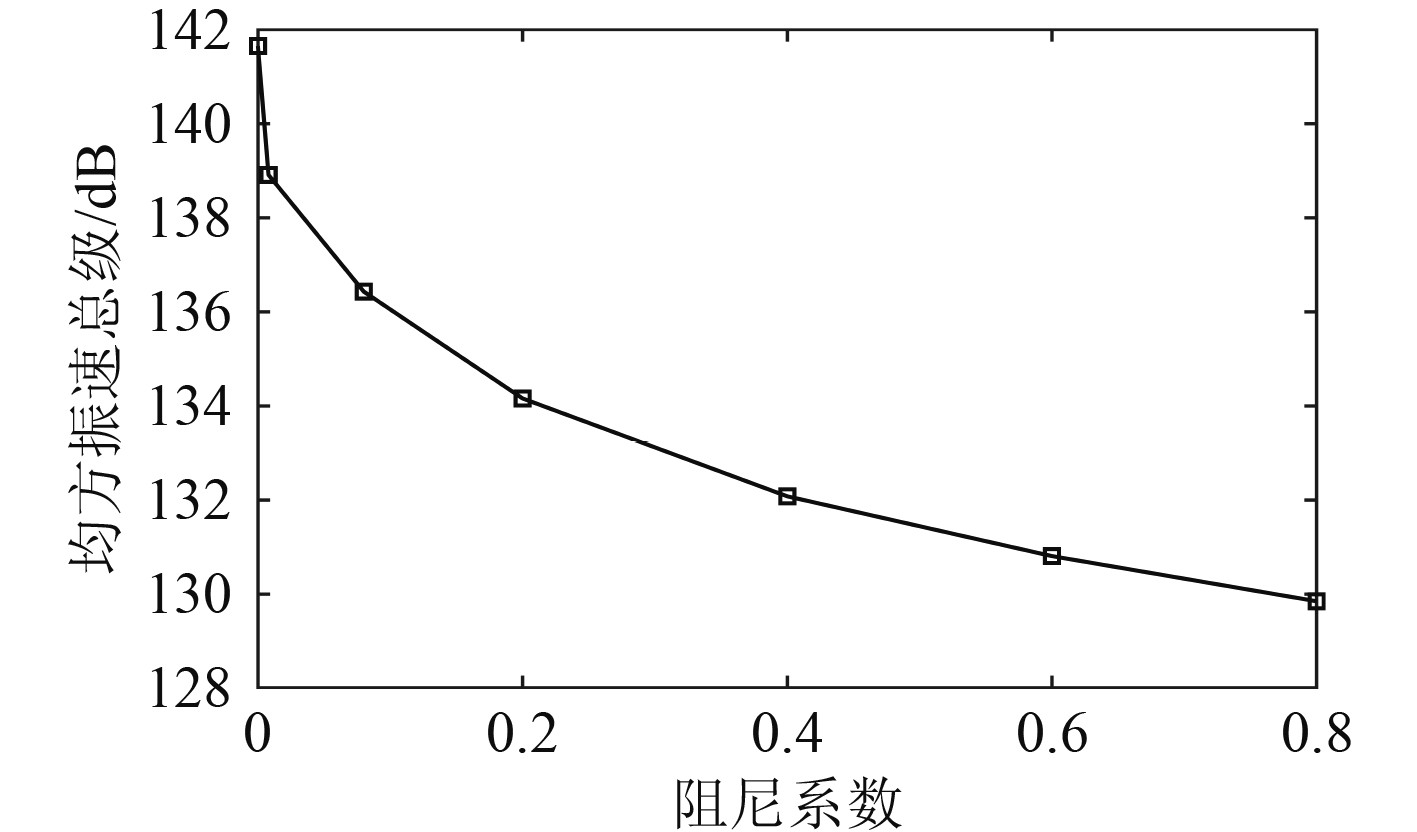
为了更加深入地探究芯材阻尼特性的变化对该复合材料结构振动特性的影响规律,采取有限元仿真的方法,改变芯材的阻尼系数,并保持其他材料属性不变,计算不同工况下的均方振速总级。总级变化如图9所示,随着芯材阻尼系数增大,总级不断降低,同时总级降低的趋势有所减缓。
|
图 9 不同工况下总级变化图 Fig. 9 Diagram of change in overall level under different conditions |
本文制作2个双层加筋板模型,其中一个模型填充了聚氨酯芯材。对模型进行振动试验,对照研究填充芯材前后该结构振动特性的变化,并与有限元方法进行对比分析。在验证有限元方法的准确性后,通过仿真手段研究了对该结构振动特性影响的主要因素。综上,可以得出如下结论:
1)两类双层加筋板振动试验结果与有限元仿真结果吻合的程度较高,说明有限元方法对该结构进行的仿真研究准确可靠。
2)填充聚氨酯芯材之后,双层加筋板固有频率试验结果平均降低6.9%,对应模态振型未发生明显变化。从均方振速总级来看,填充芯材之后,试验结果平均减振11.73 dB,说明该复合材料结构具有良好的减振效果。
3)填充芯材之后,双层加筋板板固有频率的改变跟芯材的附加质量和附加刚度有关,而均方振速曲线幅值的降低主要与芯材的阻尼性能有关。
| [1] |
马玉璞. 舰用非金属隐身材料的发展[J]. 舰船科学技术, 2001(2): 28-34. MA Y P. Development of non-metallic stealth materials for ships[J]. Ship Science and Technology, 2001(2): 28-34. |
| [2] |
BROOKING M A. The performance, safety and production benefits of SPS structures for double hull tankers[C]//The RINA Conference on Double Hull Tankers, London, 25th Feb, 2004.
|
| [3] |
中国科学院北京力学研究所固体力学研究室板壳组. 夹层板壳的弯曲稳定和振动[M]. 北京: 科学出版社, 1977: 2–10.
|
| [4] |
WANG S C, DENG Z X, SHEN W D. Sound transmission loss characteristics of unbounded orthotropic sandwich panels in bending vibration considering transverse shear deformation[J]. Composite Structures, 2010, 92: 2885-2889. DOI:10.1016/j.compstruct.2010.04.014 |
| [5] |
XIN F X, LU T J, CHEN C Q. Sound transmission through simply supported finite double-panel partitions with enclosed air cavity[J]. Journal of Vibration and Acoustics, 2010, 132: 011008-1-11. DOI:10.1115/1.4000466 |
| [6] |
薛启超. 聚氨酯弹性体钢夹层板的力学性能研究[D]. 哈尔滨: 哈尔滨工程大学, 2013.
|
| [7] |
仝博, 李永清, 朱锡, 等. 复合材料夹芯圆柱壳水下振声性能试验研究[J]. 材料导报, 2019, 33(10): 1728-1733. TONG B, LI Y Q, ZHU X, et al. Underwater vibro-acoustic behavior of composite cylindrical shell with sandwich structure: an experimental study[J]. Materials Reports, 2019, 33(10): 1728-1733. DOI:10.11896/cldb.17100158 |
| [8] |
任树伟, 辛锋先, 卢天健. 蜂窝层芯夹层板结构振动与传声特性研究[J]. 力学学报, 2013, 45(3): 349-358. REN S W, XIN F X, LU T J. Vibroacoustic performance of simply supported honeycomb sandwich panels[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(3): 349-358. DOI:10.6052/0459-1879-12-280 |
| [9] |
余敏, 查晓雄, 阳松, 等. 聚氨酯、挤塑夹芯板力学性能的有限元分析[J]. 哈尔滨工业大学学报, 2008, 40(12): 1914-1918. YU M, ZHA X, YANG S, et al. Finite element analysis on mechanical properties of polyurethane and XPS sandwich panel[J]. Journal of Harbin Institute of Technology, 2008, 40(12): 1914-1918. DOI:10.3321/j.issn:0367-6234.2008.12.013 |
| [10] |
黄梦情. 填充吸声材料的点阵增强双板隔声特性研究[D]. 武汉: 华中科技大学, 2020.
|
| [11] |
刘监波, 吴崇健, 陈乐佳, 等. 基于模态滤波的板壳类结构空间均方振速估算方法[J]. 中国舰船研究, 2014, 9(2): 48-54. LIU J B, WU C J, CHEN L J, et al. Estimation of the spatial quadratic velocity of shells and plate structures based on a modal filter[J]. Chinese Journal of Ship Research, 2014, 9(2): 48-54. DOI:10.3969/j.issn.1673-3185.2014.02.009 |
 2023, Vol. 45
2023, Vol. 45
