2. 四川大学 视觉合成图形图像技术国家级重点实验室,四川 成都 610065
2. National Key Laboratory of Fundamental Science on Synthetic Vision, Sichuan University, Chengdu 610065, China
潜艇的隐蔽性是其生存能力的重要保障,潜艇隐蔽效能研究是国内外学者重点关注的领域。卜文俊等[1]从潜艇自身隐蔽能力方面,研究新材料技术在潜艇隐身设计中的应用;朱理等[4]从敌方声呐探测系统性能[2]方面,基于被动声呐方程对于水下声学安全态势进行研究;秦锋等[5]对于非均匀温盐海洋环境中的潜艇隐蔽效能进行了仿真,研究海洋环境因素[3]对于潜艇隐蔽航行的影响;刘雄等[6]从潜艇的航行路线方面进行研究,仿真得出典型温跃层条件下潜艇不同航深的声隐蔽效能。潜艇的隐蔽效能受诸多因素影响,潜艇隐蔽效能模型应该从潜艇自身隐蔽能力、声呐探测系统性能、海洋环境因素、潜艇的运动规律等多方面评估。本文基于海洋环境温盐场数据,利用射线Bellhop模型[7]计算海洋声传播损失值,结合潜艇的运动规律以及潜艇自身隐身能力,采用被动声呐方程和概率论构建潜艇隐蔽效能模型,解决现有模型评估方法单一的问题。
由于潜艇航行的海洋环境复杂多变,潜艇隐蔽效能快速计算是研究潜艇隐蔽性的关键[17]。射线Bellhop模型因其计算精度高被广泛应用于水声领域。张朝金等[8]利用多线程技术建立了BellhopMP并行计算模型,实现了声场快速计算,但是对于不同的硬件条件,并行计算效率表现不稳定;Ulmstedt等[10]使用GPU对Bellhop模型进行了快速计算,但是该计算方法平台依赖性高,对于不同平台的通用性和适配性表现不佳。误差反向传播(back propagation,BP)神经网络[11]由于简单易行、计算量小、并行性强、可移植性等特点,成为应用最为广泛的神经网络模型之一。本文基于BP神经网络构建了BellhopBP模型,结合层次细节算法[20] 思想,提出一种基于层次细节算法[20]的快速计算方法。其主要思想是均衡考虑计算效率和准确性,即大范围场景使用BellhopBP模型实现快速计算,进行潜艇隐蔽效能预判,小范围场景使用Bellhop模型进行精确计算,2个计算模型结合使用可实现隐蔽效能准确快速的计算。
通过仿真实验与分析,验证了本文的潜艇隐蔽效能模型和快速计算方法可以快速准确地计算潜艇隐蔽效能。
1 相关理论 1.1 被动声呐方程在海洋环境噪声下的被动声呐方程[12]为:
| $ SE = SL - TL - NL - (DT - DI) 。$ | (1) |
其中,
潜艇的辐射噪声[14]为敌方被动声呐提供了跟踪定位的信息,潜艇辐射噪声的声源级大小会直接影响到潜艇的隐蔽性,对于潜艇的隐蔽航行造成极大的威胁。被动声呐检测系统中依赖的主要是潜艇的辐射噪声,潜艇辐射噪声级
| $ SL=\left\{\begin{array}{ll}25\mathrm{log}({V}_{m})+77+20a\text{,} & {V}_{m} < {V}_{T}\text{,} \\ 104+20a+\Delta\text{,} & {V}_{m}={V}_{T}\text{,} \\ 104+20a+\Delta +b({V}_{m}-{V}_{T})\text{,} & {V}_{m} > {V}_{T}。\end{array}\right. $ | (2) |
其中:
潜艇的隐蔽性不只受到敌方探测和自身性能的制约,海洋环境背景噪声[12]对潜艇的隐蔽性影响也非常大。海洋的背景噪声主要由航运噪声和风噪声组成。采用文献[12]中的经验公式可以估算得到海洋背景噪声,海洋环境噪声计算公式为:
| $ NL = 10{\log _{10}}({10^{N{L_{ship}}/10}} + {10^{N{L_{wind}}/10}})。$ | (3) |
其中:
海洋声场的计算是水声领域研究的难点所在,对于与距离有关的海洋声传播问题,基于高斯声线束的Bellhop模型[7]被广泛应用于水声学领域。本文利用射线Bellhop模型计算声传播损失值。
Bellhop模型计算需要当前区域的声速值(soundspeed, SSP),结合当前海洋环境的三维温盐场,计算水域中三维声速场[12]为:
| $ c = 1449.30 + {{\Delta }}{c_P} + {{\Delta }}{c_T} + {{\Delta }}{c_S} + {{\Delta }}{c_{TPS}} ,$ | (4) |
| $ {{\Delta }}{c_P} = 1.5848 \times {10^{ - 1}}P + 1.572 \times {10^{ - 5}}{P^2} - 3.46 \times {10^{ - 12}}{P^4} ,$ | (5) |
| $ {{\Delta }}{c_T} = 14.857T - 5.356 \times {10^{ - 2}}{T^2} + 2.604 \times {10^{ - 4}}{T^3} ,$ | (6) |
| $ {{\Delta }}{c_S} = 1.19(S - 35) + 9.6 \times {10^{ - 2}}{(S - 35)^3} ,$ | (7) |
| $\begin{aligned} & {{\Delta }}{c_{TPS}} = 1.35 \times {10^{ - 5}}{T^2}P - 7.19 \times {10^{ - 7}}T{P^2} -\\ & 1.2 \times {10^{ - 2}}(S - 35)T 。\end{aligned}$ | (8) |
其中:
| $\begin{split} P =& 1.033 + 1.028126 \times {10^{ - 1}}z + 2.38 \times\\ & {10^{ - 7}}{z^2} - 6.8 \times {10^{ - 17}}{z^4}。\end{split}$ | (9) |
利用海洋环境的温盐密数据,根据经验公式(4)计算声速值SSP并结合射线Bellhop模型即可计算潜艇在某一位置处的声传播损失

|
图 1 Bellhop模型计算TL流程 Fig. 1 Bellhop model calculation TL process |
基于被动声呐方程结合概率论计算声呐的探测概率,被动声呐方程中各个参数相互独立,满足正态分布。因此,声呐对潜艇的探测概率为:
| $ {P_{({s_r},{s_d})}} = \int_{ - \infty }^{SE} {\frac{1}{{\sqrt {2 \text{π} } }}} {e^{ - \frac{{{t^2}}}{2}}}{\rm{d}}t。$ | (10) |
其中:
| $ {P_{({s_r},{s_d})}}\left\{ {\begin{array}{*{20}{l}} { > 0.5}, \\ { = 0.5}, \\ { < 0.5}, \end{array}\begin{array}{*{20}{l}} {SE > 0} ,\\ {SE = 0} ,\\ {SE < 0}。\end{array}} \right. $ | (11) |
当声呐余量
声呐的投放深度[16]也影响其探测性能,但潜艇在进行隐蔽性评估时对于对方声呐的入水深度是未知的,所以声呐投放深度的概率分布为:
| $ {P_d} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{1}{D}},&{{d_i} \in [{D_{\min }},{D_{\max }}]},\\ 0,&{{d_i} \notin [{D_{\min }},{D_{\max }}]} 。\end{array}} \right. $ | (12) |
其中:
声呐探测到潜艇和潜艇隐蔽性为对立事件,依据概率的可列可加性,定义潜艇在某一位置处的隐蔽效能为:
| $ P = 1 - \sum\limits_{i = 1}^N {{P_{({S_r},{S_d}_{_i})}}{P_{{{{d}}_i}}}}。$ | (13) |
其中,
潜艇隐蔽效能研究的目的是确保潜艇隐蔽性和航行安全。因为潜艇隐蔽性受潜艇自身隐蔽能力、声呐探测系统性能、海洋环境因素、潜艇的运动规律等多方面因素影响,所以构建全方面评估的潜艇隐蔽效能模型非常关键。本文潜艇隐蔽效能模型进行评估的详细过程如下:
步骤1 确定潜艇艇型和经纬位置坐标 [Lat,Lon]、航行深度
步骤2 结合潜艇艇型,按照式(2)得到该潜艇的声源噪声级
步骤3 根据当前潜艇所处位置,按照式(3)估算海洋环境噪声级
步骤4 确定敌方探测设备的投放深度
步骤5 利用射线Bellhop模型计算潜艇声源噪声传播损失
步骤6 根据被动声呐方程(1)计算潜艇声源噪声到达敌方探测设备的声呐余量
步骤7 根据敌方探测设备的投放深度
BP神经网络由于简单易行、计算量小、并行性强、可移植性等特点,成为应用最为广泛的神经网络模型之一。本文基于BP神经网络构建BellhopBP模型,结合层次细节算法思想,提出一种基于层次细节算法的快速计算方法,其主要思想是均衡考虑计算效率和准确性,即大范围场景使用BellhopBP模型快速计算,进行潜艇隐蔽效能预判,小范围场景使用Bellhop模型进行精确计算,2个模型结合使用可实现隐蔽效能准确快速地计算。
3.1 BellhopBP模型 3.1.1 BP神经网络BP神经网络[11]是一种按照误差反向传播算法训练的人工神经网络。结构上,它由输入层、隐含层和输出层构成且每一层有若干个节点,相邻层之间由权值连接,但各层内的节点相互独立,实现从输入到输出的非线性映射,应用于声场快速计算极具潜力。它的基本思想就是梯度下降法,利用梯度搜索技术以使网络预测值与实际期望值的损失函数值达到目标精度要求。BP神经网络的结构如图2所示。
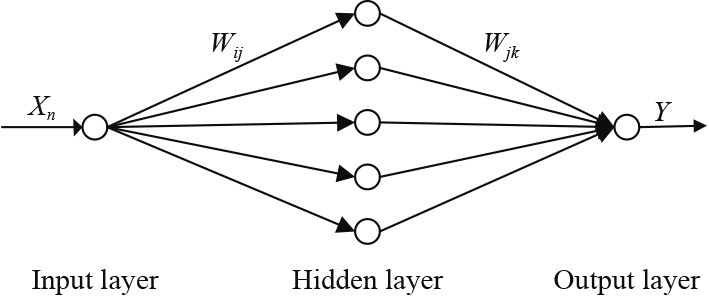
|
图 2 BP神经网络结构图 Fig. 2 BP neural network structure diagram |
图中:
潜艇航行位置处的工况用[Lat,Lon,SSP,SubDep,SonDep]五维向量描述,其中[Lat,Lon,SSP]为潜艇所处的海域经纬度位置以及该位置的声速值。[SubDep,SonDep]为潜艇的航行深度和敌方声呐的投放深度。对于潜艇所在位置处的声场模型BellhopBP可设计为:
| $ F(Lat,Lon,SSP,SubDep,SonDep) \to TL。$ | (14) |
其中:
在BellhopBP模型中,输入层神经元节点的数目主要取决于输入向量的维数,所以神经网络的输入层为5个神经元节点,神经网络的输出则是对于声场声传播损失
| $ l = 2m + 1。$ | (15) |
其中:
BellhopBP模型中采用ReLU激活函数,优化器选取的是Adam,学习率初始值在0~1之间,随着训练次数自适应调整。用平均绝对误差MAE(Mean Absolute Error)检验预测值与期望值的结果误差,用准确度Accuracy检验预测值与真实值之间的符合程度。
| $ MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{{\hat y}_i} - {y_i}} \right|},$ | (16) |
| $ Accuracy = 1 - \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{|{{\hat y}_i}{\text{ - }}{y_i}|}}{{{y_i}}}}。$ | (17) |
其中:
BellhopBP模型快速计算的声场数据与Bellhop模型计算的数据存在误差,所以导致基于BellhopBP模型计算的潜艇隐蔽效能也有误差,但是对于整个航行海域的隐蔽效能可以进行预判。对于潜艇的隐蔽航行,隐蔽效能的计算必须准确才能进行全面评估,以便进行下一步的决策规划。所以在解决计算效率问题时,需均衡考虑计算效率和准确性。
层次细节算法[20]的主要思想是均衡考虑计算效率和准确性,在保证准确性的前提下,进行快速计算。所以本文的快速计算方法是:在任务海域先基于BellhopBP模型快速计算隐蔽效能,对于潜艇保持隐蔽做出预判,后在潜艇局部范围内基于Bellhop模型精确计算隐蔽效能。由于潜艇的任务海域范围大小动态变化,所以潜艇局部范围的大小也应动态变化。
| $ {R_{acc}}(t,{R_{ini}}) = \left\{ {\begin{array}{*{20}{c}} {{R_{ini}}},&{{R_{ini}} \leqslant 10},\\ {t{R_{ini}}},&{10 < {R_{ini}} \leqslant 50},\\ {10},&{{R_{ini}} > 50} 。\end{array}} \right. $ | (18) |
其中:
在训练BellhopBP模型时,训练集数据与测试集数据分别使用的是ARGO提供的海洋环境数据,时间范围为2020年12月~2021年12月,其空间分辨率为0.25°×0.25°,该数据中包含海洋环境温度、盐度等数据,声速SSP由经验公式(4)得到,海深为0~200 m(深度在200 m以内的为浅海),浅海条件下被动声呐浮标的最佳入水深度[16]为30~170 m,此时被动声呐的最大有效探测范围[18]为2 km,因此BellhopBP模型计算潜艇位置处2 km范围内的声传播损失
|
|
表 1 Bellhop模型参数设置 Tab.1 Bellhop model parameter settings |
结合经验公式(15) 采用枚举法选取不同的隐含层神经元数量的进行训练。训练结果表明,当隐含层为2,每层的节点数为15,每个训练轮次迭代1000次,当训练轮次达到500次时,BellhopBP模型预测值与实际值误差达到预期值,且模型收敛性达到最好,训练结果如图3所示。
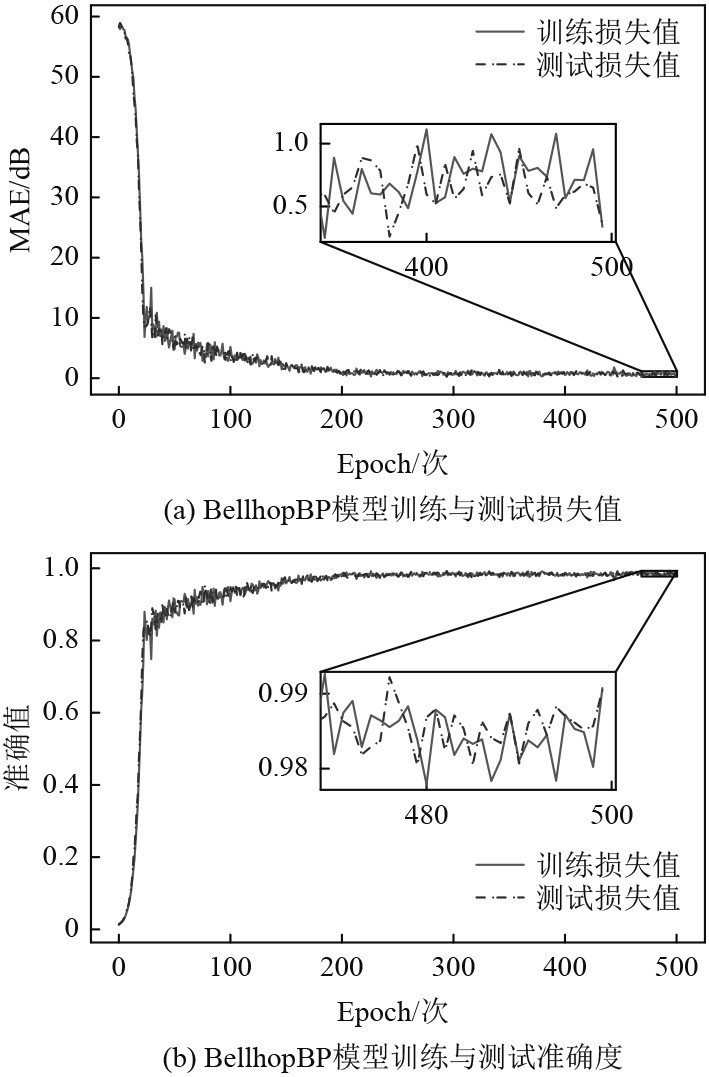
|
图 3 BellhopBP训练与测试结果图 Fig. 3 BellhopBP training and testing results |
由图3(a)可知,随着训练次数的增加,误差平均绝对值MAE在逐渐降低。当训练次数达到500次时,BellhopBP模型已经收敛,
潜艇航行在不同的海域以及不同的深度,分别用BellhopBP模型与Bellhop模型计算声传播损失值
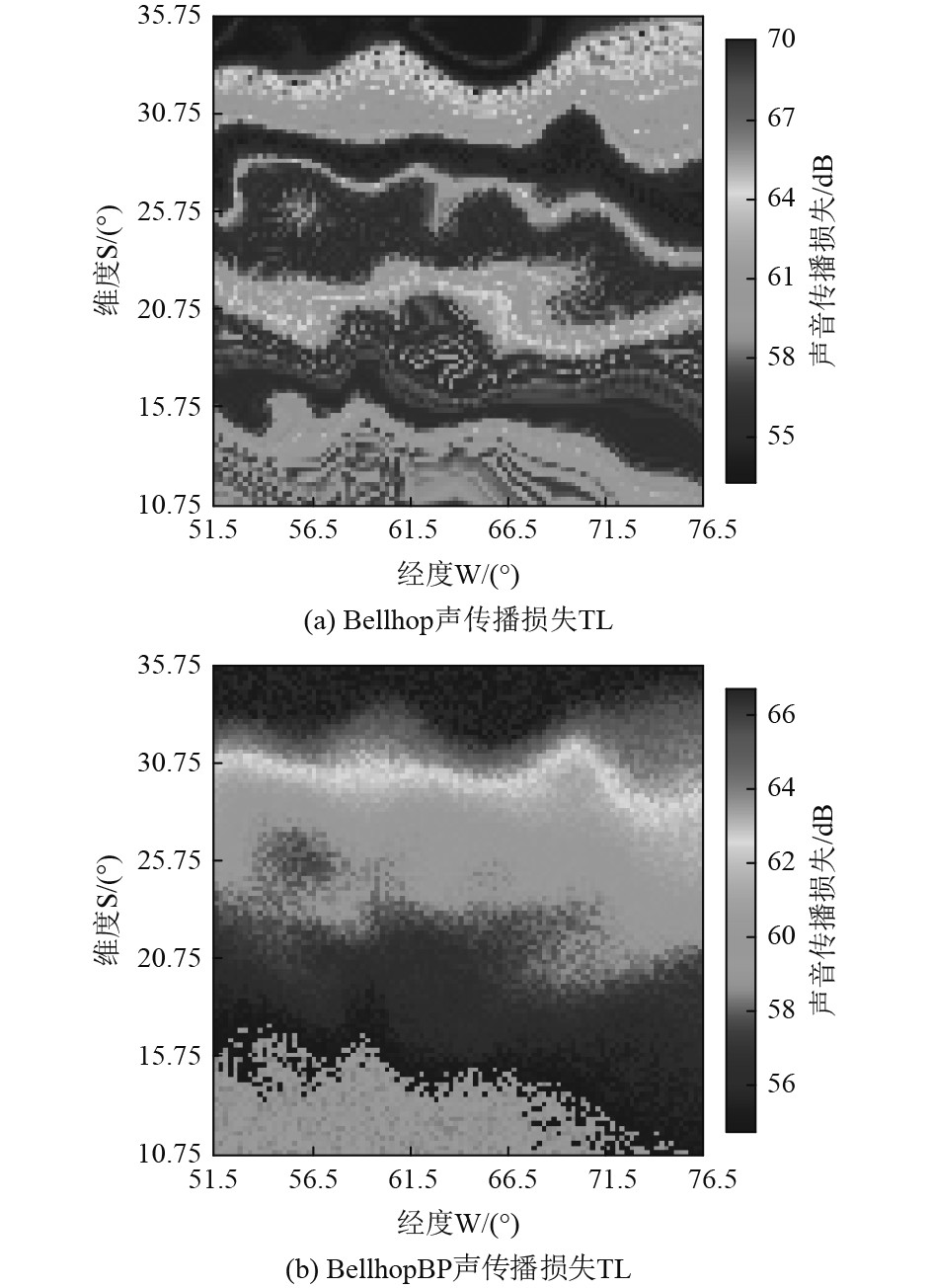
|
图 4 潜艇所在海域的声传播损失(潜艇航深30 m,敌方声呐入水深度30 m) Fig. 4 Sound transmission loss in the sea area |
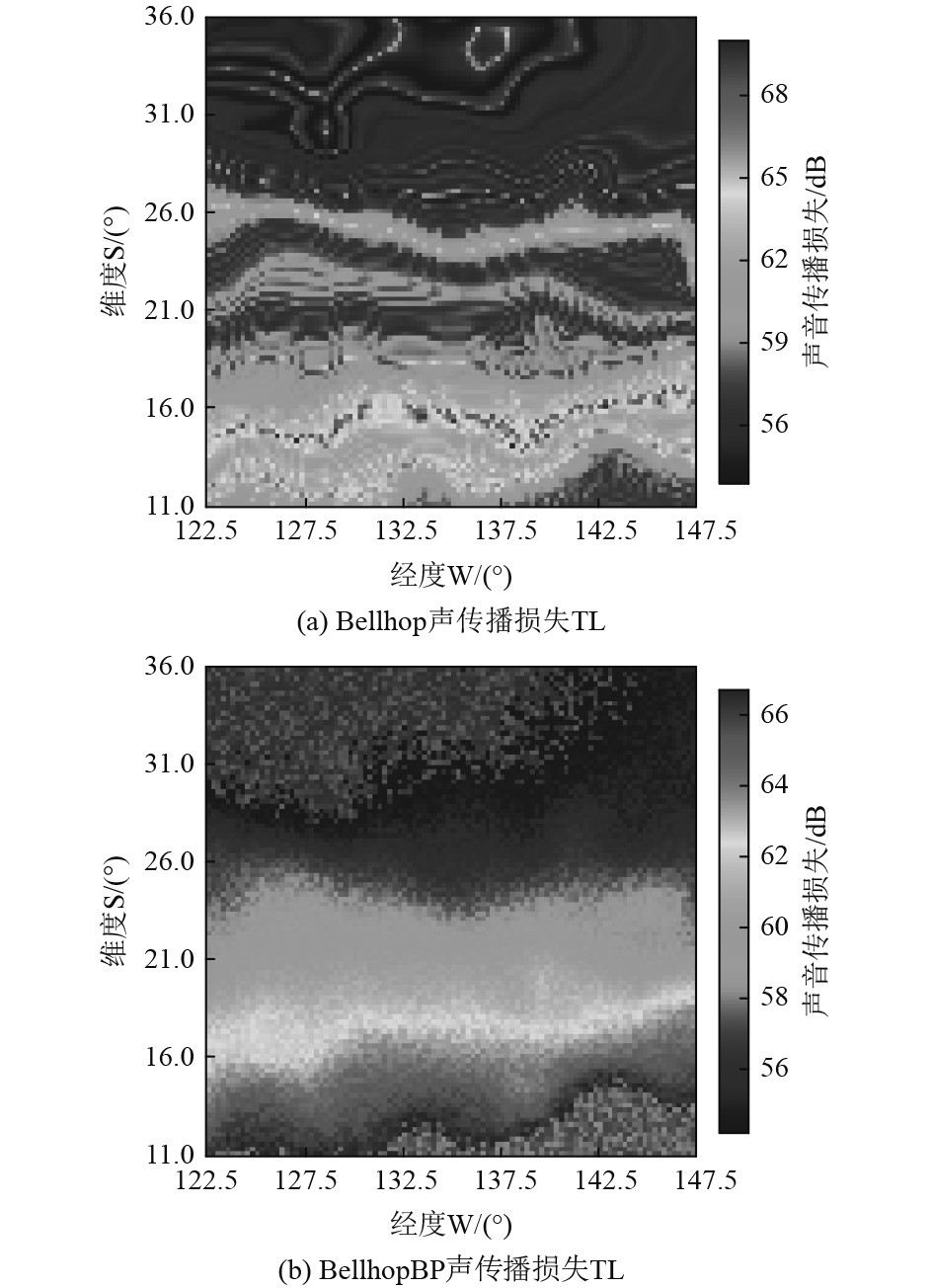
|
图 5 潜艇所在海域的声传播损失(潜艇航深100 m,敌方声呐入水深度30 m) Fig. 5 Sound transmission loss in the sea area |
图像感知哈希算法[21]是一种图像可感知内容摘要的提取算法,主要强调的是图像感知的相似性。其中感知距离是感知内容相似性的度量,感知距离的取值范围为[0,64],取值越小图像越相似。图4和图5中,Bellhop模型与BellhopBP模型计算的声音传播损失伪彩图相似性对比如表2所示。
|
|
表 2 声传播损失伪彩图相似性对比 Tab.2 Acoustic propagation loss pseudo-color map similarity comparison |
可知,在实验海域的声场分布图,感知哈希距离分别为5和6,两图的相似性分别为0.92和0.91,即声场的分布伪彩图基本一致。由此可得Bellhop模型与BellhopBP模型计算的声场分布规律基本一致。BellhopBP模型与Bellhop模型计算的声传播损失值某些位置处存在误差,但在不同海域与Bellhop模型计算得到的声场分布伪彩图都具有高的相似性,由此说明BellhopBP模型具有良好的通用性且可较为准确地计算声传播损失
由表3可知,BellhopBP模型在10°×10°大小海域范围内的计算效提升了40倍,在25°×25°大小海域范围内的计算效提升了43倍。因此,BellhopBP模型可以在保证准确性的前提下实现声场快速计算。
|
|
表 3 声传播损失计算效率对比 Tab.3 Computational efficiency comparison (time/s) |
根据模型流程计算潜艇的隐蔽效能,仿真参数设置如表4所示。
|
|
表 4 参数设置 Tab.4 Parameter settings |
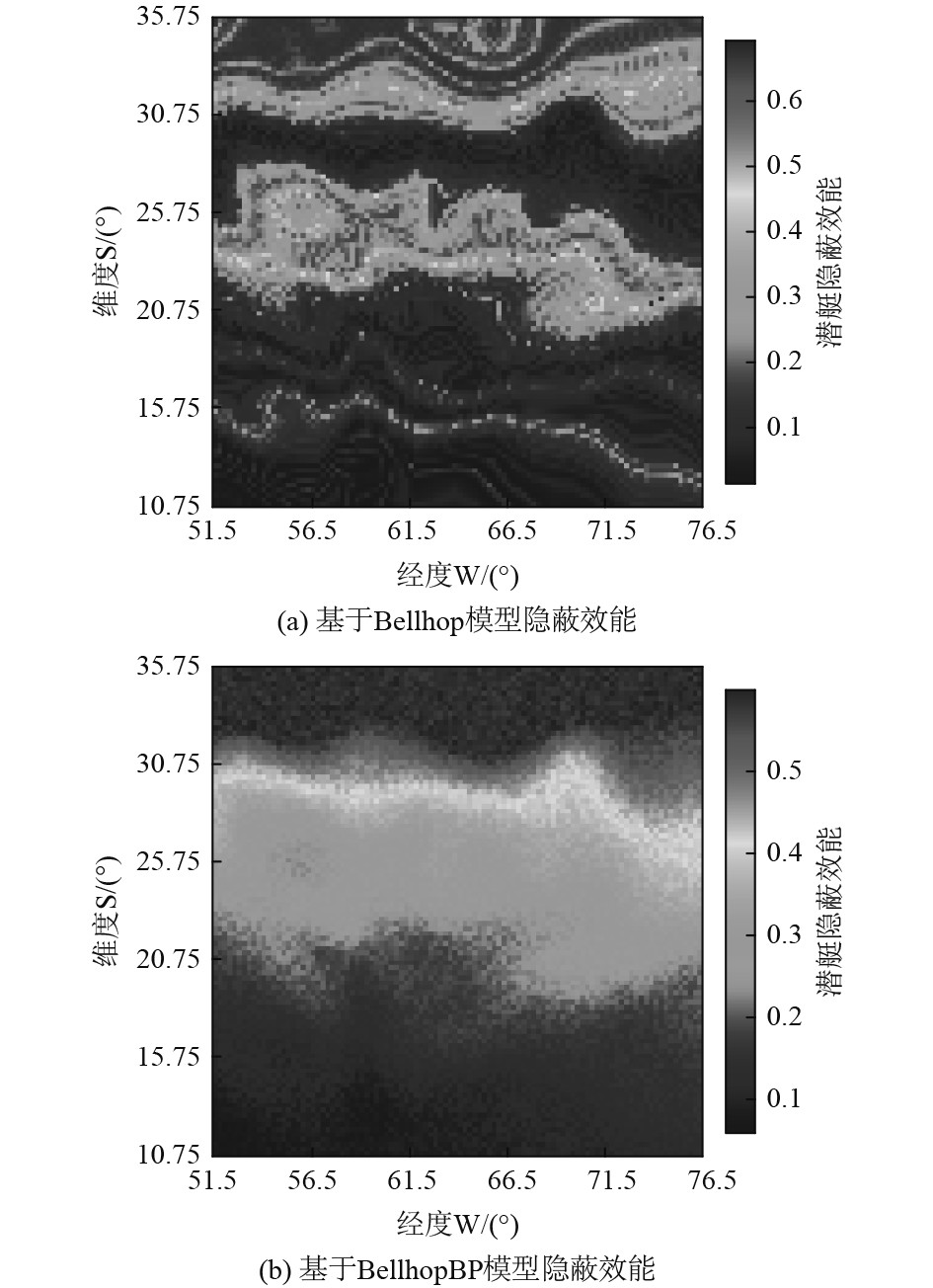
图6中,当潜艇的航深为30 m时,图6(a)与图6(b)在[51.5°W~76.5°W, 30.75°S~33.75°S]区域内航行相对安全,但是图6(b)在[51.5°W~76.5°W, 20.75°S~25.75°S]区域内的隐蔽效能计算存在误差,其他区域均为危险区域。图7中,当潜艇的航深为100 m时,图7(a)与图7(b)均可反映在[122.5°W~147.5°W, 11.0°S~16.0°S]区域航行时相对其他位置的隐蔽效能较高。由表5可知,在实验海域的隐蔽效能图,感知哈希距离分别为5和3,两图的相似性分别为0.92和0.95,即基于这2个模型的潜艇隐蔽效能分布伪彩图基本一致。由此说明基于BellhopBP模型快速计算所得的潜艇隐蔽效能伪彩图可以反映出潜艇在某一海域的隐蔽性,能够进行隐蔽航行预判。
|
图 6 潜艇航深30 m的隐蔽效能 Fig. 6 Concealment effectiveness of submarines at 30 m depth |
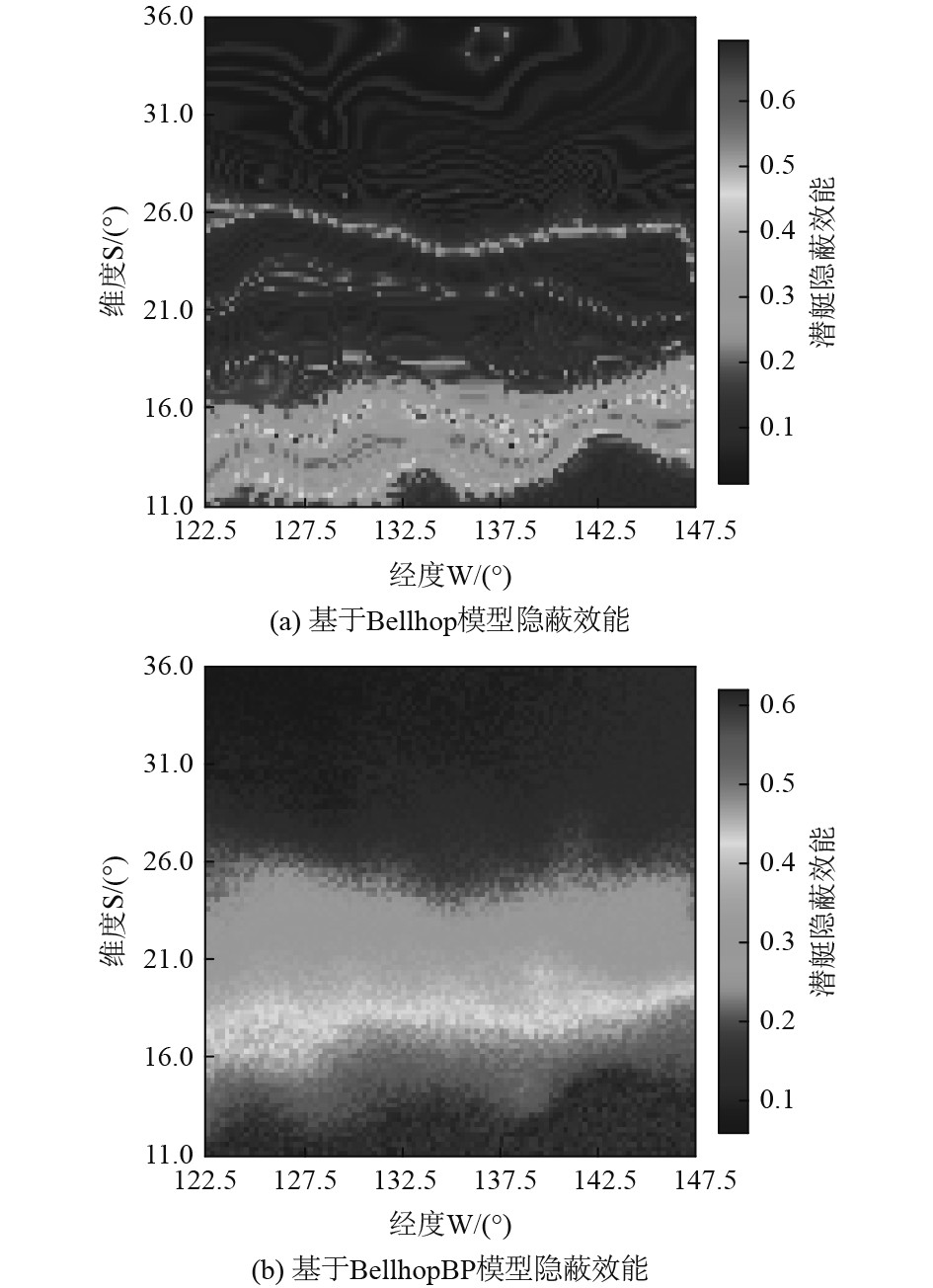
|
图 7 潜艇航深100 m隐蔽效能 Fig. 7 Concealment effectiveness of submarines at 100 m depth |
|
|
表 5 隐蔽效能伪彩图相似性对比 Tab.5 Similarity comparison of pseudo-color images for concealment effectiveness |
但是潜艇在执行任务中需要使用准确的隐蔽效能才能决定具体的航行路线,所以还需要结合Bellhop模型计算更加准确的隐蔽效能。基于本文提出的层次细节算法的快速计算方法,利用式(18)计算潜艇准确的隐蔽效能。
图8(a)为基于BellhopBP模型快速计算的潜艇隐蔽效能,图8(b)为结合Bellhop模型根据式(18)计算的潜艇所在点A处经纬度10°×10°范围内的隐蔽效能。通过基于层次细节的快速计算方法,既能快速地对整个任务海域进行隐蔽效能的预判,又能在潜艇活动小周围海域做精确计算。
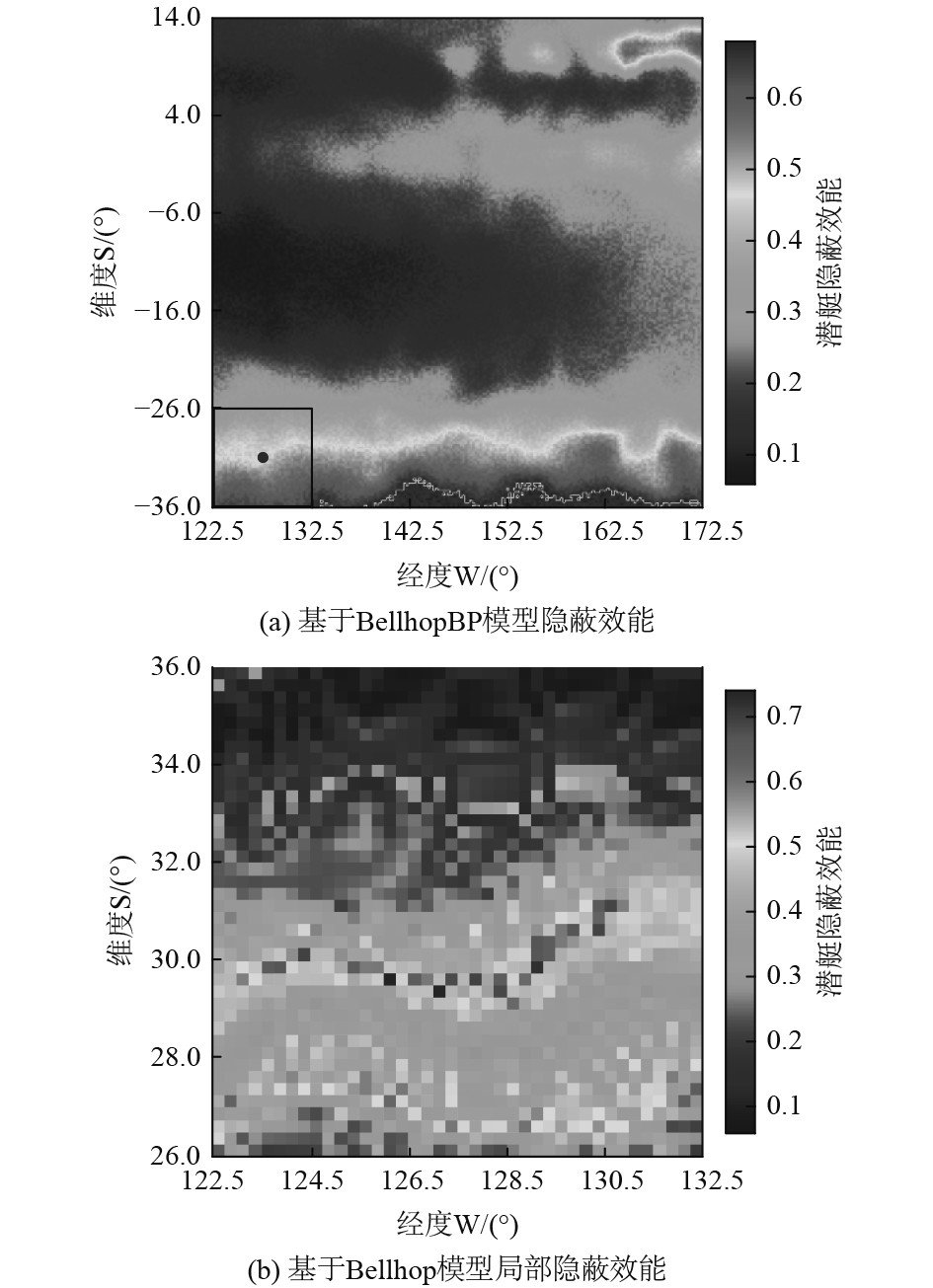
|
图 8 潜艇航深200 m隐蔽效能 Fig. 8 Concealment effectiveness of submarines at 200 m depth |
对计算效率进行对比实验。方法1:研究文献[5]中使用的传统计算方法;方法2:本文基于层次细节算法的的快速计算方法。分别选择不同大小范围的海域进行仿真实验。场景1:海域大小为经纬10°×10°;场景2:海域大小为经纬25°×25°;场景3:海域大小为经纬50°×50°。每个场景中经纬度的空间分辨率为0.25°×0.25°,敌方声呐均匀分布在30~170 m深处,针对不同场景下潜艇隐蔽效能的计算效率如表6所示。
|
|
表 6 潜艇隐蔽效能计算效率对比(时间/s) Tab.6 Submarine concealment effectiveness solution efficiency comparison (time/s) |
可知,场景1中,本文方法相较于传统方法计算效率相对提高了12.16倍。在场景3中,计算效率明显优于传统模型效率提升了24.7倍。由此可见,本文快速计算方法的计算效率在不同大小范围场景中均有提升,并且进行大范围海域计算时,本文方法的计算效率明显优于传统方法。
综上,本文提出的BellhopBP模型与传统Bellhop模型在计算潜艇隐蔽效能时对于不同的海域位置的效能分布规律基本一致。在计算准确性方面,基于层次细节算法的计算方法采用了BellhopBP模型与Bellhop模型相结合的方式,在计算效率方面有明显的提升。
5 结 语本文针对现有潜艇隐蔽效能模型评估方法单一的问题,从潜艇自身隐蔽能力、声呐探测系统性能、海洋环境因素、潜艇的运动规律等多方面构建了基于海洋环境数据与潜艇工况的潜艇隐蔽效能模型,用于潜艇隐蔽性的评估。针对现有潜艇隐蔽效能模型计算效率低等问题,利用BP神经网络建立BellhopBP模型,采用层次细节算法思想,提出一种快速计算方法。通过仿真实验可以看出,本文潜艇隐蔽效能模型在保证隐蔽效能计算准确的前提下,利用快速计算方法提高了潜艇隐蔽效能的计算效率。本文的隐蔽效能模型与快速计算方法具有显著优势与创新性,为后续潜艇航迹规划提供了数据支撑。
| [1] |
孙世岩, 刘忠. 潜艇隐蔽攻击能力分析方法研究[J]. 系统工程与电子技术, 2006(28): 564-567. |
| [2] |
季蓓, 程健庆, 曹志敏. 被动声纳作用距离预报的仿真研究[J]. 计算机仿真, 2007, 24(3): 31-34. JI Bei, CHENG Jianqing, CAO Zhimin. Simulation research on passive sonar range prediction[J]. Computer Simulation, 2007, 24(3): 31-34. DOI:10.3969/j.issn.1006-9348.2007.03.008 |
| [3] |
高学强, 杨日杰, 韩建辉. 跃变层对潜艇隐蔽性的影响仿真研究[J]. 舰船科学技术, 2008, 30(5): 147-150. GAO Xueqiang, YANG Rijie, HAN Jianhui. Simulation study on the influence of the climacteric layer on submarine concealment[J]. Ship Science and Technology, 2008, 30(5): 147-150. DOI:10.3404/j.issn.1672-7649.2008.05.035 |
| [4] |
朱理, 董博文, 王雪仁, 等. 基于被动声呐方程的水下航行器声学安全态势研究[J]. 舰船科学技术, 2021, 43(6): 90-94. DOI:10.3404/j.issn.1672-7649.2021.06.017 |
| [5] |
秦锋, 赵志允, 于振涛. 非均匀温盐场潜艇声隐蔽效能仿真研究[J]. 青岛大学学报(工程技术版), 2020(4): 62-67. |
| [6] |
刘雄, 张绳, 蔡勇. 潜艇隐蔽性建模与仿真研究[J]. 舰船科学技术, 2009, 31(8): 103-107. LIU Xiong, ZHANG Sheng, CAI Yong. Research on Submarine Concealment Modeling and Simulation[J]. Ship Science and Technology, 2009, 31(8): 103-107. |
| [7] |
李孟, 周荣艳. 基于 BELLHOP 模型的水下信道仿真方法研究[J]. 舰船电子工程, 2018, 38(8): 166-169. DOI:10.3969/j.issn.1672-9730.2018.08.037 |
| [8] |
张朝金, 孙炳文. 射线模型 Bellhop 的并行化处理[J]. 应用声学, 2019, 38(1): 1-7. |
| [9] |
Ulmstedt M, Stålberg J. GPU Accelerated Ray-tracing for Simulating Sound Propagation in Water[J]. 2019.
|
| [10] |
鲁娟娟, 陈红. BP 神经网络的研究进展[J]. 控制工程, 2006, 13(5): 449-451. DOI:10.3969/j.issn.1671-7848.2006.05.016 |
| [11] |
刘伯胜. 水声学原理[M]. 北京: 科学出版社, 2019.
|
| [12] |
刘仁义, 刘南, 尹劲峰, 等. 全球海洋环境观测数据 (ARGO) 及 ARGOGIS 系统[J]. 自然灾害学报, 2004(4): 93-98. |
| [13] |
高守勇, 王升, 马力, 等. 潜艇辐射噪声近场特性研究[C]//中国声学学会水声学分会2011年全国水声学学术会议论文集. 2011.
|
| [14] |
高学强, 杨日杰. 潜艇辐射噪声声源级经验公式修正[J]. 声学与电子工程, 2007(3): 17-18. |
| [15] |
郁红波, 鞠建波, 杨少伟. “浅海” 条件下声纳浮标最佳入水深度[J]. 探测与控制学报, 2020.
|
| [16] |
笪良龙, 胡均川. 在浅海环境中潜艇隐蔽占位航路研究[J]. 应用声学, 1997, 16(4): 18-22. DA Lianglong, HU Junchuan. Research on submarine concealed occupancy route in shallow sea environment[J]. Applied Acoustics, 1997, 16(4): 18-22. DOI:10.11684/j.issn.1000-310X.1997.04.005 |
| [17] |
张飞飞, 赵申东, 刘朝晖, 等. 近浅海条件下被动声呐浮标使用深度分析与研究[J]. 舰船科学技术, 2018, 40(3): 128-131. ZHANG Feifei, ZHAO Shendong, LIU Zhaohui, et al. Depth analysis and research of passive sonar buoys under shallow sea conditions[J]. Ship Science and Technology, 2018, 40(3): 128-131. DOI:10.3404/j.issn.1672-7649.2018.03.023 |
| [18] |
郁红波, 鞠京龙. 浅海条件下吊放声呐最佳入水深度的研究[J]. 电光与控制, 2021, 28(4): 106. DOI:10.3969/j.issn.1671-637X.2021.04.023 |
| [19] |
樊振宇. BP 神经网络模型与学习算法[J]. 软件导刊, 2011, 10(7): 66-68. FAN Zhenyu. BP neural network model and learning algorithm[J]. Software Guide, 2011, 10(7): 66-68. |
| [20] |
HEOK T K, DAMAN D. A review on level of detail[C]//Proceedings. International Conference on Computer Graphics, Imaging and Visualization, 2004. CGIV 2004. IEEE, 2004: 70-75.
|
| [21] |
NIU X, JIAO Y. An overview of perceptual hashing[J]. ACTA Electonica Sinica, 2008, 36(7): 1405. |
 2023, Vol. 45
2023, Vol. 45
