2. 中国科学院福建物质结构研究所 泉州装备制造研究中心,福建 泉州 362216
2. Quanzhou Institute of Equipment Manufacturing, Fujian Institute of Research on the Structure of Matter, Chinese Academy of Sciences, Quanzhou 362216, China
潜艇在水下执行任务时,需要同岸基无线电通信站和岸基指挥所保持可靠有效的通信联系。由于海水对电磁波的衰减特性,目前,对潜通信的有效手段仍然以甚低频(3 ~ 30 kHz)和超低频(30 ~ 300 Hz)通信为主[1]。在超低频通信系统中,接收点接收到的信号信噪比低,该信号还必须与频段内的电磁噪声进行竞争,使检测有用信号变得十分困难。因此,研究潜艇周围的电磁噪声对提高海陆通信质量和提高海上航行安全具有重要意义。
潜艇周围超低频电磁噪声来源复杂,主要包括艇体不同金属材料之间的电化学腐蚀和各种防腐措施作用产生的电磁,艇体漏电流和用电设备对外的电磁辐射,以及艇体运动产生的感应电磁场。在不同频段的电场信号中,静态电场的能量最大,主要集中在0.2 Hz以下[2-3];工频交变电场能量次之,峰值频率一般在50~100 Hz之间,并具有较高的倍频成分[4];轴频电场的能量在各频段中最小,时域上幅值量级一般为µV/m,频域上电场信号是以主轴转动为基频的低频线谱[5-6]。
目前,对水下潜艇电磁场的研究主要侧重于恒速下潜艇自身产生的电磁场,且各种理论基础和数学模型相对成熟,而对运动潜艇周围的复杂流场切割地磁场产生的感应电磁场的研究相对较少。虽然部分学者[7-9]对舰船尾流产生的感应电磁场进行了详细研究,但其频谱特性分析却不够。此外,由于实际海洋环境非常复杂,潜艇通信过程会对潜艇在水中的机动性能产生影响,包括潜艇航速和航向的限制。因此,为了改善超低频波段的通信质量,有必要对不同航速和航向下潜艇周围复杂流场的电磁噪声特性进行深入细致的研究。
本文采用RANS方程结合 RNG
三维不可压缩粘性流体的连续方程和Navier - Stokes方程[10]如下:
| $ \frac{\partial \left(\rho {\bar{u}}_{i}\right)}{\partial {x}_{i}}=0,$ | (1) |
| $ \begin{split} \frac{\partial \left(\rho {\bar{u}}_{i}\right)}{\partial t}+\frac{\partial }{\partial {x}_{j}}\left(\rho {\bar{u}}_{i}{\bar{u}}_{j}\right)=\;&-\frac{\partial \bar{p}}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{j}}\left[\mu \left(\frac{\partial {\overline{u}}_{i}}{\partial {x}_{j}}+\frac{\partial {\overline{u}}_{j}}{\partial {x}_{i}}\right)\right]-\\&\frac{\partial \left(\rho \overline{{u'}_{i}{u'}_{j}}\right)}{\partial {x}_{j}}+\rho \overline{{F}_{i}}。\\[-12pt] \end{split} $ | (2) |
式中:
湍流控制方程采用 RNG
| $ \frac{\partial \left(\rho k\right)}{\partial t}+\frac{\partial \left(\rho k{u}_{i}\right)}{\partial {x}_{i}}=\frac{\partial }{\partial {x}_{j}}\left({\alpha }_{k}{\mu }_{eff}\frac{\partial k}{\partial {x}_{j}}\right)+{G}_{k}-\rho \varepsilon +{S}_{k} ,$ | (3) |
| $ \begin{split} \frac{\partial \left(\rho \varepsilon \right)}{\partial t}+\frac{\partial \left(\rho \varepsilon {u}_{i}\right)}{\partial {x}_{i}}=&\frac{\partial }{\partial {x}_{j}}\left({\alpha }_{\varepsilon }{\mu }_{eff}\frac{\partial \varepsilon }{\partial {x}_{j}}\right)+{C}_{1\varepsilon }\frac{\varepsilon }{k}{G}_{k}-\\&{C}_{2\varepsilon }\rho \frac{{\varepsilon }^{2}}{k} +{S}_{ \varepsilon }。\end{split} $ | (4) |
式中:
| $ {G}_{k}=-\rho \overline{{u'}_{i}{{u'}_{j}}}\frac{\partial {u}_{j}}{\partial {x}_{i}}。$ | (5) |
电磁流体耦合是流体介质与电磁场之间高度非线性的相互作用,描述了导电流体在电磁场作用下的行为。导电流体在电磁场作用下产生的电磁力会影响流体的运动,反过来流体的运动也会影响电磁场。
电磁流体耦合方程是从电磁学的麦克斯韦方程和流体动力学的N-S方程推导而来。根据法拉第电磁感应定律,运动的海水切割地磁场产生感应电流,从而产生感应电磁场,电磁场通过Maxwell方程进行描述:
| $ \nabla \times H=J+\varepsilon \frac{\partial E}{\partial t},$ | (6) |
| $ \nabla \cdot B=0,$ | (7) |
| $ \nabla \times E=-\frac{\partial B}{\partial t},$ | (8) |
| $ \nabla \cdot D=\rho。$ | (9) |
电磁场对流体的作用一般通过N-S方程表示:
| $ \rho \frac{\partial v}{\partial t}=-\nabla P+\nabla \cdot \tau +F。$ | (10) |
式中:
| $ J=\sigma (E+v\times B) 。$ | (11) |
流体与电磁场之间的耦合可以通过2个基本效应理解:流体在磁场中运动所产生的电流,以及电流与磁场相互作用产生的洛伦兹力。电磁流体耦合方程如下:
| $ \rho \frac{\partial v}{\partial t}=-\nabla P+\nabla \cdot \tau +(\nabla \times H)\times B。$ | (12) |
假设流体的速度完全由潜艇的运动引起,而忽略其他所有海洋现象,如风产生的波浪和海浪等,则潜艇周围流体切割地磁场产生的感应电场为
为了更直观地分析噪声特性,采用噪声功率级(power level, PL)评估频谱特性,计算公式如下:
| $ {PL}_{f}=10{\log}_{10}\left(\frac{{w}_{f}}{{w}_{0}}\right) 。$ | (13) |
式中:
根据噪声测量系统,某一点的噪声总功率级(overall power level, OPL)可以由以下公式得到:
| $ OPL=10{\log}_{10}\left(\Delta f\sum _{f={f}_{0}}^{{f}_{1}}{10}^{0.1{PL}_{f}}\right)。$ | (14) |
式中,
选取全附体SUBOFF潜艇模型作为模拟对象。该模型包括主艇体、指挥台围壳和尾舵翼,如图1所示。潜艇总长 L 为 4.356 m,其中前体长 1.016 m,平行中体长 2.229 m,后体长 1.111 m,最大直径 D 为0.508 m,尾翼截面为NACA0020 对称翼型。

|
图 1 潜艇3D几何模型 Fig. 1 3D geometric model of the submarine |
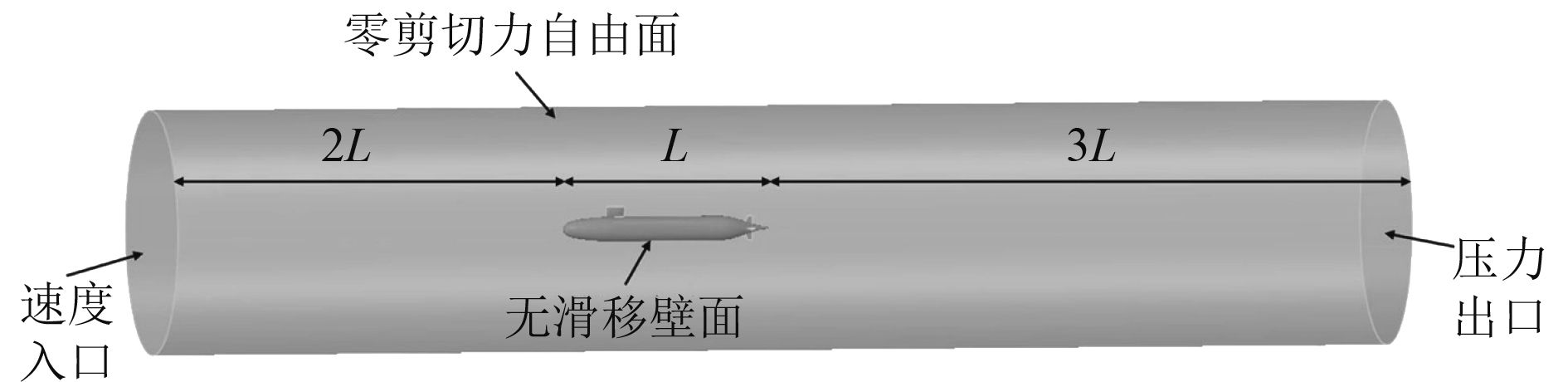
仿真模型的计算域和边界条件如图2所示。入口距离上游2倍艇长,采用速度入口边界,
|
图 2 计算域与边界条件 Fig. 2 Computational domain and boundary conditions |
网格划分策略有很多种,本文采用切割体网格技术对计算域进行离散。该网格划分策略可以生成具有最低网格偏度的高质量网格,在复杂的计算领域中更具有灵活性和适应性[12]。图3为经切片修剪过的艇体附近的局部网格示意图。对于指定的

|
图 3 潜艇周围的局部网格 Fig. 3 Local mesh around the submarine |
网格的敏感性分析是确定数值模拟中离散化误差阶数最直接的方法。使用 RNG
|
|
表 1 Re=1.2×107,不同网格的总阻力系数 Tab.1 Re=1.2×107, the total resistance coefficient of different grids |
当来流速度为
|
|
表 2 总阻力的计算值与实验值对比 Tab.2 Comparison of calculated and experimental values of total resistance |
|
|
表 3 摩擦阻力系数的计算值与经验值对比 Tab.3 Comparison of calculated and empirical values of frictional resistance coefficients |
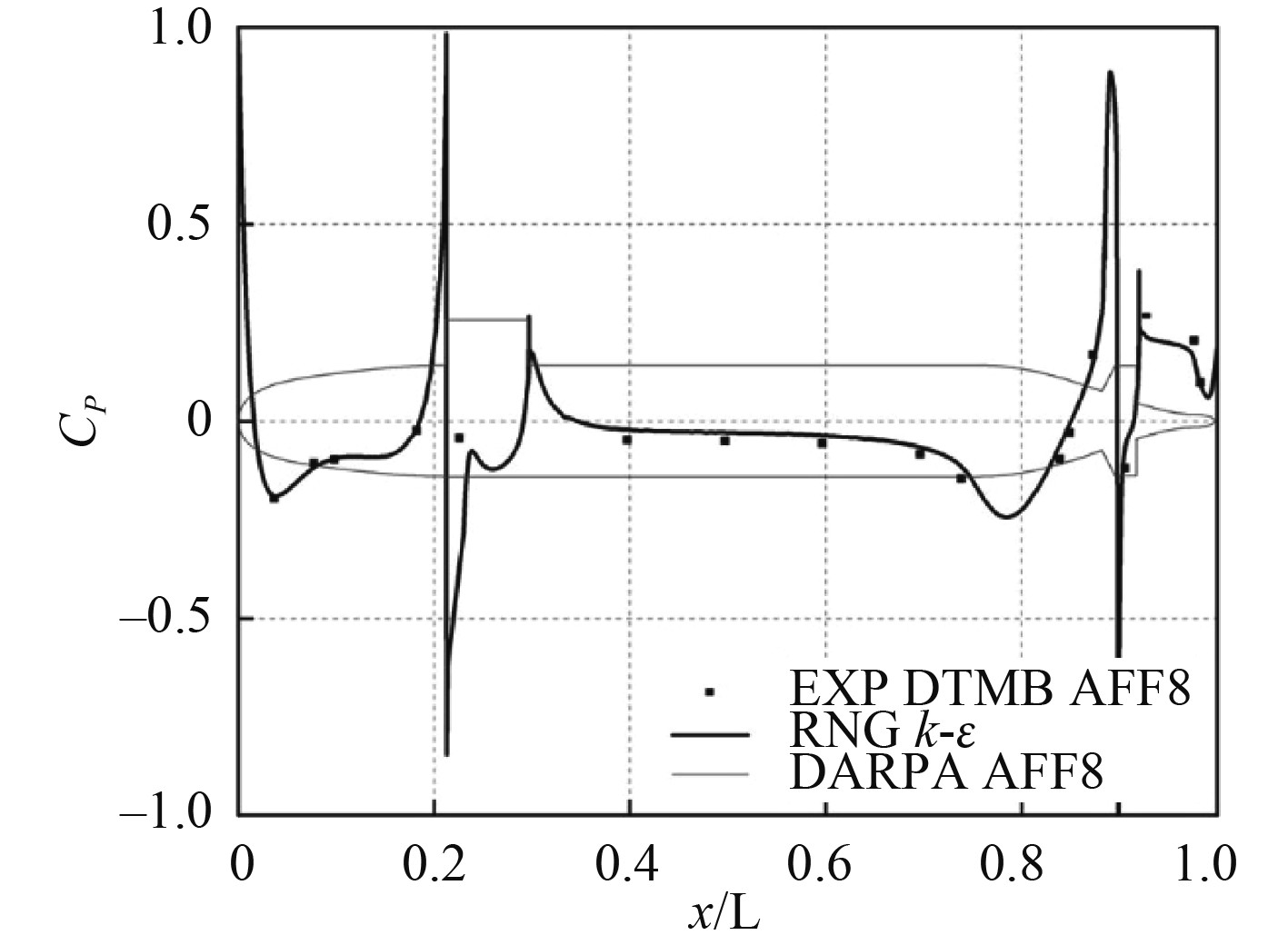
从压力系数与实验值的对比,进一步验证流场模拟的准确度。图4和图5分别为艇体表面静压分布和静压系数

|
图 4 艇体表面静压分布 Fig. 4 Static pressure distribution on submarine surface |
|
图 5 艇体纵中剖面上半缘的静压系数CP Fig. 5 The static pressure coefficient CP of the upper half edge of the submarine longitudinal midsection |
|
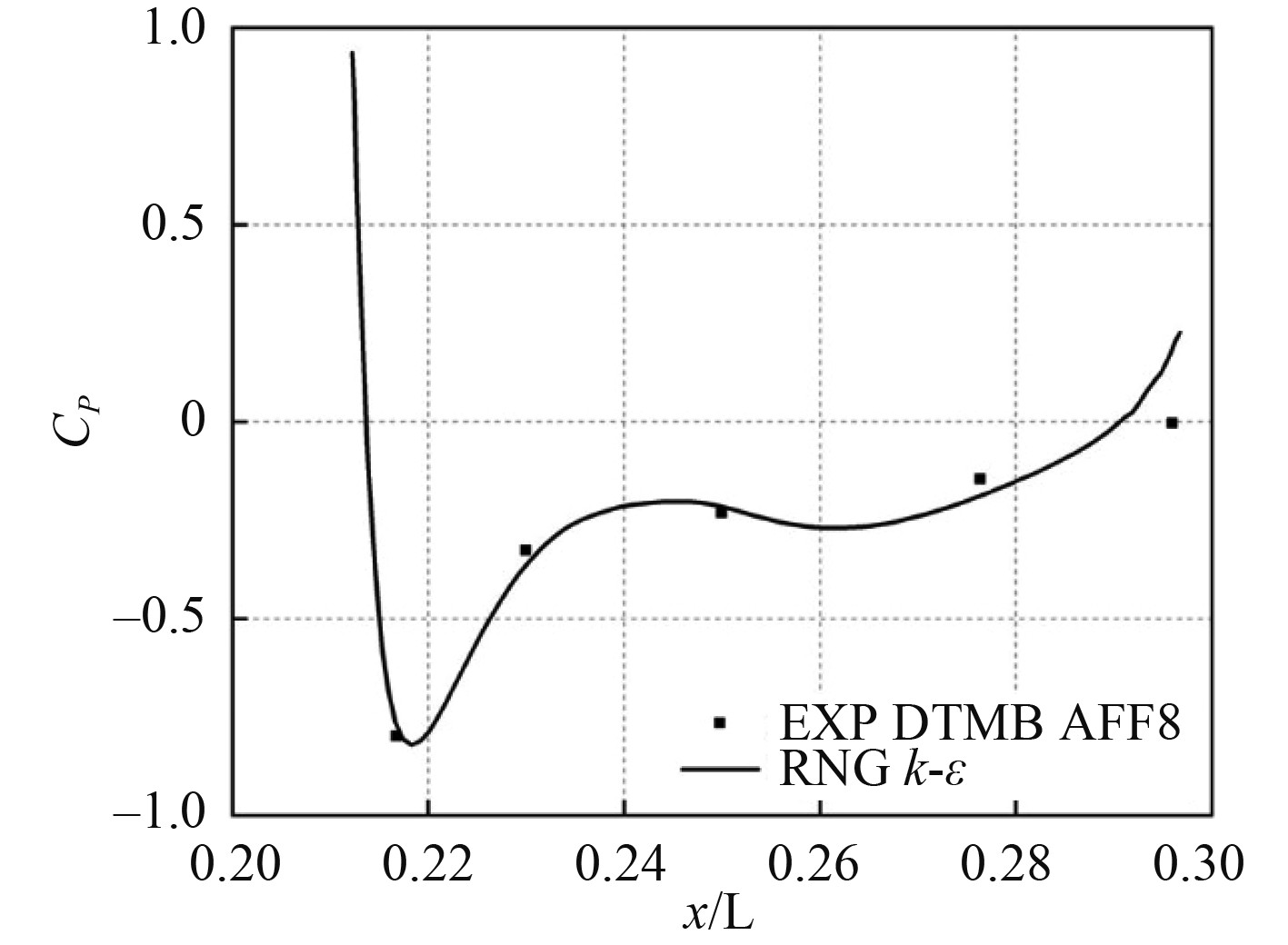
图 6 围壳前缘弦长10% 处的静压系数CP Fig. 6 Static pressure coefficient CP at 10% of the chord length of the front edge of the enclosure |
为了预测电磁噪声的数值大小和分布,沿 x 轴方向在潜艇舷侧设置13部水听器,分别为

|
图 7 水听器安装位置示意图 Fig. 7 Schematic diagram of the installation position of the hydrophone |
实际的海洋环境非常复杂,潜艇在保障通信畅通的同时,还要保证作战性能不受影响。通信过程中潜艇的机动性是影响作战性能的重要因素之一,机动性主要包括对潜艇航速和航向的限制,因此有必要对复杂海洋环境下不同航速和不同航向状态下潜艇的电磁噪声特征进行分析。
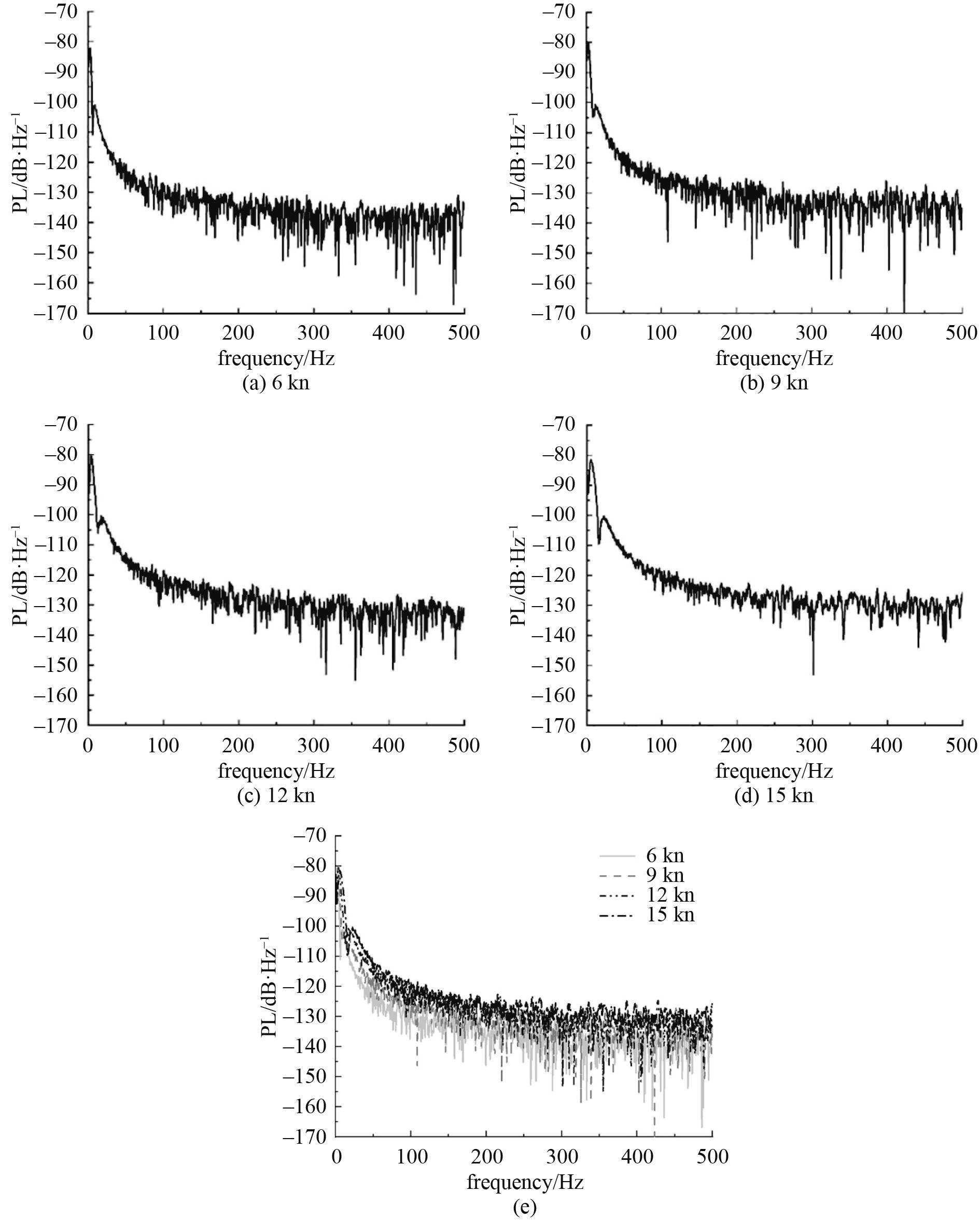
4.1 航速的影响图8为不同航速下
|
图 8
不同航速下
|
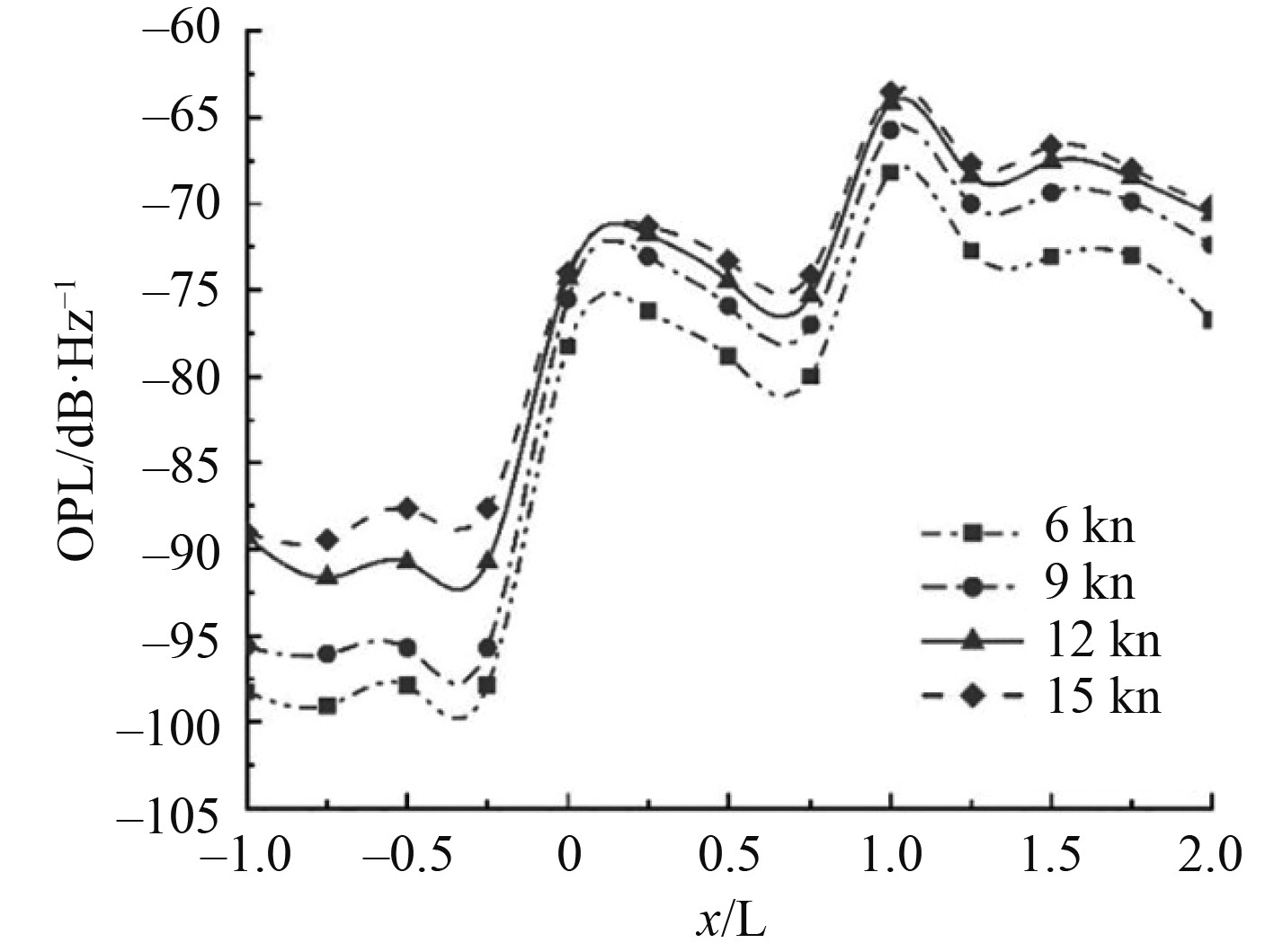
不同航速下噪声总功率级在x轴方向的变化如图9所示。随着航速的增加,同一探测点的OPL不断增大,但增大的幅度逐渐减小。同一航速下上游的OPL比下游的OPL小,噪声OPL变化最大的2个波峰分别出现在
|
图 9 不同航速下OPL在x轴方向的变化 Fig. 9 Variation of OPL in the x-axis direction at different speeds |

|
图 10 xy 平面上潜艇的电场强度分布 Fig. 10 Electric field intensity distribution of submarine on xy plane |
图11为艇体附近不同探测点的航速与OPL的关系曲线图。可知,不同探测点的噪声OPL随着速度的增加不断增大,且相同速度增量下,OPL的增长速率逐渐变缓。
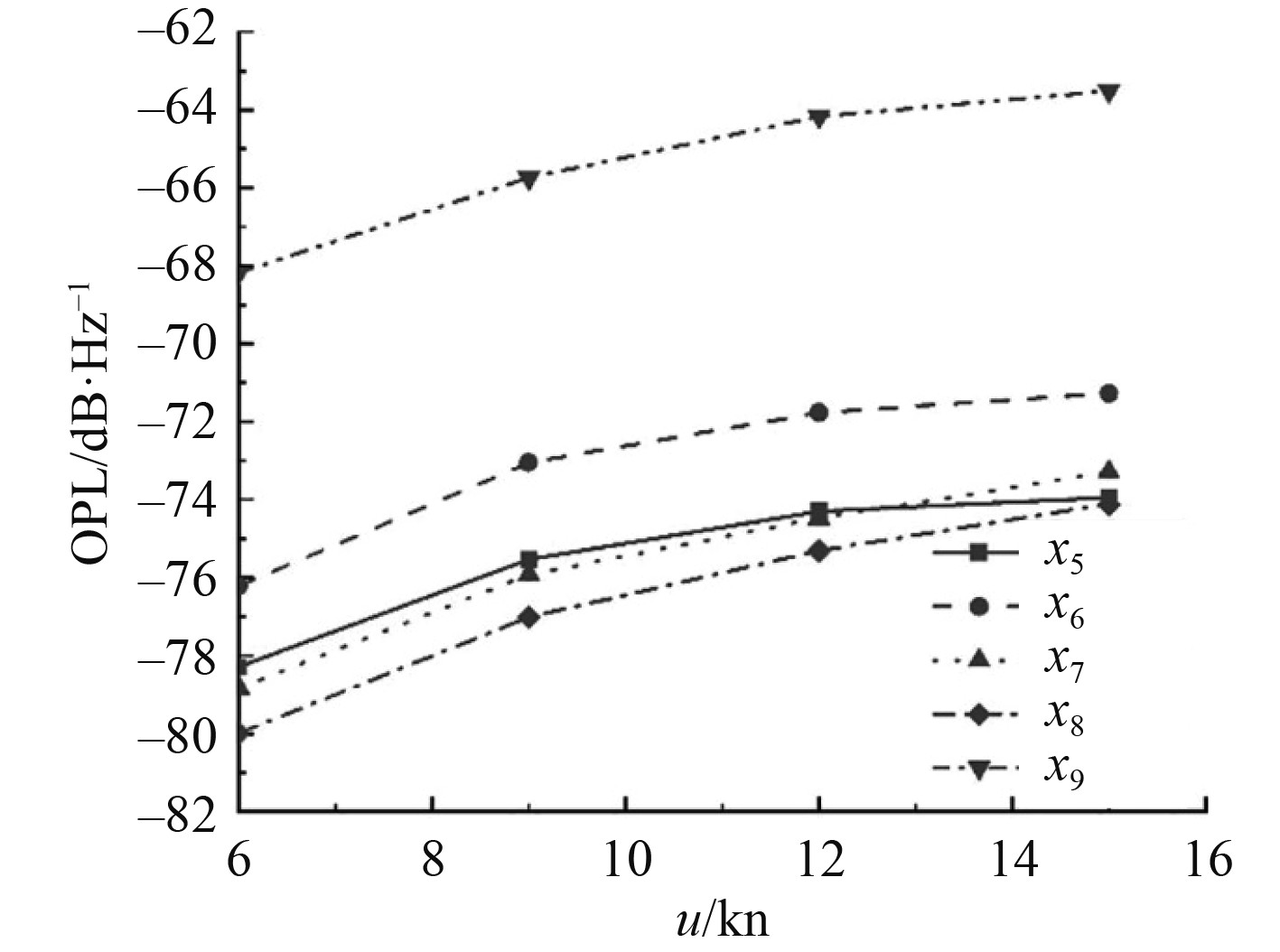
|
图 11 不同探测点的航速与OPL的关系曲线 Fig. 11 Relationship between speed and OPL at different monitoring points |
为了便于分析潜艇航向变化对电磁噪声的影响,建立图12所示的笛卡尔坐标系。以潜艇为坐标原点,其运行方向的反方向为x轴正方向,xoy平面为水平面,z轴垂直于水平面向上。
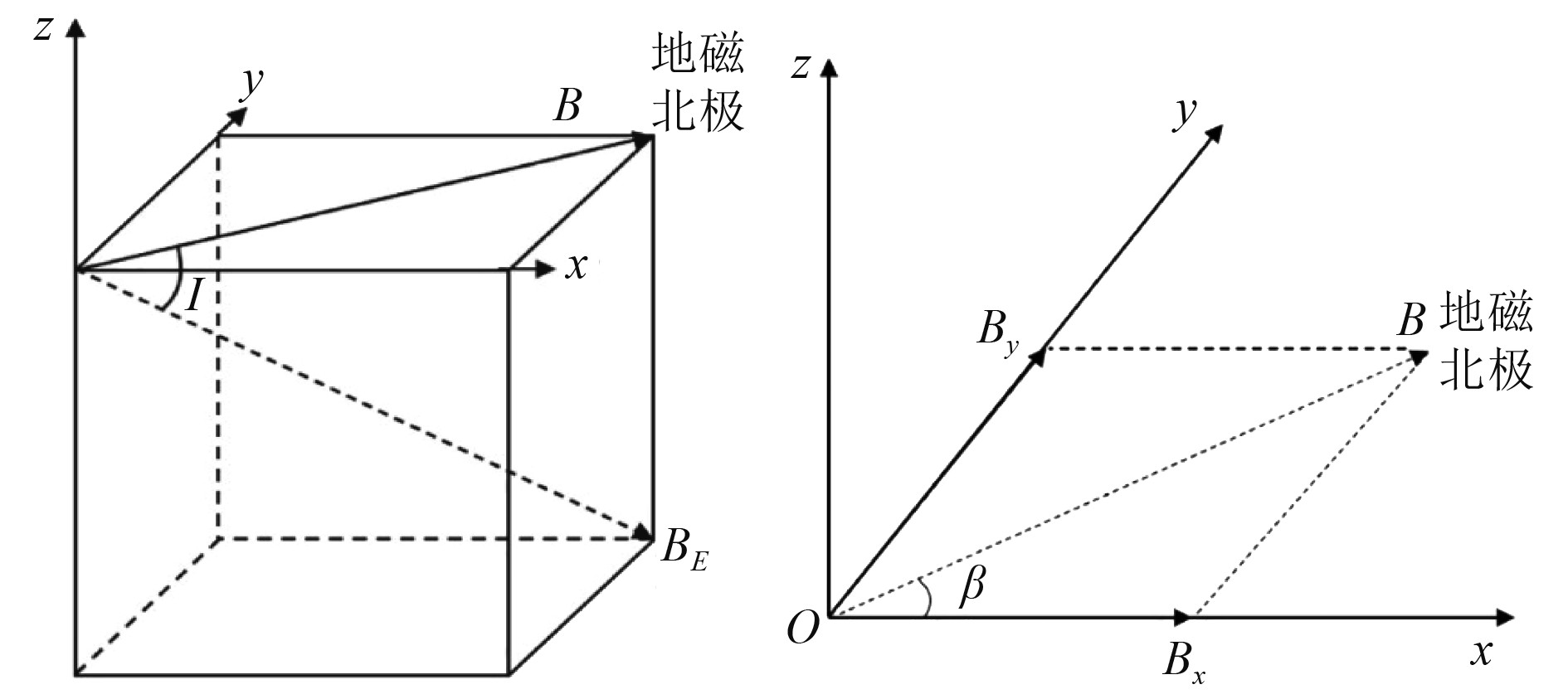
|
图 12 潜艇地磁坐标系 Fig. 12 Geomagnetic coordinate system of submarine |
| $ {B}_{E}=\left|{B}_{E}\right|(\mathrm{cos}I\mathrm{cos}\beta \vec{i}+\mathrm{cos}I\mathrm{sin}\beta \vec{j}-\mathrm{sin}I\vec{k}) 。$ |
本文只考虑水平面内潜艇的航向变化,不考虑俯仰角变化,在给定
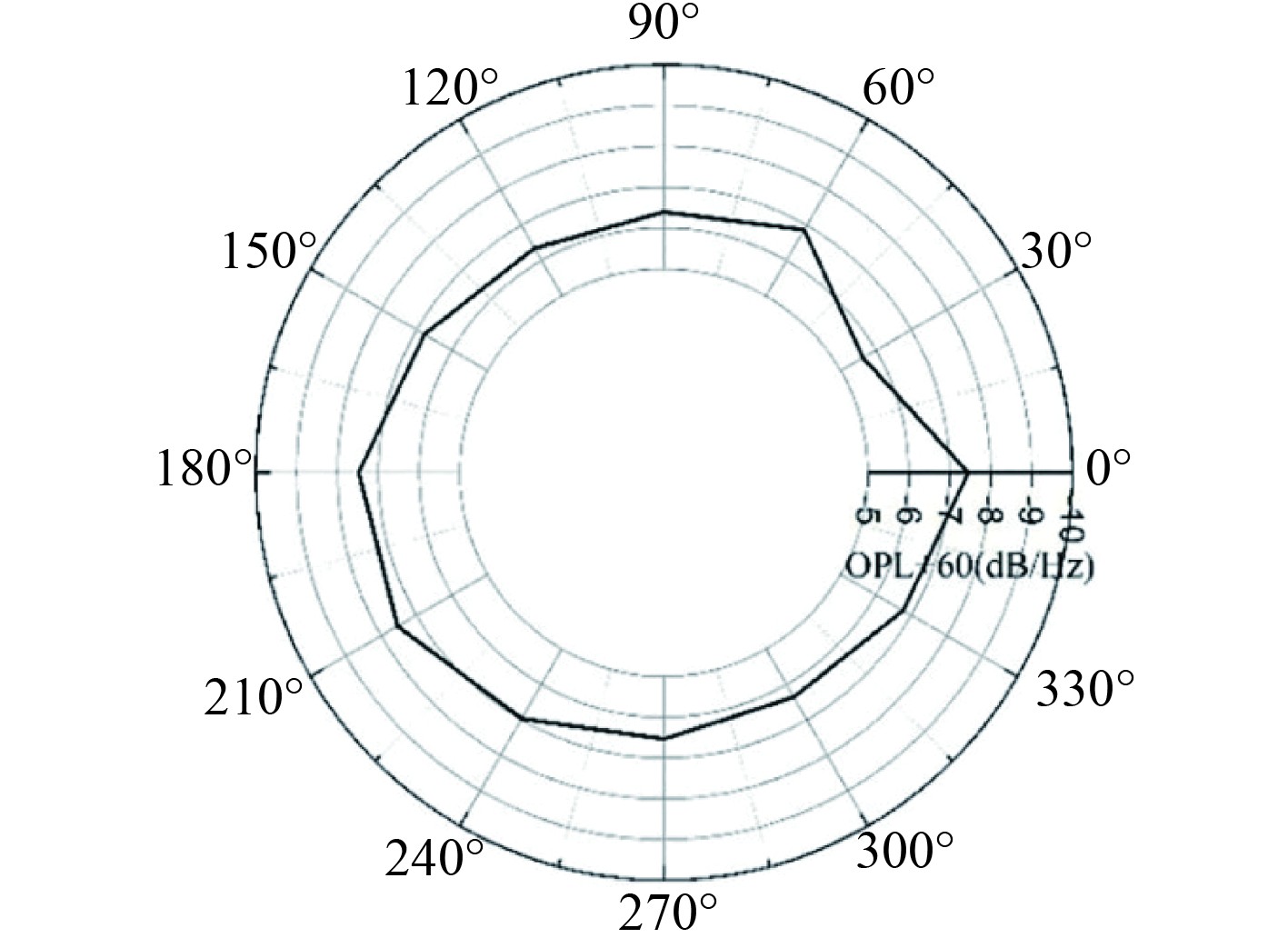
对比了不同航向下
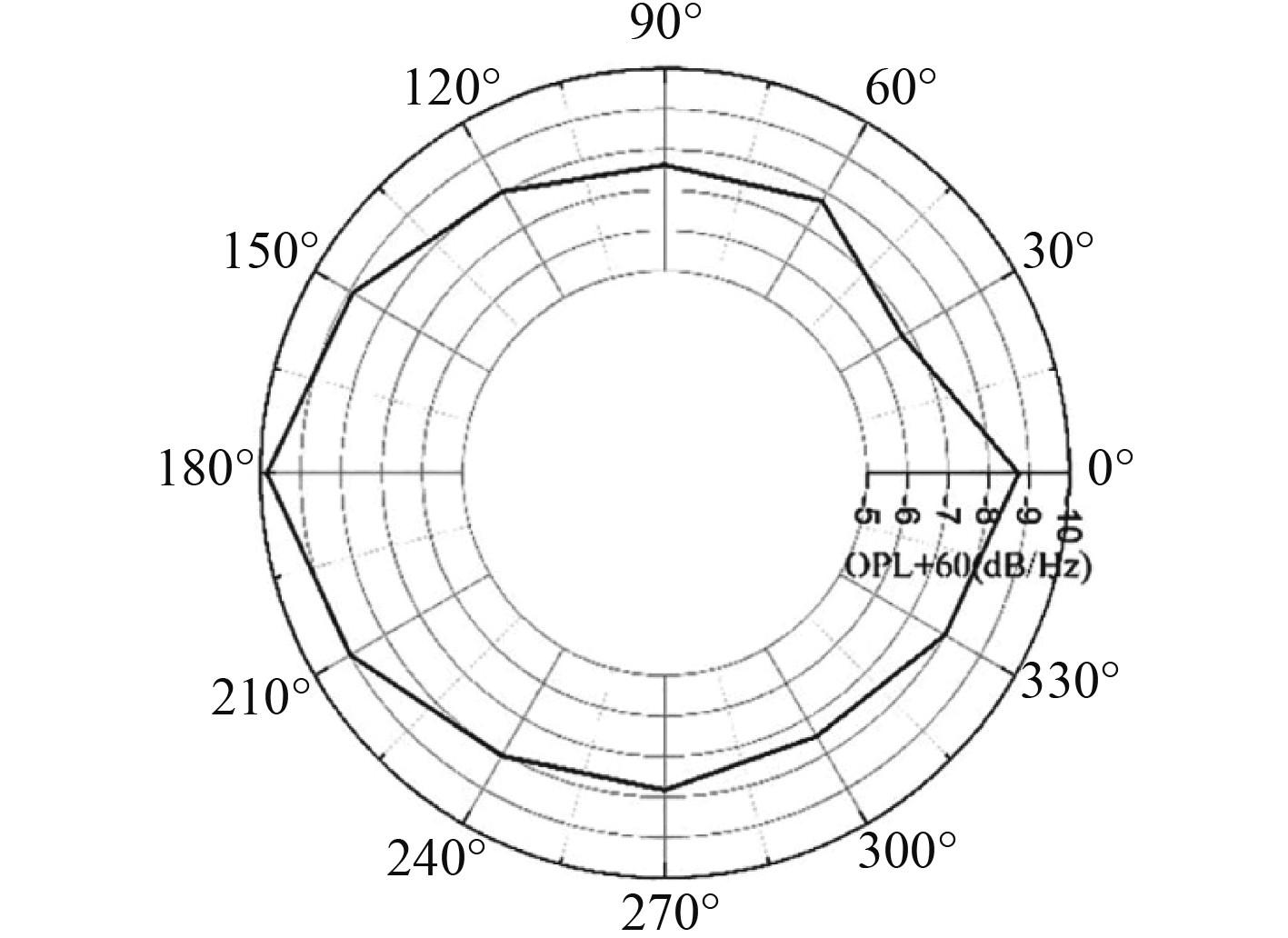
|
图 13
不同航向下 |
|
图 14
不同航向下 |
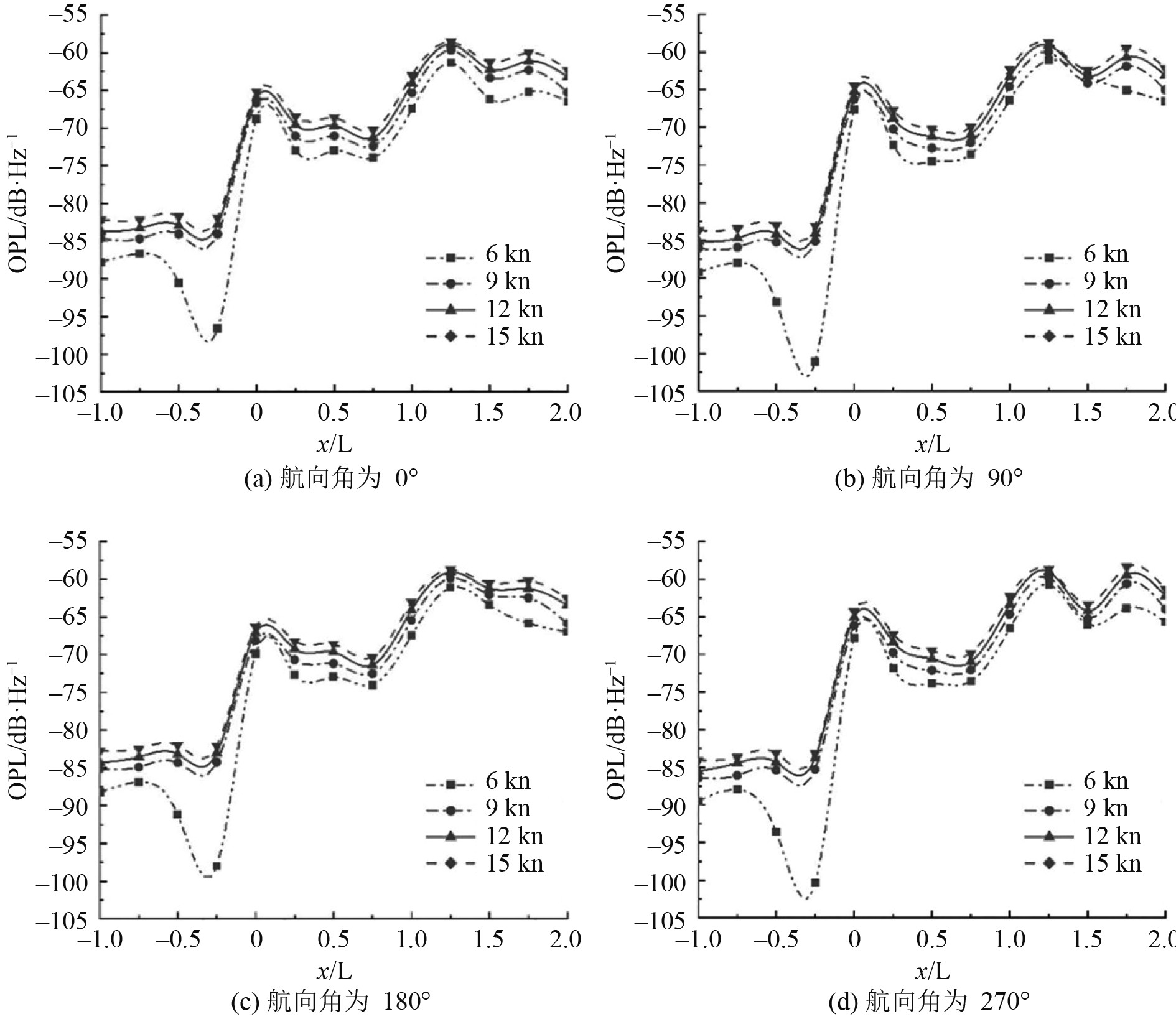
进一步研究航速和航向对电场噪声的共同影响,不同航速和不同航向下OPL在x轴方向的分布如图15所示。从图中可以清楚地看出,4个航向下噪声OPL在x轴方向的变化趋势基本相同。由于上游来流速度比较稳定,总噪声电平始终稳定在 –85 dB/Hz 左右。靠近艇首时由于来流速度变化梯度增大,导致
|
图 15 不同航速和不同航向下OPL在 x 轴方向的变化 Fig. 15 Variation of OPL in the x-axis direction at different speeds and headings |
对潜超低频通信信号会受到很强的电磁噪声干扰,为了研究潜艇周围的复杂流场切割地磁场产生的感应电磁噪声,本文采用多物理场耦合有限元仿真软件Ansys对SUBOFF 潜艇的三维流场进行建模,并对流场的模拟结果进行了分析验证。同时基于电磁学和流体动力学基础理论,提出电磁流体耦合模型,对不同航速和不同航向的复杂海洋条件下流场的感应电磁噪声的频谱特性和变化特征进行分析,得出以下结论:
1)潜艇周围的复杂流场切割地磁场产生的感应电场的噪声频谱是连续谱,具有明显的线谱特征,在低频段内的能量很强。艇首和艇尾是产生电场噪声的2个重要来源,噪声强度的分布具有空间性,与电场信号强度分布基本一致。
2)噪声幅值与航速有着密切的关系,在一定航向下,噪声能量随着航速的增大而增加,反之亦然,且相同速度增量下,OPL的增长速率逐渐变缓。
3)不同航向下的噪声电平变化不大,方向性不显著,各个航向上的噪声分量具有很大的相关性。
4)本文电磁流体耦合模型能够很好地模拟潜艇流场切割地磁场产生的感应电磁噪声,可以为对潜超低频通信电磁噪声的识别和分离提供一定支持。
| [1] |
郭定荣, 陆洪, 陈宇. 船载ULF/VLF对潜通信系统可行性分析[J]. 电波科学学报, 2011, 26(6): 1148-1152. |
| [2] |
孙明, 龚沈光, 周骏, 等. 运动舰船切割地磁场在海水中产生的电场计算[J]. 电子学报, 2003, 31(3): 464-467. |
| [3] |
张伽伟, 熊露, 龚沈光. 运动船舶磁性船体产生的感应电场[J]. 国防科技大学学报, 2015(2): 86-91. DOI:10.11887/j.cn.201502017 |
| [4] |
蒋治国, 陈聪, 谭浩. 舰船水下工频电场特性研究[J]. 华中科技大学学报(自然科学版), 2017, 45(4): 57-60. |
| [5] |
梁成浩, 于楠, 黄乃宝, 等. 船舶腐蚀相关的轴频电场特征[J]. 大连海事大学学报, 2007, 33(1): 1-5. |
| [6] |
ZHANG L, WANG Y, HUANG A. Effect of seawater on radiation field of electric dipole[C]// IEEE China Summit & International Conference on Signal & Information Processing. IEEE, 2014: 800–803.
|
| [7] |
MADURASINGHE, D, TUCK, et al. The induced electromagnetic field associated with submerged moving bodies in an unstratified conducting fluid[J]. Oceanic Engineering, IEEE Journal, 1994, 19(2): 193-199. DOI:10.1109/48.286641 |
| [8] |
张伽伟, 熊露, 姜润翔. 浅海中水下航行器尾流感应电磁场建模与仿真[J]. 系统工程与电子技术, 2016, 38(5): 1004-1009. DOI:10.3969/j.issn.1001-506X.2016.05.06 |
| [9] |
XU ZHIhua, Changping, et al. Evaluation of electromagnetic fields induced by wake of an undersea-moving slender body[J]. IEEE Access, 2017(6): 2943-2951. |
| [10] |
Groves N C , Huang T T , Chang M S . Geometric Characteristics of DARPA (Defense Advanced Research Projects Agency) SUBOFF Models (DTRC Model Numbers 5470 and 5471)[J]. Geometric Characteristics of Darpa Suboff Models, 1989.
|
| [11] |
TENNEKES H, LUMLEY J L. A first course in turbulence [M]. MIT Press, 1972.
|
| [12] |
刘洪杰, 张博, 娄万里, 等. 复杂水流环境下系泊船的水动力特性研究[J]. 舰船科学技术, 2022, 44(1): 1-6. |
| [13] |
LIU H L , HUANG T T . Summary of DARPA Suboff experimental program data[J]. 1998.
|
| [14] |
ITTC, 1957. Report of resistance committee. In: Presented at the Proceedings of 8 th ITTC[C]// Madrid, 1957.
|
| [15] |
孟庆辉, 王永斌, 赵志礼. 潜艇周围影响超低频通信的电磁噪声来源及特征分析[J]. 舰船科学技术, 2009, 31(11): 66-69. |
 2023, Vol. 45
2023, Vol. 45
