2. 中国人民解放军92485部队,辽宁 大连 116000
2. No. 92485 Unit of PLA, Dalian 116000, China
由钢铁材料制造而成的潜艇在地磁场中很容易被磁化,进而产生感应磁场,由于潜艇的铁磁体量较大,其出现会造成周围较大范围的地磁场畸变,产生磁异常效应[1-2]。随着弱磁探测技术的发展及其在航空平台上的成熟应用,潜艇磁场已成为反潜探测的重要信息源,潜艇磁场的计算对评估潜艇磁性状态、预报磁暴露概率、支撑反潜磁异探测等都有重要意义。
磁偶极子模型最常见的磁场计算方法,是指由位于目标中心的单个磁偶极子描述目标外部磁场的强度分布特性,该方法在潜艇或其他铁磁物磁场的估算中被广泛使用[3-6],在此基础上,很多研究对潜艇或类似铁磁目标的磁场模型进行了进一步的改进[7-12]。刘辉[7]在此基础上提出了同点的三轴磁偶极子数学解析模型,并明确了地磁感应下磁偶极矩的估算方法,能够根据地磁场值、潜艇尺寸及航向等推算得到潜艇磁异常。但总体来说单个磁偶极子模型相对真实潜艇的磁特性而言被严重简化,导致在计算时存在较大的误差,该误差随着场点与源点距离的变化而不同。张朝阳等[8]指出在探测距离较小(小于2.5倍铁磁体尺寸)时,该模型计算误差过大而不再推荐使用;周家新等[9]改进了该方法,用分布于潜艇内部的有限个磁偶极子阵列的叠加来描述潜艇磁状态,相比单个磁偶极子模型,在描述潜艇磁场近场特性的准确度上得到了提升。王金根[10]建立了磁偶极子阵列与椭球体模型的混合模型,提出了近、远场均适用的潜艇外空间磁场计算方法,但这种方法依赖于磁偶极子的数量与每个磁偶极子磁矩的定义值,在实际使用时难以量化。
为解决简单磁偶极子模型准确度低,磁偶极子阵列与椭球体混合模型计算复杂切量化困难的问题,本文提出一种新的潜艇外空间磁场计算方法,并推导出数学模型,在计算潜艇磁场随着位置、距离等的变化规律时,具有更高的准确度。
1 单个偶极子模型磁偶极子是最基本的磁单元,在磁场分析中有着重要的作用,潜艇的磁偶极子模型则是将潜艇对外总磁矩等价于一个位于中心位置的磁偶极子,其磁矩
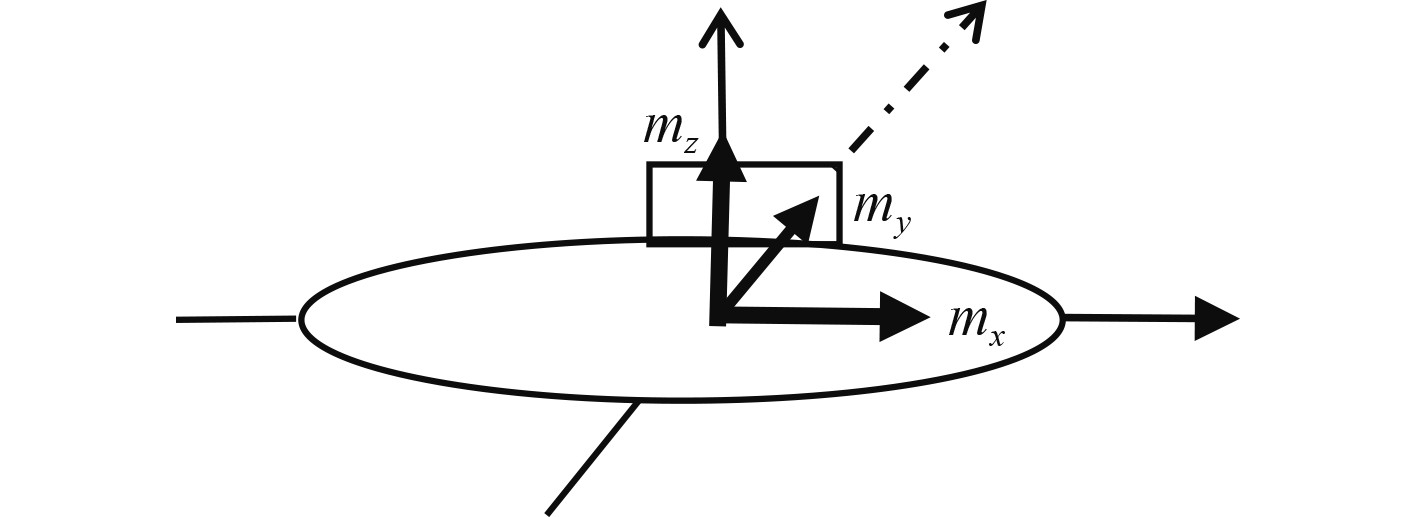
|
图 1 潜艇的单个磁偶极子模型 Fig. 1 Single magnetic dipole model for submarines |
则其在空间产生的磁场分为:
| $ \left[ {\begin{array}{*{20}{c}} {{B_{{x}}}} \\ {{B_{{y}}}} \\ {{B_{ {z}}}} \end{array}} \right] = N \cdot \vec M = N \cdot \left[ {\begin{array}{*{20}{c}} {{m_x}} \\ {{m_y}} \\ {{m_z}} \end{array}} \right],$ | (1) |
其中N为系数矩阵:
| $ \begin{gathered} N = \dfrac{{{\mu _0}}}{{4 \text{π} {r^5}}} \times \\ \left[ {\begin{array}{*{20}{c}} {2{x^2} - {y^2} - {z^2}}&{3xy}&{3xz} \\ {3yx}&{2{y^2} - {x^2} - {z^2}}&{3yz} \\ {3zx}&{3zy}&{2{z^2} - {x^2} - {y^2}} \end{array}} \right]。\end{gathered} $ | (2) |
潜艇磁偶极子模型是大量简化后的近似模型,不需要复杂计算,给潜艇磁异常的估算带来了方便,在对精度要求不高或者远距离探测条件下,可用于潜艇磁场的粗略估算。
2 潜艇磁场的椭球壳 2.1 潜艇与椭球壳的等效性如图2所示,潜艇舰桥尺寸相比整个潜艇很小,因此对潜艇感应磁场的贡献微弱,基本可以忽略。将潜艇看作旋转椭球体,由于潜艇是中空结构,铁磁物质主要集中在壳体附近,因此等价于旋转椭球壳则更为恰当[13-15]。

|
图 2 潜艇与旋转椭球体对比 Fig. 2 Submarine vs spheroid |
地磁场在潜艇的尺度范围内可以看作是匀强场,其大小与方向在该范围内保持不变,潜艇的感应磁场来源于其在地磁场中的磁化,研究证明在均匀外场下,只有旋转椭球体或椭球壳的内部磁化是均匀的[16-17],说明旋转椭球体在均匀外场中的磁化特性能够被严格计算,这也是要将潜艇等价于旋转椭球壳模型的重要原因。
2.2 椭球壳面磁矩密度铁磁学中磁化强度定义的是磁矩体密度,为方便计算薄壳铁磁体模型的磁场,提出面磁矩密度的概念定义,即假设椭球壳被磁化后的磁矩都集中在壳体表面,如图3所示,整个潜艇的磁矩是由无数个分布在壳体上的小磁矩叠加而成,由于潜艇壳体的厚度相比潜艇尺寸来说很小,因此不会引入较大的误差。

|
图 3 椭球壳磁矩面分布示意图 Fig. 3 Schematic diagram of distribution of magnetic moment surface of ellipsoid shell |
如图4所示,定义面磁矩密度矢量
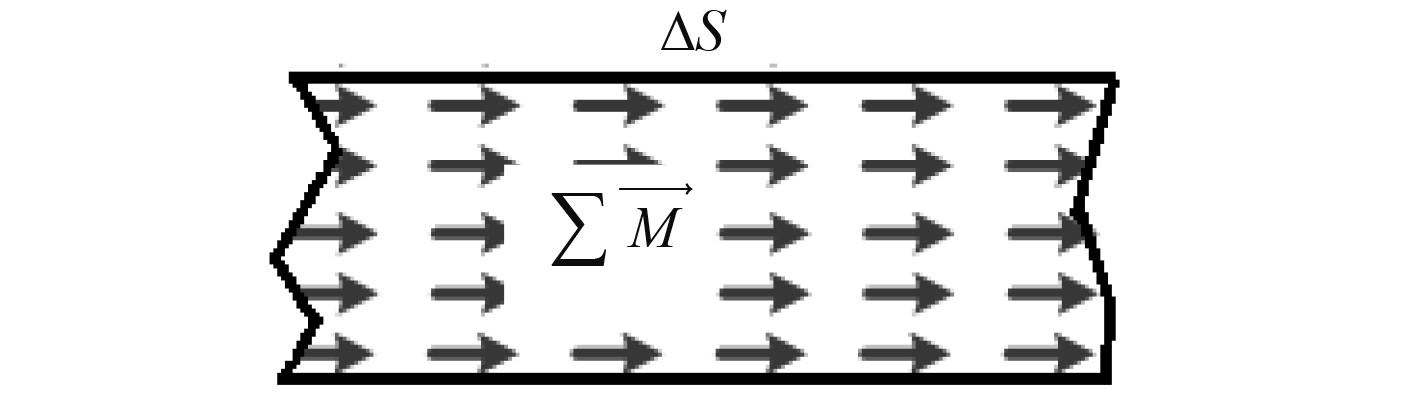
|
图 4 面磁矩密度定义 Fig. 4 Surface magnetic moment density definition |
考虑到椭球壳在均匀外场中的磁化均匀,说明椭球体表面任意位置上的面磁矩密度均相等,面磁矩密度不随着其在椭球表面上的位置而变化,则面磁矩密度可以表示为:
| $ {\vec m_{\text{s}}}{\text{ = }}\dfrac{{\vec M}}{S} 。$ | (3) |
式中:
| $ \dfrac{{x_i^2}}{{{a^2}}}{\text{ + }}\dfrac{{y_i^2{\text{ + }}z_i^2}}{{{b^2}}} = 1。$ | (4) |
椭球体表面积的近似计算为:
| $ \left\{ \begin{aligned} & S= 2\text{π} ({b^2} + \dfrac{{a \cdot b}}{e} \cdot \arcsin (e)) ,\\ & e = \dfrac{{\sqrt {{a^2} - {b^2}} }}{a} 。\end{aligned} \right. $ | (5) |
如图5所示,以旋转椭球面的正中心为坐标原点,以长轴为x轴垂直向上和水平面方向为y和z轴,建立直角坐标系,该椭球面沿着长轴x方向旋转而成。
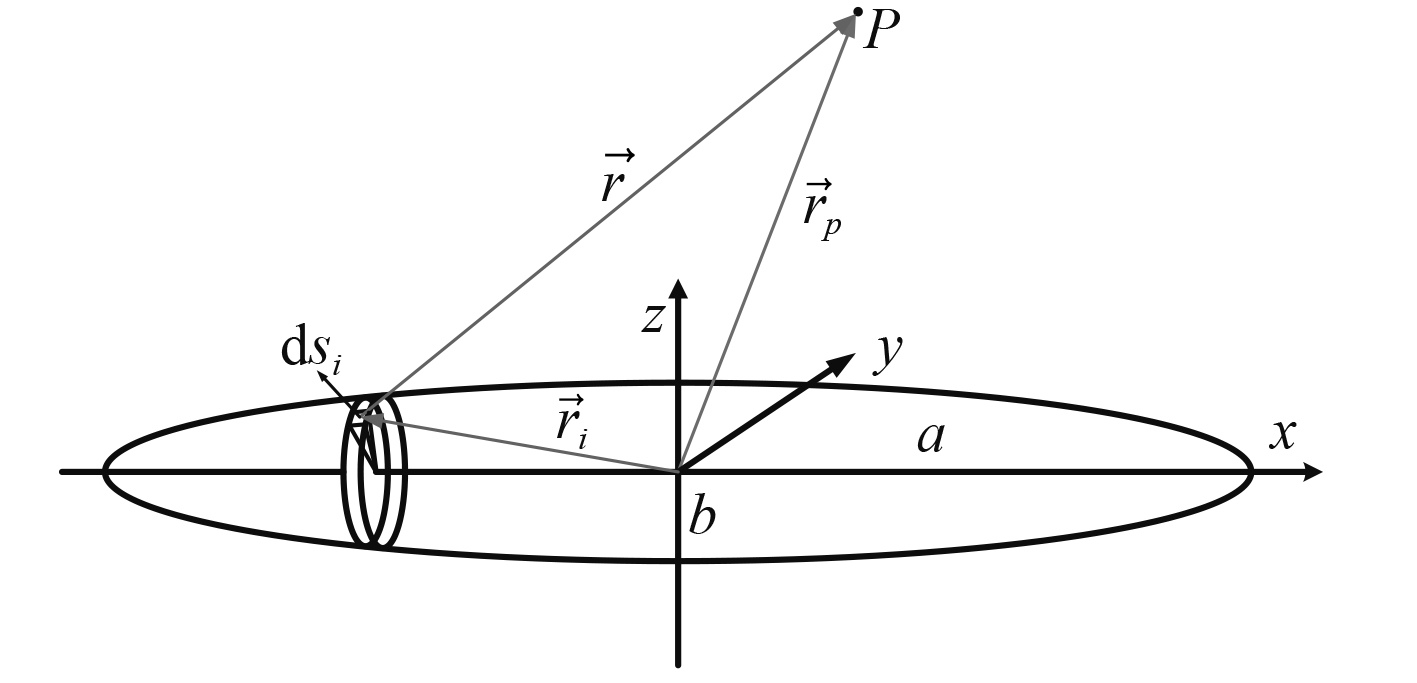
|
图 5 面磁矩元磁场计算示意图 Fig. 5 Schematic diagram of magnetic field calculation of surface magnetic moment element |
在椭球面上取一微分面元
| $ {\rm{d}}\vec B{\text{ = }}N \cdot {\vec m_{\text{s}}} \cdot {\rm{d}}{s_i}。$ | (6) |
其中N为式(2)所表达的磁偶极子磁场系数矩阵,且有:
| $ \left\{ {\begin{array}{*{20}{c}} {x = {x_p} - {x_i},\begin{array}{*{20}{c}} {}&{}&{} \end{array}} \\ {y = {y_p} - {y_i},\begin{array}{*{20}{c}} {}&{}&{} \end{array}} \\ {z = {z_p} - {z_i},\begin{array}{*{20}{c}} {}&{}&{} \end{array}} \\ {r = \sqrt {{x^2} + {y^2} + {z^2}} } 。\end{array}} \right. $ | (7) |
设面元
| $ {\rm{d}}{s_i}{\text{ = }}\dfrac{{{\rm{d}}{x_i} \cdot l \cdot {\text{d}}\theta }}{{{\text{2}}\text{π} }} ,$ | (8) |
其中l为
则有:
| $ {\rm{d}}{s_i}{\text{ = }}b\sqrt {1 - \dfrac{{{x_i}^2}}{{{a^2}}}} \cdot {\rm{d}}{x_i} \cdot {\text{d}}\theta 。$ | (9) |
根据式(5):
| $ \begin{gathered} {\rm{d}}\vec B{\text{ = }}N \cdot {{\vec m}_{\text{s}}} \cdot {\rm{d}}{s_i}= \\ N \cdot \dfrac{{\vec M}}{S} \cdot b \cdot \sqrt {1 - \dfrac{{{x_i}^2}}{{{a^2}}}} \cdot {\rm{d}}{x_i} \cdot {\text{d}}\theta 。\end{gathered} $ | (10) |
根据式(4),系数矩阵N中yi和zi可表达为:
| $ \left\{ \begin{aligned} & {x_i} = {x_i},\\ & {{y_i} = b\sqrt {1 - \dfrac{{{x_i}^2}}{{{a^2}}}} \cdot \cos \theta },\\ & {{z_i} = b\sqrt {1 - \dfrac{{{x_i}^2}}{{{a^2}}}} \cdot \sin \theta } 。\end{aligned} \right. $ | (11) |
由矢量场的叠加原理可知,整个椭球壳产生的磁场即是所有面微分元产生磁场的积分,最终可得面磁矩分布的椭球壳模型在场点P处产生的磁场为:
| $ \vec B{\text{ = }}\oint {{\rm{d}}\vec B} {\text{ = }}\int_{ - a}^a {\int_0^{2\text{π} } {N \cdot \dfrac{{\vec M}}{S} \cdot b\sqrt {1 - \dfrac{{{x_i}^2}}{{{a^2}}}} \cdot {\rm{d}}{x_i} \cdot {\text{d}}\theta } } 。$ | (12) |
在潜艇与旋转椭球壳的近似等效下,建立了磁场潜艇磁场
相比单个磁偶极子模型,基于面磁矩分布的潜艇磁场模型计算较为复杂,但更贴近真实情况。因为一般在用于测量或探测潜艇磁场的探测器有效距离内,潜艇100 m左右的尺寸都不适合看作单个磁偶极子处理,为对比分析2种计算方式的差异性,假设潜艇是沿着长轴磁化的,且总磁矩取值为
图6分别为测量高度50 m时,面磁矩分布模型(B1)同单个磁偶极子模型(B2)磁场的x,z方向分量对比,其中水平坐标是潜艇模型的x轴向距离,对于x方向磁化的潜艇模型,在其轴线上方磁场的y方向分量始终为0。
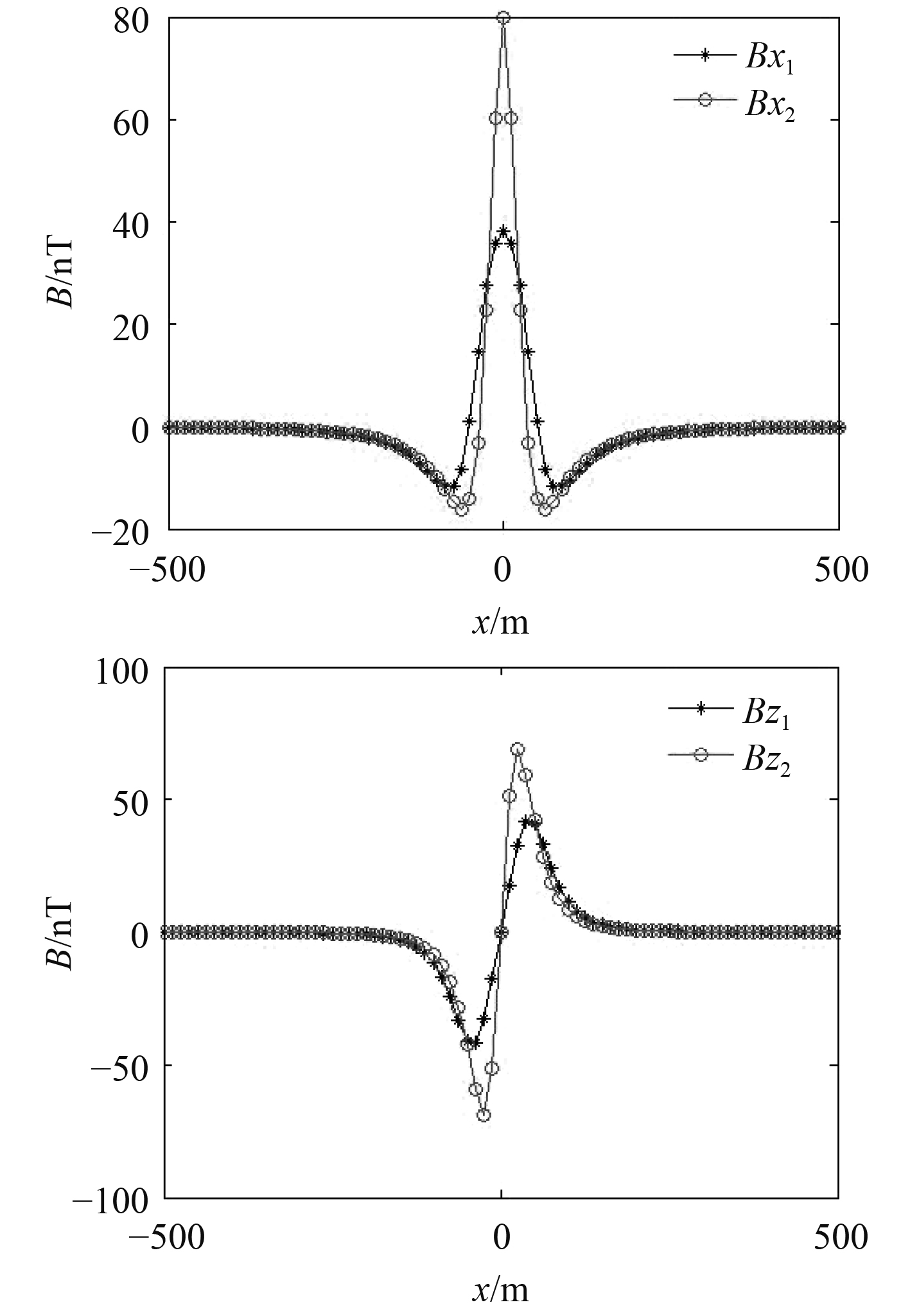
|
图 6 上方50 m高度上磁场x,z分量对比 Fig. 6 Comparison of the x and z components of the magnetic field at a height of 50 m above |
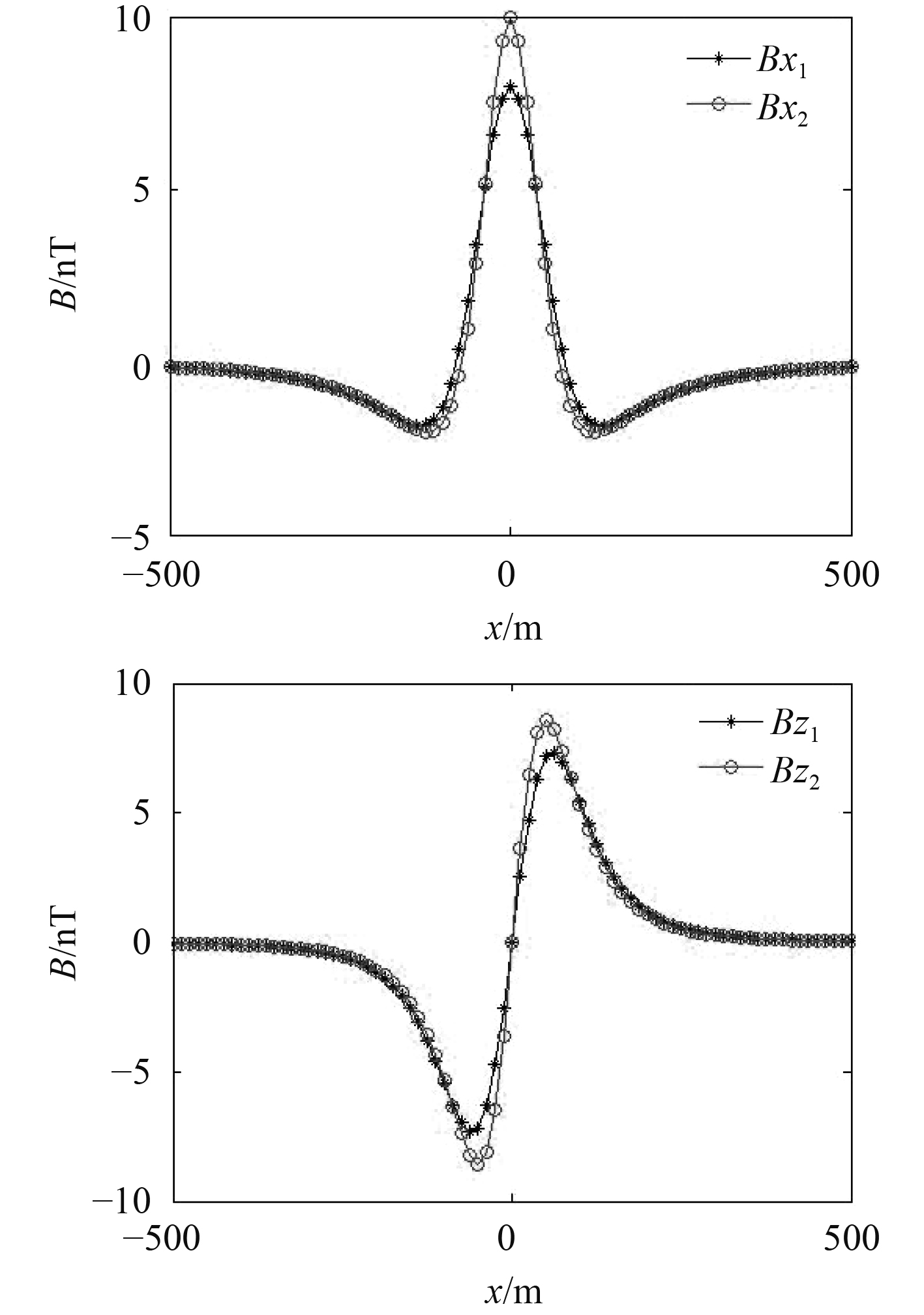
图7分别为测量高度100 m时,面磁矩分布模型(B1)同单个磁偶极子模型(B2)磁场的x方向,z方向分量对比。
|
图 7 上方100 m高度上磁场x,z分量对比 Fig. 7 Comparison of the x and z components of the magnetic field at a height of 100 m above |
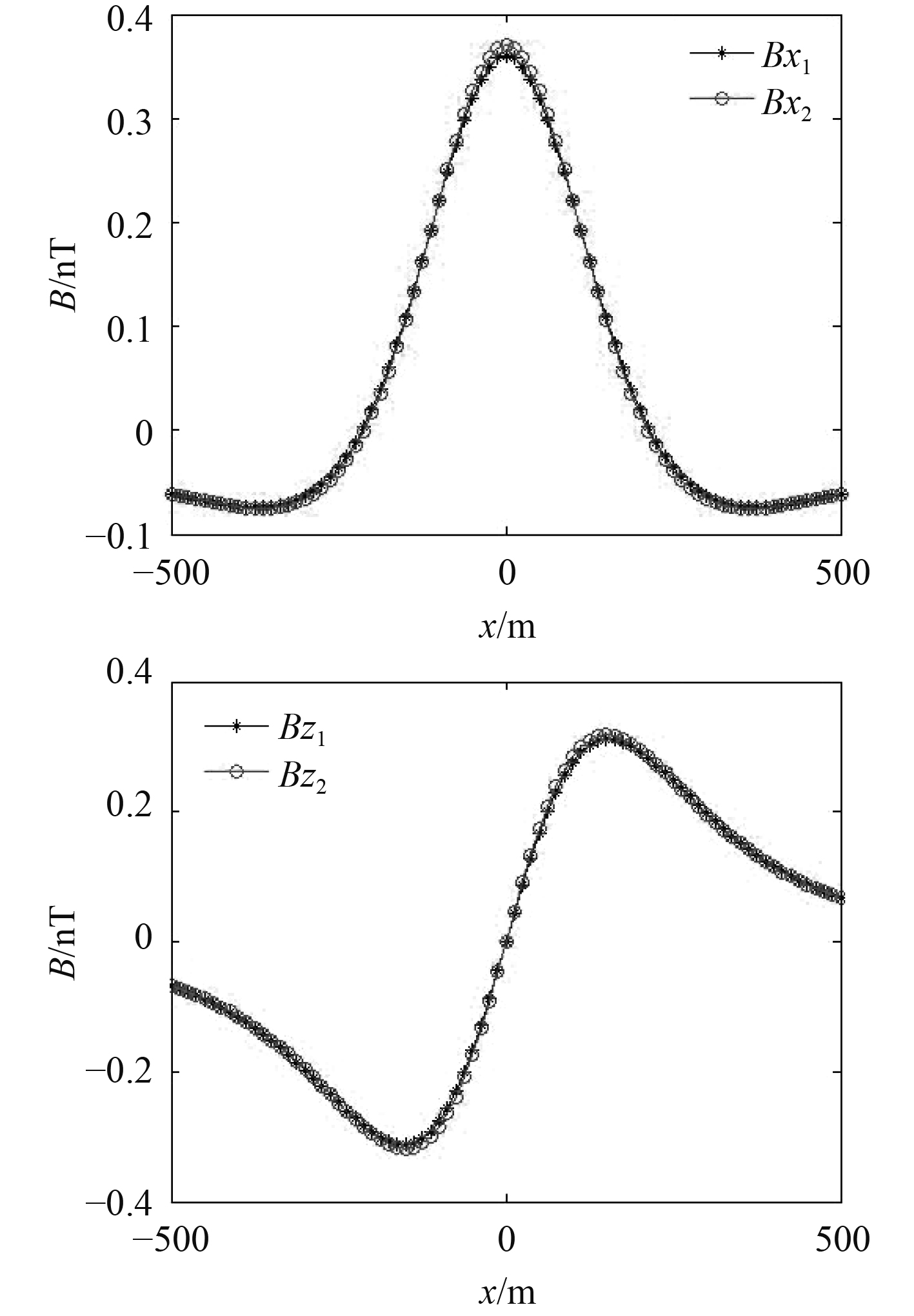
图8分别为测量高度300 m时,面磁矩分布模型(B1)同单个磁偶极子模型(B2)磁场的x方向、z方向分量对比。
|
图 8 上方300 m高度上磁场x,z分量对比 Fig. 8 Comparison of the x and z components of the magnetic field at a height of 300 m above |
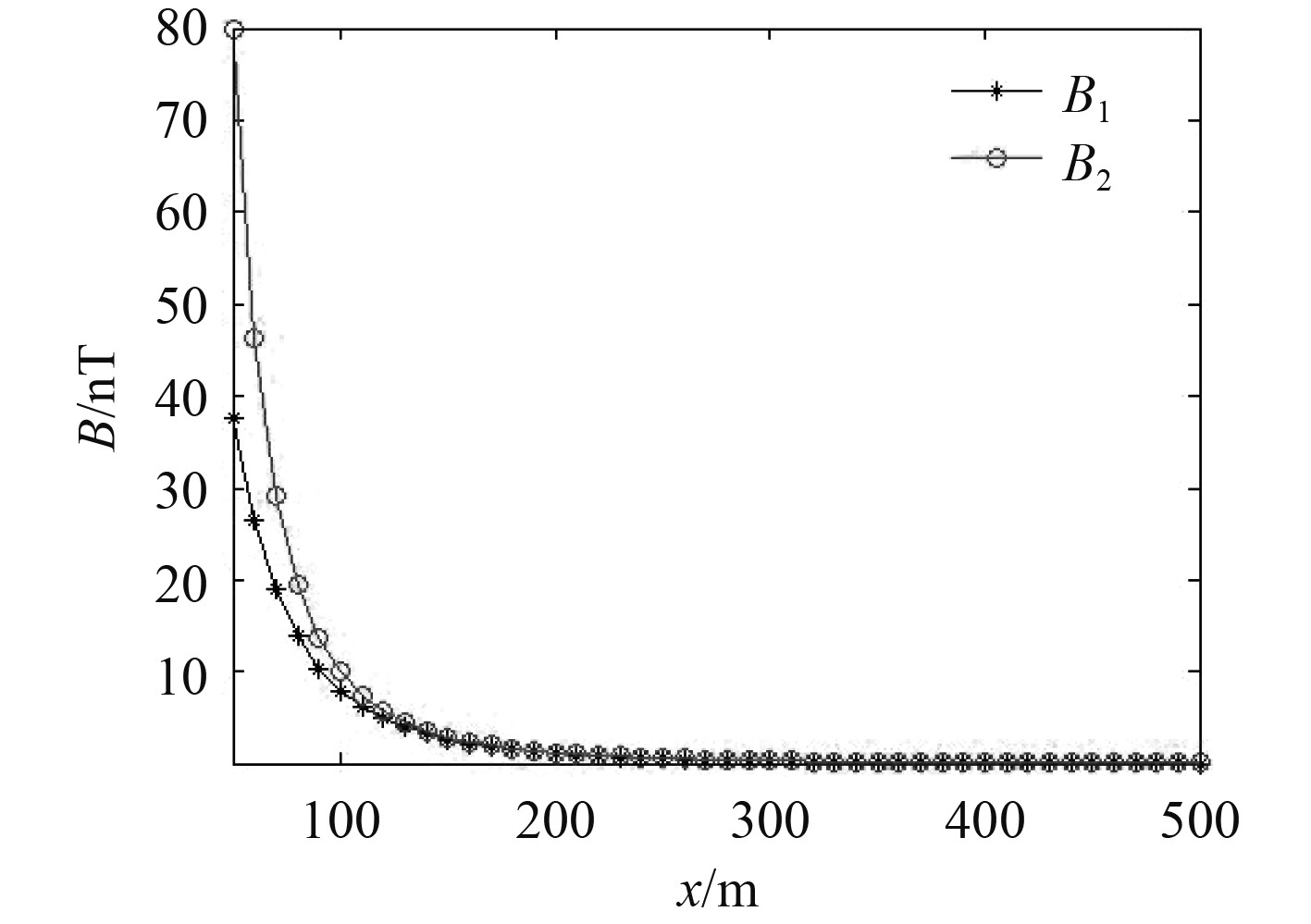
可以看出,随着测量高度的增加,2种模型的计算结果差异在逐步减小,测量高度50 m时,面磁矩分布模型的计算结果约只有磁偶极子模型的1/2,但当高度增加到300 m时几乎完全相同。将二者磁场的最大值随着距离的变化进行对比,如图9所示。
|
图 9 2种模型磁场最大值随着距离的变化 Fig. 9 The variation of the maximum magnetic field value with distance for the two models |
由此可见,在远距离探测时(探测距离大于潜艇长度3倍),可以将潜艇磁场看作单个磁偶极子模型,但在近距离测量、推算、评估潜艇磁性时,若将潜艇模型看作简单的磁偶极子模型处理,则会引入较大的误差,距离越近误差越大,与其他潜艇磁场模型的研究结论基本吻合[18-19]。
5 结 语本文将潜艇看作旋转椭球壳,并根据椭球壳在外场下的磁化特性,提出面磁矩密度的概念,以及基于面磁矩分布的潜艇磁场计算方法。通过对分布在壳体表面上的无限个磁矩面元的积分,建立了潜艇磁场的面磁矩分布计算模型,同单个磁偶极子模型对比,得到以下结论:
1)在近距离上,面磁矩模型与磁偶极子模型的计算结果存在较大差异,面磁矩模型的磁场在强度上要明显小于磁偶极子模型,且水平分量比垂直分量更明显。
2)随着距离的增加,2种模型计算结果的差异在逐渐减小,面磁矩模型下磁场的衰减要小于偶极子的三次方,衰减速度较慢。
3)在距离大于3倍潜艇尺寸时,潜艇磁场可作为单个磁偶极子模型进行处理,不会引入较大的误差。
本文研究的主要意义在于,在由潜艇磁场的实测数据推算潜艇磁性状态时,可取代单个磁偶极子模型,提高潜艇磁性状态评估的准确度,对潜艇磁场分布特性的推演、磁矩的估算以及消磁状态评估等都有重要的意义。本文建立了潜艇磁场的正演模型,在后续研究中,还将开展基于该模型的潜艇磁性状态反演评估方法研究。
| [1] |
义井胤景, 著. 胡超, 译. 磁工学[M]. 北京: 国防工业出版社, 1977.
|
| [2] |
叶平贤, 龚沈光. 舰船物理场[M]. 北京: 兵器工业出版社, 1992.
|
| [3] |
MCAULAY A D. Computerized model demonstrating magnetic submarine localization[J]. Transactions on Aerospace and Electronic Systems, 1977, 13(3): 246-254. |
| [4] |
GANG Yin, PING Li, ZHI Wei, et al. Magnetic dipole localization and magnetic moment estimation method based on normalized source strength[J]. Journal of Magnetism and Magnetic Materials, 2020, 502: 166450. DOI:10.1016/j.jmmm.2020.166450 |
| [5] |
庞学亮, 林春生, 张宁. 一种基于磁偶极子模型的潜艇信号检测方法[J]. 海军工程大学学报, 2011, 23(1): 73-76. PANG X L, LIN C S, ZHANG N. A new method of signal detection and parameter estimation based on magnetic dipole model[J]. Journal of Naval University of Engineering, 2011, 23(1): 73-76. DOI:10.3969/j.issn.1009-3486.2011.01.015 |
| [6] |
张朝阳, 虞伟乔. 基于磁偶极子等效的潜艇空间磁场分布[J]. 舰船科学技术, 2013, 35(1): 31-34. ZHANG Z Y, YU W Q. Research on spatial magnetic field distributing of submarine based on magnetic dipole equivalent[J]. Ship Science and Technology, 2013, 35(1): 31-34. |
| [7] |
刘辉. 基于感应磁场的潜艇磁异常计算模型[J]. 水下无人系统学报, 2018, 26(2): 152-160. LIU H. Magnetic Anomaly calculation model of submarine based on induced magnetic field[J]. Journal of Unmanned Undersea Systems, 2018, 26(2): 152-160. |
| [8] |
张朝阳, 肖昌汉, 高俊吉, 等. 磁性物体磁偶极子模型适用性的试验研究[J]. 应用基础与工程科学学报, 2010, 18(5): 862-868. ZHANG C Y, XIAO C H, GAO J J, et al. Experim research of magnetic dipole model applicability for a magnetic object[J]. Journal of Basic Science and engineering, 2010, 18(5): 862-868. DOI:10.3969/j.issn.1005-0930.2010.05.016 |
| [9] |
周家新, 陈建勇, 单志超, 等. 航空磁探中潜艇磁场建模方法分析[J]. 海军航空工程学院学报, 2017, 32(1): 143-148. ZHOU J X, CHEN J Y, SHAN Z C, et al. Analysis of submarine magnetic field modeling method for aero magnetic detection[J]. Journal of Naval Aeronautical and Astronautical University, 2017, 32(1): 143-148. DOI:10.7682/j.issn.1673-1522.2017.01.008 |
| [10] |
王金根, 龚沈光, 刘胜道. 磁性目标的高精度建模方法[J]. 海军工程大学学报, 2001, 13(3): 49-52. WANG J G, GONG S G, LIU S D. High accuracy method for modelling magnetic objects[J]. Journal of Naval University of engineering, 2001, 13(3): 49-52. DOI:10.3969/j.issn.1009-3486.2001.03.012 |
| [11] |
NEYMAN V YU, MARKOV A V. Comparison of finite element modelling of a magnetic field by the example of solving the magnetostatics problem[J]. Journal of Physics:Conference Series, 2020, 1661(1): 012067. DOI:10.1088/1742-6596/1661/1/012067 |
| [12] |
朱武兵, 庄劲武, 赵文春, 等. 载体感应磁场的改进积分方程法[J]. 国防科技大学学报, 2018, 40(3): 101-106. ZHU W B, ZHUANG J W, ZHAO W C, et al. Modified integral equation method for carrier's induced magnetic field solving[J]. Journal of National University of Deffense Technology, 2018, 40(3): 101-106. DOI:10.11887/j.cn.201803016 |
| [13] |
章尧卿, 毛世超. 潜艇空间磁场的建模分析与运用[J]. 舰船电子工程, 2018, 38(1): 136-139. ZHANG Y Q, MAO S C. Modeling analysis and application of submarine space magnetic field[J]. Ship Electronic Engineering, 2018, 38(1): 136-139. DOI:10.3969/j.issn.1672-9730.2018.01.033 |
| [14] |
孙权, 唐劲飞. 潜艇磁场的估算与仿真[J]. 鱼雷技术, 2011, 19(4): 318-321. SUN Q, TANG J F. Estimation and simulation of submarine magnetic field[J]. Torpedo Technology, 2011, 19(4): 318-321. |
| [15] |
曲晓慧, 杨日杰, 单志超. 潜艇磁场建模方法的分析与比较[J]. 舰船科学技术, 2011, 33(3): 7-11. QU X H, YANG R J, SHAN Z C. Analysis and comparison on magnetic field modeling method of submarine[J]. Ship Science and Technology, 2011, 33(3): 7-11. DOI:10.3404/j.issn.1672-7649.2011.03.002 |
| [16] |
赵凯华, 陈熙谋. 电磁学[M]. 北京: 高等教育出版社, 1985.
|
| [17] |
周耀忠, 张国友. 舰船磁场分析计算[M]. 北京: 国防工业出版社, 2004.
|
| [18] |
高胜峰, 朱海, 王超, 等. 基于有限元法的潜艇磁场模型适用条件分析[J]. 舰船科学技术, 2016, 38(1): 34-38. GAO S F, ZHU H, WANG C, et al. Analysis on the applicability of submarine magnetic model based on finite-element method[J]. Ship Science and Technology, 2016, 38(1): 34-38. DOI:10.3404/j.issn.1672-7649.2016.1.007 |
| [19] |
金煌煌, 庄志洪, 付梦印, 等. 最简多磁偶极子等效建模方法[J]. 系统工程与电子技术, 2021, 43(8): 2066-2075. JIN H H, ZHUANG Z H FU M Y, et al. Modeling method using simplest multiple magnetic dipoles equivalence[J]. Systems Engineering and Electronics, 2021, 43(8): 2066-2075. DOI:10.12305/j.issn.1001-506X.2021.08.06 |
 2023, Vol. 45
2023, Vol. 45
