2. 中国科学院 机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
深海运载器是一种将载荷从深海海底快速投送到指定海域水面的无动力运载工具。运载器在深海环境快速上浮,近水面则通过减速翼减速,以保证运载器安全出水速度,减小再入水冲击。减速翼不仅具有水下减速功能,同时也具有潜在的水面垂荡抑制作用,可为载荷水面释放提供稳定平台。带有减速翼的深海运载器其近水面出水和垂荡运动力学环境最为复杂,涉及流体介质突变及复杂海情,直接影响载荷的水面释放过程。因此对深海运载器的近水面运动预报和适航性分析具有重要的研究意义。
目前波浪影响下的水下垂直上浮运载器相关研究,多采用势流理论计算方法,冯学知等[1]采用STF流体切片理论和Frank源分布紧密拟合相结合的方法对不规则波中潜艇细长体在近水面瞬时潜深时的运动响应和波频波浪力响应,推导了二阶波浪力平均值的解析解。杨继锋等[2]根据二维线性波和Morison理论建立了海浪作用下的水下垂直发射导弹运动的数学模型,分析了不同航向和浪级下的运动状态变化规律。王亚东等[3]采用P-M谱和SWOP方向分布函数的双叠加模型建立了随机波浪的数学描述,根据切片理论得出波浪力的计算公式,分析了波浪对弹道参数极限偏差影响随深度变化的规律。但上述方法假设航行器主要受到波浪的粘滞和附加质量效应,没有考虑海水粘性、表面张力影响,仍需要进一步的试验验证[4]。此外基于势流理论的切片方法假定航行体表面光滑连续,对于带有舵、稳定翼、减速翼等附体,表面非连续的航行器建模难度大,因此不适用于外形复杂的水下航行体的波浪载荷建模。
近年来随着CFD(computational fluid dynamics)数值计算技术的进步,采用求解N-S方程的数值造波,并融合动网格技术计算航行体在波浪作用下受力和运动模拟的方法更为可靠[4]。权晓波等[5]建立了二阶Stokes波的数值波浪,研究了5级海况下航行体模型在近水面水下垂直发射过程中二阶波浪产生的流场和力学特性。朱坤等[6]采用数值计算方法研究了航行体在不同波浪相位出水条件下的水动力和近水面空泡几何特性,通过分析流场数据得出航行器肩部空泡空间不对称是引起实际出水姿态变化的主要原因。
无动力水下航行体的减速方式有多种形式,如减速伞、减速翼和压载水舱等。练永庆等[7]针对采用减速伞的潜伏武器水下安全着陆问题,建立了减速伞减速和舱段分离着陆运动的数学模型,研究了减速伞不同开启角度对着陆运动过程的影响及分离减速坐底运动规律。孙斌等[8]分析了潜艇集体逃生舱安装压载水舱、减速伞及减速翼的3种减速方案,均能控制安全出水速度,其中减速翼方案最优。任佰锋等[9]通过流场仿真分析得出阻尼板的存在会使水下航行体的轴向附加质量增加且尾部流速降低,减速效果明显。现有研究尚未开展减速翼对运载器近水面出水和垂荡运动特性的影响研究。
本文针对运载器携带载荷的水面释放需求,设计一种带有减速翼的深海运载器。基于CFD数值计算中的重叠网格技术、DFBI(dynamic fluid body interaction)方法以及VOF(volume of fluid)波模型,建立数值波浪水池,探究静水波环境下减速翼对运载器近水面出水和垂荡运动的影响规律;模拟计算不同海况一阶和五阶波浪短期作用下运载器受到的波浪力及其运动响应,分析运载器不同海况等级下的运动响应特性和载荷释放条件,并通过正弦和函数和非线性最小二乘法拟合,建立了短期波浪载荷的时域模型。相关研究可为水下垂直上浮运载器近水面运动预报、适航性分析和波浪载荷建模提供参考。
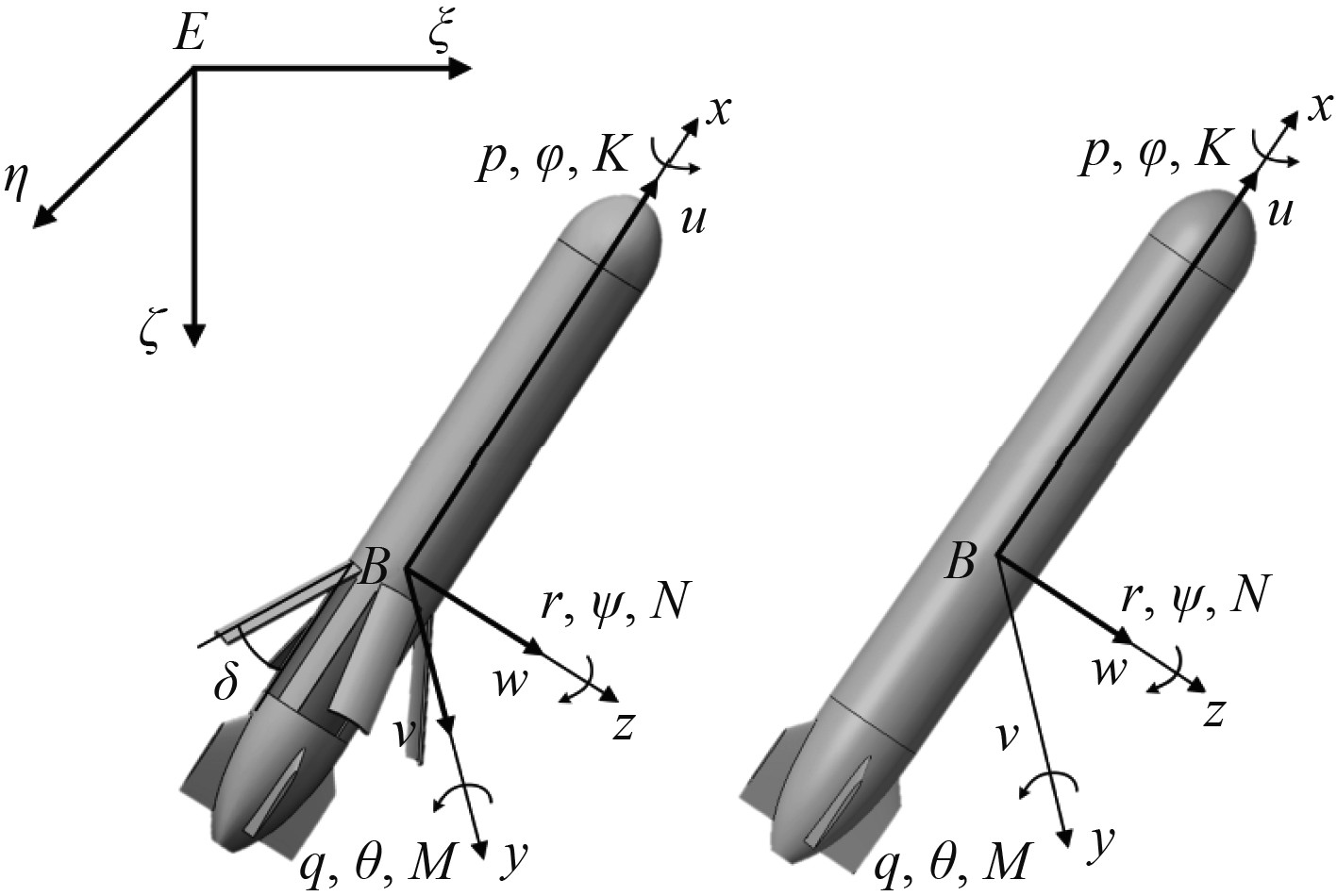
1 数值计算模型及验证 1.1 深海运载器模型简介减速翼型水下运载器模型,如图1所示。减速翼由四块周向均布的曲面板组成,深海环境快速上浮时减速翼闭合与运载器外表面共形,近水面时控制减速翼展开一定角度
|
图 1 深海运载器外形及坐标系定义 Fig. 1 Definition of shape and coordinate system of underwater vehicle |
CFD数值模型采用可实现的
| $ {\mu _t} = \rho {C_\mu }{f_\mu }kT 。$ | (1) |
湍动能
| $ \begin{split} \frac{\partial }{{\partial t}}\left( {\rho k} \right) +& \nabla \cdot \left( {\rho k{\mathbf{\bar v}}} \right) = \nabla \cdot \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\nabla k} \right] +\\ & {P_k} - \rho \left( {\varepsilon - {\varepsilon _0}} \right) + {S_k} \\ \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + &\nabla \cdot \left( {\rho \varepsilon {\mathbf{\bar v}}} \right) = \nabla \cdot \left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\nabla \varepsilon } \right]- \\ & {C_{\varepsilon 2}}{f_2}\rho \left( {\frac{\varepsilon }{{{T_e}}} - \frac{{{\varepsilon _0}}}{{{T_0}}}} \right) + \\ & \frac{1}{{{T_e}}}{C_{\varepsilon 1}}{P_\varepsilon } + {S_\varepsilon } 。\end{split} $ | (2) |
其中:
采用VOF波模型中的一阶和五阶Stokes波模型模拟气液两相交界面上的表面重力波。
1.3.1 一阶VOF波一阶VOF波模型使用Stokes波的一阶近似理论对一阶波浪建模,能够近似生成具有规则周期性正弦分布的波。一阶波浪波面水质点围绕原位置以角度
| $ \begin{split} & {\zeta _d} = {\zeta _a}\omega \cos (K\xi - \omega t) ,\\ & {V_\xi } = {\zeta _a}\omega \cos (K\xi - \omega t){e^{Kd}},\\ & {V_\zeta } = {\zeta _a}\omega \cos (K\xi - \omega t){e^{Kd}}。\end{split} $ | (3) |
其中:
为减小有限深度数值波浪水池对一阶波浪耗散的影响,通过深水逼近的方式模拟无限水深波浪水池。此时,波的耗散关系与水的深度无关,即波形与深度无关。一阶波浪在无限水深中波周期
| $ \lambda = {{g{T^2}} / {2\text{π} }}。$ | (4) |
五阶VOF波基于Fenton的五阶近似理论,相比一阶近似方法生成的波浪更接近于实际波浪。五阶波浪波面轮廓方程为[11]:
| $ \begin{split} k{\zeta _d}(x) =& {\zeta _a}\cos kx + \zeta _a^2{A_{22}}\cos 2kx + \\ & \zeta _a^3{A_{31}}(\cos kx - \cos 3kx) + \\ & \zeta _a^4{A_{42}}(\cos 2kx - {B_{44}}\cos 4kx) + \\ & \zeta _a^5[ - ({A_{53}} + {A_{55}})\cos kx + {A_{53}}\cos 3kx + \\ & {A_{55}}\cos 5kx] + kd。\end{split} $ | (5) |
式中:波幅值
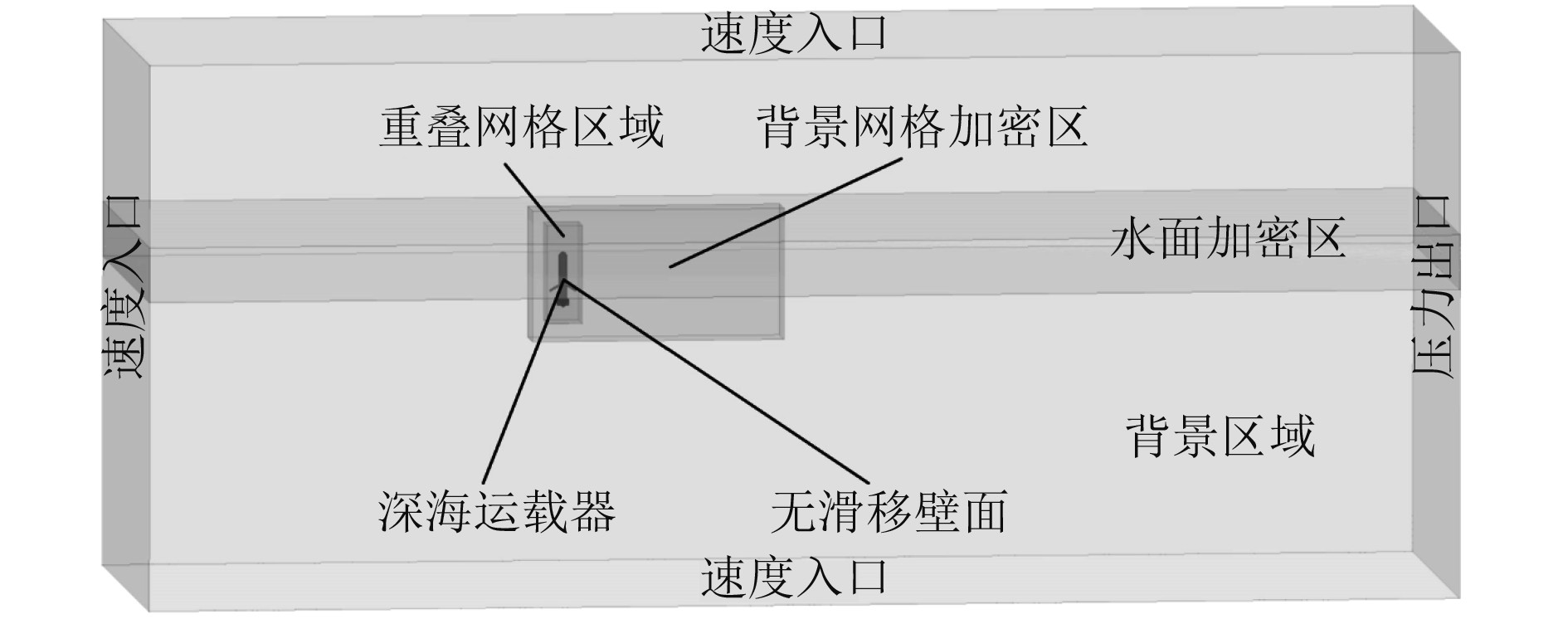
运载器近水面出水和垂荡运动由于受到波浪载荷作用,表现出强非线性特征。本文采用STAR-CCM+的重叠网格技术、DFBI方法和VOF波模型,模拟波浪作用下运载器近水面的纵垂面三自由度运动。数值模型计算域包含背景区域、重叠网格、背景网格加密区和水面加密区,其中重叠网格随运载器体坐标系运动。数值波浪水池长60 m,宽20 m,高25 m,如图2所示。VOF方法要求交界面的各相异性网格足够精细,因此根据波高,在水面上下对称建立的水面加密区。为精细捕捉出水位置的气液两相交界面,对运载器预计到达的区域再次进行背景网格的各相同性加密。背景区域除右侧设置压力出口外,其他表面设置为速度入口。根据波浪的属性,将速度入口设置为一阶波浪和五阶波浪速度的场函数,波浪的有效波高和周期根据海况等级设置。压力出口设置为一阶波浪和五阶波浪静压力的场函数,速度入口和压力出口的体积分数分别设置为不同波浪模型对应的VOF波轻流体体积分数和VOF波重流体体积分数的复合场函数。
|
图 2 计算域和边界条件设置 Fig. 2 Computational domain and boundary condition settings |
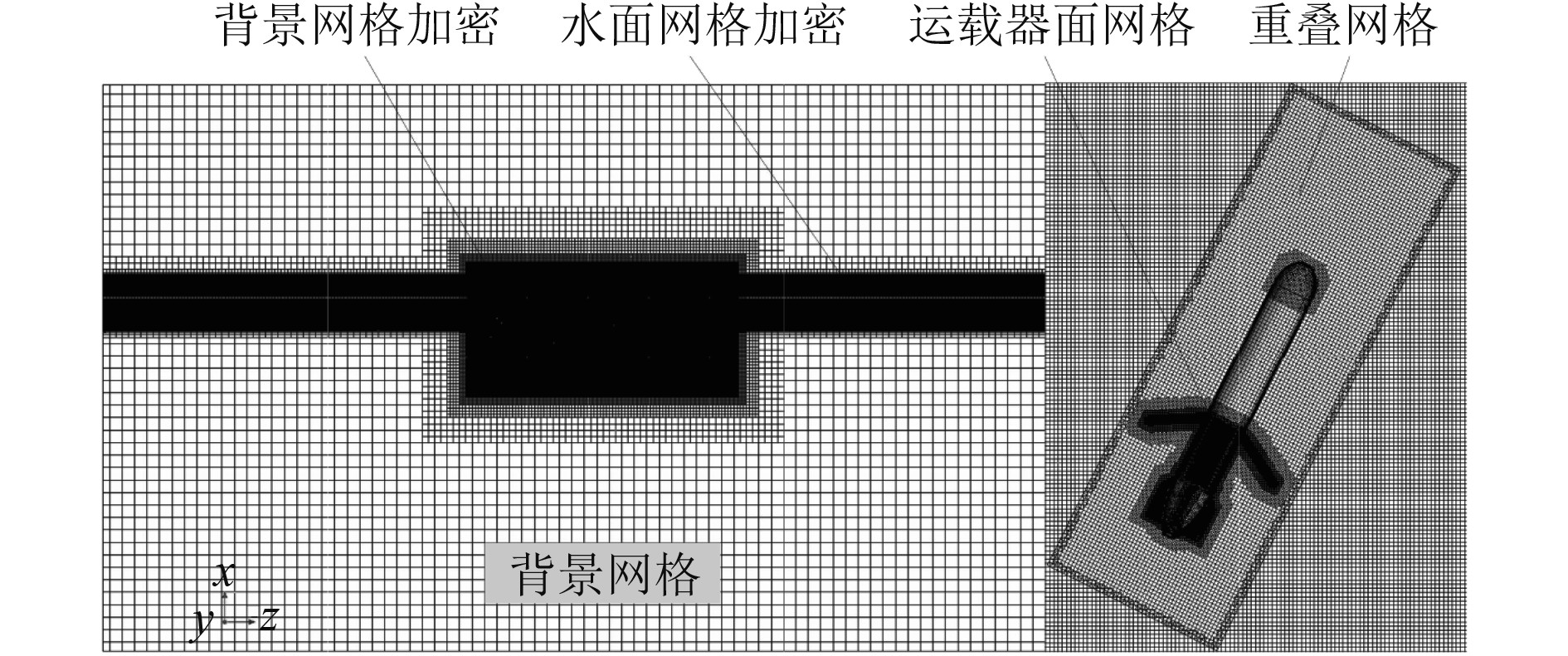
重叠网格区域是在运载器周围设置的高4.500 m,长宽均为1.600 m的长方体,并对其进行各相同性加密。在重叠网格与背景区域的交界面处设置重叠网格交界面,背景网格和重叠网格通过重叠网格交界面进行数据的传递和网格的更新。运载器表面为无滑移壁面,并采用棱柱层网格对壁面边界层进行划分,网格场景如图3所示。
|
图 3 运载器近水面运动网格场景 Fig. 3 Mesh scene of vehicle near-water motion |
世界海洋气象组织公布的各级海况下的波浪参数如表1所示[12]。5级海况有效波高在2.5~4 m属于恶劣海况,此时无动力运载器一般在海底处于静默状态,因此本文仅对2~4级海况开展研究。数值计算模型中VOF波参数,选取不同海况波浪有效波高
|
|
表 1 不同海况等级的波浪参数 Tab.1 Wave parameters of different sea states levels |
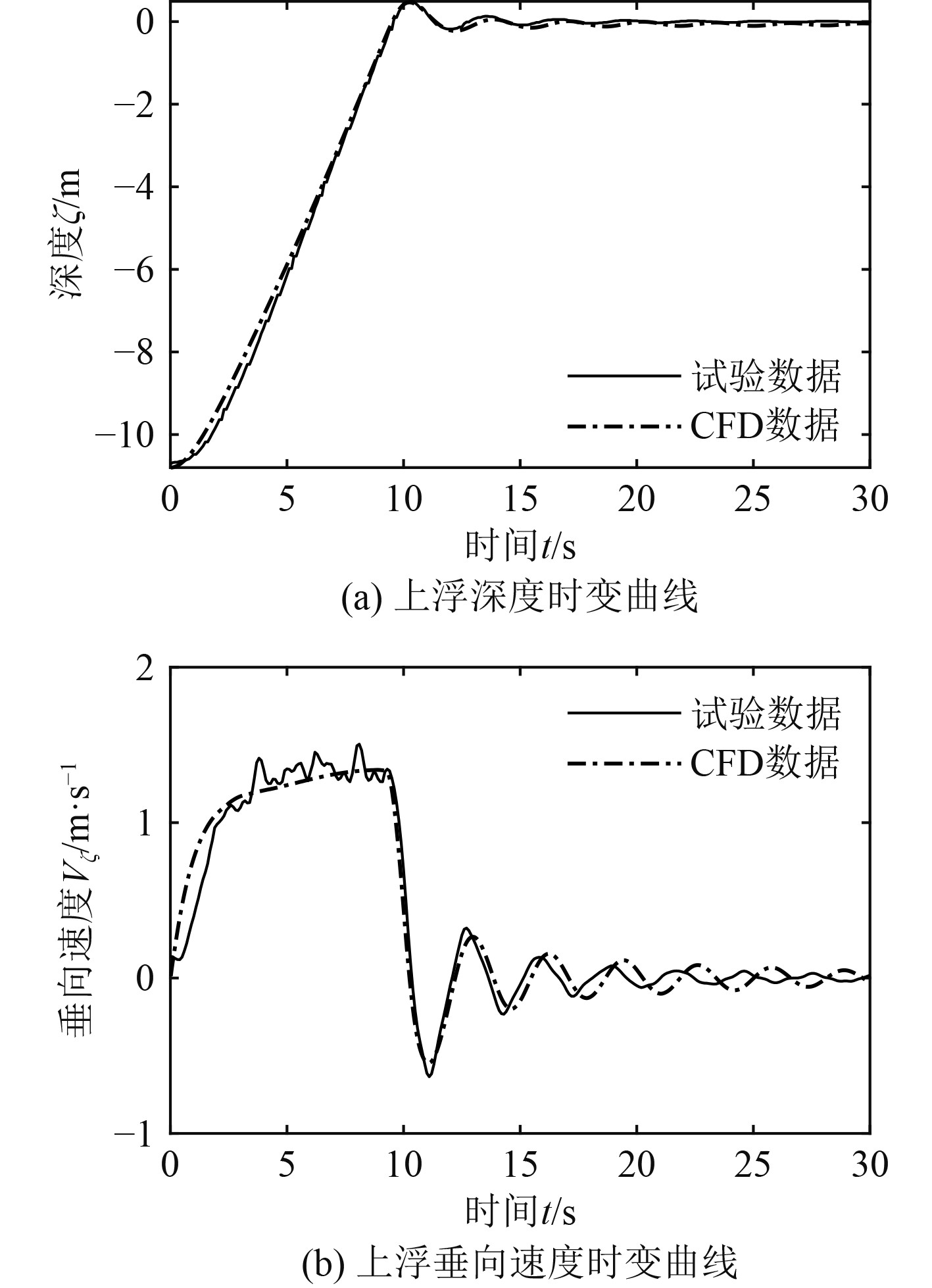
为验证本文建立的运载器近水面三自由度运动数值模型的可靠性和计算精度,采用原理样机进行水池试验验证。水池试验工况参数与数值模型相同,水池有效深度约10.7 m,VOF波模型采用静水波,运载器减速翼张角
|
图 4 运载器上浮状态参数对比分析 Fig. 4 Comparative analysis ascent motion state parameters of the vehicle |
试验和数值模拟数据表明,运载器自由释放后,约9 s加速到最大速度1.339 m/s时到达水面,经过多次垂荡后,垂向速度趋于稳定。CFD数值方法得到的运载器上浮深度和速度时变曲线与样机试验结果基本吻合,具有较高的计算精度,因此该数值方法能够用于本文运载器近水面运动特性分析。
图4中数值计算结果和试验结果之间存在偏差是由于试验样机表面配重压载、天线等附体,导致表面不同于数值模型中的理想光滑表面。此外运载器在水下脱缆释放时,也存在一定姿态偏差。
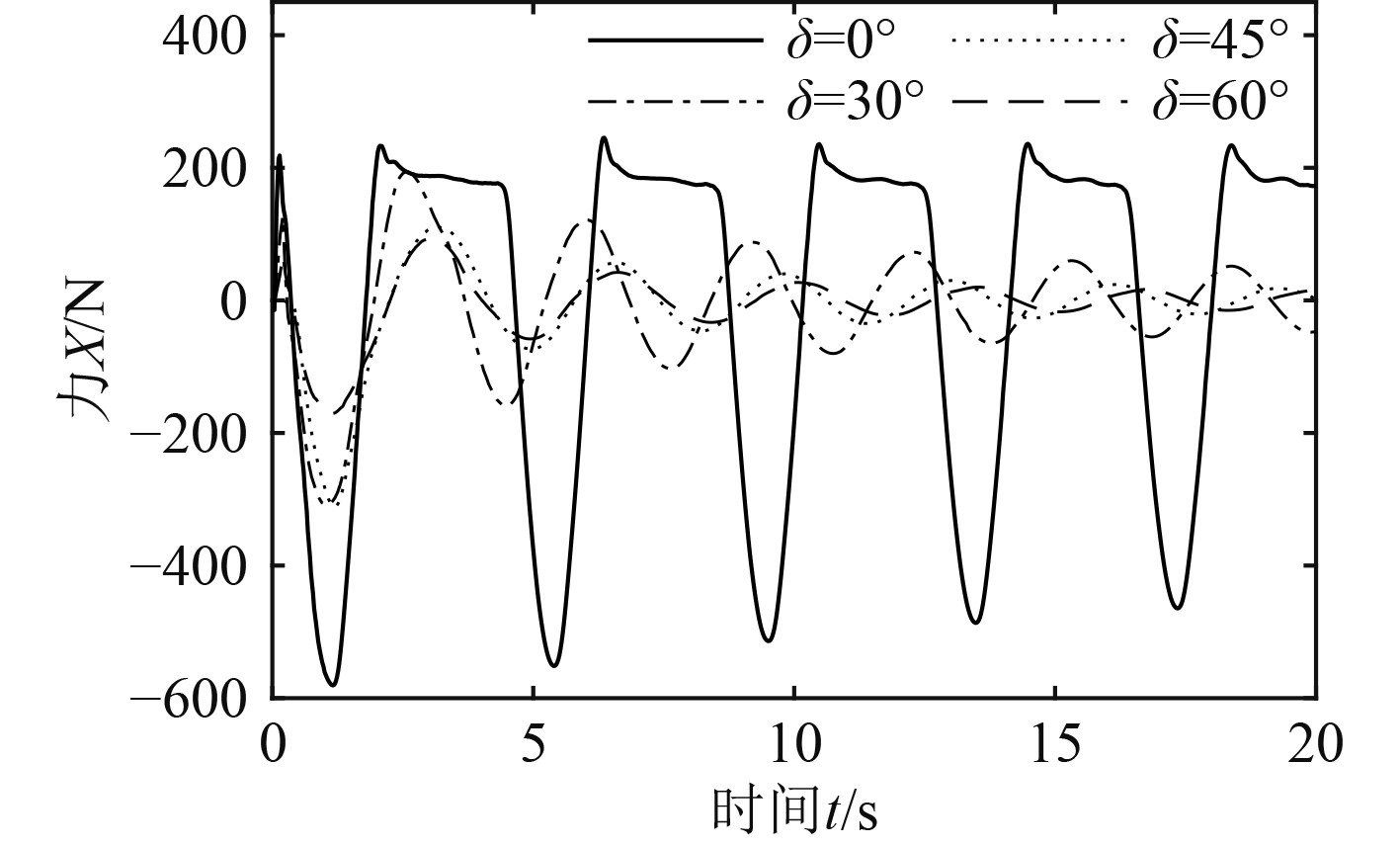
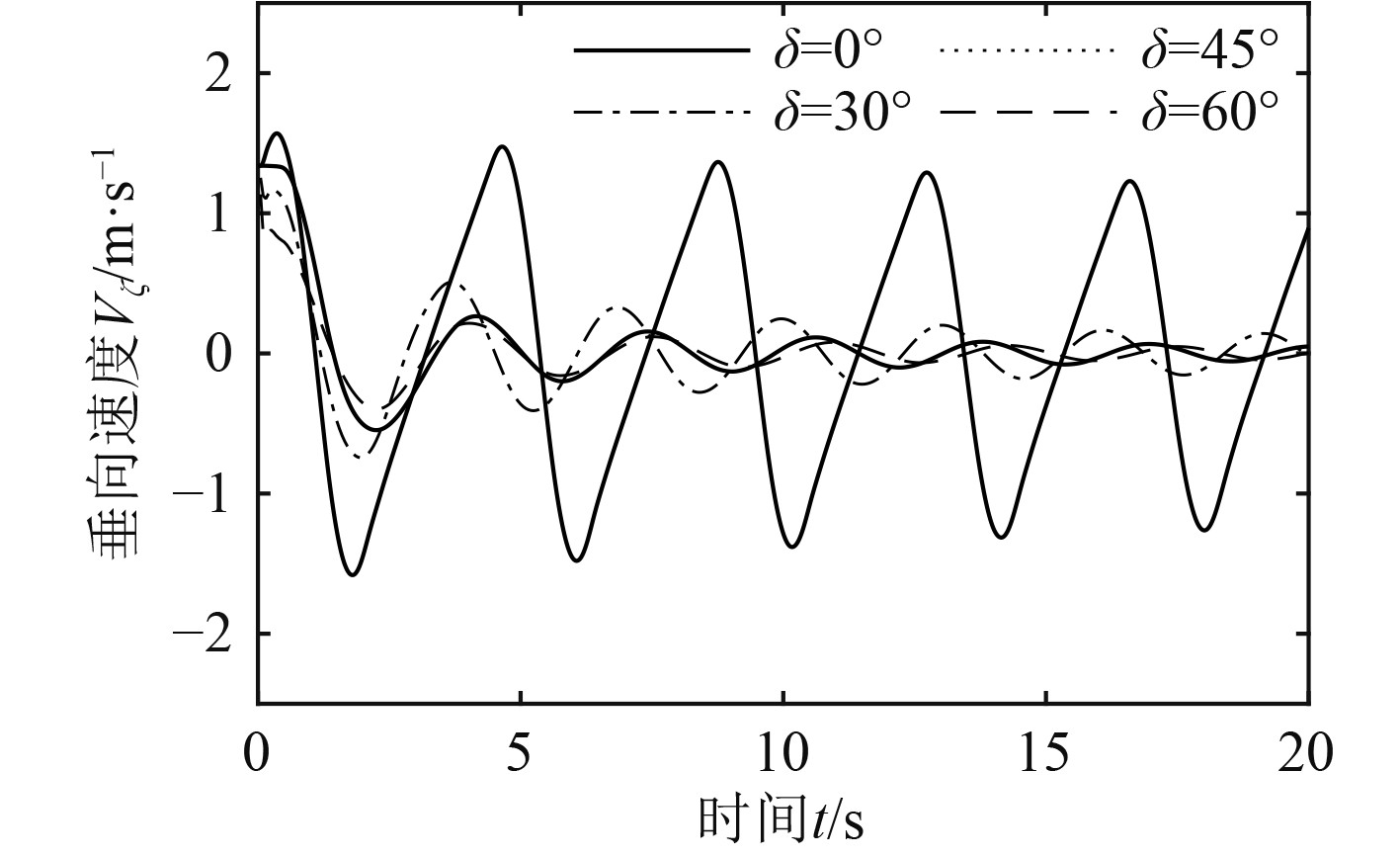
2 减速翼对近水面运动的影响 2.1 减速翼张角对近水面垂荡运动的影响为探究减速翼张角对运载器近水面运动的作用规律,分别设置减速翼张角
|
图 5 减速翼张角对运载器垂向力的影响 Fig. 5 The vertical force of the vehicle at different deceleration wing angle |
|
图 6 减速翼张角对运载器垂向速度的影响 Fig. 6 The vertical velocity of the vehicle at different deceleration wing angle |
结果表明:减速翼对无动力运载器的近水面垂荡运动起到显著抑制作用。减速翼作用下运载器受到的垂向力比无减速翼作用时波动更加平缓;减速翼张角越大,运载器实现水面稳定所需的垂荡次数和时间越少,垂荡周期越短;减速翼张角不变时,运载器作垂荡运动时的垂向速度及其受到的垂向力波动幅值逐渐减小。
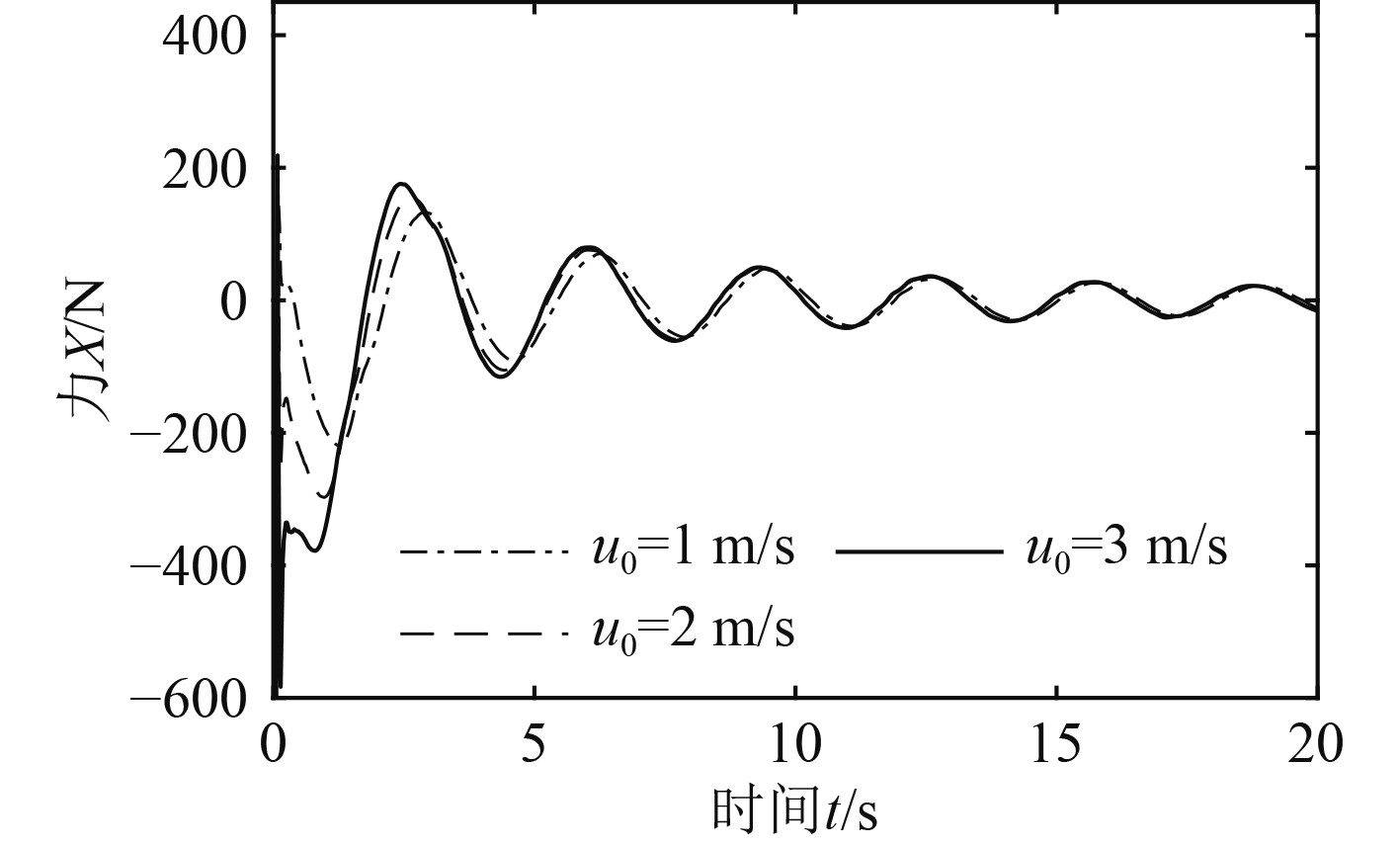
2.2 出水速度对近水面垂荡运动的影响为研究出水速度对运载器近水面垂荡运动的作用规律,设置减速翼张角
|
图 7 出水速度对运载器垂向力的影响 Fig. 7 The vertical force of the vehicle at different vertical velocity |

|
图 8 出水速度对运载器垂向速度的影响 Fig. 8 The vertical velocity of the vehicle at different water-exit velocity |
可知:出水速度越大,运载器首次穿越水面的垂向速度和受到的垂向力波动幅值越大;经过多次垂荡运动后,不同出水速度下的运载器垂荡运动状态参数变化趋于一致。
3 海况等级对波浪载荷与运动状态的影响为分析运载器的适航性及载荷的释放条件,根据实际波浪参数,模拟运载器在不同海况下的近水面三自由度运动,分析运载器受到的波浪力和运动响应特性,并通过函数拟合建立短期波浪力和力矩的时域模型。
采用正弦和函数与非线性最小二乘法对运载器在不同海况下近水面出水和垂荡过程受到的波浪力和力矩进行拟合,建立波浪力和力矩的时域模型。正弦和函数如下式:
| $ S(t) = \sum\limits_{i = 1}^n {{a_i}\sin ({b_i}t + {c_i})},\qquad n = 8,9。$ | (6) |
其中:
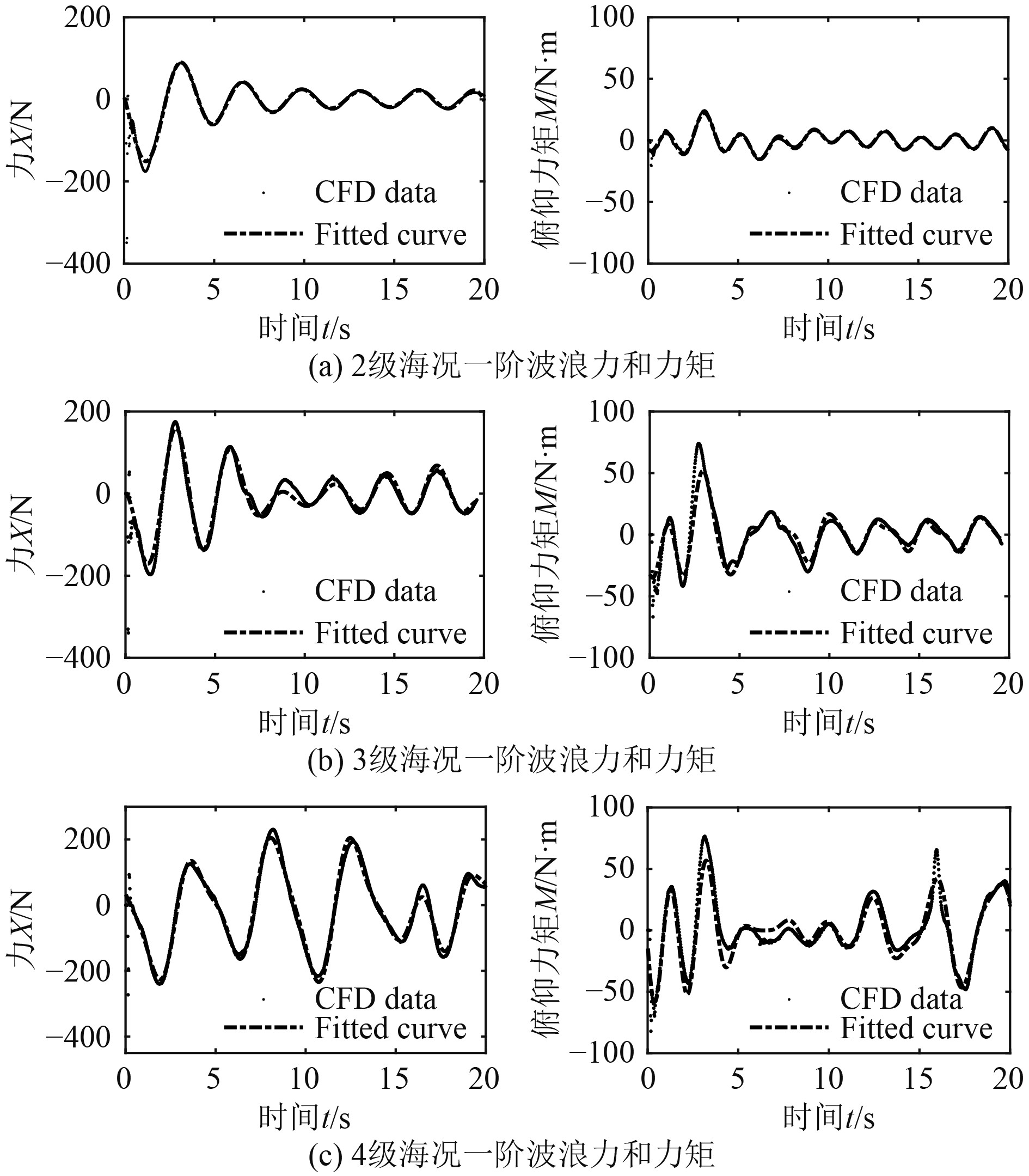
运载器近水面运动受到的一阶波浪力及其运动响应。数值模型采用一阶VOF波模型。考虑运载器以减速翼最大张角60°稳态上浮时垂向速度约为1 m/s,因此数值模型采用的工况参数,如表2所示。运载器浮心距离水面1.400 m处,以初速度1 m/s垂直释放,净浮力为154.781 N,重浮心轴向距离0.155 m,径向距离0 m。不同海况一阶波浪作用下运载器受到的力和力矩及正弦和函数的拟合效果,如图9所示。
|
|
表 2 一阶波作用下的数值模拟工况 Tab.2 Numerical simulation conditions under the action of 1st-order wave |
|
图 9 不同海况一阶波浪载荷及拟合结果 Fig. 9 First-order wave forces and fitting results at different sea state |
2~4级海况下,运载器首次穿越水面过程受到的垂向力
正弦和函数对运载器在一阶波浪作用下受到的垂向力
由图10可知,2~4级海况下运载器首次穿越水面过程垂向速度和纵倾角变化较大,纵倾角达到极小值。2级海况下,运载器垂向速度和纵倾角波动幅值逐渐减小,之后垂向速度呈等幅度振荡的趋势。3级海况2T~3T波周期内,运载器垂向速度波动范围最小,且运载器纵倾角回复到90°附近,为载荷提供了良好的水面发射条件,但随着波浪的持续作用,垂向速度和纵倾角波动幅值略有增大。
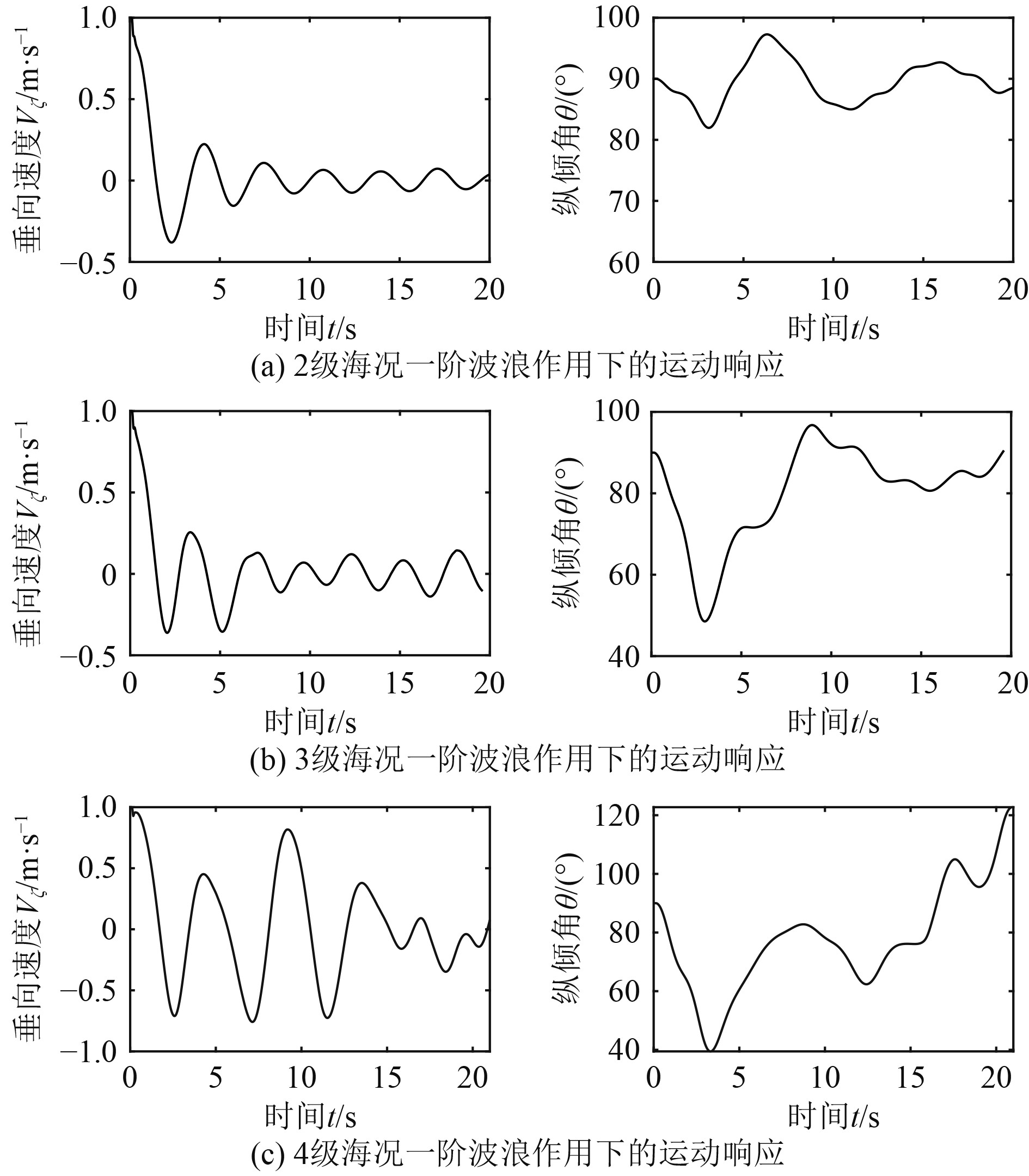
|
图 10 不同海况一阶波浪作用下的运动响应 Fig. 10 The motion response of the 1st-order wave at different sea state |
为尽可能模拟实际波浪作用,数值波浪水池采用五阶VOF波模型,并根据表3设置3种海况等级的波浪参数。运载器在不同海况五阶波浪作用下受到的力和力矩,以及函数拟合结果,如图11所示。
|
|
表 3 五阶波作用下的数值模拟工况 Tab.3 Numerical simulation conditions under the action of 5th-order wave |
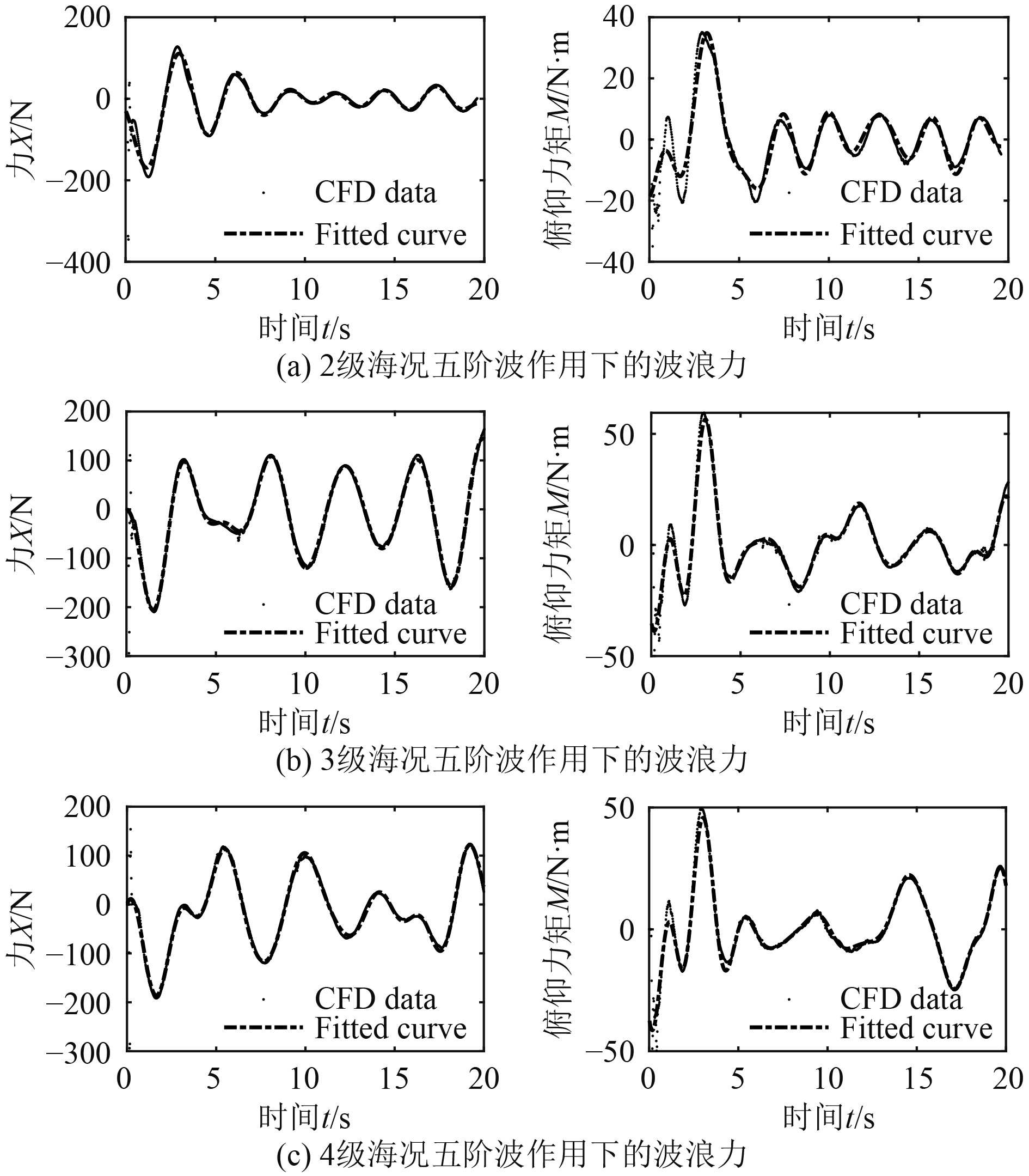
|
图 11 不同海况五阶波下的受力及拟合效果 Fig. 11 Wave forces, moments and fitting results at different sea state and 5th-order wave |
2级海况下,由于减速翼的垂荡抑制作用,
由图12可知,2级海况五阶波作用下,运载器首次穿越水面过程,纵倾角达到最小值,
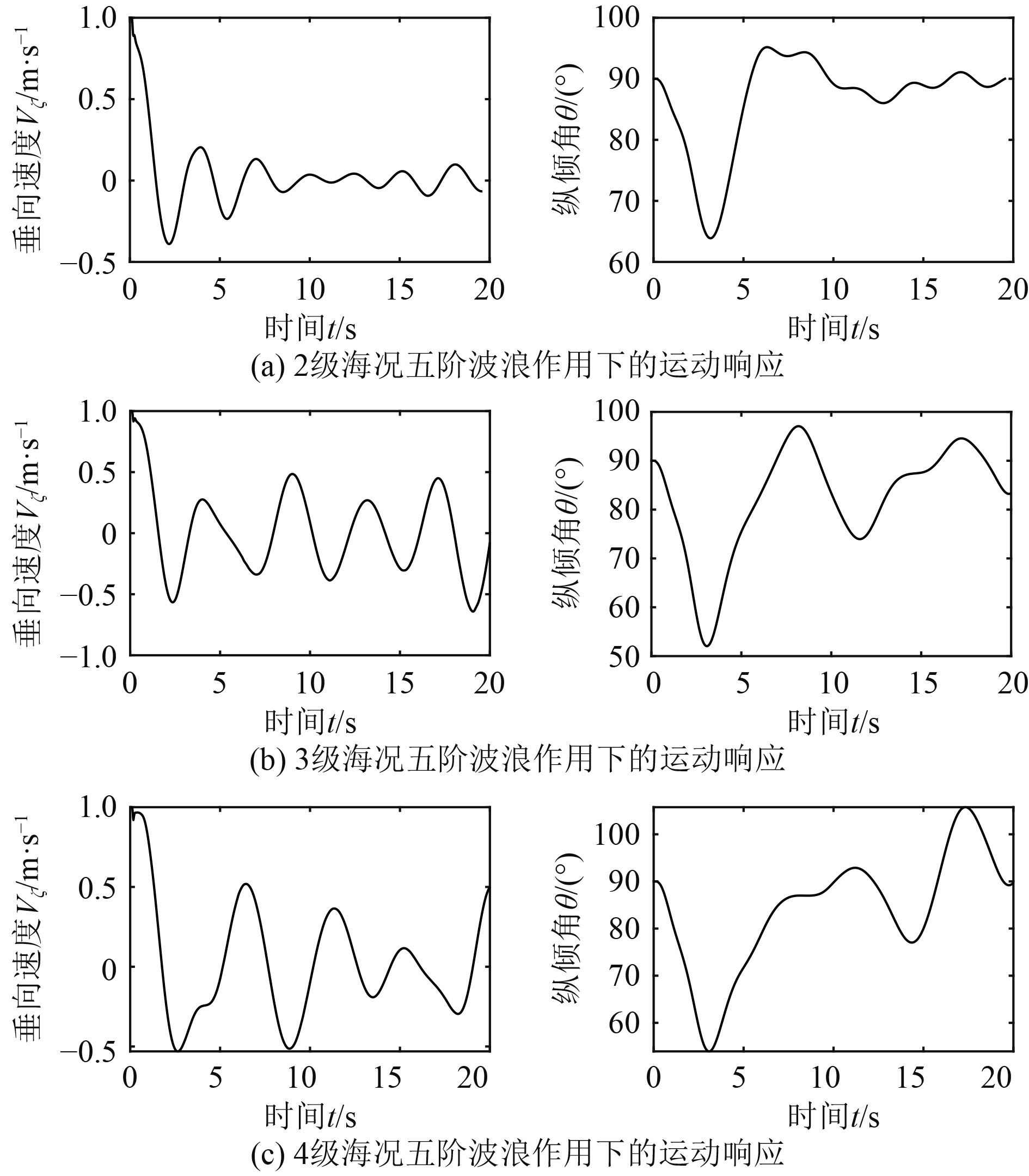
|
图 12 不同海况五阶波浪作用下的运动响应 Fig. 12 The motion response under different sea state and the fifth-order wave |
图13统计了运载器在不同海况下近水面运动纵倾角响应范围,随着海况等级的增大,纵倾角变化范围逐渐扩大。载荷的释放角度要求运载器在垂直方向上纵倾角偏差不超过45°。2~4级海况五阶波浪作用下,运载器纵倾角在垂直方向上纵倾角偏差均满足载荷的释放条件。
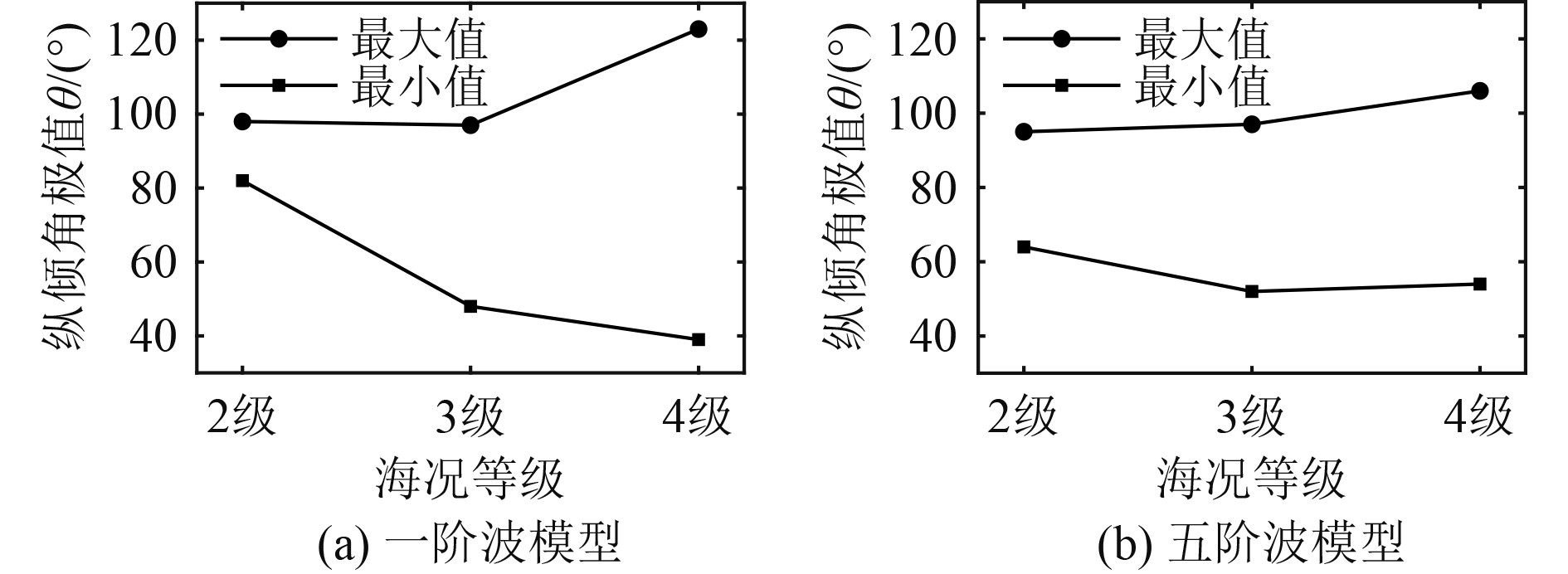
|
图 13 不同海况下运载器纵倾角变化范围 Fig. 13 Variation range of pitch angle of the vehicle under different sea state |
非线性最小二乘法的拟合优度可通过拟合系数
|
|
表 4 波浪载荷的拟合优度 Tab.4 Goodness of fit results of 5th-order wave force |
一阶和五阶波浪力和力矩的均方根误差较小,且拟合系数
针对复杂海情下减速翼深海运载器近水面运动预报难度大的问题,采用CFD数值方法,建立运载器近水面运动仿真模型,并通过水池试验验证了数值模型的准确性。在此基础上分析不同减速翼张角和海况条件对运载器近水面出水和垂荡运动的作用规律。结果表明:
1)减速翼对无动力运载器近水面垂荡运动起到显著抑制作用;随着减速翼张角的增大,运载器实现水面稳定所需要的时间和垂荡次数越小;减速翼张角不变时,运载器垂荡运动垂向速度及其受到的垂向力,波动幅值和周期均逐渐减小。
2)2~4级海况下,运载器首次穿越水面的
3)采用正弦和函数和非线性最小二乘法对不同海况波浪载荷的拟合效果较好。后续考虑将拟合后的波浪载荷时域模型添加到运载器的动力学方程中,评估运载器在波浪载荷下的操纵性。
| [1] |
冯学知, 蒋强强, 缪泉明, 等. 潜体波浪中近水面不同潜深和航向时运动和波浪力计算[J]. 船舶力学, 2002(2): 1-14. |
| [2] |
杨继锋, 刘勇志, 刘丙杰, 等. 海浪对水下垂直运动航行体出水姿态的影响分析[J]. 海洋技术学报, 2015, 34(2): 59-63. |
| [3] |
王亚东, 袁绪龙, 张宇文, 等. 波浪对导弹垂直发射水弹道影响研究[J]. 兵工学报, 2012, 33(5): 630-635. |
| [4] |
周敬国, 权晓波, 程少华. 海浪环境对航行体出水特性影响研究[J]. 导弹与航天运载技术, 2016(3): 44-49. |
| [5] |
权晓波, 孔德才, 李岩. 波浪模拟及其对水下航行体出水过程影响[J]. 哈尔滨工业大学学报, 2011, 43(3): 140-144. |
| [6] |
朱坤, 陈焕龙, 刘乐华, 等. 波浪相位对航行体出水过程水动力特性的影响[J]. 兵工学报, 2014, 35(3): 355-361. DOI:10.3969/j.issn.1000-1093.2014.03.010 |
| [7] |
练永庆, 王昕晔, 宋保维. 潜伏式武器水下减速着陆运动仿真[J]. 弹道学报, 2019, 31(3): 79-85. |
| [8] |
孙斌, 黄祥兵. 潜艇大型集体逃生舱上浮速度控制仿真计算[J]. 中国舰船研究, 2020, 15(S1): 42-49. |
| [9] |
任佰锋, 边晓阳. 阻尼板对水下航行体的力学影响作用[J]. 兵工自动化, 2018, 37(4): 1-4. DOI:10.7690/bgzdh.2018.04.001 |
| [10] |
胡坤, 何斌, 张建华, 等. 波浪环境下潜艇近水面操纵特性仿真分析[J]. 舰船科学技术, 2022, 44(2): 6-11. |
| [11] |
FENTON, JOHN D. A fifth-order stokes theory for steady waves[J]. Journal of Waterway Port Coastal and Ocean Engineering, 1985, 111(2), 216–234.
|
| [12] |
崔秀芳, 康建军, 胡勇, 等. 全海深ARV被动升沉补偿系统缆绳张力控制分析[J]. 上海海洋大学学报, 2017, 26(2): 287-293. |
 2023, Vol. 45
2023, Vol. 45
