2. 云南民族大学 计算机学院,云南 昆明 6505041
2. College of Computer Science, Yunnan Nationalities University, Kunming 650504, China
声呐作为水下探测、通信、定位、目标识别及成像的电子设备,是利用声波在水下的传播和反射特性,通过声电转换和信息处理进行导航和测距的技术,在科学研究、资源开发、水下作业、军事等方面均具有巨大的应用前景[1]。声呐按照换能器排列方式来划分,通常可分为合成孔径声呐、侧扫声呐、前视声呐及拖曳线列阵声呐等。在这几种声呐中,拖曳线列阵声呐是将水听器镶嵌在电缆上形成线列阵,并拖曳在平台尾后进行目标探测的声呐[2]。拖曳线列阵声呐能获得大的空间增益,摆脱了传统声呐的空间限制,消除了来自平台的自噪声干扰源,具有工作深度可变、基阵尺寸大、工作频率低、探测距离远、探测精度高、探测指向性好等特点,正成为未来声呐的发展方向,可广泛应用于水下目标探测、定位和跟踪、水下设备通信和制导、港口航道预警、海洋石油勘探、水文测量和海底地质地貌勘测等众多领域[3]。尤其是小口径航行器具有机动性、隐蔽性强等优点,搭载拖曳线列阵声呐具有更广的应用领域,也是海洋强国发展智能化海洋装备的研究热点[4]。
本文针对小口径航行器搭载拖曳线列阵声呐的数学建模和仿真分析,重点在保证航行器的航行品质和有效减阻角度出发,对搭载拖曳缆的导管支架截面形状及攻角进行水动力仿真、拖曳缆的流体动力仿真,进而对搭载拖曳线列阵声呐的小口径航行器进行流体动力仿真,并依据仿真分析结果对航行器的结构布局进行优化[5-6]。
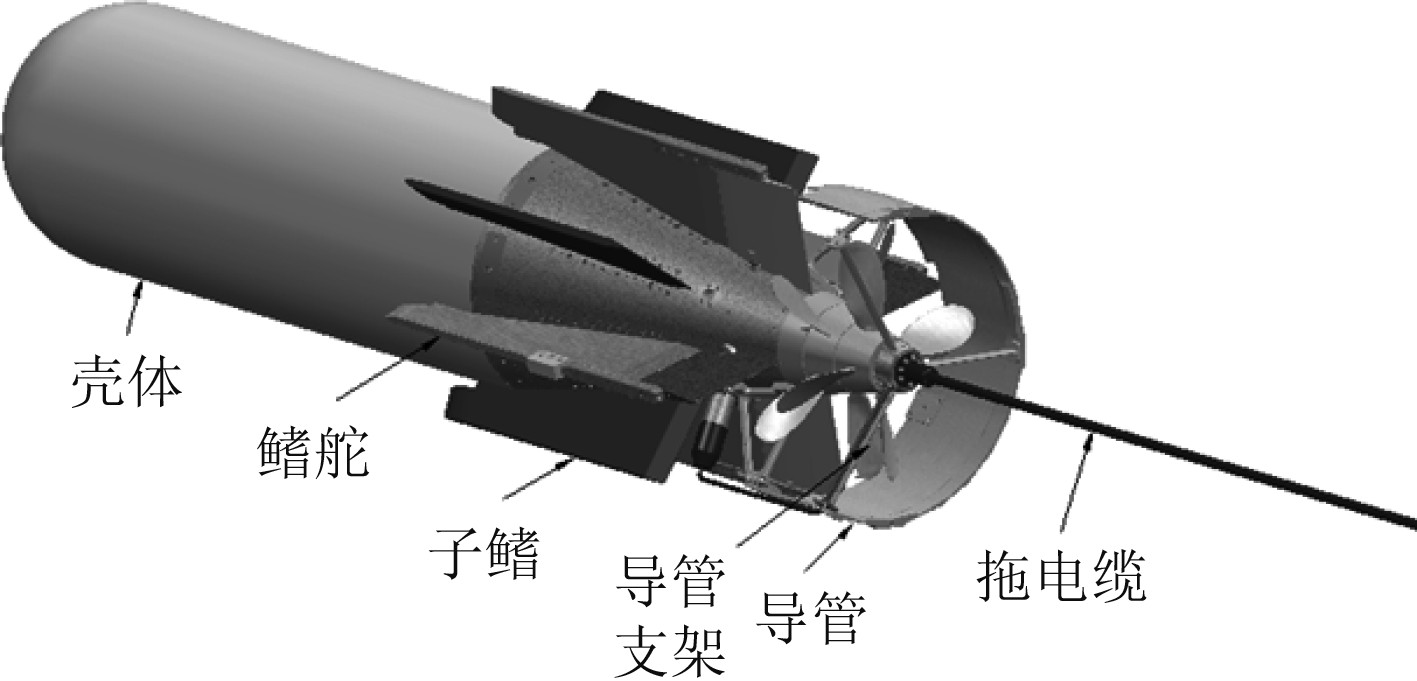
1 航行器组成及建模本文研究的带拖曳缆航行器的组成如表1所示,采用UG NX软件对航行器进行三维建模如图1所示。
|
|
表 1 航行器组成部分 Tab.1 A component of the vehicle |
|
图 1 航行器三维模型 Fig. 1 3D model of the vehicle |
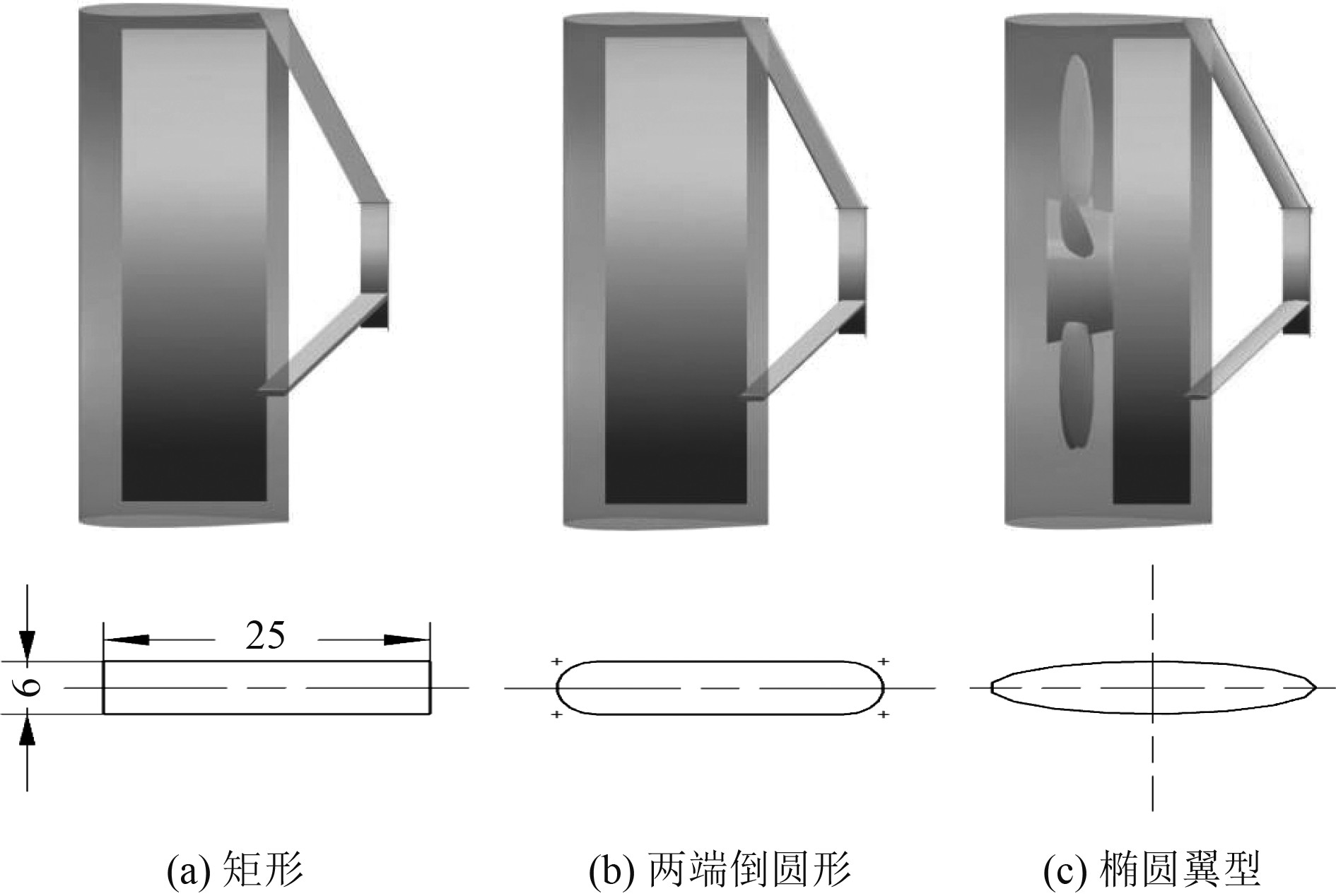
导管支架选择矩形、两端倒圆矩形和椭圆翼型3种截面形状为导管支架截面,短边和来流方向平行。其中矩形和两端倒圆形的尺寸一致,椭圆翼型的大径为12.5 mm,小径为3 mm,如图2所示。
|
图 2 导管支架的截面形状图 Fig. 2 Cross-sectional shape diagram of the catheter holder |
将3种导管支架和螺旋桨作为整体,采用计算流体力学CFD方法对其进行流体性能分析,评估3种导管支架推进器的敞水特性。采用Fluent软件对其进行模拟仿真。湍流模型采用SST湍流模型,静止域和运动域采用MRF模型传输数据,流场计算方法采用Couple算法[5],研究转速为333 r/min、来流速度在1.32~3.3 m/s工况下推进器的敞水推进特性。
收敛标准设置为均方根残差小于1E-5。经试错之后发现经过大约2 000步的迭代,控制方程的连续方程均方根残差(RMS P-Mass)达到1E-5,动量方程平均残差均降至1E-5以下并基本保持平稳时,推进装置力和力矩值相对误差小于0.002,可以认为计算已经收敛[7]。
统一假定3种不同导管截面形状的推进器以定速333 r/min旋转,通过在1.32~3.3 m/s速度范围内改变外流场进流面的速度调整螺旋桨进速比,使其在0.6~1.5区间内变化,运用CFD数值仿真方法,可以得到3种不同截面推进器的敞水性能曲线可知:
1)随着推进器进速比的增加,3种截面的推力系数Kt,扭矩系数Kq以及敞水效率
2)3种不同导管截面形状推进器的最大敞水效率点均出现在进速比为1.2附近。
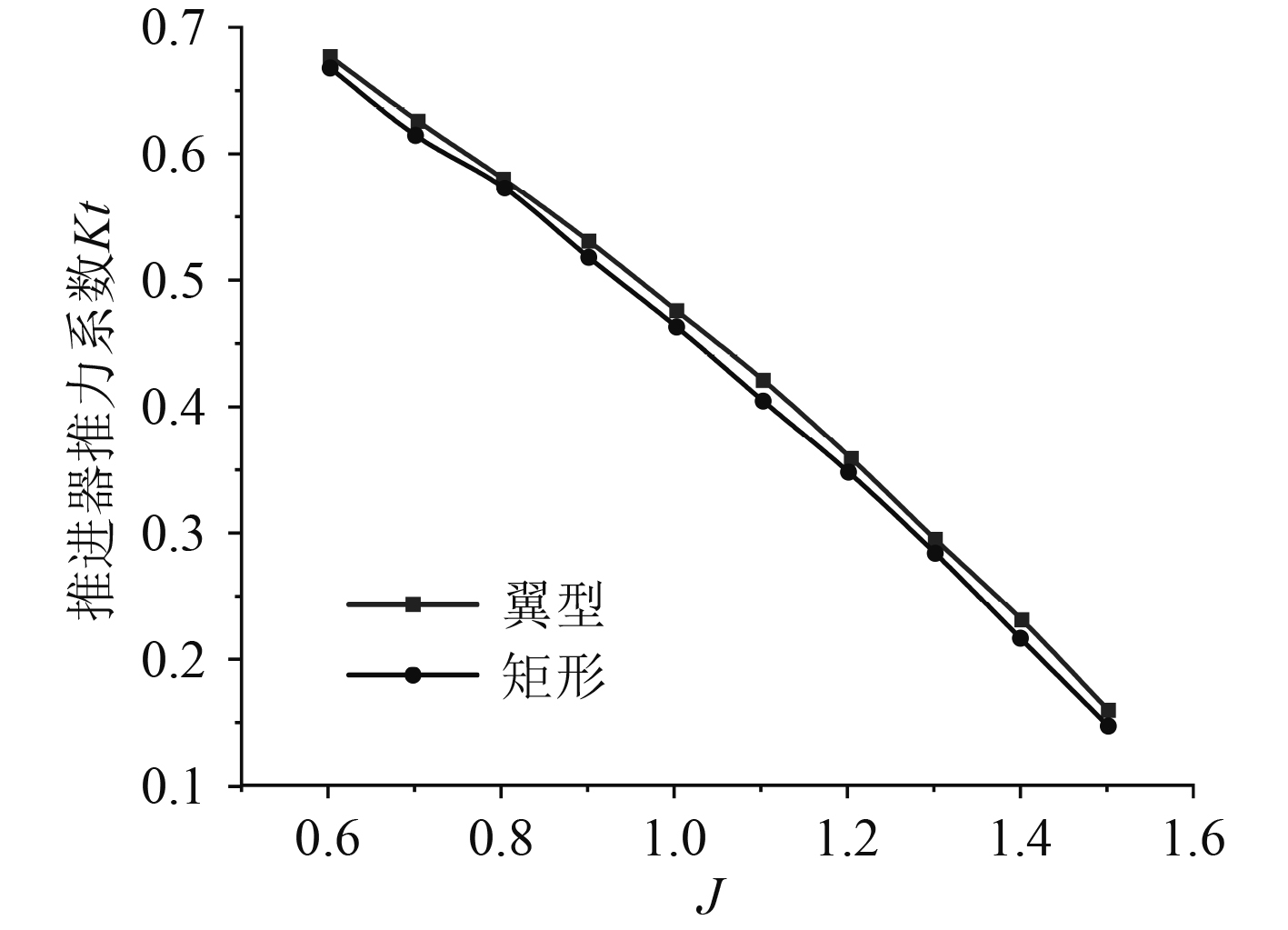
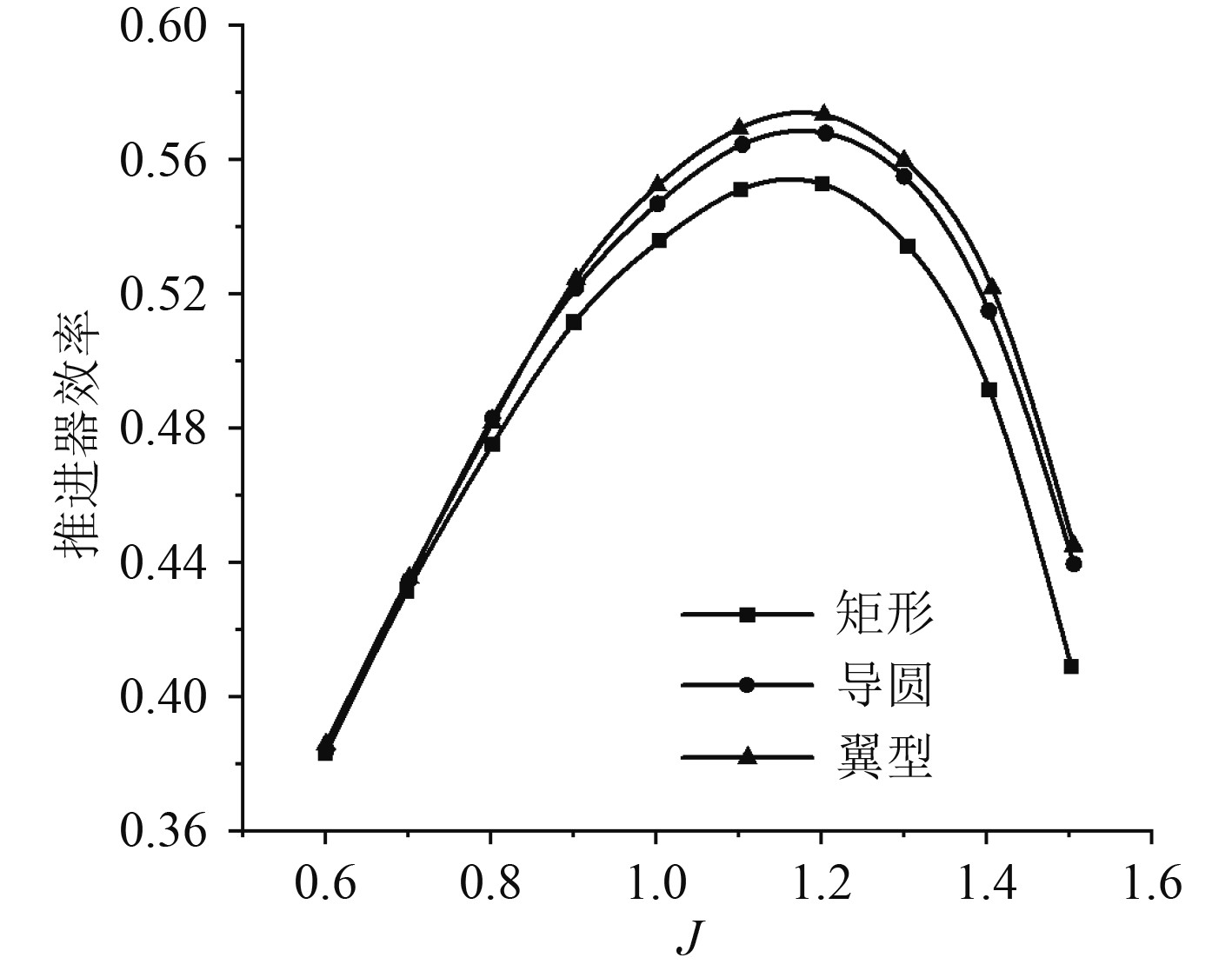
在相同工况下,通过对3种不同截面导管的推力系数和效率进行对比,从而选出最佳的导管截面形状。图3为不同截面形状推进器的推力系数对比曲线,图4为不同截面形状推进器的效率对比曲线。
|
图 3 不同截面推进器推力系数对比曲线 Fig. 3 Comparison curve of thrust coefficients with different sections |
|
图 4 不同截面推进器效率对比曲线 Fig. 4 Comparison curve of propeller efficiency with different sections |
可以看出:
1)推力系数
椭圆翼型与两侧导圆截面基本相同,但都大于矩形截面。
2)敞水效率
椭圆翼型截面稍大于两侧导圆截面,并远大于矩形截面。椭圆翼型截面导管支架的最大敞水效率出现在进速比为1.2附近,最大效率值为57.3%。
综合考虑推进器推力系数及最大敞水效率随不同导管截面形状变化的情形,最终选择椭圆翼型截面作为推进器导管的迎流截面形状。
2.3 导管支架偏转角的敞水仿真 2.3.1 导管支架偏转角除考虑导管支架截面形状对推进器推进性能的影响外,导管支架偏转角(攻角)的影响同样不容忽视,导管支架偏转角是指导管支架与推进器纵截面间的夹角,偏转角的大小直接影响到推进器导管支架轴向迎流面积的大小,从而决定了导管支架升力与阻力的大小,进而影响到推进器的流体动力特性和整体推进性能。不同导管支架偏转角如图5所示。
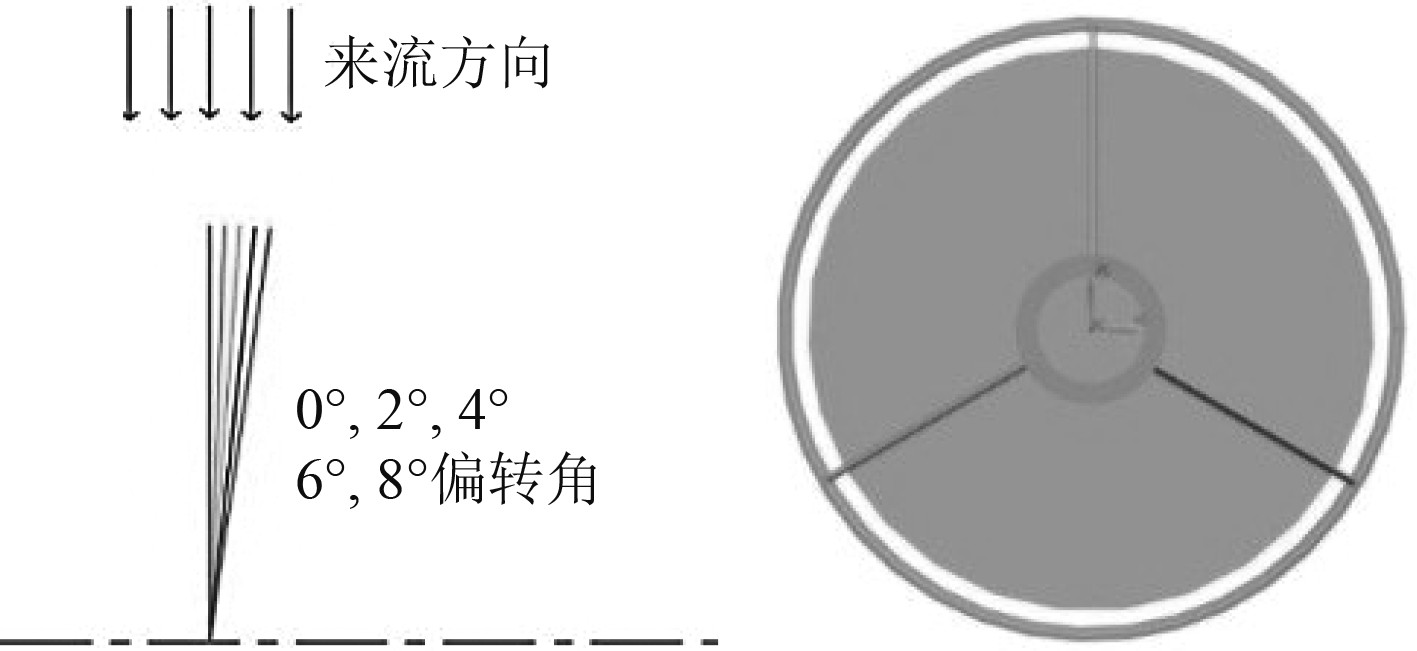
|
图 5 不同导管支架偏转角示意图 Fig. 5 Schematic diagram of deflection angles of different catheter stents |
仿真针对的椭圆翼型截面导管,分别选取偏转角为0°,2°,4°,6°,8°对推进器的推进性能进行分析,主要选取推进器的推力系数和效率这2项指标对推进器推力性能进行评估,从而选择最佳的偏转角。图6为不同偏转角下的推力系数对比曲线图,图7为不同偏转角下的效率对比图。
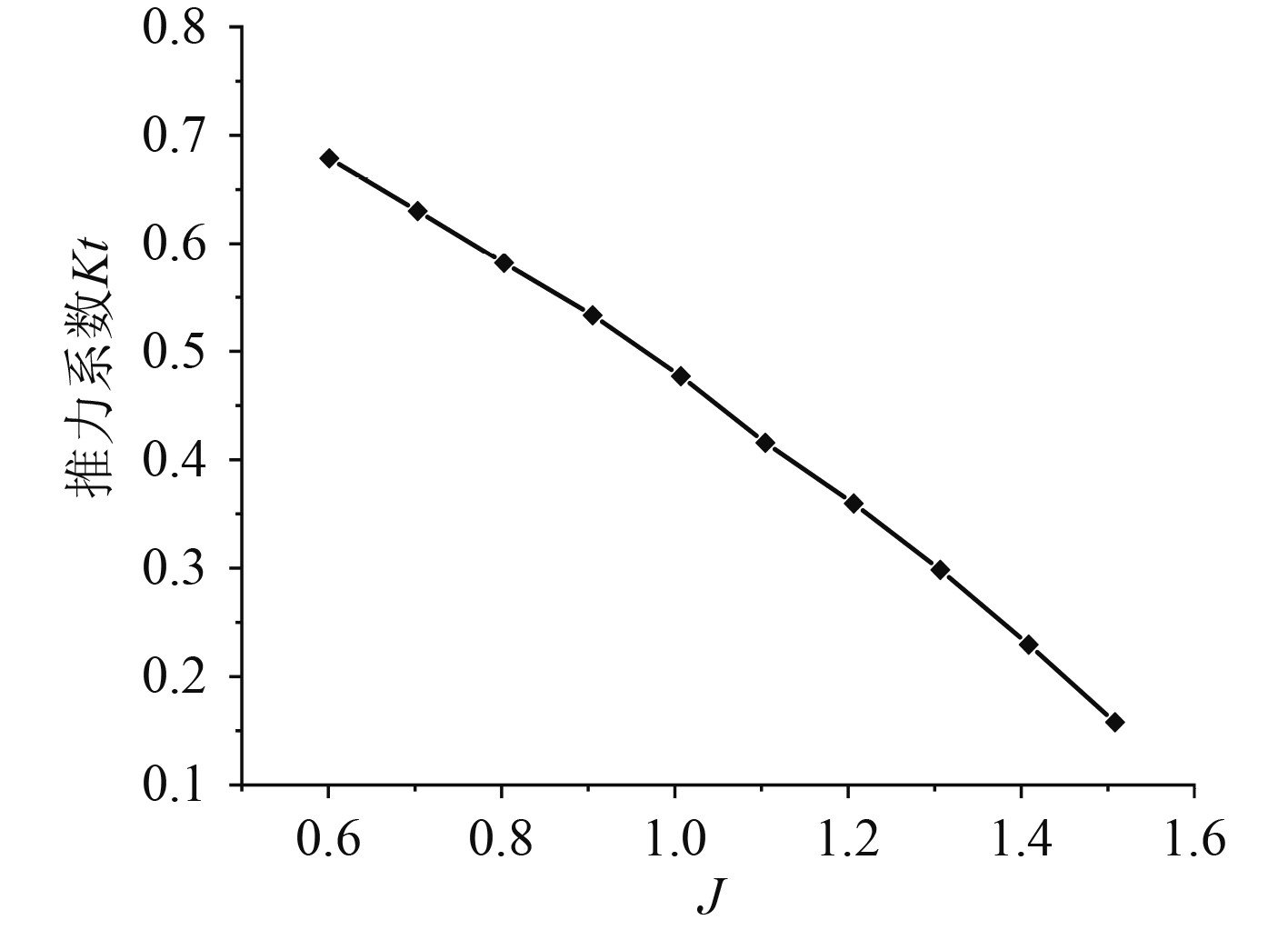
|
图 6 不同偏转角下推力系数对比图 Fig. 6 Comparison chart of thrust coefficients at different deflection angles |
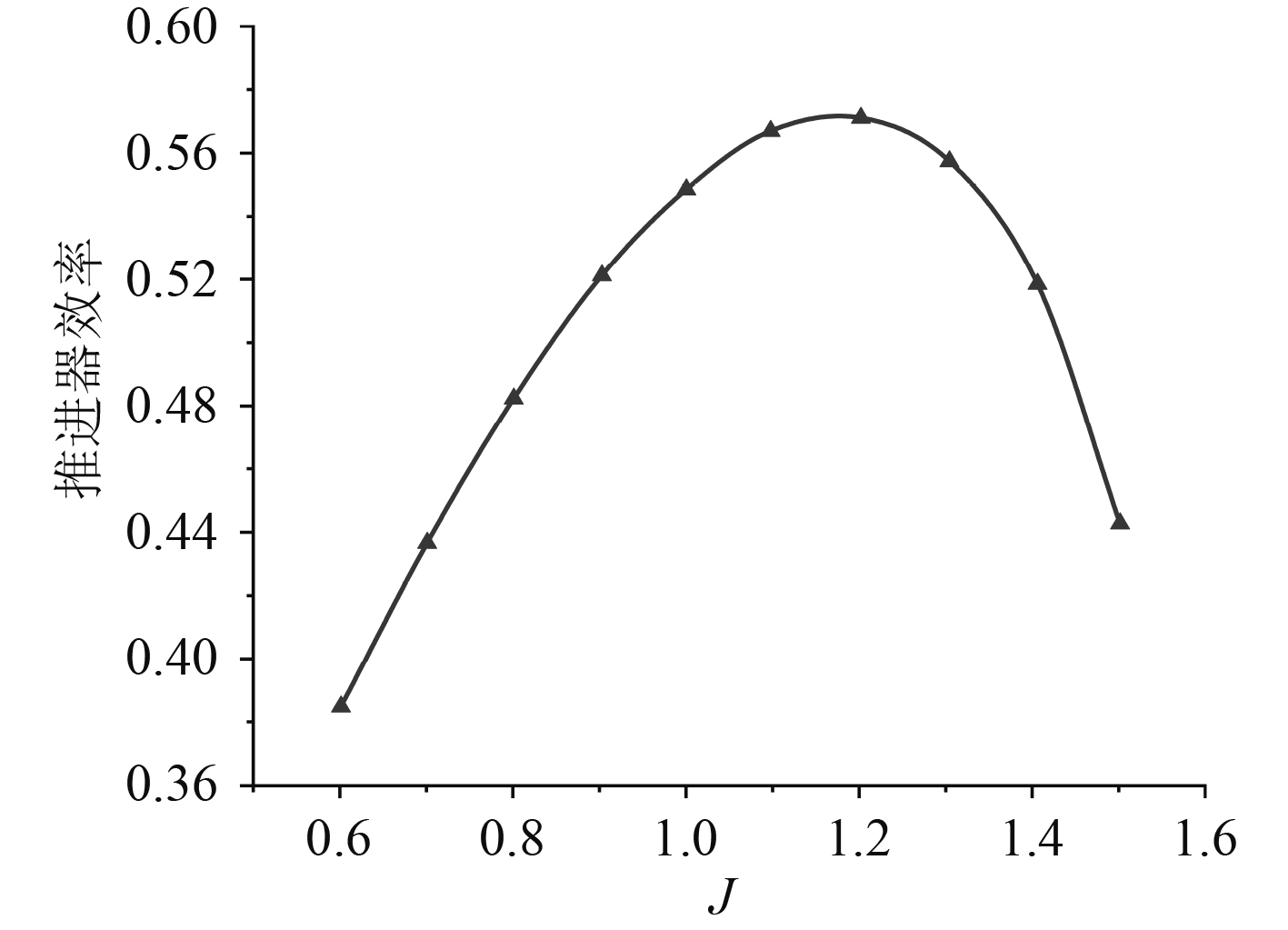
|
图 7 不同偏转角下效率对比图 Fig. 7 Comparison chart of efficiency at different deflection angles |
从图中可以得到以下结果:
1)随着进速比的不断增大,推进器的推力系数呈现不断下降的趋势,对于同一工况而言,随着导管偏转角由0°变化到8°,推进器的推力系数基本保持不变;
2)随着进速比的不断增大,推进器的敞水效率先增大后减小,并在进速比为1.2附近达到最大敞水效率,当偏转角在0°~8°的范围内变化时,在偏转角为4°时,推进器的敞水效率最大,此时的最大敞水效率为57.45%。
由不同偏转角的导管支架推力系数与敞水效率对比结果分析可知,当偏转角数值在0°~8°范围内变化时,推进器导管的最佳偏转角为4°。
3 拖曳缆流体动力仿真 3.1 裸缆阻力系数理论裸缆作为一种圆柱回转体,其阻力系数的计算可直接应用回转体阻力系数的计算公式,回转体外形阻力估算经验公式为:
| $\begin{aligned} & Cx=(2.07 - 18.44T_A - 4.154l_r + 73.25T_Al_r +3.26l_r^2 +\\ & 10.81T_AT_F - 56.96T_Al_r^2 - 38.34 T_AT_Fl_r + 37.75T_AT_Fl_r^2) \cdot C_f。\end{aligned}$ |
其中:
| $ C_f=\left\{ \begin{array}{*{20}{llll}} \dfrac{1.328}{\sqrt{{{Re}}}},& {{Re}}\leqslant 5\times 10^5 ;\\ 0.455({{\lg Re}})^{-2.58} - \dfrac{1700}{{{Re}}},& 5\times 10^5 < {{Re}}\leqslant 5\times 10^7;\\ 0.455({{\lg Re}})^{-2.58},& {{Re}} > 5\times 10^7。\end{array} \right. $ |
| $ T_F=\varPsi _H \cdot \dfrac{D}{2Lh},T_A=\varPsi_A \dfrac{D}{2LA},l_r=\dfrac{Lh+LA}{Lh+Lp+LA}。$ |
式中:Re为雷诺数;Re=v·L/υ,υ为水的运动粘性系数,υ=1.06×10−6 m2/s。由于拖缆在航行状态下的雷诺数在105<Re<107之内,这时开始出现湍流边界层段,所以在计算摩擦阻力系数时,应用混合边界层阻力系数计算公式[8]。
3.2 拖缆数学建模及CFD参数设置本次仿真运用的拖缆由缆绳与尾绳2部分组成,其中缆绳的长度为104 m,直径为15 mm,尾绳位于缆绳的尾端,长度为10 m,直径为6 mm,运用CAD绘制拖缆的几何模型如图8所示。

|
图 8 拖缆的二维几何模型图 Fig. 8 The 2D geometry of a tow cable |
建立几何模型后,应用计算流体力学数值离散仿真数学原理,在Ansys ICEM软件中完成拖缆三维几何模型的网格离散化过程,然后导入到CFD仿真软件STAR-CCM+12.06对拖缆在给定的2~7 kn航速范围内进行流体阻力计算。由于此次仿真目的是为确定裸缆在给定航速下的流体阻力,因此采用基于压力的稳态求解过程,其中湍流模型选择的是标准k-omega模型,数值计算算法选择couple算法,库朗数设置为20,收敛标准设置为均方根残差小于1E-6,参考值设置时设置特征面积参考值为2,参考密度值为1,使得Fluent软件输出结果即为拖缆流体阻力的数值[4,7]。
3.3 拖缆阻力仿真在给定的2~7 kn航速下,由Fluent计算得到的拖缆(裸缆)流体阻力随速度变化的拟合曲线如图9所示。
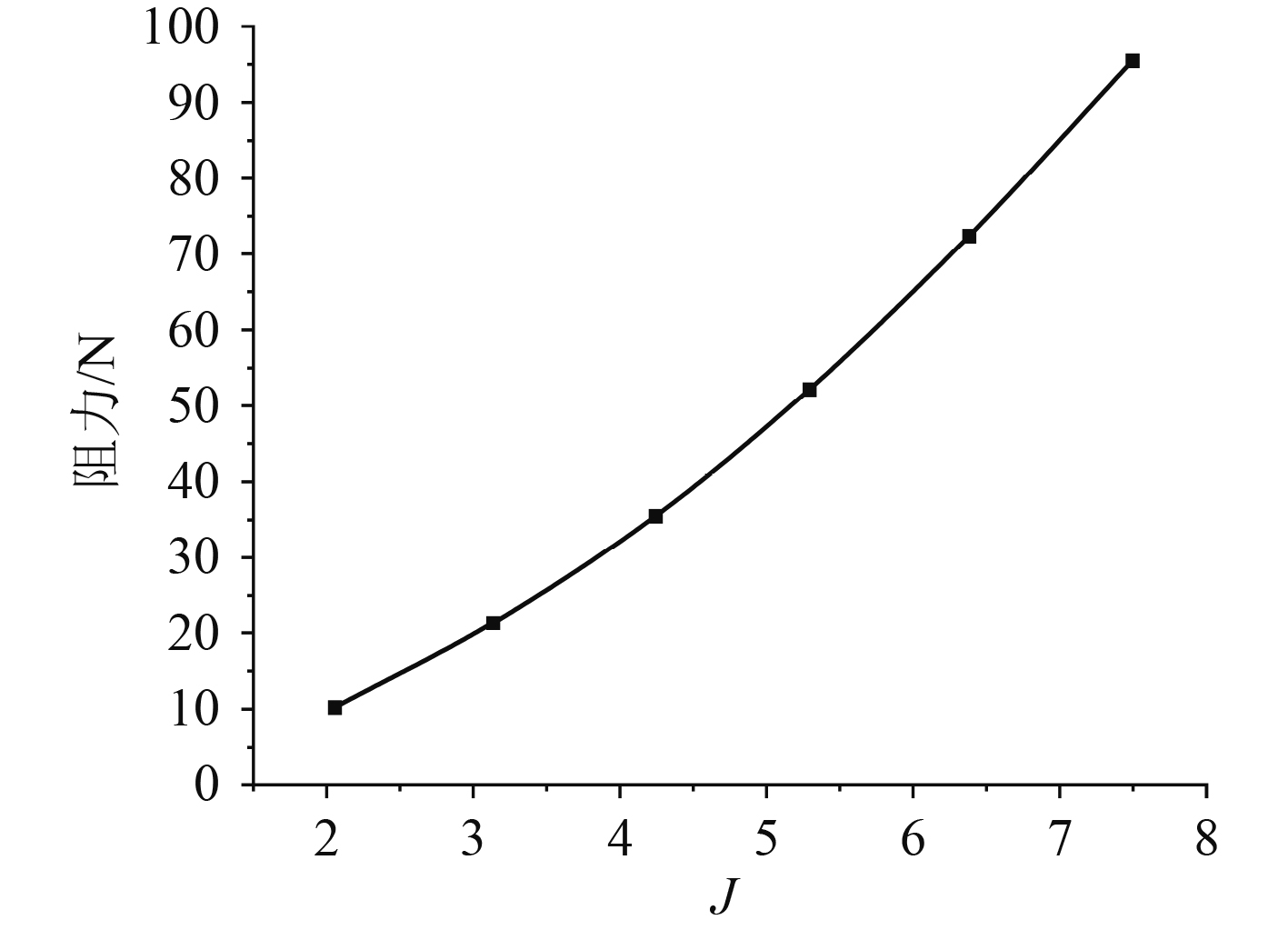
|
图 9 拖缆阻力随拖缆速度变化曲线 Fig. 9 The drag resistance curve varies with the speed of the tow cable |
可以看出,在裸缆的流体数值仿真过程中,随拖缆航速不断增大,拖缆的流体阻力不断增大,在航速2 kn时,拖缆的阻力为10.59 N,在航速7 kn时,拖缆的阻力为96.07 N。
4 航行器流体动力仿真在得到主要影响航行器流体动力的导管支架和裸缆流体仿真结果情况下,为得到航行器完整的流场分布及实船推力,并进一步得到航行器实船推进效率和最大实船航速,对带有拖缆的航行器完全体进行CFD仿真计算。
4.1 航行器实船性征仿真在研究螺旋桨的水动力性能时,通常并不应用推力和转矩的绝对数值,而是以无因次系数表示,这样对于不同尺寸的几何相似螺旋桨有相同的水动力性能图。根据因次分析,螺旋桨的推力及转矩可用无因次系数表示[8]。
推力系数:
| $ {{{K_T}}} = \dfrac{T}{{\rho {n^2}{D^4}}},$ |
转矩系数:
| $ {K_Q} = \dfrac{Q}{{\rho {n^2}{D^5}}} 。$ |
式中:T为推力;Q为转矩;ρ为水的密度;n为螺旋桨转速;D为螺旋桨直径。
螺旋桨的效率η0也可用无因次系数KT,KQ及J表示:
| $ {\eta }_{0}=\dfrac{T{V}_{A}}{2\text{π} nQ}=\dfrac{{K}_{T}}{{K}_{Q}}\cdot \dfrac{{V}_{A}}{2\text{π} nD}=\dfrac{{K}_{T}}{{K}_{Q}}\cdot \dfrac{J}{2\text{π} }。$ |
式中,J为进速系数。
航行器实船推进效率是基于螺旋桨敞水效率采用等推力法计算得到的。对于几何形状一定的螺旋桨而言,推力系数KT、转矩系数KQ及效率η0仅与进速系数J有关。图10为航行器的实船性征曲线。
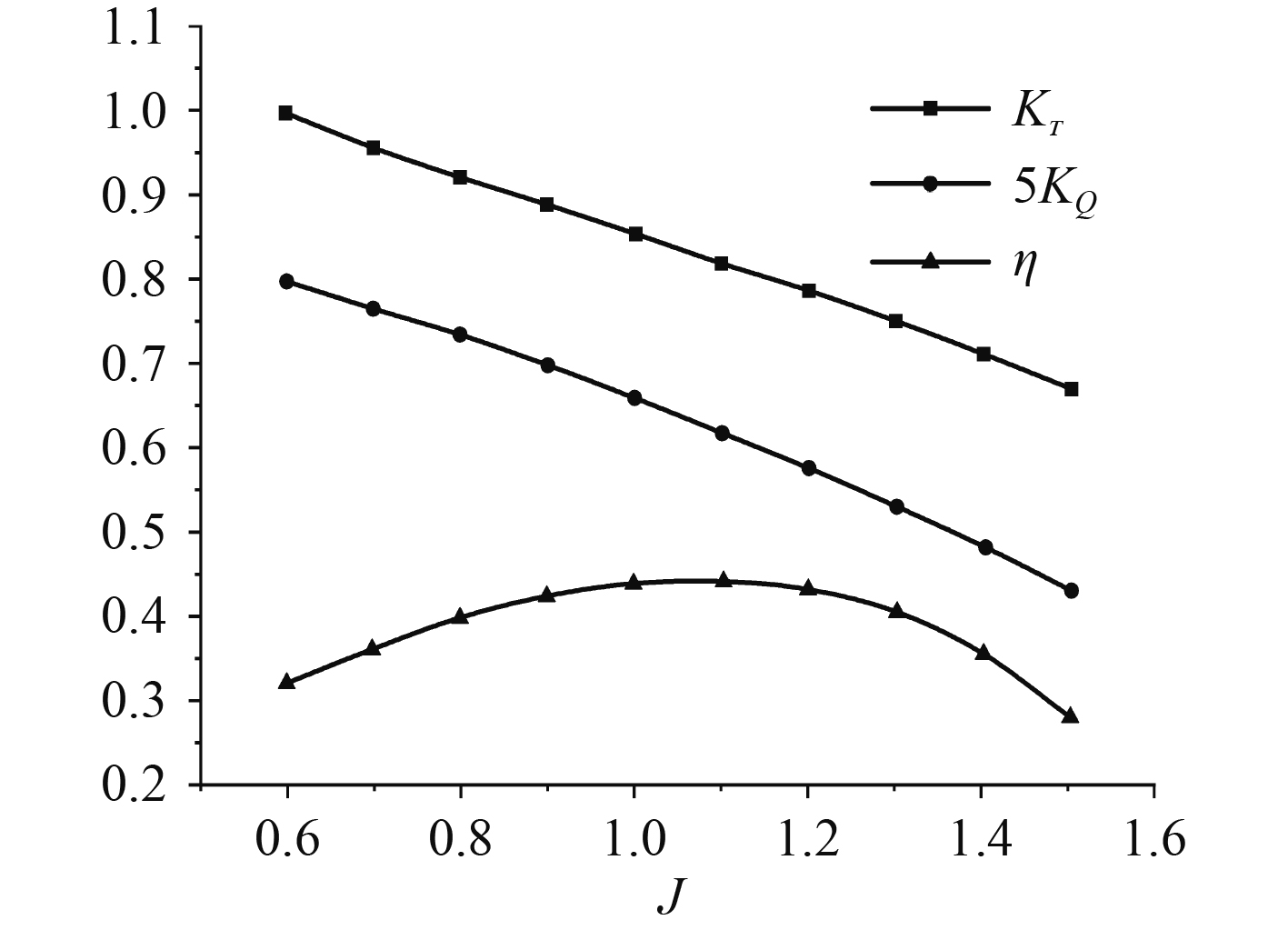
|
图 10 航行器实船性征曲线 Fig. 10 The actual characteristic curve of the vehicle |
可以看出,在给定进速比工况范围内,随进速比J增加,推力系数KT不断减小,转矩系数KQ也呈现不断减小的趋势,推进器的实船推进效率η则表现为先增大后减小的态势,并在进速比J为1.1附近出现峰值,给定工况下推进器的最大实船推进效率为44.66%。
4.2 航行器的实船最大航速航行器总推力由航行器壳体阻力、螺旋桨推力、鳍板阻力、导管阻力、导管支架阻力及拖缆阻力组成,运用流体仿真软件Fluent对航行器进行流体仿真计算,得到在给定不同实船航速工况下航行器的流场分布情形及航行器各组成部分的受力和转矩情况。表2为航行器实船推力随航速变化表。可以看出,随着航行器实船航速由2.57 kn变化到6.41 kn,航行器实船推力先由468.8 N减小到0,然后转变为航行器运动阻力并不断增大。分析可知,航行器最大实船航速出现在加速度最小处,即出现在航行器推力为0处。运用数学中线性插值的方法,可以近似得到在航行器推力为0时的实船航速为6.36 kn,这就是航行器所能达到的最大实船航速。
|
|
表 2 航行器实船航速与航行器推力关系表 Tab.2 Table of the relationship between the actual speed of the vehicle and the thrust of the vehicle |
由以上分析可知,选用椭圆翼型截面导管且偏转角为4°时,推进器的推进性能最佳。在CFD数值仿真过程中,推进器转速设定为333 r/min,来流速度在1.32~3.3 m/s范围内,得到图11所示的航行器推进器敞水性能曲线和图12所示的航行器实船性能曲线。
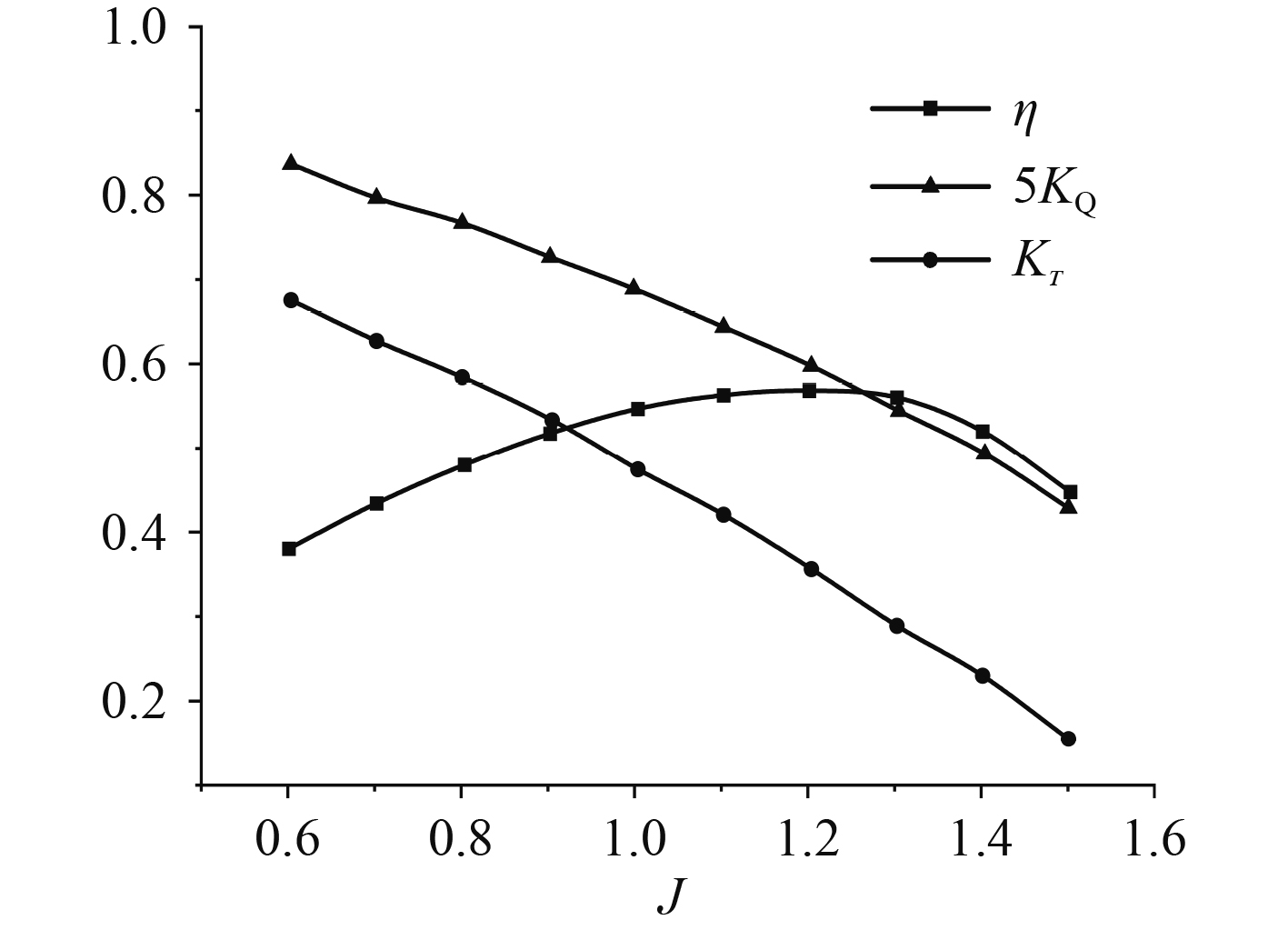
|
图 11 航行器敞水性能仿真曲线 Fig. 11 Simulation curve of open water performance of the vehicle |
可以看出:
1)无论是其敞水性能曲线还是实船性能曲线,随着进速比的增大(来流速度增大),推力系数KT均不断减小,转矩系数KQ也不断减小,效率均呈现先增大后减小的趋势。
2)敞水时航行器推进器的最大效率点出现在进速比为1.2处附近,其最大效率值约为57.45%,而实船推进时推进器的最大效率点出现在进速比为1.1处前后,最大效率值为51.34%。
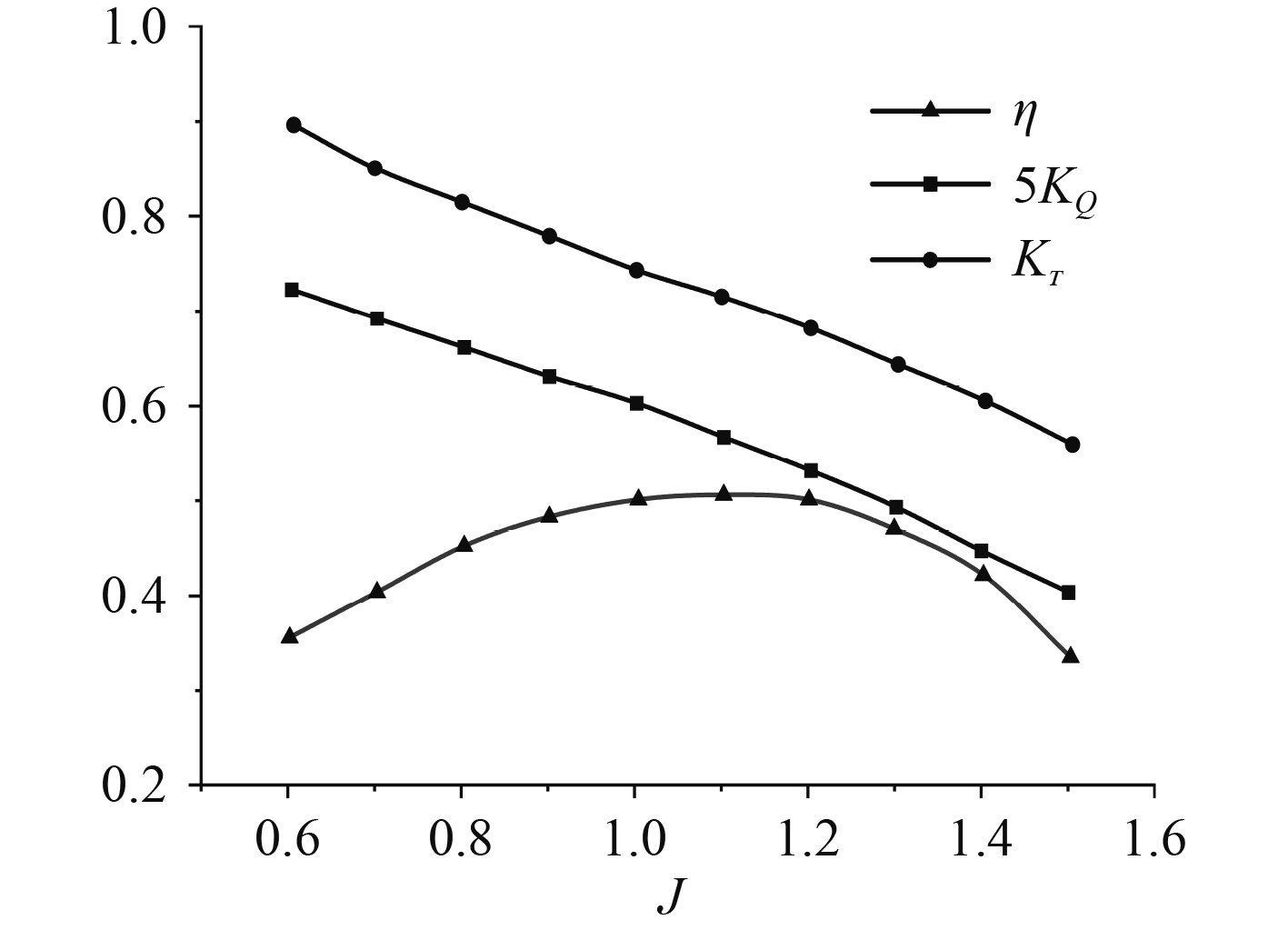
|
图 12 航行器实船性能曲线 Fig. 12 Performance curve of the vehicle |
从图13及图14可以看出,在给定的0.6~1.5进速比范围内,航行器推进器实船的推进系数均大于敞水时推力系数,且随进速比增加,两者间推力系数的差值呈不断扩大的趋势。在给定工况下,航行器推进器实船的推进效率要稍低于敞水时所得的推进效率。这是由于螺旋桨在敞水中工作时,盘面上各处的进速都相同,而在船后工作时,盘面上各处的局部进速不同。所以在同一进速系数时,两者的推力和转矩不同。采用等推力法求解实船推进效率,
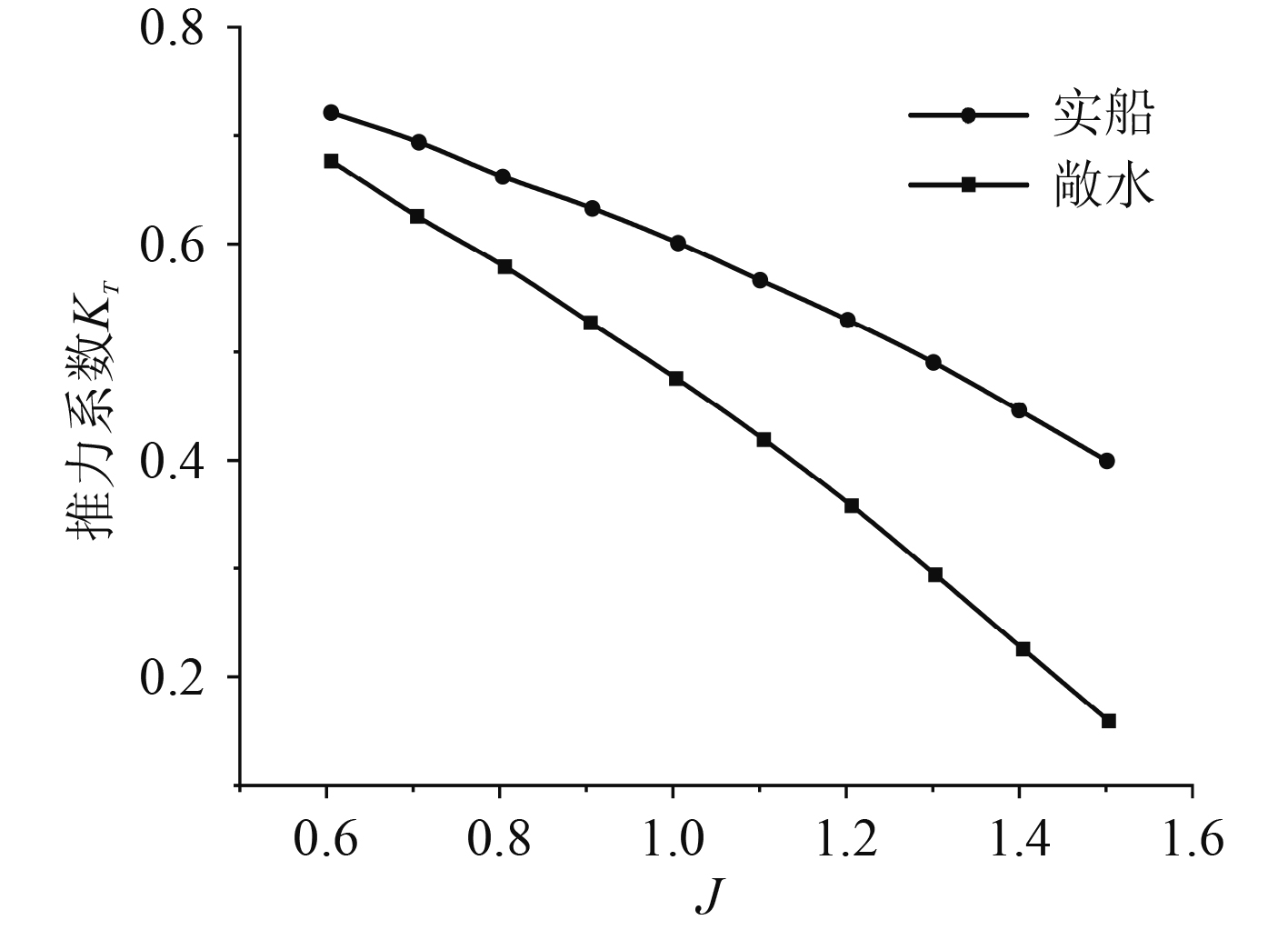
|
图 13 敞水仿真与实船推力系数对比曲线 Fig. 13 Comparison curve of open water simulation and real ship thrust coefficient |
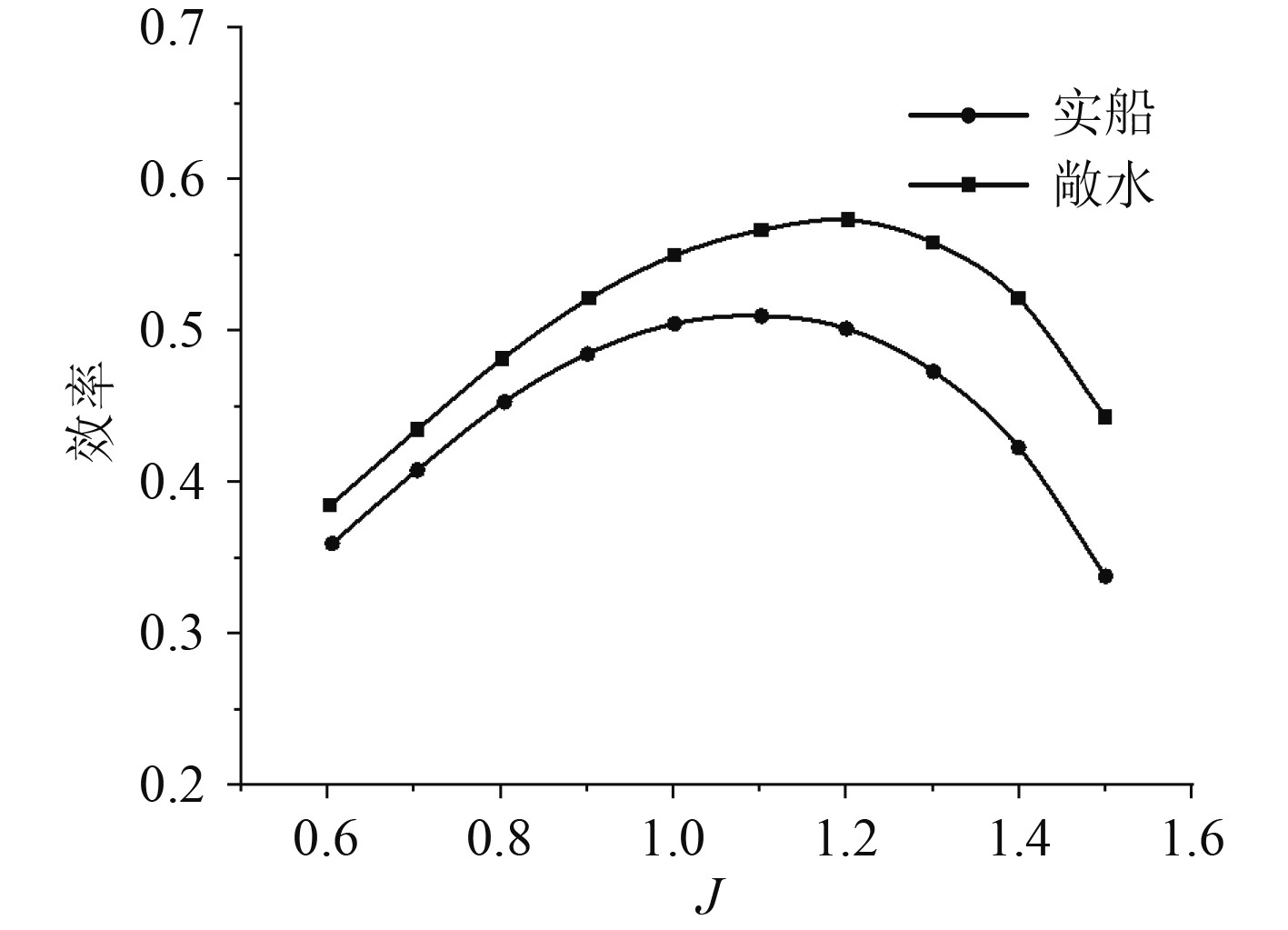
|
图 14 敞水仿真与实船效率对比曲线 Fig. 14 Open-water simulation versus real ship efficiency curve |
数学建模和动态仿真是开展小口径航行器搭载线列拖曳阵声呐推进技术的一种重要方法,对航行器总体系统及线列阵进行数学建模和动态仿真结果的分析,有助于进一步认识航行器推进技术,了解航行器、线列阵声呐及组成部分在各种工况下的工作情况,特别是深入了解总体与动力推进之间的工作匹配状况,从而为影响航行器航行品质的关键组件进行优化提供依据。另外,在航行器的设计阶段,通过数学建模和动态仿真研究,不但可定量分析主要组件的水动力特性对系统整体性能的影响,还可为不同配置方案的优劣比较提供可信的分析结果,从而使航行器的设计科学、正确和总体最优。
| [1] |
傅仁琦, 曹焱, 王晓林. 无人水下航行器声呐装备现状与发展趋势[J]. 舰船科学技术, 2020, 42(3): 82-87. FU Kaiqi, CAO Yan, WANG Xiaolin. Current status and developing trend of sonar equipments for unmanned undersea vehicle[J]. Ship Science and Technology, 2020, 42(3): 82-87. DOI:10.3404/j.issn.1672-7649.2020.02.016 |
| [2] |
刘孟庵. 拖曳线列阵声呐技术发展综述[J]. 声学与电子工程, 2006(3): 1-5. |
| [3] |
陈仕林. 拖曳线列阵声呐运动响应分析研究[D]. 大连: 大连理工大学, 2021.
|
| [4] |
陈小星. 拖曳线列阵声呐动态阵形仿真计算研究[J]. 声学与电子工程, 2018(3): 1-3. |
| [5] |
孔庆福, 吴家明, 曾凡明. 船舶喷水推进系统数学建模及仿真研究[J]. 船舶工程, 2006(2): 12-16. KONG Q F, WU J M, ZENG F M. Mathematical modeling and simulation of ship water jet propulsion system[J]. Ship Engineering, 2006(2): 12-16. DOI:10.3969/j.issn.1000-6982.2006.01.009 |
| [6] |
韩占忠. FLUENT流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2008.
|
| [7] |
叶凡滔. 水下拖曳线列阵动力学分析[D]. 北京: 中国舰船研究院, 2017.
|
| [8] |
董志荣. 拖曳线列阵声呐目标运动分析数学模型[J]. 电光与控制, 2007(5): 34-42. DONG Zhirong. Mathematical models for towed linear array sonar's target moving analysis[J]. Electronics Optics and Control, 2007(5): 34-42. DOI:10.3969/j.issn.1671-637X.2007.05.008 |
 2023, Vol. 45
2023, Vol. 45
