2. 常熟理工学院 汽车工程学院,江苏 常熟 215500;
3. 哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001
2. Automotive Engineering, Changshu Institute of Technology, Changshu 215500, China;
3. College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China
随着计算机技术的不断进步,基于CFD数值模拟技术的船舶水动力性能计算已经成为当下主流方法。孙志远等[1]采用RANS方法模拟了某滑行艇在静水中的阻力、纵摇和垂荡运动,并与实验值进行对比,最终验证了CFD数值模拟在滑行艇水动力性能计算中的可行性。针对某大型船舶,吴江涛等[2]提出了基于RANS方程和VOF方法的液舱晃荡及制荡计算方法,为液舱晃荡的计算提供一定理论依据。祝启波等[3]采用CFD数值方法计算了某船舶在水线面处大开口状态下的船体总阻力。Kramer等[4]采用CFD方法和航线模拟模型计算了某货船在4种简化模型下的水动力性能。Kim[5]采用RANS方法研究了波高对KCS船舶操纵性能的影响。船体型线对船体水动力性能起着决定性作用,合适的船体形状能够有效改善船体阻力,提高航行安全。叶萌等[6]采用RBF插值函数方法修改载重46 000 t油船几何,采用粒子群算法通过优化得到了总阻力最小的优良船型。Liu等[7]采用FFD方法修改DTMB-5415船型首部形状,采用遗传算法获得水动力性能最佳的船型。Nazemian等[8]同样采用FFD方法修改某三体船首部和尾部形状,采用NSGA-III优化算法对其进行优化,最终得到了阻力和尾流系数最佳的船体形状。
良好的船体型线对于船体阻力的降低有着非常大的作用。在船舶初始设计阶段,在满足一定要求下,合适的船型参数成为设计的重点。为了探讨船型参数与船体水动力性能之间的关系,本文以KCS船型为例,首先采用CFD方法建立三维数值水池,计算船体在不同速度下的总阻力和纵摇、升沉幅值。然后将计算结果与实验值和文献值进行对比,验证本文采用的方法对KCS船体阻力、纵摇和升沉幅值计算的可行性。最后根据相应的缩放因子修改船体形状,研究船体长度和船体宽度的变化对船体水动力性能(阻力和纵摇、升沉幅值)的影响,为船型设计提供一定参考。
1 CFD仿真方法 1.1 控制方程及湍流模型整个CFD数学模型的流场控制方程由连续方程和运动方程构成,表示如下[9]:
| $ \frac{{\partial \left( {\rho {{\bar u}_i}} \right)}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{{\partial (\rho {{\bar u}_i})}}{{\partial t}} = \frac{{\partial {{\bar \tau }_{ij}}}}{{\partial {x_j}}} - \frac{{\partial \bar p}}{{\partial {x_i}}} - \frac{{\partial (\rho {{\bar u}_i}{{\bar u}_j} + \rho \overline {u{'_i}u{'_j}} )}}{{\partial {x_j}}}。$ | (2) |
式中:ρ为密度;p 为平均压力;
采用可实现的k-ε模型作为整个流场的湍流模型,封闭上述方程组。
1.2 两相流捕捉本文涉及到两相流自由分界液面的问题,采用VOF模型模拟计算。VOF方法[10]是一种在固定的欧拉网格下的表面跟踪方法,可以精确捕捉自由液面情况。对于某时刻的网格单元内部,可知[11]:
1)若比例函数为0,说明该单元全部为气体;
2)若比例函数在0~1之间,说明该单元为含有两相流体的交界面;
3)若比例函数1,说明该单元全部为液体。
2 KCS船型水动力性能计算与验证采用KCS船型作为研究模型。图1为KCS船体三维实体模型,船尾带有舵。表1为KCS船体主尺度。采用CFD方法建立三维数值水池,图2为流域网格划分图。在自由液面上对网格进行加密,远离船体和自由液面的区域网格逐步扩大,从而减小网格总数量。最终整个计算域网格总数量为1376749。

|
图 1 KCS船体三维模型 Fig. 1 3-dimension ship hull model |
|
|
表 1 KCS船型主尺度 Tab.1 Geometric parameters of KCS ship |

|
图 2 计算域网格划分 Fig. 2 Mesh on the computational domain |
图3为母型船在设计航速Fr=0.26工况中船体纵摇、升沉稳定后船体表面的剪切应力云图。可以看出,在球鼻艏位置处有一块明显的应力最高区域。合适的球鼻艏布置有效地减小了靠近球鼻艏附近区域的船体表面剪切应力,从而产生有利的波形,达到减小船体总阻力的目的。

|
图 3 KCS船体表面剪切应力云图 Fig. 3 The wall shear stress distribution on the KCS ship hull surface |
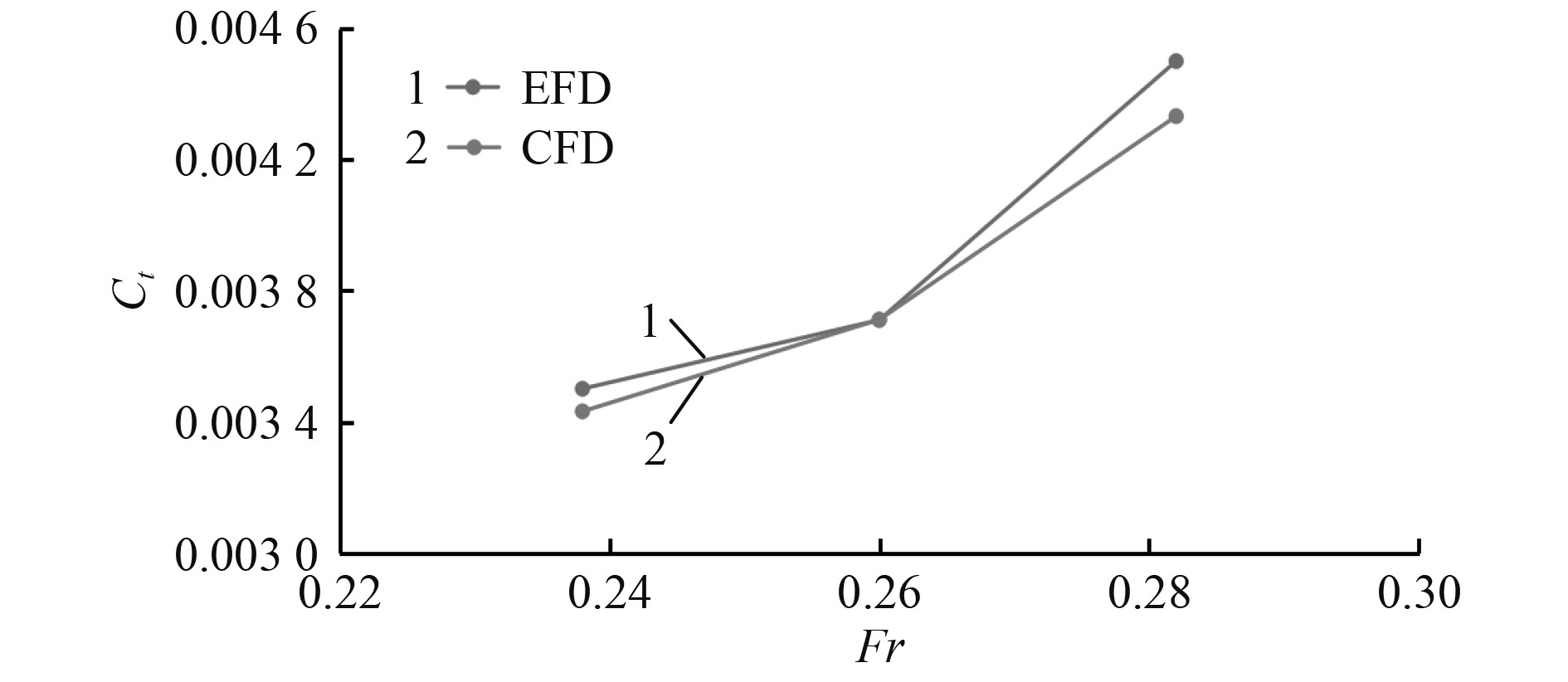
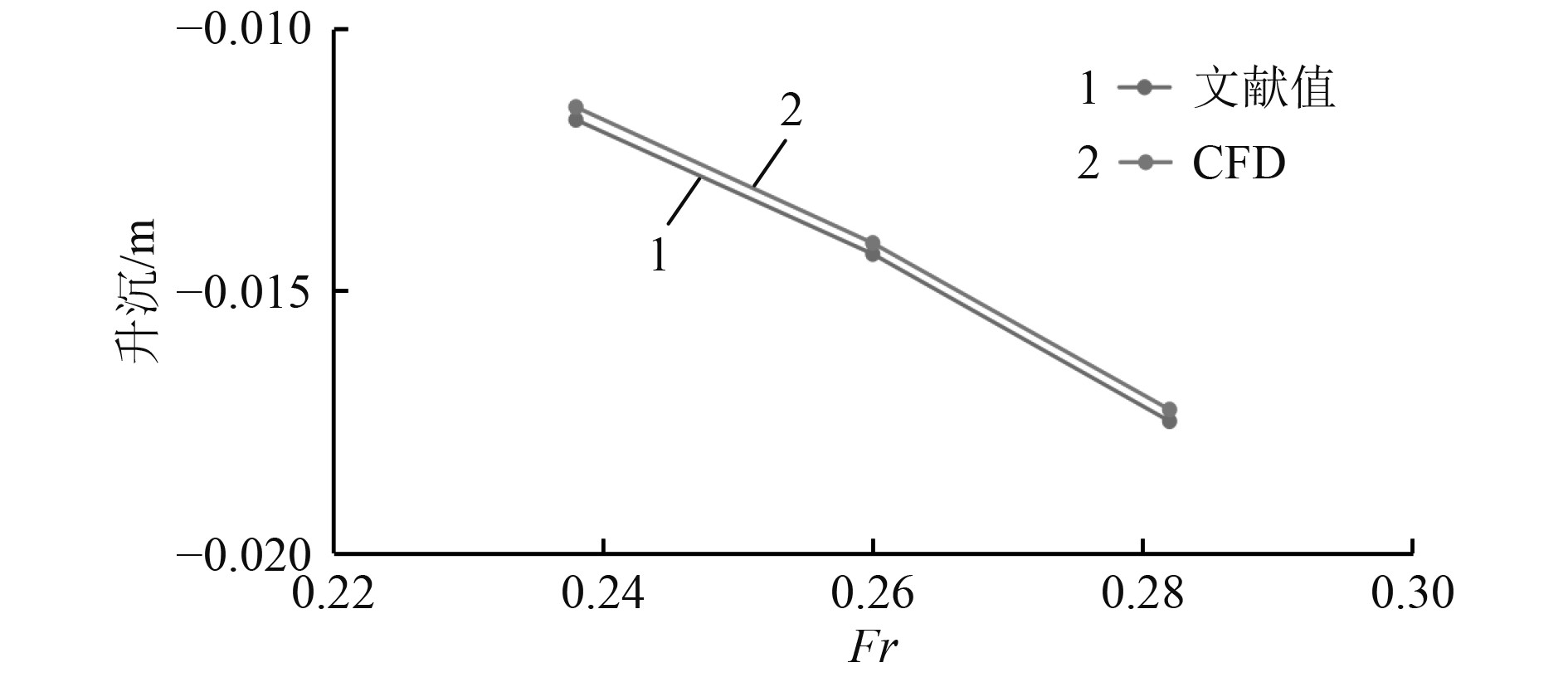
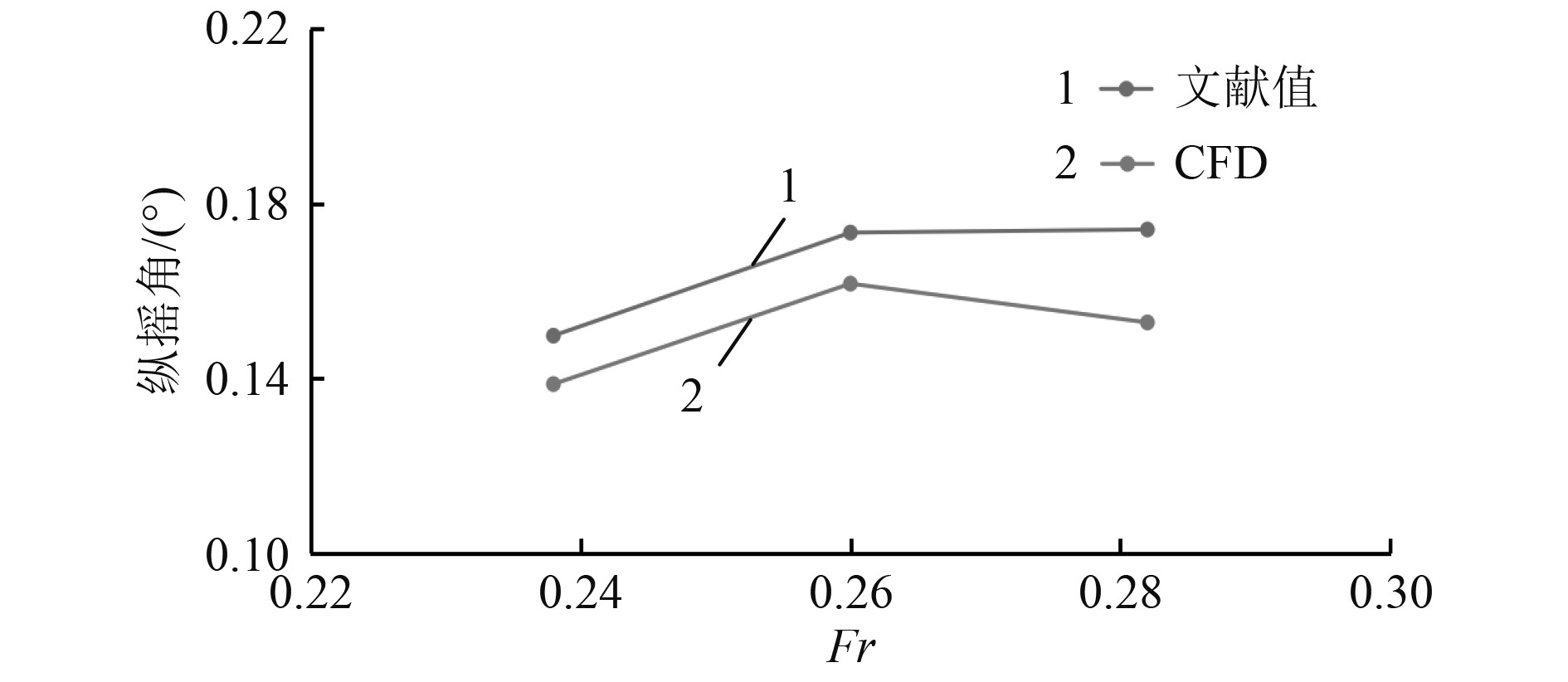
图4为采用CFD方法计算的不同速度下船体阻力和实验值[12]对比结果。可以看出,随着船速的增加,采用CFD方法计算的船体阻力结果趋势符合实验数据结果。在设计航速Fr=0.26时,总阻力误差最小,为0.027%。3个速度下总阻力的平均误差为1.91%。图5为采用CFD方法计算的船体升沉幅值和文献[12]数据对比结果。可以看出,采用本文的CFD方法能够很好地预测船体升沉幅值,误差较小,趋势与文献值相同。3个速度下升沉幅值的平均误差仅为1.59%。图6为采用CFD方法计算的船体纵摇角度和文献[12]数据对比结果。与阻力和升沉幅值相比,本文采用的CFD方法在纵摇角计算上误差略大,设计航速下,纵摇角度与文献值之间的误差为6.74%,总的平均误差为8.79%。虽然误差和文献值有一定差别,但是误差在可以接受的范围内。
3 船型参数对船体性能的影响
本文选择船长和船宽2个参数研究船型参数的变化对船体性能的影响。为了清楚地对比计算结果,分别改变船长和船宽参数,采用船体缩放因子对原始母型船进行缩放获得变化后的船体形状,然后通过修改船体的吃水保证不同船型的排水量固定不变。
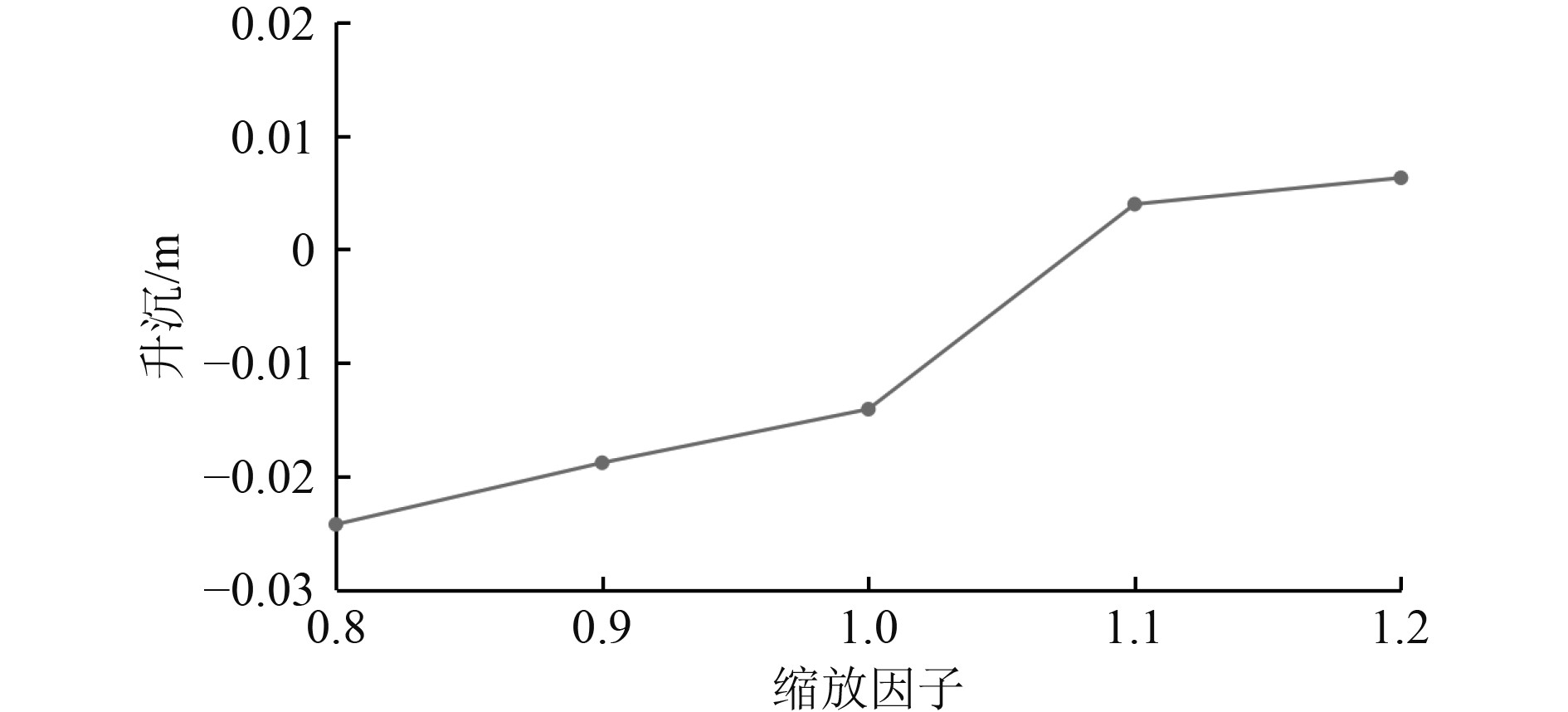
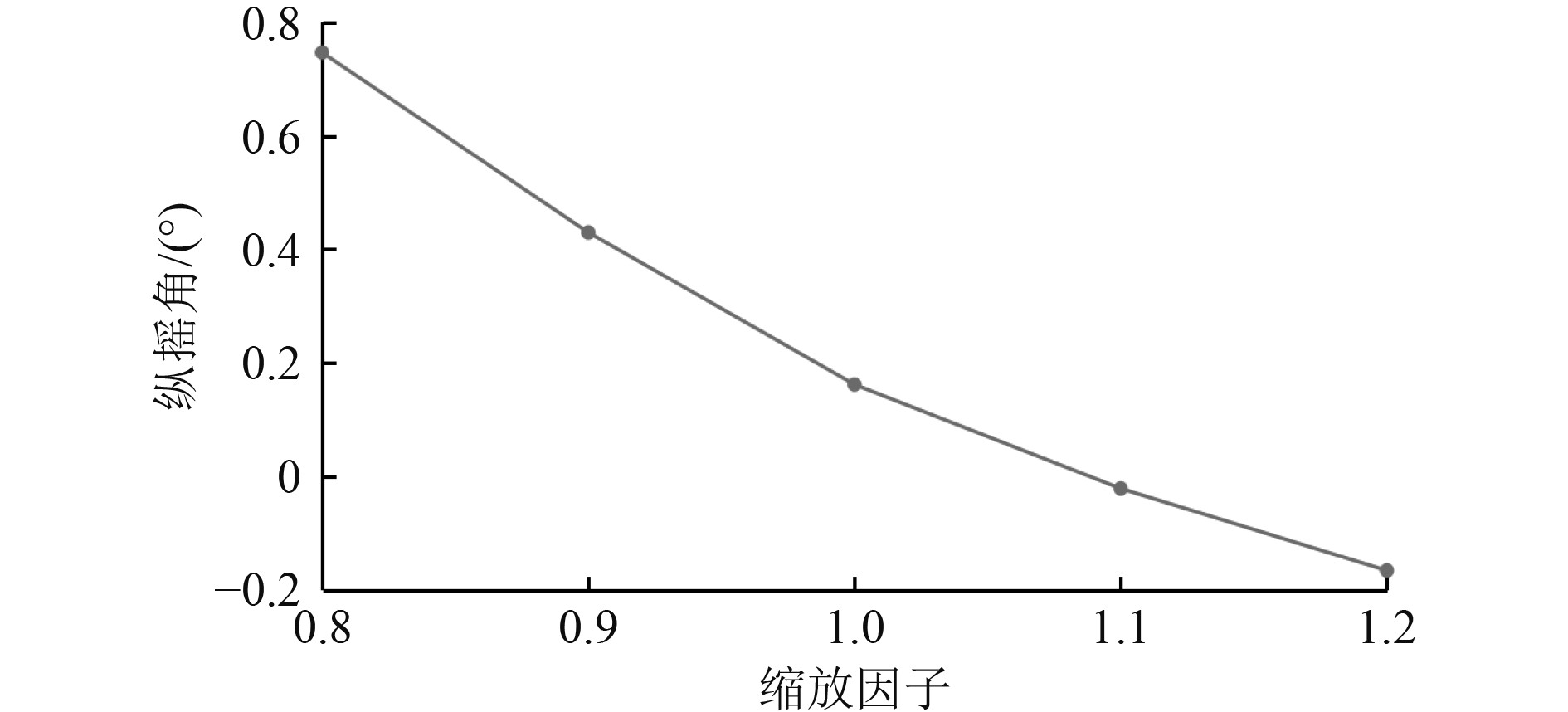
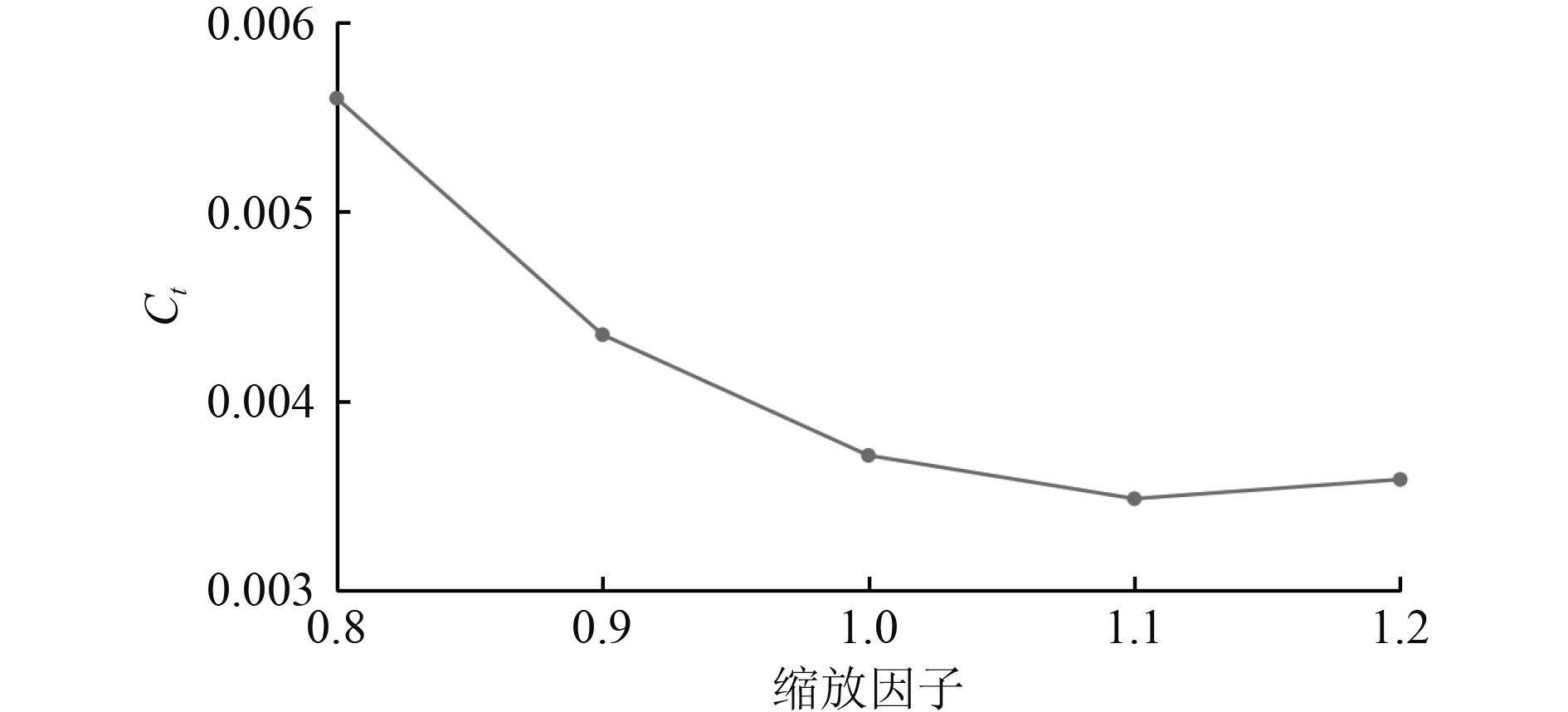
3.1 船长对船体性能的影响图7为在设计航速Fr=0.26工况中船体升沉幅值随着船长的变化规律。可以发现,总体上随着船长的增长,升沉幅值也呈递增的变化规律。随着船体长度的增加,船体升沉幅值在0.8~1.1缩放因子中急剧增加,然而当船长缩放因子继续增加时,升沉幅值增长变缓。图8为在设计航速Fr=0.26工况中船体纵摇角度随着船长的变化规律。可以看出,随着船长的增加,纵摇角度呈单调线性递减的变化规律。因此可知,船长的变化对船体的纵摇角度影响较大。图9为在设计航速Fr=0.26工况中船体总阻力系数随着船长的变化规律。可以发现,随着船长的增加,船体总阻力先单调递减,当船长继续增加时,总阻力开始呈现缓慢上升趋势。可见,通过设计合适的船长能够有效地减小船体阻力。
|
图 7 Fr=0.26不同船长升沉幅值计算结果对比 Fig. 7 Comparison of the sinkage for different ship length at Fr=0.26 |
|
图 8 Fr=0.26不同船长纵摇角度计算结果对比 Fig. 8 Comparison of the trim for different ship length at Fr=0.26 |
|
图 9 Fr=0.26不同船长船体总阻力计算结果对比 Fig. 9 Comparison of the total resistance for different ship length at Fr=0.26 |
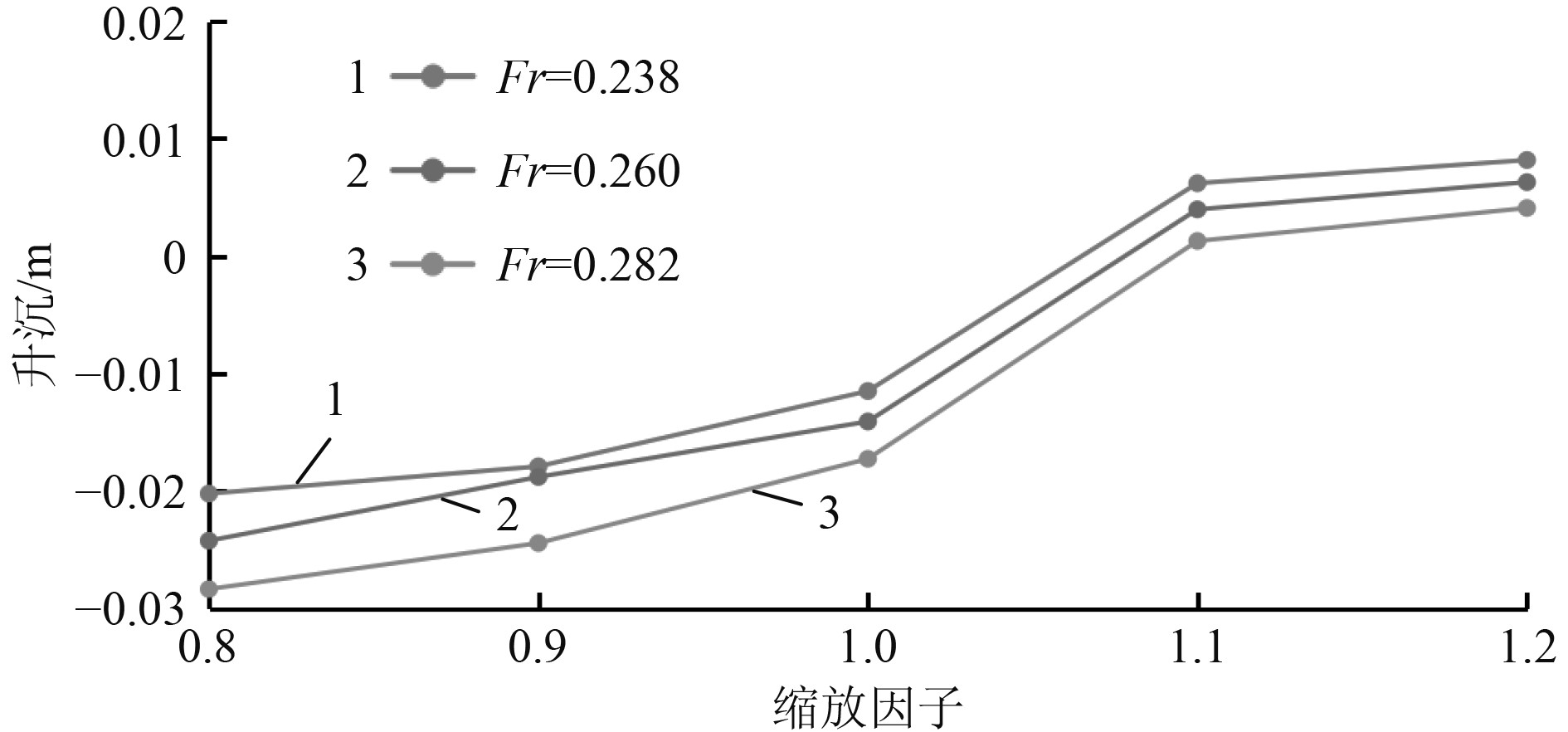
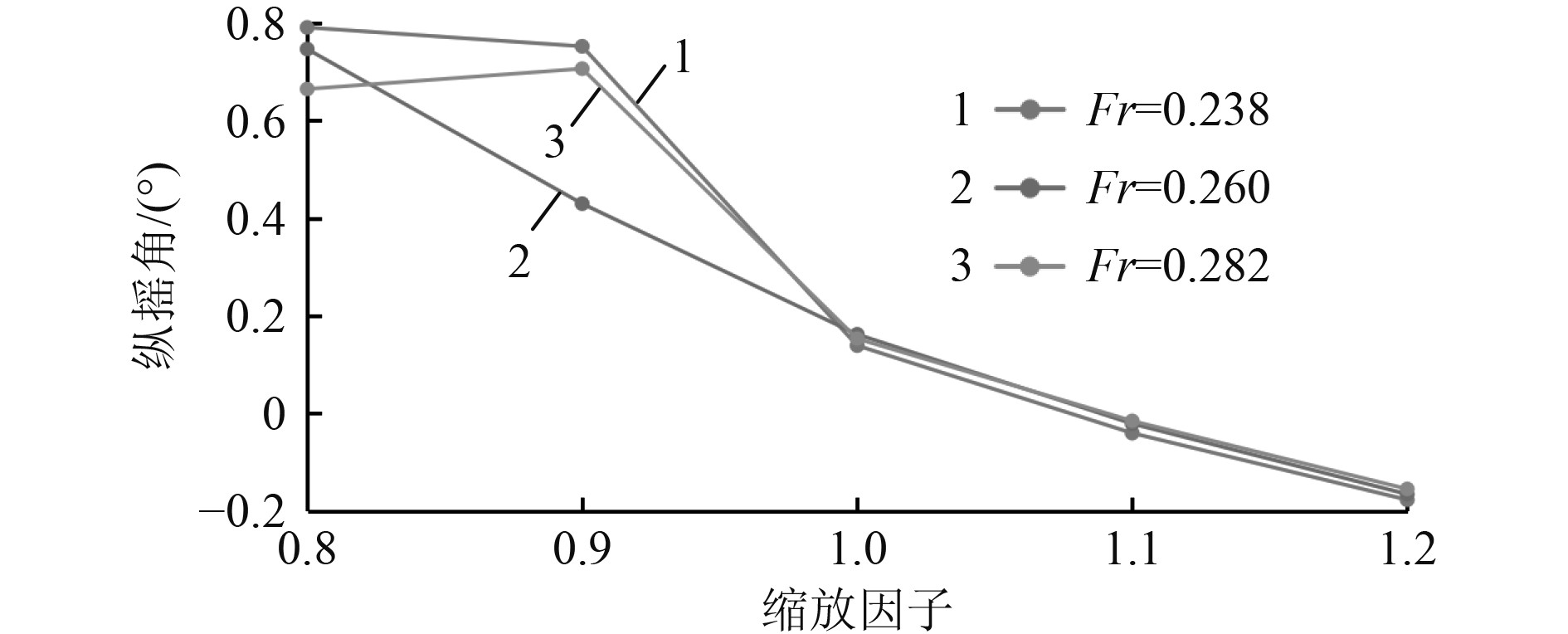
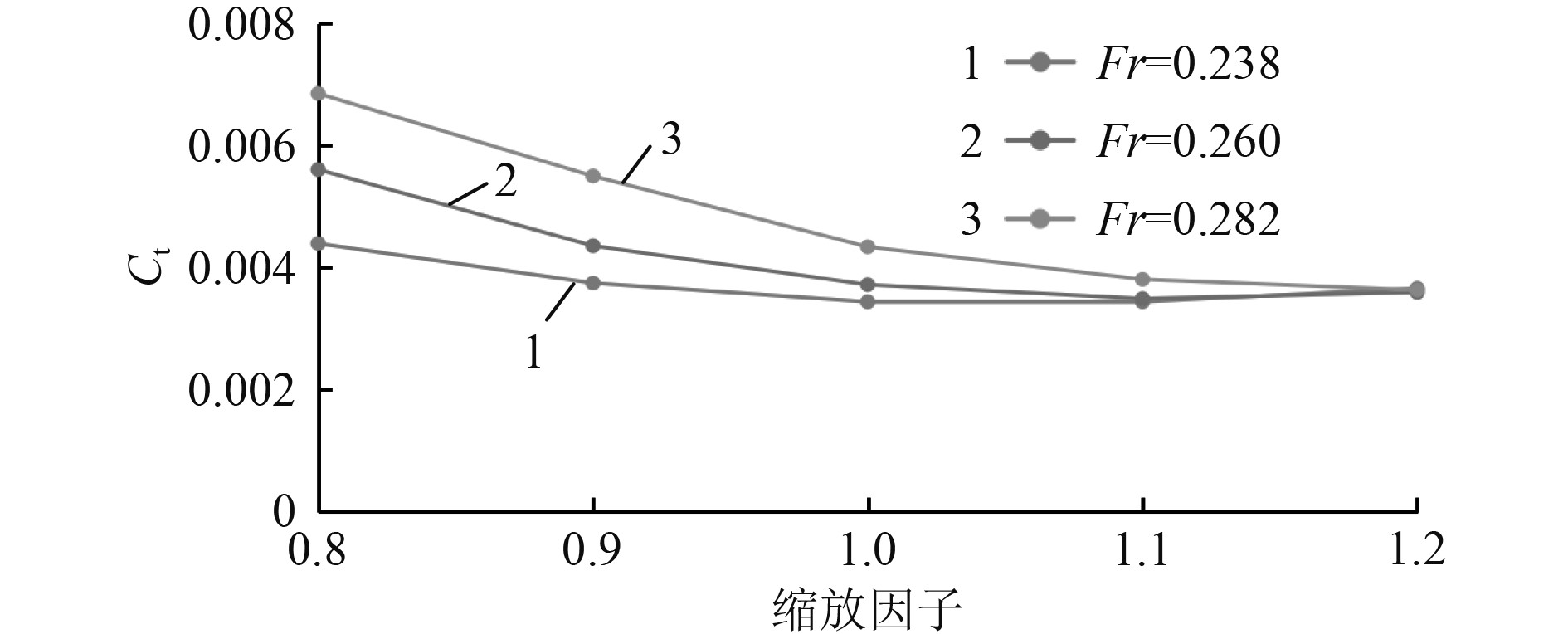
图10为不同船速下不同船长的升沉幅值计算对比结果。可以看出,不同航速下升沉幅值随着船长的变化规律基本相同,先是急剧上升,之后增加较缓慢。图11为不同船速下不同船长的纵摇角度计算对比结果。可以看出,速度的不同对应的纵摇角度变化的规律略有不同,主要集中在船长较短时。在Fr=0.238时,船长缩放因子从0.8变化到0.9时,纵摇角度略微降低,但是从0.9到1.0时,纵摇角度急剧下降,之后随着船长的增加,纵摇角度单调递减。在Fr=0.282时,船长缩放因子从0.8增加到0.9时,纵摇角度略微增加,当船长继续增加时,纵摇角度和其他速度下的变化规律相同。图12为不同船速下不同船长的总阻力计算对比结果。可知,不同速度下,随着船长的变化,船体总阻力的变化规律大体相同,只是随着速度的提高,这种阻力减小的百分比有所提高。
|
图 10 不同速度下不同船长升沉幅值计算结果对比 Fig. 10 Comparison of the sinkage for different ship length at different speeds |
|
图 11 不同速度下不同船长纵摇角度计算结果对比 Fig. 11 Comparison of the trim for different ship length at different speeds |
|
图 12 不同速度下不同船长船体总阻力计算结果对比 Fig. 12 Comparison of the total resistance for different ship length at different speeds |
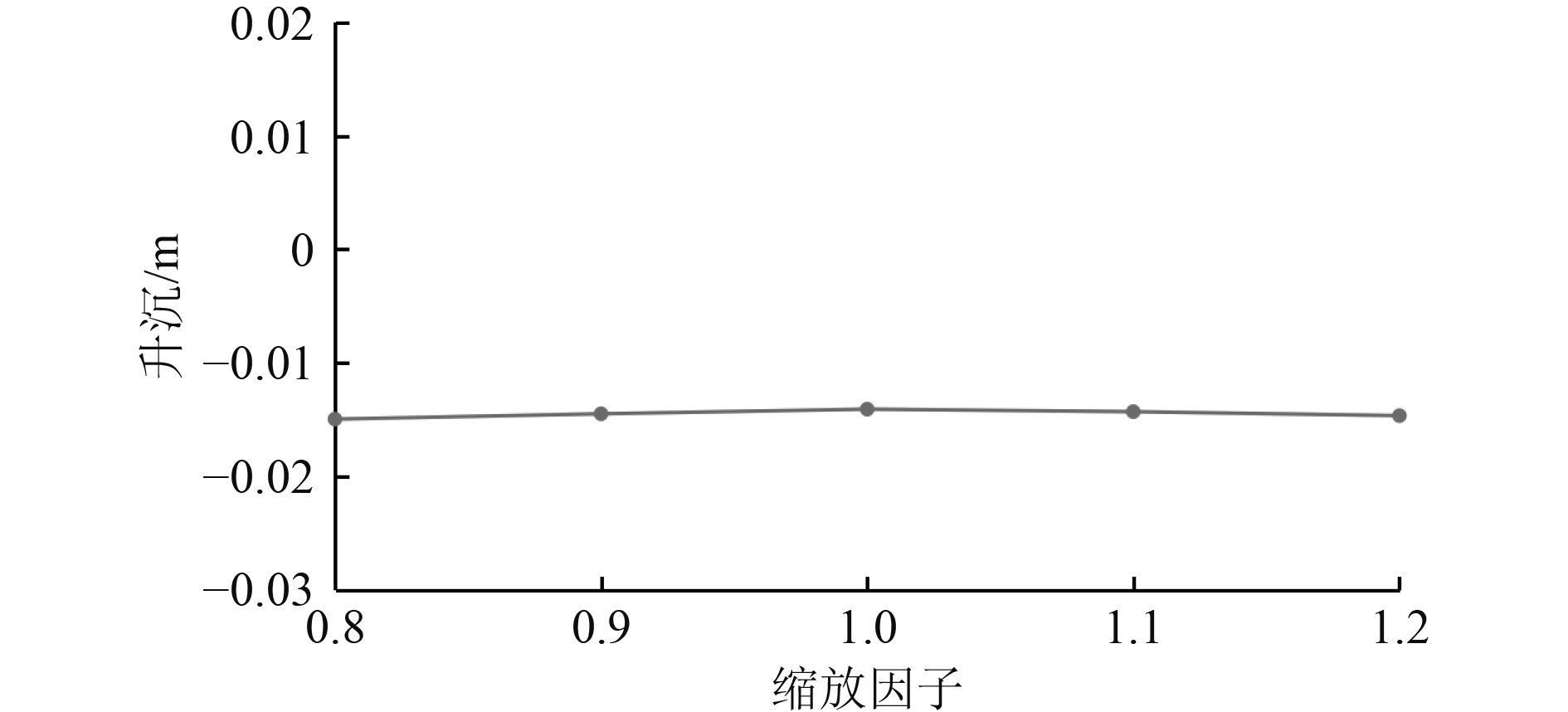
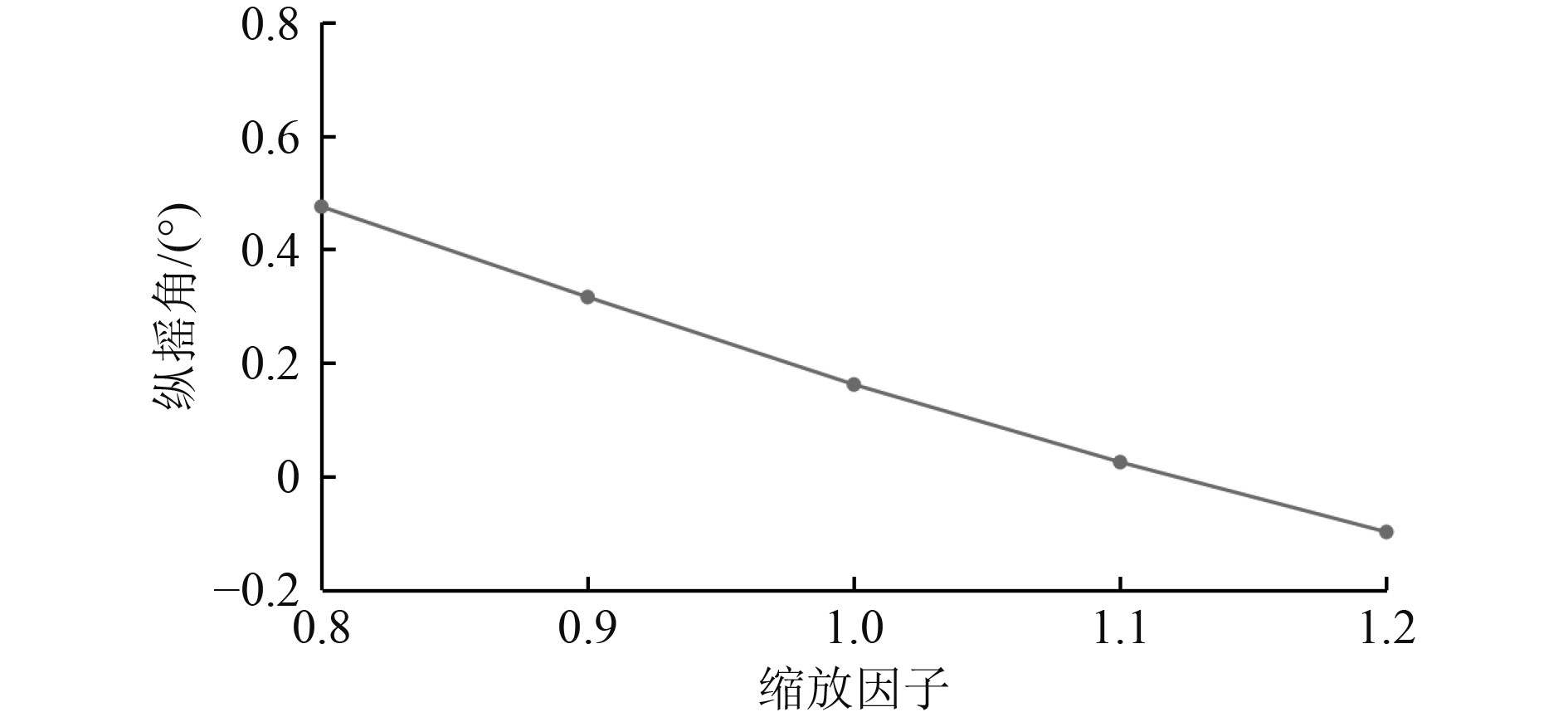
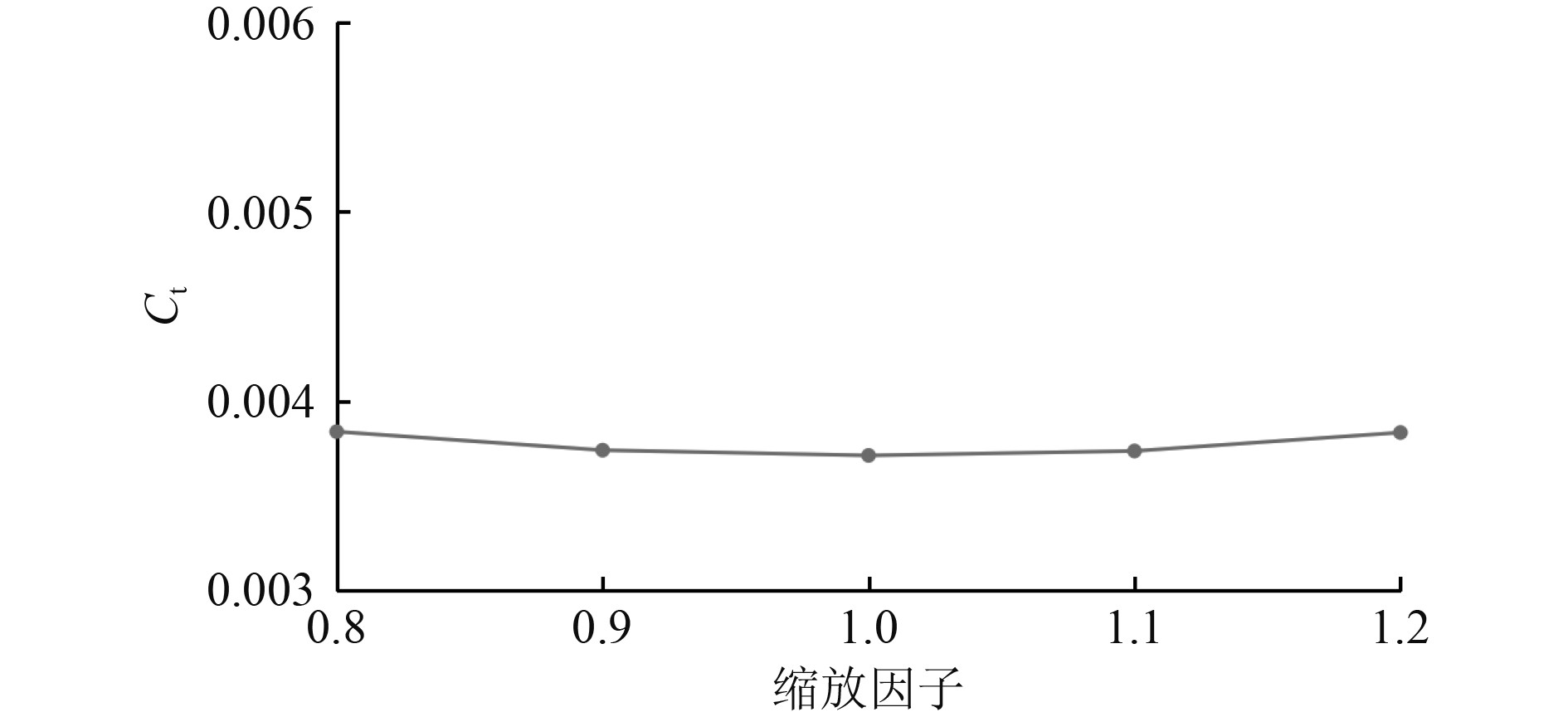
图13为设计航速Fr=0.26时不同船宽的升沉幅值计算对比结果。可以看出,随着船体宽度的增加,船体的升沉幅值变化不大。图14为设计航速Fr=0.26时不同船宽的纵摇角度计算对比结果。可以看出,随着船宽的增加,船体纵摇角度成单调递减趋势,这与设计航速下船长变化的规律基本相同。图15为设计航速Fr=0.26时不同船宽的船体总阻力计算对比结果。与图10相比,随着船宽的变化,船体总阻力变化依旧不明显,总阻力系数在0.00371~0.00384之间小幅度变化。
|
图 13 Fr=0.26不同船宽升沉幅值计算结果对比 Fig. 13 Comparison of the sinkage for different ship breadth at Fr=0.26 |
|
图 14 Fr=0.26不同船宽纵摇角度计算结果对比 Fig. 14 Comparison of the trim for different ship breadth at Fr=0.26 |
|
图 15 Fr=0.26不同船宽船体总阻力计算结果对比 Fig. 15 Comparison of the total resistance for different ship breadth at Fr=0.26 |
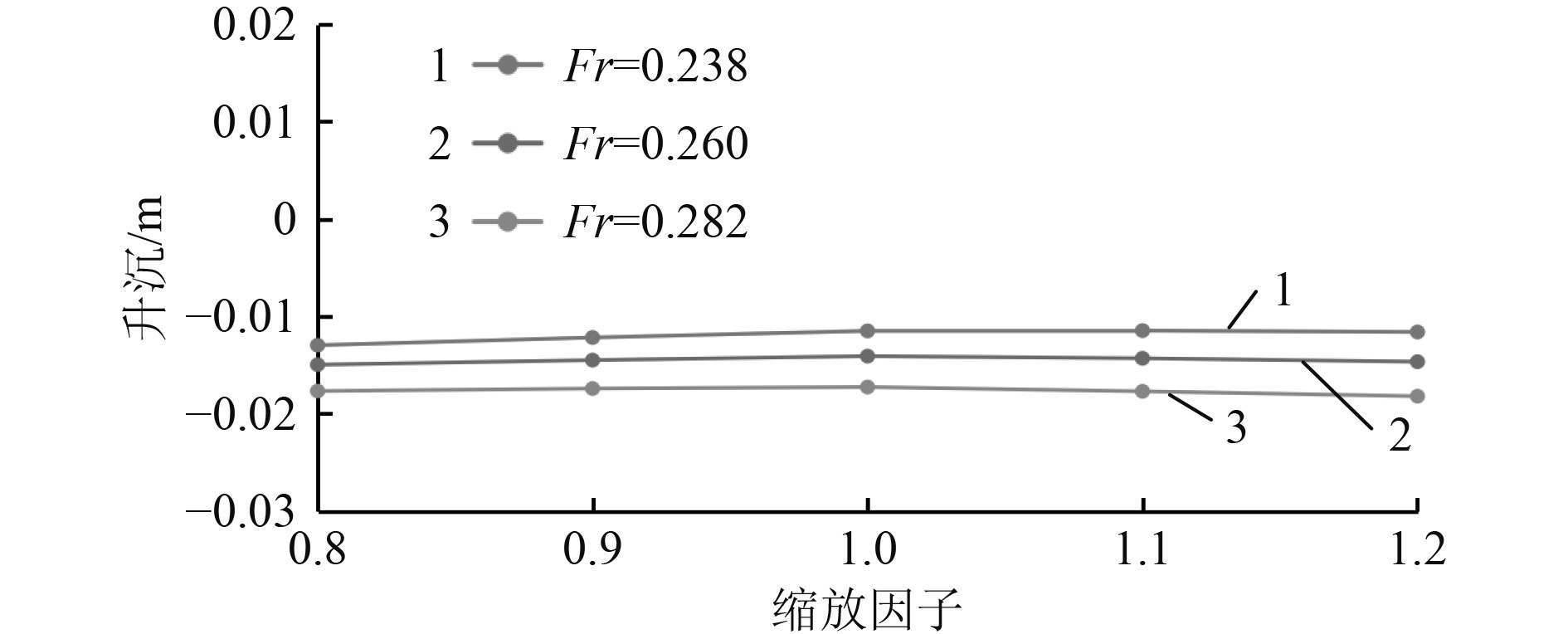
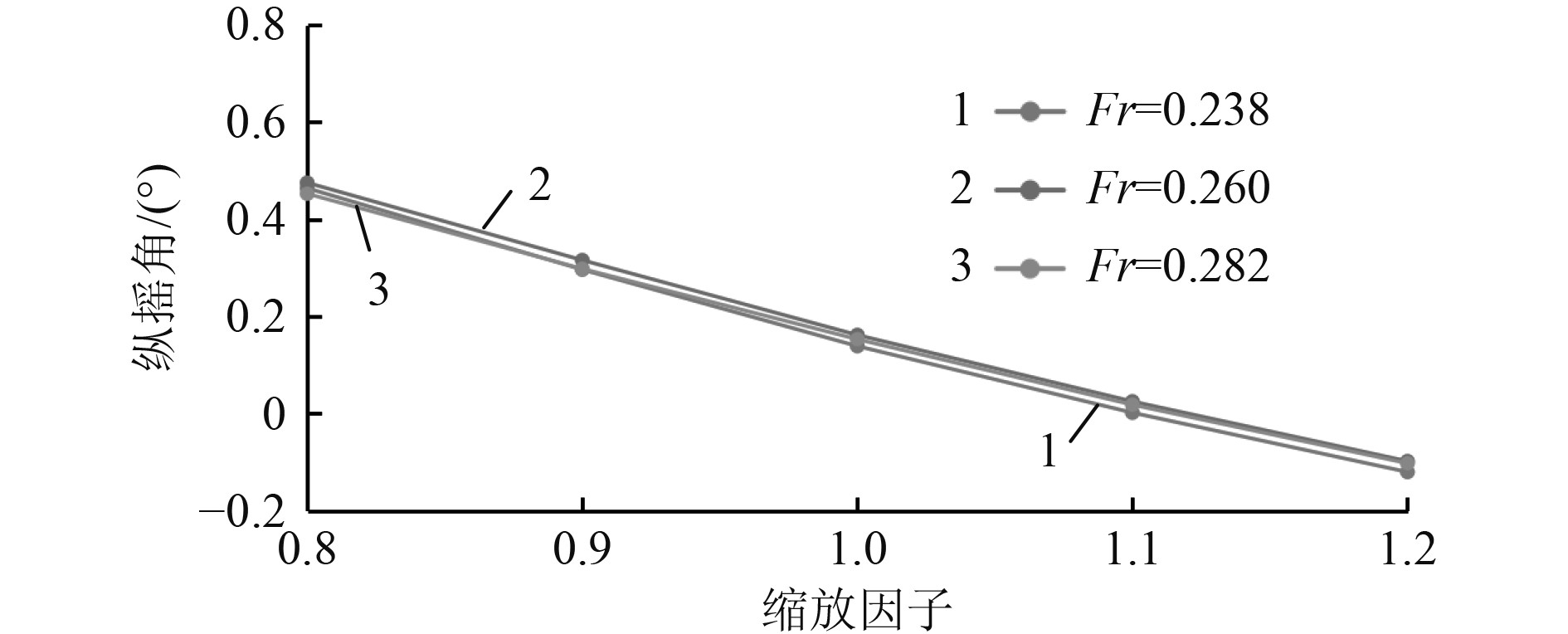
图16为不同速度下不同船宽的升沉幅值计算对比结果,图17为不同速度下不同船宽的纵摇角度计算对比结果,图18为不同速度下不同船宽的船体总阻力计算对比结果。可以看出,不同船速下,船体总阻力、纵摇和升沉幅值随着船宽的变化规律相同,整体上变化不明显。因此可知,船宽的增加对船体的总阻力和升沉幅值影响不大,但是对船体纵摇角度影响非常大。
|
图 16 不同速度下不同船宽升沉幅值计算结果对比 Fig. 16 Comparison of the sinkage for different ship breadth at different speeds |
|
图 17 不同速度下不同船宽纵摇角度计算结果对比 Fig. 17 Comparison of the trim for different ship breadth at different speeds |

|
图 18 不同速度下不同船宽船体总阻力计算结果对比 Fig. 18 Comparison of the total resistance for different ship breadth at different speeds |
本文建立基于KCS船型的船体水动力性能计算模型,通过VOF方法捕捉自由液面,采用RANS方程作为流域控制方程,模拟船体在不同速度下的船体阻力和纵摇角度和升沉幅值。然后分别变换船长和船宽,对比不同速度下的计算结果,得到结论如下:
1)本文采用的CFD方法模拟船体在设计航速下的总阻力与实验值误差为0.027%,纵摇角度和升沉幅值与文献值之间的误差分别为6.74%和1.45%。本文建立的CFD数学模型能够很好地模拟船体在静水中的水动力性能。
2)采用不同的缩放因子修改船体长度,随着船长的增加,船体的升沉幅值先急剧上升,当继续增加船长时,升沉幅值增加变缓。除了在Fr=0.282高航速外,船体的纵摇角度随着船长的增加逐渐降低。总阻力系数随着船长的增加逐渐变小,最后缓慢增加。
3)船宽的增加对船体的总阻力和升沉幅值影响不大,但是对船体纵摇角度影响非常大。随着船宽的增加,船体的纵摇角度单调递减。
| [1] |
孙志远, 邹劲, 谈果戈, 等. 基于STAR-CCM+的滑行艇阻力研究[J]. 船舶, 2017, 28(3): 16-20. |
| [2] |
吴江涛, 陈作钢. 基于 CFD 的大型船舶液舱晃荡研究[J]. 舰船科学技术, 2021, 43(12): 37-43. |
| [3] |
祝启波, 曾江易. 基于 CFD 的水线面大开口船舶阻力预报[J]. 广东造船, 2020, 39(5): 16-19. |
| [4] |
KRAMER JV, STEEN S. Simplified test program for hydrodynamic CFD simulations of wind-powered cargo ships[J]. Ocean Engineering, 2022, 244(1): 1–19.
|
| [5] |
KIM D, SONG S, JEONG B, et al. Unsteady RANS CFD simulations of ship manoeuvrability and course keeping control under various wave height conditions[J]. Applied Ocean Research, 2021, 117: 102940.
|
| [6] |
叶萌, 冯佰威, 常海超. 基于近似模型的载重46000 t油船阻力性能优化[J]. 造船技术, 2020, 355(12): 6-12. DOI:10.3969/j.issn.1000-3878.2020.03.002 |
| [7] |
LIU X, ZHAO W, WAN D. Multi-fidelity Co-Kriging surrogate model for ship hull form optimization[J]. Ocean Engineering, 2022, 243: 1-20. |
| [8] |
NAZEMIAN A, GHADIMI P. Multi-objective optimization of ship hull modifcation based on resistance and wake feld improvement: combination of adjoint solver and CAD-CFD-based approach[J]. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 2022, 44(27): 1-27. |
| [9] |
OWEN D, DEMIREL Y. K, OGUZ E, et al. Investigating the effect of biofouling on propeller characteristics using CFD[J]. Ocean Engineering, 2018, 159: 505-516. DOI:10.1016/j.oceaneng.2018.01.087 |
| [10] |
HIRT C W, NICHOLS B D. Volume of fluid method for the dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39(1): 201-225. |
| [11] |
陈辉, 陈克强. M船型阻力数值模拟[J]. 船海工程, 2012, 41(5): 51-53. |
| [12] |
郭春雨, 王恋舟, 赵庆新, 等. 一种计及姿态变化的船舶阻力预报方法[J]. 船舶工程, 2015, 37(1): 31-34. |
 2023, Vol. 45
2023, Vol. 45