激光网络能够实现对目标的跟踪、检测和识别[1],在实际应用过程中[2],回波信号极易受到噪声或遮挡等因素影响,不利于信息的提取[3]。因此激光网络回波信息增强方法的研究对于激光网络应用具有重要意义。
山雨等[4]在研究回波信号增强问题过程中,利用贝叶斯因子分析模型的参数求解问题取代信号增强过程,并对参数进行求解。张涛等[5]在研究回波信号增强问题时,针对信号频谱扩散问题进行加权补偿,通过目标周边多帧信号实施联合处理,由此实现信号增强目的。但它样均未考虑信号的异步传输问题,由此造成最终的增强效果受到一定影响,为此提出大数据异步传输环境下舰船激光网络回波信号增强处理方法,在回波信号中获取更多有用的信息。
1 舰船激光网络回波信号增强处理方法 1.1 基于信号累积增强的激光网络回波信号采集信号累积增强即将舰船激光网络范围内的若干个回波信号积累在一起,由此形成一个高强度的回波信号,并以此为基础实现目标检测。激光网络回波信号积累则增强过程描述如下:以f,
| $ \left\{ \begin{gathered} N = {E \mathord{\left/ {\vphantom {E {\Delta t}}} \right. } {\Delta t}} ,\\ \Delta U = {{c\Delta t} \mathord{\left/ {\vphantom {{c\Delta t} 2}} \right. } 2}。\\ \end{gathered} \right. $ | (1) |
式中,
舰船激光网络回波信号被划分成N个部分,为完成M个回波信号的累积增强,就要通过加法设定信号累积标准。由此将M个舰船激光网络回波信号相对应的N个部分依次输入至M个累加器,由此完成舰船激光网络回波信号的M次累积。
| $ {D_R}{\text{ = }}\sum\limits_{k = 0}^S {x_k^2} ,$ | (2) |
| $ {D_\xi }{\text{ = }}\sum\limits_{k = 0}^S {\varepsilon _k^2} ,$ | (3) |
由此得到功率信噪比,公式描述如下:
| $ SN{R_i} = \frac{{{D_R}}}{{{D_\xi }}} = \frac{{\displaystyle\sum\limits_{k = 0}^S {x_k^2} }}{{\displaystyle\sum\limits_{k = 0}^S {\varepsilon _k^2} }},$ | (4) |
| $ SN{R_n} = \frac{{{n^2}{D_R}}}{{n{D_\xi }}} = nSN{R_i}。$ | (5) |
通过n次信号累积处理后,舰船激光网络回波信号噪声功率与幅值分别得以提升,通过信号累积技术能够提升舰船激光网络回波信号的信噪比。
1.2 大数据异步传输环境下的异常回波信号清除由于舰船激光网络回波信号采集过程中,采用信号累积增强的方式,将多个回波信号积累成一个高强度的回波信号,这一过程中将产生异步传输特性,而信号的异步传输将导致异常信号产生,因此在采用信号累积增强方式对舰船激光网络回波信号实施增强处理过程中,需通过分形特征法清除回波信号异步传输条件下产生的异常信号。异常信号清除过程中,将盒维数作为舰船激光网络异步传输过程中的连接分形维数。S(k)和
| $ \phi = \dfrac{{\displaystyle\sum\limits_{{k_1},{k_2}} {\dfrac{{\log \left( {\dfrac{{{k_1}\tilde t}}{{{k_2}\tilde t}}} \right)}}{{T\log \left( {\dfrac{{{k_1}}}{{{k_2}\tilde t}}} \right)}}} }}{B}。$ | (6) |
式中:
| $ k\tilde t = \frac{{\left( {{L_{k\tilde t}} - {L_{\tilde t}}} \right)\phi }}{{S_n^{\left( i \right)} \cdot \displaystyle\sum {i{k_1}\tilde t \cdot j{k_1}\tilde t} }},$ | (7) |
式中,
根据式(7)可获取时刻
| $ \dim \left( \phi \right) = \frac{{\displaystyle\sum\limits_{{k_1},{k_2}} {\frac{{\log \left( {{k_1}\tilde t} \right) - \log \left( {{k_2}\tilde t} \right)}}{{\left( {\log \left( {{k_1}} \right) - \log \left( {{k_2}} \right)} \right)}}} }}{B} 。$ | (8) |
利用式(8)可获取异步传输条件下舰船激光网络连接于不同时刻盒维数。非异常状态下,检出激光网络连接分形维数趋于恒值,可通过hn表示,则hc(i)可表示hn对应的动态舰船激光网络连接于不同时刻ti的分形维数,则利用式(9)计算hn与hc(i)间的差异值:
| $ p\left( i \right) = \left| {{h_c}\left( i \right) - {h_n}} \right| \cdot \dim \left( \phi \right)。$ | (9) |
设定阈值
清除异常信号后,舰船激光网络ti时刻的回波信号将处于缺失状态,会导致舰船激光网络通信性能的下降,针对这一问题,采用贝叶斯因子分析模型恢复缺失的回波信号,并对回波信号进行去噪处理。贝叶斯因子分析模型以模型参数求解过程替代舰船激光网络回波信号缺失信号恢复过程,通过变分贝叶斯期望最大算法求解模型参数,通过求解过程确定不同参数的后验概率分布。
1)因子加载矩阵的后验概率满足高斯分布
| $ q\left( D \right) = \prod\limits_{k = 1}^k {p\left( {{d_k}\left| {{m_{k,}}{\Sigma _k}} \right.} \right)},$ | (10) |
式中:
| $ \left\{ \begin{gathered} {m_k} = {\Sigma _k}\left( {\left\langle \upsilon \right\rangle {y^{\rm{T}}}\left\langle s \right\rangle } \right),\\ {\Sigma _k} = {\left( {\left\langle \upsilon \right\rangle \left( {\Theta \left\langle {{s_k}s_k^{\rm{T}}} \right\rangle + \left\langle {diag\left( \alpha \right)} \right\rangle } \right)} \right)^{ - 1}} ,\\ \end{gathered} \right. $ | (11) |
式中,<>和diag()表示求期望运算和对角矩阵。
2)
| $ q\left( s \right) = p\left( {s\left| {\varsigma ,{\boldsymbol{M}}} \right|} \right) ,$ | (12) |
均值
| $ \left\{ \begin{gathered} {\boldsymbol{M}} = {\left( {I + \left\langle \upsilon \right\rangle \left\langle {{w^{\rm{T}}}{\Theta ^{\rm{T}}}\Theta w} \right\rangle } \right)^{ - 1}},\\ \varsigma = \left\langle \upsilon \right\rangle {\boldsymbol{M}}\left\langle {{w^{\rm{T}}}} \right\rangle {\Theta ^{\rm{T}}}y 。\\ \end{gathered} \right. $ | (13) |
3)参数ak的后验概率满足伽马分布标准
| $ q\left( {{a_k}} \right) = p\left( {{a_k}\left| {{c_k},{w_k}} \right|} \right),$ | (14) |
其中:
| $ \left\{ \begin{gathered} {c_k} = {c_0} + P ,\\ {w_k} = {w_0} + \left\langle {w_k^{\rm{T}}w_k^{}} \right\rangle ,\\ \end{gathered} \right. $ | (15) |
依照伽马分布标准,ak的后验概率分布均值计算公式如下:
| $ \left\langle {{a_k}} \right\rangle = \frac{{{c_k}}}{{{w_k}}}。$ | (16) |
4)参数
| $ q\left( \upsilon \right) = p\left( {\upsilon \left| {\tilde a,\tilde b} \right|} \right),$ | (17) |
其中:
| $ \left\{ \begin{gathered} a = {a_0} + P ,\\ b = {b_0} + {y^{\rm{T}}}y + \sum\limits_{k = 1}^k {w_k^{\rm{T}}S} + tr\left( {\left\langle {w_k^{}w_k^{\rm{T}}} \right\rangle \left( {s{s^{\rm{T}}}} \right)} \right) 。\\ \end{gathered} \right. $ | (18) |
式中,tr()为求迹运算。
依照伽马分布标准,
| $ \left\langle \upsilon \right\rangle = \frac{a}{b}。$ | (19) |
在满足迭代次数上限或接连两次迭代参数波动低于设定阈值的条件下即可终止迭代过程。
由此获取完成噪声抑制与缺失数据复原等增强过程的舰船激光网络回波信号。
2 测试结果与分析测试对象波长与输出功率分别为910 mm和65 mW,所输出的信号功率经由分数器分为两部分,分别是本振光与信号光,分别占输出功率的5%和95%。研究对象回波信号光直接投射至目标上,并通过投射望远镜接收回波信号,利用保偏光纤耦合器对本振光与接收光进行耦合处理,通过模数转换采集器采集后传输至计算机内实施增强处理。
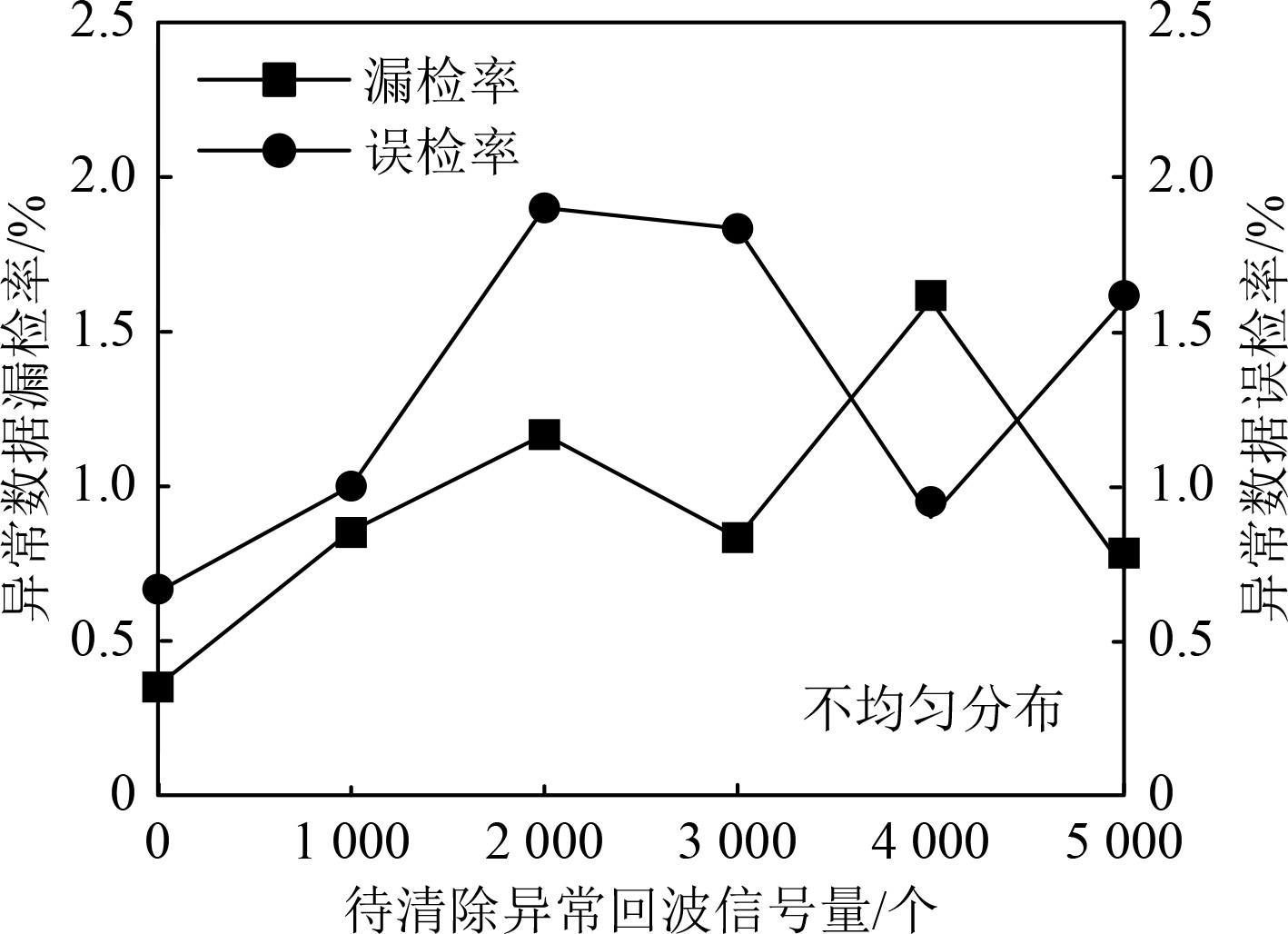
2.1 异步传输环境下异常数据漏检率与误检率为验证清除回波信号中异常数据应用性能,以漏检率与误检率为性能分析指标,结果如图1所示。分析图1得到,随着待清除异常回波信号量的提升,回波信号中的异常信号漏检率整体表现出提升趋势,但整体控制在2%以下。而回波信号中异常信号的误检率随着待清除异常回波信号量的提升表现出明显的波动性,但始终低于2%。以上数据充分说明本文方法在异步传输环境下的异常回波信号清除过程具有较高的准确率。
|
图 1 异步传输环境下异常数据漏检率与误检率 Fig. 1 Abnormal data leak rate and false detection rate under asynchronous transmission environment |
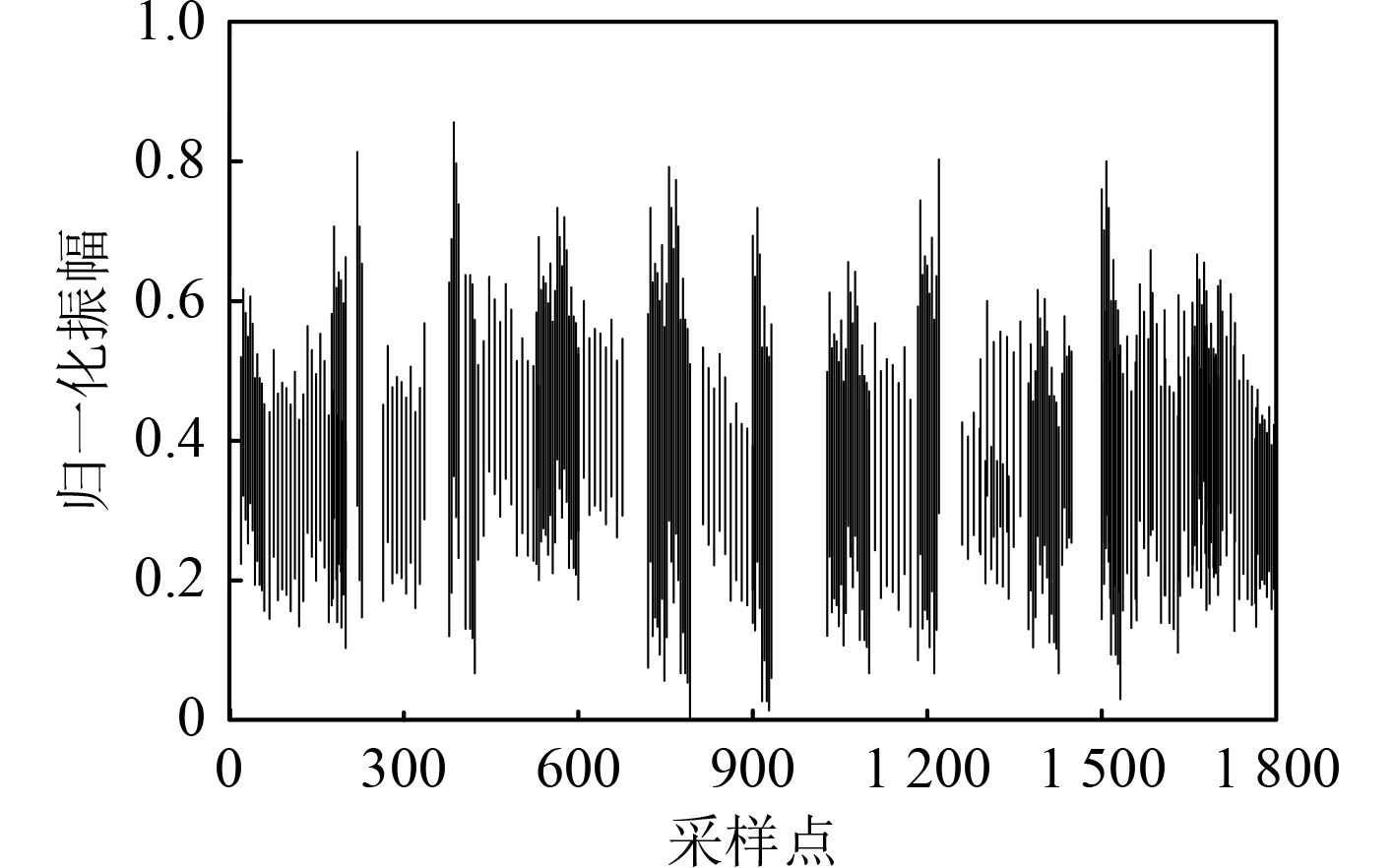
通过在所采集回波信号内引入高斯白噪声的方式测试本文方法的增强效果。图2和图3分别为信噪比0 dB时激光雷达回波数据和本文方法的去噪性能。由图2和图3能够得到,所采集回波信号在噪声污染状态下,周期性变弱,在此信号内提取有用信息较为困难。采用本文方法对其进行增强处理,能够彻底抑制信号内的噪声分量,较好地保留所采集信号内的有用信息。
|
图 2 信噪比为0 dB条件下的回波信号 Fig. 2 Echo signal with SNR of 0 dB |
|
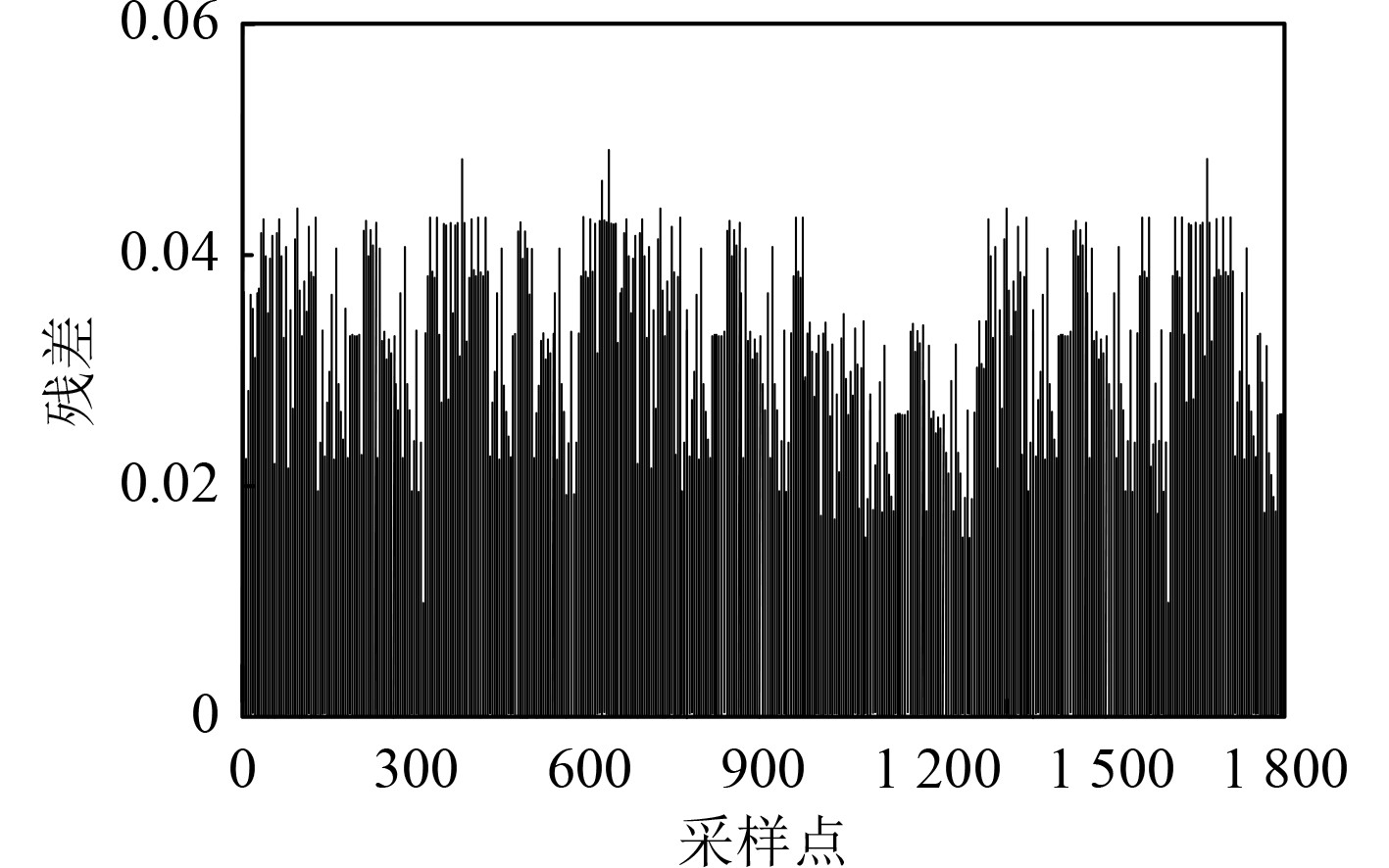
图 3 回波信号噪声抑制结果 Fig. 3 Echo signal noise suppression results |
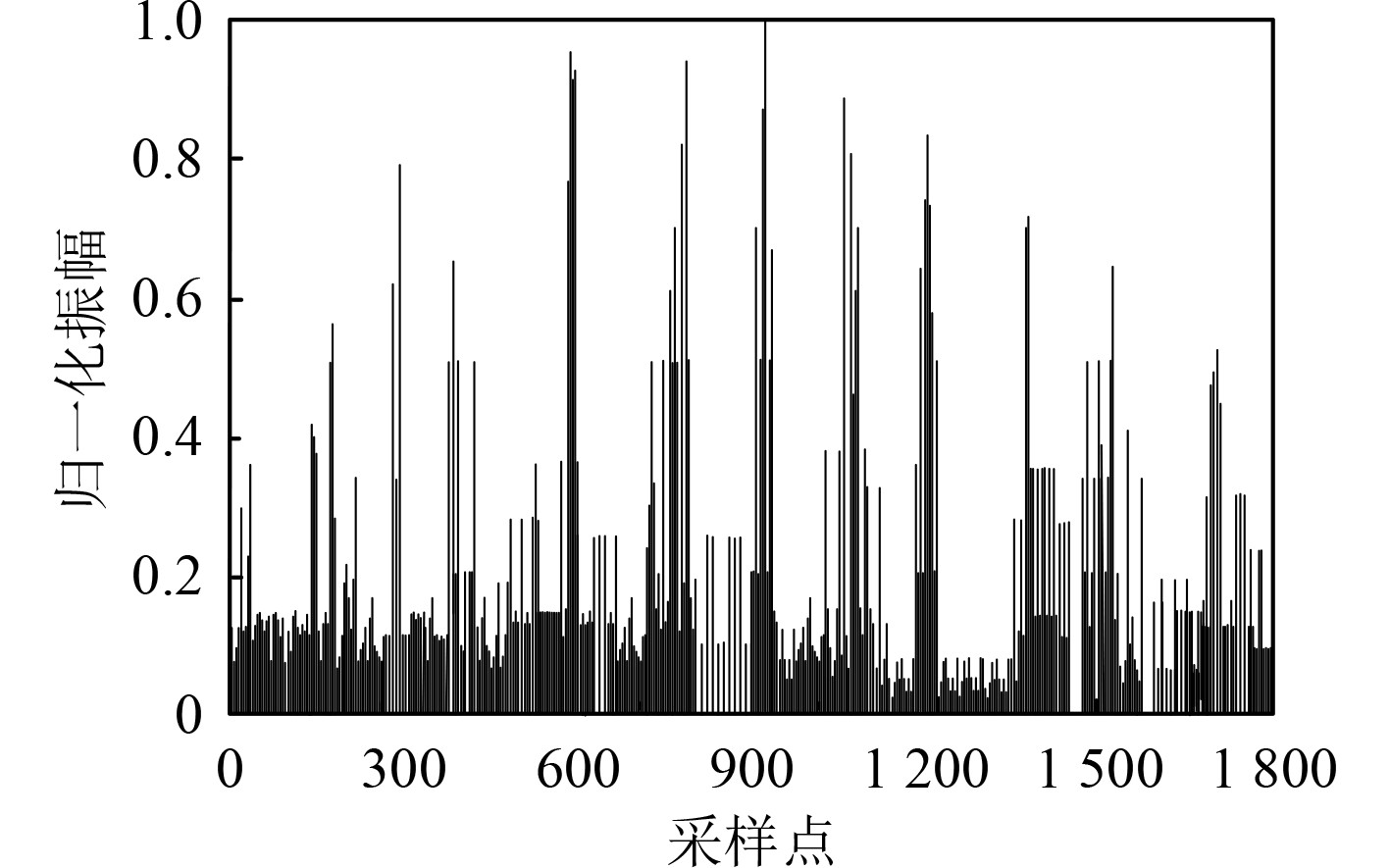
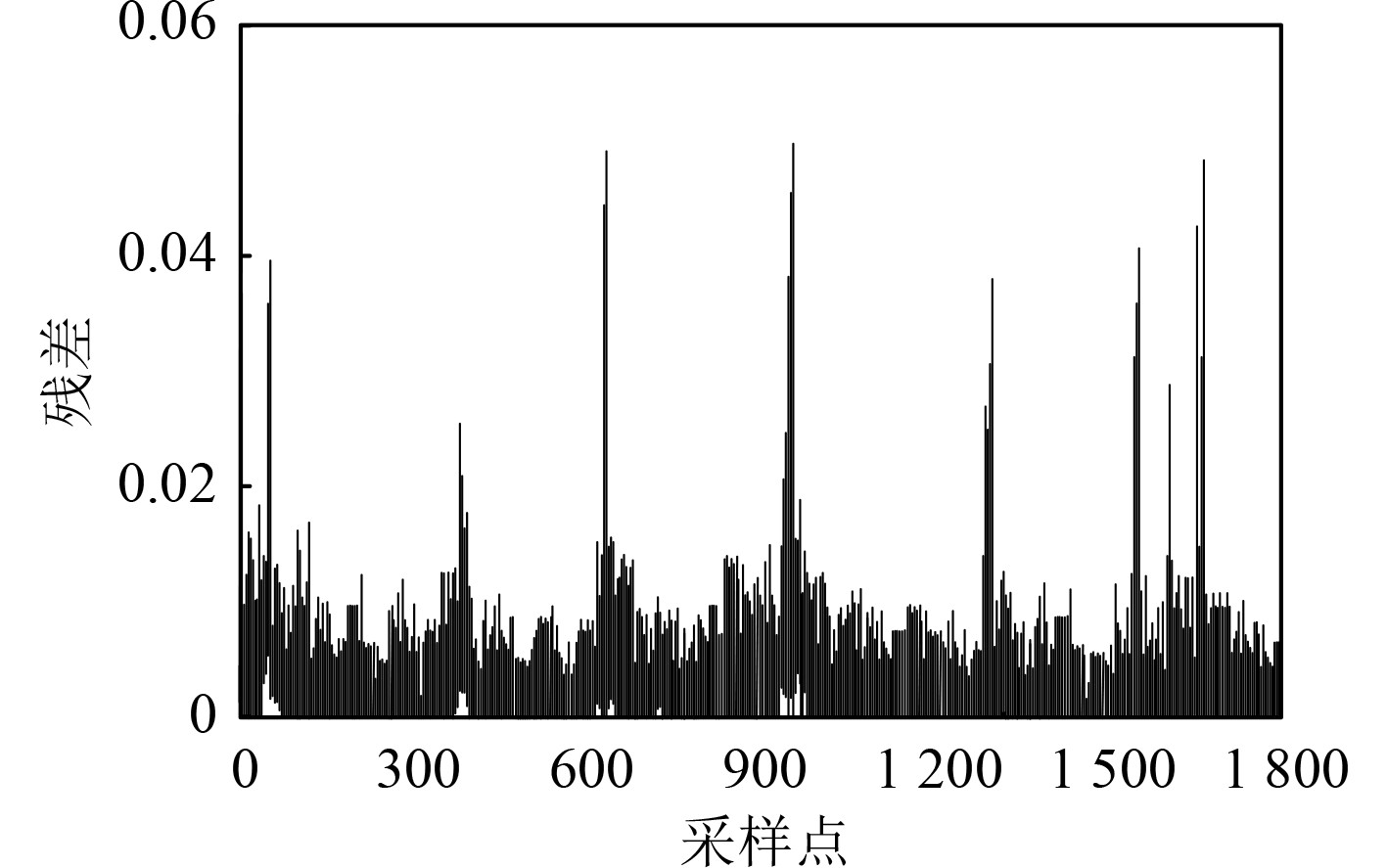
图4和图5分别为缺失率为25%条件下的回波数据和本文方法缺失数据恢复结果。分析图4和图5能够得到,采用本文方法进行缺失信号恢复时,恢复结果中不同采样点的残差波动较为微弱,这表明本文方法具有较好的信号恢复精度。
|
图 4 缺失率为25%条件下的回波信号 Fig. 4 Echo data with a missing rate of 25% |
|
图 5 回波信号恢复结果 Fig. 5 Echo signal recovery results |
本文设计了大数据异步传输环境下舰船激光网络回波信号增强处理方法,通过信号累积增强、异常信号清除与缺失信号恢复等过程实现回波信号增强的目的,并通过实验结果验证了本文方法的有效性。
| [1] |
徐沛拓, 刘东, 周雨迪, 等. 海洋激光雷达多次散射回波信号建模与分析[J]. 遥感学报, 2020, 24(2): 142-148. XU Peituo, LIU Dong, ZHOU Yudi, et al. Modeling and analysis of oceanic lidar returns with multiple scattering[J]. Journal of Remote Sensing, 2020, 24(2): 142-148. DOI:10.11834/jrs.20208266 |
| [2] |
董志伟, 闫勇吉, 姜玉刚, 等. 基于神经网络的条纹管激光雷达回波信号分类(英文)[J]. 红外与激光工程, 2020, 49(S2): 124-130. DONG Zhiwei, YAN Yongji, JIANG Yugang, et al. Classification technique of echo signal from streak-tube LiDAR based on neural network[J]. Infrared and Laser Engineering, 2020, 49(S2): 124-130. |
| [3] |
孙佳琦, 胡淼, 李鹏, 等. 不同风速下侧向散射激光雷达的回波信号分析[J]. 光子学报, 2020, 49(4): 53-60. SUN Jiaqi, HU Miao, LI Peng, et al. Echo signals analysis of side-scattering LiDAR under different wind speed conditions[J]. Acta Photonica Sinica, 2020, 49(4): 53-60. |
| [4] |
山雨, 常亮, 张希兵, 等. 基于贝叶斯因子分析模型的激光回波信号增强方法[J]. 应用激光, 2021, 41(1): 161-166. SHAN Yu, CHANG Liang, ZHANG Xibing, et al. Laser echo waveform enhancement method based on Bayesian factor analysis model[J]. Applied Laser, 2021, 41(1): 161-166. DOI:10.14128/j.cnki.al.20214101.161 |
| [5] |
苟晔鹏, 刘星, 郭甲崇, 等. 基于小波分析的脉冲激光回波信号分离方法[J]. 激光与红外, 2022, 52(1): 136-144. GOU Yepeng, LIU Xing, GUO Jiachong, et al. Pulse laser echo signal separation method based on wavelet analysis[J]. Laser & Infrared, 2022, 52(1): 136-144. DOI:10.3969/j.issn.1001-5078.2022.01.022 |
 2023, Vol. 45
2023, Vol. 45
