0 引　言

船舶作为海事管理中监管对象，每天会有海量船舶图像存入海事管理数据库里。为了满足用户检索需求，研究船舶图像检索算法可提高用户检索船舶图像效率^[1-3]。潘丽丽等^[4]研究三元组网络图像检索算法，在提取船舶图像特征后，利用三元组网络，对船舶图像实施分类，实现船舶图像的检索。但该方法的特征提取过程比较复杂，实时性较差。马绍覃等^[5]研究PCA的哈希图像检索算法，该算法包括投影和量化步骤，利用主成分分析去除船舶原始图像特征冗余信息，通过哈希编码完成船舶图像的检索。但该算法在编码时计算量较大，导致检索时间长。

针对以上方法在船舶图像检索中存在的局限性，研究集成局部和全局特征的船舶图像检索算法。

局部特征有利于图像中某一个区域的识别，全局特征能够有效展示图像信息。因此集成局部和全局特征，全面表征船舶图像，可提高船舶图像检索能力。

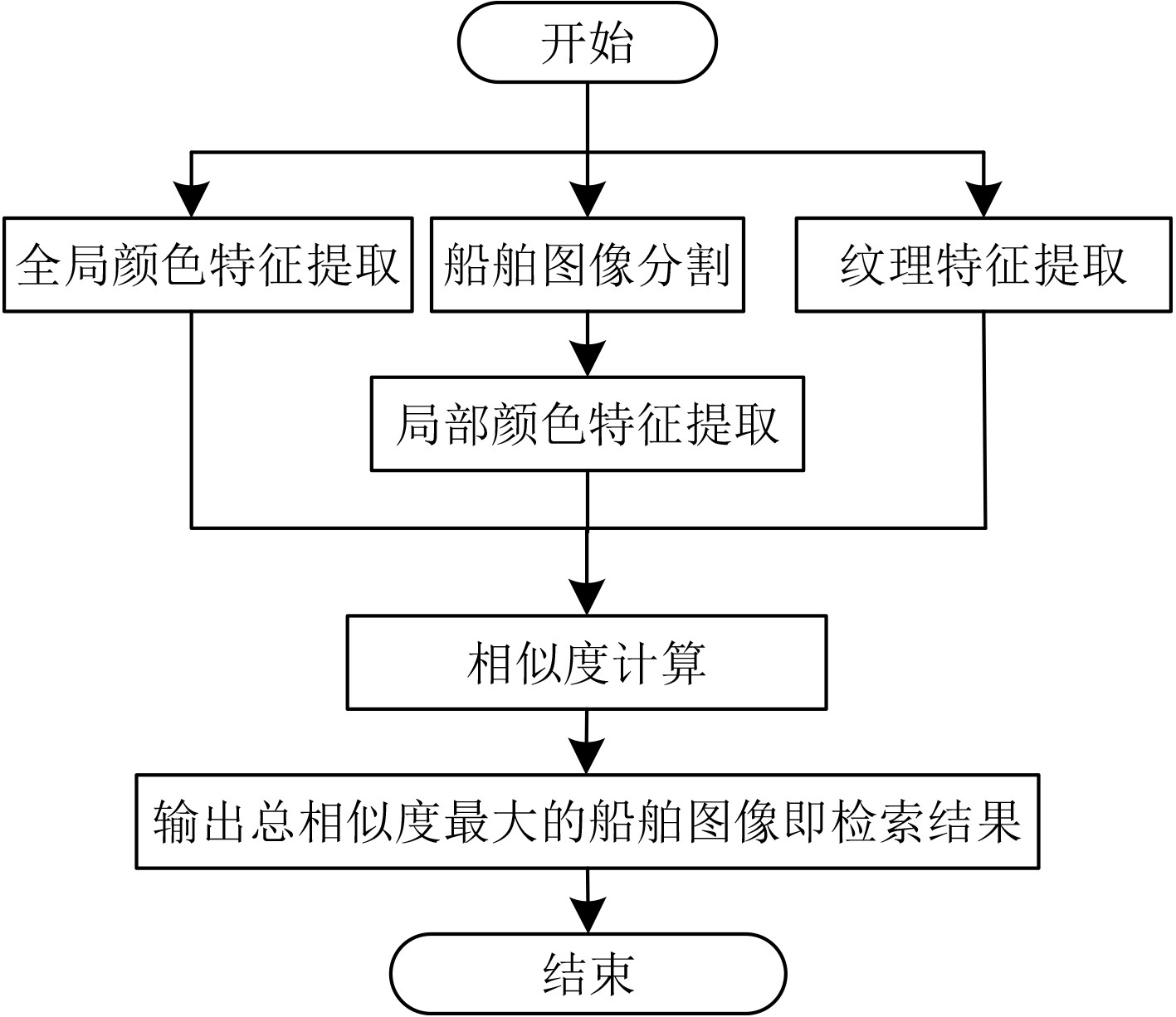
1 船舶图像检索算法

为了提高用户检索所需船舶图像效率，研究集成局部和全局特征的船舶图像检索算法，该算法流程如图1所示。由图1可知，船舶图像检索算法流程为：通过颜色矩方法提取船舶图像全局颜色特征；基于块截断量化编码理念，采用模糊C－均值聚类算法对船舶图像实施分割预处理，并构建分割处理后船舶图像的二值位图，表征船舶图像局部颜色特征；通过小波变换提取船舶图像纹理特征；依据3项特征求解待检索船舶图像与数据库中船舶图像的特征相似度，选取总相似度最大船舶图像作为从船舶图像数据库的检索输出结果，该结果为用户检索所需船舶图像。

1.1 船舶图像全局颜色特征提取

集成局部和全局特征的过程：在对船舶图像实施分割处理后，分别提取图像的局部和全局特征后并融合，求解用户搜索的船舶图像和船舶图像数据库的相似度，选取相似度最大船舶图像作为搜索结果。因船舶图像颜色特征在低阶矩中比较多，因此通过颜色矩方法(一阶矩、二阶矩)提取船舶图像全局颜色特征，用1个矢量表示船舶图像的每1个像素，该矢量公式如下：

$ {Q_i} = {\left( {{R_i}^{}{G_i}^{}{B_i}} \right)^{\rm{T}}}，1 \leqslant i \leqslant H。$

(1)

其中：R_i、G_i、B_i为船舶图像内第 $ i $ 个像素红、绿、蓝颜色分量值；Q_i为船舶图像内第 $ i $ 个像素颜色值； $ H $ 为船舶图像总像素。

一阶矩表达式为：

$ \chi = \left( {1/H} \right)\sum\limits_i^H {{Q_i}}, $

(2)

二阶矩表达式为：

$ \delta = {\left\{ {\left[ {1/\left( {H - 1} \right)} \right]{{\sum\limits_{i = 1}^H {\left( {{Q_i} - \chi } \right)} }^2}} \right\}^{0.5}}, $

(3)

红、绿、蓝颜色分量一阶矩表达式如下：

$ \chi = {\left( {\chi {R^{}}\chi {G^{}}\chi {B^{}}} \right)^{\rm{T}}}, $

(4)

红、绿、蓝颜色分量二阶矩表达式如下：

$ \delta = {\left( {\delta {R^{}}\delta {G^{}}\delta {B^{}}} \right)^{\rm{T}}}, $

(5)

一阶矩表示船舶图像索引图，二阶矩阵表示船舶图像边缘信息，2个矩阵可提取船舶图像全局颜色特征。

1.2 船舶图像局部颜色特征提取

基于块截断量化编码技术的船舶图像局部颜色特征提取流程为：将图像分为多个图像子块，求解各图像子块的方差、均值后，构建二值位图，表示图像局部颜色特征。依据块截断量化编码理论，提取图像局部颜色特征，采用模糊C－均值聚类算法对图像实施分割预处理，将图像分为4×4子块， $ {F_\alpha } = \left( {{q_1},{q_2},{q_3} \cdots {q_l}} \right) $ 表示第 $ \alpha $ 个图像子块，其中 $ 1 \leqslant x \leqslant z $ ，图像总子块数量用 $ z $ 描述，船舶图像子块总像素数量用 $ l $ 描述。图像子块一阶矩阵计算公式为：

$ {\chi _{{B_x}}} = \left( {1/l} \right)\sum\limits_{j = 1}^z {{Q_j}}，$

(6)

其中，第 $ j $ 个图像子块用Q_j描述。

红、绿、蓝颜色分量一阶矩表达式如下：

$ \chi = \left( {\chi {R_{{F_x}}}^{}\chi {G_{{F_x}}}^{}\chi {B_{{F_x}}}^{}} \right)。$

(7)

对比全局船舶图像均值和船舶图像子块均值确定二位值图特征，当船舶图像子块均值小于全局船舶图像均值时，该船舶图像颜色分量为0。

1.3 船舶图像纹理特征提取

对于船舶二维图像，小波变换是通过对某个函数ε(x₁,x₂)实施平移、缩减后生成以函数族 $ {\varepsilon _{a,{b_1},{b_2}}} \left( {{x_1},{x_2}} \right) $ 为基底的船舶图像，分解船舶图像(x₁,x₂)，得出船舶图像在函数族的系数。小波变换计算公式为：

$ \begin{split} W{T_f}\left( {a,{b_1},{b_2}} \right) = &\left( {1/a} \right)\iint {\left( {{x_1},{x_2}} \right)}\times \\ &\varepsilon \left[ {\left( {{x_1} - {b_1}} \right)/a,\left( {{x_2} - {b_2}} \right)/a,} \right]{\rm{d}}{x_1}{\rm{d}}{x_2}, \end{split} $

(8)

船舶图像函数族为：

$ {\varepsilon _{a,{b_1},{b_2}}}\left( {{x_1},{x_2}} \right) = \left( {1/a} \right)\varepsilon \left[ {\left( {{x_1} - {b_1}} \right)/a,\left( {{x_2} - {b_2}} \right)/a,} \right]。$

(9)

其中：b₁，b₂为平移因子； $ a $ 为缩放因子。

采用二维离散小波变换提取船舶图像纹理特征，为船舶图像检索提供数据支持。在保留船舶图像纹理小波分解频域后，通过调整小波系数抑制船舶图像非纹理特征。船舶图像纹理特征提取流程为：

1) 设图像纹理集中在5层和6层，需重构船舶图像5层和6层的高频分量，求出3组系数[U_n, V_n, D_n]，第 $ n $ 层的水平系数用U_n描述，垂直系数用V_n描述，对角线系数用D_n描述。

2)计算各分量的标准差 $ {S_{{U_n}}} $ ， $ {S_{{V_n}}} $ ， $ {S_{{D_n}}} $ ，表示图像不同方向纹理特征。

3)归一化处理。第 $ n $ 层总差异性M_n表达式为：

$ {M_n} = {S_{{U_n}}} + {S_{Vn}} + {S_{{D_n}}}\mathop {}\nolimits^{} n = 5,6, $

(10)

图像纹理特征向量求解公式为：

$ {\beta _{no}} = {S_{no}}/{M_n}\mathop {}\nolimits^{} o = U,V,D 。$

(11)

依据式(11)求出船舶图像六维纹理特征向量 $ \left[ {{\beta _{U5}},{\beta _{V5}},{\beta _{D5}},{\beta _{U6}},{\beta _{V6}},{\beta _{D6}}} \right] $ 。

1.4 基于相似度计算的检索结果生成

采用欧式距离与皮尔逊相关系数求解出船舶图像特征相似度，假设用户需要检索船舶图像特征向量为X=(x₁,x₂,···,x_n)，船舶数据集中特征向量为Y=(y₁,y₂,···,y_n)，则欧式距离求解公式为：

$ \theta \left( {X,Y} \right) = \sqrt {\sum\limits_{i = 1}^n {\left[ {\left( {{x_i} - {y_i}} \right)*\left( {{x_i} - {y_i}} \right)} \right]} } ,\mathop {}\nolimits^{} i = 1,2,3, \cdots n ,$

(12)

欧式距离越小，说明待检索图像与图像检索结果相似度越大。

皮尔逊相关系数求解如下：

$ {{V}}\left( {X,Y} \right) = Cov\left( {X,Y} \right)/\sqrt {Var\left[ X \right]*Var\left[ Y \right]}。$

(13)

其中：向量X方差用Var[Y]描述；向量X、Y协方差用Cov(X,Y)；向量Y方差用Var[Y]描述；当V(X,Y)越接近0时，说明待检索图像与图像检索结果相似度越小，反之，当V(X,Y)越接近1时，相似度越大。

归一化处理局部、全局颜色特征和纹理特征后，实施加权，得出船舶图像总相似度，具体公式如下：

$ P = {w_{e1}}{p_{e1}}\left( {{E_{\eta 1}},{E_{k1}}} \right) + {w_{e2}}{p_{e2}}\left( {{E_{\eta 2}},{E_{k2}}} \right) + {w_t}{p_t}\left( {{T_\eta },{T_k}} \right)。$

(14)

其中：w_e1，w_e2为局部、全局颜色相似度权重，p_e1，p_e2为局部、全局颜色相似度；w_t为纹理相似度权重，p_t为纹理相似度；E_η1，E_η2为需要检索船舶图像局部、全局颜色特征，E_k1，E_k2为船舶数据集中局部、全局颜色特征；T_η为需要检索船舶图像纹理特征；T_k为船舶数据集中纹理特征。

在求解用户搜索的船舶图像和船舶图像数据库的总相似度后，选取总相似度最大的船舶图像为用户需要船舶图像检索图像。

2 实验结果分析

为了验证本文船舶图像检索算法的有效性，选取某地区船舶管理部门的船舶图像数据库作为实验对象。船舶图像样本数据库如表1所示。

2.1 船舶图像特征提取测试

船舶图像样本数据库中选取其中一张客运船图像(见图2(a))，采用本文算法对该客运船图像实施特征提取，其中纹理特征提取结果见图2(b)。分析图2可知，本文算法可有效提取客运船图像纹理特征，在保留船的图像纹理小波分解频域后，通过调整小波系数抑制船的图像非纹理特征，为图像检索提供数据支持。

2.2 检索性能测试

为了测试本文算法的检索性能，将匹配率和匹配时间作为检索性能测试指标，分别采用本文算法、三元组网络检索算法和PCA的哈希图像检索算法，对船舶图像进行检索实验，经过50次反复实验，求出3种算法的检索性能的对比结果，如表2所示。

分析表2可知，在船舶图像3种变化(尺度变化、光照变化、旋转)条件下，与三元组网络检索算法PCA的哈希图像检索算法相比，本文算法平均匹配率97.94%，平均匹配时间为11.9 ms，说明本文算法检索性能较好，具有较高的匹配精确度，检索速度快，能够满足用户实时性检索的需要，验证了本文算法的有效性。

2.3 检索效果展示

使用本文算法能够实现船舶图像检索，检索后结果界面见图3。分析图3可知，本文检索算法在船舶图像检索应用时效果较好，操作比较简单，用户将需要检索船舶图像拖拽至检索船舶数据库内，自动检索与待检索船舶相似图像，并生成检索结果，选取相似度为100%的船舶图像检索结果，说明本文算法具有较高的图像检索能力。

3 结　语

本文通过提取局部和全局特征，并计算相似度，选取总相似度最高的船舶图像，实现船舶图像的检索。通过大量试验分析发现，本文算法的检索效果较好，操作便捷，将需要检索船舶图像拖拽至检索数据库内，点击检索键自动检索与待检索船舶相似图像，依据相似度高低选取最高相似度的船舶图像，完成船舶图像的检索。