0 引　言

海上交通快速发展，在进行海上交通管理过程中，为保证航道和港口资源的高效、合理利用和安全运行，避免发生交通事故^[1]，需精准掌握船舶交通流量情况。船舶交通流量指的是海面上或者内河航运内发生连续运动的全部船舶数量^[2]，其包含交通流量、交通流密度、宽度以及速度等。由于船舶类型较多^[3]，大小也存在差异，在海上的航行速度也存在显著区别，外加海上环境较为多变，导致船舶交通流量预测难度较高^[4]，预测结果误差较大。刘敬贤等^[5]针对船舶交通流量预测需求展开相关研究，结合卷积神经网络及长短时记忆网络提出预测方法。但该方法主要用于短时间内的船舶交通流量预测，对于长时间内的预测效果较差。张矢宇等^[6]为实现船舶交通流量预测，提出组合模型预测方法，该方法主要针对航道整治区域内的船舶交通流进行预测，对于海上的船舶交通流预测误差较大。

支持向量机(SVM)是一种通过监督学习实现目标二元分类的一种典型方法，其在多个识别领域中均具有较好的应用效果。因此，本文利用SVM的优势，提出基于SVM的船舶交通流量预测方法。

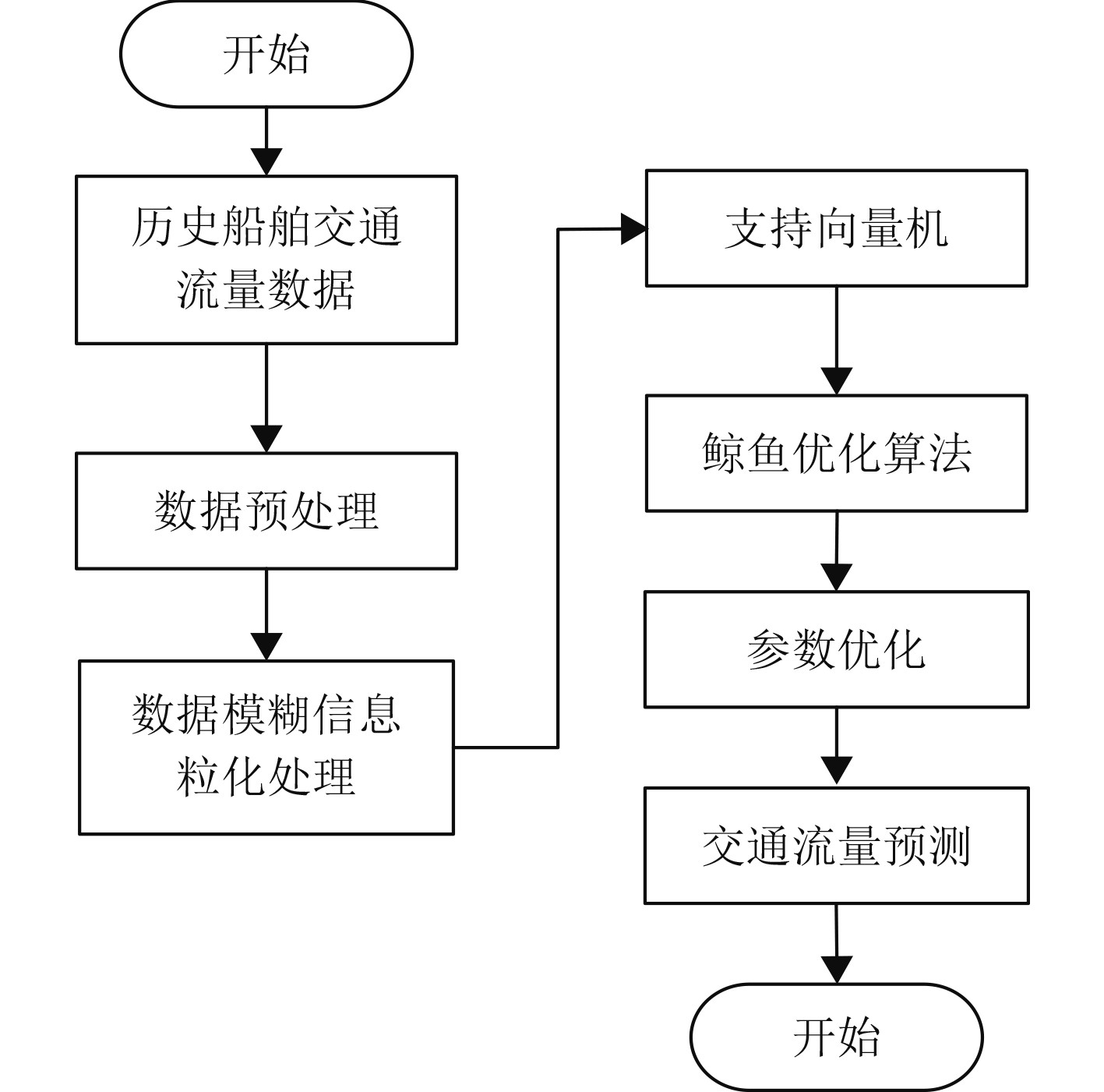
1 船舶交通流量预测 1.1 船舶交通流量预测方法架构

交通流量预测是港口管理的重要部分，其对于海上交通调度和协调控制以及安全管理具有重要意义，因此需可靠完成船舶交通流量预测。本文结合在交通流量预测时存在的不确定因素以及周期性或者区间性等特征，提出SVM的船舶交通流量预测方法，其总体流程用图1描述。

该方法在进行船舶交通流量预测时，以历史船舶交通流量数据为基础，对数据进行预处理，并采用模糊信息粒化对数据进行二次处理，以保证数据的完整性，同时更好地刻画数据的语义，为预测提供可靠的数据依据。将处理后的数据输入SVM模型中，该模型通过输入数据和输出结果之间的映射，完成船舶交通流量预测。为保证预测结果的可靠性，采用鲸鱼算法对SVM参数进行优化，获取最优参数值，减少SVM模型的构建时间，提升交通流量预测的精确度。

1.2 基于SVM的船舶交通流量预测

SVM的本质是一个凸二次规划问题，能够获取高维空间内数据集的最佳拟合结果。本文选择SVM作为船舶交通流量预测方法的基础，将归一化处理后的船舶历史交通流量数据作为样本数据，进行交通流量预测。如果归一化处理后的已知数据样本集合用 $ {\boldsymbol{X}} = \left( {{x_i},{y_i}} \right) $ 表示，其中， $ {x_i} $ 和 $ {y_i} $ 分别为输入值和输出值，均为第 $ i $ 个，则SVM的学习即为 $ {x_i} $ 和 $ {y_i} $ 之间的映射关系，用f()表示。该映射能够保证任意的 $ {\boldsymbol{X}} $ 均具有f()=y_i关系，通常情况下f()的计算公式为：

$ f\left( . \right) = w\phi \left( x \right) + b 。$

(1)

式中： $ w $ 为权重； $ b $ 为阈值； $ \phi \left( x \right) $ 为映射关系，其可将输入量映射至高维特征空间内。

在进行船舶交通流量预测时，为保证预测精度，需保证参数的合理性，确保结构的风险最小，因此引入经验风险函数，其计算公式为：

$ {\psi _{emp}} = \frac{1}{m}\sum\limits_{i = 1}^m L 。$

(2)

式中： $ m $ 为样本数据数量； $ L $ 为损失函数，计算公式为：

$ L\left( . \right) = \left\{ \begin{aligned} & {0,}&{{\rm{if}}\left| {{y_i} - f\left( {{x_i}} \right)} \right| < \varepsilon ,} \\ & {\left| {{y_i} - f\left( {{x_i}} \right)} \right| - \varepsilon ,}&{{\rm{else}}} 。\end{aligned} \right. $

(3)

式中， $ \varepsilon $ 为小数，且大于0。

在预测时如果数据样本数量较少，则结合SRM准则进行回归函数的选择，其公式为：

$ f\left( x \right) = {{\rm{sgn}}} \left[ {\sum\limits_{i = 1}^m {{w_i}\phi \left( x \right) + b} } \right]。$

(4)

依据SVM的最大间隔概念对船舶交通流量预测的非线性回归问题进行转换，形成函数规划问题，其表达式为：

$ \min \left[ {\frac{1}{2}{{\left\| w \right\|}^2} + C\sum\limits_{i = 1}^m {\left( {{\xi _i} + \xi _i^ * } \right)} } \right] 。$

(5)

在实际应用过程中，将上述公式转换成对偶形式进行求解，其公式为：

$ f\left( x \right) = \sum {\left( {\alpha _i^ * - {\alpha _i}} \right)K\left( {{x_i},x} \right)} + b 。$

(6)

式中： $ {\alpha _i} $ 为拉格朗日乘子； $ K\left( {{x_i},x} \right) $ 为核函数。选择径向基函数作为核函数，是考虑船舶交通流量预测问题具有非线性特点。保证预测可靠的预测效果，同时确保数据存在不可分情况时，也可完成数据映射，实现预测。

在进行船舶交通流量预测时，输入SVM中的输入量包含对船舶交通流量存在影响的因素，输出的结果为预测得出的交通流量结果。通过上述确定的核函数和SVM的其他相关参数，进行输入量和输出量之间的映射，获取船舶交通流量预测结果。

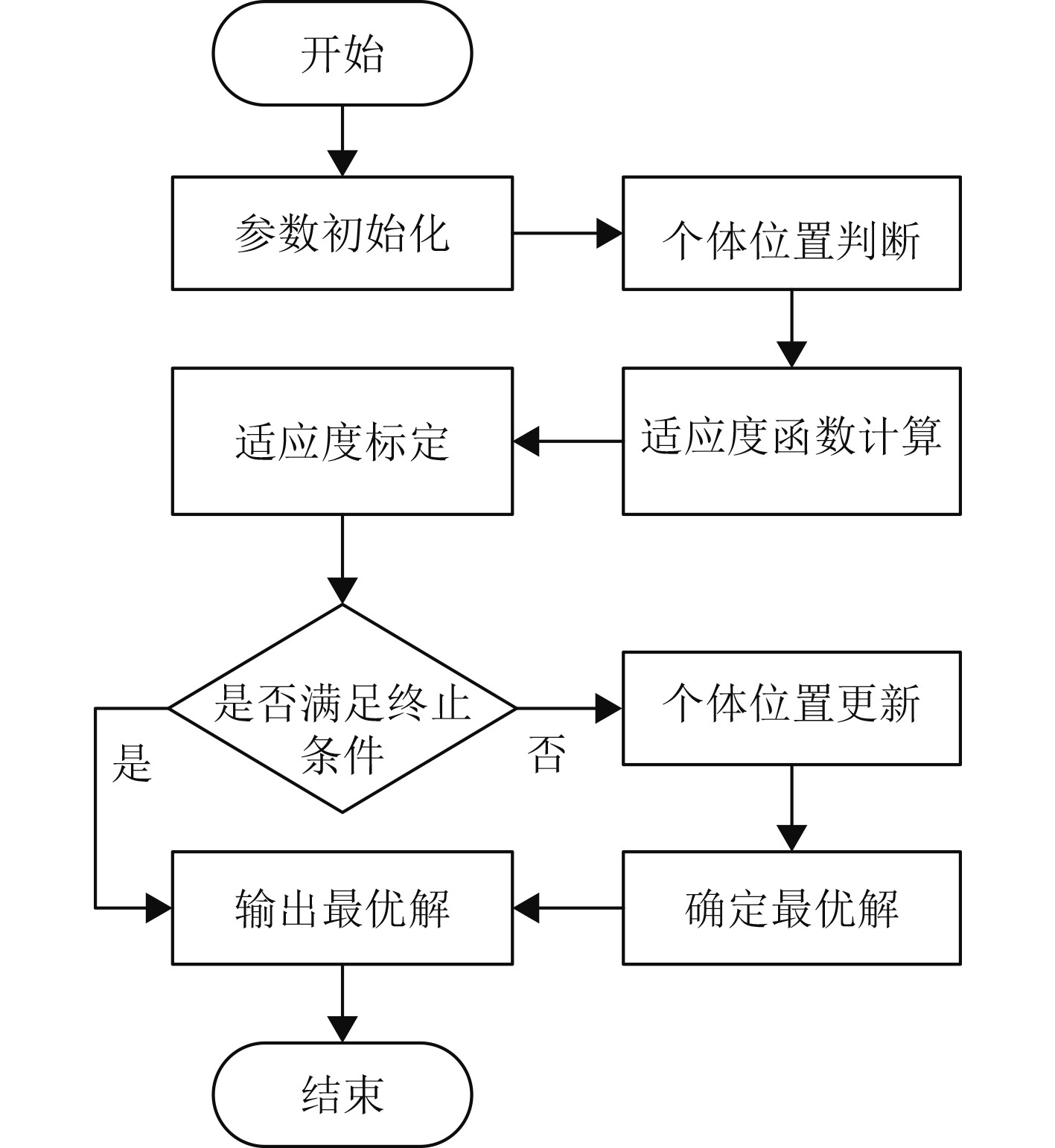
1.3 SVM参数优化

SVM对船舶交通流量预测过程中，K(x_i,x)的参数 $ g $ 和 $ C $ 的取值对于SVM的预测效果存在直接影响，因此，为保证船舶交通流量预测精度，对上述2个参数进行寻优，选择鲸鱼优化算法(WOA)完成。在优化时，为保证最佳参数的获取，先利用网格搜索法对 $ g $ 和 $ C $ 两个参数进行大范围寻优，获取初始的寻优结果；再将该结果输入至WOA算法中，进行精确寻优，获取全局最优解，其寻优流程用图2描述。

参数优化详细步骤如下：

步骤1　对WOA相关参数初始化处理，包含搜索代理X^*(t)的维数、最大迭代次数、搜索范围的上限和下限等。

步骤2　判断寻优搜索时个体位置是否位于搜索范围内，如果越限后则对其进行调整。

步骤3　计算适应度函数，X^*(t)当前位置定义为 $ g $ 和 $ C $ 参数，以此获取当前的SVM预测模型，获取该模型的预测精准度，并将其作为WOA的适应度函数。

步骤4　当前最优解更新，通过WOA算法对X^*(t)当前位置进行更新，以此获取全局最佳适应度函数，并完成当前X^*(t)的更新。其更新公式为：

$ X\left( {t + 1} \right) = X_{rand}^ * - A.D 。$

(9)

式中： $ X_{rand}^ * $ 为群体中的某个个体位置； $ A $ 为系数向量； $ D $ 为距离，对应鲸鱼当前位置和当前最优个体之间。

步骤5　判断计算结果是否满足终止条件，如果预测结果精度是当前适应度函数和全局适应度函数的差值，即满足终止条件，则将SVM预测模型进行更新，使其为最佳模型。

步骤6　输出 $ {X^ * } = \left\{ {best\mathop {}\nolimits^{} c,best\mathop {}\nolimits^{} g} \right\} $ 结果，该结果即为SVM预测模型的最优参数。

2 实验结果分析

为验证本文方法对于船舶交通流量的预测效果，获取某港口管理中心通过海上船舶自动识别系统获取的2021年连续3个月的海上交通流量数据作为测试数据。该港口为中型港口，作为重要的海运枢纽，承载近邻多个城市的海运中转。该港口相关海域和航道在3个月内实际共经过83522艘船舶，包含货船、客船以及巡查船舶。

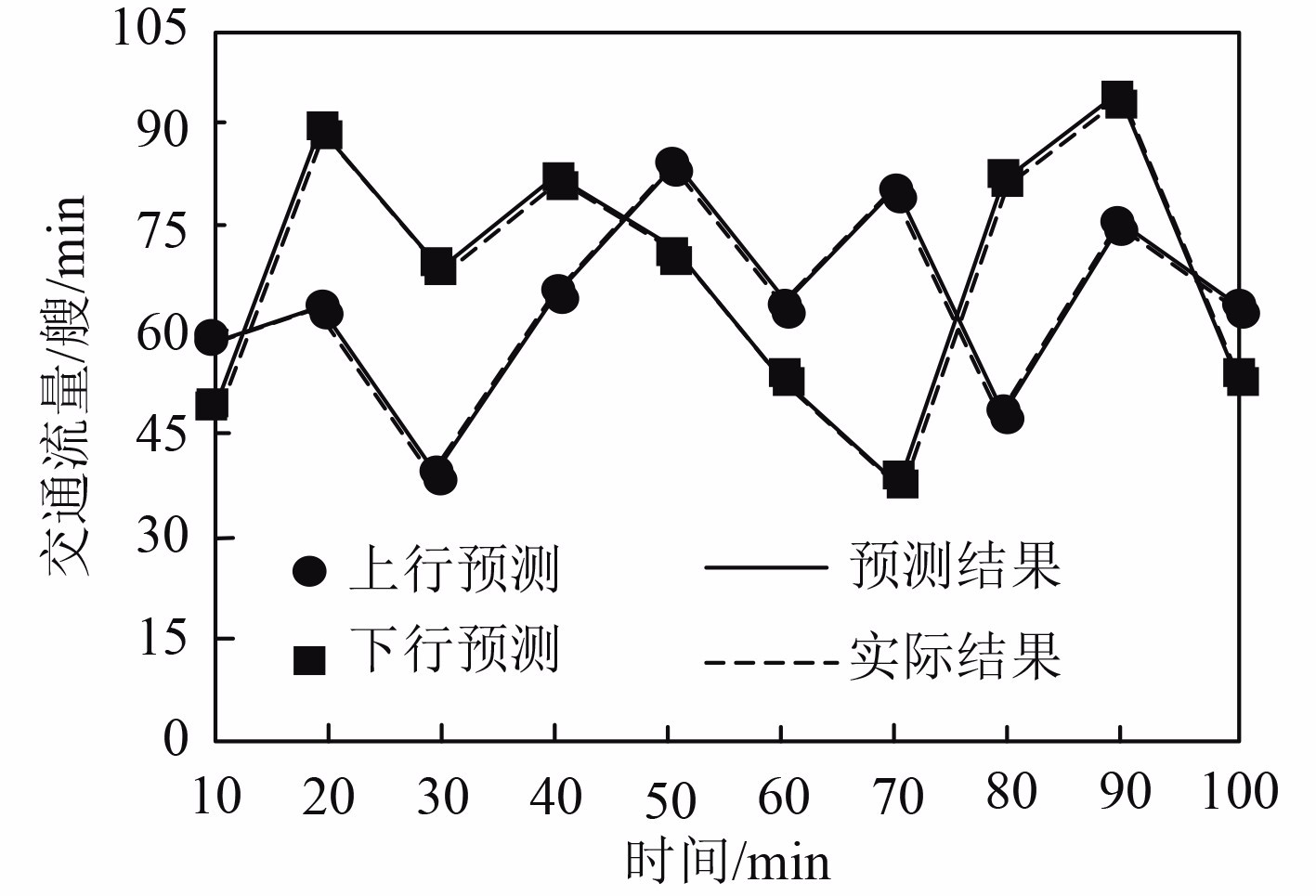
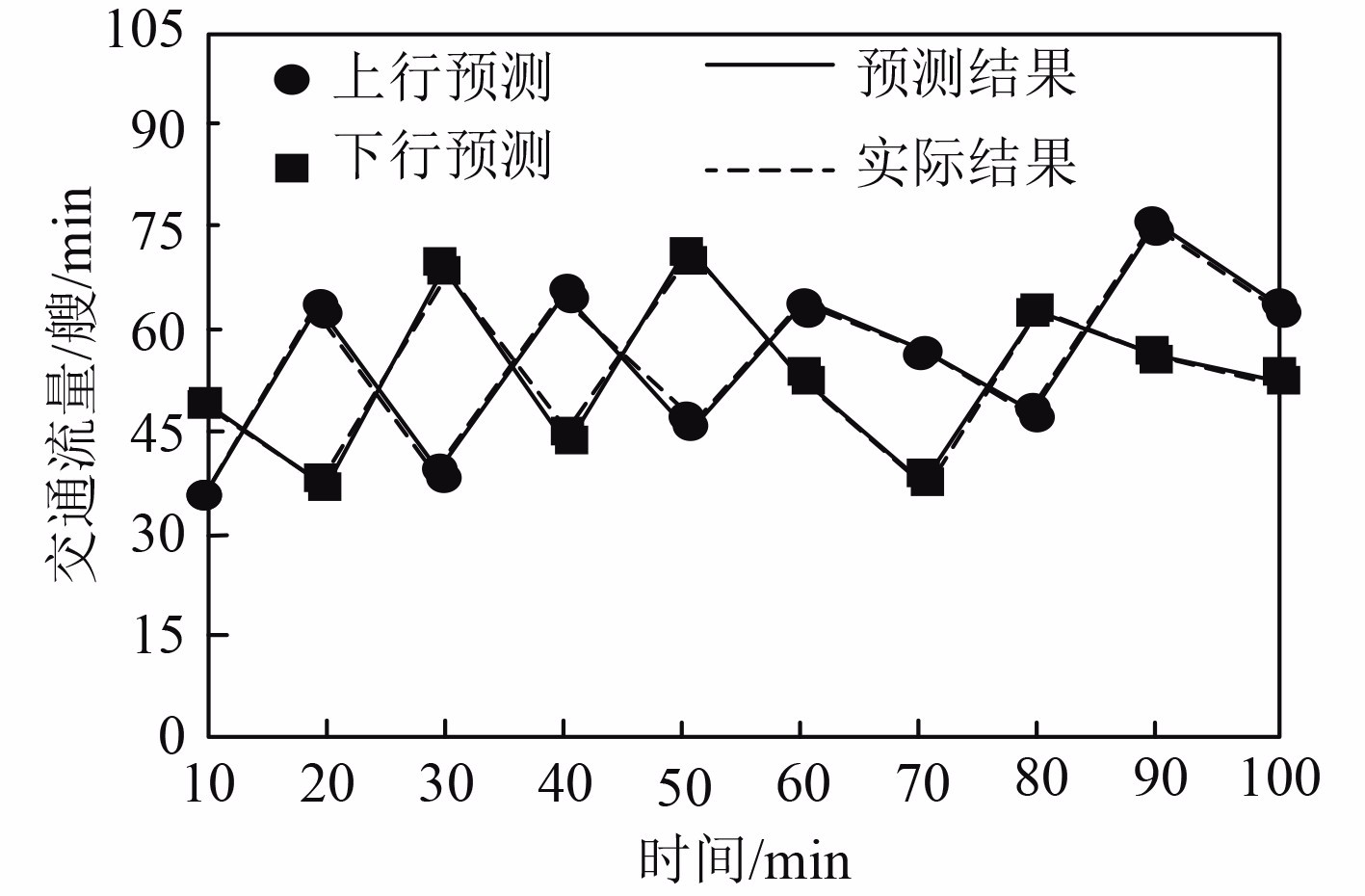
为验证本文方法对于船舶交通流量的预测效果，获取本文方法在海面和航道2种航行环境下，对于船舶交通流量的预测结果，如图3和图4所示。由图3和图4可知，本文方法应用后，能够精准预测不同时间段内，海上和航道内的船舶流量结果，预测结果和实际结果的吻合程度依较高。因此，本文方法具有较好的船舶交通流量预测能力，可靠完成船舶交通流量预测，为港口的船舶管理和调度提供可靠依据。

为进一步验证本文方法对于船舶交通流量的预测效果，采用均等系数 $ \eta $ 作为评价指标，测试本文方法在进行不同数量船舶交通流量预测时的预测效果。该指标取值在0～1之间，其值越大表示预测结果的误差越大。计算在不同数量船舶下，本文方法的预测结果，用表1描述。由表1可知，在雾天和雨天2种天气下，随着海上船舶数量的逐渐增加，本文方法均可精准完成船舶交通流量预测， $ \eta $ 结果均在0.019以下，极大程度接近0。存在的少许误差对于船舶的管理影响极小，可忽略不计。

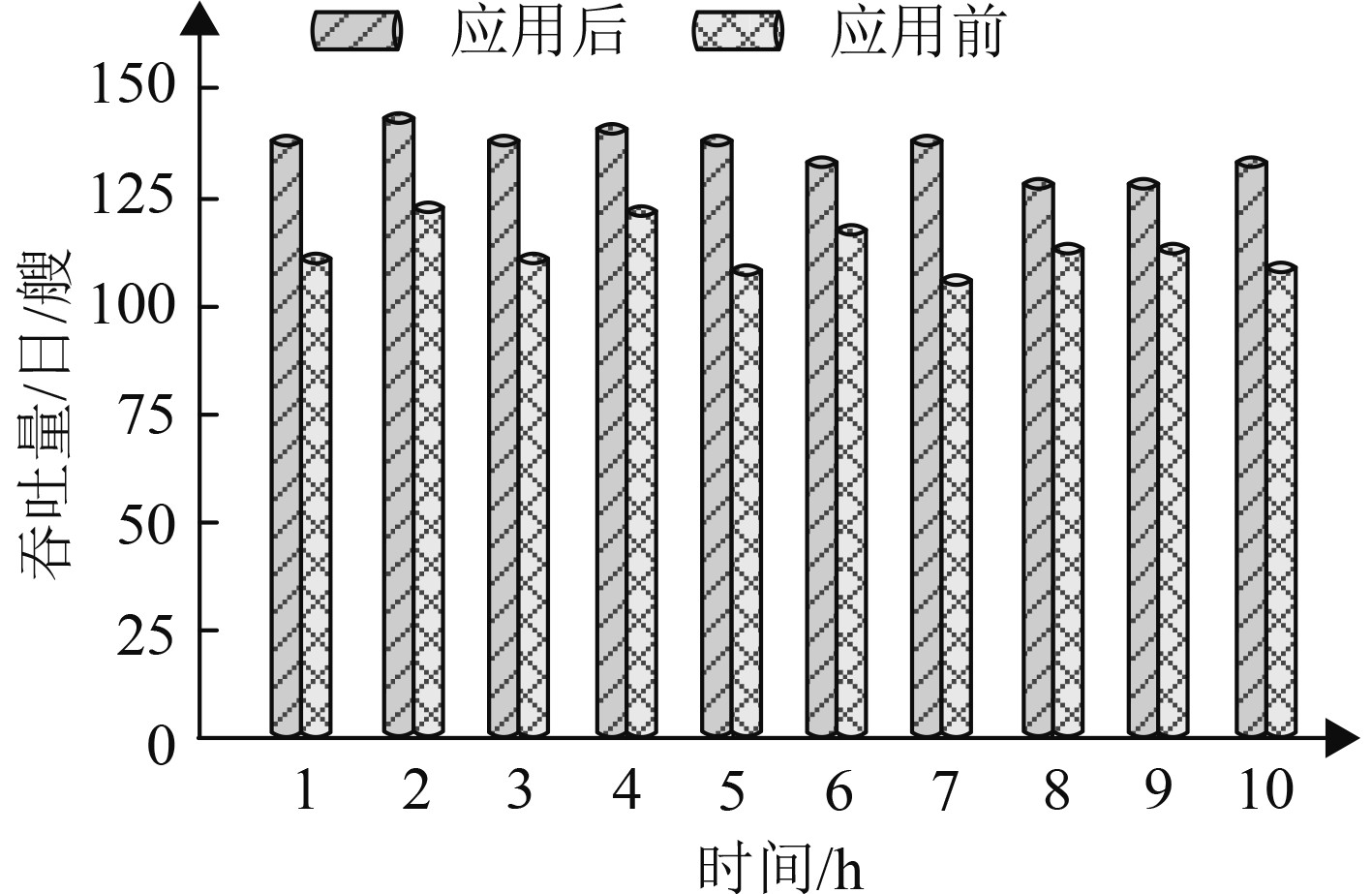
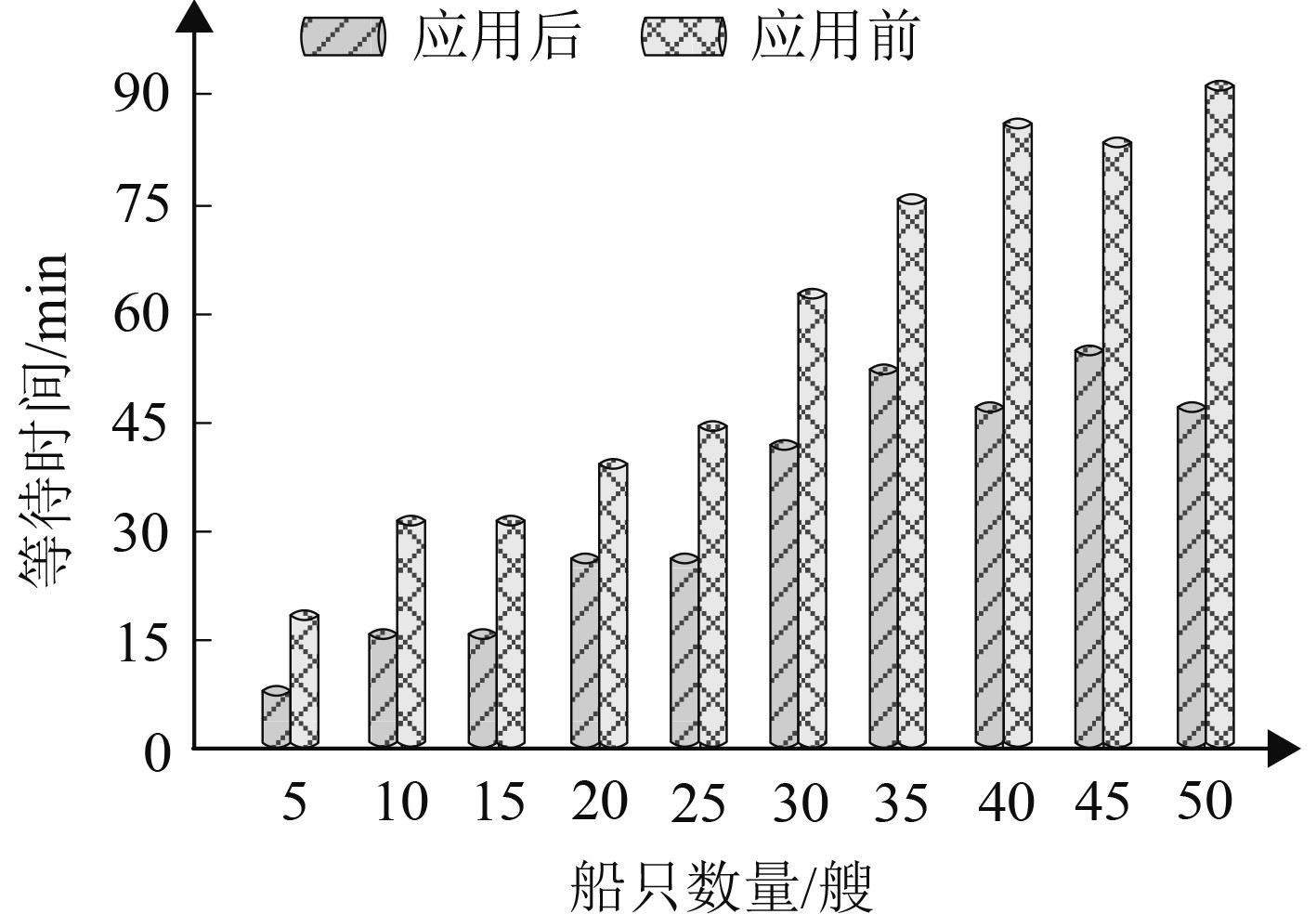
为直观验证本文方法的应用性，获取本文方法应用前后，港口管理部门依据交通流量预测结果对港口资源进行调度，获取调度后船舶吞吐量变化情况和航道内船舶等待进港的等候时间变化情况，结果用图5和图6描述。由图5和图6可知，本文方法应用后，能够可靠获取船舶流量情况，港口调度中心可依据预测结果对船舶进行调度，高效、合理实现港口资源利用，减少船舶等待进港时间，提升船舶吞吐量。因此，本文方法具有良好的应用性，对于港口的船舶管理具有重要作用。

3 结　语

船舶交通流量会受到多种因素的影响，产生一定变化，对于港口的管理和资源的合理化应用造成一定影响。因此，港口管理部门需可靠掌握船舶交通流量情况，为港口管理提供数据依据。基于此，本文提出基于支持向量机的船舶交通流量预测方法，预测船舶交通流量情况。对该方法进行相关测试后可知：本文方法具有较好的应用效果，能够完成船舶交通流量预测，掌握船舶流量情况，为港口调度提供可靠依据。