0 引　言

近年来国际贸易交流愈加频繁，大宗货物流通均通过海上运输方式实现，海上运输方式是远距离货物运输最主要方式^[1-2]，具备较高的能源效率。但船舶在航行过程中，会遭遇特殊天气状况、洋流以及冰山等障碍物，导致航行轨迹发生偏移，对航行轨迹进行异常检测是船舶航行安全保障之一，因此船舶航迹异常检测在航海领域意义重大。郁舒昊等^[3]提出船舶轨迹聚类方法，该方法通过采集船舶航向、航速、坐标等数据，提取该数据特征后，使用聚类方法得到船舶航行轨迹异常检测。但该方法在应用时，其聚类方法容易陷入极值情况，导致其输出结果不够准确。魏辉等^[4]提出船舶调用轨迹异常检测方法，该方法以物联网为基础，建立轨迹异常检测框架，通过该框架输出船舶轨迹异常检测结果。但该方法对框架运行环境要求较高，因此应用范围较为狭窄。大数据驱动是通过采集海量大数据，通过聚类、统计等数据运算方法，从海量大数据内提取到有用信息的过程或方法。大数据驱动可实现目标的检测、诊断、预测等目的，在各个领域应用较为广泛^[5]。本文以大数据驱动技术为基础，研究船舶航行轨迹异常检测，为保障船舶安全航行提供技术支持。

1 船舶航行轨迹异常检测研究 1.1 船舶观测大数据相似度方程构建

利用角度传感器、速度传感器、方位传感器采集船舶在海上航行时的角度、速度和坐标等大数据，为保障该大数据来自于同一目标区域，构建传感器相似度方程，利用该方程得到某一艘船舶的航行大数据。船舶传感器观测方程表达式如下：

$ E(t) = Y(t)X(t) + W(t)。$

(1)

式中： $ t $ 为时刻； $ E(t) $ 为传感器在时刻为 $ t $ 时的观测向量； $ W(t) $ 为船舶航行大数据内存在的干扰噪声； $ Y(t) $ 为船舶航行状态转移矩阵； $ X(t) $ 为船舶航行状态观测矩阵。

当时刻为 $ t $ 时，获取到 $ N $ 个传感器观测大数据，其由下式表示：

$ \left\{ \begin{gathered} {T_l} = \left\{ {{Z_i}(t),i = 1,2, \cdots ,N} \right\}, \\ {E_i}(t) = \left\{ {{E_{i1}}(t),{E_{i2}}(t), \cdots ,{E_{im}}(t),m = 1,2, \cdots ,N} \right\} , \\ {E_{ij}}(t) = \left\{ {{E_{ij1}}(t),{E_{ij2}}(t), \cdots ,{E_{ijk}}(t),j = 1,2, \cdots ,m} \right\}。\\ \end{gathered} \right. $

(2)

式中： $ N $ 为传感器总数； $ {m_i} $ 为第 $ i $ 个传感器采集到的船舶航行大数据数量； $ k $ 为大数据属性数量； $ {E_{ijk}}(t) $ 为第 $ i $ 个传感器采集第 $ j $ 个船舶航行大数据第 $ k $ 个属性值。

为便于计算，对式(2)进行简化处理，其变更如下：

$ \left\{ \begin{gathered} {E_{ij}}(t) = {B_l}(t) , \\ l = (i - 1) \times M + j 。\\ \end{gathered} \right. $

(3)

式中： $ {B_l}(t) $ 为在第 $ l $ 个时刻，若干个传感器采集到的船舶航行大数据集合； $ M $ 为传感器观测最大目标数量。

依据式(3)则传感器观测船舶航行大数据相似度方程如下：

$ {\rm{dist}}({B_i}(t),{B_j}(t)) = {\omega _k} \cdot \sqrt {\sum\limits_{k = 1}^N {\Delta {{({B_i}(t),{B_j}(t))}^2}} } 。$

(4)

式中： $ {B_i}(t) $ ， $ {B_j}(t) $ 为第 $ i $ 和 $ j $ 个船舶航行大数据； $ {\rm{dist}}( \cdot ) $ 为相似度函数； $ {\omega _k} $ 为调节参数； $ \Delta $ 为变量符号。

设置传感器观测船舶航行大数据相似度阈值 $ \varepsilon $ ，当 $ {\rm{dist}}({B_i}(t),{B_j}(t)) $ > $ \varepsilon $ 时，则输出船舶航行大数据，该大数据来自于同一个目标船舶。

1.2 基于大数据驱动技术的船舶正常轨迹模型构建

以同一个目标船舶航行大数据为基础，建立其正常轨迹模型。使用大数据驱动技术中的多特征大数据聚类方法建立船舶正常轨迹模型，利用该模型获得船舶航行正常轨迹，其详细过程如下：

步骤1　将同一目标船舶航行大数据采样点看做船舶轨迹类簇，在每个类簇内，航迹点航向为其平均值，将航向看做类簇向^[6-7]，每一个航迹类簇均具备独立的类簇向，则航向表达式如下：

$ {U_w} = \frac{{{U_1}}}{n} + \frac{{{U_2}}}{n} + \cdots \frac{{{U_n}}}{n}。$

(5)

式中： $ {U_w} $ 为航迹类簇的总航向； $ {U_n} $ 为第 $ n $ 个船舶轨迹点航向； $ n $ 为航迹点数量。

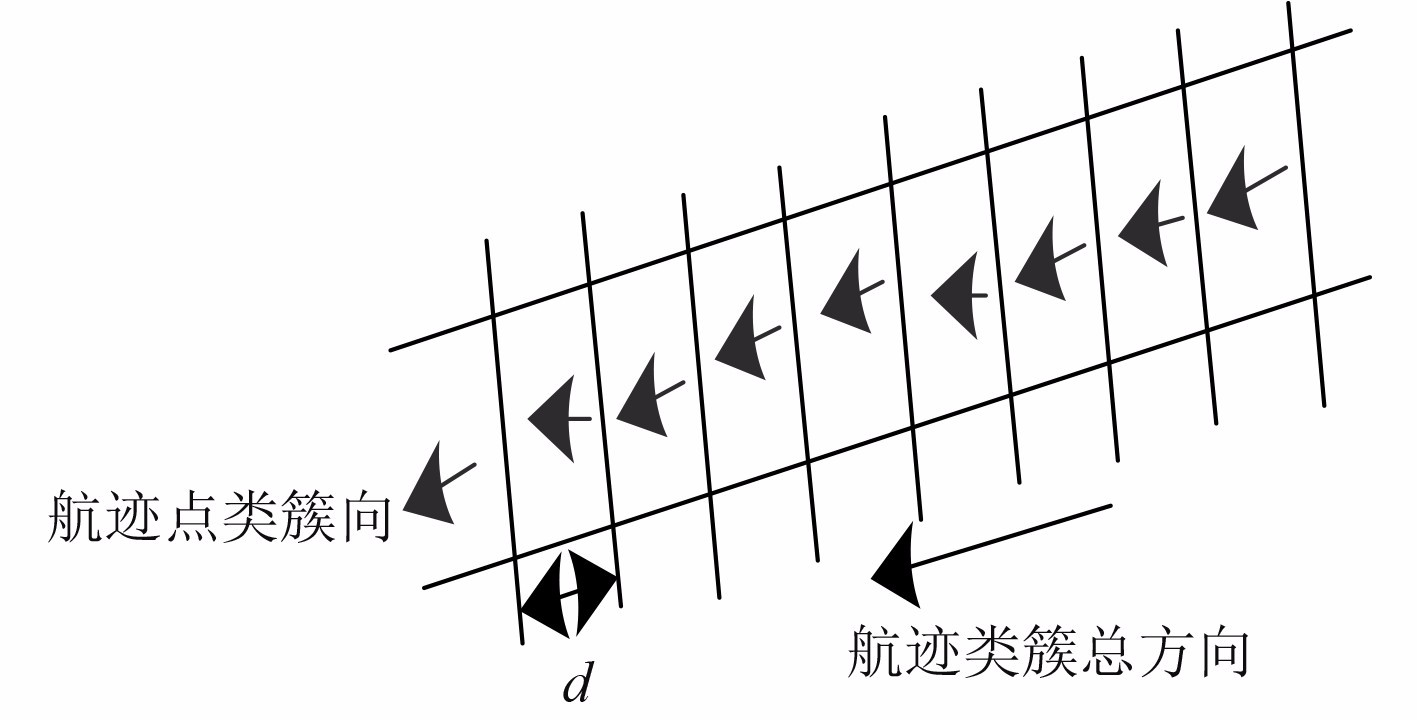
步骤2　按照航迹类簇向，划分轨迹点网格。航迹类簇网格划分示意图如图1所示，其网格宽度阈值为 $ d $ 。

步骤3　建立船舶航行轨迹采样点。在图1内，每个网格均为一个船舶航迹采样点，该采样点与船舶航行轨迹点不同，每个采样点均具备平均航速、平均航向、平均经纬度和中位数距离等特征属性。船舶航行轨迹采样点表达式如下：

$ S{G_i} = \left\{ {CO{U_{avg}},SG{E_{avg}},LO{N_{avg}},LA{T_{avg}},{D_{median}}} \right\}。$

(6)

式中： $ S{G_i} $ 为第 $ i $ 个船舶航行轨迹采样点； $ CO{U_{avg}} $ ， $ SG{E_{avg}} $ ， $ LO{N_{avg}} $ ， $ LA{T_{avg}} $ 分别为船舶航行平均航向、平均航速、平均经度、平均纬度； $ {D_{median}} $ 为中位数距离。

经过上述步骤，利用式(6)即可得到船舶航行正常轨迹。

1.3 基于大数据驱动技术的船舶轨迹异常检测算法

依据得到的船舶航行正常轨迹，使用大数据驱动技术内的Spark Streaming数据实时计算框架，实现船舶航行轨迹异常检测。船舶航迹位置异常检测是以实时接收到的船舶航迹点位置展开测定的，令 $ {G_i} $ 为待检测的船舶航行轨迹点， $ S{G_j} $ 为船舶实际采样轨迹点，通过计算 $ {G_i} $ 和 $ S{G_j} $ 之间的距离 $ \sigma $ ，并将与位置距离阈值进行比较，即可实现船舶航行异常轨迹检测。 $ {G_i} $ 和 $ S{G_j} $ 之间的距离 $ \sigma $ 计算公式如下：

$ \sigma = \sqrt {{{({G_{i \cdot lon}} - S{G_{j \cdot lon}})}^2}} + \sqrt {{{({G_{i \cdot lat}} - S{G_{j \cdot lat}})}^2}}。$

(7)

式中： $ {G_{i \cdot lon}} $ ， $ S{G_{j \cdot lon}} $ 为待检测轨迹点的经度和纬度； $ {G_{i \cdot lat}} $ ， $ S{G_{j \cdot lat}} $ 为船舶实际轨迹采样点经度和纬度。

令 $ \tilde \sigma $ 表示航迹点位置距离阈值，当式(7)结果高于该阈值时，则判断当前船舶航迹异常。

由于船舶航线较长，为降低轨迹异常检测难度，需将其航线划分为若干个航迹段。设置航迹段长度为 $ len $ ，航迹段起点和终点之间的间隔时间为 $ \Delta t $ ，依据长度 $ len $ 划分船舶航迹段，判断其航迹点起点和终点时间间隔是否在航行规定时间内，若是则选定该航迹段，反之则缩小航迹段选取长度。经过上述步骤，得到船舶航行时若干个航迹段。

$ T $ 和 $ SubT $ 分别表示待检测航迹段和船舶实时航迹段，该2个航迹段之间的夹角为 $ H $ ，其计算公式如下：

$ H = \arccos \left(\frac{{{Q_1} \cdot {Q_2}}}{{\left| {{Q_1}} \right|\left| {{Q_2}} \right|}}\right) \times \frac{{180}}{{\text{π}} } 。$

(8)

式中： $ {S_1} $ ， $ {S_2} $ 分别为待检测轨迹段向量和船舶航行实际轨迹段向量。 $ \tilde H $ 为船舶航迹段夹角阈值，当式(8)结果高于 $ \tilde H $ 时，则表示当前船舶航迹异常。

经过上述步骤，实现船舶航行轨迹异常检测。

2 性能分析

以某长距离海运船作为实验对象，该船航程较长，且航行海域暗礁、洋流错综复杂，为保障该船航行安全，使用本文方法对异常航迹展开检测，同时验证本文方法实际应用效果。

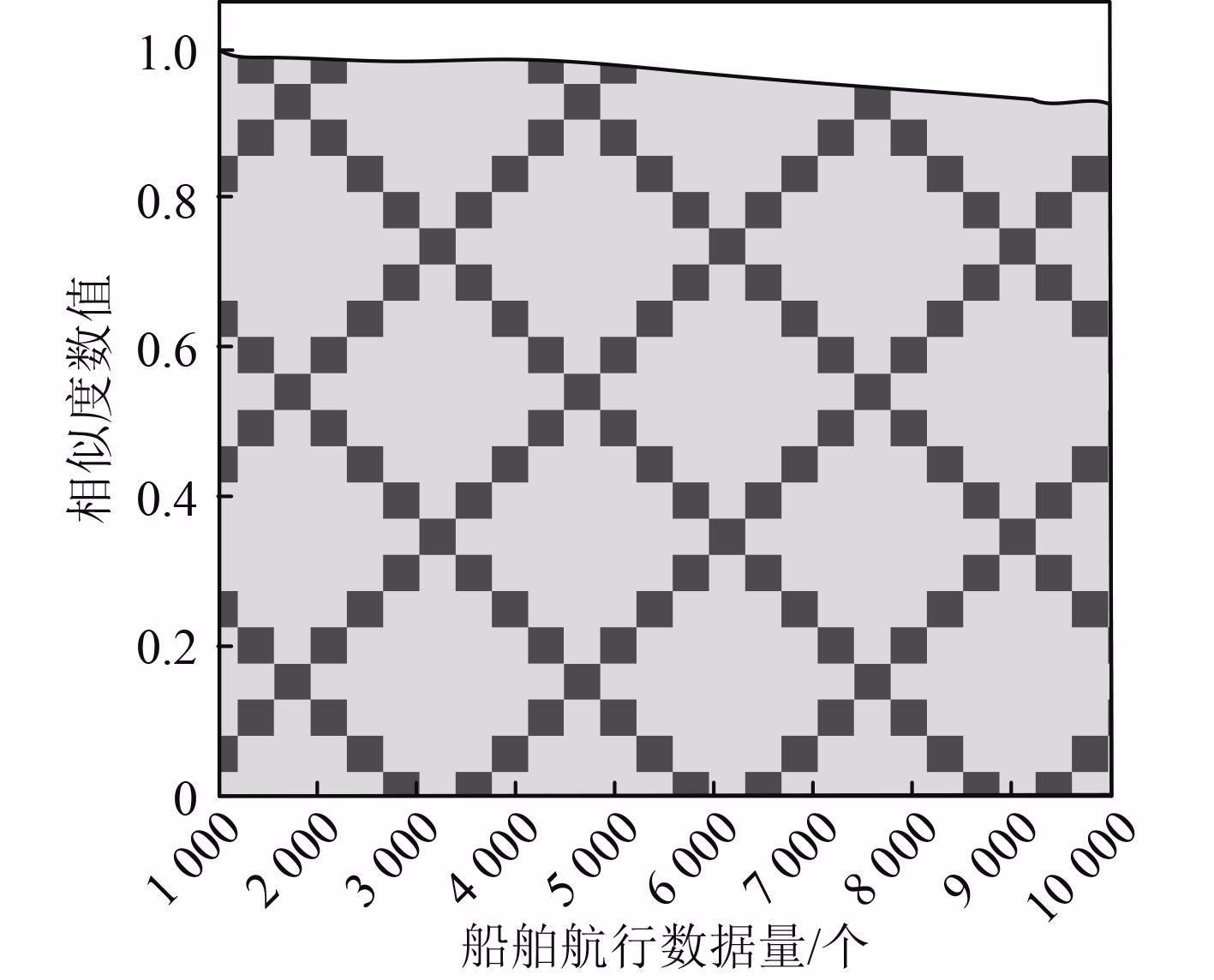
本文方法利用船舶大数据相似度方程获得实时航行数据，测试其在获得航行实时数据量不同情况下，数据相似度变化情况，结果如图2所示。分析可知，本文方法计算船舶航行数据相似度数值随着航行数据量的增加而降低。在航行数据量为6000个左右之前时，本文方法计算航行数据相似度数值接近1.0，当船舶航行数据量超过6000个之后，航行数据相似度数值呈现小幅度下降趋势。在航行数据量为10000个时，船舶航行数据相似度数值为0.95左右。该结果说明：本文方法可有效从海量船舶航行数据中获得同一船舶航行数据，从侧面说明其获得实际航迹和异常航迹检测能力较好。

验证本文方法获得船舶航行正常航迹能力。选择该船在海上航行某时间段，使用本文方法获取该时间段船舶航迹，结果如表1所示。分析可知，应用本文方法获取该船在该时间段内航迹时，航迹点经度和纬度数值与其实际数值吻合度极高，仅在08:30和16:30时，获得船舶经度与其实际数值存在偏差，在12:30船舶纬度与其实际数值存在偏差，但偏差区间仅为0.001°～0.002°之间，偏差数值较小。综上可知，本文方法可有效获得船舶实际航行轨迹，且获取结果精度较高。

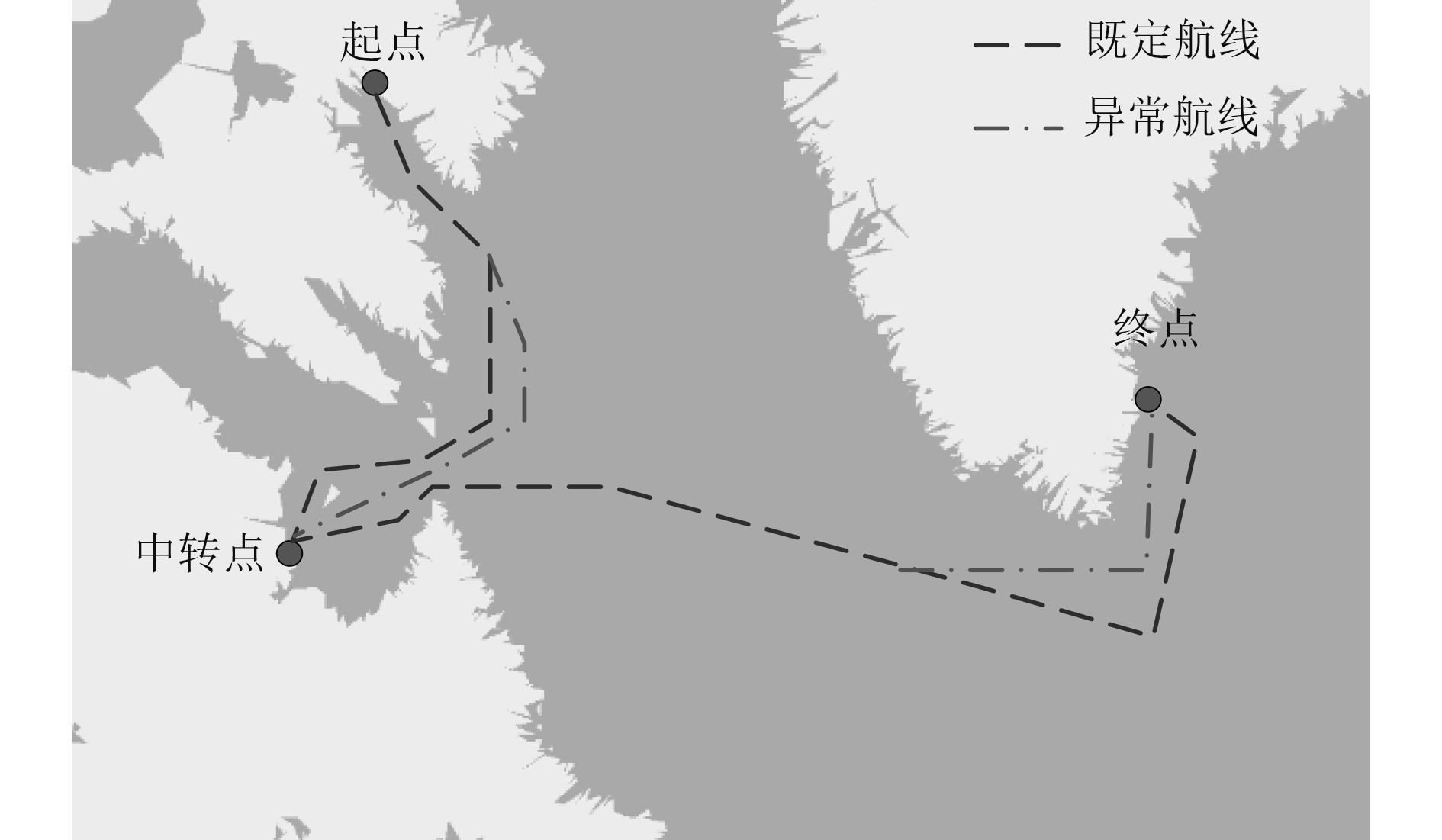
验证本文方法检测异常航迹能力。选择该船舶完整航线，检测其在既定航线航行过程中航迹异常情况，结果如图3所示。由图3可知，该船在航行过程中，存在2段航迹异常情况。该结果说明，本文方法可有效检测船舶航行异常航迹，具备较为显著的应用效果。

3 结　语

本文研究基于大数据驱动的船舶航行轨迹异常检测方法。该方法应用大数据驱动技术，从海量的船舶航行数据内获取其航向偏差、航迹点偏差等数据，依此实现船舶航行轨迹异常检测。对本文方法展开实际验证，从验证结果得知，本文方法可有效检测船舶航行异常航迹，为船舶安全航行提供数据支持。