2. 江苏海洋大学 理学院,江苏 连云港 222005
2. Jiangsu Ocean University, Lianyungang 222005, China
舰船受地磁作用影响后会形成一定的磁化现象[1],由此造成磁信号异常,影响舰船磁引信炮弹等所依赖的目标信息源[2]。而舰船在实际航行过程中受外界环境因素影响将导致舰船姿态产生变化,而舰船的姿态变化也将对舰船的磁异常信号分布产生影响[3]。因此研究姿态与舰船感应磁性间关系,对于保障舰船行驶安全,提升舰船炮弹发射的准确性具有重要意义。
郭成豹等[4]在研究舰船感应磁性问题中,主要针对斜航向进行分析,根据不同航向上的测量数据确定横向与纵向磁场特性。该方法研究过程中仅考虑了舰船航向问题,没有考虑舰船姿态。王锴松等[5]采用仿真平台模拟地磁,获取舰船地磁数据,分析舰船行驶过程中受地磁影响的特征。但该方法主要研究的是舰船感应磁状态,对于姿态的研究并未涉及。针对上述问题,本文提出姿态与舰船感应磁性间关系的建模分析方法,对于认识舰船磁性目标特征提供新的方向。
1 姿态与舰船感应磁性间关系模型构建 1.1 舰船姿态坐标系构建与姿态角定义构建地磁坐标系、舰船坐标系与地理坐标系,分别以
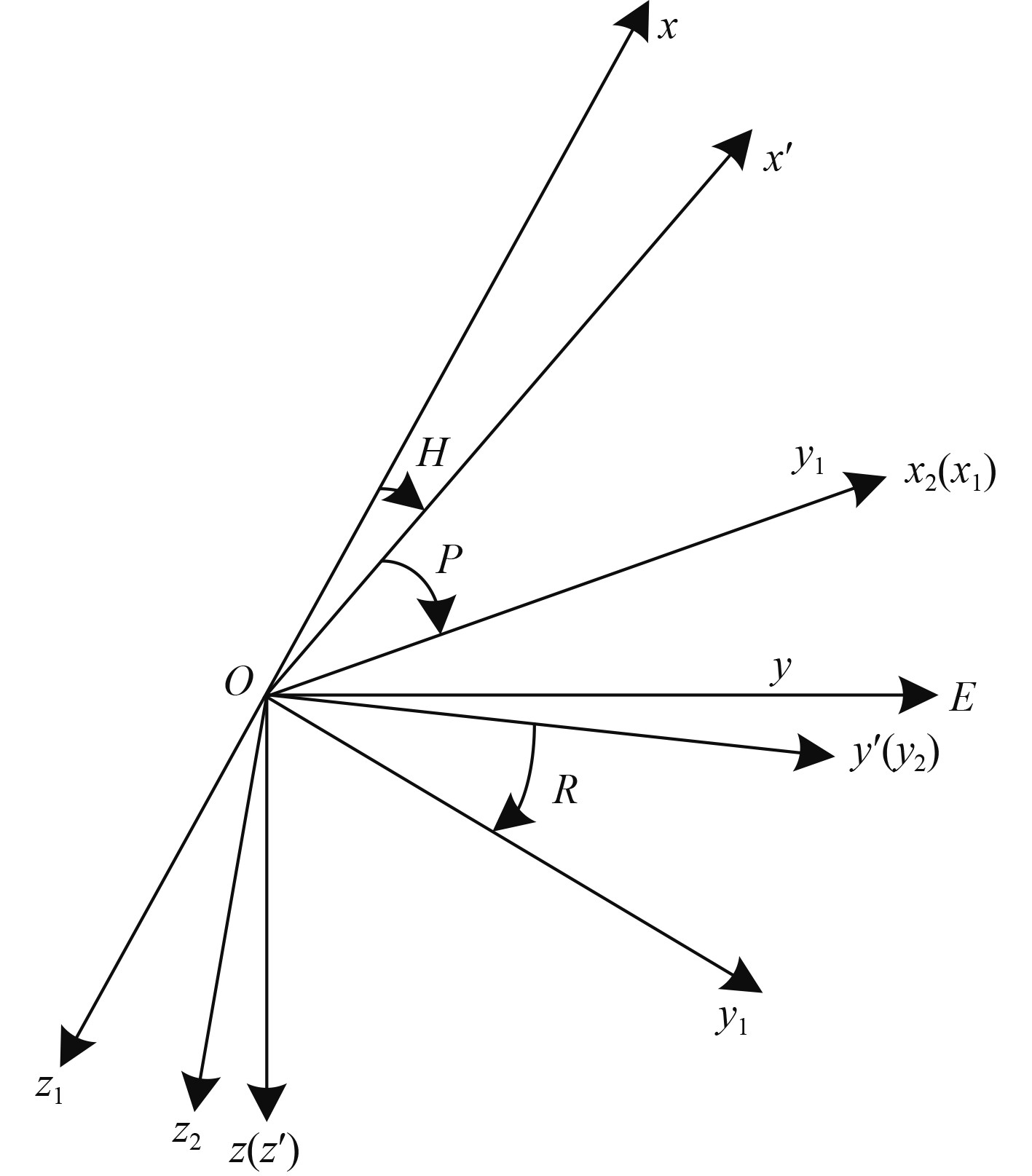
|
图 1 坐标轴转换关系 Fig. 1 Coordinate axis conversion relationship |
在仿真舰船感应磁性过程中,选择单椭球体和磁偶极子阵列混合模型仿真舰船感应磁场,图2为舰船感应磁性模型。
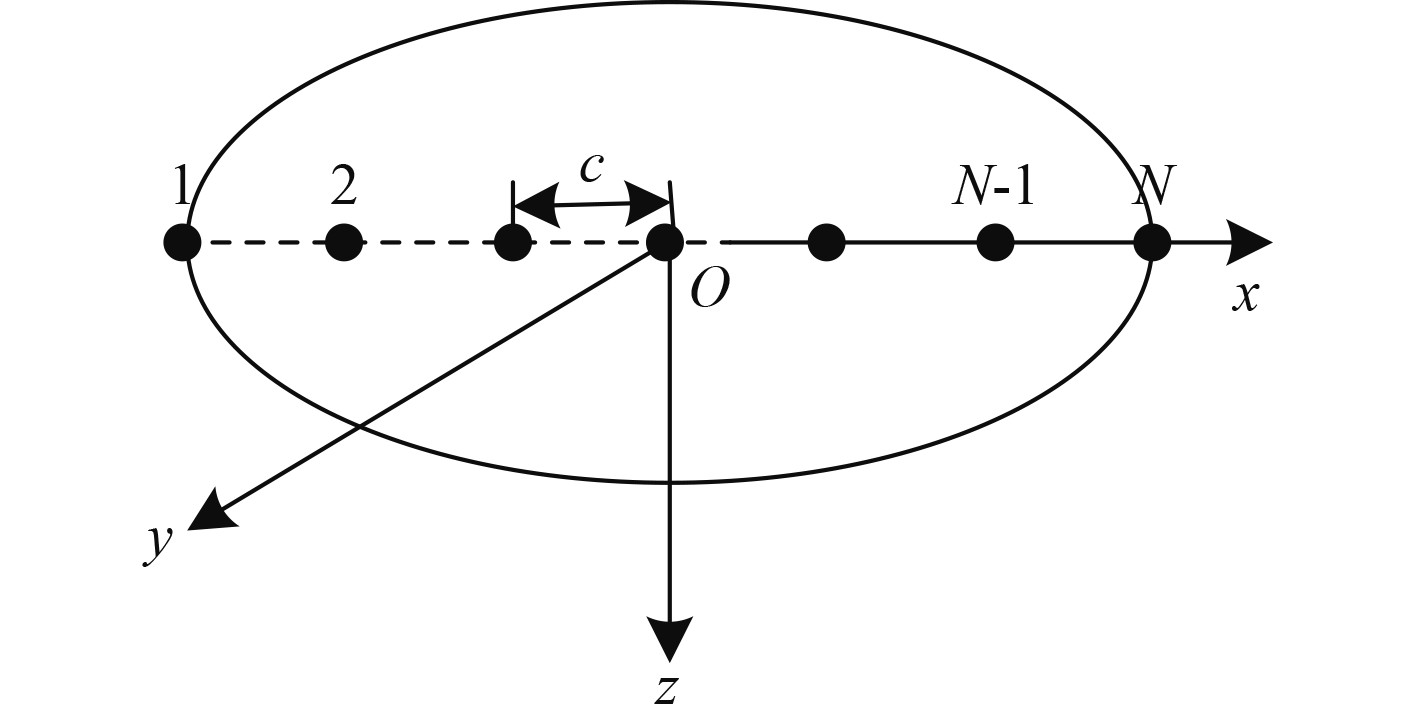
|
图 2 舰船感应磁性模型 Fig. 2 Ship induction magnetic model |
图2中单椭球体用于仿真舰船的主磁场,椭球心同舰船质心重叠,其长半轴
| $ \left\{ \begin{array}{l} \alpha = \dfrac{L}{2},\\ \beta = \dfrac{B}{2}。\end{array} \right. $ | (1) |
式中,
以奇数N和
| $ \varepsilon = \frac{L}{{N - 1}}, $ | (2) |
由此可利用
| $ \left\{ \begin{gathered} {C_{xj}} = \sum\limits_{i = 0}^N {\left( {{\alpha _{xji}}{G_{xi}} + {\alpha _{yji}}{G_{yi}} + {\alpha _{zji}}{G_{zi}}} \right)}, \\ {C_{yj}} = \sum\limits_{i = 0}^N {\left( {{\beta _{xji}}{G_{xi}} + {\beta _{yji}}{G_{yi}} + {\beta _{zji}}{G_{zi}}} \right)}, \\ {C_{zj}} = \sum\limits_{i = 0}^N {\left( {{\varepsilon _{xji}}{G_{xi}} + {\varepsilon _{yji}}{G_{yi}} + {\varepsilon _{zji}}{G_{zi}}} \right)}, \\ \end{gathered} \right. $ | (3) |
对式(3)进行简化处理,可得:
| $ C = FG。$ | (4) |
式中,
基于此利用式(3)能够确定舰船在磁传感器区域的感应磁场值。
1.3 基于感应磁性的舰船姿态计算在分析姿态与舰船感应磁性间关系的过程中,将磁传感器安装在舰船船体上,传感器与舰船坐标系处于平行状态,利用式(5)能够确定地磁场在传感器轴上的投影:
| $ {\vec G_b} = {T_{{E_b}}}{\vec G_E}, $ | (5) |
式中,
以
| $ \frac{{{\rm{d}}\vec V}}{{{\rm{d}}t}} = \frac{{\text{δ} \vec V}}{{\text{δ} t}} + \vec \psi = {\left( {{w_{{x_1}}},{w_{{y_1}}},{w_{{z_1}}}} \right)^{\rm{T}}} \times \vec V, $ | (6) |
式中:
将式(6)与地磁矢量相结合,能够得到:
| $ \frac{{{\rm{d}}{{\vec G}_E}}}{{{\rm{d}}t}} = \frac{{{\rm{d}}{{\vec G}_b}}}{{{\rm{d}}t}} + {\vec w_b} \times {\vec G_b}。$ | (7) |
在以舰船质心代表地理坐标系原点的条件下,式(7)并不会产生变化,
| $ \left\{ \begin{gathered} \frac{{{\rm{d}}{G_x}}}{{{\rm{d}}t}} = - {w_{{y_1}}}{G_{{z_1}}} + {w_{{z_1}}}{G_{{y_1}}}, \\ \frac{{{\rm{d}}{G_y}}}{{{\rm{d}}t}} = {w_{{x_1}}}{G_{{z_1}}} - {w_{{z_1}}}{G_{{x_1}}}, \\ \frac{{{\rm{d}}{G_z}}}{{{\rm{d}}t}} = - {w_{{x_1}}}{G_{{y_1}}} + {w_{{y_1}}}{G_{{x_1}}}。\\ \end{gathered} \right. $ | (8) |
式(8)并不具备线性独立特征,无法直接获取舰船角速率。但针对部分舰船
| $ \left\{ \begin{gathered} {w_{{y_1}}} = \dfrac{{\dfrac{{{\rm{d}}{G_{{z_1}}}}}{{{\rm{d}}t}} + {w_{{x_1}}}{G_{{y_1}}}}}{{{G_{{x_1}}}}}, \\ {w_{{z_1}}} = \dfrac{{ - \dfrac{{{\rm{d}}{G_{{y_1}}}}}{{{\rm{d}}t}} + {w_{{x_1}}}{G_{{z_1}}}}}{{{G_{{x_1}}}}}。\\ \end{gathered} \right. $ | (9) |
为验证本文姿态与舰船感应磁性间关系建模分析方法在分析舰船姿态与感应磁间相关性方面的应用效果,以某小型舰艇为实验对象,采用以高效率、低功耗为主要优势的BM1422AGMV三轴磁传感器采集实验对象感应磁数据,采用本文方法分析实验对象姿态与感应磁间的关系。分析过程中选用船模实验验证方法,图3为实验示意图,实验过程中共设27个采样点。
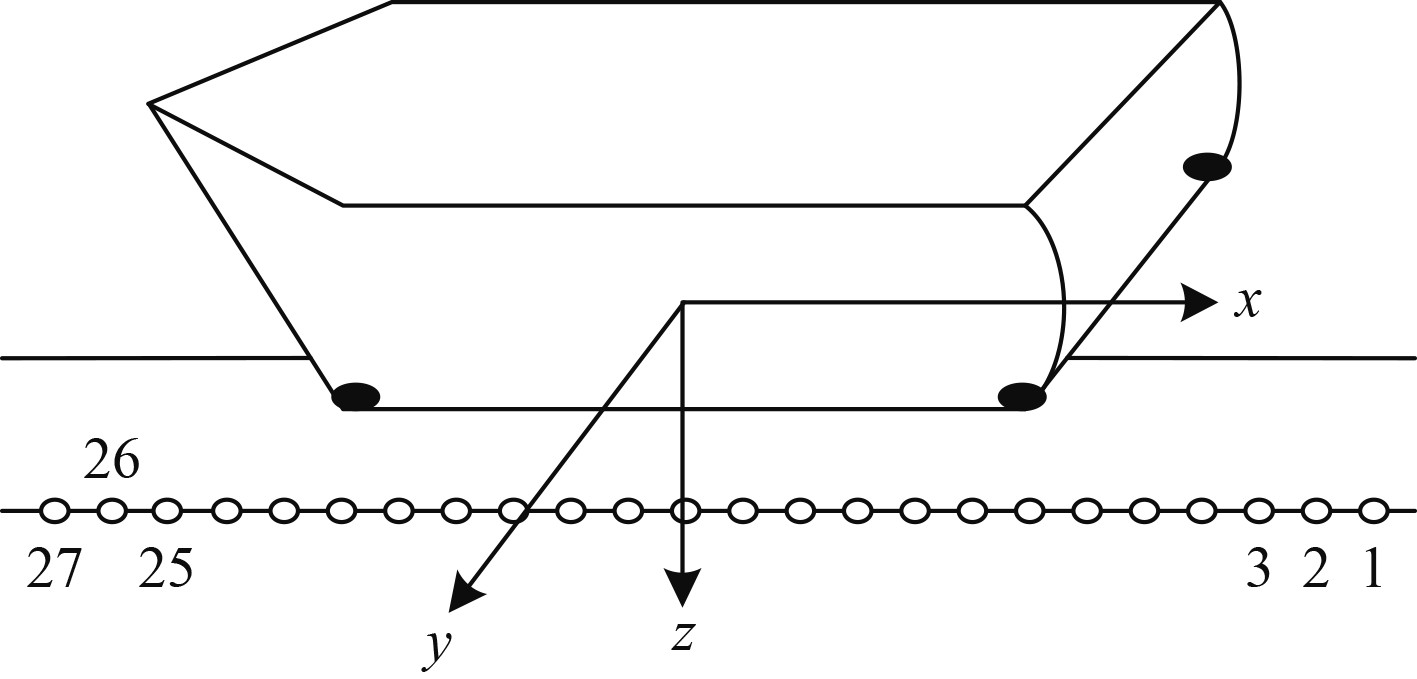
|
图 3 实验示意图 Fig. 3 Schematic diagram of experiment |
分析本文方法所采集的感应磁数据,并与实际感应磁性数据进行对比,由此验证本文方法感应磁性数据分析精度,所得结果如图4所示。分析图4得到,采用本文方法能够准确分析坐标系下不同轴上的感应磁性数据,有利于后续姿态与舰船感应磁性间关系分析准确性的提升。
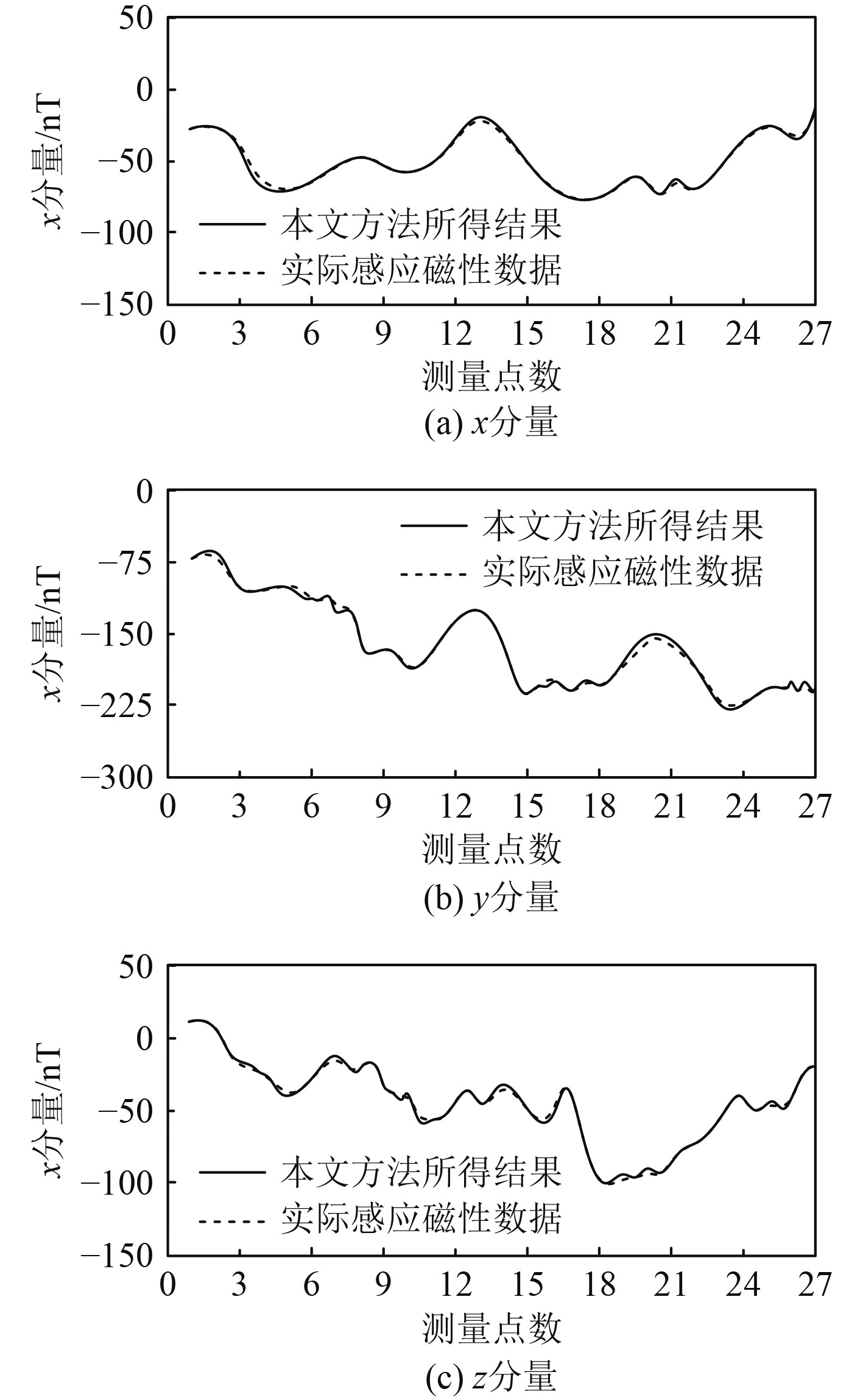
|
图 4 本文方法感应磁性数据采集结果 Fig. 4 Data acquisition results of induction magnetism in this method |
图5~图7为采用本文方法分析所得对应感应磁性下的舰船姿态角误差分析结果。由图5~图7可知,采用本文方法在相应的感应磁性条件下分析研究对象姿态信息,俯仰角误差、磁航向角误差与滚转角误差分别控制在±0.8°,±0.5°和±1.3°范围内。以上数据能够说明采用本文方法能够准确分析姿态与舰船感应磁性间的关系。
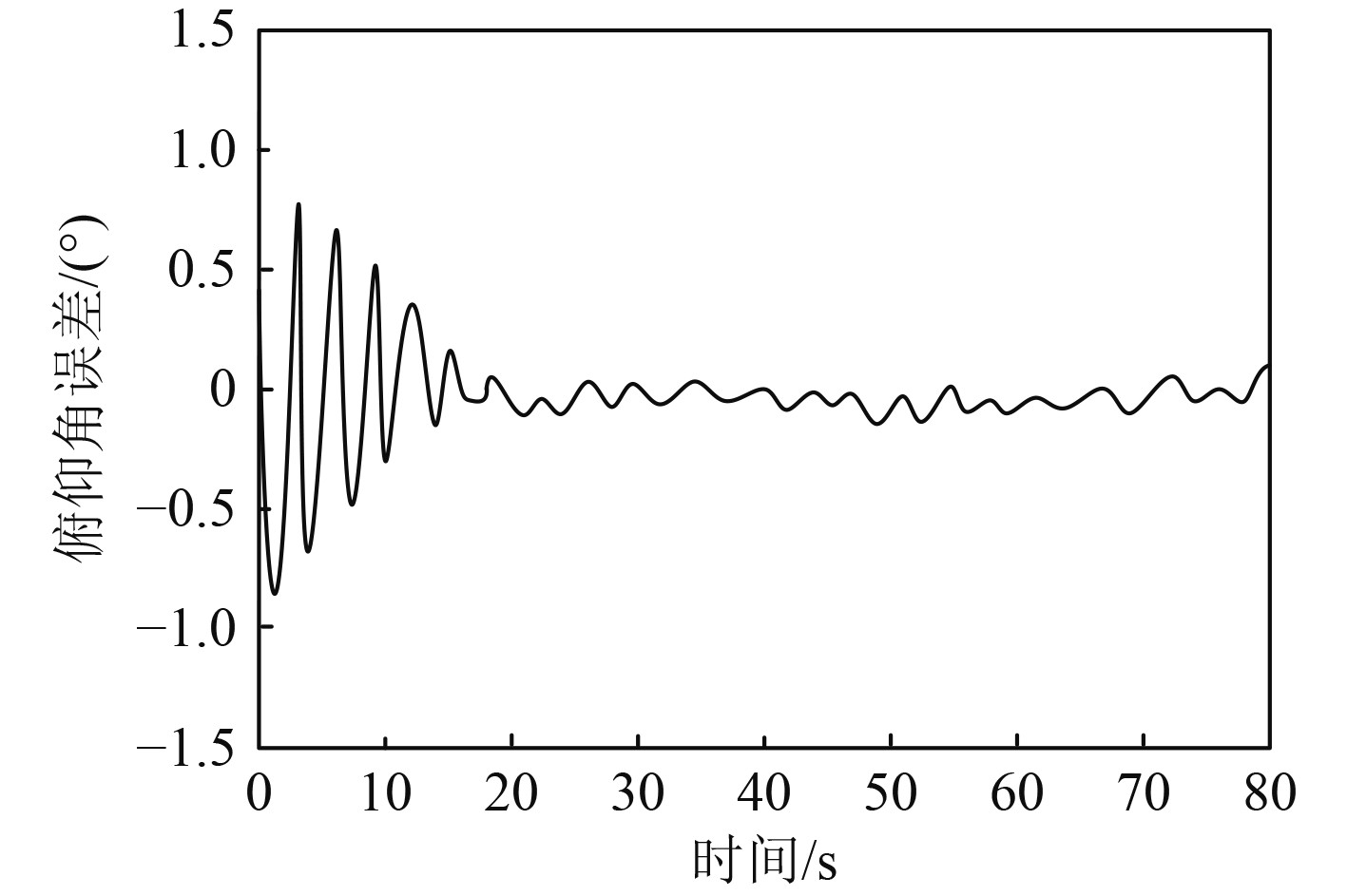
|
图 5 俯仰角误差曲线 Fig. 5 Pitch angle error curve |
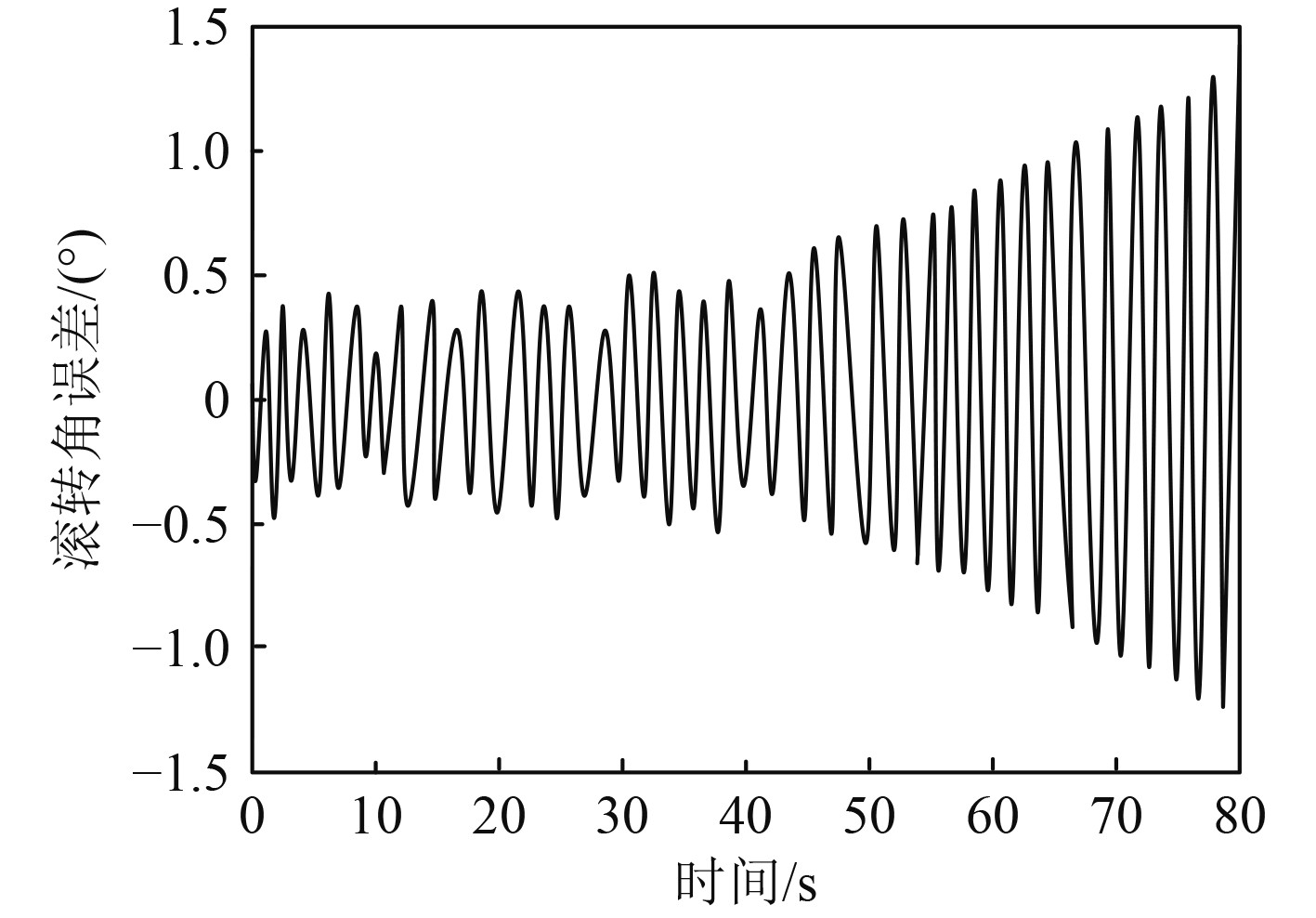
|
图 7 滚转角误差 Fig. 7 Roll angle error |
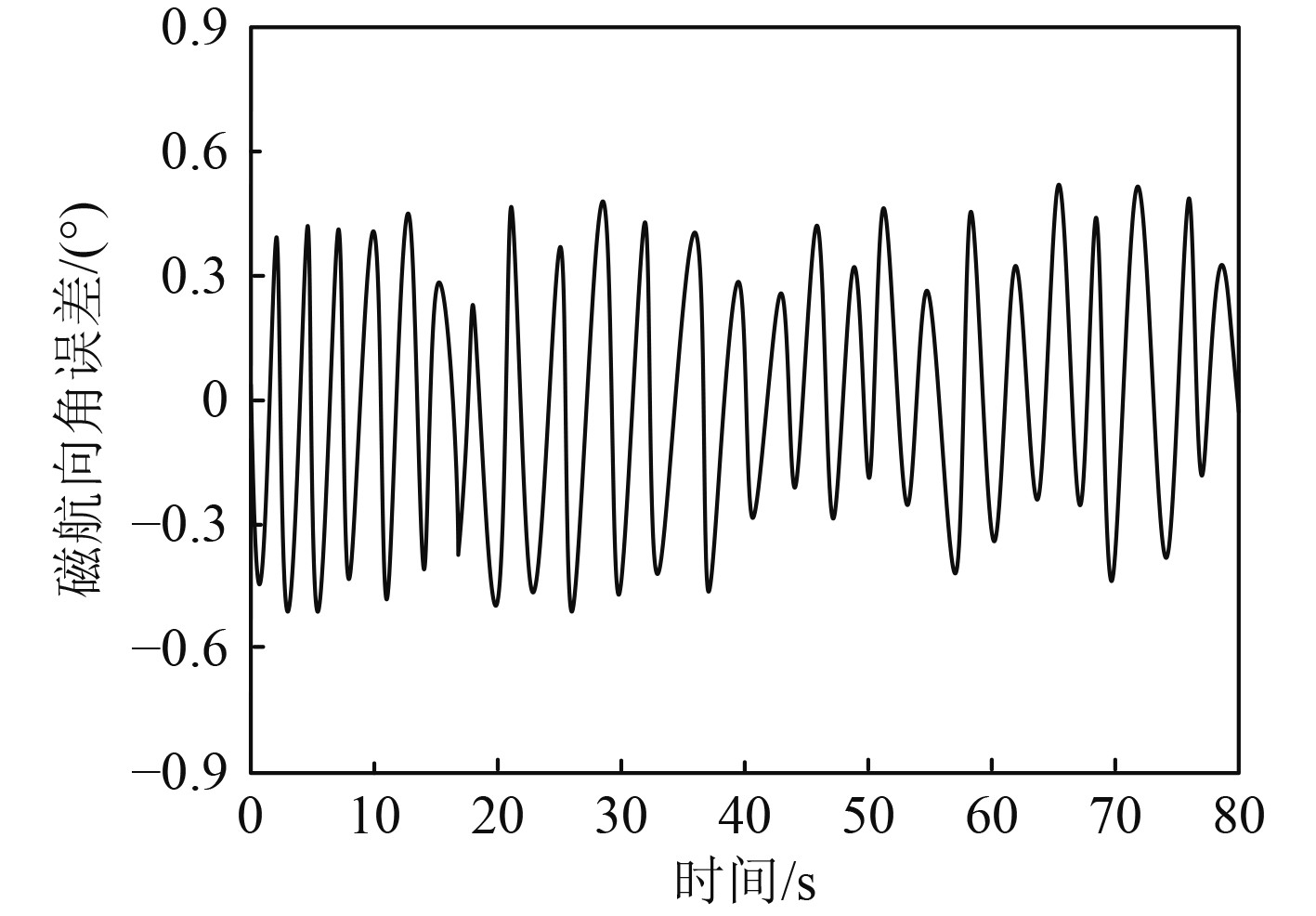
|
图 6 磁航向角误差 Fig. 6 Magnetic heading angle error |
本文研究姿态与舰船感应磁性间关系的建模分析方法,基于舰船模型与舰船感应磁性模型,分析相应感应磁性条件下舰船姿态。实验结果表明本文方法具有较高的分析精度,能够提升舰船在恶劣海况条件下的安全性。
| [1] |
王阳, 曾庆军, 戴晓强, 等. 基于多电机协同推进的遥控水下航行器姿态控制研究[J]. 中国舰船研究, 2022, 17(6): 223-235+251. WANG Yang, ZENG Qingjun, DAI Xiaoqiang, et al. ROV attitude control based on multi-motor cooperative propulsion[J]. Chinese Journal of Ship Research, 2022, 17(6): 223-235+251. |
| [2] |
贾敬蓓, 宗智, 金国庆, 等. 航行姿态对半滑行三体船型静水阻力影响的数值研究[J]. 中国舰船研究, 2020, 15(6): 106-114. JIA Jingbei, ZONG Zhi, JIN Guoqing, et al. A numerical investigation of sinkage and trim effects on the resistance of trimaran hull form in calm water[J]. Chinese Journal of Ship Research, 2020, 15(6): 106-114. |
| [3] |
王毅, 武晓康, 王康君, 等. 利用改进Elman神经网络预测舰船感应磁场[J]. 海军工程大学学报, 2022, 34(4): 31-35. WANG Yi, WU Xiaokang, WANG Kangjun, et al. Application of improved Elman neural network in predicting ship′s induced magnetic field[J]. Journal of Naval University of Engineering, 2022, 34(4): 31-35. DOI:10.7495/j.issn.1009-3486.2022.04.006 |
| [4] |
郭成豹, 胡松, 王文井, 等. 斜航向上舰船感应磁性磁场分离方法讨论[J]. 大学物理, 2021, 40(6): 48-52. GUO Chengbao, HU Song, WANG Wen-jing, et al. Discussion on the decomposition of ship induced magnetism and magnetic fields in oblique courses[J]. College Physics, 2021, 40(6): 48-52. |
| [5] |
王锴松, 周国华, 刘月林, 等. 地磁模拟法测量舰船感应磁场的数值模拟[J]. 兵工学报, 2022, 43(3): 617-625. WANG Kaisong; ZHOU Guohua; LIU Yuelin, et al. Numerical simulation of measuring ship's induced magnetic field by geomagnetic field simulation method[J]. Acta Armamentarii, 2022, 43(3): 617-625. |
 2023, Vol. 45
2023, Vol. 45
