2. 北京卫星环境工程研究所,北京 100190;
3. 中国科学院国家空间科学中心,北京 100190
2. Beijing Institute of Satellite Environmental Engineering, Beijing 100190, China;
3. National Space Science Center, Chinese Academy of Sciences, Beijing 100190, China
海水的平均密度约为1 035 kg/m3,含有约3.50 wt%的盐(NaCl),盐的浓度约为35 kg/m3。在25oC(298 K)的海水中水分子之间距离较小,能够形成氢键,从而在水分子之间出现缔合现象。水分子中,O原子的电负性较大,导致氢、氧虽然共用电子,但电子对总是偏向O原子,称之为“带有部分负电荷”,而两端的H原子就接近于失去电子,即“带有部分正电荷”。这样,一个水分子中的O原子与另一个水分子中的H原子因为所带电荷符号相反,可以在静电力的作用下互相吸引,这种静电吸引力就是一般所说的氢键。海水中只有一部分水分子因氢键而缔合,其他水分子则填充于空隙中。对于2个水分子之间形成的氢键,可以用O-H-O表示。部分H2O分子缔合成双分子准粒子(H2O)2,其他的单个水分子充斥其间。海水的体积弹性系数约为
| $ p(T,h)=K(T,h)\{\mathrm{l}\mathrm{n}[\left(\rho \left(T,h\right)\right]-\mathrm{ln}\left({\rho }_{o}\right)\}, $ |
式中:T为海水的温度;h为海水的深度;
| $\begin{split} {c}_{s}=& \left(\dfrac{\partial p}{\partial \rho }\right)^{1/2}=(\dfrac{K}{{\rho }_{o}+\Delta \rho }{)}^{1/2}\approx \\ & (2.32\times {10}^{9}/1\;035{)}^{1/2}=1\;497\;{\rm{m}}/{\rm{s}}。\end{split} $ |
海水的电导率约为
| $ \mathrm{\delta }=\left(\dfrac{2}{\omega {\mu }_{o}\sigma }\right)^{1/2}=\left(\dfrac{1}{\text{π} f{\mu }_{o}\sigma }\right)^{1/2}。$ |
如果电磁波的频率约为10 kHz,其在海水中的趋肤深度约为:
| $ \begin{aligned} & \mathrm{\delta }\left(f=10\; \mathrm{k}\mathrm{H}\mathrm{z}\right)=\\ & \left(\dfrac{1}{3.14\times {10}^{4}\times 4\times 3.14\times {10}^{-7}\times 4}\right)^{1/2}=2.5\;{\rm{m}} 。\end{aligned} $ |
10 kHz的声波在海水中衰减仅约1 dB/km。而磁声波的传播必须依赖于传播的磁流体介质。磁流体介质的电离率如果降低到零,或介质中没有磁场存在,磁声波也就完全退化成声波。
在磁化海水中垂直地磁场传播的磁声波与常规电磁(横)波是完全不同特性的、带有电磁成分的纵波。研究海水中磁声波传播的特性,可以派生出一门交叉学科—海洋电磁动力学(oceanic electro-magneto dynamics)[3]。海水中的磁声波更加类似于声波,是传播介质密度疏密变化的纵波,只是磁声波有自己的特点,磁声波垂直于介质中磁场传播,在电离成分介质密度疏密涨落的同时,磁场的磁力线也出现疏密的涨落。磁声波是磁流体介质中的快模式波,磁声波电离介质成分的密度涨落与磁场感应强度涨落正相关[4]。
1 海水的磁流体简化模型为了分析海洋中磁流体波动现象,需要建立简单的海洋磁流体力学模型[5-6]。假设海水是均匀的粒子密度分布和温度分布。海水的温度是25oC(298 K),海水中有50%的水分子缔合成双分子准粒子,还有50%的水分子以单分子充斥于缔合分子之间。海水中缔合准粒子(H2O)2和水分子H2O在动力学过程中始终保持电中性,不会出现电离或复合等过程。海水中盐完全解离成Na+离子和Cl−离子,提供海水导电的载流子。北半球海水中地磁场假设成垂直海平面向下
| $ {v}_{dh}=\sqrt{\dfrac{8kT}{\text{π} {m}_{dh}}}=\sqrt{\dfrac{8\times 1.38\times {10}^{-23}\times 298}{3.14\times 6.01\times {10}^{-26}}}=417.5\;{\rm{m}}/{\rm{s}}, $ |
海水中H2O,Na+,Cl-的热速度分别为:
| $ {v}_{H2O}=\sqrt{\dfrac{8kT}{\text{π} {m}_{H2O}}}=\sqrt{\dfrac{8\times 1.38\times {10}^{-23}\times 298}{3.14\times 3.01\times {10}^{-26}}}=590.3\;{\rm{m}}/{\rm{s}}, $ |
| $ {v}_+=\sqrt{\dfrac{8kT}{\text{π} {m}_+}}=\sqrt{\dfrac{8\times 1.38\times {10}^{-23}\times 298}{3.14\times 3.84\times {10}^{-26}}}=522.2\;{\rm{m}}/{\rm{s}}, $ |
| $ {v}_-=\sqrt{\dfrac{8kT}{\text{π} {m}_-}}=\sqrt{\dfrac{8\times 1.38\times {10}^{-23}\times 298}{3.14\times 5.85\times {10}^{-26}}}=423.3\;{\rm{m}}/{\rm{s}} 。$ |
Na+,Cl-在地磁场中的回旋半径分别为:
| $\begin{split} {r}_{L+}=&\dfrac{{m}_+ < {v}_{\perp +} > }{q{B}_{\perp }}\approx \dfrac{\sqrt{2{m}_+kT}}{e{B}_{\perp }}=\\ & \dfrac{\sqrt{2\times 3.84\times {10}^{-26}\times 1.38\times {10}^{-23}\times 298}}{1.6\times {10}^{-19}\times 4\times {10}^{-5}}=2.79\;{\rm{m}}, \end{split}$ |
| $\begin{aligned} {r}_{L-}=& \dfrac{{m}_- < {v}_{\perp -} > }{q{B}_{\perp }}\approx \dfrac{\sqrt{2{m}_-kT}}{-e{B}_{\perp }}=\\ & \dfrac{\sqrt{2\times 5.85\times {10}^{-26}\times 1.38\times {10}^{-23}\times 298}}{-1.6\times {10}^{-19}\times 4\times {10}^{-5}}=-3.44\;{\rm{m}}。\end{aligned} $ |
正离子是右手螺旋旋转(+),而负离子是左手螺旋旋转(–)。海水中声波的传播速度约为1500 m/s,如果声波的频率约为1 kHz,声波的波长约为:
| $ {\lambda }_{s}=\dfrac{{c}_{s}}{f}=\dfrac{1\;500}{1\;000}=1.5\;{\rm{m}}。$ |
声波波长与海水中盐离子的回旋半径在同一个量级,在声波传播过程中盐离子在地磁场中的回旋运动特性将对声波的传播起到一定的影响。
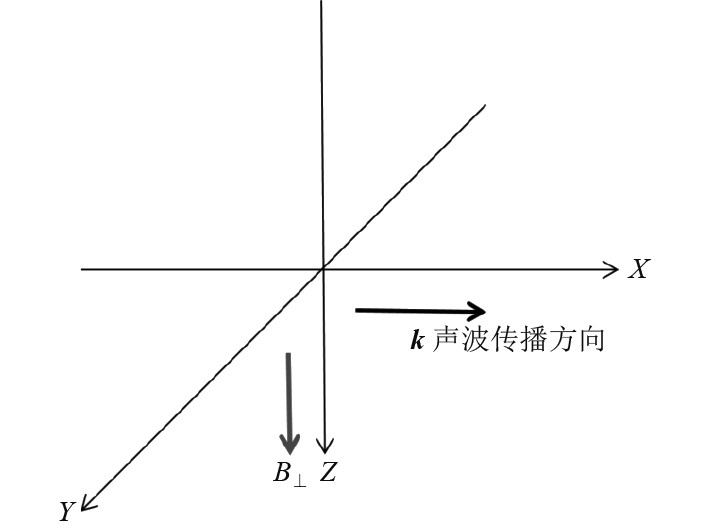
2 声波密度扰动驱动的离子密度群聚[7-8]为了分析海水中声波传播过程中盐离子对声波传播的响应,需要建立一个直角坐标系(X,Y,Z),X方向指向声波的传播方向,并假设声波的传播方向平行于海平面,是一维的平面波。假设海洋中的地磁场是垂直海平面向下的,平行于Z轴方向,Y轴构成XYZ右手坐标系。
|
图 1 海水中的直角坐标系及声波传播方向和垂直地磁场方向 Fig. 1 Cartesian coordinate system in seawater and the direction of sound wave propagation and vertical geomagnetic field |
假设在海水中有一支沿X轴传播的一维声波,海水的深度约为10 m,海水的平均压力约为2.026·105Pa(2个大气压)。声波的声压约为10 MPa。远远小于海水的静压。假设声波的频率约为1000 Hz,声速约为1500 m/s,声波的波长
| $ {n}_{s}\left(x,t\right)=\Delta n\mathrm{sin}\left(kx-{\omega }_{s}t+{\phi }_{o}\right)+{n}_{stat}\left({\rm{A}}\right)。$ |
式中:
在t=0时刻,假设初始相位
| $ {n}_{s}\left(x\right)=\Delta n\mathrm{sin}\left(kx+3\text{π} /2\right)+{n}_{stat}\left(B\right)。$ |
在原点
在
在
在
在
如果只考察声波振荡造成的海水密度涨落,而减去海水的静止密度,则声波的密度振荡形式变换为:
| $ {n}_{s}\left(x\right)=2\Delta n\mathrm{sin}\left(\dfrac{\text{π} }{{\lambda }_{s}}x+\dfrac{3\text{π} }{2}\right)。$ |
在
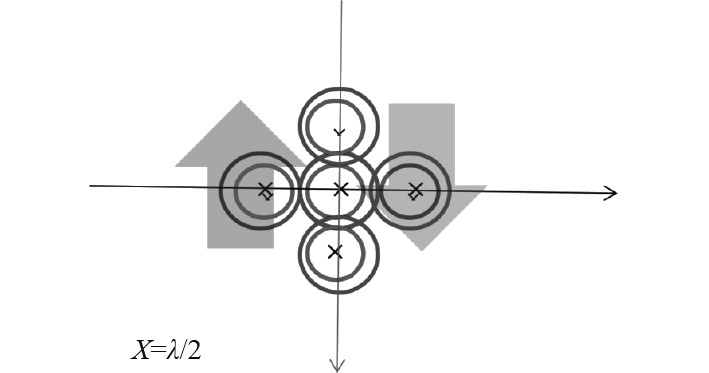
如果海水中不存在垂直于声波传播方向的地磁场,声波振荡的声压,引起海水中所有的粒子(缔合双分子准粒子、水分子、Na+和Cl-离子)都遵守相同的振荡规律。当地磁场存在时,海水的粒子密度振荡,使得盐离子的密度梯度在地磁场中形成密度梯度漂移电流,如图2所示。地磁场是垂直纸面向下,内圆圈是右手螺旋旋转(正离子),而外圆圈是左手螺旋旋转(负离子)。正离子和负离子旋转得到环电流方向是相同的,电流的方向是右手螺旋的。在
|
图 2 密度梯度形成的盐离子漂移电流示意图 Fig. 2 Schematic diagram of salt ion drift current formed by density gradient |
声波传播中离子密度梯度的漂移电流在密度极大值区产生的感应磁场
海水中Na+的分布函数遵守麦克斯韦分布:
| $ {f}^{\left(+\right)}\left(x,\overrightarrow{v}\right)={N}_+\left(x\right)\left(\dfrac{{m}_+}{2\text{π} k{T}_{o}}\right)^{3/2}\mathrm{exp}\left[-\dfrac{{m}_+}{2k{T}_{o}}\left({v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}\right)\right], $ |
其中
| $ {f}^{(-)}\left(x,\overrightarrow{v}\right)={N}_-\left(x\right)\left(\dfrac{{m}_-}{2\text{π} k{T}_{o}}\right)^{3/2}\mathrm{exp}\left[-\dfrac{{m}_-}{2k{T}_{o}}\left({v}_{x}^{2}+{v}_{y}^{2}+{v}_{z}^{2}\right)\right], $ |
由于海水是电中性的,
在
| $ \dfrac{{\rm{d}}{N}_+\left(x\right)}{{\rm{d}}x} > 0, $ |
满足
| $ \left|\dfrac{1}{{N}_{+o}}\dfrac{{\rm{d}}{N}_+\left(x\right)}{{\rm{d}}x}\right|\dfrac{ < {v}_{\perp +} > }{\left|{\omega }_{c+}\right|}\ll 1\left(C\right)。$ |
在一个平均Na+离子回旋半径[
| $ {\overrightarrow{J}}_+\left(x=\dfrac{\lambda }{2}-\left|\Delta x\right|\right)=e{N}_+\left(x=\dfrac{\lambda }{2}-\left|\Delta x\right|\right){\overrightarrow{V}}_{D+}, $ |
| $ {\overrightarrow{V}}_{D+}=-\dfrac{k{T}_{o}}{e{B}_{\perp }}\dfrac{1}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{y}\left(D\right), $ |
| $ {\overrightarrow{J}}_{D+}=-\dfrac{k{T}_{o}}{{B}_{\perp }}\dfrac{1}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{y}\left(E\right)。$ |
在
虽然Cl-离子在地磁场中是左手螺旋旋转的,但Cl-离子所带电荷是负电荷,因此Cl-离子的电流环的方向与Na+离子的电流环方向相同。同理,Cl-离子因在地磁场中的密度梯度而形成的密度梯度漂移速度。
| $ {\overrightarrow{V}}_{D-}=\dfrac{k{T}_{o}}{e{B}_{\perp }}\dfrac{1}{{n}_-}\dfrac{{\rm{d}}{n}_-}{{\rm{d}}x}{\overrightarrow{e}}_{y}\left(F\right), $ |
| $ {\overrightarrow{J}}_{D-}=-\dfrac{k{T}_{o}}{{B}_{\perp }}\dfrac{1}{{n}_-}\dfrac{{\rm{d}}{n}_-}{{\rm{d}}x}{\overrightarrow{e}}_{y}\left(\mathrm{G}\right)。$ |
海水中存在垂直于声波传播方向(x方向)的地磁场(z方向),由于声波传播而声压造成的海水密度沿传播方向的密度不均匀,在声波密度极大值的两边形成密度梯度漂移电流,密度梯度漂移电流密度为:
| $\begin{aligned} {\overrightarrow{J}}_{D}=& e{\overrightarrow{V}}_{D+}+\left(-e{\overrightarrow{V}}_{D-}\right)=-e\dfrac{k{T}_{o}}{e{B}_{\perp }}\dfrac{1}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{y}-\\ & e\dfrac{k{T}_{o}}{e{B}_{\perp }}\dfrac{1}{{n}_-}\dfrac{{\rm{d}}{n}_-}{{\rm{d}}x}{\overrightarrow{e}}_{y}, \end{aligned}$ |
在海水里
| $ {\overrightarrow{J}}_{D}=-\dfrac{2k{T}_{o}}{{B}_{\perp }}\dfrac{1}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{y}。$ |
地磁场对Na+和Cl-离子的密度梯度漂移电流的作用力也是相等的,地磁场作用于密度梯度漂移电流为:
| $ {\overrightarrow{F}}_{L+}={\overrightarrow{J}}_{D+}\times \overrightarrow{B}=-\dfrac{k{T}_{o}}{{B}_{\perp }}\dfrac{1}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{y}\times {B}_{\perp }{\overrightarrow{e}}_{z}=\dfrac{k{T}_{o}}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{x}, $ |
| $ {\overrightarrow{F}}_{L-} = {\overrightarrow{J}}_{D-}\times \overrightarrow{B} = \left(-e\right)\dfrac{k{T}_{o}}{e{B}_{\perp }}\dfrac{1}{{n}_-}\dfrac{{\rm{d}}{n}_-}{{\rm{d}}x}{\overrightarrow{e}}_{y} \times {B}_{\perp }{\overrightarrow{e}}_{z} = \dfrac{k{T}_{o}}{{n}_-}\dfrac{{\rm{d}}{n}_-}{{\rm{d}}x}{\overrightarrow{e}}_{x}。$ |
因此在声波密度极大值左右两边单位面积上的电磁作用力为:
| $\begin{aligned} {F}_{em1}=&{\overrightarrow{F}}_{L+}+{\overrightarrow{F}}_{L-}=\dfrac{k{T}_{o}}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{x}+\dfrac{k{T}_{o}}{{n}_-}\dfrac{{\rm{d}}{n}_-}{{\rm{d}}x}{\overrightarrow{e}}_{x}=\\ & \dfrac{2k{T}_{o}}{{n}_+}\dfrac{{\rm{d}}{n}_+}{{\rm{d}}x}{\overrightarrow{e}}_{x}。\end{aligned} $ |
由于离子密度梯度漂移电流的载流子分别是Na+和Cl−,虽然Na+和Cl−离子的密度梯度漂移电流密度大小和方向都相等,漂移电流所受到地磁场的作用力也是相等的。在声波传播的粒子密度极大值前后两边由于海水处于含有垂直分量的地磁场,形成离子密度漂移电流;地磁场对离子密度梯度漂移电流的作用,就是将离子(正、负离子)更加群聚到中性粒子密度极大值区,海水中盐离子与垂直磁场的耦合作用,增加了海水体积弹性系数。海水密度不仅随着声压增加而密度增加,且垂直声波传播方向的地磁场也额外增加盐离子的密度,也就是海水的粒子总密度,这就是磁声波的特征。
3 磁场脉冲驱动的离子密度群聚在海水中沿着X方向激励一个传播的一维磁脉冲,磁场振动幅度为
| $ {B}_{z}\left(x\right)={B}_{\perp }+{B}_{\delta }\mathrm{s}\mathrm{i}\mathrm{n}({k}_{x}x-\text{π} /2), $ |
扰动磁场的方向与海水中地磁场的方向相同。磁场在x轴方向上有梯度,为
| $ \dfrac{\partial {B}_{z}}{\partial x}={B}_{\delta }{k}_{x}\mathrm{c}\mathrm{o}\mathrm{s}({k}_{x}x-\text{π} /2)。$ |
带电离子在具有梯度的磁场中,产生磁场梯度漂移运动,其漂移运动速度为:
| $ {\overrightarrow{V}}_{DBG+}=\dfrac{{W}_{\perp +}}{{q}_+{B}^{3}}\overrightarrow{B}\times \nabla B=-\dfrac{{\mu }_+}{{q}_+{B}^{2}}(\nabla B\times \overrightarrow{B})。$ |
其中:
| $ {\overrightarrow{V}}_{DBG-}=\dfrac{{W}_{\perp -}}{{q}_-{B}^{3}}\overrightarrow{B}\times \nabla B=-\dfrac{{\mu }_-}{{q}_-{B}^{2}}(\nabla B\times \overrightarrow{B})。$ |
其中:
磁场梯度漂移运动导致正、负离子将沿相反的方向漂移,假设正离子漂移运动的方向设定为正,正离子的磁场梯度漂移电流为正;负离子漂移运动的方向为负,但负离子的磁场梯度漂移电流与正离子的漂移电流方向相同也为正。
| $ {B}_{z}\left(x\right)={B}_{\perp }+{B}_{\delta }\mathrm{s}\mathrm{i}\mathrm{n}({k}_{x}x-\text{π} /2)。$ |
在x=0处,磁场处于极小值;在
| $\begin{aligned} & {\overrightarrow{J}}_{DBG+}={q}_+{\overrightarrow{V}}_{DBG+}{n}_+=-\dfrac{{\mu }_+}{{B}^{2}}{n}_+\left(\nabla B\times \overrightarrow{B}\right)=\\ & - \dfrac{{\mu }_+}{{B}^{2}}\dfrac{\partial B}{\partial x}{{n}_+\overrightarrow{e}}_{x} \times B{\overrightarrow{e}}_{z} = \dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+({\overrightarrow{e}}_{z}\times {\overrightarrow{e}}_{x}) = \dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+{\overrightarrow{e}}_{y}, \end{aligned} $ |
负离子在磁场极大值左侧的磁场梯度漂移电流为:
| $\begin{aligned} & {\overrightarrow{J}}_{DBG-}={q}_-{\overrightarrow{V}}_{DBG-}{n}_-=-\dfrac{{\mu }_-}{{B}^{2}}{n}_-\left(\nabla B\times \overrightarrow{B}\right)=\\ & - \dfrac{{\mu }_-}{{B}^{2}}\dfrac{\partial B}{\partial x}{{n}_-\overrightarrow{e}}_{x}\times B{\overrightarrow{e}}_{z} = \dfrac{{\mu }_-}{B}\dfrac{\partial B}{\partial x}{n}_-\left({\overrightarrow{e}}_{z} \times {\overrightarrow{e}}_{x}\right) = \dfrac{{\mu }_-}{B}\dfrac{\partial B}{\partial x}{n}_-{\overrightarrow{e}}_{y}, \end{aligned}$ |
因此在磁场脉冲的左侧介质离子的磁场梯度漂移电流为:
| $\begin{aligned} {\overrightarrow{J}}_{DBG}=& {\overrightarrow{J}}_{DBG+}+{\overrightarrow{J}}_{DBG-}=\dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+{\overrightarrow{e}}_{y}+\dfrac{{\mu }_-}{B}\dfrac{\partial B}{\partial x}{n}_-{\overrightarrow{e}}_{y}=\\ & \dfrac{({\mu }_++{\mu }_-)}{B}\dfrac{\partial B}{\partial x}{n}_+{\overrightarrow{e}}_{y}, \end{aligned}$ |
介质离子在磁脉冲极大值左侧的磁场梯度漂移电流密度与背景磁场相互作用,表达式为:
| $\begin{aligned} {\overrightarrow{F}}_{L}=&{\overrightarrow{J}}_{DBG}\times \overrightarrow{B}=\dfrac{({\mu }_++{\mu }_-)}{B}\dfrac{\partial B}{\partial x}{n}_+{\overrightarrow{e}}_{y}\times B{\overrightarrow{e}}_{z}=\\ & ({\mu }_++{\mu }_-)\dfrac{\partial B}{\partial x}{n}_+\left({\overrightarrow{e}}_{y}\times {\overrightarrow{e}}_{z}\right)=({\mu }_++{\mu }_-)\dfrac{\partial B}{\partial x}{n}_+{\overrightarrow{e}}_{x}, \end{aligned}$ |
在
| $ {\overrightarrow{J}}_{DBG+} = e{\overrightarrow{V}}_{DBG+}{n}_+ = \dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+\left({\overrightarrow{e}}_{z}\times {\overrightarrow{e}}_{x}\right) = - \left|\dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+\right|{\overrightarrow{e}}_{y}。$ |
在磁脉冲的右侧,磁场梯度漂移电流密度与背景磁场的相互作用为:
| $\begin{aligned} {\overrightarrow{F}}_{R}=&{\overrightarrow{J}}_{DBG}\times \overrightarrow{B}=-\left|\dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+\right|{\overrightarrow{e}}_{y}\times B{\overrightarrow{e}}_{z}=\\ & -\left|\dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+\right|\left({\overrightarrow{e}}_{y}\times {\overrightarrow{e}}_{z}\right)=-({\mu }_++{\mu }_-)\dfrac{\partial B}{\partial x}{n}_+{\overrightarrow{e}}_{x}, \end{aligned}$ |
磁场梯度的作用会造成正负离子向磁场极大值区群聚。在磁脉冲感应强度极大值的两边,单位面积介质上电离成分所受的电磁力为:
| $ {\overrightarrow{F}}_{em2}={\overrightarrow{F}}_{L}=({\mu }_++{\mu }_-)\dfrac{\partial B}{\partial x}{n}_+。$ |
磁脉冲在海水中垂直于背景磁场传播,磁场梯度漂移电流与背景磁场的相互作用,使得海水中的离子向磁脉冲极大值区域群聚。
4 海水中的磁声波速度由于海水中含有3.50wt%的盐,且盐在海水中完全解离成Na+和Cl-离子,使得海水的电导率约为4 S/m,海水处于地磁场中,因此海水具有磁流体的基本特征。海水粒子密度不仅受到声压作用而密度压缩,而且受到垂直于声波传播方向的地磁场作用而进一步密度压缩(离子群聚)。在带有磁场垂直分量的磁流体海水中,纵波垂直于背景磁场方向传播时,其介质密度包含两部分:一是声压致压缩项,二是电离成分的漂移电流密度与垂直磁场相互作用的压缩项。
海水假设成三流体成分,中性的水分子流体、Na+离子流体和Cl-离子流体。根据前面海水简单模型,海水中中性粒子密度约为:
| $ {n}_{o}={n}_{H2O}+{n}_{dh}=2.5\times {10}^{28}\;{{\rm{m}}}^{-3}。$ |
其中:
| $ {n}_+=9.11\times {10}^{26}{{\rm{m}}}^{-3}={n}_-。$ |
其中,
| $ {\sigma }_{s}=5\times {10}^{-17}\;{\rm{{m}}}^{2}, $ |
Na+(Cl-)离子在海水中的平均自由程为:
| $ {\lambda }_{+mfp}=\dfrac{1}{{\sigma }_{o}{n}_{o}}=\dfrac{1}{{1.8\times 10}^{-16}\times 2.5\times {10}^{28}}=2.2\times {10}^{-13}\;{\rm{m}}, $ |
Na+(Cl-)离子在海水中的弹性碰撞频率为:
| $ {\nu }_{+o}=\dfrac{{v}_+}{{\lambda }_{+mfp}}=\dfrac{522.2}{2.2\times {10}^{-13}}=2.4\times {10}^{14}\;{\rm{Hz}}, $ |
因此海水中的电导率为:
| $\begin{aligned} \mathrm{\sigma }=& \dfrac{2{n}_+{e}^{2}}{{m}_{*}{\nu }_{+o}}=\dfrac{2\times 9.11\times {10}^{26}\times 2.56\times {10}^{-38}}{5.4\times {10}^{-26}\times 2.4\times {10}^{14}}=\\ & \dfrac{2\times 9.11\times 2.56}{5.4\times 2.4}=3.6\;{\rm{S}}/{\rm{m}}。\end{aligned} $ |
其中,
| $ \begin{aligned} {v}_{A}=&\sqrt{\dfrac{{B}^{2}}{4{\mu }_{o}{m}_{*}{n}_+}}=\sqrt{\dfrac{16\times {10}^{-10}}{16\times 3.14\times 5.4\times {10}^{-26}\times 9.11\times {10}^{26}}}=\\ & 8\times {10}^{-7}{\rm{m}}/{\rm{s}}\ll {c}_{s}, \end{aligned}$ |
海水中磁声波的速度
| $ {c}_{ms}=({c}_{s}^{2}+{v}_{A}^{2}{)}^{1/2}\approx {c}_{s}。$ |
海水中磁声波的传播速度约等于声波速度,约为1500 m/s。
5 海水中无人潜航器激励磁声波传播特征海水中无人潜航器(UUV或鱼雷),一般采用铝合金做外壳,尺寸在
| $\begin{aligned} {R}_{m}=&\dfrac{UL}{{\nu }_{m}}=\sigma {\mu }_{o}UL=3.6\times {10}^{7}\times 4\times 3.14\times \\ & {10}^{-7}\dfrac{8\times{10}^{4}}{3600}\times 3=4\times 3.14\times 240=3014 \gg 1。\end{aligned}$ |
因此UUV可以看成是良好导体,其在水下运动时,地磁场磁力线可以认为是冻结在UUV的铝合金导体内,导致UUV前端不仅出现声压增加和海水密度增加,同时也造成磁场感应强度的增加。UUV在向前运动时,类似于一个铲雪车,将雪铲起堆积在雪铲的前端。UUV在向前运动时,也将地磁场“铲起”,堆积在UUV的前端。当磁场达到饱和时,UUV前端的磁场不在增加。在UUV前端形成地磁场的负梯度(随着向更远的前方,磁场感应强度下降)。
UUV的速度约为22 m/s,UUV的直径约为0.5 m,地磁场垂直海平面向下,磁感应强度约为40000 nT。在UUV艇体上,产生感应电场,表达式为:
| $ \overrightarrow{E}=-\overrightarrow{V}\times \overrightarrow{B}=-VB\left({\overrightarrow{e}}_{x}\times \right)=VB\left({\overrightarrow{e}}_{z}\times {\overrightarrow{e}}_{x}\right)=VB{\overrightarrow{e}}_{y}。$ |
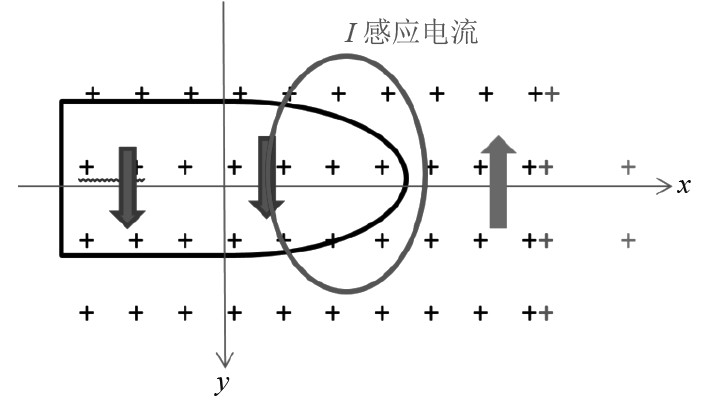
|
图 3 UUV高速运动在海水中激励声波和磁声波示意图 Fig. 3 Schematic diagram of the excitation of acoustic waves and magneto-acoustic waves in seawater by UUV high-speed motion |
由于海水是导电体,UUV艇体上的电场,通过外部的导电海水形成电流回路,且电流回路产生的感应磁场在艇体内部是减弱地磁场,而在艇体的前端是增强地磁场
| $ {\overrightarrow{B}}_{G}\left(\overrightarrow{r},t\right)=const, $ |
在UUV定速运行过程中:
| $ \dfrac{\partial {\stackrel{~}{B}}_{z}}{\partial t}=0, $ |
| $ \nabla \times \left({\stackrel{~}{B}}_{z}{\overrightarrow{e}}_{z}\right)\ne 0 ,$ |
在UUV前端与声压增加近似的位置上:
| $ \dfrac{\partial {\stackrel{~}{B}}_{z}}{\partial x} < 0。$ |
也就是UUV前端的感应磁场是随着x三次方衰减的,感应磁场是还电流产生的类偶极子磁场。如前面分析,磁场梯度在海水中产生-y方向的漂移电流。
在
| $\begin{aligned} {\overrightarrow{J}}_{DBG+}=& e{\overrightarrow{V}}_{DBG+}{n}_+=\dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+\left({\overrightarrow{e}}_{z}\times {\overrightarrow{e}}_{x}\right)=\\ & -\left|\dfrac{{\mu }_+}{B}\dfrac{\partial B}{\partial x}{n}_+\right|{\overrightarrow{e}}_{y}。\end{aligned}$ |
这个漂移电流将感应磁场的扰动向前传播。因此UUV不仅在海水中通过压力扰动激励声波传播,而且由于海水是导电流体,且存在地磁场,UUV高速运动时,在艇体前端激励感应磁场,感应磁场的梯度又将磁场扰动向前传播。如果海水不导电或者海水中不存在垂直海平面的地磁场分量,则不会出现平行海平面传播的磁声波。但显示状态下,UUV不仅激励声波,而且激励平行海平面传播的磁声波。对磁声波的探测可以利用搜索线圈进行探测。其探测灵敏度远远高于声波换能器的灵敏度,在海洋中,磁声波的干扰信号源远远小于声波的干扰信号源。只有高速运动、金属壳体的船体才可能在海水下激励磁声波。磁声波与声波类似,都是沿着传播方向震荡的纵波,因此常识中电磁波在海水中的衰减远远大于声波的结论对于磁声波并不一定适用。电磁波是横波,由于海水是导体,海水对电磁波的屏蔽深度,决定了电磁波在海水中的衰减。海水的电导率
| $ \mathrm{\delta }=\left(\dfrac{2}{\omega {\mu }_{o}\sigma }\right)^{1/2}=\left(\dfrac{1}{\text{π} f{\mu }_{o}\sigma }\right)^{1/2}, $ |
如果电磁波的频率
| $ \mathrm{\delta }=\left(\dfrac{1}{3.14\times 1000\times 4\times 3.14\times {10}^{-7}\times 4}\right)^{1/2}=8.0\;\mathrm{m}。$ |
磁声波在磁流体力学波中是一支快波,磁声波垂直背景磁场传播,在传播过程中造成磁流体的质量密度和扰动磁场的疏密变化,且快波的特征是密度扰动和磁场扰动正相关。磁声波的速度大于声波速度,这是由于磁场使得海水中的正负离子具有向磁场极大值群聚的特性,也就增加了磁流体的弹性,海水在外磁场作用下,海水的体积弹性系数
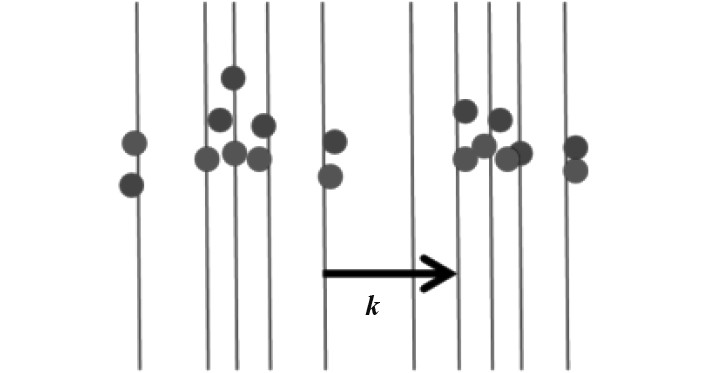
|
图 4 海水磁流体中纵波磁声波传播示意图 Fig. 4 Schematic diagram of longitudinal-wave magneto-acoustic wave propagation in seawater magnetic fluid |
海水磁流体具有始终保持宏观电中性的特征。UUV在激励声波的同时,也激励磁声波。且磁声波的离子密度扰动与声波的中性粒子密度扰动是同步涨落。声波的声压涨落同时将部分热能转换成磁扰动的能量,带来垂直磁场分量的涨落。磁场扰动产生海水离子的磁场梯度漂移运动,离子与海水中性粒子的碰撞又将磁扰动能量转换成海水粒子的热能。海水中声波垂直于背景磁场传播时,伴随着磁声波传播。海水的热能与磁扰动能量之间相互转换。因此可以通过高灵敏磁感应搜索线圈探测UUV产生的磁场扰动,探测灵敏度可以达到10−4nTHz−1/2。如果搜索线圈的工作频段设定为100 Hz~10 kHz,在海水下的背景磁噪声(100 Hz~10 kHz)是非常平静地。探测相对灵敏度约为2.5*10−9。假设搜索线圈的横截面积为
| $ V={S}_{\sigma }N{\mu }_{r}{\mu }_{o}\dfrac{\partial B}{\partial t}={S}_{\sigma }N{\mu }_{r}{\mu }_{o}f\left(\delta B\right)。$ |
因此利用搜索线圈探测UUV产生和传播的磁声波,是一种有效的非声探测方法。
6 结 语本文通过分析海水的基本特性,含有大量的中性粒子、Na+、Cl-离子,海水宏观上呈现电中性。海水处于地球的地磁场中,还有垂直海平面的地磁场分量。如果海水中有一支垂直地磁场传播的声波,同时也激励磁声波的传播,磁声波的速度与声波速度相近,约为1500 m/s。声波传播过程中,声压驱动海水粒子的密度涨落,盐离子密度梯度与中性粒子密度同步。离子密度梯度漂移运动产生漂移电流,感应产生磁场涨落,扰动磁场的方向与背景磁场方向相同。扰动磁场的能量是声压驱动离子移动形成密度梯度的热能转换而来;扰动磁场的梯度又产生磁场梯度漂移运动,离子的漂移运动与中性粒子的弹性碰撞又将磁场扰动能量转换成海水粒子的热能。海水中垂直于背景磁场的磁声波传播过程中,声压热能与磁扰动能量相互转化,始终伴随着磁声波传播。
水下潜航器(UUV)由于其在海水中运行速度较快,不仅激励出声波,同时还激励出较大的磁脉冲在海水中以磁声波的模式传播。磁声波传播的磁场扰动信号可以是一种高灵敏非声探测磁声波激励源的技术途径之一。磁扰动信号通过搜索线圈获得非常高的相对探测灵敏度,并且在海水中,磁扰动信号的背景噪声远远低于声波的背景噪声,搜索线圈的磁探测是一种有效的、远距离探测磁声波激励源的技术。
| [1] |
王强, 赫冀成, 岩井一彦, 等. 在强磁场中传播的磁声波的特性研究[J]. 自然科学进展, 2002, 12(10): 1026-1030. WANG Q, HAO J C, YAN J Y Y, et al. Research on the characteristics of magnetoacoustic waves propagating in strong magnetic fields[J]. Advances in Natural Science, 2002, 12(10): 1026-1030. DOI:10.3321/j.issn:1002-008X.2002.10.004 |
| [2] |
LIU, N, etal. Magnetosonic harmonic falling and rising frequency emissions potentially generated by nonlinear wave‐wave interactions in the van allen radiation belts[J]. Geophysical Research Letters, 2018, 16(45): 7985-7995. |
| [3] |
吕俊军, 陈凯, 苏建业, 等. 海洋中的电磁场及其应用[M]. 上海: 上海科学技术出版社, 2020: 35–41.
|
| [4] |
陈轩, 周家海. 船舶吃水深度数据检测关键技术及应用[J]. 舰船科学技术, 2022, 44(8): 183-185. CHEN X, ZHOU J H. Key technology and application of ship draft data detection[J]. Ship science and technology, 2022, 44(8): 183-185. |
| [5] |
石志东, 李中元. 空间尘埃等离子体中尘粒电荷的相关涨落对尘埃磁声波的影响[J]. 空间科学学报, 1997(4): 303-308. SHI Z D, LI Z Y. Influence of correlated fluctuation of dust particle charge in space dust plasma on dust magnetoacoustic waves[J]. Journal of Space Science, 1997(4): 303-308. |
| [6] |
尼古拉斯. 希洛斯[美]. 数学磁流体力学(英文)[M]. 哈尔滨: 哈尔滨工业大学出版社, 2020.
|
| [7] |
陈芸, 吴晋生. 海洋电磁学及其应用[J]. 海洋科学, 1992, 3(2): 19-21. CHEN Y, WU J S. Marine Electromagnetics and Its Applications[J]. Marine Science, 1992, 3(2): 19-21. |
| [8] |
肖晖, 周庆华. 多离子空间等离子体中快磁声波与粒子的回旋共振特性[J]. 空间科学学报, 2018, 38(3): 332-341. XIAO H, ZHOU Q H. Cyclotron resonance properties of fast magnetoacoustic waves and particles in multi-ion space plasmas[J]. Chinese Journal of Space Science, 2018, 38(3): 332-341. DOI:10.11728/cjss2018.03.332 |
| [9] |
徐家鵉, 金尚宪. 等离子体物理学[M]. 太原: 原子能出版社, 1981: 121–135.
|
| [10] |
李兵. 部分电离等离子体中离子声波的阻尼[J]. 湖南城市学院学报, 2013, 22(2): 45-47. LI B. Damping of ion acoustic waves in partially ionized plasma[J]. Journal of Hunan City University, 2013, 22(2): 45-47. |
 2023, Vol. 45
2023, Vol. 45
