2. 水下信息与控制国防重点实验室,陕西 西安 710077
2. Science and Technology on Underwater Information and Control Laboratory, Xi′an 710077, China
水声通信是实现水下各类装备信息化发展的重要基础。近年来,各种水下无人航行器快速发展,其智能化和信息化对移动水声通信技术提出了日益迫切的需求。移动水声通信是水下移动节点执行任务、传输信息的重要途径,也是构建水下网络、提升水下信息化整体发展能力的必备技术[1]。但目前定点水声通信研究较多,移动水声通信技术研究相对而言尚存不足,特别是收发两端相对运动速度较快的高速移动水声通信技术研究甚少。
移动水声通信中收发两端的相对运动会导致通信信号出现时间压缩或扩展而产生多普勒效应,由于声波的传播速度低,因此移动水声通信中的多普勒效应影响相对严重。较大的多普勒频偏将引起严重的载波频率偏移,直接影响通信系统性能。通过采用帧同步信号作为同步码,为接收信息码信号准确开窗,并进行多普勒因子准确估计与补偿,是实现移动水声通信和保证高质量通信的前提。
针对移动水声通信中的帧同步和多普勒估计,国内外学者已经开展了一系列的研究,并提出不同的处理方法。Sharif等[2]提出了在数据块前后添加LFM信号,接收端根据相关峰值估计多普勒因子。李云飞[3]提出了利用Zadoff-Chu序列,通过给训练序列分别添加循环前缀和后缀,进行多普勒因子估计。岳玲等[4]提出了利用HFM信号和单频脉冲信号等估计多普勒频移。同时,还将宽带模糊度函数方法引入水声通信同步技术,以实现高精度多普勒因子估计。
总体来看,可以将当前这些多普勒估计方法分别归结为利用LFM信号、m序列、HFM信号的3类移动水声通信帧同步方法,这些方法均从不同角度给出了移动水声通信的帧同步解决途径。但对于特定的移动水声通信应用需求,还需要充分了解各种方法的具体适用环境和技术优势与特点等,这就需要对不同方法进行全面深入的性能分析与对比,为各方法优化选取和实际应用提供有效指导。
本文在分别研究LFM信号、m序列信号、HFM信号3种帧同步方法实现原理的基础上,针对AWGN信道和实测多途衰落信道,通过计算机仿真分析,分别从信噪比、信道特性、收发相对多普勒速度、计算复杂度等方面,对这3种帧同步方法在不同条件和应用环境的多普勒因子估计性能进行全面对比分析,为水下各类无人航行器移动水声通信帧同步方法的具体选择和综合应用提供参考。
1 移动水声通信的帧同步对于发射和接收端存在相对运动速度的移动水声通信系统,在收发端多普勒效应的影响下,水声信号不仅在频域发生频率偏移,同时也表现为时域信号波形的压缩或扩展效果[5]。因此,在水声通信中,接收信号通常建模为时域波形上的伸缩效应,即
| $ r(t) = s\left( {(1 + \alpha )t} \right) 。$ | (1) |
式中:
| $ \alpha = \frac{v}{c} 。$ | (2) |
一般情况下,当通信双方相向移动时,
水声信号经过不同的路径到达接收端,接收信号是所有路径传送信号的叠加。一般情况下,每条传播路径上的多普勒因子不同,但其主要部分都是由收发两端相对运动引起的,故假设所有传播路径上的多普勒因子均相等,且多普勒因子在一帧信号持续时间内保持不变。
因此,对于频率为
| $ {f_r} = f(1 + \alpha ) 。$ | (3) |
水声通信信号的时间展宽或压缩,将导致码元信号同步误差的累积。例如,对于水下相对运动速度30 kn的收发系统,则会产生1%的时间压缩或扩展量,其影响表现为在传输100个码元信息后,同步误差累计为1个码元宽度[5],严重影响后续码元信息的解调和解码。因此,高速移动水声通信必须减缓严重多普勒效应的影响。
帧同步是移动水声通信中消除严重多普勒效应影响的重要方法。发射端在码元信号前后附加一定的帧同步信号作为同步码,接收端通过解析同步码,为接收信息码信号准确开窗,并对多普勒因子进行准确估计。因此,多普勒因子估计性能是帧同步方法的主要性能指标。在此基础上,利用多普勒补偿技术,可以消除多普勒效应对码元信号的影响,从而保证高质量的信息通信。
接收端根据帧同步信号的多普勒因子估计结果,可以通过重采样的方式进行多普勒补偿,也就是通过多普勒效应的逆过程实现对多普勒因子的补偿,即
| $ \hat s(t) = r \left(\frac{1}{{1 + \alpha }}t\right)。$ | (4) |
式中,
LFM信号是指瞬时频率随着时间线性变化的一种信号,其时间函数可以表示为:
| $ s(t)=A\mathrm{exp}[ j(2{\text{π}} {f}_{0}t\pm {\text{π}} k{t}^{2})] 。$ | (5) |
式中:
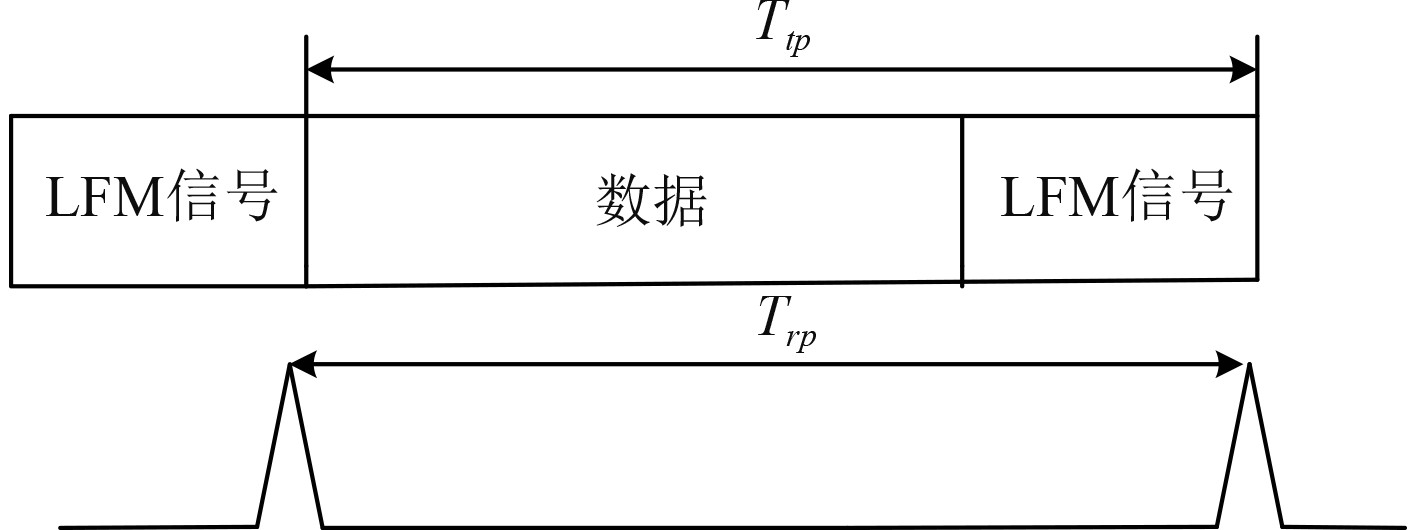
块估计方法是在传输数据前后各加上一段相同的多普勒不敏感信号,常用LFM信号,通过比较接收信号与发射信号的帧长度变化估计多普勒因子[2,6]。
假设发射信号的帧长度为
| $ \hat \alpha = 1 - \frac{{{T_{rp}}}}{{{T_{tp}}}} 。$ | (6) |
式中,
|
图 1 块估计方法 Fig. 1 Block estimation method |
图中,多普勒估计的分辨率取决于LFM信号的带宽
| $ \Delta \hat \alpha \approx {1 \mathord{\left/ {\vphantom {1 {B{T_{tp}}}}} \right. } {B{T_{tp}}}}。$ | (7) |
可见,该方法实现简单,仅需要进行2次相关运算即可获得
同时,宽带LFM信号的多普勒容限[7]为:
| $ {v_d} = \frac{{2610}}{{BT}}{\text{ kn}}。$ | (8) |
根据式(7)和式(8)可知,发射信号带宽
| $ R(n) = \frac{1}{N}\sum\limits_{k = 1}^N s [k]{s^*}{[k + n]_N} = \left\{ {\begin{array}{*{20}{c}} {1,}&{n = 0} ,\\ { - 1/N,}&{0 < n < N} 。\end{array}} \right. $ | (9) |
式中:
宽带模糊度函数定义为:
| $ \chi (\tau ,\alpha ) = \int {{s^ * }((1 + \alpha )t)} r(t - \tau ){\rm{d}}t ,$ | (10) |
式中,
基于模糊度函数估计多普勒因子的帧同步方法,其数据帧格式如图2所示,前导信号使用对多普勒敏感的m序列。

|
图 2 模糊度函数方法的帧格式 Fig. 2 Frame format for the ambiguity function method |
在实际应用中,由于接收机无法知道
|
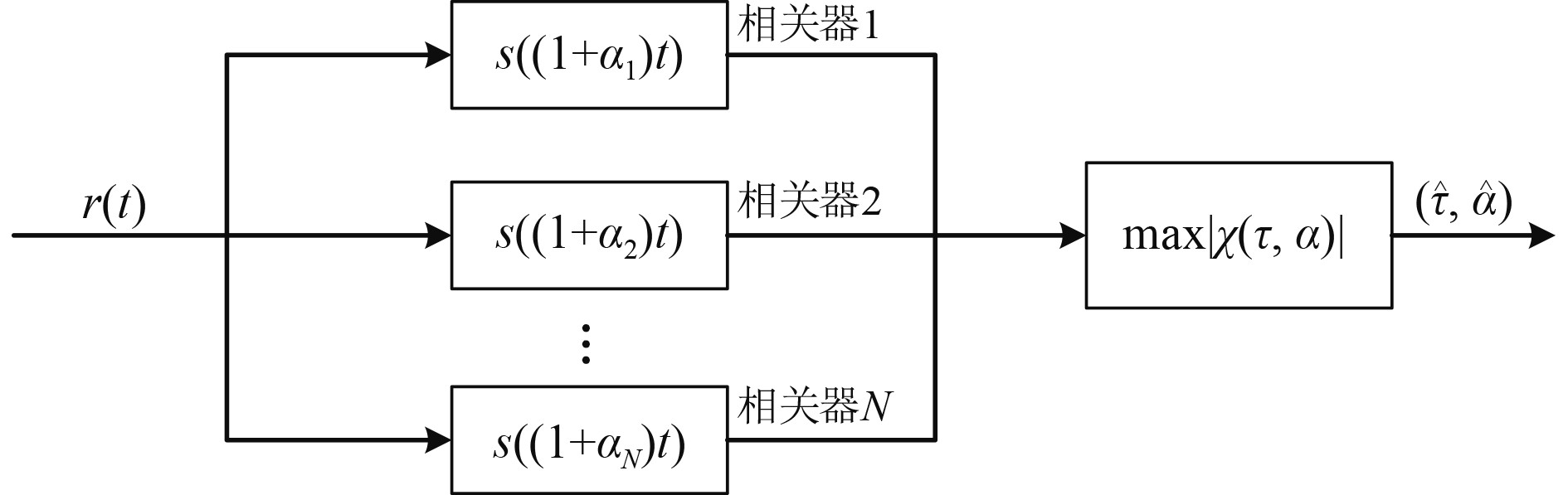
图 3 多普勒因子估计结构图 Fig. 3 Doppler factor estimation structure diagram |
由图3可知,在接收端,将本地保存的受不同多普勒效应影响的副本信号与接收信号中的前导信号作拷贝相关,相关器组输出的最大峰值便是多普勒估计结果,即
| $ (\hat \tau ,\hat \alpha ) = \arg \mathop {\max }\limits_{\tau ,\alpha } \left| {\chi (\tau ,\alpha )} \right| 。$ | (11) |
该方法可以实时处理数据,其多普勒估计精度主要依赖于前导信号对多普勒的敏感程度以及接收端相关器的个数。为了获得最佳的多普勒分辨率,前导信号的自模糊度函数应具有非常尖锐的主峰,因此常用伪随机信号。接收端相关器的个数主要由多普勒估计范围与精度决定,如果多普勒因子的搜索范围为
HFM信号的瞬时频率随着时间呈对数变化,其上扫频和下扫频HFM信号的时间函数[8]分别为:
| $ {s_{up}}(t) = A\exp \left[ {j\frac{{2{\text{π}} }}{{{\gamma _{up}}}}\ln \left( {1 + {\gamma _{up}}{f_{\min }}t} \right)} \right],$ | (12) |
| $ {s_{down}}(t) = A\exp \left[ {j\frac{{2{\text{π}} }}{{{\gamma _{down}}}}\ln \left( {1 + {\gamma _{down}}{f_{\max }}t} \right)} \right] 。$ | (13) |
式中:
以上扫频HFM信号为例,它的瞬时频率为:
| $ {f_{up}}(t) = \frac{{{f_{\min }}}}{{1 + {\gamma _{up}}{f_{\min }}t}},$ | (14) |
当存在多普勒效应时,该信号的瞬时频率改变为:
| $ {f_{dop}}(t) = \frac{{(1 + \alpha ){f_{\min }}}}{{1 + (1 + \alpha ){\gamma _{up}}{f_{\min }}t}} ,$ | (15) |
比较式(14)和式(15),可以发现存在一个时延差
| $ \tau = - \frac{\alpha }{{{\gamma _{up}}{f_{\min }}(1 + \alpha )}}。$ | (16) |
由此可见,通过解算时延
通过时序连续发射或者同时叠加发射上扫频与下扫频HFM信号作为前导信号,同步帧结构分别如图4所示。其中,图4(b)的帧结构中前导信号持续时间更短,可以降低发送端能耗,提高帧的数据利用率。

|
图 4 发射帧结构 Fig. 4 The structure of transmitted frame |
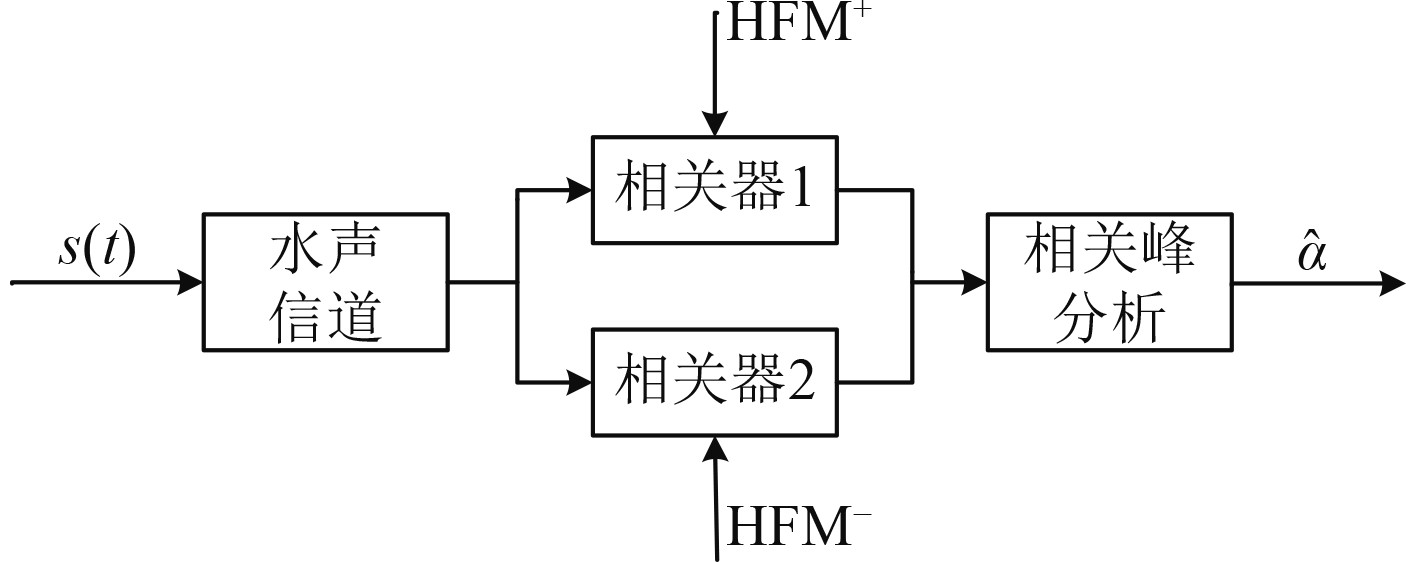
接收端设置2个并行相关器对接收信号进行拷贝相关处理[9],分别对接收信号中的
|
图 5 多普勒因子估计结构图 Fig. 5 The structure of Doppler factor estimation |
图中,通过拷贝相关处理,2个并行相关器分别输出上扫频和下扫频HFM信号的相关峰偏移量
| $ {\tau _1} = \frac{{ - \alpha T{f_{\max }}}}{{({f_{\min }} - {f_{\max }})(1 + \alpha )}},$ | (17) |
| $ {\tau _2} = \frac{{\alpha T{f_{\min }}}}{{({f_{\min }} - {f_{\max }})(1 + \alpha )}} 。$ | (18) |
由式(17)和式(18)可得,2个相关峰之间的差值
| $ \Delta \tau = {\tau _1} - {\tau _2} = \frac{{\alpha T({f_{\min }} + {f_{\max }})}}{{({f_{\max }} - {f_{\min }})(1 + \alpha )}} ,$ | (19) |
因此,通过式(19)可以解算出多普勒因子
| $ \hat \alpha = \frac{{\Delta \tau ({f_{\max }} - {f_{\min }})}}{{T({f_{\max }} + {f_{\min }}) - \Delta \tau ({f_{\max }} - {f_{\min }})}} 。$ | (20) |
由式(20)可以看出,多普勒因子
针对AWGN信道和实测水声多径信道条件下高速移动节点水声通信的2种典型应用场景,利用3种多普勒因子估计方法进行计算机仿真。仿真时,发射信号的帧结构分别如图1和图2及图4(b)所示。LFM信号和HFM信号的参数设置均为起始频率
分别针对不同信噪比、信道特性、收发相对多普勒速度、计算复杂度等条件,进行仿真分析,每种情况下仿真次数均为1000次,统计分析各种方法对多普勒因子估计的均方误差性能。
3.2 不同信道特性条件下对比分析实测水声多径信道参数如表1所示,其中信道的多普勒扩展为1 Hz。
|
|
表 1 水声信道仿真参数 Tab.1 Underwater acoustic channel simulation parameters |
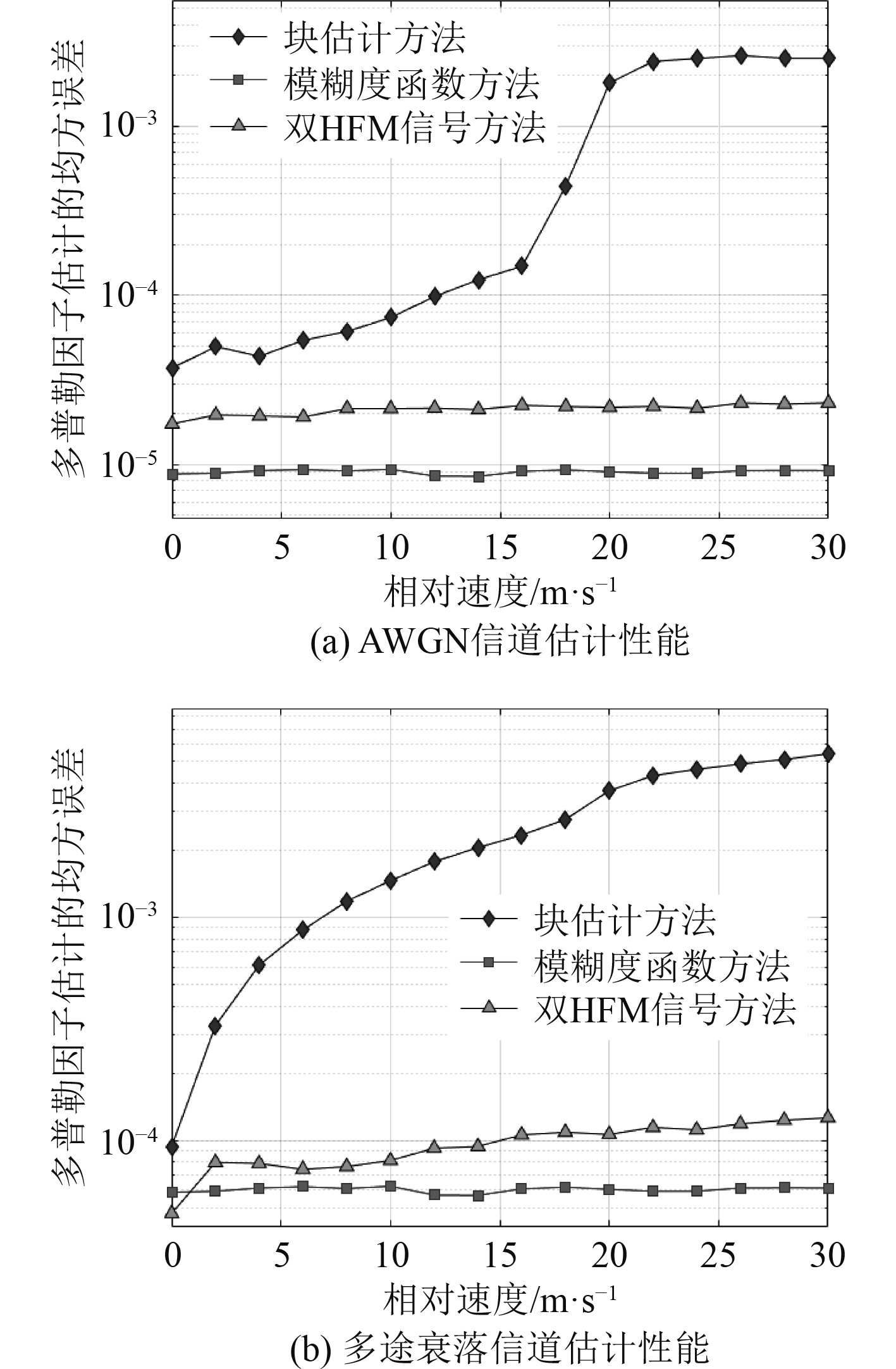
在−10 dB信噪比情况下,分别针对AWGN信道和时变多途衰落信道,各种方法多普勒估计性能仿真结果如图6所示。
|
图 6 多普勒因子估计性能 Fig. 6 Doppler factor estimation performance |
对比分析图6可以发现,多途衰落信道条件下的多普勒估计性能明显低于AWGN信道,这是由于多径效应的存在,增加了各路径信号之间的干扰,导致多普勒因子估计误差增大。从图6均可以看出,m序列模糊度函数算法的多普勒因子估计性能最好,双HFM信号估计方法次之,LFM信号块估计方法最差。
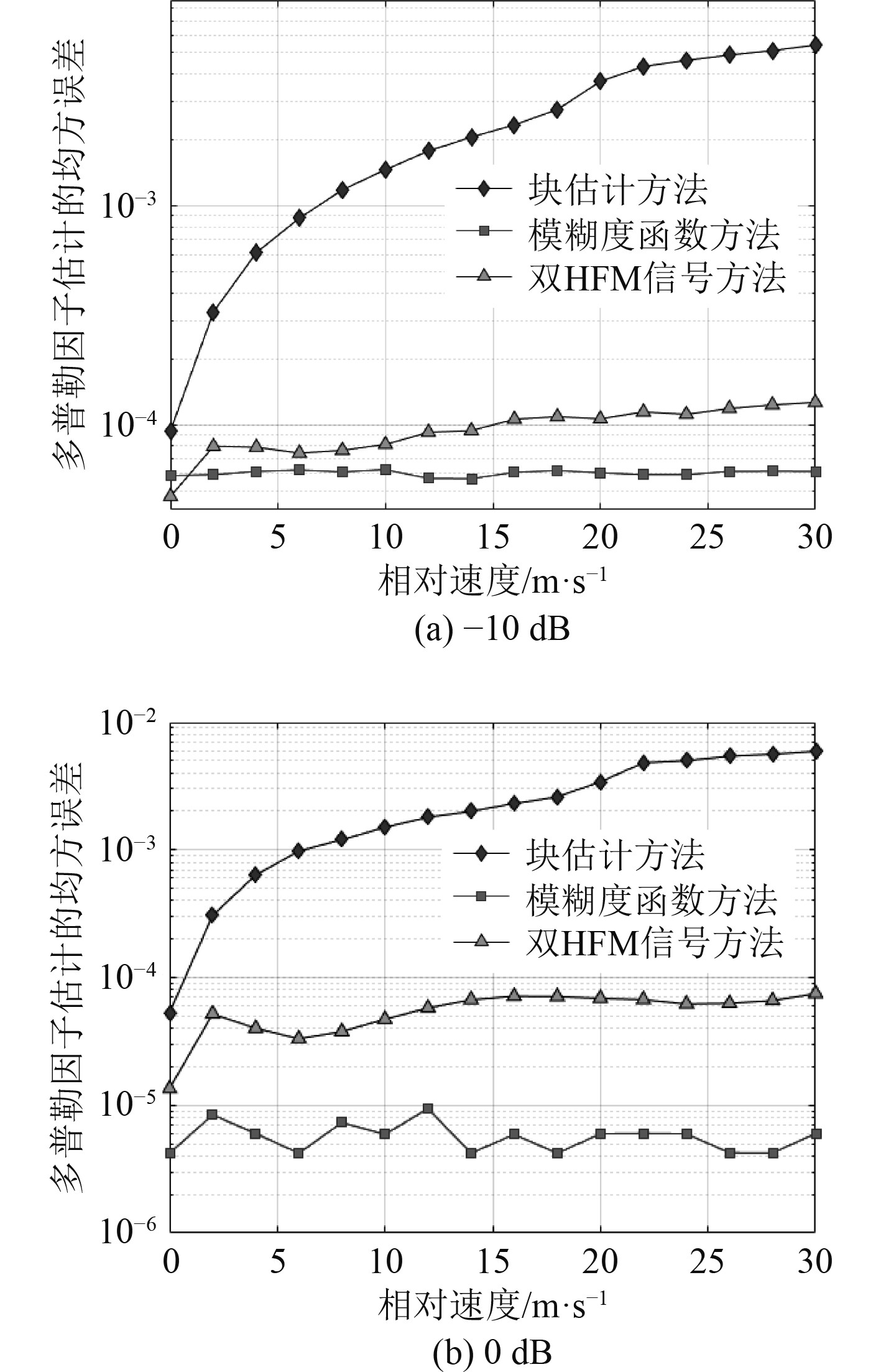
3.3 不同信噪比条件下对比分析在实测水声信道中,为分析3种方法在不同信噪比条件下的多普勒因子估计性能,将各方法分别在−10 dB和0 dB下进行仿真对比,结果如图7所示。
|
图 7 多普勒因子估计性能 Fig. 7 Doppler factor estimation performance |
可以看出,当信噪比从−10 dB增大到0 dB,m序列模糊度函数方法的估计性能提升到
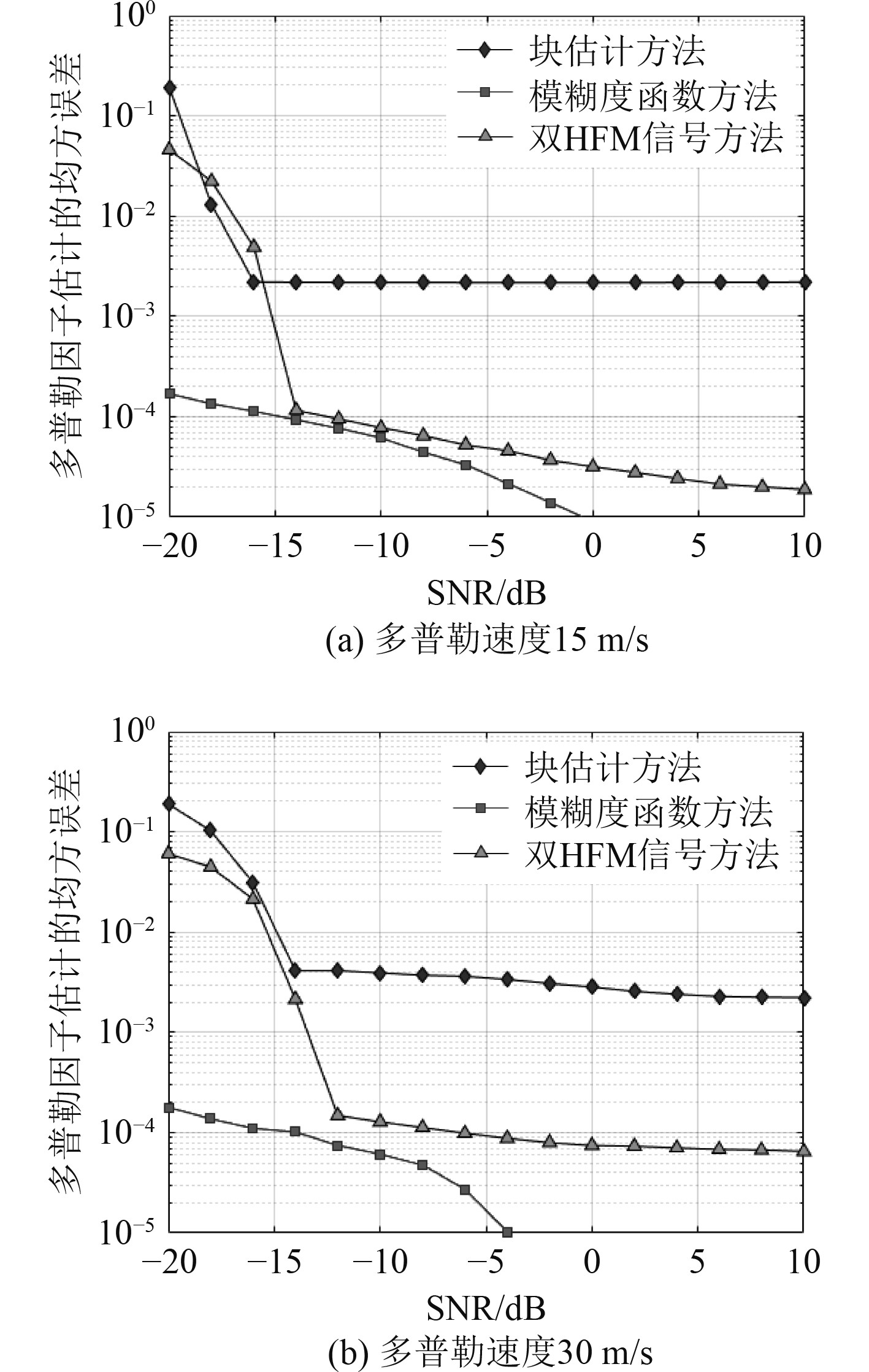
在实测水声信道中,为分析3种方法在不同多普勒速度条件下的多普勒估计性能,将3种多普勒估计方法分别在相对运动速度15 m/s和30 m /s条件下作对比,仿真结果如图8所示。
|
图 8 多普勒因子估计性能 Fig. 8 Doppler factor estimation performance |
可知,给定多普勒速度,3种多普勒估计方法的估计误差随信噪比增大而减小。由于仿真的多普勒速度远远超过LFM信号的多普勒容限,即使增大信噪比,块估计方法也不能得到理想的估计性能。模糊度函数方法在多普勒速度15 m/s和30 m/s时均表现出良好的估计性能,但是付出了计算复杂度大的代价,工程实现起来较为困难。当多普勒速度分别为15 m/s和30 m/s时,基于双HFM信号的多普勒估计方法分别在−14 dB和−12 dB信噪比实现
假定各方法使用拷贝相关器的计算复杂度均相等。LFM信号块多普勒估计方法和双HFM信号多普勒估计方法均仅需要2次拷贝相关,而对于m序列模糊度函数方法,采用粗细两步搜索,即先以
|
|
表 2 三种多普勒估计方法的计算复杂度比较 Tab.2 Comparison of computational complexity of three Doppler estimation methods |
根据以上仿真分析可以得出下面结论:基于LFM信号的块多普勒估计方法适用于静止节点或者移动速度较低,且对多普勒估计精度要求不高的水声通信设备;基于m序列的模糊度函数方法计算复杂度高、运算量大,对移动水声通信接收机设备提出了十分严苛的要求;基于双HFM信号多普勒估计方法的计算复杂度与块估计方法相同,且该方法在低信噪比和高多普勒速度条件下,仍能实现
综上,双HFM信号多普勒估计方法估计精度高、计算复杂度低、帧数据利用率高,可以在−10 dB信噪比下实现对多普勒速度30 m/s的多普勒因子精确估计,同时也可以实现复杂信道移动水声通信的帧同步。
4 结 语对于移动水声通信系统,利用帧同步信号进行精确多普勒估计是不可或缺的。本文在分析多普勒效应对水声通信信号影响的基础上,分别研究LFM信号、m序列信号、HFM信号3种帧同步方法,给出了各种方法的具体实现原理,针对AWGN信道和实测多途衰落信道,通过计算机仿真分析,分别从信噪比、信道特性、收发相对多普勒速度、计算复杂度等方面,全面对比分析了这3种帧同步方法在不同条件和应用环境的多普勒因子估计性能,明确了各方法的优缺点和可适用的应用场景。仿真结果表明,3种方法各有优势,均可适用不同的移动水声通信应用环境。但相对而言,HFM信号同步方法多普勒估计精度高、数据传输速率快、计算复杂度低、稳健性强,可以实现复杂信道移动水声通信的帧同步。研究结果可为水下各类无人航行器移动水声通信帧同步方法的具体选择和综合应用提供参考。
| [1] |
岳玲, 樊书宏, 冯西安. 鱼雷协同制导对水声通信能力的需求分析[J]. 水下无人系统学报, 2018, 26(5): 427-432. YUE L, FAN S H, FENG X A. Capability requirements analysis of underwater acoustic communication for torpedo cooperative guidance[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 427-432. |
| [2] |
SHARIF B S, NEASHAM J, HINTON O R. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE Journal of oceanic engineering, 2000, 25(1): 52-61. DOI:10.1109/48.820736 |
| [3] |
李云飞. 基于Zadoff-Chu序列的水声通信同步算法[D]. 上海: 上海交通大学, 2018.
|
| [4] |
岳玲, 樊书宏, 王明洲. 高速移动水声通信中的多普勒频移估计方法研究[J]. 系统仿真学报, 2011, 23(11): 2366-2370. |
| [5] |
何成兵, 黄建国, 孟庆微, 等. 水声多径信道多普勒因子精确估计方法[J]. 电声技术, 2010, 34(12): 57-59. |
| [6] |
王小阳, 郑思远, 李斌, 等. 基于AD变采样抑制多普勒的移动水声通信系统[J]. 水下无人系统学报, 2018, 26(5): 465-469. WANG X Y, ZHENG S Y, LI B, et al. Mobile underwater acoustic communication system based on AD variable sampling[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 465-469. |
| [7] |
李志舜. 鱼雷自导信号与信息处理[M]. 西安: 西北工业大学出版社, 2004: 143-149.
|
| [8] |
KHUC B, VYLEGZHANIN E, CHILINGAROV A, et al. Preamble signals for detection timing and Doppler synchronization in underwater acoustic communications[C]//International Youth Conference on Electronics, Telecommunications and Information Technologies, 2021: 683-698.
|
| [9] |
WANG K X, CHEN S M, LIU C Z, et al. Doppler estimation and timing synchronization of underwater acoustic communication based on hyperbolic frequency modulation signal[C]//2015 IEEE 12th International Conference on Networking, Sensing and Control, 2015: 75-80.
|
 2023, Vol. 45
2023, Vol. 45
