当前,随着降噪技术的发展,以及水下目标声反射强度的不断降低[1-2],使得水下目标定位的难度逐渐增加,单基地水下目标定位的精度不能满足其定位需求,为此可以联合多个测量平台组成多基地声呐定位系统,增加对目标的观测数据,实现联合定位。多基地声呐系统可分为[3-4]:一发多收型(T-Rn型)、多发一收型(Tn-R型)和多发多收型(T-Rn型),其中T-Rn型相比于另外2种具有结构简单、成本低,隐蔽性好的优点,因此研究T-Rn型多基地声呐系统更具有应用前景。在多个平台进行联合定位时,各个平台在接收观测信息后,不同平台产生的误差不一样,并且存在不知道其误差统计特性的情况,因此针对不同条件,为达到最优的定位误差,需要使用不同的线性优化算法。为此分析T-Rn型多基地声呐系统的定位算法,能够为未来的多平台联合定位提供参考,具有实际应用前景。本文主要对T-Rn型多基地声呐系统基于到达时间差定位(TDOA)信息进行水下目标定位的算法以及由此产生的定位误差进行研究,为此建立基于TDOA信息的多基地声呐系统的定位模型,分析系统中不同误差的具体表达式,推导在未知误差和已知误差条件下的最优线性算法,并给出不同算法定位误差的计算公式,最后利用仿真对理论结果进行验证和分析。
1 建立定位模型在多基地声呐定位系统中,接收站声呐的作用距离通常要远高于定位目标的深度[5],针对深度可通过测量其俯仰角确定,因此为简化问题只考虑二维空间的定位。由于是一发多收的定位系统,以发射站为原点建立基于TDOA信息的T-Rn型多基地声呐系统定位模型几何图如图1所示。
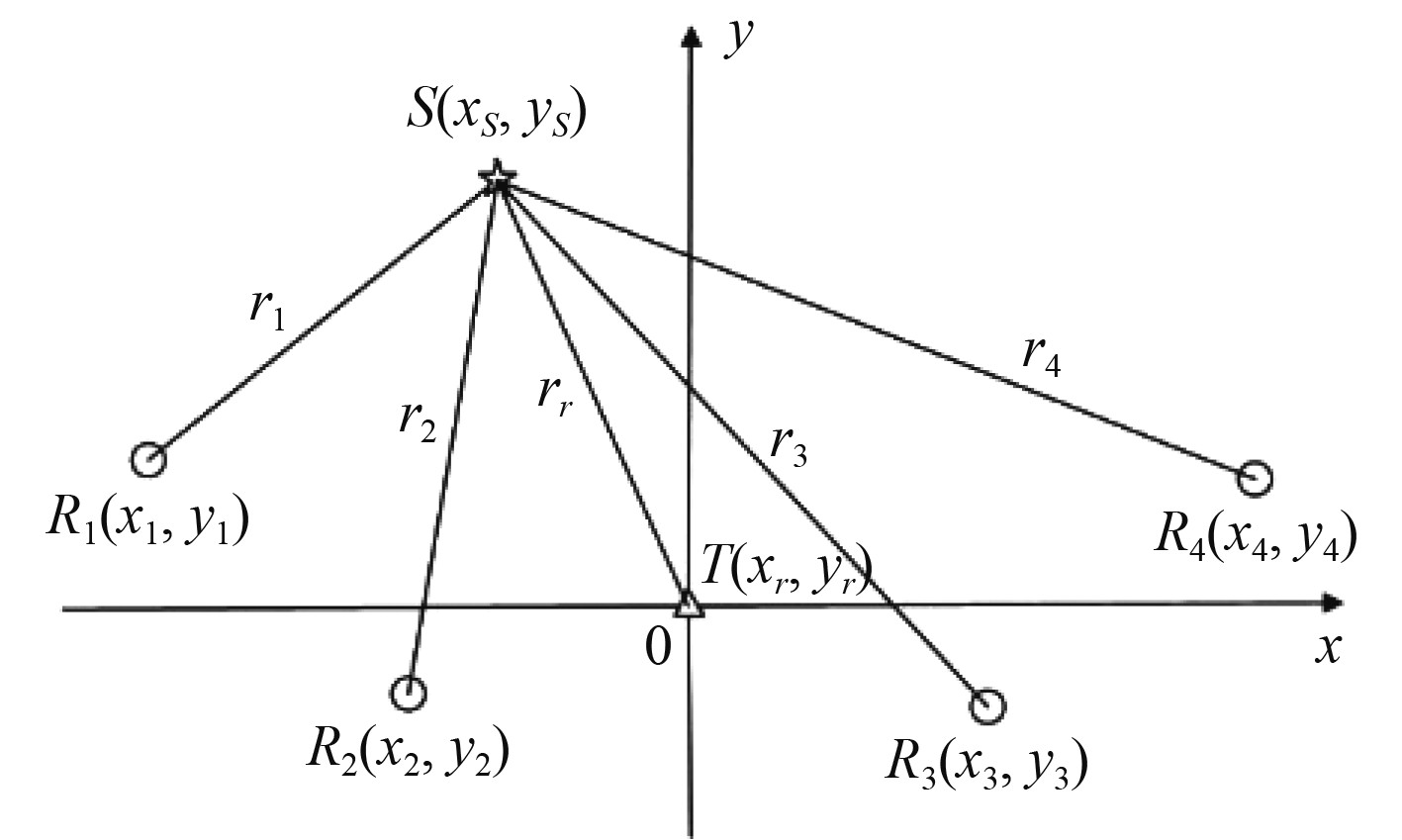
|
图 1 T-Rn型多基地声呐系统定位模型几何图 Fig. 1 Geometric diagram of positioning model of T-Rn multistatic sonar system |
在T-Rn型多基地声呐系统中,由1个发射站和n个接收站组成,发射站为发声声源,通常用T表示,其坐标为
建立基于TDOA信息的T-Rn型多基地声呐系统目标定位方程,假设有N个测量时延信息的接收站
| $ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} \sqrt {{{({x_1} - {x_S})}^2} + {{({y_1} - {y_S})}^2}} + \\ \sqrt {{{({x_T} - {x_S})}^2} + {{({y_T} - {y_S})}^2}} = c{t_1},\\ \end{gathered} \\ \vdots \\ \begin{gathered} \sqrt {{{({x_N} - {x_S})}^2} + {{({y_N} - {y_S})}^2}} + \\ \sqrt {{{({x_T} - {x_S})}^2} + {{({y_T} - {y_S})}^2}} = c{t_N}。\\ \end{gathered} \end{array}} \right. $ | (1) |
在实际定位过程中,其发射站、接收站的站址和接收时间都可能产生误差,因此需要对上述理想条件的定位方程作变换,因此作如下假设:
1)发射站及接收站站址误差分为X轴误差和Y轴误差;
2)所有误差均为先验信息,且为均值为0方差已知的相互独立的误差;
3)在通过时延信息计算距离时,声速保持不变。
通过以上假设,可以将上述理想定位方程化为带误差的定位方程:
| $ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} \sqrt {{{({x_1} + \Delta {x_1} - {x_S})}^2} + {{({y_1} + \Delta {y_1} - {y_S})}^2}} + \\ \sqrt {{{({x_T} + \Delta {x_T} - {x_S})}^2} + {{({y_T} + \Delta {y_T} - {y_S})}^2}}= \\ c({{\tilde t}_1} - \Delta {t_1}),\\ \end{gathered} \\ \vdots \\ \begin{gathered} \sqrt {{{({x_N} + \Delta {x_N} - {x_S})}^2} + {{({y_N} + \Delta {y_N} - {y_S})}^2}} + \\ \sqrt {{{({x_T} + \Delta {x_T} - {x_S})}^2} + {{({y_T} + \Delta {y_T} - {y_S})}^2}} = \\ c({{\tilde t}_N} - \Delta {t_N})。\\ \end{gathered} \end{array}} \right. $ | (2) |
其中,
由于在实际中各项误差很小,因此可以忽略其中二次项的误差,同时为计算方便,将发射站定为坐标原点,即有
| $ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} ({x_1} - {x_T}){x_S} + ({y_1} - {y_T}){y_S} - c{{\tilde t}_1}{r_{ST}} + {w_1} = \\ {{\left[ {r_1^2 - r_T^2 - {{(c{{\tilde t}_1})}^2}} \right]} \mathord{\left/ {\vphantom {{\left[ {r_1^2 - r_T^2 - {{(c{{\tilde t}_1})}^2}} \right]} 2}} \right. } 2},\\ \end{gathered} \\ \vdots \\ \begin{gathered} ({x_N} - {x_T}){x_S} + ({y_N} - {y_T}){y_S} - c{{\tilde t}_N}{r_{ST}} + {w_N} = \\ {{\left[ {r_N^2 - r_T^2 - {{(c{{\tilde t}_N})}^2}} \right]} \mathord{\left/ {\vphantom {{\left[ {r_N^2 - r_T^2 - {{(c{{\tilde t}_N})}^2}} \right]} 2}} \right. } 2} 。\\ \end{gathered} \end{array}} \right. $ | (3) |
其中:
1)观测时间误差
由于声源在水中传播时会有环境噪声和衰减[6],从而导致接收到的观测时间与实际观测时间有误差,用
| $ {w_{i\_\Delta t}} = ({r_{ST}} - c{\tilde t_i})\Delta t。$ | (4) |
2)接收站的站址误差
在多基地定位系统中,接收站所在的平台可能为水下固定节点、水中UUV或是水面船只调放的接收装置,其在水中位置不像在陆地或空中做到位置实时精确,同时不同平台其产生的误差也各不相同,用
| $ {w_{i\_R}} = ({x_S} - {x_i})\Delta {x_i} + ({y_S} - {y_i})\Delta {y_i},$ | (5) |
其中方程组中的每个
3)发射站址误差
发射站同接收站一样存在站址误差,用
| $ {w_{i\_T}} = \left({x_i} - {x_T} + \frac{{{x_S}c\tilde t}}{{{r_{ST}}}}\right)\Delta {x_T} + \left({y_i} - {y_T} + \frac{{{y_S}c\tilde t}}{{{r_{ST}}}}\right)\Delta {y_T},$ | (6) |
其中,
由此每个接收方程中的误差可以表示为:
| $ {w_i} = {w_{i\_\Delta t}} + {w_{i\_R}} + {w_T},$ | (7) |
将上述三元一次方程组化为矩阵形式:
| $ AX + W = G。$ | (8) |
其中:
上式即为基于TDOA信息的多基地T-Rn型多基地声呐系统目标定位模型。
2 定位算法及误差分析针对上述模型,要求解出目标的坐标,可分为线性方法和非线性方法。仅分析线性算法,其主要有3种,分别为最小线性二乘法(LLS)、加权最小线性二乘法(WLLS)和两步加权最小线性二乘法(2-WLLS),其定位精度也是逐渐提高。目标的定位误差主要是以定位精度的几何解释(GDOP)[7]表示,其可以作为衡量定位算法好坏的一个指标。
2.1 最小二乘法上述模型为线性矩阵,为求出目标的坐标,当只知道误差矩阵均值为零的随机分布,而其方差未知时,为求出无偏估计,则最小二乘法的解
| $ \begin{array}{*{20}{c}} {\min }&{{\varepsilon _{LLS}} = {{({\boldsymbol{A}}{{\boldsymbol{X}}_{LLS}} - {\boldsymbol{G}})}^{\rm{T}}}({\boldsymbol{A}}{{\boldsymbol{X}}_{LLS}} - {\boldsymbol{G}})} ,\end{array} $ | (9) |
据此可以求出
| $ {{\boldsymbol{X}}_{{\boldsymbol{LLS}}}} = {({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}})^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{G}},$ | (10) |
为分析该算法的定位精度好坏,可以用GDOP作为指标,其定义为:
| $ GDOP = \sqrt {E\left[ {{{({x_S} - {{\tilde x}_S})}^2} + {{({y_S} - {{\tilde y}_S})}^2}} \right]} ,$ | (11) |
其中,
| $ {\boldsymbol{X}} - {({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}})^{ - 1}}{\boldsymbol{AG}} = \left[ {{{({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}})}^{ - 1}}{\boldsymbol{AW}}} \right],$ | (12) |
代入上述根据最小二乘法得到的定位结果,即有:
| $ {\boldsymbol{X}} - {{\boldsymbol{X}}_{LLS}} = \left[ {{{({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}})}^{ - 1}}{\boldsymbol{AW}}} \right],$ | (13) |
根据上式,可以看出
| $ \begin{gathered} E\left[ {({\boldsymbol{X}} - {{\boldsymbol{X}}_{LLS}}){{({\boldsymbol{X}} - {{\boldsymbol{X}}_{LLS}})}^{\rm{T}}}} \right] = \\ {({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}})^{ - 1}}{\boldsymbol{A}} \cdot E({{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{W}}) \cdot {{\boldsymbol{A}}^{\rm{T}}}{({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{A}})^{ - 1}} ,\\ \end{gathered} $ | (14) |
设
| $ \left\{\begin{gathered} {P_{LLS,11}} = E\left[ {{{({x_S} - {x_{S\_LLS}})}^2}} \right],\\ {P_{LLS,22}} = E\left[ {{{({y_S} - {y_{S\_LLS}})}^2}} \right]。\\ \end{gathered}\right. $ | (15) |
所以有最小二乘法的GDOP为:
| $ GDO{P_{LLS}} = \sqrt {{P_{LLS,11}} + {P_{LLS,22}}}。$ | (16) |
由于上面的最小二乘法是在误差矩阵未知其方差时的最优线性解,而当已知误差矩阵的方差时,则可以将其利用起来构建加权最小二乘法,则加权最小二乘法的解
| $ \begin{array}{*{20}{c}} {\min }&{{\varepsilon _{WLLS}} = } {{{({\boldsymbol{A}}{{\boldsymbol{X}}_{WLLS}} - {\boldsymbol{G}})}^{\rm{T}}}{\boldsymbol{K}}({\boldsymbol{A}}{{\boldsymbol{X}}_{WLLS}} - {\boldsymbol{G}})} ,\end{array} $ | (17) |
其中,K为误差权值矩阵,根据参考文献[8]有:
| $ {\boldsymbol{K}} = {\left[ {E({{\boldsymbol{W}}^{\rm{T}}}{\boldsymbol{W}})} \right]^{ - 1}},$ | (18) |
据此可以求出
| $ {{\boldsymbol{X}}_{WLLS}} = {({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{KA}})^{ - 1}}{{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{KG}} ,$ | (19) |
利用同样的方式在定位模型的两边乘以
| $ GDO{P_{WLLS}} = \sqrt {{P_{WLLS,11}} + {P_{WLLS,22}}} 。$ | (20) |
其中,
在加权最小二乘法求出的自变量
| $ {{\boldsymbol{A}}_2}{{\boldsymbol{X}}_2} + {{\boldsymbol{W}}_2} = {{\boldsymbol{G}}_2}。$ | (21) |
其中:
| $ \begin{gathered} {{\boldsymbol{W}}_2} \approx {\rm{diag}}(2{x_{S\_WLLS}},2{y_{S\_WLLS}},2{r_{ST\_WLLS}}) \times \\ \left[ {\begin{array}{*{20}{c}} {{x_{S\_WLLS}} - {x_S}} \\ {{y_{S\_WLLS}} - {y_S}} \\ {{r_{ST\_WLLS}} - \sqrt {x_S^2 + y_S^2 + z_S^2} } \end{array}} \right],\\ \end{gathered} $ | (22) |
| $ {{\boldsymbol{K}}_2} = {\left[ \begin{gathered} {\rm{diag}}(2{x_{S\_WLLS}},2{y_{S\_WLLS}},2{r_{ST\_WLLS}}) \cdot \\ {({{\boldsymbol{A}}^{\rm{T}}}{\boldsymbol{KA}})^{ - 1}} \cdot \\ {\rm{diag}}(2{x_{S\_WLLS}},2{y_{S\_WLLS}},2{r_{ST\_WLLS}}) \\ \end{gathered} \right]^{ - 1}}。$ | (23) |
据此可以求出两步加权最小二乘法的定位结果为:
| $ \left\{ \begin{gathered} {{{\boldsymbol{\tilde X}}}_{2 - WLLS}} = \sqrt {{{({\boldsymbol{A}}_2^{\rm{T}}{{\boldsymbol{K}}_2}{{\boldsymbol{A}}_2})}^{ - 1}}{\boldsymbol{A}}_2^{\rm{T}}{{\boldsymbol{K}}_2}{{\boldsymbol{G}}_2}},\\ {x_{2 - WLLS}} = {\rm{sign}}({x_{WLLS}})\sqrt {{{{\boldsymbol{\tilde X}}}_{2 - WLLS}}(1)} ,\\ {y_{2 - WLLS}} = {\rm{sign}}({y_{WLLS}})\sqrt {{{{\boldsymbol{\tilde X}}}_{2 - WLLS}}(2)} 。\\ \end{gathered} \right. $ | (24) |
其中,
为求解两步加权最小二乘法的GDOP,在第2个线性方程组的两边乘以
| $ \left\{ {\begin{array}{*{20}{l}} {{\boldsymbol{H}} = {\rm{diag}}(2{x_{S\_2 - WLLS}},2{y_{S\_2 - WLLS}},2{z_{S\_2 - WLLS}})},\\ {GDO{P_{2 - WLLS}} = \sqrt {tr\left[ {{{({{\boldsymbol{H}}^{\rm{T}}}{\boldsymbol{A}}_2^{\rm{T}}{\boldsymbol{K}}{{\boldsymbol{A}}_2}{\boldsymbol{H}})}^{ - 1}}} \right]} } 。\end{array}} \right. $ | (25) |
其中,
分析可知,两步加权最小二乘法是在加权最小二乘法的基础上利用了自变量矩阵中的目标到发射站的距离信息,因此其性能也要优于加权最小二乘法。
2.4 影响算法优劣因素的分析通过分析利用信息的角度,得出了在未知误差分布时,线性二乘法为最优线性算法,在已知误差分布时,两步加权最小二乘法为最优算法。定义平均
| $ \overline {GDOP} = {{\sum\limits_{({x_i},{y_i}) \in S}^M {GDOP({x_i},{y_i})} } \mathord{\left/ {\vphantom {{\sum\limits_{({x_i},{y_i}) \in S}^M {GDOP({x_i},{y_i})} } M}} \right. } M}。$ | (26) |
其中:S为系统的定位区域;M为在定位区域内定位目标数目。
由于每个线性方程中的误差不同,同时根据前面对误差表达式的推导可以看出,在每个线性方程中的误差不仅与系统产生的误差有关,还与目标与发射站和接收站的距离有关,其距离越远,误差也越大,因此导致线性方程组中的误差分布不均匀,为衡量不均匀度,定义误差的平均值
| $ \left\{ {\begin{array}{*{20}{l}} {\overline w = {{\displaystyle\sum\limits_{i = 1}^N {{w_i}} } \mathord{\left/ {\vphantom {{\displaystyle\sum\limits_{i = 1}^N {{w_i}} } N}} \right. } N}},\\ {\eta = \displaystyle\sum\limits_{i = 1}^N {{{(1 - {{{w_i}} \mathord{\left/ {\vphantom {{{w_i}} {\overline w }}} \right. } {\overline w }})}^2}} } 。\end{array}} \right. $ | (27) |
通过对3个算法
为比较3种算法的优劣,以3个算法的
为分析观测时间误差对算法的影响,将4个接收站接收的观测时间误差分别设为:0.8 ms,3 ms,6 ms和9 ms并逐渐增加,图2为不同观测时间误差下3种算法的
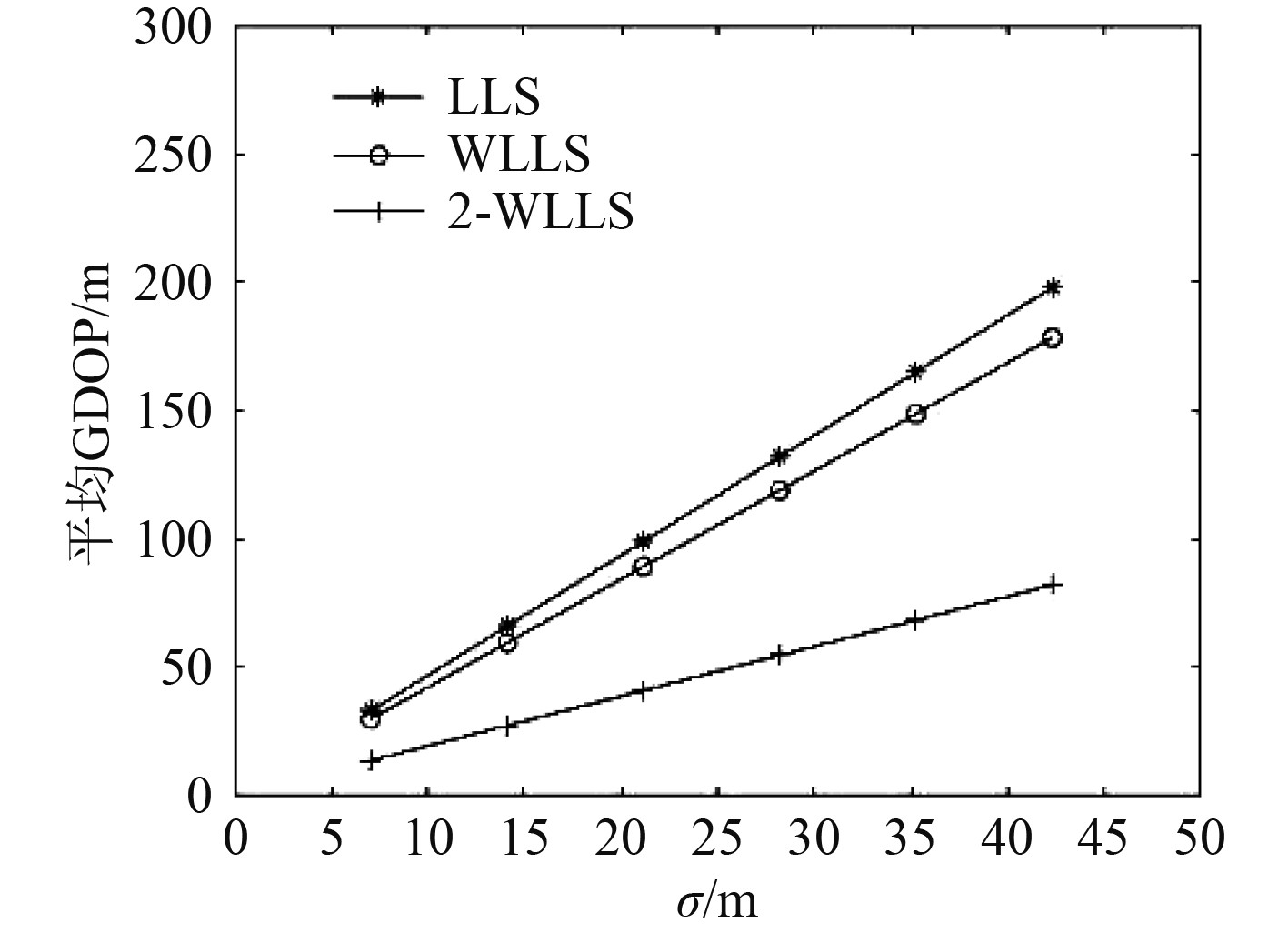
|
图 2
3种算法
|
可以看出:随着观测时间误差的增加,3种算法的
为与前面的观测时间误差比较,将每个接收站的站址误差设为和观测时间误差一致,分析接收站站址误差对算法的影响。将4个接收站的站址误差分别设为:1.2 m,4.5 m,9 m和13.5 m并逐渐增加,图3为不同接收站站址误差下3种算法
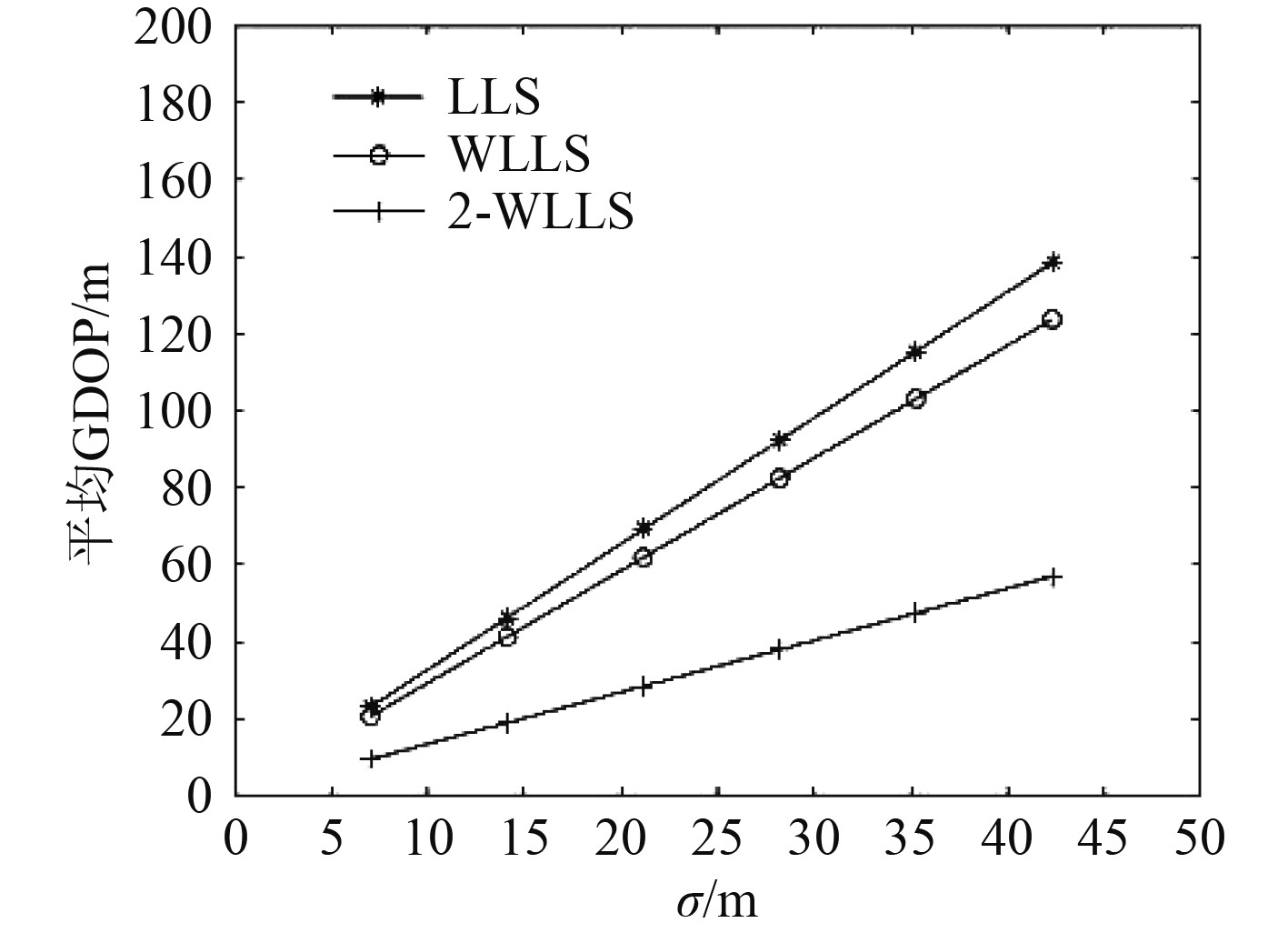
|
图 3
3种算法
|
可以看出:随着接收站站址误差的增加,3种算法的
为与前面的观测时间误差和接收站站址误差比较,分析发射站站址误差对算法的影响。将发射站的站址误差设为7.05m并逐渐增加。由于在T-Rn型多基地声呐系统中发射站只有一个,当误差仅为发射站站址误差时其
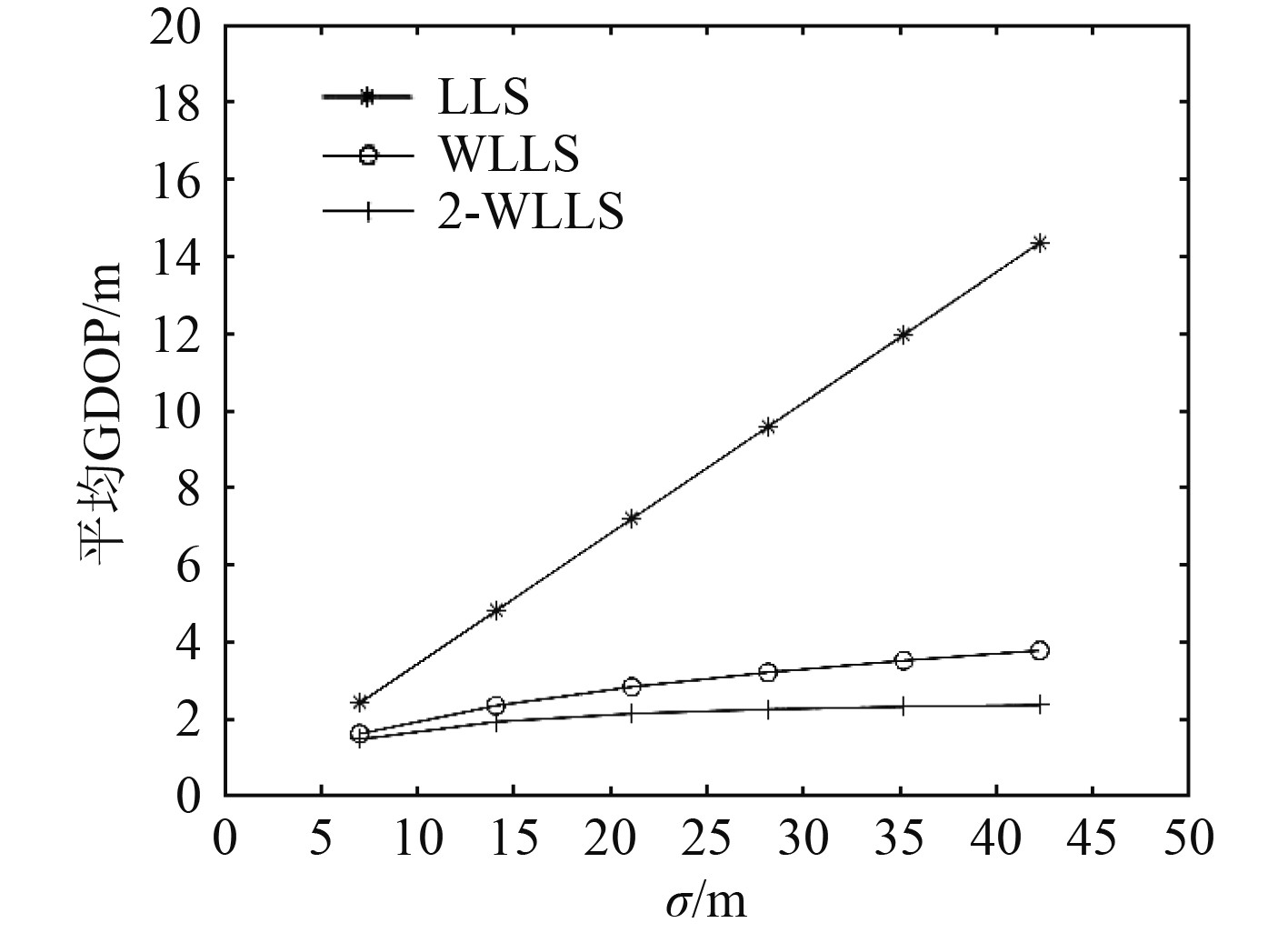
|
图 4
3种算法
|
可以看出:随着发射站站址误差的增加,3种算法的
根据仿真研究可以看出,观测时间误差对定位算法的影响最大,因此为分析误差不均匀对3种算法
|
|
表 1 参数设置 Tab.1 Parameter setting |
据此,得到3种算法的
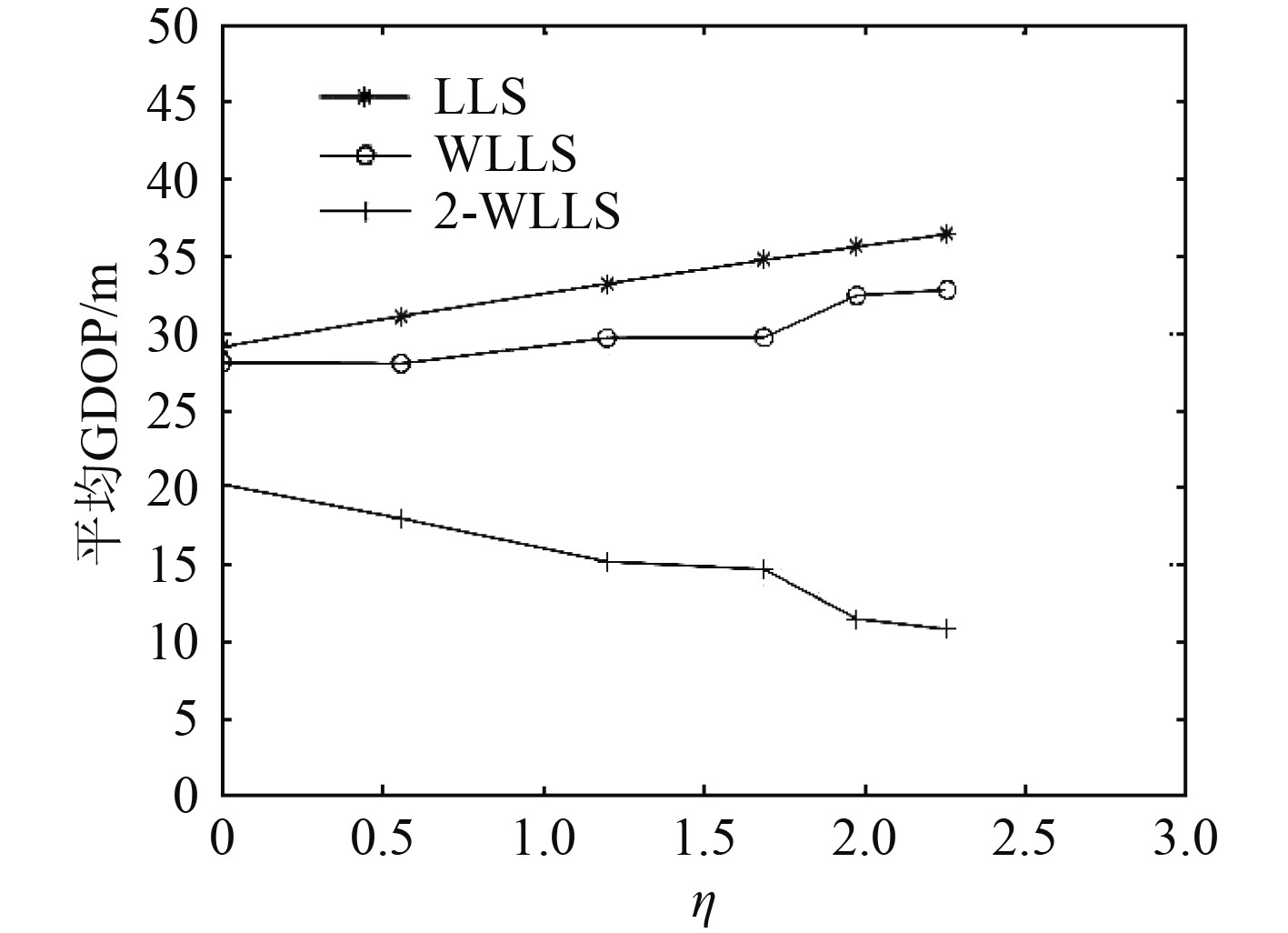
|
图 5
3种算法
|
本文建立T-Rn型多基地声呐的定位几何模型,在基于TDOA时间信息进行定位时,分析模型中存在的3种误差的计算公式,并根据模型分别推导了在未知误差信息和已知误差的条件下的最优线性算法以及相应的
| [1] |
CRAPARO E, KARATAS M. Optimal source placement for point coverage in active multistatic sonar networks[J]. Naval Research Logistics (NRL), 2020, 1-12. |
| [2] |
KUHN T U . Optimal sensor placement in active multistatic sonar networks[R]. Approved for Public release: Distribution is Unlimited, 2014.
|
| [3] |
EMC A, ARMIN F B, CHRISTOPHHOF, et al. Optimizing source and receiver placement in multistatic sonar networks to monitor fixed targets[J]. European Journal of Operational Research, 2019, 273(3): 816-831. |
| [4] |
徐景峰, 舒象兰, 韩树平, 等. T2-R型多基地声纳定位精度研究[J]. 兵工学报, 2014(7): 1052-1059. XU Jingfeng, SHU Xianglan, HAN Shuping, et al. Research on accuracy of localization algorithm for T2-R multistatic sonar[J]. Acta Armamentarii, 2014(7): 1052-1059. DOI:10.3969/j.issn.1000-1093.2014.07.018 |
| [5] |
李涛, 屈也频, 梅风华. 基于总体最小二乘的多基地声纳系统定位算法[J]. 探测与控制学报, 2015, 37(3): 2015,37(3):82-85. LI Tao, Qu Yepin, MEI Fenghua. Multistatic sonar space location algorithm based on total least squares method[J]. Journal of Detection & Control, 2015, 37(3): 2015,37(3):82-85. |
| [6] |
ROBERT J U. 水声原理(洪申, 译)[M]. 哈尔滨: 哈尔滨船舶工程学院出版社, 1990: 160−168.
|
| [7] |
张小凤. 双/多基地声呐定位及目标特性研究 [D]. 西安: 西北工业大学, 2003: 23−25.
|
| [8] |
SO H C. Handbook of Position Location: Theory, Practice, and Advances[M]. 2011: 90−110.
|
 2023, Vol. 45
2023, Vol. 45
