2. 福州大学 电气工程与自动化学院,福建 福州 350108;
3. 福建水口发电集团有限公司,福建 福州 350004
2. College of Electrical Engineering and Automation, Fuzhou University, Fuzhou 350108, China;
3. Fujian Shuikou Power Generation Group Co., Ltd., Fuzhou 350004, China
面对国际环保战略的不断推进,航海业的减排脱碳重任迎来了新挑战[1]。电动船舶作为船舶动力从传统柴油转向清洁能源的有效手段,是船舶行业实现“双碳”目标的必然趋势,同时也是未来船舶动力革新的重要途径。随着碳排放指标的提升,未来纯电动船舶的需求将不断扩大[2-3]。截至2021年底,全国拥有水上运输船舶12.59万艘,未来纯电动船舶的推广应用,将改变水运产业的能源结构[4]。
尽管电动船舶在安全、质保、环保、节能等方面有显著的发展潜力,但也存在着动力电池初装费用及运维费用高、船舶长时间靠岸充电导致运行效率低、占用岸线资源滞缓水运行业经济发展等阻碍。为改进靠岸充电的传统模式,目前正推行一种“船电分离、换电租赁”的新思路,该运营模式下,动力电池做成了可移动的模块化集装箱式,并采用换装方式为船舶提供电池动力。因此,船舶用户不再需要花费大量时间占据岸线资源等待电池充电,在一定程度上解决了岸线交通资源分配紧张问题。同时可移动的更换方式有利于缩短换电操作时间,可以有效提高船舶的运营效率和动力电池利用率。但由于电动船舶可携带动力电池数量有限,若充换电站配置电池数量过多,将导致部分电池使用率降低;反之,充换电站配置电池数量太少,将无法满足船舶用户的换电需求。因此采取合理的规划方案进而避免动力电池使用率分配不均将成为推动电动船舶发展的关键性问题之一。
目前,关于电动船舶的发展已经有了一定的研究。李振兴等[5]采用纵倾优化减少电动船舶的航行阻力,进而延长续航里程,减少充电次数。裴宝浩等[6]设计了一种结合氢燃料电池技术的电动船舶,详细研究了其动力系统的整体设计、仿真测试等。李利杰等[7]提出增加燃料电池、电动机等动力来源来提高能量转化率,通过建立动力系统和控制电路模型优化混合动力系统的能量配置。张晋源等[8]利用模型预测提前设置相关调度策略,以增大风电利用率为目标减轻电动船舶充电对电网造成的扰动。王伟等[9]建立了纯电动船舶直流并网配电系统主电路等效仿真模型,提出一种保护纯电动船直流并网短路的方法。孙士茼等[10]提出兼顾电能质量与能源消耗的海岛微电网船舶充电站多目标规划模型,考虑以化石能源耗量最小为目标规划充电站的选址定容。
然而,在上述文献中,其研究内容多是以电动船舶靠岸充电为背景下的传统运营模式,未能从船电分离的角度考虑电动船舶的发展。相比之下,张文芬等[11]提出了一种船电分离的动力电池充换电运营管理模式,从船舶运行效率、经济效益和社会效益等3个方面分析了新型运营模式的优势,但忽略了对岸线充换电站的选址布局以及站内配置的动力电池箱数量进行优化。
针对上述研究存在的不足,本文建立船电分离新型运营模式下的电动船舶充换电站选址定容优化模型,该模型综合考虑充换电站一体化的位置规划、充换电站内集装箱式动力电池的数量配置,在满足船舶航行情况的基础上优化船舶充换电站选址定容,提高动力电池利用率。
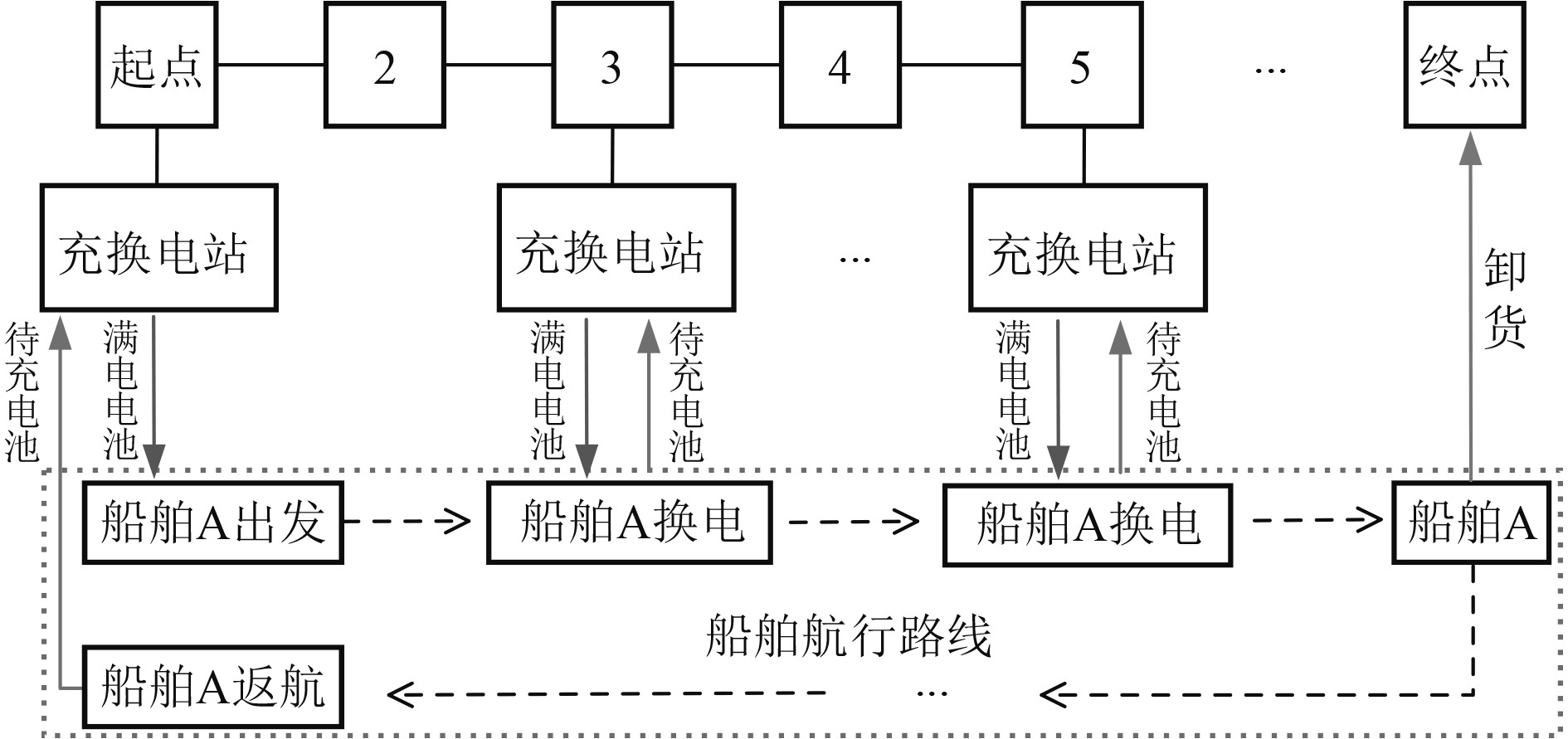
1 基本原理船用集装箱式动力电池运营模式,是指船舶不配备固定电池动力组,而是将电池组做成可移动的集装箱式动力电池,其运营模式示意图如图1所示。
|
图 1 集装箱式动力电池运营模式示意图 Fig. 1 Schematic diagram of the operation mode of containerized battery |
图中数字表示各个站点的编号,船舶从起点充换电站携带电池箱出发,航行途中船东根据船舶电池相剩余电量选择是否更换动力电池,当电量不足时,船舶航行至充换电站直接更换动力电池,无需长时间等待电池充电,可快速续航。考虑到调运时间过长影响电池箱供给效率,因此更换后的待充电池多在电站附近完成充电,实现充换电模式一体化。此外,由于租赁模式下电池箱归充换电站所有,船舶返航后使用完的电池箱需要归还给充换电站。
电动船舶充换电站一体化的位置规划和充换电站内集装箱式动力电池的数量配置同时还应保证船舶的航运条件及需求,因此需要设置相应的约束模拟船舶运行情况。首先模型综合考虑船舶换电需求、船舶出发时间、各航线站点间距、岸线充换电站规划建设数量、航运需求等因素,然后设置充换电站选址布局约束、充换电站配置动力电池箱数量约束、充换电站可用动力电池箱数量状态约束、船舶航行状态约束、船舶动力电池可用电量状态约束、船舶更换电池决策等约束,最后求解优化模型获得最佳的充换电站布局位置和充换电站内配置的动力电池箱数量。
2 模型建立 2.1 目标函数本文在保证船舶航运需求的前提下,通过构建新型运营模式下充换电站的选址定容优化模型,计算充换电站内配置船用可移动电池箱的最优数量,以提高航运过程动力电池箱的利用率,其目标函数为最小化动力电池箱数量
| $ \min F = \sum\limits_{m = 1}^{{N_{\text{C}}}} {(N_m^{{{PB}}}} )。$ | (1) |
式中:
1)充换电站最大可建设电池箱数量约束
| $ 0 \leqslant N_m^{{{PB}}} \leqslant N_{}^{{{PB,{\rm{max}}}}} ,$ | (2) |
式中,
2)充换电站动力电池箱可用数量状态约束
式(3)表示起点充换电站动力电池箱可更换数量的状态约束,船舶出发前只有装设电池箱的操作,没有卸下的更换操作;式(4)表示航途中充换电站的动力电池箱在更换完并满充后可再次投入使用;式(5)表示充换电站可更换电池数量的上下限约束。
| $ M_{1,t}^{{{PB}}} = M_{1,t - 1}^{{{PB}}} - \sum\limits_{n = 1}^{N_{\text{S}}^{}} {\sum\limits_{i = 1}^{{N_{\text{G}}}} {\left( {W_{1,n,i,t}^{}} \right)} },$ | (3) |
| $ M_{m,t}^{{{PB}}} = M_{m,t - 1}^{{{PB}}} - \sum\limits_{n = 1}^{{N_{\text{S}}}} {\sum\limits_{i = 1}^{{N_{\text{G}}}} {(W_{m,n,i,t}^{})} } + \sum\limits_{n = 1}^{{N_{\text{S}}}} {\sum\limits_{i = 1}^{{N_{\text{G}}}} {(W_{m,n,i,t - T_{{{PB}}}^{\text{C}} - T_{{{PB}}}^{{R}}}^{})} },$ | (4) |
| $ 0 \leqslant M_{m,t}^{{{PB}}} \leqslant N_m^{{{PB}}}。$ | (5) |
式中:
3)船舶航行约束
式(6)表示船舶航行距离约束;式(7)表示船舶开/停船约束;式(8)表示船舶的航行时长要满足一定时间才能被认定为完成一次货运输送;式(9)和式(10)表示船舶到达终点的状态约束;式(11)表示船舶到达终点后卸货停船的决策约束;式(12)表示船舶最短停泊时间需要满足卸装货物时间或者换电时间;式(13)表示船舶返航回到起点的状态约束;式(14)和式(15)表示船舶在航行过程不能无故停船,其中,式(14)表示船舶只有在更换电池、到达终点卸装货物或者返航回到起点时可进行停船决策,式(15)表示船舶完成卸货或者更换完电池箱后应立即航行。
| $ D_{n,t}^{} = D_{n,t - 1}^{} + U_{n,t - 1}^{}{V_n}\Delta t,$ | (6) |
| $ U_{n,t}^{} = U_{n,t - 1}^{} + U_{n,t}^{{{on}}} - U_{n,t}^{{{off}}},$ | (7) |
| $ \sum\limits_{t = {T_{{\text{S,}}n}}}^{{N_{{T}}}} {U_{n,t}^{}} = \alpha, $ | (8) |
| $ {D_{n,t}}{Q_{n,t}}{\kern 1pt} = ({H_{{{TR}}}}/2){\kern 1pt} {Q_{n,t}}, $ | (9) |
| $ \sum\limits_{t = 1}^{{N_{{T}}}} {{Q_{n,t}}} = 1 ,$ | (10) |
| $ U_{n,t}^{{{off}}} \geqslant Q_{n,t}^{},$ | (11) |
| $ \left\{ \begin{gathered} {U_{n,t}} \leqslant 1 - \sum\limits_{\tau = 1}^{T_{{S}}^{{P}}} {Q_{n,t - \tau }^{}} ,\\ {U_{n,t}} \leqslant 1 - \sum\limits_{\tau = 1}^{T_{{{PB}}}^{{R}}} {W_{m,n,i,t - \tau }^{}}。\\ \end{gathered} \right. $ | (12) |
| $ {D_{n,t}}{Y_{n,t}}{\kern 1pt} = {H_{{{TR}}}}{Y_{n,t}},$ | (13) |
| $ U_{n,t}^{{{off}}} \leqslant \sum\limits_{i = 1}^{{N_{{G}}}} {W_{m,n,i,t}^{}} + {Q_{n,t}} + {Y_{n,t}},$ | (14) |
| $ \left\{ \begin{gathered} {U_{n,t}} \geqslant U_{n,t - T_{{{PB}}}^{{R}}}^{{{off}}} - Q_{n,t - {T_{\min }}}^{} - {Y_{n,t{\text{ - }}T_{{{PB}}}^{{R}}}} ,\\ {U_{n,t}} \geqslant Q_{n,t - {T_{\max }}}^{} ,\\ {T_{\min }} = \min \left\{ {T_{{{PB}}}^{{R}},T_{{S}}^{{P}}} \right\},{T_{\max }} = \max \left\{ {T_{{{PB}}}^{{R}},T_{{S}}^{{P}}} \right\} 。\\ \end{gathered} \right. $ | (15) |
式中:
4)船舶动力电池约束
式(16)表示船舶动力电池可用电量状态约束;式(17)表示船舶电池可用电量的上下限约束;式(18)~式(20)表示船舶更换电池决策约束,其中,式(18)~式(19)表示船舶在到达充换电站所在站点时才可进行更换电池的决策,式(20)表示船舶更换电池与船舶航行的互斥约束。
| $ S_{n,t}^{{{PB}}} \leqslant S_{n,t - 1}^{{{PB}}} - U_{n,t - 1}^{}{\beta _n}\Delta t + {\kern 1pt} {\kern 1pt} \left( {\sum\limits_{m = 1}^{{N_{\text{C}}}} {\sum\limits_{i = 1}^{{N_{\text{G}}}} {W_{m,n,i,t - 1}^{}} } } \right) \cdot \gamma ,$ | (16) |
| $ 0 \leqslant S_{n,t}^{{{PB}}}{\kern 1pt} \leqslant {N_{\text{G}}} \cdot {\kern 1pt} {\kern 1pt} \gamma ,$ | (17) |
| $ \left\{ \begin{gathered} {D_{n,t}}W_{m,n,t}^{{S}} = \left(\sum\limits_{q = 1}^{{N_Z}} {{A_{m,q}}{H_q}}\right) W_{m,n,t}^{{S}},\\ {D_{n,t}}W_{m,n,t}^{{R}} = \left(\sum\limits_{q = {N_Z}}^{2{N_Z} - 1} {{A_{m,q}}{H_q}}\right) W_{m,n,t}^{{R}}。\\ \end{gathered} \right. $ | (18) |
| $ W_{m,n,i,t}^{} \leqslant W_{m,n,t}^{{S}}{\text{ + }}W_{m,n,t}^{{R}},$ | (19) |
| $ U_{n,t}^{}{\text{ + }}W_{m,n,i,t}^{} \leqslant 1。$ | (20) |
式中:
式(9)、式(13)、式(18)中,
| $ \left\{ \begin{gathered} Q{Q_{n,t}} \leqslant M \cdot {Q_{n,t}},\\ Q{Q_{n,t}} \leqslant {D_{n,t}},\\ Q{Q_{n,t}} \geqslant {D_{n,t}} - M(1 - {Q_{n,t}}) ,\\ Q{Q_{n,t}}{\text{ = }}({H_{{{TR}}}}/2){Q_{n,t}}。\\ \end{gathered} \right. $ | (21) |
| $ \left\{ \begin{gathered} Y{Y_{n,t}} \leqslant M \cdot {Y_{n,t}},\\ Y{Y_{n,t}} \leqslant {D_{n,t}},\\ Y{Y_{n,t}} \geqslant {D_{n,t}} - M(1 - {Y_{n,t}}),\\ Y{Y_{n,t}}{\text{ = }}{H_{{{TR}}}}{Y_{n,t}}。\\ \end{gathered} \right. $ | (22) |
| $ \left\{ \begin{gathered} WW_{m,n,t}^{{S}} \leqslant M \cdot W_{m,n,t}^{{S}},\\ WW_{m,n,t}^{{S}} \leqslant {D_{n,t}} ,\\ WW_{m,n,t}^{{S}} \geqslant {D_{n,t}} - M(1 - W_{m,n,t}^{{S}}),\\ AA_{m,n,t}^{{S}} \leqslant M \cdot W_{m,n,t}^{{S}} ,\\ AA_{m,n,t}^{{S}} \leqslant \sum\limits_{q = 1}^{{N_Z}} {{A_{m,q}}{H_q}} ,\\ AA_{m,n,t}^{{S}} \geqslant \sum\limits_{q = 1}^{{N_Z}} {{A_{m,q}}{H_q}} - M(1 - W_{m,n,t}^{{S}}),\\ WW_{m,n,t}^{{S}} = AA_{m,n,t}^{{S}} 。\\ \\ \end{gathered} \right. $ | (23) |
| $ \left\{ \begin{gathered} WW_{m,n,t}^{{R}} \leqslant M \cdot W_{m,n,t}^{{R}},\\ WW_{m,n,t}^{{R}} \leqslant {D_{n,t}},\\ WW_{m,n,t}^{{R}} \geqslant {D_{n,t}} - M(1 - W_{m,n,t}^{{R}}) ,\\ AA_{m,n,t}^{{R}} \leqslant M \cdot W_{m,n,t}^{{R}},\\ AA_{m,n,t}^{{R}} \leqslant \sum\limits_{q = {N_Z}}^{2{N_Z} - 1} {{A_{m,q}}{H_q}} ,\\ AA_{m,n,t}^{{R}} \geqslant \sum\limits_{q = {N_Z}}^{2{N_Z} - 1} {{A_{m,q}}{H_q}} - M(1 - W_{m,n,t}^{{R}}),\\ WW_{m,n,t}^{{R}} = AA_{m,n,t}^{{R}} 。\\ {\kern 1pt} {\text{ }} \\ \end{gathered} \right. $ | (24) |
式中:
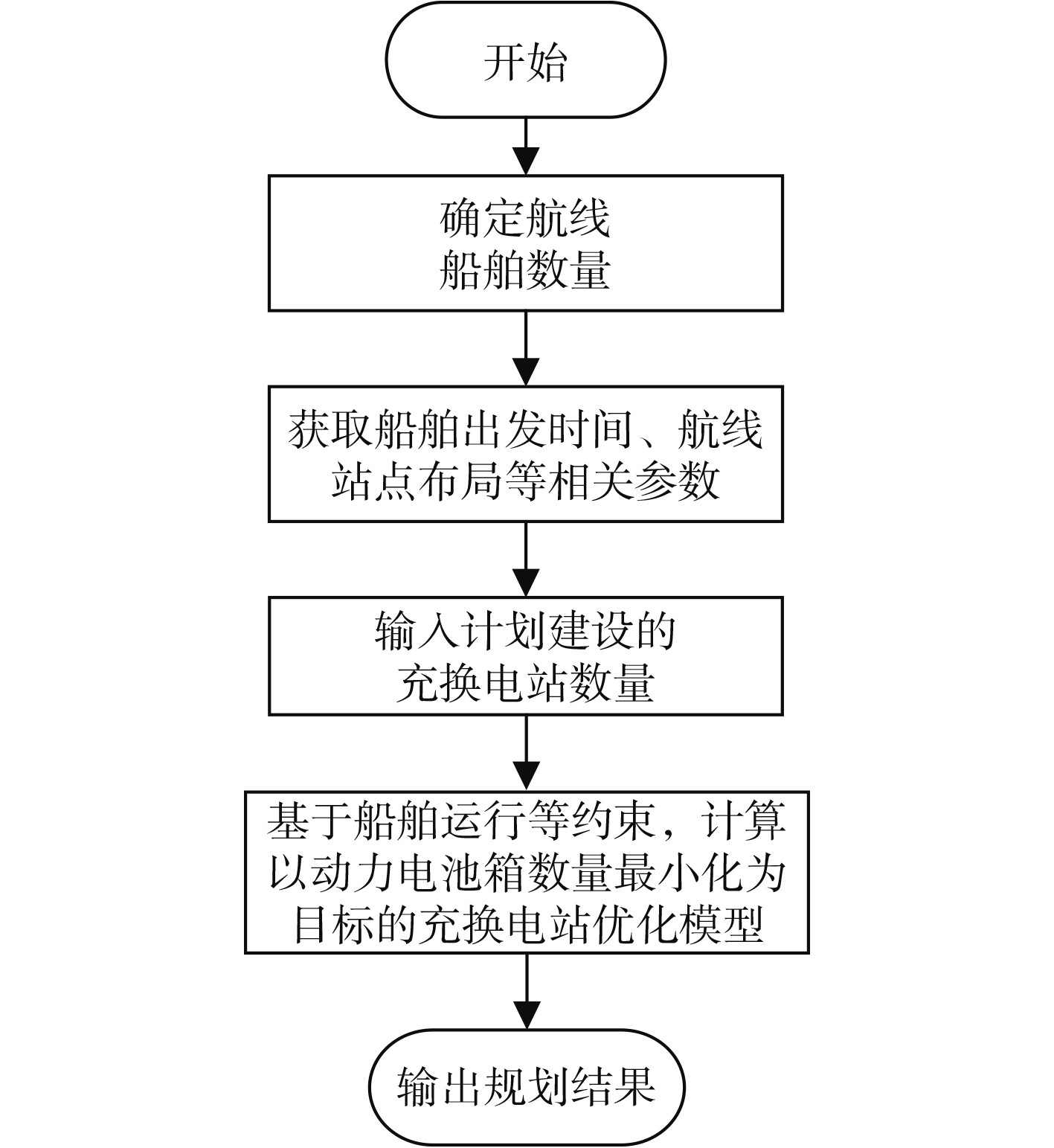
线性化处理后的模型为混合整数线性规划模型,因此可采用Matlab调用GUROBI的方法求解不同变量在约束范围内的目标最小值,实现充换电站模型的优化。模型求解的流程图如图2所示。
|
图 2 充换电站模型求解流程图 Fig. 2 Flow chart of solving the charging and replacing station model |
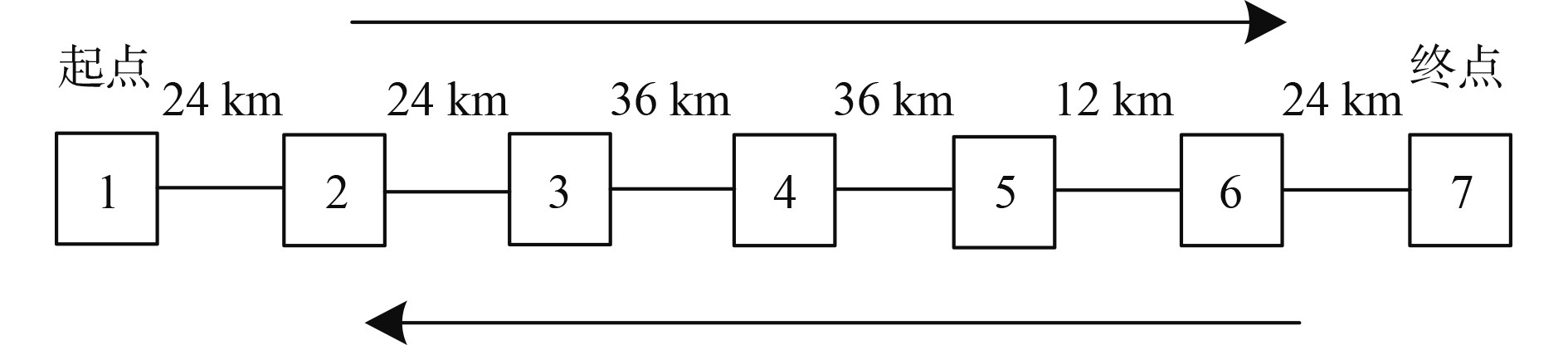
为了验证本文所提优化模型的可行性,对图3所示的航线站点拓扑图进行充换电站的选址定容规划。设定图3航线同时运输的在线船舶通常为21艘,船上最多可搭载2个标准20英尺集装箱动力电池,单个电池容量为1000 kWh,可用电量为800 kWh。设定船舶在目标航线上匀速航行,平均航速为12 km/h,船舶每小时耗电120 kWh,则按照图3航线距离船舶完成一次往返需要航行26 h。其他参数为:
|
图 3 航线站点拓扑图 Fig. 3 Ship station topology |
基于给定参数,考虑21艘船舶在2点同时出发的场景并设置以下2种方案:方案1不采用本文优化模型,按照船舶耗尽电量才更换电池的传统规划思路建设充换电站,计划建设2个充换电站;方案2采用本文优化模型,计划建设2个充换电站。2种方案的规划结果如表1所示。
|
|
表 1 两种方案充换电站选址定容规划结果 Tab.1 Planning results of location and capacity of charging and replacing stations in two cases |
方案1中,船舶出发时携带的2个动力电池箱可用电量为1600 kWh,能够续航13.3 h,即可航行13 h到达终点站点7后更换2个动力电池箱再返航回到起点,充换电站总共需要配置84个动力电池箱;方案2中,采用优化模型后,航途中的充换电站电池箱数量减少了一半。
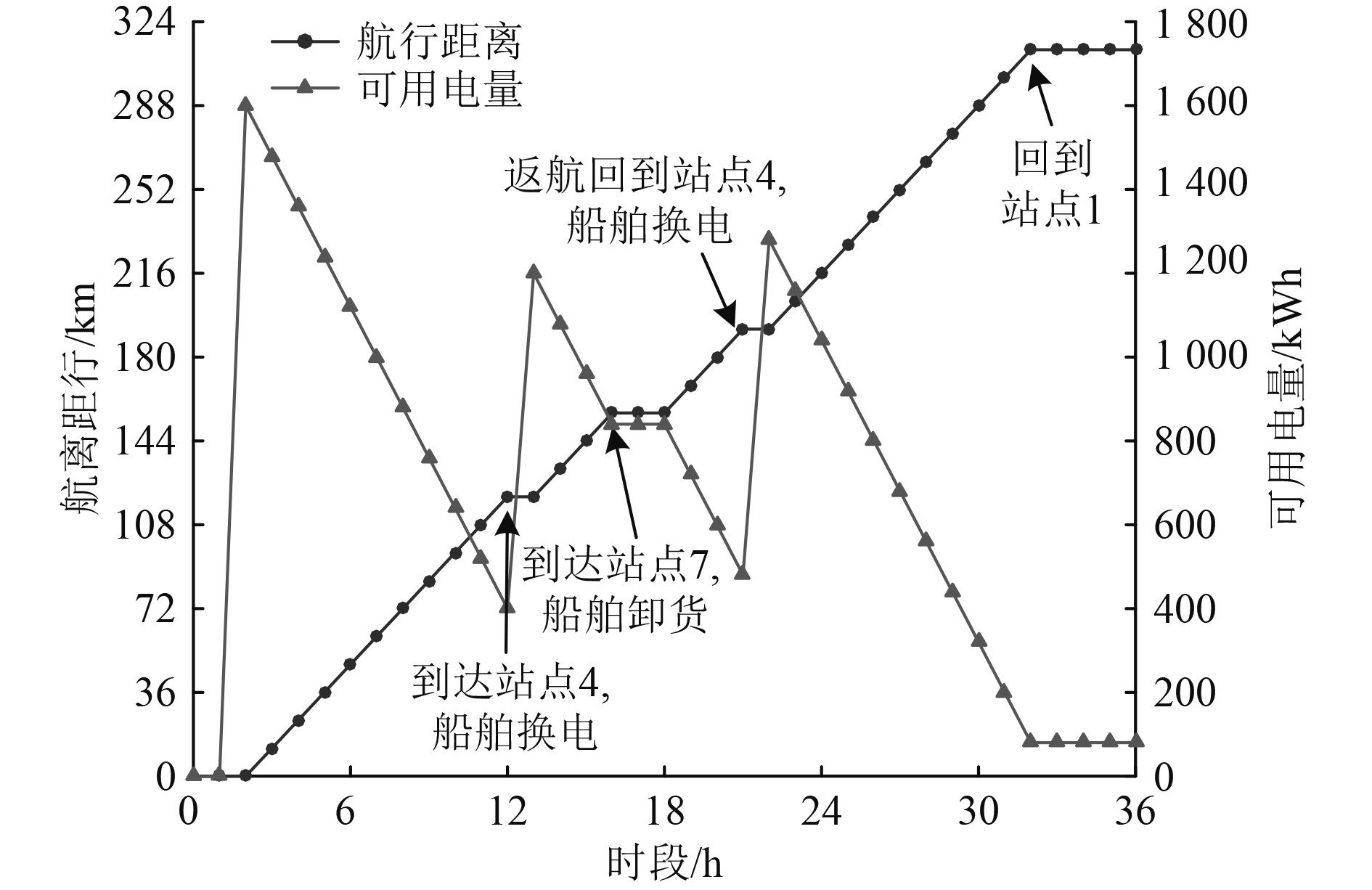
为分析方案2船舶航行过程电池耗量及电池箱更换决策,图4给出了方案2中其中1艘船舶航行距离变化与船内电池可用电量状态变化曲线,图5给出了充换电站动力电池箱可用数量变化曲线。
|
图 4 方案2船舶航行距离与电池电量状态变化图 Fig. 4 Schematic diagram of ship sailing distance and battery state change in case 2 |
|
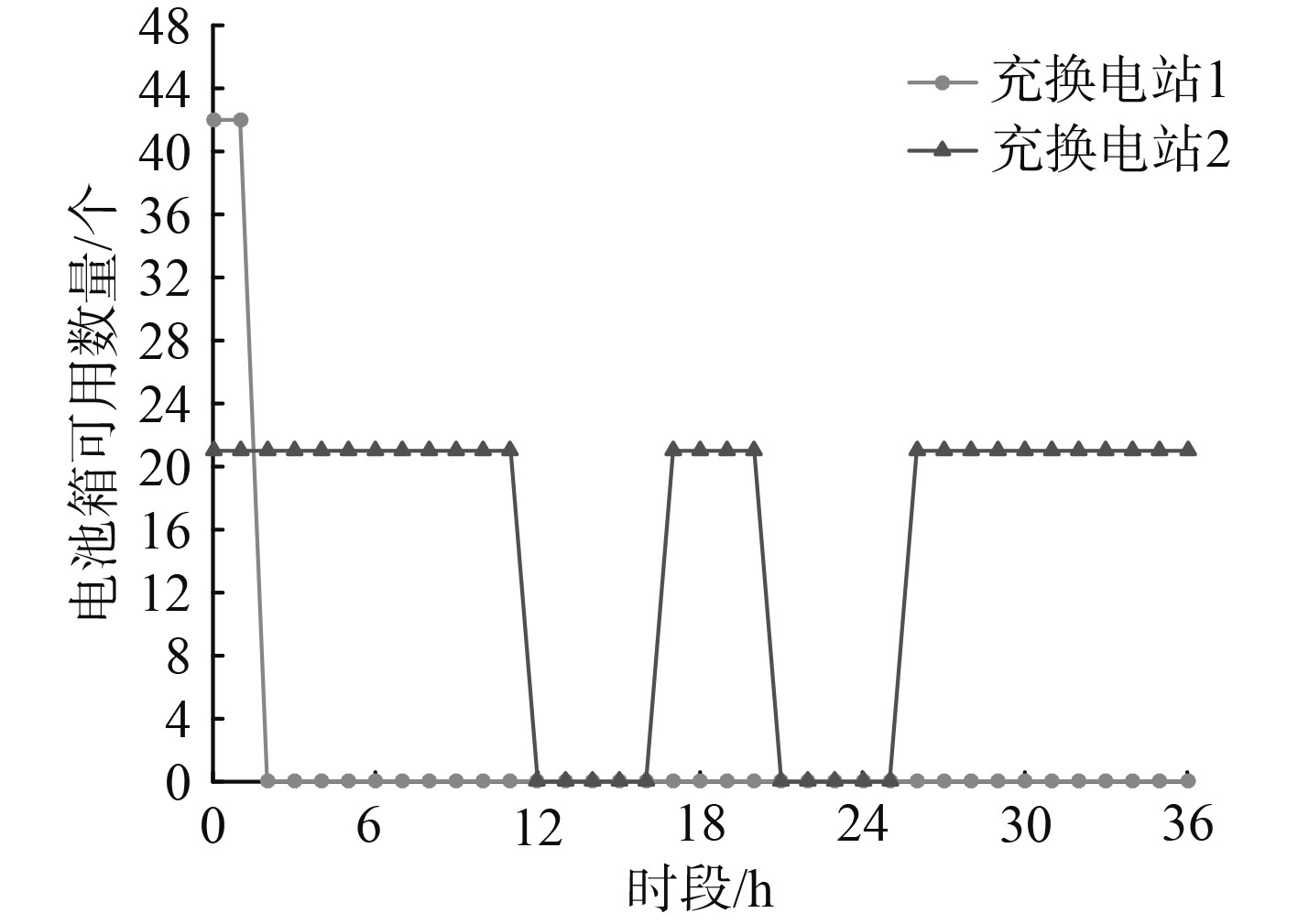
图 5 方案2动力电池箱可用数量变化图 Fig. 5 Variation diagram of available quantity of battery in case 2 |
由图4可知,方案2中船舶航行10 h后到达站点4,剩余可用电量400 kWh,此时船舶更换1个动力电池,经过1 h换电时间后,可用电量为1200 kWh,航行3 h到达终点开始卸货,返航过程到达站点4更换一个动力电池再继续航行10 h回到起点,完成整个运输的往返过程。此外,电池箱最小化的目标引导还能限制船舶的换电次数,船舶在航行过程有电量需求时才可进行换电,由图4电量曲线变化可知,船舶仅更换了4个电池箱,即刚好满足航行需求的电池电量。
由图5可知,方案2中船舶在12时更换的动力电池,经过1 h的换电与4 h的充电又可以投入使用,能够提供给返航过程的船舶,配置在站点4的同一批电池箱得到了二次利用,通过提高电池箱的利用率来减少电池箱的配置数量。
3.3 敏感性分析1)船舶错峰出行对规划的影响
船舶的错峰出行会错开电池箱的换充,实现电池箱的循环使用,从而减少动力电池箱的配置数量。设置3个场景分析船舶出发时间对规划的影响,各场景船舶的出发时间见表2。
|
|
表 2 船舶出发时间情况 Tab.2 Ship departure time |
按照优化模型,计算得到3个场景均计划建设3个充换电站的优化结果如表3所示。
|
|
表 3 建设三个充换电站选址定容优化结果 Tab.3 Optimization results of location and capacity for the three charging and replacing stations |
由表3可知,场景2电池箱的总数量相比场景1减少了6个,这是因为2点出发的3艘船舶在站点2和站点4更换完3个电池箱经过4 h的充电后,可提供给7点出发的3艘船舶,从而节省了电池箱的配置数量。说明当船舶错开出行的时间长于电池充换电时间时,船舶交替使用电池箱将有利于减少充换电站配置的电池箱数量;场景3中2点和7点出行的船舶数量增多,充换电站配置的电池箱数量继续减少,说明错开出行的船舶数量越多,动力电池箱减少的幅度也越明显。
2)充换电站建设数量对规划的影响
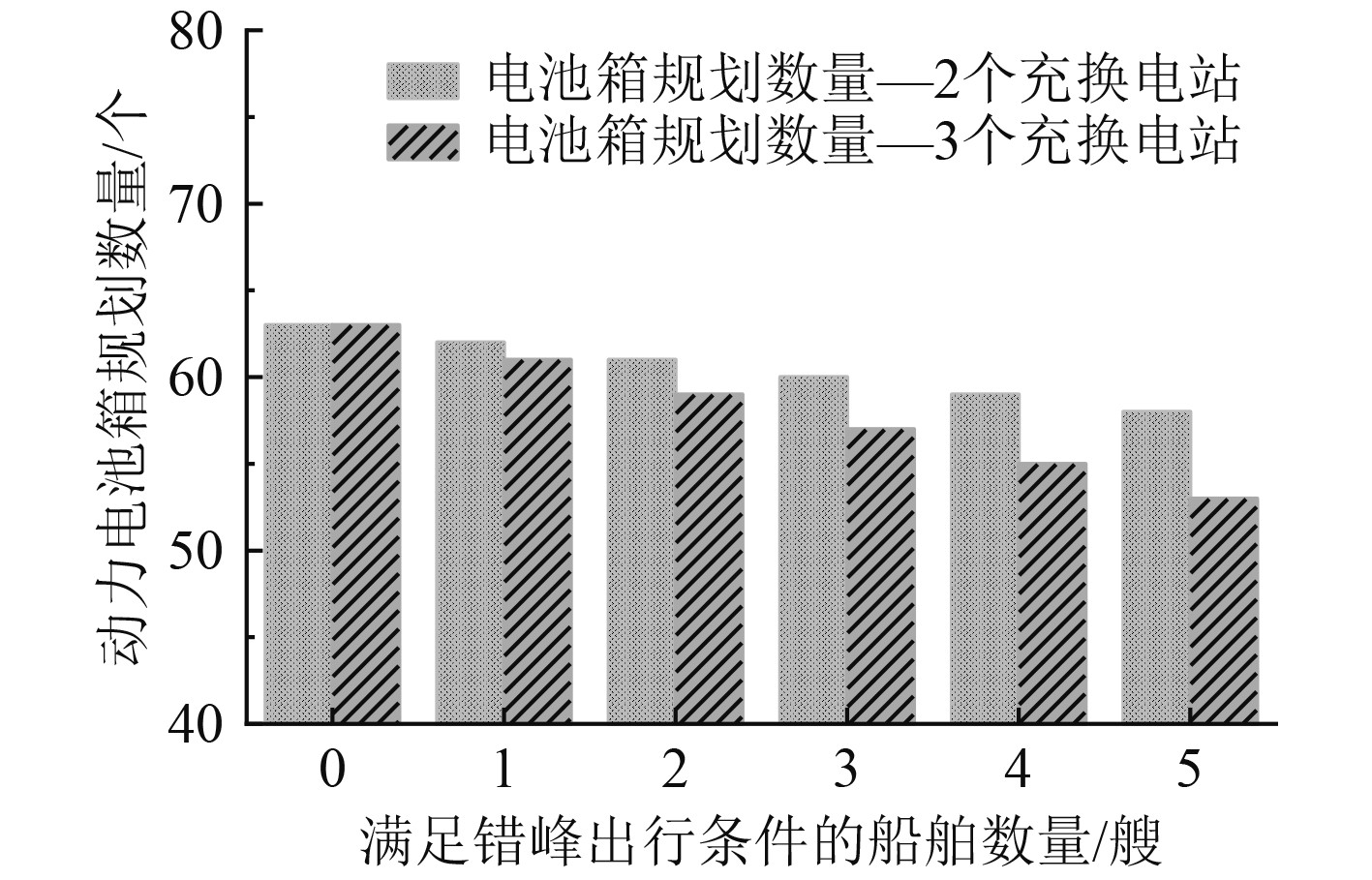
为分析不同充换电站数量对规划的影响,图6展示了建设2个充换电站和3个充换电站对动力电池箱整体数量的情况变化。其中横坐标满足错峰出行条件的船舶是指出发相差的时间不短于电池箱充换电时间对应的船舶。
|
图 6 不同充换电站动力电池箱数量变化图 Fig. 6 Changes in the number of battery for different charging and replacing stations |
航线建设2个充换电站时,如果航途中的充换电站设置在站点2或站点3,船舶到达该站点时更换的2个电池箱则无法实现返航;如果航途中的充换电站设置在4~7中的一个,则出发时必须携带2个电池箱才可到达站点进行更换。因此航线建设2个充换电站的情况下,起始站点必须要满足船舶携带2个动力电池,即站点1需要配置42个电池箱。相比建设3个充换电站,船舶可以在出发时只携带1个动力电池,并在航途中灵活更换电池补充电量,不仅可以减少起始站点配置的电池箱数量,而且可以通过充电的再利用减少航途充换电站的电池箱数量。由图6可知,随着满足错峰出行条件的船舶数量增加,建设3个充换电站的电池箱数量不断减少,其中,满足错峰出行条件的船舶数量为5艘时,建设3个充换电站的电池箱数量比建设2个减少了5个。
4 结 论基于新型电动船舶运营模式,本文提出一种电动船舶充换电站选址定容的优化方法,所得结论如下:
1)所构建的模型能够优化充换电站的选址布局以及动力电池箱的规划数量,从而提高动力电池箱利用率。当所有的船舶同时出发时,采用本文优化模型建设2个充换电站的方案相比传统规划方案,电池箱规划总数减少了50%;
2)船舶错峰出行交替使用电池箱将有利于减少充换电站配置的电池箱数量,同时错开出行的船舶数量越多,动力电池箱减少的幅度也越明显;
3)当有5艘船舶满足错峰出行条件时,建设3个充换电站的电池箱总数比建设2个减少了5个,说明增加一定的充换电站数量能够提升船舶在航行过程更换电池的灵活性,在减少充换电站的电池箱数量的前提下保证船舶的运行效率。
| [1] |
吕龙德, 熊莹. 船舶动力路径从常规燃料到低碳零碳排放[J]. 广东造船, 2021, 40(6): 3-11. |
| [2] |
孙玉伟, 胡克容, 严新平, 等. 新能源船舶混合储能系统关键技术问题综述[J]. 中国造船, 2018, 59(1): 226-236. |
| [3] |
瞿小豪, 袁裕鹏, 范爱龙. 动力电池系统在运输船舶上的应用现状与展望[J]. 船舶工程, 2019, 41(10): 98-104. DOI:10.13788/j.cnki.cbgc.2019.10.20 |
| [4] |
刘艳良. 浅谈磷酸铁锂电池及其在电动船舶行业应用与发展[J]. 科学技术创新, 2020(15): 43-44. DOI:10.3969/j.issn.1673-1328.2020.15.024 |
| [5] |
李振兴, 徐轶群, 陈皓雯. 小型电动船舶纵倾优化[J]. 舰船科学技术, 2022, 44(13): 26-30. DOI:10.3404/j.issn.1672-7649.2022.13.006 |
| [6] |
裴宝浩, 周娟, 于蓬. 氢燃料电池动力技术在船舶动力能效改进的应用[J]. 舰船科学技术, 2022, 44(5): 97-100. |
| [7] |
李利杰. 船舶混合动力系统能量配置优化策略研究[J]. 舰船科学技术, 2021, 43(22): 82-84. DOI:10.3404/j.issn.1672-7649.2021.11A.028 |
| [8] |
张晋源, 林湘宁, 张哲原. 基于模型预测控制的远洋海岛交通船舶充电调度方案[J]. 三峡大学学报(自然科学版), 2019, 41(3): 75-80. DOI:10.13393/j.cnki.issn.1672-948x.2019.03.016 |
| [9] |
王伟, 张瀚宸. 纯电动船舶直流并网短路保护功能设计及仿真分析[J]. 控制与信息技术, 2021(6): 71-76. |
| [10] |
孙士茼, 何英发, 汪致洵, 等. 兼顾电能质量与化石能源消耗的全电船舶充电站多目标规划[J]. 中国电机工程学报, 2018, 38(S1): 45-52. |
| [11] |
张文芬, 汤旭晶, 严新平, 等. 船用模块化集装箱式动力电池的运营模式设计[J]. 中国水运, 2021(10): 6-9. DOI:10.13646/j.cnki.42-1395/u.2021.10.001 |
 2023, Vol. 45
2023, Vol. 45
