船载无人机可实时采集船舶航行环境的相关信息,为驾驶员提供船舶航行的水域信息,及时发现危险物体,避免发生碰撞事故[1]。船载无人机具备垂直起降与高效巡航特性,可提升无人机飞行效率,延长飞行时间[2]。现代船载无人机的使用特点,导致对其结构重量提出更高的要求。减轻船载无人机结构重量,还可有效降低材料的消耗量[3]。为实现船载无人机的轻量化设计,需研究无人机参数化设计方法。有学者通过网格重构法,建立船载无人机参数化模型,该方法可有效完成船载无人机的参数化设计,设计完成的船载无人机应用性较优[4]。有学者通过分析船载无人机的气动/推进耦合特性,对船载无人机进行参数化设计。该方法设计的船载无人机重量较轻,续航性能较优。但这2种方法均只实现了船载无人机的轻量化设计,并未考虑船载无人机的力学性能,导致船载无人机的结构柔度较大,降低船载无人机结构间连接的光滑性与全连通性。3D打印是通过粉与块等形状的材料,逐层堆叠构造物体的一种技术,可完全根据设计者的创意加工获取其需要的目标物体,具备材料利用率高,废料形成量少的优势[5]。为此研究基于3D打印的船载无人机参数化设计方法,降低船载无人机的结构柔度,提升船载无人机的力学性能。
1 船载无人机参数化设计 1.1 船载无人机的三维建模采用面向3D打印技术的SolidWorks软件提供的API接口实施二次开发,设计友好的船载无人机参数化设计交互界面,由该界面建立船载无人机的三维模型。船载无人机的三维建模流程如图1所示。

|
图 1 船载无人机的三维建模流程 Fig. 1 3D modeling process of shipborne UAV |
船载无人机的三维建模具体步骤如下:
1) 拉伸船载无人机机架与桨叶等零部件的外框实体,切除外框实体得到各零部件间的连接口,并进行修整操作,完成船载无人机三维建模过程的确定。
2) 以船载无人机结构柔度最小为目标,建立船载无人机设计参数确定模型,通过变权重变异鸽群优化算法,求解该模型,得到最小结构柔度对应的船载无人机设计参数。
3) 界面设计,在该界面内输入确定的船载无人机设计参数,自动生成船载无人机各部件的三维模型。
4) 通过设计界面,先确定主体框架,再通过SolidWorks软件提供的API接口,启动SolidWorks软件的建模程序,达到船载无人机自动三维建模的目的。
5) 当船载无人机三维建模成功时,则输出船载无人机的三维模型;反之,返回步骤4,重新建模。
1.2 面向3D打印的船载无人机设计参数确定利用面向3D打印技术的Solidworks软件,建立船载无人机三维模型过程中,需要先确定船载无人机的设计参数。利用船载无人机的结构柔度,衡量其全局刚度,结构柔度越小,全局刚度越大,船载无人机的力学性能越佳。对3D打印船载无人机进行轻量化设计,可降低船载无人机重量,节约生产消耗。为此以最小结构柔度为目标,体积、应变与梯度为约束条件,建立船载无人机设计参数确定模型,公式如下:
| $ F = \min y\left( {u,t,p} \right) 。$ | (1) |
式中:
| $ y\left( u \right) = \int_\varOmega {Efu{\rm{d}}\varOmega } + \int_\varGamma {Egu{\rm{d}}s}。$ | (2) |
式中:
为防止船载无人机结构过度突变导致结构曲率较大,出现应力集中问题,在式(1)内添加梯度约束、应变约束与体积约束,要求船载无人机在指定的体积结构内具有最大的刚度,降低船载无人机重量,提升船载无人机的力学性能。为此将式(1)变更为如下的连续形式,即
| $ \min F = \int_{{\varOmega _{\max }}} {fu{\rm{d}}} B + \int_\varGamma {sud\left( {t,p} \right)}。$ | (3) |
式中:
式(3)的体积、梯度、应变约束条件为:
| $ \left\{\begin{array}{l}{\displaystyle {\int }_{{\varOmega }_{\mathrm{max}}}E:\delta \left(u\right):\delta \left(v\right){\rm{d}}B}={\displaystyle {\int }_{{\varOmega }_{\mathrm{max}}}fv{\rm{d}}B}+{\displaystyle {\int }_{\varGamma }svd\left(t,p\right)}\\ u=\overline{u}on\varGamma \text{,}{\displaystyle {\int }_{{\Omega }_{\mathrm{max}}}{\rm{d}}B}\leqslant \overline{B},\\ \Vert \nabla t\Vert \leqslant h\text{,}\mathrm{max}\sigma < \varepsilon。\end{array} \right.$ | (4) |
式中:
为防止船载无人机三维建模过程中,重新剖分网格,引入Heaviside函数Z,变更式(3)获取:
| $ \min F = \int_{{\varOmega _{\max }}} {Z\left( \lambda \right)fu{\rm{d}}} B + \int_\varGamma {sud\left( {t,p} \right)},$ | (5) |
式中,
式(4)的约束条件变更为:
| $ \left\{\begin{array}{l}{\displaystyle {\int }_{{\varOmega }_{\mathrm{max}}}Z\left(\lambda \right)E:\delta \left(u\right):\delta \left(v\right){\rm{d}}B}={\displaystyle {\int }_{{\varOmega }_{\mathrm{max}}}Z\left(\lambda \right)fv{\rm{d}}B}+\\ \qquad\qquad {\displaystyle {\int }_{\varGamma }svd\left(t,p\right)},\\ u=\overline{u}on\varGamma \text{,}{\displaystyle {\int }_{{\varOmega }_{\mathrm{max}}}Z\left(\lambda \right){\rm{d}}B}\leqslant \overline{B},\\ \Vert \nabla t\Vert \leqslant h\text{,}\mathrm{max}\sigma < \epsilon。\end{array}\right. $ | (6) |
Z(λ)的计算公式如下:
| $ Z\left( \lambda \right) = \left\{ \begin{array}{*{20}{l}} 1,& \lambda > \eta ,\\ \dfrac{{3 - 3\alpha }}{4}\left( {\dfrac{\lambda }{\eta } - \dfrac{{{\lambda ^3}}}{{3{\eta ^3}}}} \right) + \dfrac{{1 + \alpha }}{2},& - \eta \leqslant \lambda \leqslant \eta ,\\ \alpha ,& \lambda < - \eta ,\end{array} \right. $ | (7) |
式中:
利用变权重变异鸽群优化算法,求解式(5),获取最小结构柔度的船载无人机设计参数。
步骤1 参数初始化。
步骤2 鸽群速度与位置更新公式如下:
| $ \begin{split} &{Q_i}\left( l \right) = {Q_i}\left( {l - 1} \right)\exp \left( { - Rl} \right) + \gamma \left( {{X_{best}} - {X_i}\left( {l - 1} \right)} \right) \\ & {X_i}\left( l \right) = {X_i}\left( {l - 1} \right) + {Q_i}\left( l \right) 。\end{split} $ | (8) |
式中:Qi,Xi为第
步骤3 更新种群,计算新位置的适应度值,以式(5)的目标函数为适应度值,更新适应度最差鸽群的速度与位置,公式如下:
| $ \begin{split} & {Q_{worst}}\left( l \right) = {Q_{worst}}\left( {l - 1} \right)w - \gamma \left( {{X_{best}} - {X_{worst}}\left( {l - 1} \right)} \right) ,\\ & {X_{worst}}\left( l \right) = {X_{worst}}\left( {l - 1} \right) + {Q_{worst}}\left( l \right) ,\\ & w = \exp \left( { - \frac{{f\left( {{X_i}} \right)Rt}}{{f\left( {{X_{best}}} \right)}}} \right) 。\end{split} $ | (9) |
式中:Qworst(l),Qworst(l)为最差鸽群速度与位置;f(Xi),f(Xbest)为Xi,Xbest的适应度值。
步骤4 计算全局最佳位置Xbest,分析
在3D打印软件内,输入面向3D打印技术的Solidworks软件建立的船载无人机三维模型,进行船载无人机的3D打印,船载无人机3D打印流程如图2所示。具体步骤如下:

|
图 2 船载无人机3D打印流程 Fig. 2 3D printing process of shipborne UAV |
1)3D打印软件内导入船载无人机三维模型。
2)通过Magics修复导入的船载无人机三维模型;在导入三维模型过程中,可能会出现较小的缺陷,采用Magics技术可自动修复该缺陷;
3)分层处理。在打印船载无人机前,需分层处理船载无人机三维模型,获取每层的无人机数据,确定打印方向,以及开始与结束指令;
4)通过3D打印软件读取每层无人机数据,并实施打印,得到船载无人机,完成船载无人机参数化设计。
2 性能测试与分析以某KVLCC2船为实验对象,利用本文方法为该船设计船载无人机,用于实时观测航行环境信息。该船长8 m,宽1.2799 m,排水体积3.3835 m3。该船载无人机的设计需求为最大平飞速度在30~35 m/s之间,最大应力范围在60~70 MPa之间。
利用本文方法确定该船载无人机的设计参数,最小结构柔度的计算结果如图3所示。可知,本文方法可有效计算船载无人机的最小结构柔度,当迭代次数达到7次左右时,便完成收敛,结构柔度降至最低,本文方法计算结构柔度时的收敛速度快。

|
图 3 最小结构柔度计算结果 Fig. 3 Determination results of minimum structure compliance |
最小结构柔度对应的船载无人机设计参数如表1所示。可知,本文方法可有效确定最小结构柔度对应的船载无人机设计参数。对比初始值可知,本文方法确定的船载无人机设计参数,均低于初始值,有效节约船载无人机的制造材料,达到船载无人机轻量化设计的目的。
|
|
表 1 船载无人机设计参数 Tab.1 Design parameters of shipborne UAV |
利用本文方法根据确定的船载无人机设计参数,建立船载无人机三维模型,如图4所示。可知,本文方法可根据确定的船载无人机设计参数,完成无人机的三维建模,本文方法建立的三维模型,可清晰呈现船载无人机的细节信息。实践证明,本文方法具备船载无人机三维建模的可行性。

|
图 4 船载无人机三维模型 Fig. 4 Three-dimensional model of shipborne UAV |
利用本文方法对船载无人机进行3D打印,3D打印结果如图5所示。可知,本文方法可有效根据船载无人机的三维模型,得到船载无人机的3D打印结果。实践证明,本文方法可有效完成船载无人机参数化设计。

|
图 5 船载无人机3D打印结果 Fig. 5 3D printing results of shipborne UAV |
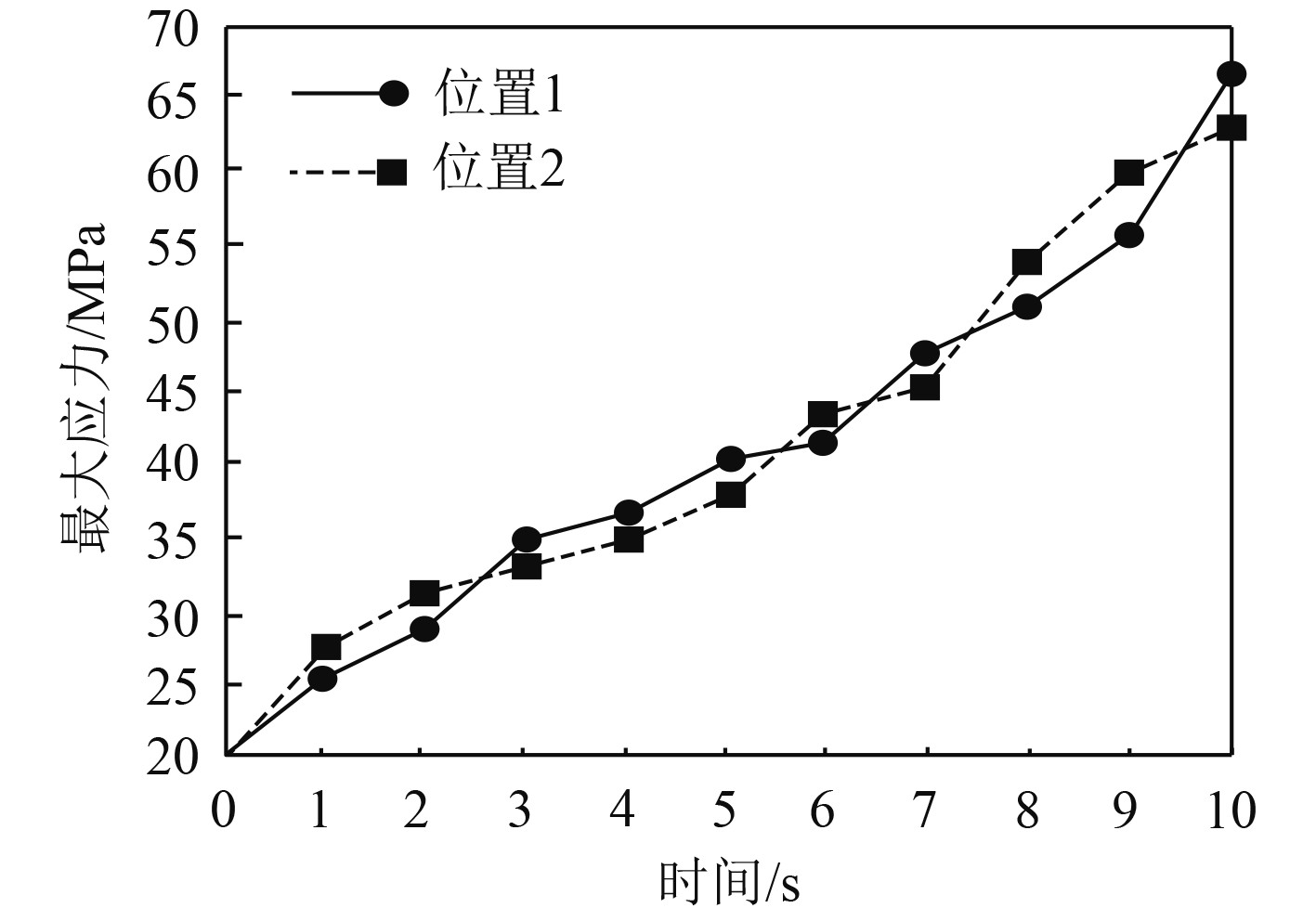
在本文方法设计的船载无人机中,随机选择2个位置,分别在这2个位置处施加一竖直方向的集中力150 N,分析本文方法设计的船载无人机的最大应力,分析结果如图6所示。可知,随着时间的延长,船载无人机2个位置承受的最大应力越大,位置1处的最大应力在67 MPa左右,位置2处的最大应力在63 MPa左右,均在船载无人机最大应力的控制范围内,说明本文方法设计的船载无人机符合强度与刚度等力学性能的需求。
|
图 6 船载无人机的最大应力分析结果 Fig. 6 Maximum stress analysis results of shipborne UAVs |
针对船载无人机制造过程繁琐、材料消耗较多等问题,研究基于3D打印的船载无人机参数化设计方法,利用3D打印技术成本低、过程简单、制造效率高等优势,提升船载无人机参数化设计效果。在降低船载无人机结构重量的同时,加强船载无人机的力学性能。
| [1] |
蔡玉良, 向林浩, 何洪磊, 等. 面向船舶检验的无人机关键技术解决方案[J]. 船海工程, 2020, 49(1): 10-14. |
| [2] |
尹项迎, 常瑜, 刘宝顺. 基于SGS模型与AHP的侦测无人机造型设计研究[J]. 包装工程, 2022, 43(14): 45-50. |
| [3] |
杨鸿. 基于Moldflow的无人机上盖模流优化分析与模具设计[J]. 中国塑料, 2020, 34(6): 92-99. |
| [4] |
张振扬. 玻纤增强聚丙烯无人机机身轻量化设计及优化分析[J]. 塑料科技, 2022, 50(1): 108-111. DOI:10.15925/j.cnki.issn1005-3360.2022.01.025 |
| [5] |
陈晓霞, 龙妍婷, 张楚, 等. 基于侧面DLP的3D打印技术制作微流控芯片[J]. 微纳电子技术, 2022, 59(5): 437-444. |
 2023, Vol. 45
2023, Vol. 45
