2. 中国人民解放军91999 部队,山东 青岛 266000
2. No. 91999 Unit of PLA, Qingdao 266000, China
泵喷推进器[1](简称泵喷)是一种带定子的导管类组合式推进器,因其具有推迟空泡发生、降低水下航行体辐射噪声、提高推进效率等优势,已被广泛应用于水下航行体上。为避免摩擦和满足运行需求,泵喷转子梢部端面与导管内壁之间不可避免地存在一定的间隙,泵喷再运转过程中会在叶梢间隙内形成较强的复杂涡系结构,这种非定常的涡系结构不但会诱发流动噪声,还会在叶梢端面和梢涡的涡核处形成低压区,引发梢隙空化和梢涡空化,产生空化噪声,最终导致推进器的噪声显著增加。
目前国内外有不少针对梢隙流动及梢涡控制方面的研究。王涛等[2-3] 对泵喷推进器的梢隙三维复杂粘性流场进行研究,揭示了间隙流的形成机理及对性能安全方面的影响。鹿麟等[4]对不同叶顶间隙的泵喷推进器进行数值模拟计算,着重对叶顶间隙进行精细化处理,结果显示在相同进速系数下,间隙尺寸越大,泵喷推进器的整体效率值越低。施卫东等[5] 在轴流泵的模拟实验中,发现随着叶顶间隙的增大,模型泵的临界空化数增大。Dreyer等[6]通过调节叶尖和壁面之间的间隙,利用高速摄像机和立体粒子图像测速技术研究漩涡的轨迹和叶尖泄漏涡(TLV)诱导的三维速度场,结果清楚地揭示了间隙宽度对TLV的轨迹和强度的强烈影响。翁凯强等[7]考虑间隙流动模型,可更加准确地预报泵喷推进器水动力性能。
抑制梢涡空化[8]的的方法有很多,主要分为主动控制和被动控制2种,主动控制方法主要是向梢涡空化中进行质量注入,要抑制梢涡空化产生一般注入水或聚合物;被动控制方法主要是通过修改翼型,在梢部安装平板、翼板或球帽,在螺旋桨或水翼叶面或边缘加粗糙等。在工程实际中被动控制更具优势。Ahn等[9] 通过对泵喷推进器进行改进设计,在转子叶梢处加装周向圆环,数值分析结果表明该结构有助于降低梢涡强度、抑制梢涡空化的形成。于丰宁等[10] 针对转子叶片带冠结构进行研究,结果表明其能有效改善间隙涡结构,降低流体辐射噪声。叶金铭等[11-13] 借鉴航空发动机中的“处理机匣”技术,在泵喷推进器的导管内壁上开设系列凹槽结构,以达到降低泵喷梢涡强度、抑制梢涡空化的目的。
本文设计一种转子梢部带圆环并嵌入导管内壁凹槽的改进型泵喷推进器,属于一种被动控制方法。基于RANS方程,结合SST k-ω湍流模型,采用分块网格技术[14],分别对原始泵喷和改进型泵喷进行水动力性能数值模拟,分析梢部带圆环并嵌入导管内壁凹槽结构对梢隙空化与梢涡空化的控制效果以及对泵喷推进器敞水性能的影响。
1 数值计算方法及其验证 1.1 控制方程及湍流模型在不考虑推进器内部流场空化影响的前提下,可假设流体为不可压缩的单相流,基于RANS方法的控制方程可写为[15]:
| $ \frac{\partial {U}_{i}}{\partial {x}_{i}}=0 ,$ | (1) |
| $ \begin{aligned} &\rho \frac{\partial {U}_{i}}{\partial t}+\rho \frac{\partial {U}_{i}{U}_{j}}{\partial {x}_{j}}=-\frac{\partial P}{\partial {x}_{i}}+\frac{\partial }{\partial {x}_{j}}\left[\mu \left(\frac{\partial {U}_{i}}{\partial {x}_{j}}+\frac{\partial {U}_{j}}{\partial {x}_{i}}\right)\right]+\\ & \frac{\partial }{\partial {x}_{j}}\left(-\rho \bar{{u}_{i}'}\bar{{u}_{j}'}\right)。\end{aligned} $ | (2) |
式中:i,j = 1,2,3;
在RANS方法中常用SST k-ω 湍流模型来对控制方程进行封闭,它综合了近壁k-ω模型的稳定性及边界层外部k-ε模型独立性的优点。计算时收敛性好、效率高,对复杂流场的适应性好。
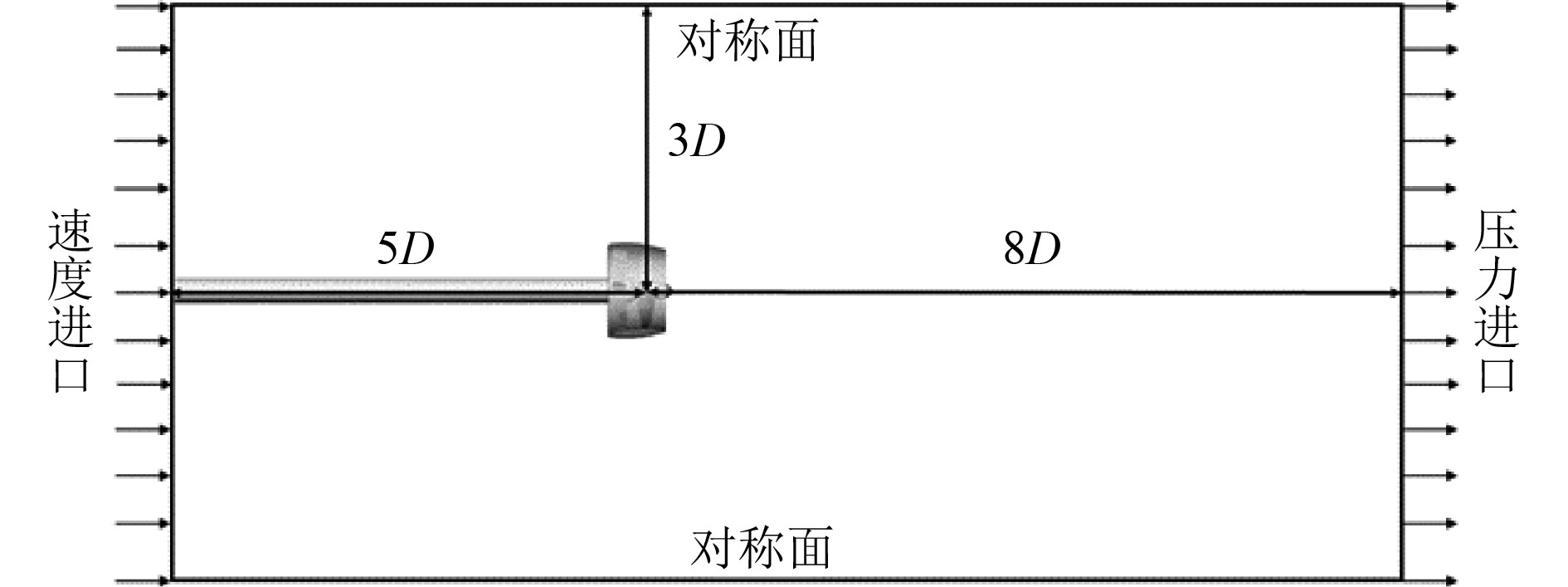
1.2 数值计算方法验证选取有试验值的泵喷推进器[16]对数值计算方法的准确性进行验证,该泵喷为前置定子式,由9叶弦长为50.8 mm的定子和 4 叶直径为254 mm的转子构成,如图1所示。转子叶梢端面与导管内表面之间最小间隙为 1.5 mm。计算域及其边界条件设置如图2所示,以泵喷推进器的转子直径D作为基准尺寸和转子盘面中心为坐标原点对计算域进行布置,计算域进口与转子盘面的距离为5D,边界条件设置为速度进口,

|
图 1 泵喷推进器几何示意图 Fig. 1 Geometry of pumpjet propulsorr |
|
图 2 计算域及边界条件设置 Fig. 2 Calculation domain and boundary condition setting |
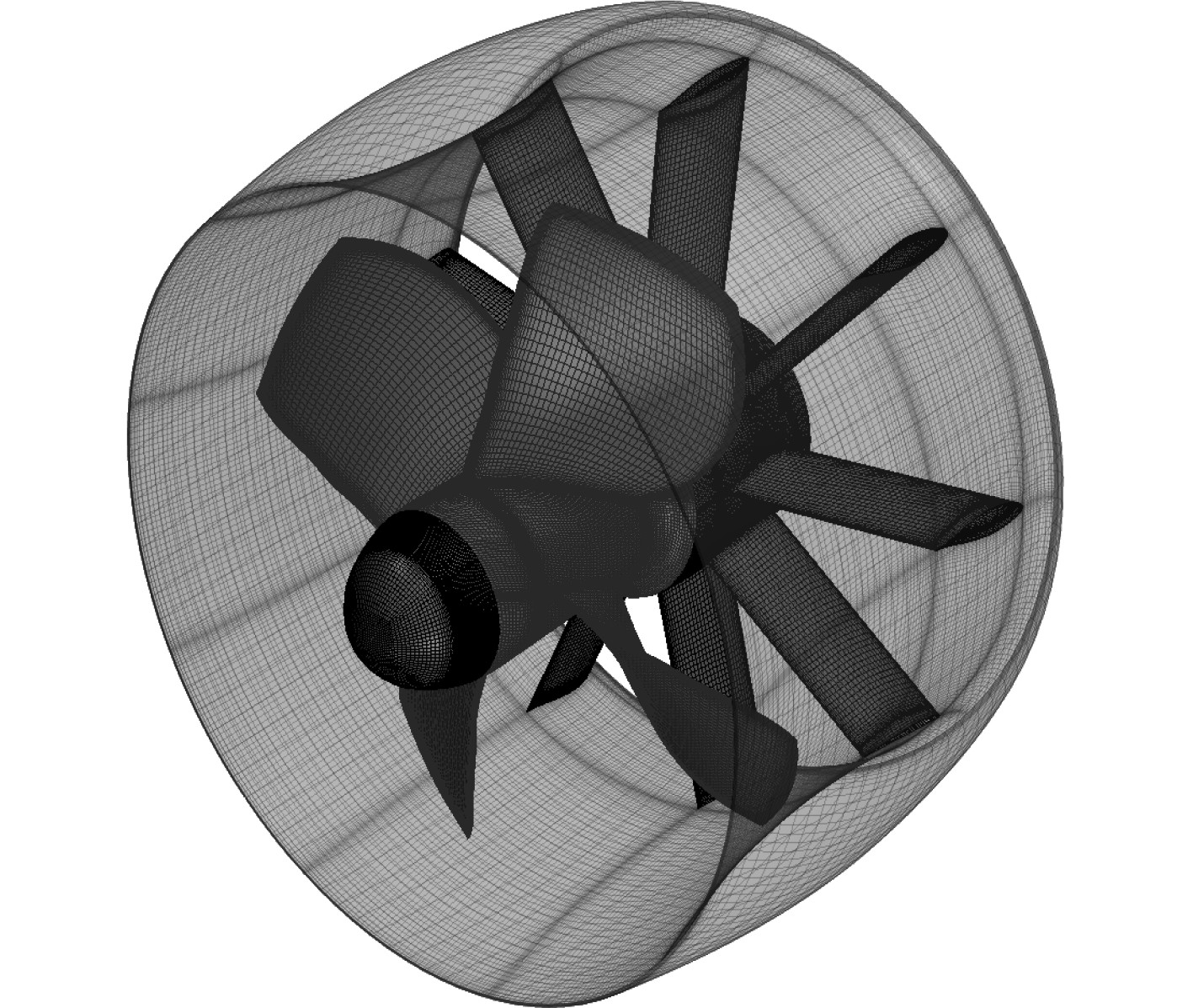
采用分块结构网格技术对泵喷推进器进行网格划分,将计算域划分成如图3所示的外域、转子域和定子域。其中转子域和定子域中的叶片为周期性分布,可采用周期性拓扑结构的形式进行网格划分,由包含单叶片的单通道网格通过周期性旋转得到全通道网格,单通道中对叶片采用 O 型网格和H 型网格相结合的拓扑结构,在转子域中对转子叶梢端面采用Y型网格拓扑形式以提高网格质量,网格如图4所示。

|
图 3 计算区域划分 Fig. 3 The division of calculation area |
|
图 4 泵喷推进器网格 Fig. 4 The mesh of pumpjet propulsor |
通过固定转子转速
为验证数值方法的精度,对数值计算结果(CFD)进行无量纲化处理,各系数的计算公式如下:
| $ J=\frac{{V}_{S}}{nD}, $ | (3) |
| $ KTr=\frac{{T}_{r}}{\rho {n}^{2}{D}^{4}} ,$ | (4) |
| $ KQr=\frac{{Q}_{r}}{\rho {n}^{2}{D}^{5}} ,$ | (5) |
| $ KT=\frac{T}{\rho {n}^{2}{D}^{4}} ,$ | (6) |
| $ \eta =\frac{J}{2 \text{π}}\times \frac{KT}{{KQ}_{\mathrm{r}}} 。$ | (7) |
式中:
将数值计算(CFD)得到的结果与试验值(EXP)进行比较,结果如图5所示。可以看出数值计算结果与试验值吻合较好,各个系数的误差均在 3%以内,由此可见在研究中所使用的数值计算方法是可靠的。

|
图 5 泵喷推进器敞水性能曲线 Fig. 5 Open water performance curve of pumpjet propulsor |
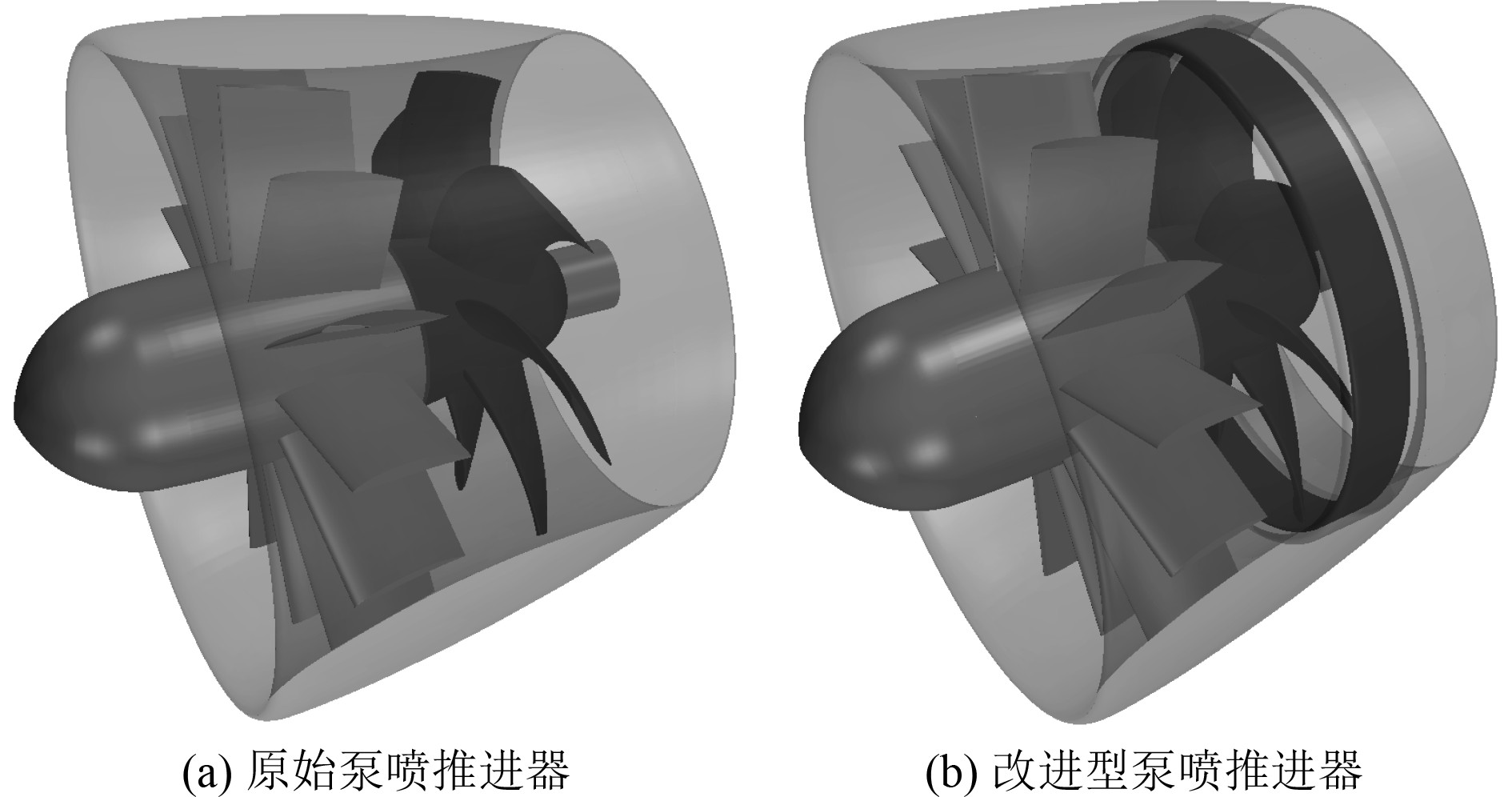
研究对象结构形式如图6所示。原始泵喷为前置定子式泵喷,定子为13叶,转子为7叶,导管采用加速型导管 ,转子叶梢端面与导管内壁表面的间隙为1.5~2.6 mm。改进型泵喷主要是在原始泵喷转子叶片的基础上在其叶片梢部加装圆环,并在导管相应位置开设环形凹槽,将上述叶梢圆环嵌入导管内壁环形凹槽内,圆环与导管内壁凹槽之间留有一定间隙,圆环前端面位于叶片梢部导边之前,圆环后端面位于叶片梢部随边之后,圆环内壁沿用之前导管相应处的内壁线型,如图7所示。
|
图 6 泵喷推进器结构模型 Fig. 6 Structure model of pumpjet propulsor |

|
图 7 改进型泵喷推进器梢部结构 Fig. 7 Top structure of improved pumpjet propulsor |
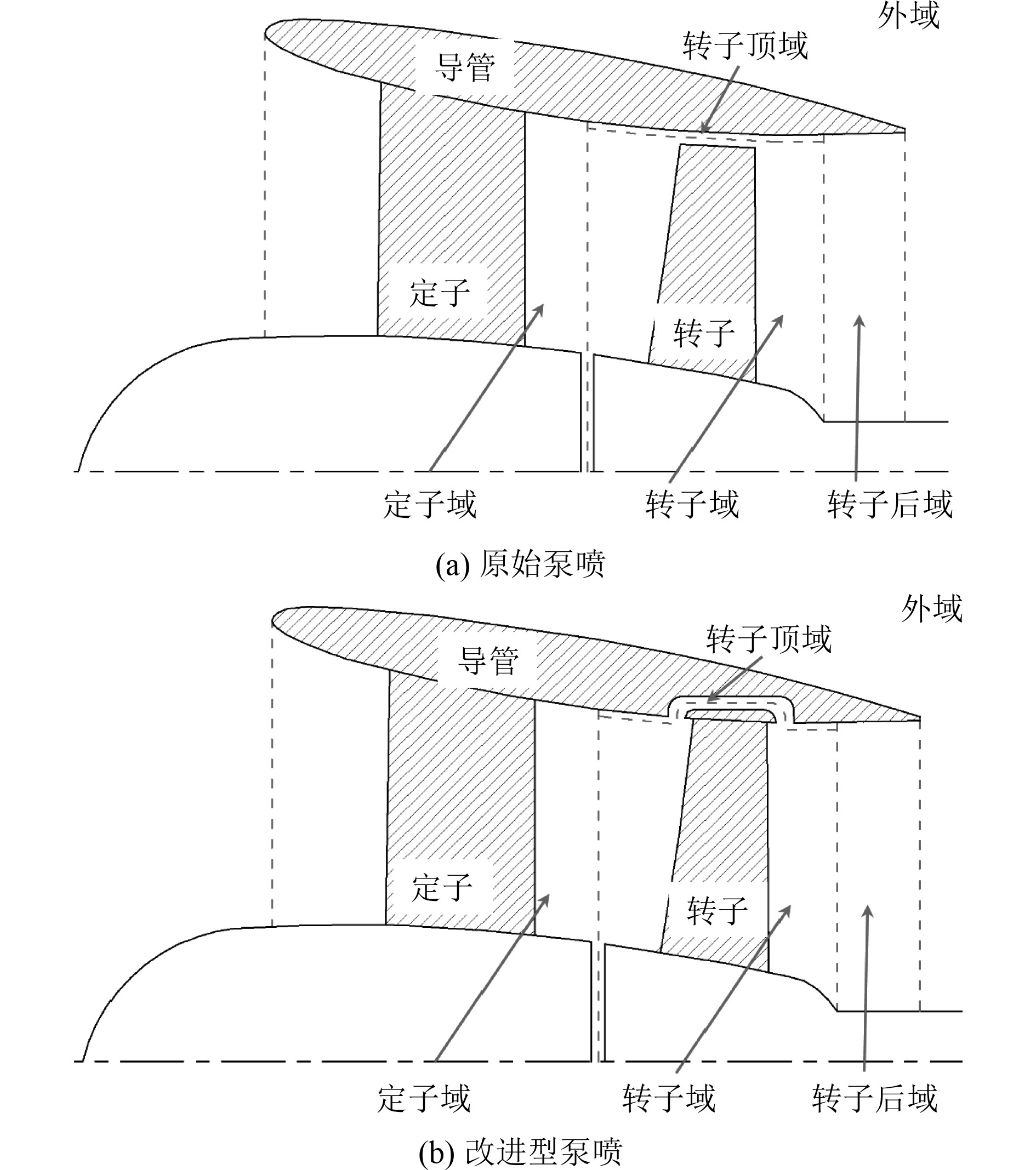
计算域边界条件及导管外域网格如图8所示。采用上述相同的方法布置,同样采用分块结构网格技术对计算模型进行结构化网格划分。原始泵喷与改进型泵喷结构形式仅在转子梢部及对应导管区域有所不同,为保持2种泵喷推进器网格尽可能的一致,对导管内域的网格进一步进行细分。如图9所示。导管内域分为转子域和静止域,静止域中包括定子域、转子顶域和转子后域。转子域的轴向位置和尺寸保持一致,除了叶梢附近转子域的径向尺寸分布也保持一致。定子域和转子后域采用相同的网格,转子域网格划分时,叶梢以下区域的网格节点分布保持基本一致,转子顶域网格节点分布形式也保持基本一致。为更好地研究转子梢部带圆环并嵌入导管内壁凹槽结构对梢涡的控制效果,对转子梢部和转子与导管内壁面间的网格进行加密,其他壁面也进行相应的加密处理,网格细节见图10。

|
图 8 计算域边界条件设置及导管外域网格 Fig. 8 The setting of computational domain boundary conditions and the external mesh of duct |
|
图 9 导管内计算域划分 Fig. 9 The division of computational domains in duct |
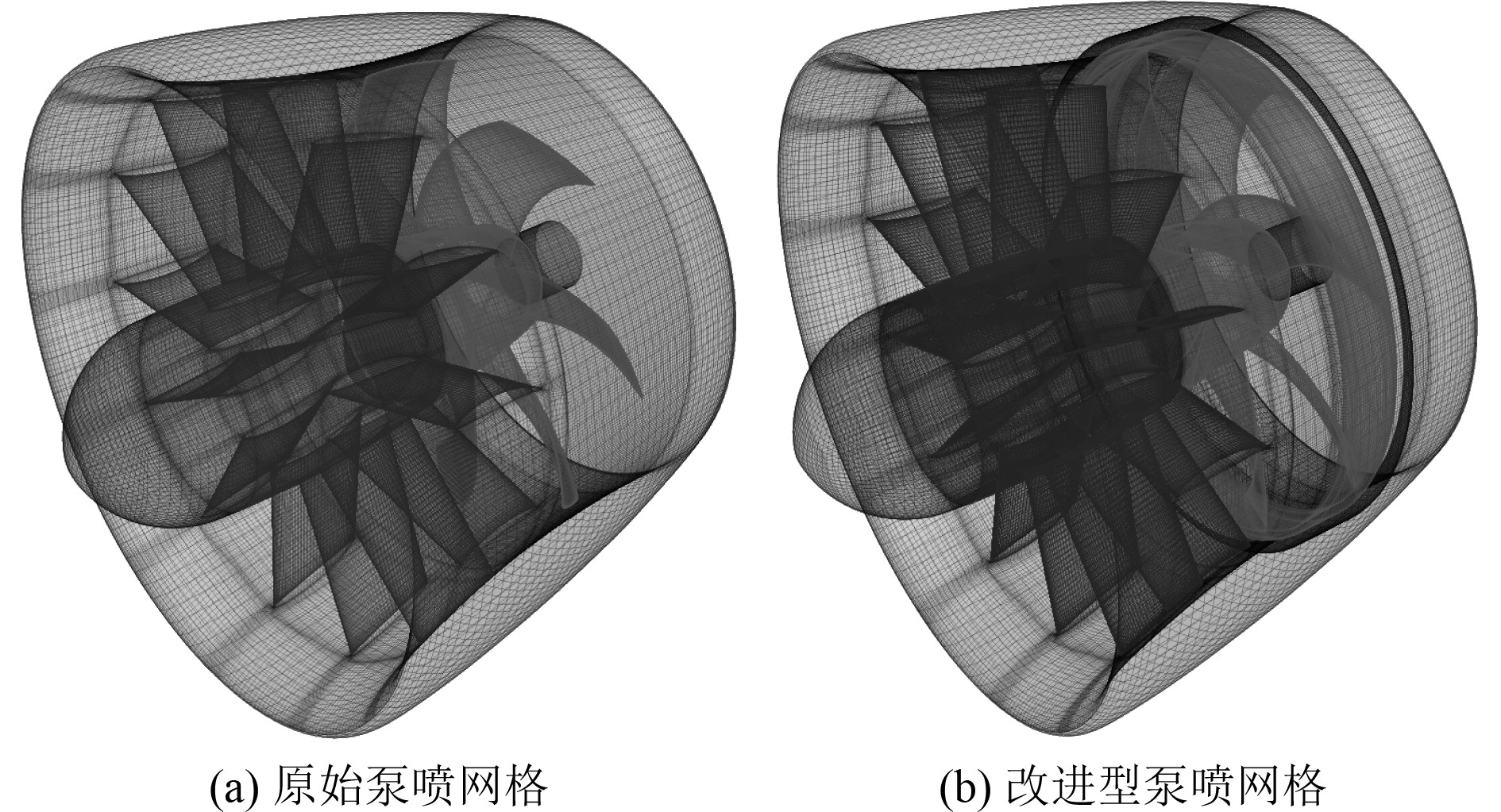
|
图 10 泵喷推进器网格 Fig. 10 The mesh of pumpjet propulsor |
由于在转子叶片表面和叶梢端面的过渡存在明显的夹角,当流体经过叶梢端面时,边缘附近会发生强烈的流动分离现象,形成梢隙分离涡,进而导致转子叶梢附近区域的压力急剧降低,发生梢隙空化。同时在转子压力面和吸力面的压差作用下,流体会从叶梢的压力面越过叶梢端面翻转到吸力面一侧,流体的翻转会在转子梢部的叶背附近和叶梢尾流中形成泄出涡—梢涡,在梢涡的涡核处,压力很低,极容易形成梢涡空化。
为更直观观察改进型泵喷对分离涡和梢涡的控制效果,使用CFD计算软件中提供的基于Q准则的等值面法对旋涡形态进行标记和直观表达。Q准则由Hunt等在1988年提出[17],定义流场中速度梯度张量
| $ Q=\frac{1}{2}\left(\|\varOmega\|^2-\|S\|^2\right)。$ | (8) |
式中:
取Q为
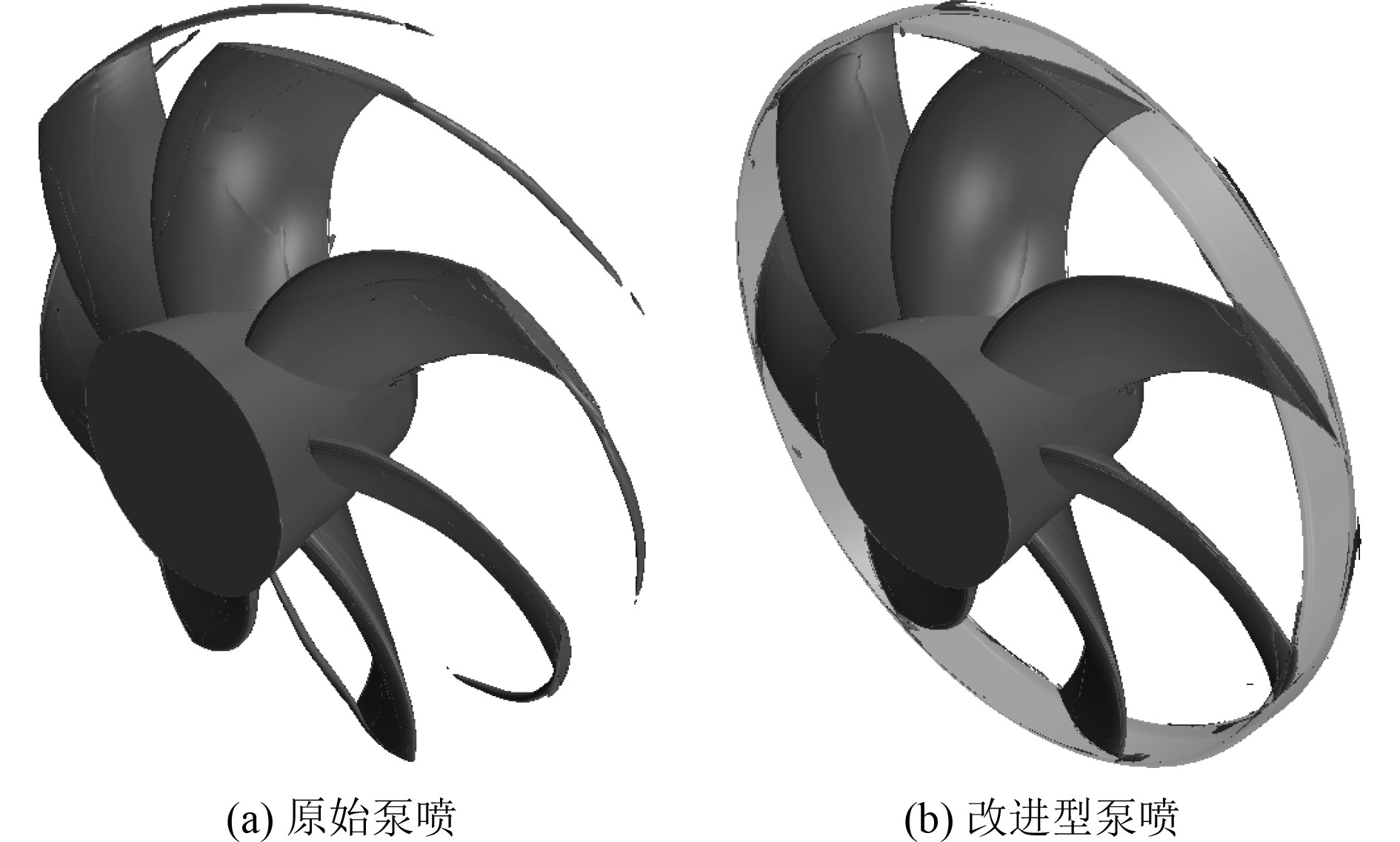
|
图 11 转子域涡可视化结果 Fig. 11 Visualization results of rotor domain vortex |
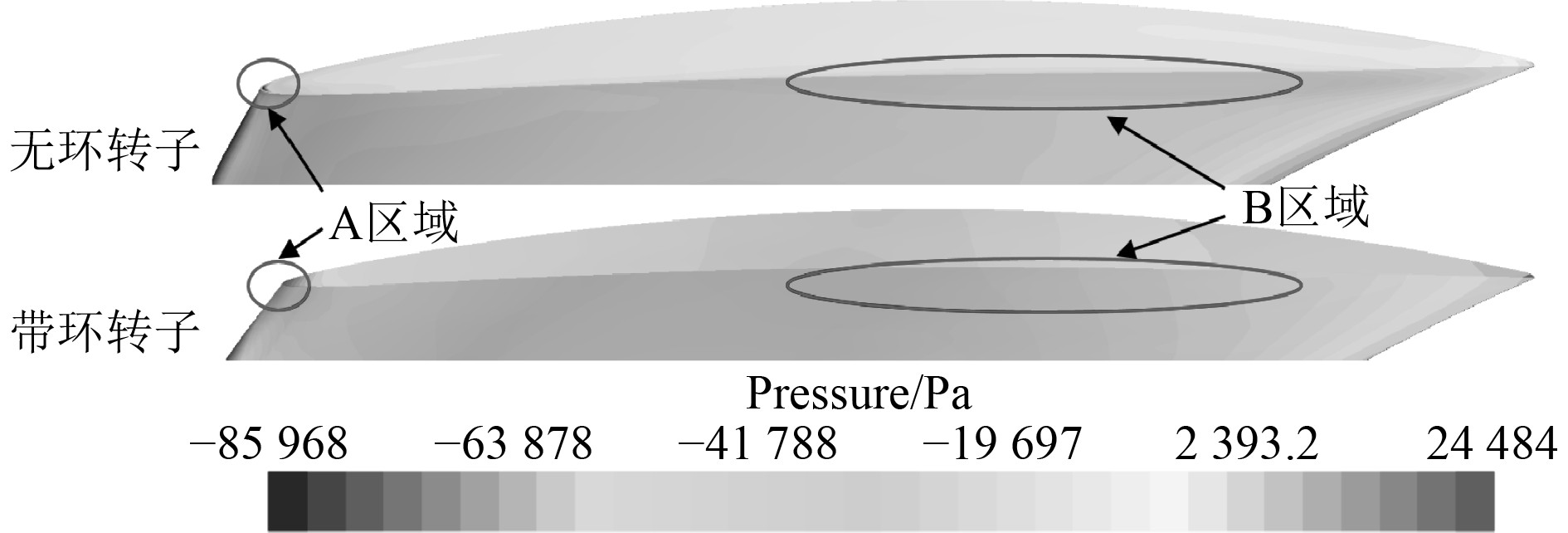
|
图 12 转子梢部表面压力分布 Fig. 12 Pressure distribution on rotor tip surface |
通过固定转子转速
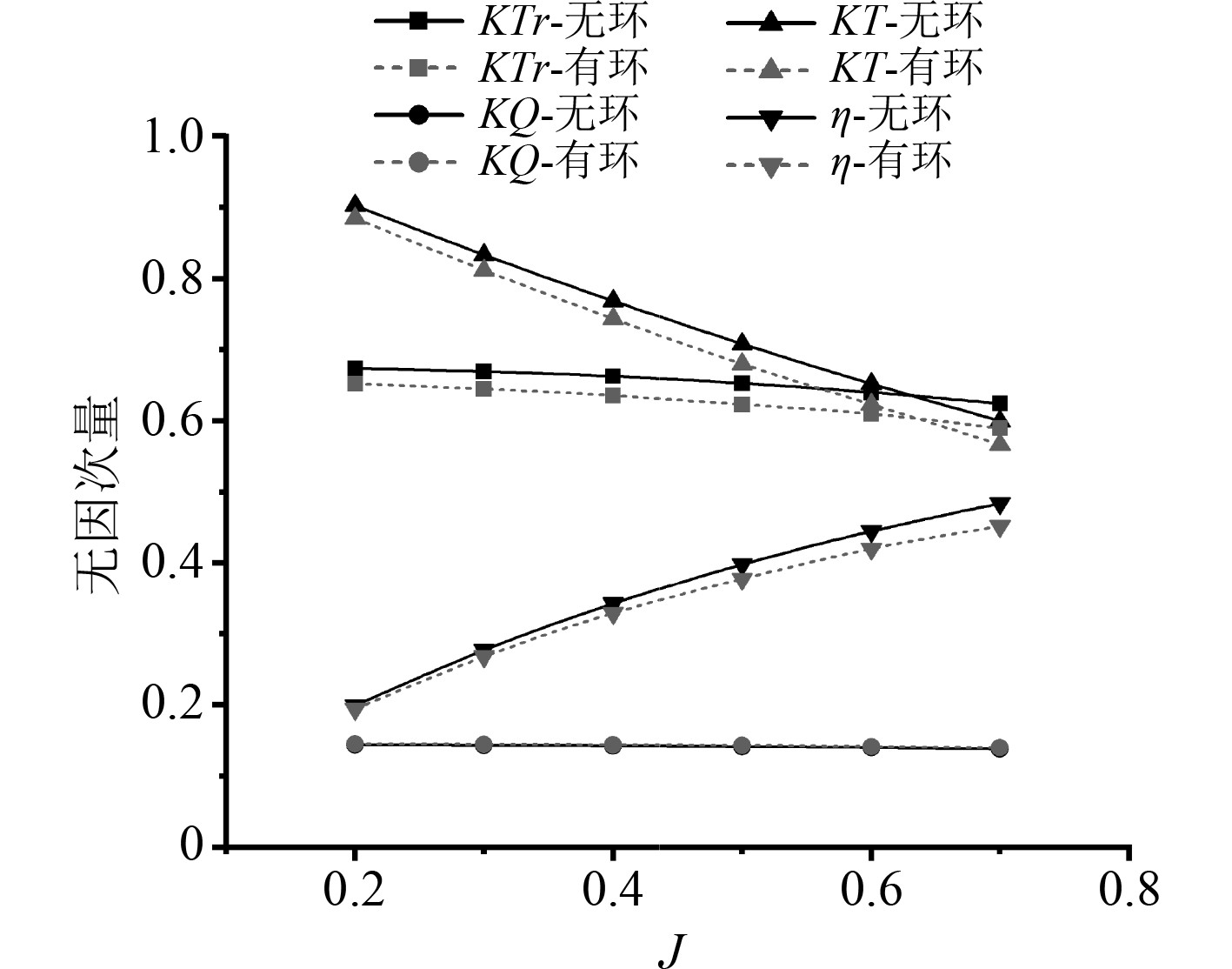
|
图 13 泵喷推进器敞水性能曲线 Fig. 13 Open water performance curve of pumpjet propulsor |
梢部圆环在旋转的过程中,由于粘性的作用,会引起圆环周围的流体产生周向的旋转速度,该周向旋转速度与转子的旋转方向一致,流体在转子叶片梢部附近的相对旋转速度减小,在转子叶片梢部附近剖面的相对来流攻角减小,导致转子叶片梢部的负荷下降,从而使转子叶片的推力和扭矩变小。另外,由于粘性的作用,转子梢部圆环在旋转时,流体在圆环表面会产生与圆环旋转方向相反的摩擦力,在梢部圆环上产生一定的扭矩。
转子梢部加装圆环结构后,一方面会使转子叶片梢部的负荷下降,叶片产生的推力和扭矩下降,另外一方面,梢部圆环还会产生一定的扭矩,在该泵喷推进器运转过程中,圆环上形成的扭矩增量略大于叶片扭矩的降低量,导致改进型泵喷的转子推力和推进器总推力减小,而转子扭矩略微增大。进而使推进器推进效率有所降低。
3 结 语通过对计算结果和试验结果的分析,得到以下结论:
1)改进型泵喷转子梢部没有了梢部端面,高速流体经过转子梢部不会发生分离现象,转子梢部的分离涡可基本消除,避免了梢隙空化的发生;同时梢部圆环结构能阻止流体从叶面高压区经梢部端面翻转到叶背低压区,梢涡也得到了有效抑制,延迟梢涡空化的发生。
2)通过对原始泵喷和改进型泵喷的敞水性能进行对比分析,发现改进型泵喷相比原始泵喷在转子推力系数和泵喷推进器总推力系数有所降低,最大降低4.72%和4.41%,转子扭矩系数有小量增加,最大增加了0.81%,推进效率方面有所下降,最大降低5.12%。
| [1] |
杨琼方, 王永生. 泵喷推进器的低噪声设计机理与设计应用[M]. 武汉: 华中科技大学出版社, 2015.
|
| [2] |
王涛, 周连第. 泵喷推进器内间隙流与主流相互作用的数值模拟和机理研究[C]//2004年船舶水动力学学术会议论文集, 2004: 215–226. WANG T, ZHOU L D. Numerical simulation and mechanism study on the interaction between interstitial flow and main flow in pump jet propeller[C]//Papers of the 2004 Ship Hydrodynamics Conference, 2004. |
| [3] |
王涛, 周连第. 高速旋转状态下间隙流动对主流影响的数值模拟和机理研究[C]//第十七届全国水动力学研讨会暨第六届全国水动力学学术会议, 2003: 278–291. WANG T, ZHOU L D. The Numerical Simulation and Mechanism Research for the Influence of Tip-Clearance Flow on Main Flow inside Duct Under the High Rotational Speed Operation[C]//Proceedings of the 17th National Symposium on hydrodynamics and the 6th National Academic Conference on hydrodynamics, 2003: 278–291. |
| [4] |
鹿麟, 李强, 高跃飞. 不同叶顶间隙对泵喷推进器性能的影响[J]. 华中科技大学学报(自然科学版), 2017, 45(8): 110-114. LU L, LI Q, GAO Y F. Numerical investigation of effect of different tip clearance size on the pumpjet propulsor performance[J]. Journal of Huazhong University of science and Technology (NATURAL SCIENCE EDITION), 2017, 45(8): 110-114. |
| [5] |
施卫东, 李通通, 张德胜, 等. 不同叶顶间隙对轴流泵空化性能及流场的影响[J]. 华中科技大学学报(自然科学版), 2013, 41(4): 21-25. SHI W D, LI T T, ZHANG D S, et al. Effect of tip clearance on cavitation and flow field of axial flow pumps[J]. Journal of Huazhong University of science and Technology (NATURAL SCIENCE EDITION), 2013, 41(4): 21-25. DOI:10.13245/j.hust.2013.04.019 |
| [6] |
DREYER M, DECAIX J, MÜNCH-ALLIGNÉ C, et al. Mind the gap-tip leakage vortex in axial turbines[J]. IOP Conference Series: Earth and Environmental Science, 2014, 22(5). |
| [7] |
翁凯强, 王超, 胡健, 等. 间隙流动模型对泵喷推进器水动力性能的影响[J]. 哈尔滨工程大学学报, 2021, 42(1): 21-26. WENG K Q, WANG C, HU J, et al. Effect of the gap-flow model on the hydrodynamic performance of pump-jet propulsor[J]. Journal of Harbin Engineering University, 2021, 42(1): 21-26. DOI:10.11990/jheu.201907001 |
| [8] |
潘森森, 彭晓星. 空化机理[M]. 北京: 国防工业出版社, 2013.
|
| [9] |
AHN S J, KWON O J. Numerical investigation of a pump-jet with ring rotor using an unstructured mesh technique[J]. Journal of Mechanical Science and Technology, 2015, 29(7): 2897-2904. DOI:10.1007/s12206-015-0619-7 |
| [10] |
于丰宁. 新型泵喷推进器结构设计及其流激振动噪声特性研究[D]. 上海: 上海交通大学, 2019. YU F N. Structural design and flow-induced vibration noise characteristics of new pump-jet thruster[D]. Shanghai: Shanghai Jiaotong University, 2019. |
| [11] |
张凯, 叶金铭, 张颖军. 凹槽结构对泵喷推进器梢涡控制效果及规律研究(英文)[J]. 船舶力学, 2020, 42(3): 57-62. |
| [12] |
张凯, 叶金铭. 基于凹槽结构的泵喷推进器梢涡控制效果及计算方法[J]. 舰船科学技术, 2020, 42(3): 57-62. ZHANG K, YE J M. Research on the tip vortex control effect and calculation method of pump jet thruster based on groove structure[J]. Ship Science and Technology, 2020, 42(3): 57-62. |
| [13] |
叶金铭, 孙大鹏, 史宝雍. 基于矩形凹槽结构的泵喷推进器梢部流动控制效果研究[J]. 中国造船, 2021, 62(3): 70-84. YE J M, SUN D P, SHI B Y. Research on controlling tip flow of pump-jet propeller based on rectangular groove structure[J]. Shipbuilding of China, 2021, 62(3): 70-84. |
| [14] |
张凯, 叶金铭, 于安斌. 基于分块结构网格的泵喷推进器敞水性能模拟[J]. 船舶工程, 2018, 40(11): 49-54. ZHANG K, YE J M, YU A B. Simulation of open performance of pumpjet propeller based on block structured mesh[J]. Ship Engineering, 2018, 40(11): 49-54. |
| [15] |
WILCOX, C D. Turbulence modeling for CFD[M]. 3rd ed. California: DCW Industries, 2006.
|
| [16] |
HUGHES M J, KINNAS S A. An analysis method for a ducted propeller with pre-swirl stator blades[C]//Propeller/Shafting 91 Symposium Virginia Beach, 1991.
|
| [17] |
郭嫱, 黄先北, 仇宝云, 等. 涡判据在翼端间隙涡流分析中的应用与评价[J]. 华中科技大学学报(自然科学版), 2018, 46(11): 23-28. GUO Q, HUANG X B, QIU B Y, et al. Application and evaluation of vortex criteria in analysis on tip clearance vortical flow around hydrofoil[J]. Journal of Huazhong University of science and Technology (Natural Science Edition), 2018, 46(11): 23-28. |
 2023, Vol. 45
2023, Vol. 45
