2. 深海技术科学太湖实验室,江苏 无锡 214082;
3. 中国舰船研究设计中心,上海201108
2. Taihu Laboratory of Deepsea Technological Science, Wuxi 214082, China;
3. China Ship Development and Design Center, Shanghai 201108, China
金属夹芯板是由上下两层金属面板以及中间金属芯材,通过激光焊接技术构成一个整体的夹层结构,对比传统的船体加筋板结构,金属夹芯结构具有高强度、刚度/重量比的特点,可大幅降低结构的重量。因此,采用金属夹芯结构替代船体加筋板结构,将成为实现船体结构轻量化的一个重要技术途径[1]。
金属夹芯结构与传统加筋板结构的结构型式差异较大,其结构的载荷传递特性和承载机理有待深入研究。模型试验是研究结构承载特性的一种直观可靠方法,也是检验理论分析和数值计算结果准确性的一个重要手段。通过模型试验可以直观、清楚地了解船体结构的破坏过程,揭示载荷的传递规律,特别是针对新结构、新材料,模型试验无疑是一种揭示船体结构崩溃机理和捕获承载特性最根本、最有效的方法。因此,针对金属夹芯结构,开展典型结构极限承载特性模型试验研究具有重要的意义。
模型试验方法分为实船模型试验和缩比模型试验。实船模型试验能够准确反映船体结构实际的逐渐崩溃过程,然而,实船试验成本巨大且周期较长,难以满足经济性、可行性等客观条件的限制,因此,缩比模型试验是研究船体结构极限强度的一个理想选择。
金属夹芯结构的极限承载机理目前尚未完全知晓,并且新的结构型式使得现有相似关系的适用性有待论证,亟需开展金属夹芯结构缩比模型的承载特性影响分析,以探索缩尺比对其极限承载能力的影响,为金属夹芯结构试验的缩比模型设计提供支撑。
本文针对典型I型金属夹芯板,采用非线性有限元法,开展不同缩比条件下金属夹芯板单轴压缩极限承载能力对比分析,探索缩尺比对其极限承载能力的影响规律,为典型金属夹芯结构试验缩比模型的设计提供参考,为金属夹芯结构模型试验研究提供技术支撑。
1 钢质缩比模型试验相似准则开展船体结构缩比模型试验时,由于结构的板厚与长度相差多个量级,模型设计时常将板厚缩比独立出来。采用方向性量纲分析方法[2-3],将尺度和厚度作为2个相互独立的长度量纲,分别记为L和t,可推导得到如下相似准则:
| $ {{\text{C}}_{{M}}} = {{\text{C}}_{{E}}}{\text{C}}_{{L}}^{\text{2}}{{\text{C}}_{{t}}} \text{,} {{\text{C}}_{{W}}} = {\text{C}}_{{L}}^{\text{2}}{{\text{C}}_{{t}}} \text{,} {{\text{C}}_{{I}}} = {\text{C}}_{{L}}^{\text{3}}{{\text{C}}_{{t}}} ,$ | (1) |
| $ {{\text{C}}_{\textit{σ}} } = {{\text{C}}_{{E}}} \text{,} {{\text{C}}_\mu } = {\text{1}} \text{,} {{\text{C}}_{{A}}} = {\text{C}}_{{L}}^{}{{\text{C}}_{{t}}}。$ | (2) |
由于非线性因素的影响以及方向性量纲分析在极限强度缩比模型设计中的局限性,上述相似关系使得缩比模型的非线性特性在一定程度上存在偏差。当
试验缩比模型和原型之间保持一定的相似关系,才能根据缩比模型试验结果推算至原型。因此,开展船体结构极限强度缩比模型试验时,应尽可能既保证试验模型与原型的弹性阶段相似,也应满足非线性阶段的结构行为相似性[4]。
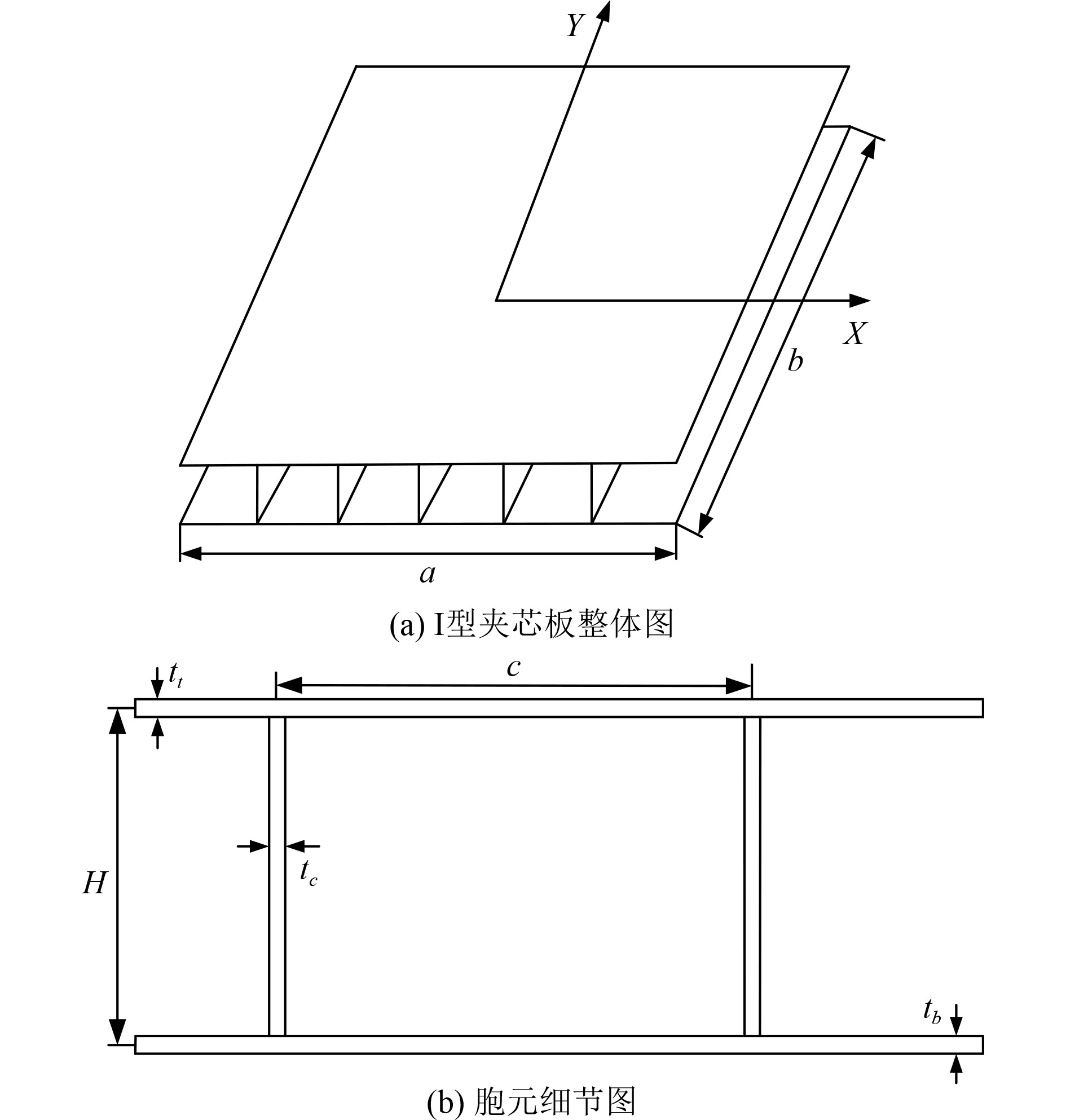
2 I型金属夹芯板几何特性I型夹芯板由上、下金属面板及I型金属夹芯组成。夹芯板横向长度为
|
图 1 典型I型金属夹芯板结构示意图 Fig. 1 Schematic diagram of type I corrugated sandwich plate |
|
|
表 1 典型I型金属夹芯板尺寸参数 Tab.1 Dimensional parameters of sandwich plate |
针对典型I型金属夹芯板,分别采用1∶1.2,1∶1.5,1∶2三种长度缩尺比和1∶1.2,1∶1.5,1∶2三种板厚缩尺比,通过2种缩比关系进行组合设计缩比模型。采用非线性有限元法对单轴压缩作用下的不同构型缩比模型极限承载能力进行对比分析,探索其尺度效应对极限承载能力的影响规律。缩尺比具体组合如表2所示。
|
|
表 2 计算模型缩尺比 Tab.2 The scaling of calculation model |
针对设计的金属夹芯板结构,利用大型通用有限元软件Abaqus,采用四节点shell单元,分别创建有限元计算模型,如图2所示。模型芯材间距及夹芯高度均划分为6个单元,纵向单元大小保证单元长宽比接近1。有限元模型中,忽略了结构初始缺陷的影响,均采用理想弹塑性材料,材料屈服极限为235 MPa。

|
图 2 I型夹芯板有限元模型 Fig. 2 FE model of Type I corrugated sandwich plate |
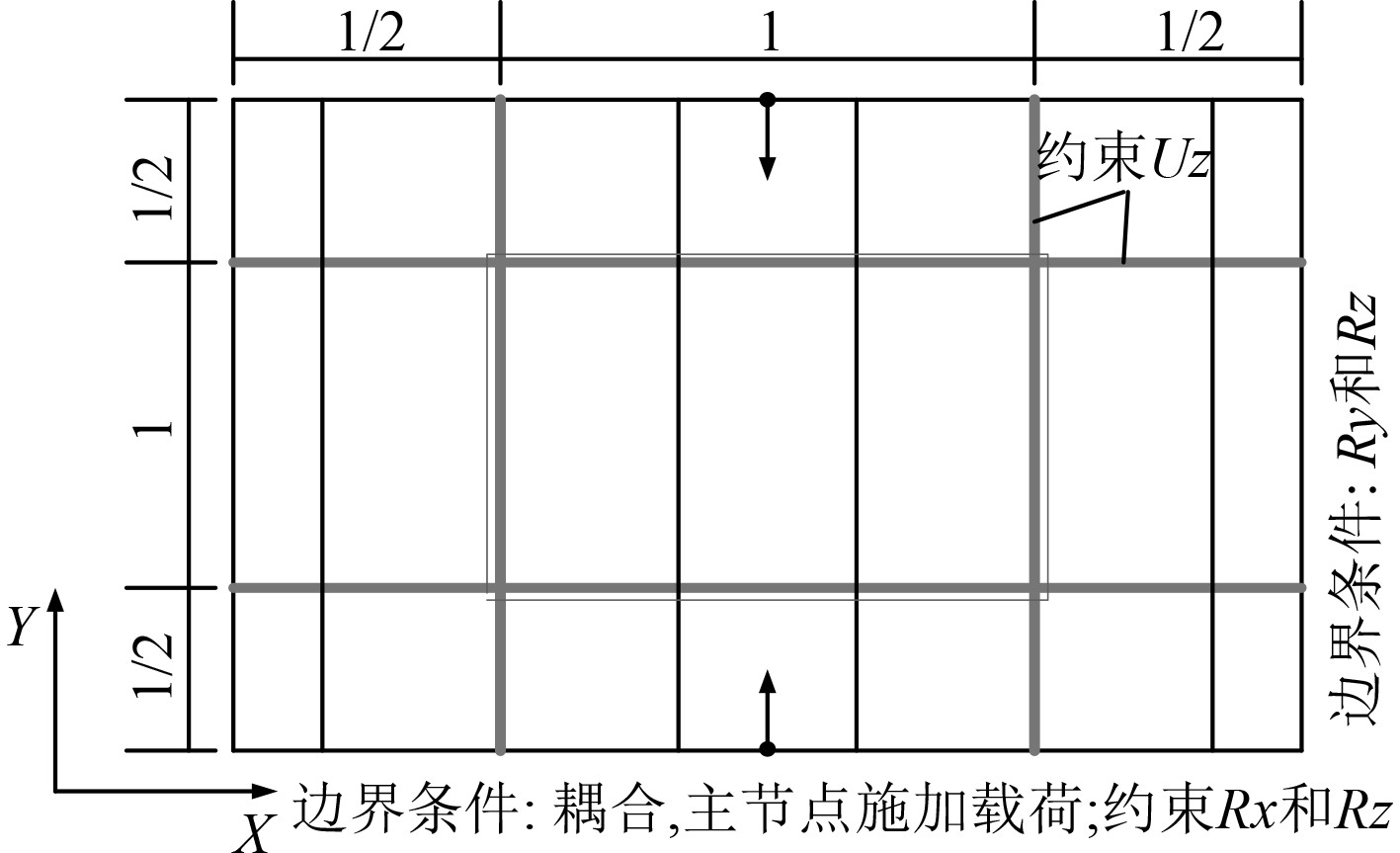
参考加筋板结构单轴压缩作用下极限承载能力非线性有限元分析所采用的模型范围和边界条件[5-7],计算模型采用“1/2+1+1/2”的模型范围,即目标结构四周各延伸半个模型范围,四周采用对称边界条件,并约束其垂向位移[8]。金属夹芯板模型主要承受纵向压缩载荷,考虑平断面假定,其受压端部采用耦合的方式约束,在横截面形心处创建主节点,截面所有节点与主节点耦合,在主节点施加集中强制位移载荷。有限元模型边界条件示意图如图3所示。
|
图 3 有限元模型边界条件示意图 Fig. 3 Boundary conditions of finite element model |
采用Abaqus软件的显式准静态分析模块,在模型的主节点处施加强制位移载荷,分载荷步光顺加载,对设计的计算模型开展极限分析,获取不同缩比组合状态下模型的极限承载能力,以探讨缩比条件对不同模型承载能力的影响。
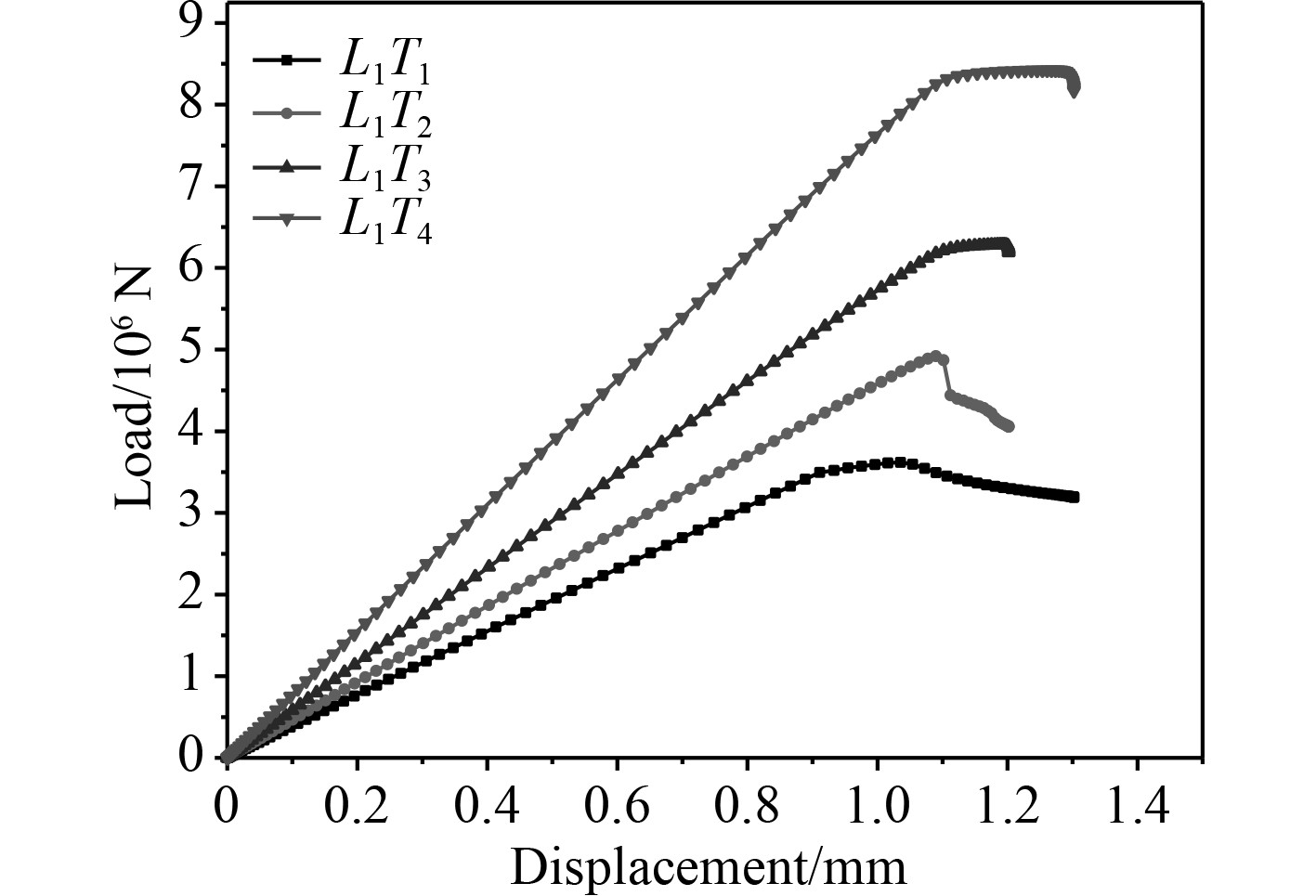
通过主节点处的位移载荷和支反力,绘制模型端部的位移-载荷曲线。图4给出了不同板厚缩比下模型端部的位移-载荷曲线。可以看出,随着板厚增加,弹性阶段曲线斜率增加,模型的刚度逐步增大;载荷到达极限后,4条曲线下降的趋势差异较大,表明4个模型塑性阶段对应的后屈曲特性存在差异。
|
图 4 不同板厚缩比模型端部位移载荷曲线 Fig. 4 Load-displacement curves of different thickness scaling models |
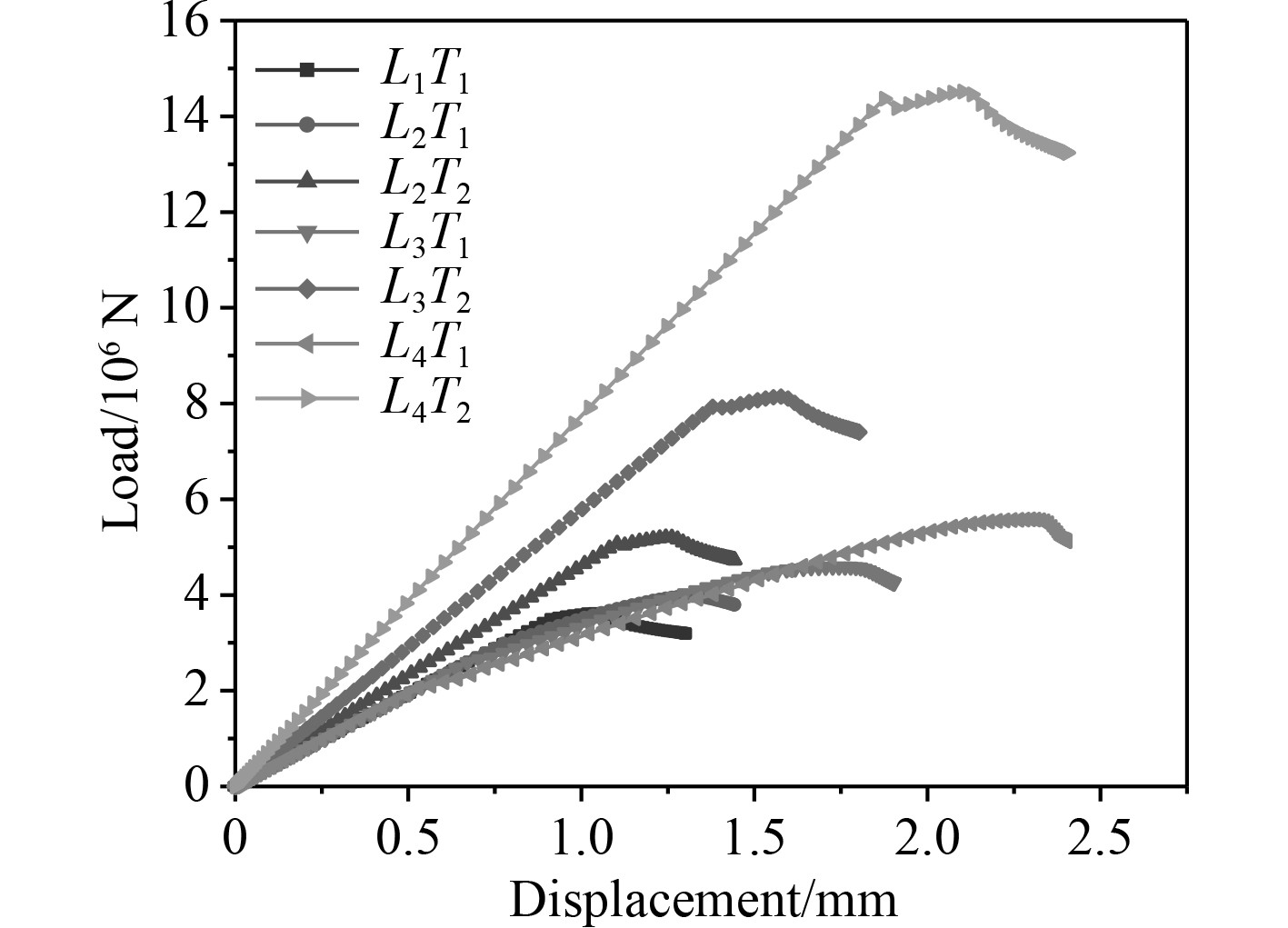
图5给出了不同缩比组合下计算模型端部位移—载荷曲线。原始板厚不同长度缩比计算模型的曲线较为集中,表明长度缩比对刚度的影响相对板厚的影响较小;板厚缩比和长度缩比相同组合模型的曲线变化趋势较为一致,与原型模型的曲线成比例吻合。
|
图 5 不同缩比组合下模型端部位移载荷曲线 Fig. 5 Load-displacement curves of structure models with different scaling |
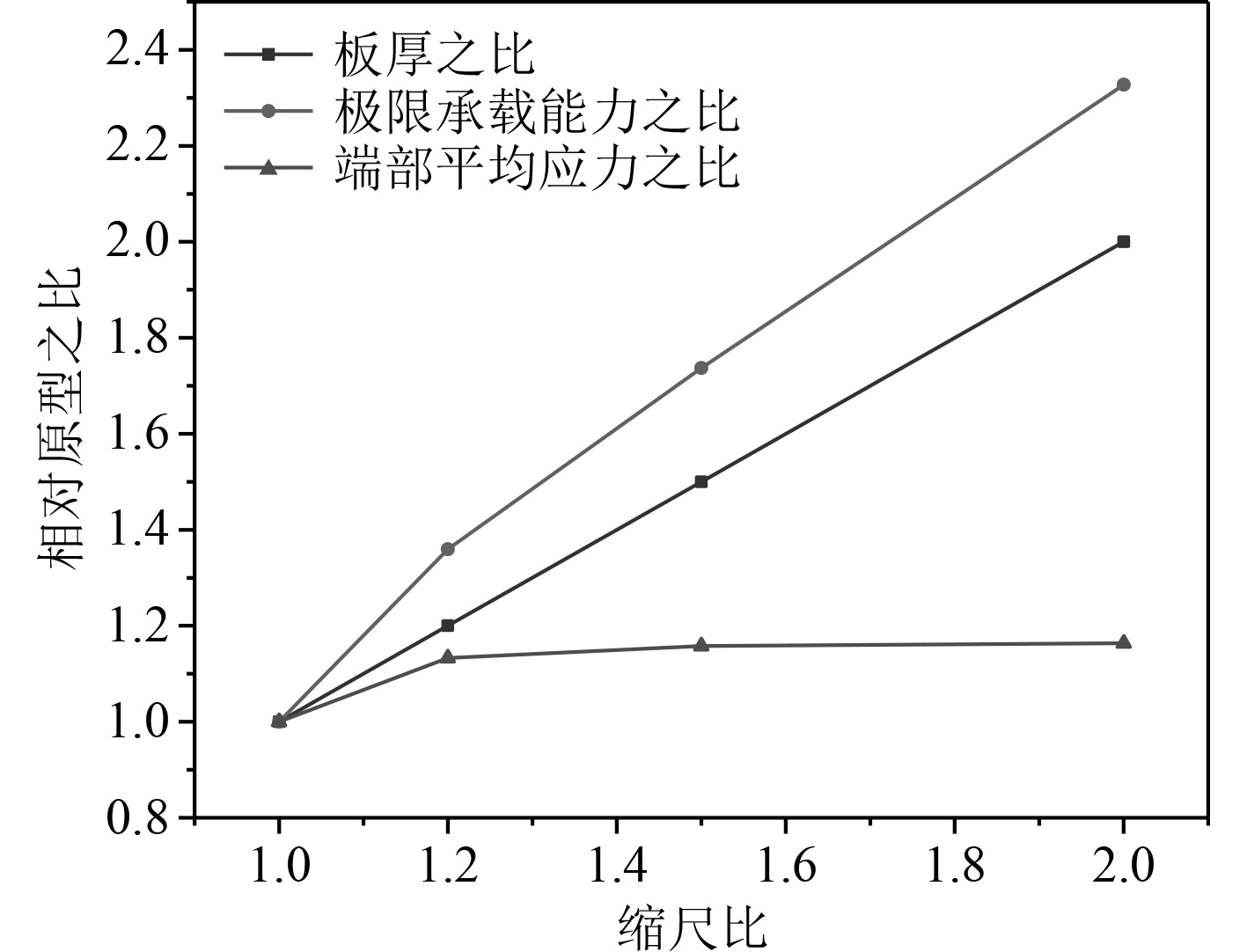
通过模型的端部位移-载荷曲线,可得到模型的极限承载能力;端部极限载荷与端部截面面积之比,即可得到模型的端部平均应力。表3和图6分别给出了不同板厚缩比条件下模型的极限承载能力的对比情况和模型承载特性与缩比之间的关系。4个模型的端部平均应力均小于材料的屈服应力,随着板厚增加,其端部平均应力向材料屈服应力接近;板厚增加至一定程度时,模型由屈曲失效向屈服失效转变;由于失效模式变化,使得模型的极限承载能力与缩比呈现非线性。
|
|
表 3 不同板厚缩比模型极限承载能力对比 Tab.3 Comparison of ultimate bearing capacity of different thickness scaling models |
|
图 6 不同板厚缩比下模型承载特性与缩比的关系 Fig. 6 Relationship between load bearing characteristics and scale of model under different thickness scaling |
表4给出了不同缩比组合下模型极限承载能力的对比情况。当板厚缩比与长度缩比相同时,不同缩比条件下模型的端部平均应力较为一致,这与端部的载荷位移曲线成比例的规律相吻合;板厚缩比相同时,随着长度缩比的增加,其模型的承载能力增加,但端部平均应力有所下降,这是由于长度增加使得结构端部承载面积增加,但模型刚度降低,板的柔度系数增加,使得板的屈曲强度降低。
|
|
表 4 不同缩比组合下模型极限承载能力对比 Tab.4 Comparison of ultimate bearing capacity of models under different scales |
图7给出了原型结构极限状态下的Mises应力分布云图,图8给出了L2T2模型极限状态下的Mises应力分布云图。L3T3和L4T4模型极限状态应力分布与L2T2以及原型的应力分布相同,均呈现典型的板格屈曲失效模式,横向一个胞元内板格表现为一个失稳波形,纵向范围表现为多个失稳波形,4个模型仅变形幅值存在差异。

|
图 7 L1T1极限状态应力分布云图 Fig. 7 Mises stress distribution of L1T1 |

|
图 8 L2T2极限状态应力分布云图 Fig. 8 Mises stress distribution of L2T2 |
图9和图10分别给出了L2T2和L1T3模型极限状态下的Mises应力分布云图。L1T4应力分布与L1T3模型应力分布一致,随着板厚增加,其失效模式发生变化,L1T1(原型)整个模型屈曲失效,L1T2模型中间范围屈曲失效导致整体崩溃,L1T3和L1T4呈现横截面整体进入塑性,屈服失效。

|
图 9 L1T2极限状态应力分布云图 Fig. 9 Mises stress distribution of L1T2 |

|
图 10 L1T3极限状态应力分布云图 Fig. 10 Mises stress distribution of L1T3 |
图11和图12分别给出了L2T1和L3T1模型极限状态下的Mises应力分布云图。L4T1模型极限状态下的Mises应力分布与之接近,其失效模式与原型的失效模式类似,均呈现屈曲失效。

|
图 11 L2T1极限状态应力分布云图 Fig. 11 Mises stress distribution of L2T1 |

|
图 12 L3T1极限状态应力分布云图 Fig. 12 Mises stress distribution of L3T1 |
基于非线性有限元法,对设计的I型金属夹芯板单轴压缩作用下的极限承载特性进行对比分析,以探索不同缩尺比对其极限承载能力的影响,为金属夹芯结构的试验缩比模型设计提供支撑。计算结果表明:
1)板厚缩比与长度缩比相同时,不同缩比模型的极限承载特性成比例吻合,因此,模型设计时应尽可能使板厚缩比与长度缩比接近,以降低缩尺比奇异性的影响;
2)板厚缩比与长度缩比不一致时,板厚的变化将导致模型的失效模式产生偏差,降低缩比模型计算结果的相似吻合度,缩比模型的极限承载能力与缩尺比呈现非线性。
3)由于尺度效应的影响,金属夹芯结构试验缩比模型设计时,在保证几何相似的前提下,还应考虑结构承载特性的非线性影响,尽可能保证缩比模型的失效模式相似,提高其非线性相似度。
| [1] |
陈杨科, 何书韬, 刘均, 等. 金属夹层结构的舰船应用研究综述[J]. 中国舰船研究, 2013, 8(6): 6-13. CHEN Y K, HE S T, LIU J, et al. Application and prospect of steel sandwich panels in warships[J]. Chinese Journal of Ship Research, 2013, 8(6): 6-13. |
| [2] |
谢仲安. 舱段极限强度试验模型设计研究[D]. 上海: 上海交通大学, 2010
|
| [3] |
朱志辉, 极限强度模型试验非线性相似准则研究[D]. 武汉: 武汉理工大学, 2017.
|
| [4] |
程瑞琪, 裴志勇, 等. 极限强度模型试验非线性相似方法研究[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(1): 195-200. Cheng Rui-qi, Pei Zhi-yong, et al. Research on nonlinear similarity method for ultimate strength model test[J]. Journal of Wuhan university of technology (transportation science & engineering), 2020, 44(1): 195-200. |
| [5] |
FUJIKUBO M, HARADA M, YAO T, et al. Estimation of ultimate strength of continuous stiffened panel under combined transverse thrust and lateral pressure Part 2: Continuous stiffened panel[J]. Marine Structures, 2005, 18(5-6): 411-427. DOI:10.1016/j.marstruc.2006.01.001 |
| [6] |
PAIK J K, KIM B J, SEO K W. Methods for ultimate limit state assessment of ships and ship-shaped offshore structures: Part II stiffened panels[J]. Ocean Engineering, 2008, 35(2): 271-280. DOI:10.1016/j.oceaneng.2007.08.007 |
| [7] |
PAIK J K, SEO J K. Nonlinear finite element method models for ultimate strength analysis of steel stiffened-plate structures under combined biaxial compression and lateral pressure actions-part II: stiffened panels[J]. Thin-walled Structures, 2009, 47(8/9): 998-1007. |
| [8] |
李政杰, 黄路, 赵南, 等. 单轴压缩下金属夹层板极限承载性能分析[J]. 中国舰船研究, 2020, 15(4): 53-58. LI Z J, HUANG L, ZHAO N, et al. Ultimate bearing capacity for steel sandwich panels under uniaxial compression[J]. Chinese Journal of Ship Research, 2020, 15(4): 53-58. DOI:10.19693/j.issn.1673-3185.01554 |
 2023, Vol. 45
2023, Vol. 45
