2. 江苏省船海机械先进制造及工艺重点实验室,江苏 镇江 212003
2. Jiangsu Provincial Key Laboratory of Advanced Manufacture and Process for Marine Mechanical Equipment, Zhenjiang 212003, China
柱形壳因为其结构简单承载能力好而应用广泛,其中海洋平台桩腿是其应用最多的领域之一[1]。海水具有较强的腐蚀性,海水腐蚀破坏在海洋环境中十分常见,如深海管道、远洋船体和海洋平台桩腿等,一直受到腐蚀危害。海洋平台桩腿因为常年在海洋环境下工作,桩腿的外壁会产生局部腐蚀,严重情况下会导致桩腿发生非线性屈曲,影响海洋平台的稳定与安全[2]。
在腐蚀的情况下柱形壳的轴向临界载荷的计算十分复杂。Philippe [3]在外压圆柱壳缺陷敏感性研究领域中,证明几何缺陷不容忽视。Blachut[4] 利用有限元方法研究了许多不同形状缺陷对圆柱壳屈曲特性的影响,其中包括了样条形缺陷和矩形凹陷等。Arbelo等[5]在复合材料圆柱壳邻域进行了研究,主要研究多点凹陷的复合材料对圆柱壳极限载荷产生的影响,最终发现多点扰动载荷更加保守。Kreilos[6]以及Virot等[7]分别从理论和试验的角度研究了局部凹坑缺陷对轴压圆柱壳屈曲强度的影响。MacKay等[8]在腐蚀损伤对稳定性产生的影响进行了研究,通过设计铝钢瓶试验,发现人为制造的减薄区域在失稳过程中产生应力集中,其抗压能力与人为减薄厚度相关。Inoue等[9]在对102号直管管材破坏行为影响的要素研究中,利用人为壁厚减薄模拟海洋腐蚀损耗,对减薄的形状和位置等因素进行了研究。这些研究局部腐蚀的对象多种多样,然而目前轴压圆柱壳研究中,探索局部腐蚀缺陷对柱形壳屈曲特性有何影响的研究鲜见报道。
本文利用壁厚减薄模拟海洋中柱壳的腐蚀损失,尝试加工了4种不锈钢局部减薄柱形壳试验模型,以及一个未进行减薄加工的完好柱壳试验模型,对这些试验模型进行三维光学扫描、超声波无损测试和轴向外压试验,并采用数值方法分析局部减薄壳体的屈曲特性,考察局部减薄缺陷位置、局部减薄缺陷形状对壳体的影响。
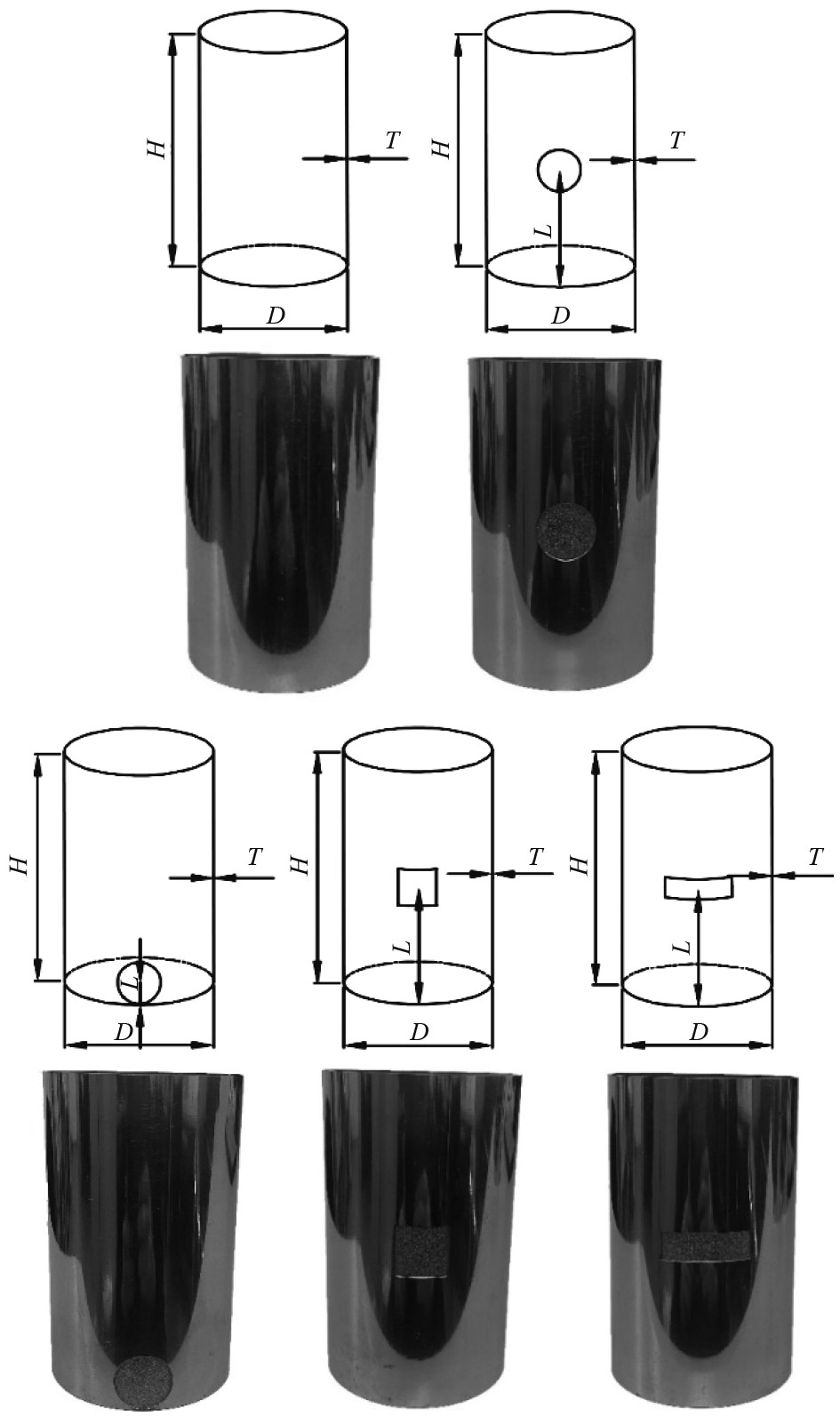
1 材料与方法研究对象是海洋平台的桩腿,该桩腿的结构是圆柱壳,实际尺寸如下:每段圆柱壳高度为4500 mm,一共由13段构成,每段圆柱壳的厚度为48 mm,直径为2800 mm,对其中一段圆柱壳进行40∶1的缩小,得到本文的研究对象。其尺寸如下:外径D=70 mm,高度或长度H=112.5 mm,厚度T=1.2 mm,T/R=0.034,根据Zhang等[10]对耐压壳的研究,T/R=0.05为厚壳、薄壳的分界值。如图1所示,不锈钢柱形壳的5种实物模型分别为未减薄的完好柱壳(PE),中部圆形减薄柱壳(RC),端部圆形减薄柱壳(RE),中部方形减薄柱壳(SC),中部长方形减薄柱壳(OC)。对于减薄缺陷处,减薄的体积为柱壳总体积的1%,本文研究了3种减薄形状,分别为:直径d=20 mm的圆形、边长为17.72 mm的方形和长宽分别为31.4 mm,10 mm的长方形。减薄处厚度t=0 .7 mm,即与原来的壁厚相比t/T约为60%的厚度,减薄处的面积都近似相等于314 mm2。
|
图 1 柱形壳模型图 Fig. 1 Cylindrical shell model drawing |
减薄缺陷几何中心距底端长度为L,L在图1四个减薄模型中分别为56.25 mm,10.5 mm,56.25 mm,56.25 mm,与柱壳高度相比T/H分别为50%,9.33%,50%,50%。这些缺陷形状是指柱壳展开后表面上的形状,与直接投影至柱壳有所区别。
共有5种类型的试件,分别称为PE,RC,RE,SC,OC,为保证数据可重复性,每个试件均制作了4个,分别编号1,2,3,4,共20个试件。这样就可以通过试验对局部减薄柱壳的屈曲特性进行研究。
1.1 加工与测试材料是一种奥氏体不锈钢,其无明显屈服极限,因此以产生0.2%残余变形的应力值作为其屈服极限。测试3次,0.2%残余变形应力值分别为452.00 MPa,458.85 MPa和460.15 MPa,其均值屈服强度
试验柱形壳利用激光从长圆柱钢管上切割下来,相较于传统砂轮切割有更小的误差,为轴压实验提供了更好的轴心受压条件。柱形壳上的局部减薄是采用电火花加工方式实现,其原理是电蚀作用蚀除导电材料,利用此种加工方法在良好的加工条件下可以获得相对较好的表面粗糙度[11]。
采用Cronos 3D光学扫描仪测量每个试验壳体外表面形状,获取表面点云的坐标数据,用具有三维误差检测功能的软件GOM Inspect软件对扫描结果进行处理。软件会将光学扫描仪的点云数据转换为三维网格数据,之后对比网格数据和CAD名义尺寸数据进行圆柱壳的表面误差检测。之后,采用超声波测量仪PX-7对6个柱形壳进行厚度测量,沿模型周向均分10组,每组沿轴向测量7个点位(落入缺陷处的点不计入结果),减薄缺陷内等间距取三横三竖的9个交点并测量其厚度,测量结果列于表1。
|
|
表 1 模型壁厚测量结果 Tab.1 Measured wall thickness data for specimens |
形状和壁厚测量之后,对柱壳试验模型进行轴向压力测试,获取壳体屈曲载荷和最终失稳模式。试验采用万能压缩试验机,试件是由激光切割而成,两端面非常平整,压缩试验机平台水平放置一个圆盘,将柱壳试件放置于圆盘上。将压力机压头慢慢调至刚与柱壳的上端部接触后,开始正式压缩试验。压头下降的速率为1 mm/min,压缩变形量设置为4 mm。
1.2 数值模型按照测量尺寸采用有限元法对20个试验柱形壳进行数值建模。采用ANSA软件进行数值模型网格划分,单元数量根据网格收敛性分析确定。单元的类型主要使用四边形壳通用单元S4,部分使用三角形通用壳单元S3,使用Abaqus软件进行处理分析。
首先,在Abaqus软件中进行线性屈曲分析,本次材料使用的是奥氏体不锈钢,这种材料的各向异性不明显,所以在仿真过程中不予特殊考虑。不锈钢材料参数定义为:杨氏模量
|
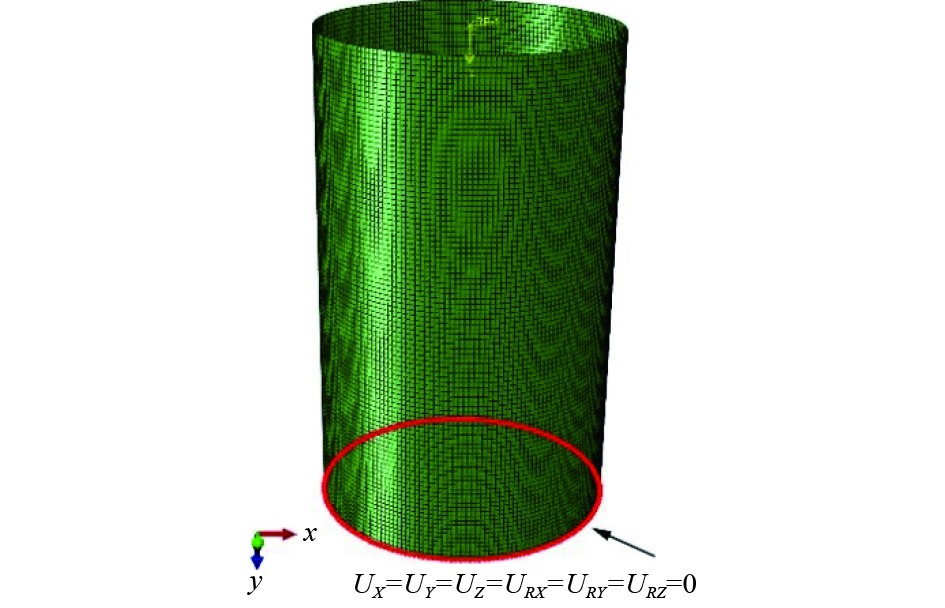
图 2 有限元模型 Fig. 2 Finite element model |
线性屈曲分析仅能分析理想情况下线弹性壳体的屈曲特性,无法对非线性特性进行分析[13]。为了得到更为准确的结果,进行非线性屈曲分析。在Abaqus软件中,使用其Riks弧长法进行非线性屈曲分析,理想弹塑性模型如下式:
| $ \sigma =\left\{\begin{array}{c}Eϵ\sigma \leqslant {\sigma }_{yp},\\ {\sigma }_{yp}\sigma > {\sigma }_{yp}{\text{。}}\end{array}\right. $ | (1) |
式中:
在分析步模块中利用Riks弧长法进行非线性屈曲分析,其基本参数为:初始弧长0.01 mm,最大弧长0.01,最小弧长1×10−50 mm,总弧长1 mm的最大迭代步数为3000。初始载荷为50000,此外采用和线性屈曲分析相同的边界条件。
由此可以获得柱形壳模型非线性屈曲过程的平衡曲线,此曲线极值点即为临界屈曲载荷。
2 结果分析与讨论 2.1 测量结果分析图3为20个柱形壳的扫描模型相对于理想模型的误差云图。误差大小的范围可以从右侧数值带数据看出,误差频数分布情况可以从右侧曲线看出。图中减薄柱壳的误差比完好柱壳的误差要大,且减薄柱壳的上偏差多集中在减薄区域的上下两侧,其可能和减薄缺陷的加工过程相关,总体上20个试件的误差基本在−0.1~0.3 mm之间。

|
图 3 柱壳扫描模型及其几何误差云图 Fig. 3 Cylindrical shell scanning model and geometric error cloud |
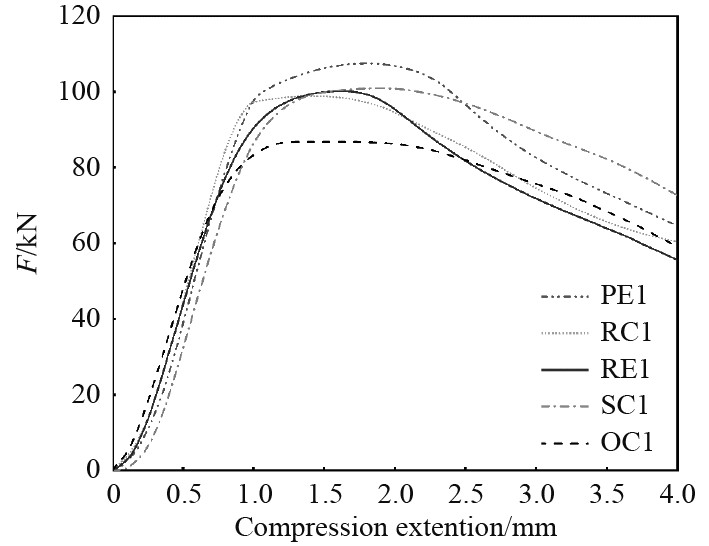
计算机通过数据采集系统在试验过程中采集数据,本次试验中主要采集位移与载荷数据,试验的位移量为0~4 mm。如图4所示,以第1组5个柱形壳为例,根据它们的数据进行位移载荷图的绘制。
|
图 4 第一组柱壳试验载荷位移曲线 Fig. 4 Load displacement curves of the first set of cylindrical shell tests |
图4局部减薄柱壳与完好柱壳拥有相似的位移-载荷曲线。所有的曲线都有上升阶段、屈曲临界点和屈曲失稳阶段。由于此种类型的不锈钢具有较高的韧性,故没有破坏阶段。开始时载荷并没有出现迅速增长,导致这种现象的原因可能是壳体上下两端存在的长度缺陷。随着位移的继续增大,载荷上升出现屈曲临界点。经过临界点后,载荷开始缓慢降低。
表2为5种柱壳试验测得的最大屈曲载荷数值,各组柱壳试件的试验数值具有良好重复性。由表2可见,未减薄完好柱壳的屈曲载荷明显大于其他4种局部减薄柱壳,最大差值达到20.69 kN,表明腐蚀减薄在会很大程度上削弱了柱壳的承载能力;在4个完好柱壳中,根据作用在截面平均壁厚上的力,求得的压强均未达到材料的屈服强度457 MPa,还未达到塑性失效的范围,所以本次试验的完好柱壳都是失效在弹性区间或者是弹塑性区间。在中部腐蚀减薄的3种试件RC,SC,OC中,中部长方形减薄柱壳OC的临界载荷值则明显小于其他2种柱壳,最大差值达到14.53 kN,其差异程度约为其承载能力的16.7%,这表明腐蚀形状对柱壳的承载能力有非常大的影响,其还可能与周向方向的缺陷尺寸成正相关,有待进一步研究。中部圆形减薄柱壳OC和中部方形减薄柱壳SC的承载能力相差不大可能是由于其形状相似。对于缺陷位置不同的柱壳RC和RE而言,RC的最大载荷都要小于RE的最小载荷,载荷最大差值为2.57 kN,约为其承载能力的2.6%,显然,缺陷位置对柱壳的承载能力是有影响的。
|
|
表 2 数值计算与试验极限载荷值 Tab.2 Numerical calculation and test limit load value |
局部减薄缺陷柱形壳的后屈曲模式如图5所示,可知,各组模型的试验结果具有良好重复性。完好柱壳PE的4个试件中1号,2号和4号试件上端发生鼓曲,3号试件下端发生鼓曲,这表明鼓曲位置的发生不是固定的。可能与柱壳存在的初始缺陷有关。腐蚀柱壳的后屈曲一般呈现为腐蚀区域的凹陷,腐蚀区域上下相邻区域的凸起。

|
图 5 柱形壳后屈曲模式 Fig. 5 Post-buckling mode of cylindrical shells |
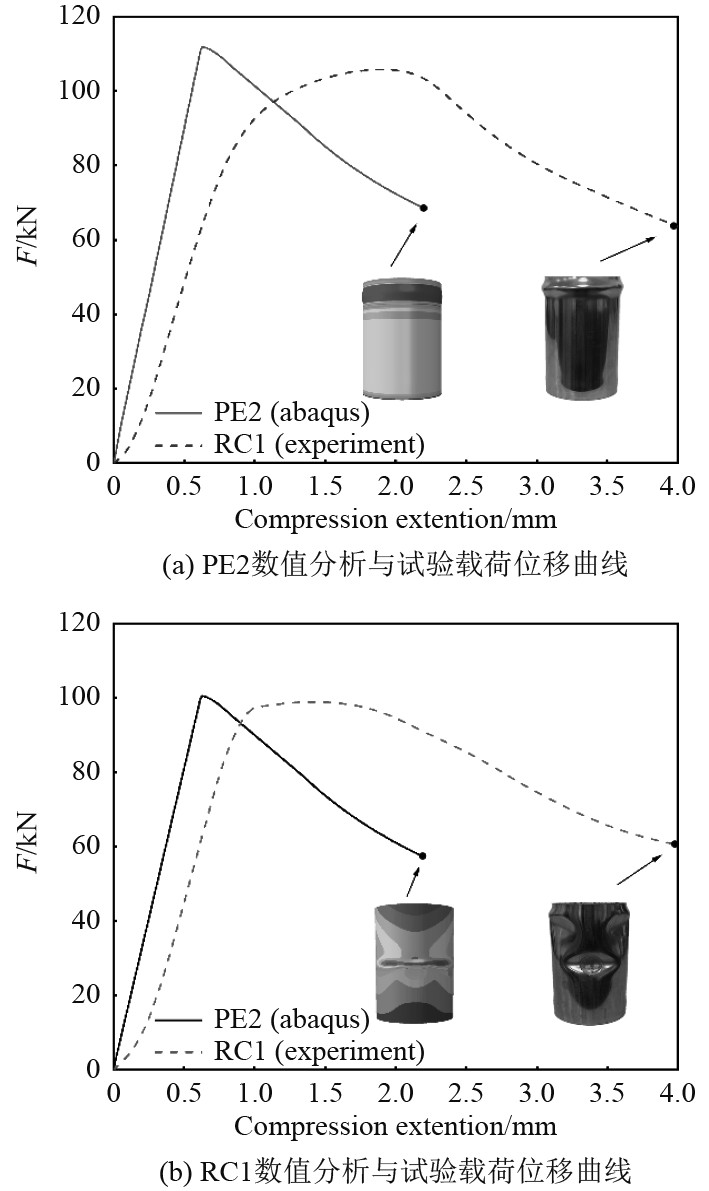
非线性屈曲分析中获得柱壳的平衡路径曲线和后屈曲模式,分别将曲线、屈曲模式与试验所得结果进行对比,以完好柱壳PE2和腐蚀柱壳中的RC1为例,如图6所示。
|
图 6 数值分析与试验载荷位移曲线比较 Fig. 6 Load-displacement curves for experimental and numerical analysis |
由图6可以直观看出,两者初始阶段的斜率存在偏差。图中数值计算 所得上升段几乎为直线,试验曲线上升阶段斜率先逐渐增大之后缓慢减小,减小到0时即出现临界载荷。上升阶段试验曲线的综合斜率要小于数值分析曲线,这会使出现极限载荷的位移值有比较大的偏差。Ifayefunmi[14]认为这种位移偏差可以通过边界条件改变。图中有限元与试验柱壳的后屈曲模式,两者之间都有很好的印证。完好柱壳的破坏应力和变形主要集中在上端部,对于减薄柱壳而言,不仅上端部同样存在着较大的破坏应力与变形,其减薄处的变形量更大。
5种柱壳非线性分析临界载荷值见表2,与试验值相近,且重复性良好,其中完好柱壳相差最大,但其中最大的差值也仅有6.2%,证明有限元模型建立的正确性。其次非线性分析减薄柱壳的临界载荷的误差是小于完好柱壳的,表明有限元在分析轴压局部减薄柱壳的问题上也是有效的。
3 结 语本文进行5种柱形壳的轴向压力测试,测试结果具有良好重复性,并进行了壳体的数值计算,数值结果与试验结果吻合良好,结论如下:
1)柱形壳对腐蚀减薄形状和腐蚀减薄位置都具有敏感性。尤其对于柱壳周向长方形缺陷形状的敏感性更强,而对于缺陷位置的敏感则稍弱。
2)完好柱壳的应力应变主要分布在柱壳两端,失效在弹性或者弹塑性区间,而减薄柱壳的最大应力应变主要存在于减薄缺陷附近。
3)存在减薄柱壳临界载荷远小于完好柱壳的情况,表明腐蚀是桩腿承载能力下降的重要原因,柱壳对腐蚀具有较强的敏感性的。
4)有限元分析结果与试验结果具有较好的重复性,平均误差仅为3%,这表明有限元在分析轴压局部减薄柱壳问题上的有效性。
| [1] |
金晔. 自升式风电安装船桩腿强度分析和优化[J]. 舰船科学技术, 2021, 43(3): 131-135. DOI:10.3404/j.issn.1672-7649.2021.02.027 |
| [2] |
邱少华. 导管架海洋平台整体结构海冰载荷环境下响应分析[J]. 船海工程, 2020, 49(4): 30-33. DOI:10.3963/j.issn.1671-7953.2020.04.008 |
| [3] |
PHILIPPE L G, PASCAL C, DOMINIQUE C. Influence of residual stresses and geometric imperfections on the elastoplastic collapse of cylindrical tubes under external pressure[J]. Marine Structures, 2009, 22(4): 836-854. DOI:10.1016/j.marstruc.2009.09.003 |
| [4] |
BLACHUT J. Imperfection sensitivity of externally pressurised shells[J]. Revue Européenne des- Eléments, 2012, 13(8): 787-810. |
| [5] |
MARIANO A. Arbelo et al. Numerical characterization of imperfection sensitive composite structures[J]. Composite Structures, 2014, 108: 295-303. DOI:10.1016/j.compstruct.2013.09.041 |
| [6] |
TOBIAS K, TOBIAS M S. Fully localized post-buckling states of cylindrical shells under axial compression[J]. Proceedings of the Royal Society A, 2017, 473(2205).
|
| [7] |
VIROT E, et al. Stability Landscape of Shell Buckling.[J]. Physical review letters, 2017, 119(22): 224101. DOI:10.1103/PhysRevLett.119.224101 |
| [8] |
JOHN R, MACKAY, et al.. Experimental investigation of the strength and stability of submarine pressure hulls with and without artificial corrosion damage[J]. Marine Structures, 2010, 23(3): 339-359. DOI:10.1016/j.marstruc.2010.06.001 |
| [9] |
INOUE K, TAKAHASHI K, ANDO K, et al. Finite element analysis on the failure behavior of straight pipe with wall thinning[J]. Pessure Vessel and Piping Codes and Standards, 2004, 480: 1-7. |
| [10] |
ZHANG J, ZHANG M, TANG W X, et al. Buckling of spherical shells subjected to external pressure: A comparison of experimental and theoretical data[J]. Thin-Walled Structures, 2017, 111: 58-64. DOI:10.1016/j.tws.2016.11.012 |
| [11] |
李晓舟, 孙宇博, 许金凯, 等. 304不锈钢电火花线切割加工表面性能研究[J]. 表面技术, 2015, 44(6): 104-108. DOI:10.16490/j.cnki.issn.1001-3660.2015.06.020 |
| [12] |
周通, 唐文献, 王纬波, 张建. 轴压复合材料蛋形壳屈曲特性[J]. 船舶力学, 2018, 22(2): 174-188. DOI:10.3969/j.issn.1007-7294.2018.02.006 |
| [13] |
王黎辉, 李其凡, 张建, 唐文献, 朱永梅. 轴压柱形壳非线性屈曲试验与理论研究[J]. 船舶力学, 2021, 25(5): 645-651.
|
| [14] |
IFAYEFUNMI O. Buckling behavior of axially compressed cylindrical shells: Comparison of theoretical and experimental data[J]. Thin-Walled Structures, 2016, 98: 558-564. DOI:10.1016/j.tws.2015.10.027 |
 2023, Vol. 45
2023, Vol. 45
