2. 中国船舶及海洋工程设计研究院,上海 200011
2. Marine Design and Research Institute of China, Shanghai 200011, China
近年来随着我国极地海事活动的频繁,冰载荷的研究也逐渐发展起来,船体结构在冰体作用下的结构响应计算分析是评估船体结构安全性的重要前提,因此,建立合理的试验方法和数值分析方法为极地船舶的结构安全性评估提供了新的思路和方法。
基于海冰原型数据的观测,在试验中通常利用原型参数对海冰进行物理模拟。Tryde[1]结合德国、挪威和丹麦的人工冰和天然冰的模型试验,提出冰力的测量和计算方法并给出影响计算精度的原因。Schultz等[2]提出一种MON冰,将多种有机物浇铸在水面上,这种模型冰确切地模拟了断裂强度和破碎后冰体大小。王永学等[3]给出DUT-1模型冰,其成分包含聚丙烯粉、塑料微粒、水泥及水等材料,产品周期为7d左右,并给出了这种模型冰的物理力学指标和试验验证方法。
对于船-冰碰撞模型试验研究,Vegard[4]进行了停泊在平整冰中的船冰试验,测量了船首与冰的相互作用,建立了船首局部冰力的计算方法。Leira等[5]根据2年的冬季实测数据,将监测数据与实船载荷进行联系,对船舶冰载荷进行估算,并研究了冰厚和船速对应变测量值的影响。
对于船-冰碰撞数值模拟的研究,张健等[6]分析冰体材料和钢材的材料特性,分别提出其本构模型及失效准则,并给出最可能发生碰撞的区域进行计算,得到了多部位多角度碰撞力和船体结构响应。任慧龙等[7]提出了冲撞式破冰模式下有限元建模准则,重点计算了由冲撞式破冰引起的船舯垂向弯矩,指出冰的破坏过程和冰荷载的不连续作用。
1 船体板架-模型冰碰撞模型试验 1.1 模型冰制备模型冰的制备准则必须满足物理和力学的性能指标,对于物理模型的相似性,需要满足弗劳德数和柯西数一致的条件。
1)满足傅汝德数一致
| $ \frac{{V_m^2}}{{{g_m}{L_m}}} = \frac{{V_p^2}}{{{g_p}{L_p}}}{\text{。}} $ | (1) |
式中:
2)满足柯西数一致
| $ \frac{{V_m^2{\rho _m}}}{{{E_m}}} = \frac{{V_p^2{\rho _p}}}{{{E_p}}}。$ | (2) |
式中:
记几何缩尺比
|
|
表 1 主要物理量的比尺 Tab.1 Scale of main physical quantities |
根据文献[8],通过考察走航的实际监测冰厚数据,此次航行过程中北极海冰的平均厚度700 mm左右,根据研究经验,将缩尺比
对于力学指标,需要在完成模型冰制备后进行力学性能的测试,所以首先完成模型冰的制备,基于以往的研究经验,取聚丙烯材料含量80%,水泥含量20%,再添加机油,食用盐,混凝土消泡剂作为添加剂和水均匀混合进行模型冰的制备,时间8 d左右。
对制作完成的模型冰进行物理力学性能的测定。选取小块模型冰进行性能测试。对于密度测定,采用原位浮力法,且保持浸水1 h的稳定密度值。对小块的模型冰进行弯曲强度的测量,上和向下弯曲强度结果相同,表明该模型冰各向同性。采用同样的方法进行弹性模量的测定。最后将另一小块模型冰放在压板中心,单轴均匀缓慢施加载荷直至模型破坏并记录压缩强度。试验测得模型冰的物理力学性能结果如表2所示。
|
|
表 2 模型冰物理力学性能测量结果 Tab.2 Measurement results of physical and mechanical properties of model ice |
根据以上物理性能和力学性能的确定,均在缩尺比为
根据某极地航行船舶的船首肩部冰载荷作用区域,其钢材屈服强度315 MPa,选取包含最低冰区水线和最高冰区水线在内的垂向5000 mm,纵向跨越4个肋位的船体板架,根据傅汝德数和柯西数一致的条件,选用和制备模型冰同样的缩尺比,根据表1的物理量比尺,忽略板架弱构建的影响,设计缩尺比船体板架,其结构图如图1所示。
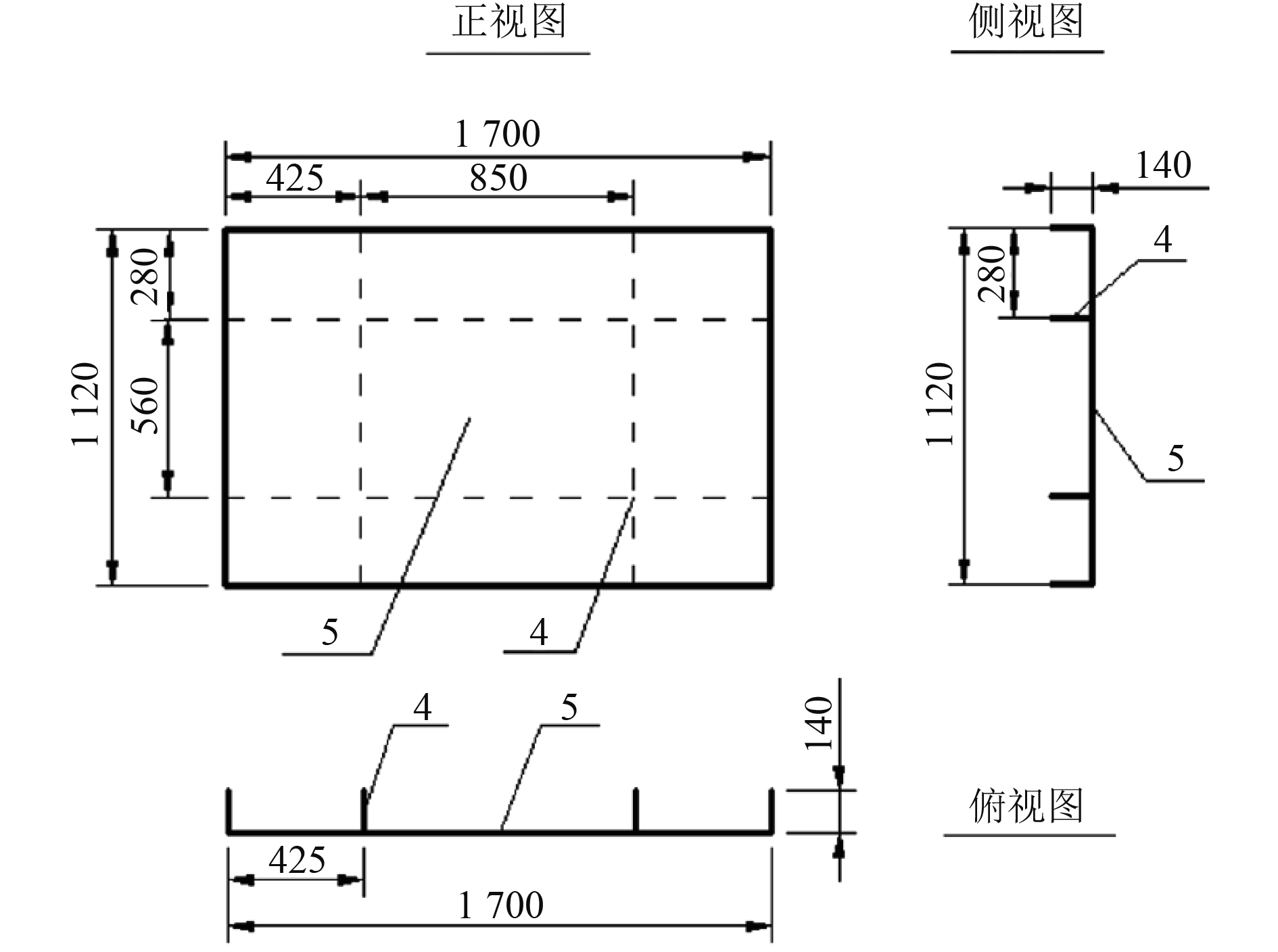
|
图 1 缩尺比船体板架结构模型图 Fig. 1 Structural model drawing of hull plate frame |
将缩尺比船体板架近似为平板,骨材横向间距560 mm,纵向间距850 mm。板架板厚度5 mm,骨材腹板厚度4 mm,选用和实船相同的材料,其弹性模量E为206000 MPa,泊松比为0.3。
完成模型冰和缩尺比船体板架的制备后,设置合理的试验工况参数,进行碰撞的响应研究,在试验中选取2个撞击点位置进行对照试验。
1.3 试验工况极地航行船舶的连续破冰航速较低,一般在1~4 kn之间,根据表1的相似关系,根据破冰均值航速2.5 kn设计试验速度为1.12 kn。
由于实船的船肩碰撞区域为曲面,船冰碰撞行为是以一定的角度进行的,根据研究经验,在模型试验中,取碰撞角度为15°,不同于实际航行的是,试验中将船体板架进行除z方向的位移约束,给模型冰一个匀速撞击板的速度。
模型冰相同,选取板架面板有骨架支撑位置和无骨架支撑位置进行对照实验,考虑到船体板架材料的弹塑性,第1次试验对第2次实验的影响,利用2块尺寸材料都相同的船体板架模型同进行,根据文献[9],长方体模型冰的碰撞发生在棱边上,而棱角的碰撞力体现出最大的特征,基于此特点设置2种试验工况,在每种工况的板上标定2个撞击位置,每个撞击点位置沿x方向布置5个测点,如图2所示。
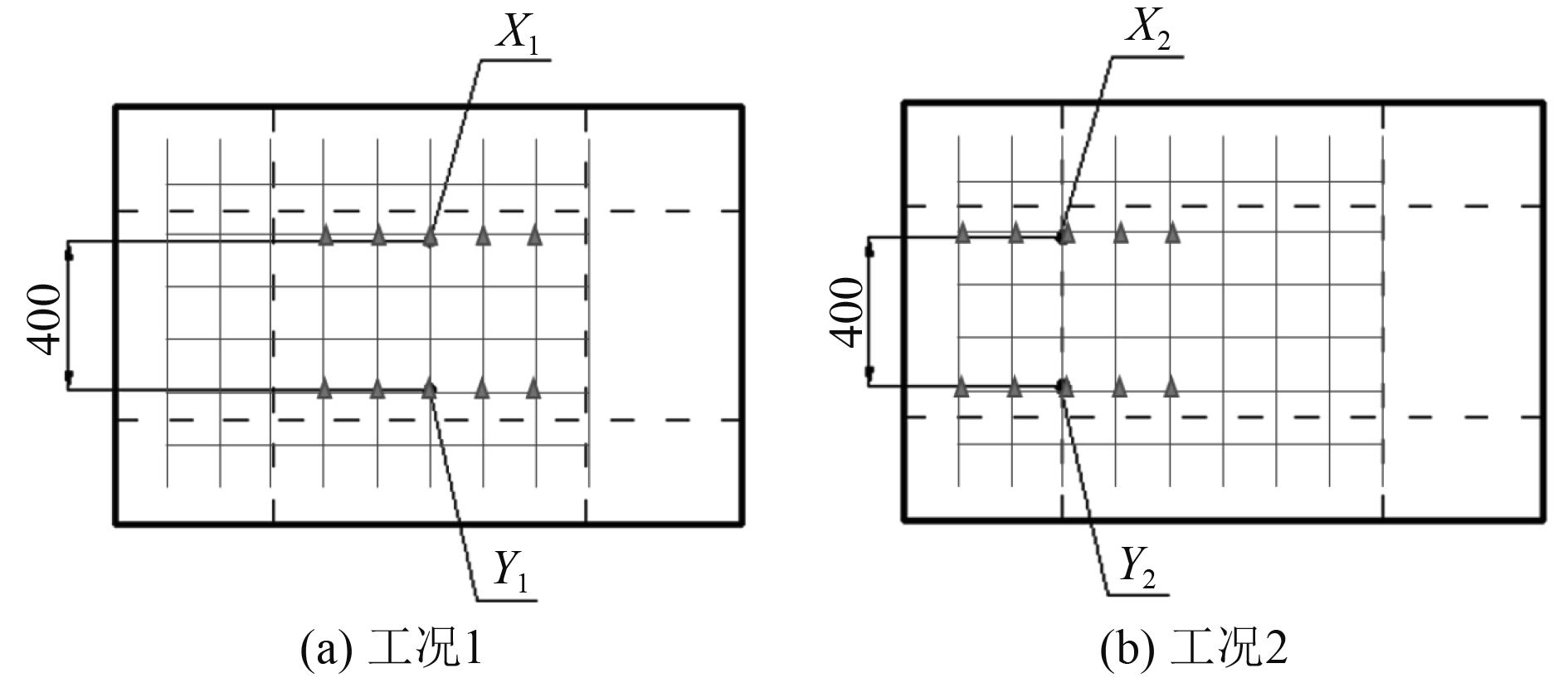
|
图 2 测点布置图 Fig. 2 Layout of measuring points |
每个测点响应监测方法为传感器监测,其中应变传感器为三向应变电阻应变计,置于碰撞面的背侧,所有电阻应变计都可以测3个方向的应变;对于碰撞力的监测运用压力传感器,每个工况均设定2个竖直方向和4个水平方向的压力传感器。
1.4 试验结果 1.4.1 应力应变结果根据碰撞试验所得的监测数据分析结构的响应,对于应变传感器的监测数据,对每个测点测得的应变值
| $ {\sigma _{vm}} = \sqrt {\frac{1}{2}[{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _3} - {\sigma _1})}^2}]}{\text{。}} $ | (3) |
式中:
工况1测点1~测点5和测点6~测点10对称分布。如图3所示,测点3和测点8的应力最大,随着到撞击点的距离的增加应力逐渐变小,对称测点显示出相同的变化特性,并且随时间的增加,处测点5和测点10受水波动影响大以外,其他测点应力值平稳,在0.7 s附近突然急速增大并达到峰值,然后迅速下降,在0.8 s时呈现出另一个波动峰值。
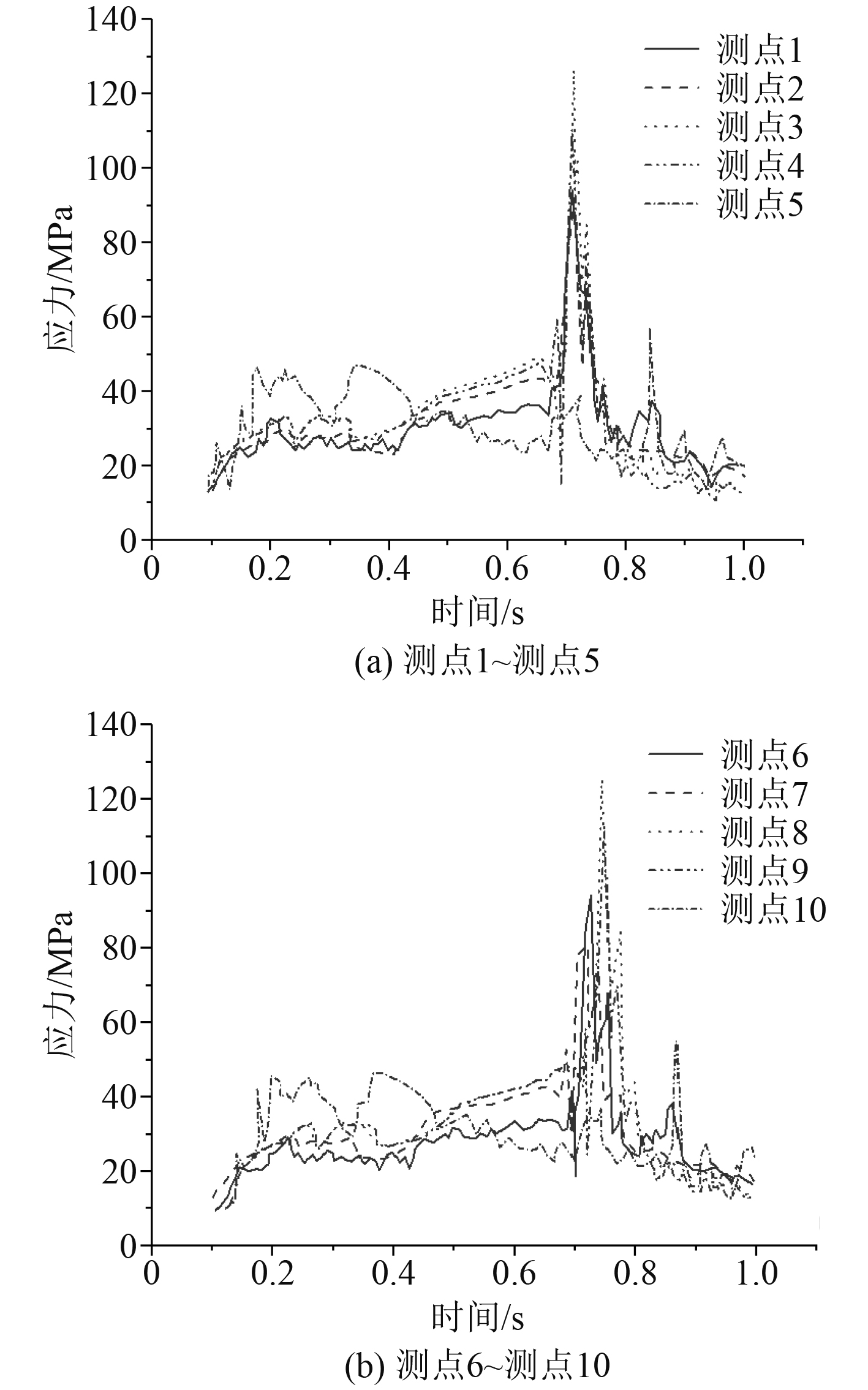
|
图 3
工况1船体板架测点应力
|
从试验结果来看,产生这种现象的原因是在0.7 s结构产生最大的响应时,发生了第1次碰撞,产生应力峰值,随后模型冰破碎,前部的模型冰破碎后给后部分的模型冰继续运动的空间,这时候应力急剧下降,再随着后部分的模型冰继续接触,产生下一个应力峰值,这样便形成了后续应力起伏的变化趋势。
工况2应力结果如图4所示,测点11~测点15和测点16~测点20对称分布。工况2的应力结果也呈现出在增加到一个大峰值后急剧下降然后连续上下波动的特点。和工况1的结果相对比,因为工况2模型撞击点位于纵桁上,最大应力100 MPa左右,而工况1最大应力120 MPa左右。另外,碰撞点应力最大,越向四周延伸,应力越小,而且结构较弱的变形范围及变化程度更大,对于2种工况的规律一致。
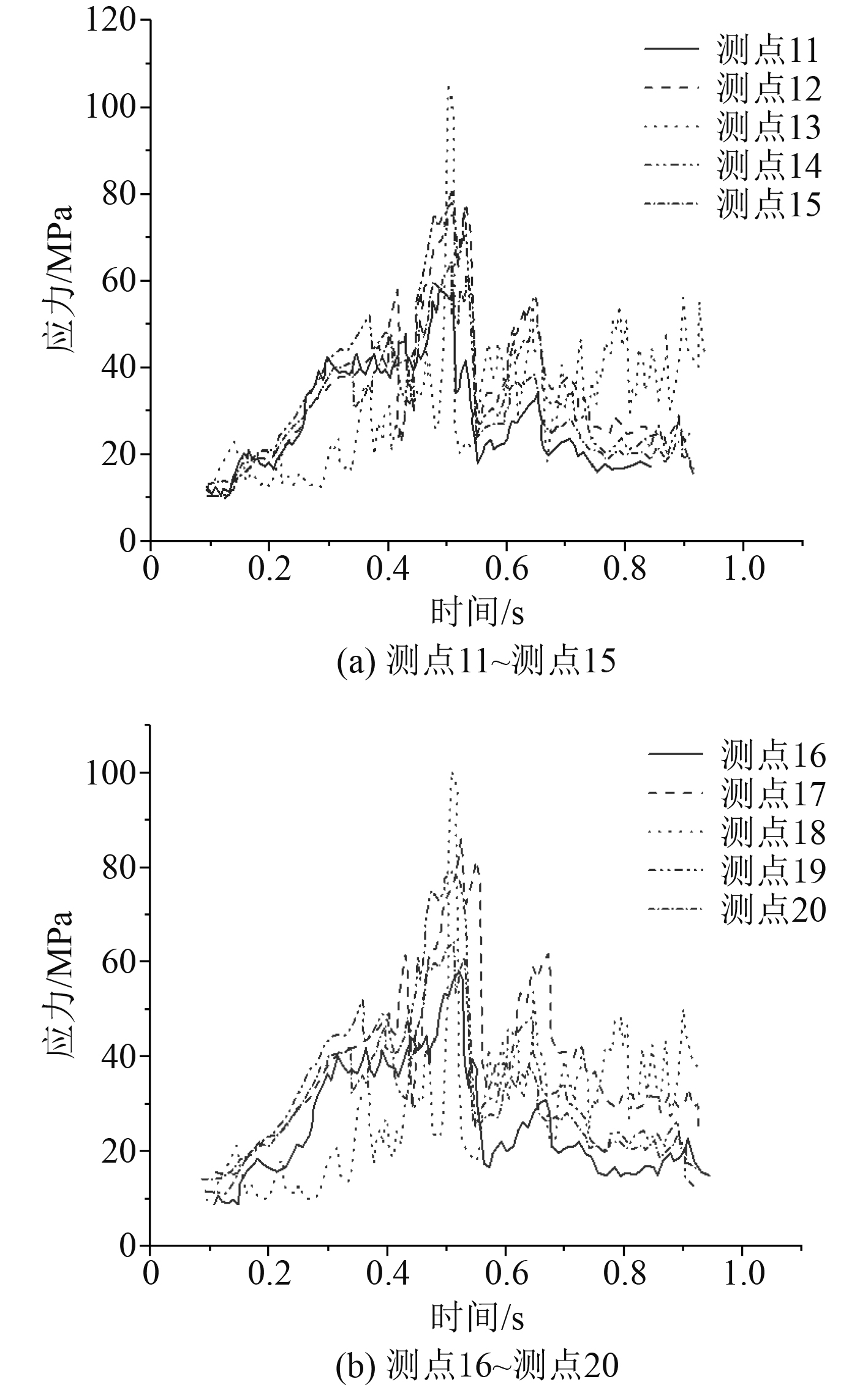
|
图 4
工况二船体板架测点应力
|
根据试验数据进行碰撞力的计算,计算公式如下:
| $ {N}_{水平}={N}_{1}+{N}_{2} ,$ | (4) |
| $ {N}_{竖直}={N}_{3}+{N}_{4}+{N}_{5}+{N}_{6},$ | (5) |
| $ {N}_{总}=\sqrt{{N}_{水平}{}^{2}+{N}_{竖直}{}^{2}},$ | (6) |
| $ {N}_{碰撞力}={N}_{总}{\text{。}} $ | (7) |
式中:
碰撞力随时间变化的曲线如图5所示。工况1的碰撞力在0.6 s之前呈现出缓慢增加的趋势,在0.7 s时急剧上升产生峰值,根据应力变化曲线可知这个峰值由于第1次碰撞产生,之后碰撞力快速下降到最小值并保持平稳,工况2的变化曲线与工况一相似,只是时间上更靠前,这与应力曲线相对应。
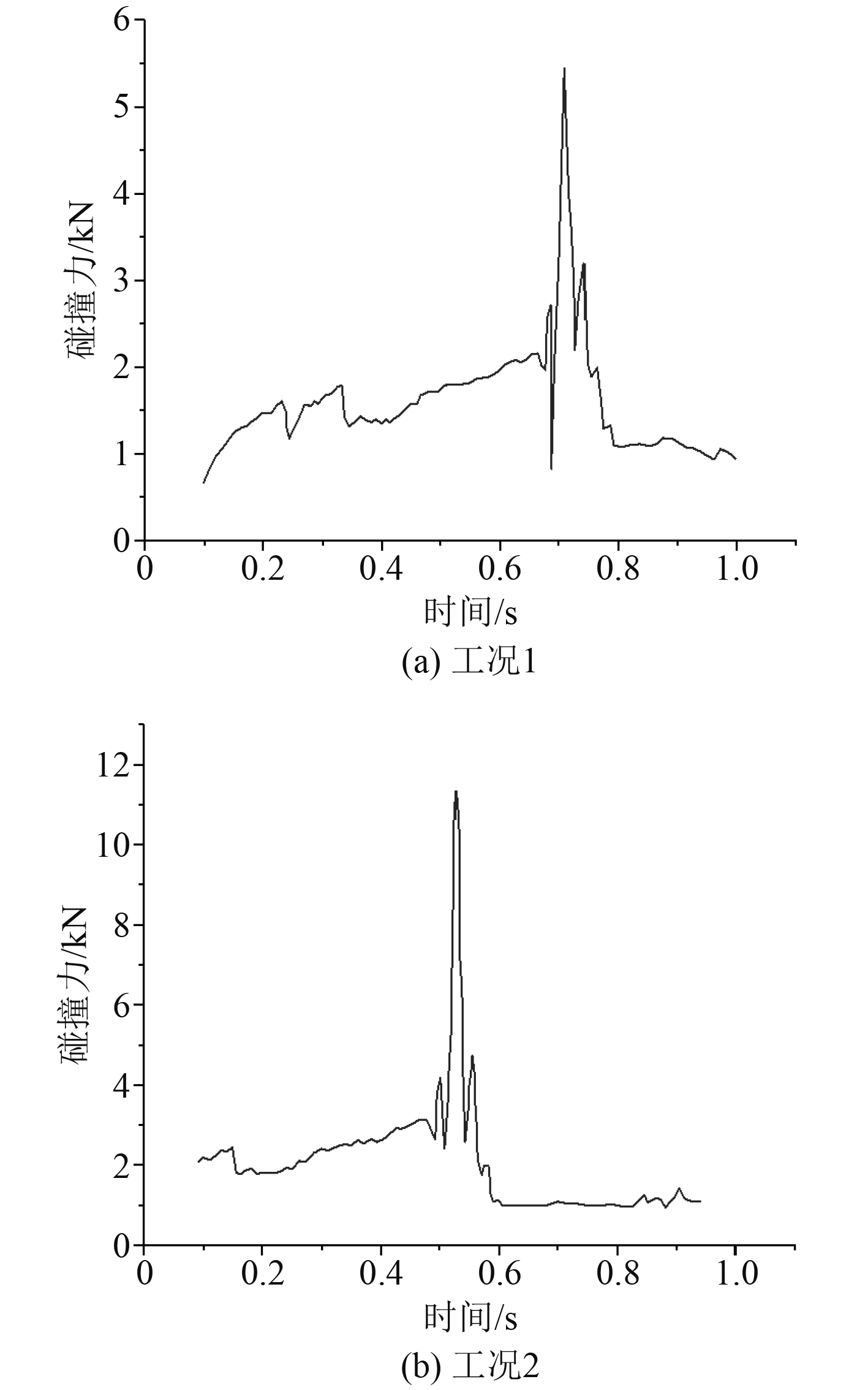
|
图 5 模型试验碰撞力-时间变化曲线 Fig. 5 Impact force time curve of model test |
根据第1部分试验所确定的试验模型参数以及工况参数,利用有限元软件 MSC. PATRAN 建立尺寸为1700 mm×1120 mm×140 mm的单层板架结构,骨材横向间距560 mm,纵向间距850 mm。设定板架模型的网格大小10 mm×10 mm,单元类型设为SHELL。
导入Ls-dyna的前处理器中,对其进行材料参数等关键字的设定。基于数值模拟尽量符合实际情况的原则,考虑冰载荷作用时船体结构先发生弹性变形再发生塑性变形设定为弹塑性材料参数,屈服函数选用Von Mises。考虑应变率影响,对于低速航行的冰载荷均为较低应变率,选用Cowper-Symonds材料模型。船体板架模型参数设定如表3所示。
|
|
表 3 船体材料参数取值 Tab.3 Value of hull material parameters |
对于模型冰的数值仿真依据实验所制备的物理力学参数,弹性屈服函数选用Von Mises,材料的破坏模式选定为塑性破坏。
同样利用有限元软件建立尺寸为长400 mm,宽400 mm,厚140 mm的长方体模型冰,网格大小为10 mm×10 mm×10 mm,单元类型设为SOILD。模型冰材料参数如表4所示。
|
|
表 4 模型冰材料相关参数 Tab.4 Relevant parameters of model ice material |
通过以上模型参数建立与试验相同的计算工况,试验速度均为1.12 kn,船体板架与水平面的初始夹角均为15°,边界条件均为船体板架底部对板进行x和y方向的位移约束,z方向和转角均不做约束。工况1的碰撞位置为架面板有骨架支撑位置,工况2设置为无骨架支撑位置,仿真场景如图6和图7所示。
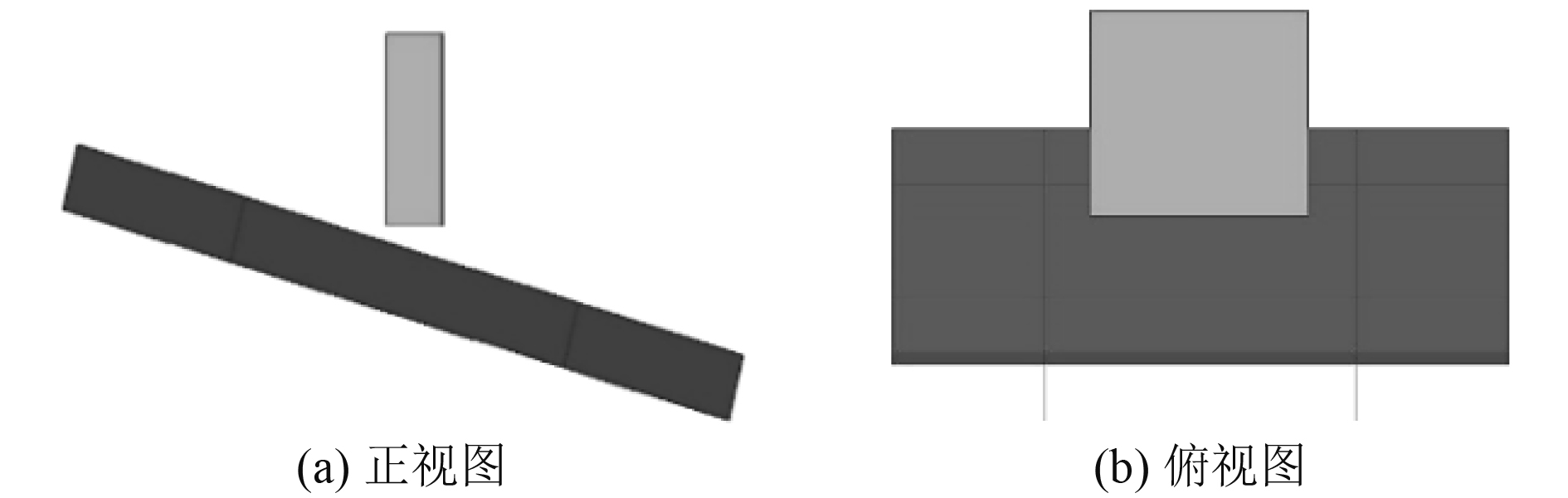
|
图 6 工况1船体板架-模型冰碰撞仿真场景图 Fig. 6 Simulation scenario diagram of hull grillage model ice collision under condition I |
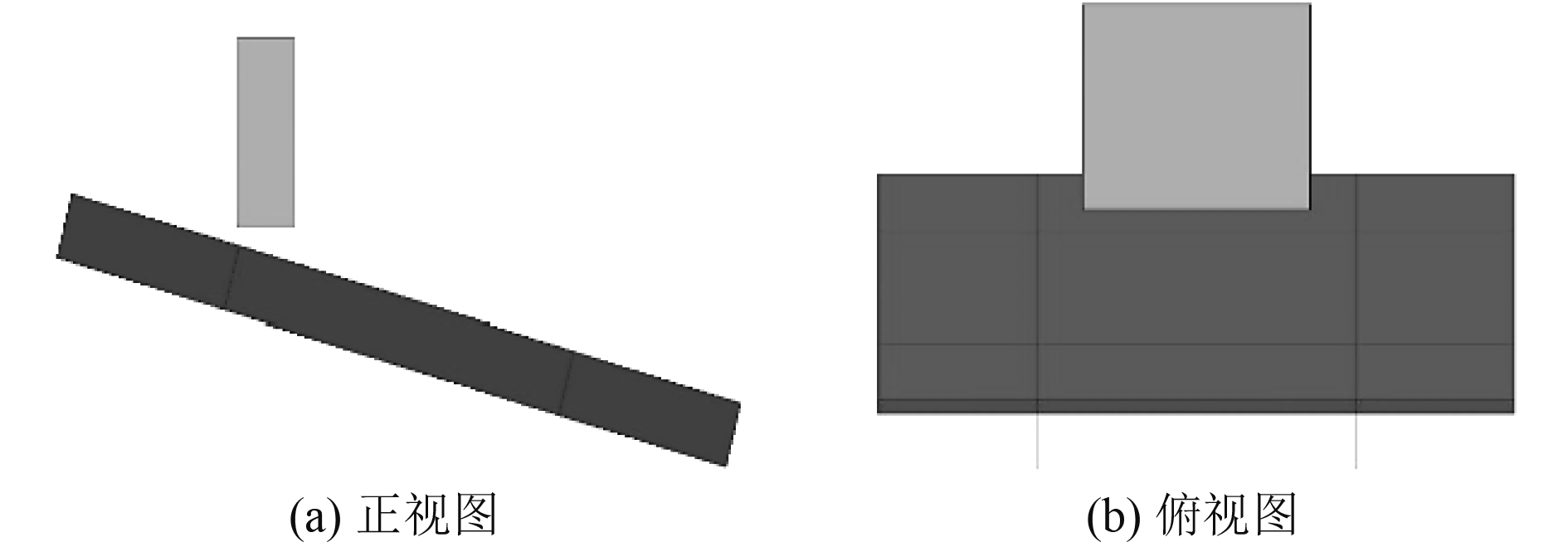
|
图 7 工况2船体板架-模型冰碰撞仿真场景图 Fig. 7 Simulation scenario diagram of hull grillage model ice collision under condition II |
数值仿真结果体现出和试验相同的变换规律。两工况的应力云图如图8所示。从应力结果来看,总体上工况2的结构响应比工况1的结构响应小,通过2个工况的对照可得,相同撞击条件下结构响应的大小是船体板架模型撞击点结构的强弱所决定的。
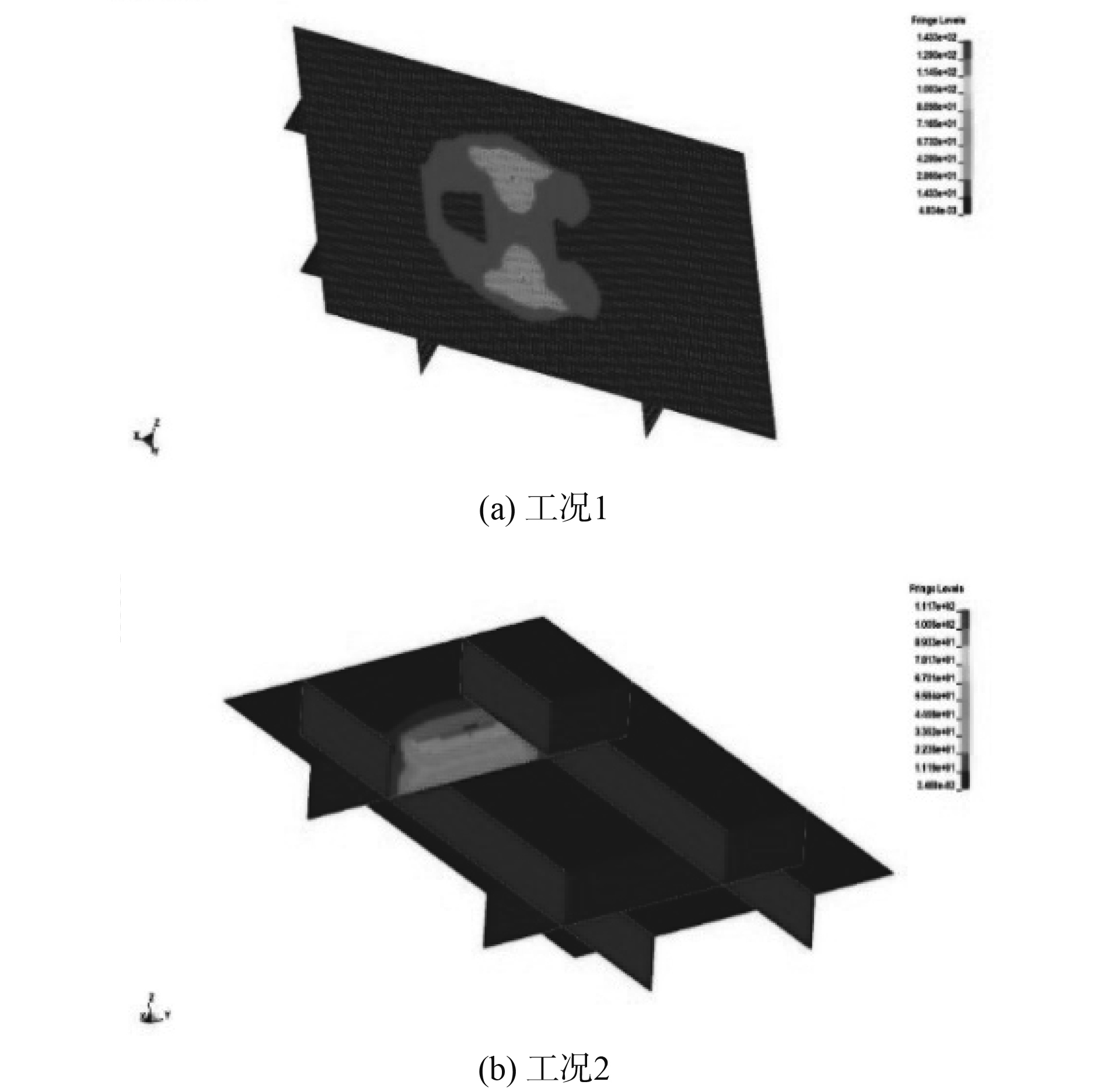
|
图 8 船体板架的应力云图 Fig. 8 Stress nephogram of hull plate frame |
从应力云图可以明显看出响应在关于x轴呈现对称的现象,选取相同的测点位置进行数据分析,证实了试验测点数据的准确性,并且响应在测点位置最大,在x方向上向两边逐渐变小,也与试验结果向对应。另外,对于工况2的应力云图结果,纵桁处的结构响应在沿纵桁左右两边差别较大,在有限元模型中,由于纵桁为强构件,在发生碰撞时更大程度的承受作用力,由于试验的倾斜角度,顺着作用力方向一边的面板响应更大。
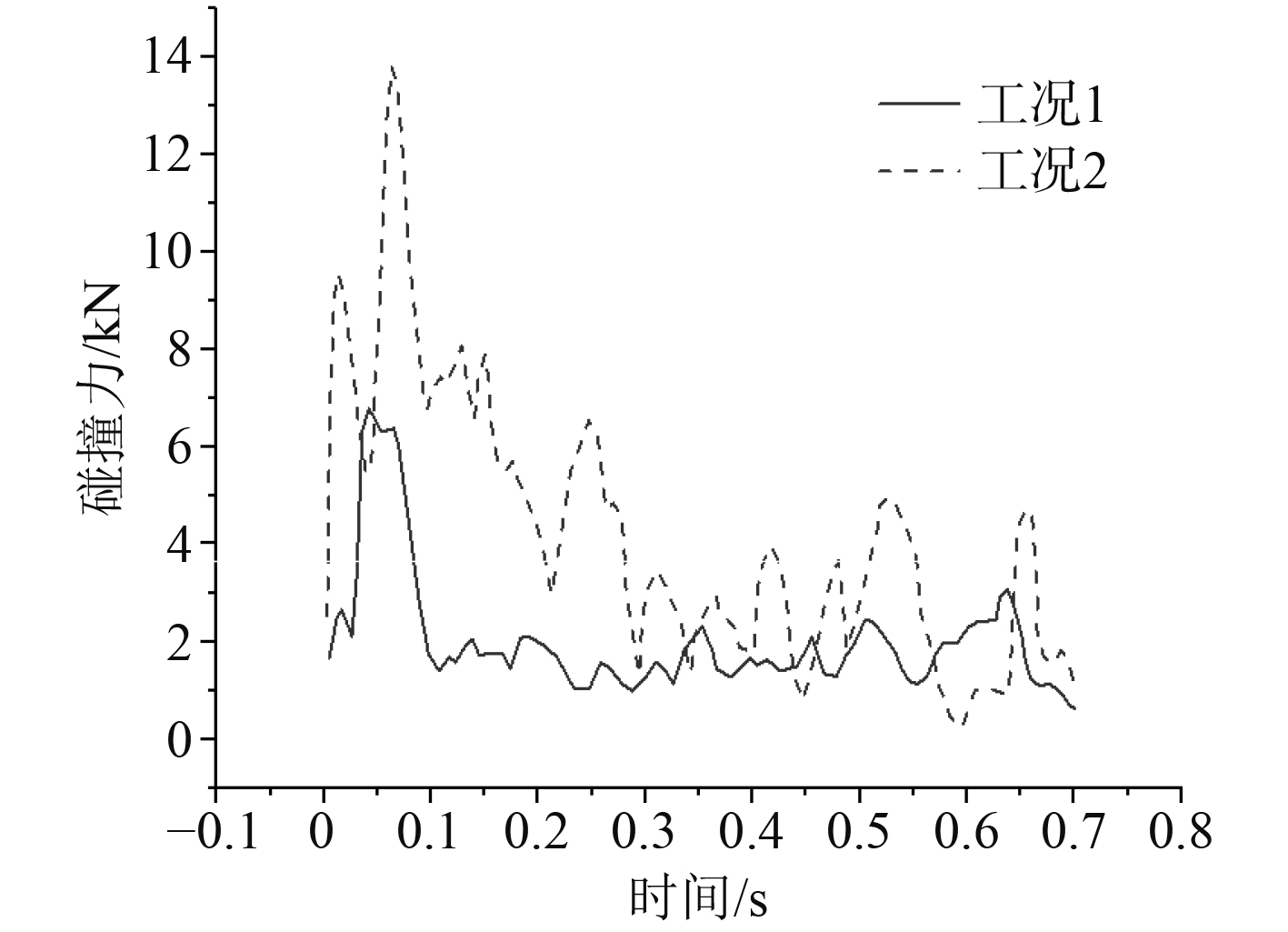
对于碰撞力的数值仿真结果,绘制碰撞点的碰撞力随时间的变化曲线,如图9所示。在数值模拟中,碰撞力在第1次峰值后的上下波动更明显,这主要是因为数值模拟是一个理想的模型冰挤压破碎过程,而在模型试验中,由于环境误差,微小的碰撞力很难监测,经过一次碰撞后很快便进入平稳。另外,在模型试验中的碰撞力在初始阶段会产生一个缓慢的变化,这是由于在碰撞前模型一直处于饱和水的状态,而在数值模拟过程中,在碰撞之前没有排净吸附水的过程,所以碰撞力从开始接触时捕获。
|
图 9 碰撞力-时间变化曲线 Fig. 9 Impact force time curve |
由数值仿真结果可知,工况2的碰撞力持续时间更长,且在数值大小上,工况2的最大碰撞力为工况1的2倍。
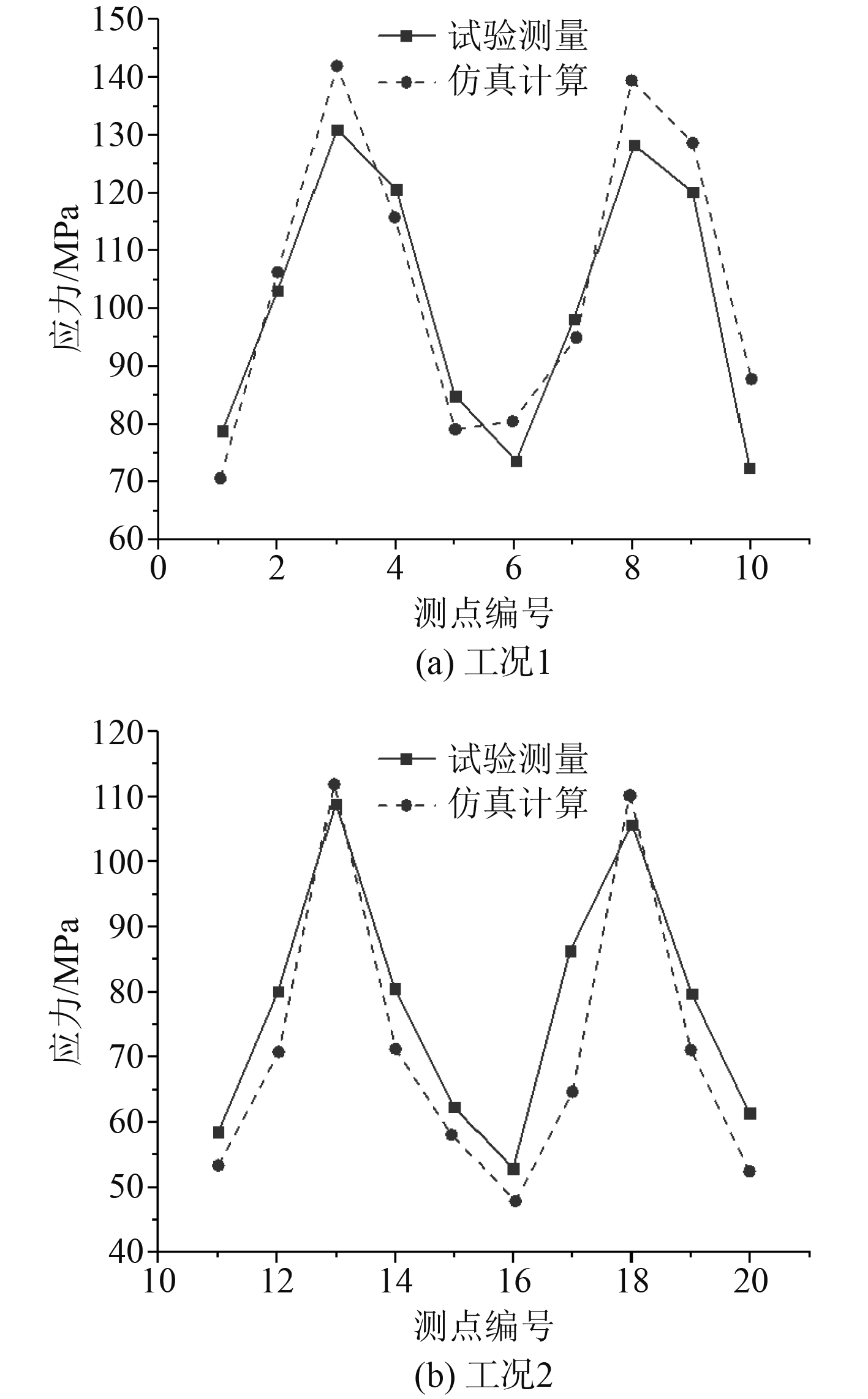
3 数值仿真及模型试验结果比较 3.1 应力比较对于应力结果的比较,选取各个测点的时历最大值绘制各工况的试验数据和仿真数据如图10所示。2个工况的试验结果和仿真结果能较好吻合,对于工况1对弱构件的撞击最大应力,仿真结果更大,而对于工况2强构件,应力最大值几乎吻合;对于幅值来讲,工况2的响应幅值在60 MPa左右,而工况1的幅值在70 MPa左右,相差不大。
|
图 10 数值仿真及模型试验应力值比较 Fig. 10 Comparison of stress values between numerical simulation and model test |
计算各测点的误差,工况1各个测点的平均误差为7.9%,在10号测点误差最大,为17.43%,在碰撞测点3和测点8的误差分别为8.7%和8.8%;工况2各个测点的平均误差为10.5%,在测点17处误差最大,为31.85% ,在碰撞测点13和测点18的误差分别为2.7%和4.3%,可见除了个别点的误差较大,整体吻合效果较好。
因为测点等距布放,应力的变化速度随着和撞击点的距离变近而变快。而且1~5号测点和6~10测点(11~15号测点和16~20测点)的变化规律相同,所以在试验中在相同曲率的船体板模型可以只取一列测点,代表整个面的变化规律,另外可以再增加测点的个数,以提高试验精度。
3.2 碰撞力比较对于碰撞力结果的比较,提取每个工况的最大碰撞力汇总在表5中。
|
|
表 5 数值仿真与模型试验的碰撞力的最大值 Tab.5 Maximum value of collision force of numerical simulation and model test |
和应力的对比结果有相同的特点,碰撞力结果的最大值也大于模型试验,而且工况2的误差也表现出相对较小的特点,对于2种方法的误差都在20%的可接受范围内,可以证明在碰撞力的计算方面,数值仿真结果也是合理的。
4 结 语通过以上研究得到如下结论:
1)所制备的非冻结模型冰的物理和力学性能,在缩尺比
2)对比不同工况的应力和碰撞力结构,响应随时间的变化的规律相似,且响应的大小与结构的强弱有关;
3)试验结果和数值模拟结果相吻合,验证了本文所提出的试验方法的正确性以及所采用的数值模拟方法的准确性,对后续研究具有一定的参考意义。
| [1] |
TRYDE P. Intermittent ice forces acting on inclined wedges[C]// Proeeedings of the IAHR 3rd International Symposium on Ice, August, Hanover, New Hampshire, USA. International Association for Hydraulic Researeh, 1975: 339−343.
|
| [2] |
SCHULTZ L, FREE A P. Recent experience in conducing ice model tests using a synthetic ice modeling material[C]// Proceedings of the IAHR. International Symposium on Ice, 1984, August, Hamburg, Germany. International Association for Hydraulic Research, 1984: 229−239.
|
| [3] |
王永学, 李志军, 李广伟. 非冻结合成模型冰物理模拟冰作用力的试验技术[J]. 冰川冻土, 2003(S2): 227−233. WANG Yongxue, LI Zhijun, LI Guangwei Experimental technology of physical simulation of ice force by non freezing synthetic model ice [J]. Glacial Permafrost, 2003 (S2): 227−233 |
| [4] |
VEGARD, AKSNES. A panel method for modelling level ice actions on moored ships. Part 1: Local ice force formulation[J]. Cold Regions Science and Technology, 2011.
|
| [5] |
LEIRA B, BØRSHEIM L, ESPELAND Ø, et al. Ice-load estimation for a ship hull based on continuous response monitoring[J]. Proceedings of the Institution of Mechanical Engineers, Part M:Journal of Engineering for the Maritime Environment, 2009, 223(4): 529-540. DOI:10.1243/14750902JEME141 |
| [6] |
张健, 张淼溶, 万正权, 等. 冰材料模型在船-冰碰撞结构响应数值仿真中的应用研究[J]. 中国造船, 2013, 54(4): 100−108. ZHANG Jian, ZHANG miaolun, WAN Zhengquan, et al. Application of ice material model in numerical simulation of structural response of ship ice collision [J]. China shipbuilding, 2013, 54 (4): 100−108. |
| [7] |
任慧龙, 王川, 李辉, 等. 冲撞式破冰引起的船舯垂向弯矩计算方法研究(英文)[J]. 船舶力学, 2014, 18(9): 1109−1116. REN Huilong, WANG Chuan, LI Hui, et al. Study on calculation method of midship vertical bending moment caused by collision ice breaking [J]. Ship mechanics, 2014, 18 (9): 1109−1116. |
| [8] |
马德毅. 中国第五次北极科学考察报告[M]. 北京: 海洋出版社, 2013.
|
| [9] |
张健. 冰载荷作用下船舶结构动态响应及损伤机理[M]. 北京: 国防工业出版社, 2015: 162.
|
| [10] |
刘海冬. 船水冰耦合技术及船冰碰撞模型试验研究[D]. 镇江: 江苏科技大学, 2018.
|
 2023, Vol. 45
2023, Vol. 45
