半潜航行器纵平面流体动力数值计算与试验研究

引用本文

李超, 宋健, 刘金勇, 艾艳辉, 佘湖清. 半潜航行器纵平面流体动力数值计算与试验研究. 舰船科学技术, 2023, 45(5): 36-43 复制到剪切板

LI Chao, SONG Jian, LIU Jin-yong, AI Yan-hui, SHE Hu-qing. Numerical calculation and experimental study on hydrodynamic characteristics at the longitudinal plane of a semi-submersible vehicle. Ship Science and Technology, 2023, 45(5): 36-43 复制到剪切板

半潜航行器纵平面流体动力数值计算与试验研究

李超, 宋健, 刘金勇, 艾艳辉, 佘湖清

中国船舶集团有限公司第七一〇研究所，湖北宜昌 443000

收稿日期: 2022-05-05.

基金项目: “十三五”预先研究课题（3020604030103）

作者简介: 李超(1991-)，男，博士研究生，研究方向为水下特种装备探测与控制

摘要: 半潜航行器因航行深度介于水面航行器和潜器之间而得名。为预报半潜航行器纵平面流体动力性能，开展数值仿真与风洞试验。研究航行器不同攻角、不同舵角下受力情况，计算速度系数、舵角系数以及耦合系数，并与风洞试验数据进行对比。针对耦合工况中舵效降低的情况进行了流场分析。仿真和试验结果表明：CFD仿真结果与试验结果吻合较好，具有较高预报精度；增加航行器攻角会影响前、后舵板贴体端稍涡的形成，迫使稍涡向上偏移，在吸力面形成一个直径与舵板弦长相当的涡。研究结论可指导航行器运动控制和前后舵布局优化。

关键词: 半潜航行器流体动力数值计算风洞试验局部流场分析

Numerical calculation and experimental study on hydrodynamic characteristics at the longitudinal plane of a semi-submersible vehicle

LI Chao, SONG Jian, LIU Jin-yong, AI Yan-hui, SHE Hu-qing

The 710 Research Institute of CSSC, Yichang 443000, China

Abstract: The navigation depth of a semi-submersible vehicle is between a surface vehicle and a submersible vehicle, so it is called a semi-submersible vehicle. To predict the longitudinal plane hydrodynamic performance of the semi-submersible vehicle, numerical simulation and wind tunnel tests are carried out. The forces on the vehicle at different angles of attack and rudder angles are studied. The velocity coefficient, rudder angle coefficient, and coupling coefficient are calculated, and the results are compared with the wind tunnel test data. The flow field is analyzed for the reduction of rudder efficiency under coupling conditions. The simulation and experimental results show that the CFD simulation results have high prediction accuracy and are in good agreement with the experimental results. Increasing the attack angle of the vehicle will affect the formation of slight vortices at the body fitted ends of the front and rear rudder plates. The existence of the body-fitted ends will force the slight vortices to shift upward and finally form a vortex with a diameter equivalent to the chord length of the rudder plate on the suction surface. The research conclusions can guide the motion control of the vehicle and the optimization of the front and rear rudder layout.

Key words: the semi-submersible vehicle hydrodynamic numerical calculation wind tunnel test local flow field analysis simulation

0 引　言

半潜航行器作为一种近水面航行器，通过自身舵板调节姿态，借助舵板和主体产生定深力控制航行深度，降低波浪干扰，提高海况适应性。研究航行器流体动力性能并求解相关系数，有助于预报半潜航行器运动特性，掌握控制规律。

针对半潜航行器流体动力性能研究方法主要有模型试验、数值计算、半经验估算等。Mori等^[1]提出一种带翼板的高速半潜式航行器，借助翼板产生的向下升力增加潜深，翼板也有助于消减行波，降低兴波阻力，之后Mori等^[2]采用数值模拟方法研究了半潜航行器的运动特性，分析了不同航行深度、翼板位置和攻角下的流场。谈果戈^[3]通过CFD方法模拟平面运动机构，计算了不同航行深度下半潜航行器惯性类和速度水动力系数。Ueno等^[4]基于Hirayama^[5]提出的半潜航行器模型通过理论和半经验公式估算了航行器线性流体动力系数，阐明了该航行器在垂直面和水平面运动中的动力特性，同时指出通过试验确定流体动力系数的必要性。后续通过水池试验，确定了不同潜深下速度和舵角流体动力系数，并指出通过估算的方法对舵某些系数的准确度有待提高^[6]。为了验证半潜航行器多状态转换的可行性，Cong^[7]对带有压载水舱的半潜式航行器开展了自航试验，研究了不同前后翼角组合对航行器状态转变的影响，测量了航行过程中翼和主体的阻力、升力和纵摇力矩的变化。Cong指出航行器运动的非线性、非线性水动力和剩余浮力等因素增加了状态转换的难度，准确测量机翼上的流体动力有助于更好地理解多状态转换过程的机理。对于该种类型的半潜式航行器，董文才等^[8]也做过相关研究。大多数研究集中在半潜航行器的速度系数、舵角系数、加速度系数的求解，并对半潜航行器航态转换性能进行了分析，对关系到半潜航行器大幅度运动性能的速度和舵角的耦合系数研究较少。

针对目前研究的不足，通过数值方法对半潜航行器的纵向速度和舵角系数进行仿真计算，并与风洞试验结果进行对比验证，通过最小二乘法回归了速度、舵角耦合系数。对于耦合系数中舵效降低的情况结合局部流场进行了深入分析，确定了适用于该航行器的最佳舵角范围。

1 数值计算模型及空间离散 1.1 几何模型

图1所示的半潜航行器由回转体、桅杆、下附体、前水平舵、后水平舵及后垂直舵组成。前舵左右对称分布，后舵为十字分布。航行器长 $L$ 为6.8 m，回转体部分直径 $\varphi$ 为0.92 m，总高度 $H$ 为3.6 m，宽度 $B$ 为1.84 m，前后舵板采用NACA0012翼型。计算域划分和边界条件设置见图2，流体域入口到首部为1倍航行器长度，出口到尾部为3倍航行器长度，左右到中垂线各2倍航行器长度。图中①号面设为对称平面，②号面为压力出口，其余面为速度入口。

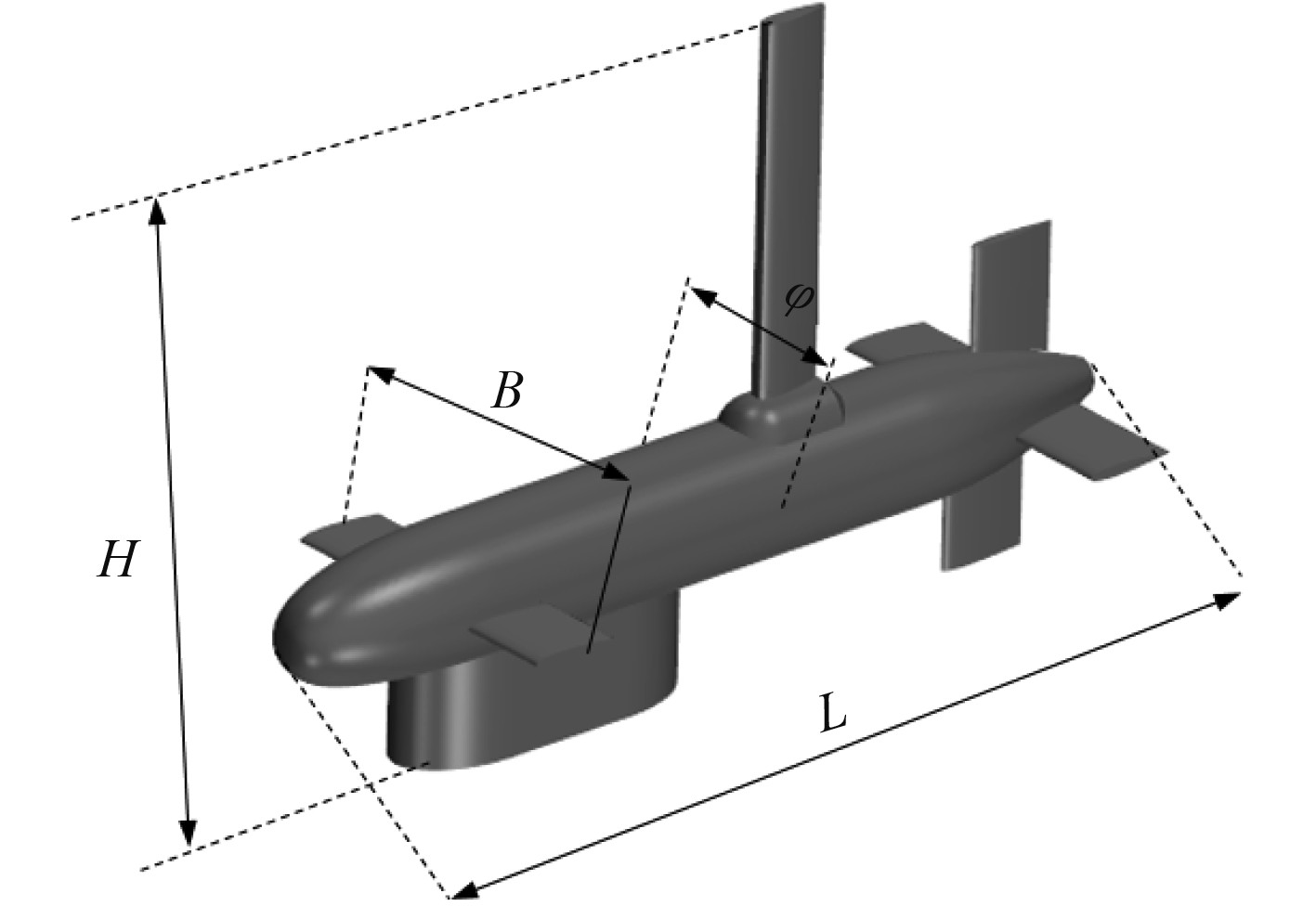
图 1 航行器外型 Fig. 1 Vehicle appearance

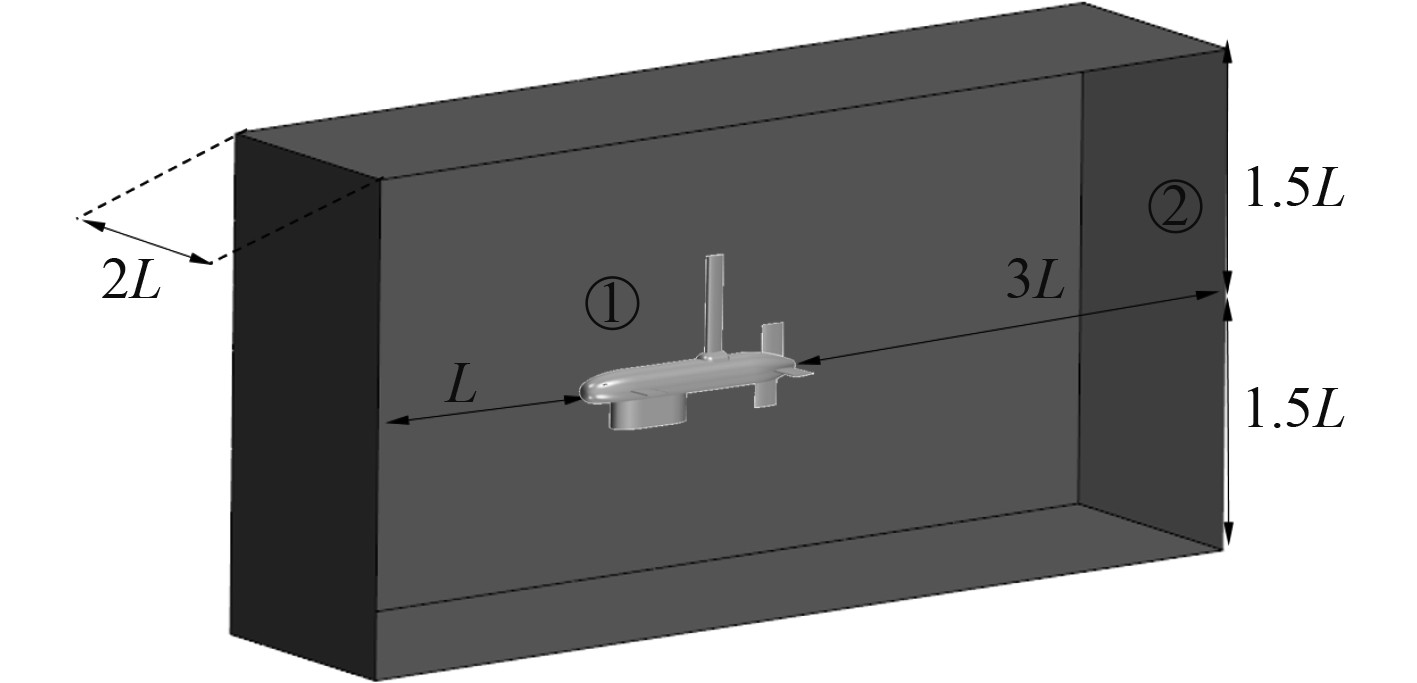
图 2 流体域划分 Fig. 2 Division of fluid domain

1.2 数值方法

数值模拟主要通过求解RANS方程得到仿真结果，其控制方程如下：

$\frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}}{\text{ + }}\frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho \overline {u_i'u_j'} } \right] + {S_i} 。$

(1)

Reynolds应力实际上有6个不同的应力项，为了构成封闭方程组，需要引入其他条件对方程进行求解。剪切应力输运 $k - \omega$ 模型^[9](简称SST $k - \omega$ 模型)在计算航行器绕流方面应用广泛^[10-12]。其方程表示如下：

$\frac{{\partial \rho k}}{{\partial t}} + \frac{{\partial \rho k{u_i}}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}\right)\frac{{\partial k}}{{\partial {x_j}}}\right] + {G_k} - {Y_k} + {S_k} \text{，}$

(2)

$\frac{{\partial \rho \omega }}{{\partial t}} + \frac{{\partial \rho \omega {u_i}}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[\left(\mu + \frac{{{\mu _t}}}{{{\sigma _\omega }}}\right)\frac{{\partial \omega }}{{\partial {x_j}}}\right] + {G_\omega } - {Y_\omega } + {D_\omega } + {S_\omega } \text{。}$

(3)

式中：

${\mu _t} = \dfrac{{\rho k}}{\omega }\dfrac{1}{{\max \left(\dfrac{1}{\alpha },\dfrac{{S{F_2}}}{{{\alpha _1}\omega }}\right)}} \text{，}$

(4)

${\sigma _k} = \frac{1}{{{F_1}/{\sigma _{k,1}} + (1 - {F_1})/{\sigma _{k,2}}}} \text{，}$

(5)

${\sigma _\omega } = \frac{1}{{{F_1}/{\sigma _{\omega ,1}} + (1 - {F_1})/{\sigma _{\omega ,2}}}} \text{，}$

(6)

${D_\omega } = \max \left[2\rho \frac{1}{{{\sigma _{\omega ,2}}}}\frac{1}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}},{10^{ - 10}}\right] 。$

(7)

式中： ${F_1}$ ， ${F_2}$ 为混合函数。

$\left. \begin{gathered} {F_1} = \tanh ({\varPhi _1}^4) ，\\ {\varPhi _1} = \min \left[\max \left(\frac{{\sqrt k }}{{{\beta ^*}\omega y}},\frac{{500\mu }}{{\rho {y^2}\omega }}\right),\frac{{4\rho k}}{{{\sigma _{\omega ,2}}{D_\omega }^ + {y^2}}}\right] \\ \end{gathered} \right] \text{，}$

(8)

$\left. \begin{aligned} & {F_2} = \tanh ({\varPhi _2}^2) \\ & {\varPhi _2} = \max \left[\frac{{2\sqrt k }}{{{\beta ^*}\omega y}},\frac{{500\mu }}{{\rho {y^2}\omega }}\right] \end{aligned} \right] 。$

(9)

式中： ${G_k}$ ， ${G_\omega }$ 分别为湍动能和 $\omega$ 方程； ${Y_k}$ ， ${Y_\omega }$ 分别为 $k$ 和 $k - \omega$ 的发散项； ${G_\omega }$ 为正交发散项。

1.3 网格划分及无关性讨论

半潜航行器航行深度超过0.35 $L$ ，该深度下水面文丘里效应对航行器影响不再明显^[13]，航行器通过流线型桅杆与水面接触，兴波对升阻力影响暂不考虑，因此在计算流体动力系数的过程中不考虑自由液面。影响航行器计算精度的要素主要有湍流模型、网格密度、时间步长等，其中网格密度是网格无关性问题谈论的重点^[14-15]。本文航行器基础网格分别为0.8 m，0.65 m，0.5 m，如图3和图4所示。为了更好地契合舵面物理形状，需对舵板表面、端面进行网格加密，网格大小为航行器表面网格的一半，航行器周围整体网格进行多层加密，网格大小为表面网格的2倍、4倍、8倍。按此规律得到网格分别为258万、325万、384万，3种网格能够贴合舵面形状，继续加密会消耗更多的计算资源，使得计算周期变长。

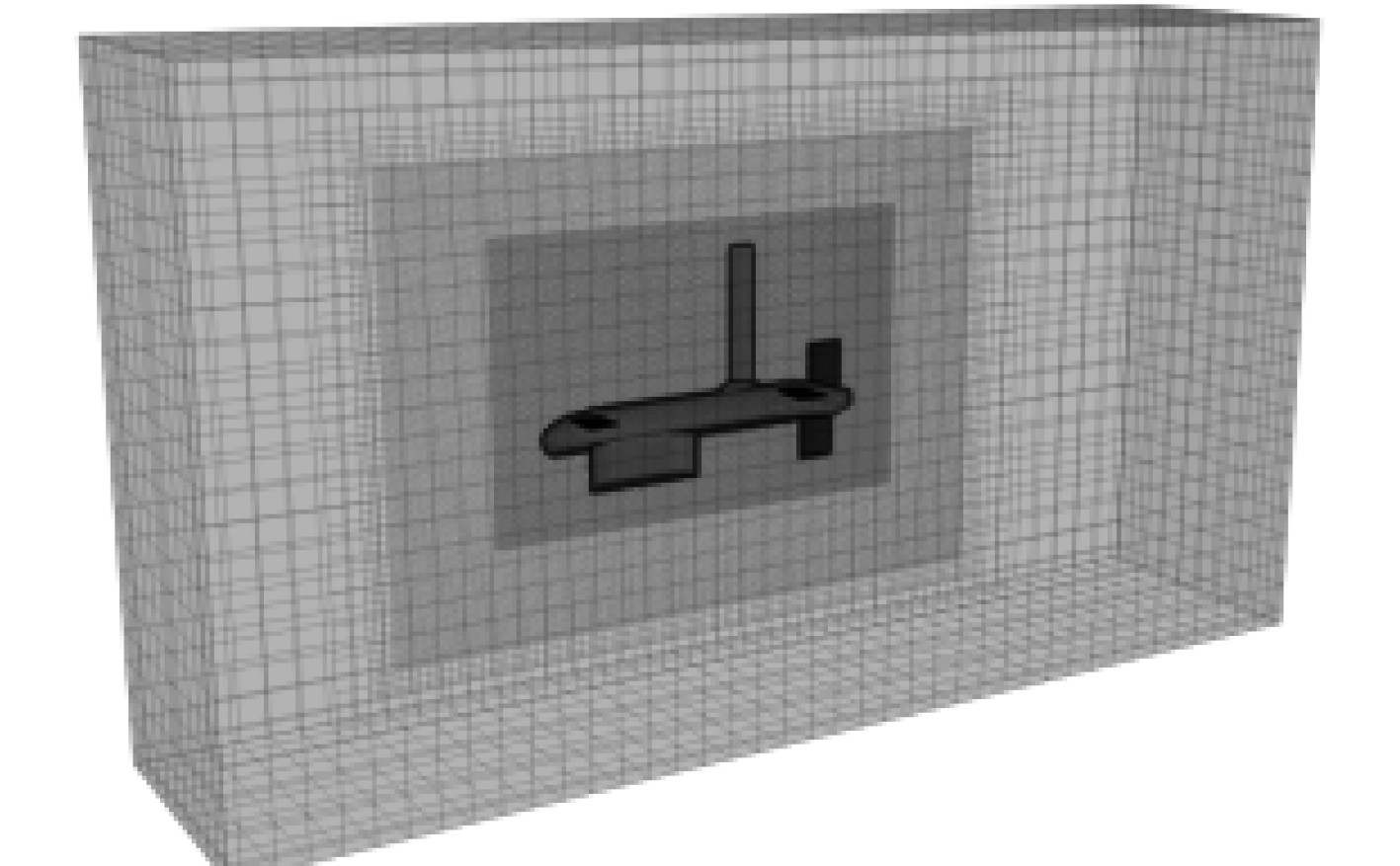
图 3 流体域网格 Fig. 3 Grid of fluid domain

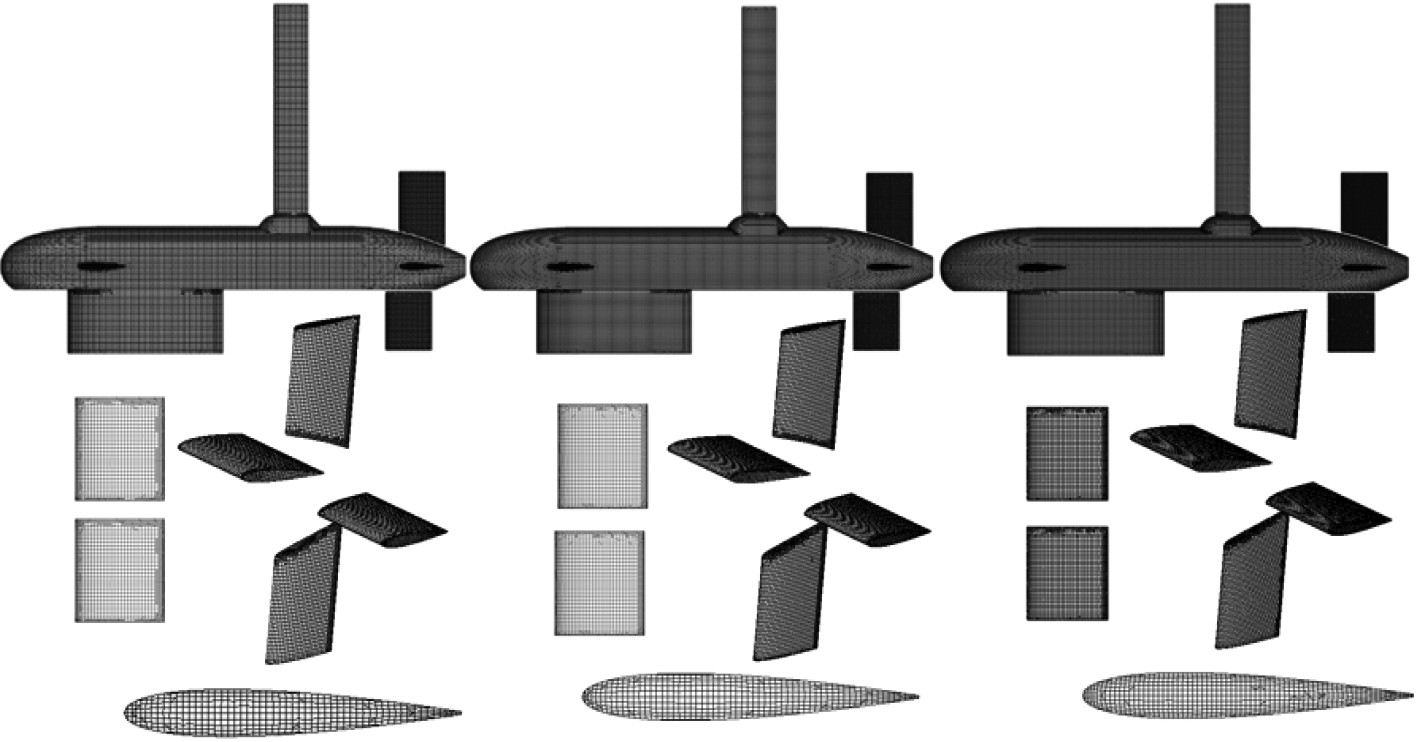
图 4 不同表面网格密度 Fig. 4 Different surface mesh density

对正浮态下不同网格密度航行器进行仿真计算，得到不同航速下升、阻力结果，如表1所示。阻力和升力随网格数量的增加有变小的趋势，以最密网格为基准，剩余2种网格阻力结果与之平均误差分别为2.2%和5.15%，升力结果平均误差2.1%和5.25%，低速情况下因基础数值较小，误差较大。综合考虑计算成本与结果准确度，网格基础为0.65 m。

表 1 主要参数 Tab.1 Primary parameters

2 风洞试验模型及内容 2.1 网格划分及无关性讨论

试验模型主体为玻璃钢，内设钢骨架，表面喷漆。风洞模型试验在西北工业大学风洞试验室进行。采用PSI8400电子扫描阀数据系统采集天平输出的电压信号，采集速度为5万点/秒，测量精度为0.1%。模型支撑方式为单支杆腹部支撑，为减少撑杆对试验结果的影响，撑杆进行导流处理，测力天平采用内测式六分量应变天平。模型缩比为1∶2，试验平均气温10℃。

图 5 试验模型 Fig. 5 Test model

2.2 试验内容

由于风洞试验雷诺数小于航行器实际雷诺数，首先验证雷诺数对试验结果的影响，风速40 m/s，50 m/s，60 m/s；然后开展航行器速度和舵角系数试验，固定航速，通过改变航行器攻角来改变其垂向速度，攻角变化范围为–9°～9°，中间间隔3°，保持航行器正浮态，依次改变前、后舵角，舵角变化范围–15°～15°。为了消除腹部支撑杆对结果的影响，还需进行支撑杆干扰消除试验。

3 结果分析 3.1 雷诺数影响分析

航行器最低航速下雷诺数Re=1.6×107，该雷诺数下需要风洞风速为76 m/s，现有试验风速最大到60 m/s，该风速下模型雷诺数超过了阻力系数变化较大的过渡区，但仍无法满足雷诺相似，因此需要研究雷诺数对结果的影响规律。舵角保持0°，风速60 m/s，50 m/s，40 m/s，30 m/s，航行器攻角α角度范围–9°～9°。图6中曲线斜率即为航行器的流体动力系数，可以看出雷诺数对阻力系数曲线影响较大，对升力系数 $C_Z^\alpha$ 和纵摇力矩系数 $C_M^\alpha$ 影响较小。风速从60m/s到30m/s，对应的阻力系数 $C_X^\alpha$ 分别为1.08×10^–4，1.07×10^–4，1.04×10^–4，9.8×10^–5，正浮状态下阻力系数 ${C_{X0}}$ 分别为–0.0188，–0.0185，–0.0179，–0.0173。根据结果趋势，76 m/s风速下各力和力矩系数可采用60 m/s风速的结果，初始阻力系数需按式(10)进行拟合修正。

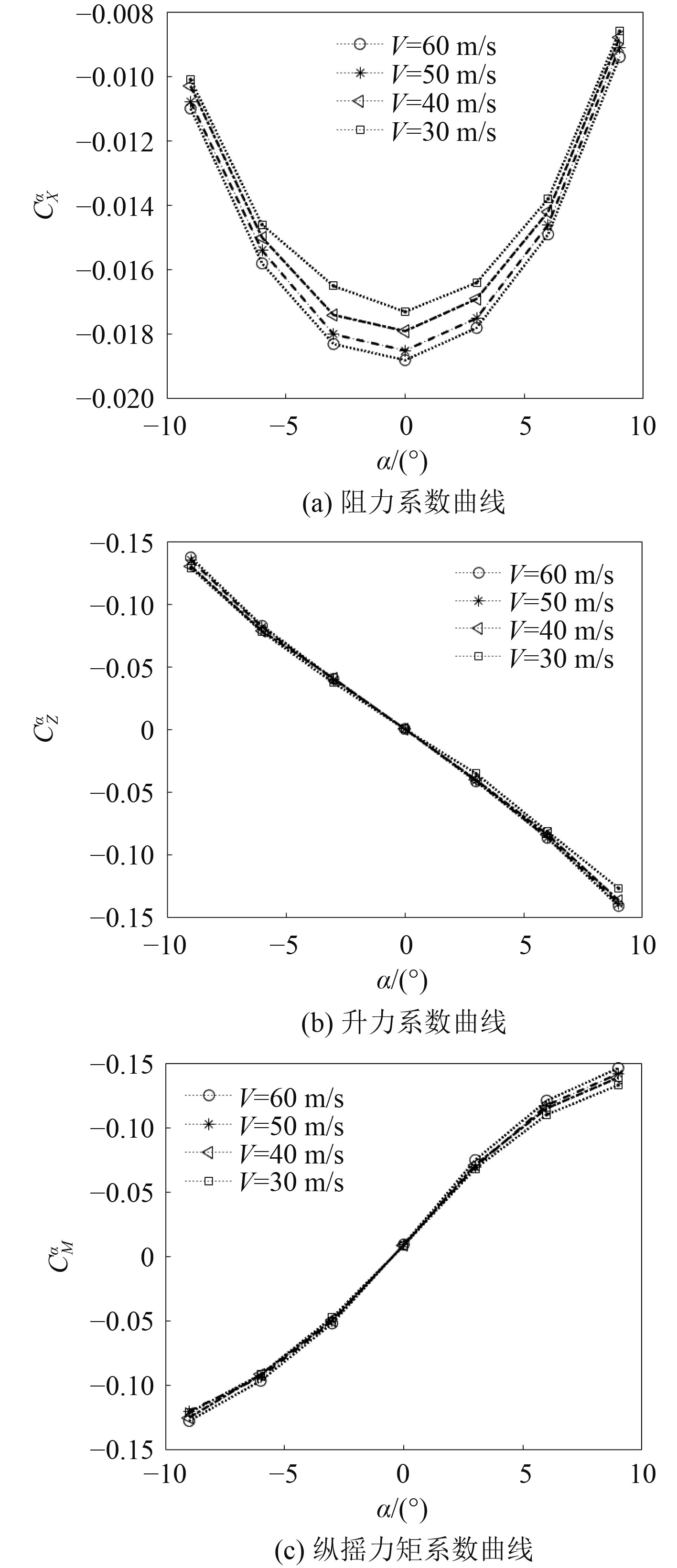
图 6 不同风速结果曲线 Fig. 6 Result curves of different wind speeds

$C_{X0}^{}(V) = 9{e^{ - 7}}{V^2} - 1{e^{ - 4}}V - 0.014。$

(10)

3.2 结果换算

本文水动力系数采用潜艇方程表达形式^[13]，将试验数据按式(11)～式(18)方式进行处理。 $X$ ， $Z$ ， $M$ 分别表示局部坐标下的阻力、升力和纵摇力矩，按右手坐标系建立局部坐标 $o - xyz$ ， $x$ 轴指向航行器首部， $z$ 轴竖直向下。下标 $m$ 和 $s$ 分别表示模型数据和仿真数据， ${*^{efd}}$ 为风洞试验结果， $*_{}^{EFD}$ 为试验换算后结果， ${ *'}_{}^{EFD}$ 为换算后的无因次化结果。

换算公式如下：

$X_{}^{EFD} = {X^{efd}}/({\rho _m} \times V_m^2 \times {S_m}) \times {\rho _s} \times V_s^2 \times {S_s} \text{，}$

(11)

$Z_{}^{EFD} = {Z^{efd}}/({\rho _m} \times V_m^2 \times {S_m}) \times {\rho _s} \times V_s^2 \times {S_s} \text{，}$

(12)

$M_{}^{EFD} = {M^{efd}}/({\rho _m} \times V_m^2 \times {S_m} \times {L_m}) \times {\rho _s} \times V_s^2 \times {S_s} \times {L_s} \text{，}$

(13)

${X'}_{ww}^{EFD} = X_{ww}^{EFD}/(1/2 \times {\rho _s} \times L_s^2) \text{，}$

(14)

${Z'}_w^{EFD} = Z_w^{EFD}/(1/2 \times {\rho _s} \times L_s^2 \times {V_s}) \text{，}$

(15)

${Z'}_{w|w|}^{EFD} = Z_{w|w|}^{EFD}/(1/2 \times {\rho _s} \times L_s^2) \text{，}$

(16)

${M'}_w^{EFD} = M_w^{EFD}/(1/2 \times {\rho _s} \times L_s^3 \times {V_s}) \text{，}$

(17)

${M'}_{w|w|}^{EDF} = M_{w|w|}^{EFD}/(1/2 \times {\rho _s} \times L_s^3) \text{，}$

(18)

${Z'}_{\delta} ^{EFD} = Z_\delta ^{EFD}/(1/2 \times {\rho _s} \times L_s^2 \times V_s^2) \text{，}$

(19)

${M'}_{\delta} ^{EFD} = M_\delta ^{EFD}/(1/2 \times {\rho _s} \times L_s^3 \times V_s^2) 。$

(20)

3.3 结果对比分析 3.3.1 速度系数

航行器初始航速10 kn，对应的不同攻角下纵向速度分别为–0.805 m/s，–0.538 m/s，–0.269 m/s，0，0.269 m/s，0.538 m/s，0.805 m/s，正、负号表示方向，航行器抬首，攻角为正，垂向速度为正。图(7)给出了局部坐标系下航行器阻力、升力、纵摇力矩CFD仿真和风洞试验曲线。由图7(a)可以看出，阻力随航行器垂向速度变化呈较强的偶函数性质，垂向速度较小时，CFD结果和试验结果误差较小，垂向速度–0.805 m/s时，二者误差达到9%。根据函数性质和式(14)求得无因次化后的流体动力系数 ${X'}_{ww}^{EFD}$ 和 ${X'}_{ww}^{CFD}$ ，具体结果如表2所示。

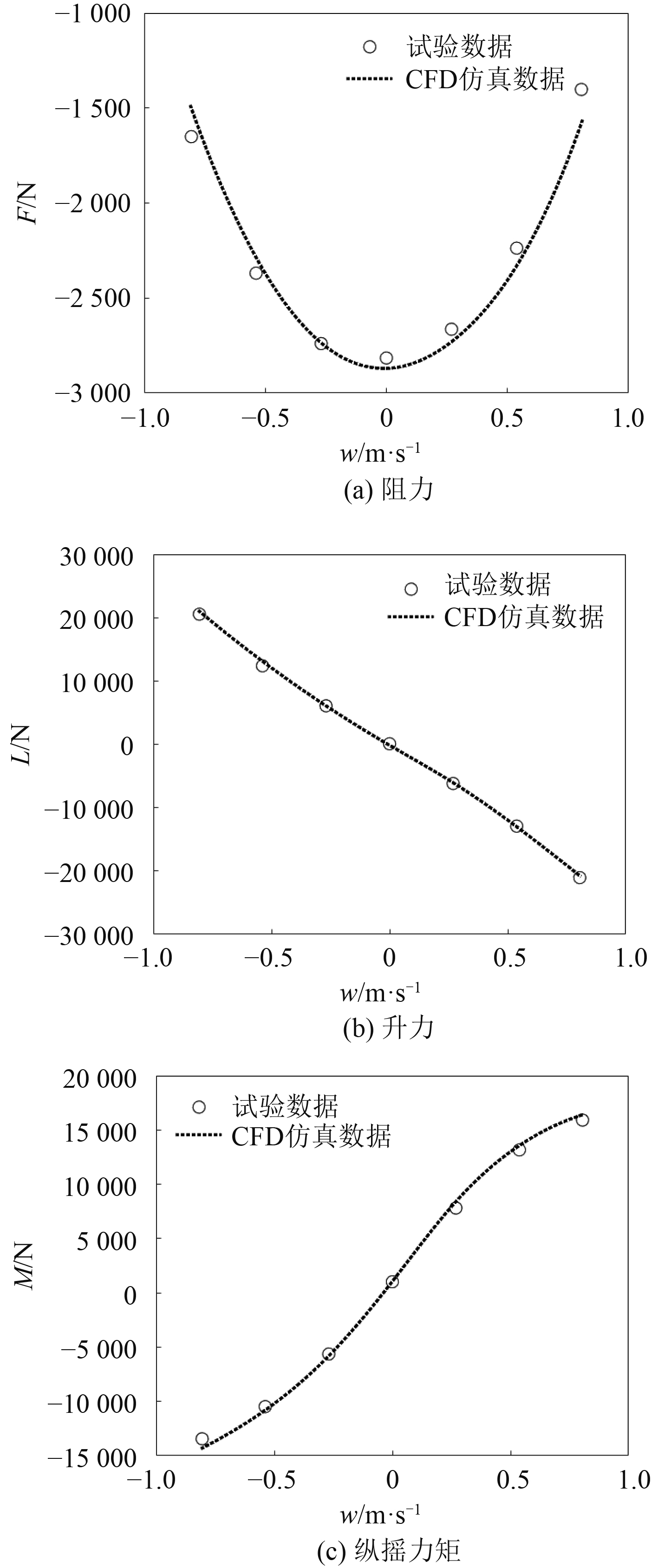
图 7 速度系数曲线 Fig. 7 Velocity coefficient curve

表 2 速度系数 Tab. 2 Velocity coefficient

试验系数	数值	CFD系数	数值	误差/%
${X'}_{ww}^{EFD}$	0.0718	${X'}_{ww}^{CFD}$	0.0734	2.2
${Z'}_w^{EFD}$	–0.139	${Z'}_w^{CFD}$	–0.1446	4
${Z'}_{w\|w\|}^{EFD}$	–0.246	${Z'}_{w\|w\|}^{CFD}$	–0.22	10
${Z'}_0^{EFD}$	–0.0002	${Z'}_0^{CFD}$	–0.0002	0
${M'}_w^{EFD}$	0.0266	${M'}_w^{CFD}$	0.0276	3.7
${M'}_{w\|w\|}^{EFD}$	–0.0626	${M'}_{w\|w\|}^{CFD}$	–0.0643	2.7
${M'}_0^{EFD}$	0.0002	${M'}_0^{CFD}$	0.0002	0

表 2 速度系数 Tab.2 Velocity coefficient

图7(b)与图7(c)中CFD仿真结果和风洞试验结果误差较小，最大误差分别为4.9%和6.3%。升力和纵摇力矩系数随航行器垂向速度变化呈奇函数特征，半潜航行器上下结构不对称导致曲线未呈现完全对称，抬首产生的升力和力矩都略大于埋首。垂向速度大于0.269m/s(对应航行器抬首或埋首3°以上)，升力和纵摇力矩呈现非线性。航行器抬首产生会抬首力矩，埋首自身产生埋首力矩，表明航行器本身的流体动力并未提供相应的回复力矩。

根据函数性质和式(15)～式(18)求得无因次化后的流体动力系数 ${Z'}_w^{EFD}$ ， ${Z'}_{w|w|}^{EFD}$ ， ${Z'}_0^{EFD}$ ， ${Z'}_w^{CFD}$ ， ${Z'}_{w|w|}^{CFD}$ ， ${Z'}_0^{CFD}$ ， ${M'}_w^{EFD}$ ， ${M'}_{w|w|}^{EFD}$ ， ${M'}_0^{EFD}$ ， ${M'}_w^{CFD}$ ， ${M'}_{w|w|}^{CFD}$ ， ${M'}_0^{CFD}$ ，具体结果见表2。

3.3.2 舵角系数

半潜航行器由前水平舵、后水平舵、后垂直舵组成，航行过程中通过前、后水平舵保持航行器的航行深度和调节运动姿态。前、后舵角变化范围从−15°～15°，间隔3°，对应的舵角从−0.209 rad到0.209 rad，正负号代表方向，负号表示打下舵角。

由图8可以看出，前、后舵舵角变化产生的阻力曲线接近偶函数性质，前舵最大误差3.8%，后舵最大误差6.1%，求得无因次舵角系数 $X{'_{{\delta _b}{\delta _b}}}$ ，如表3所示。

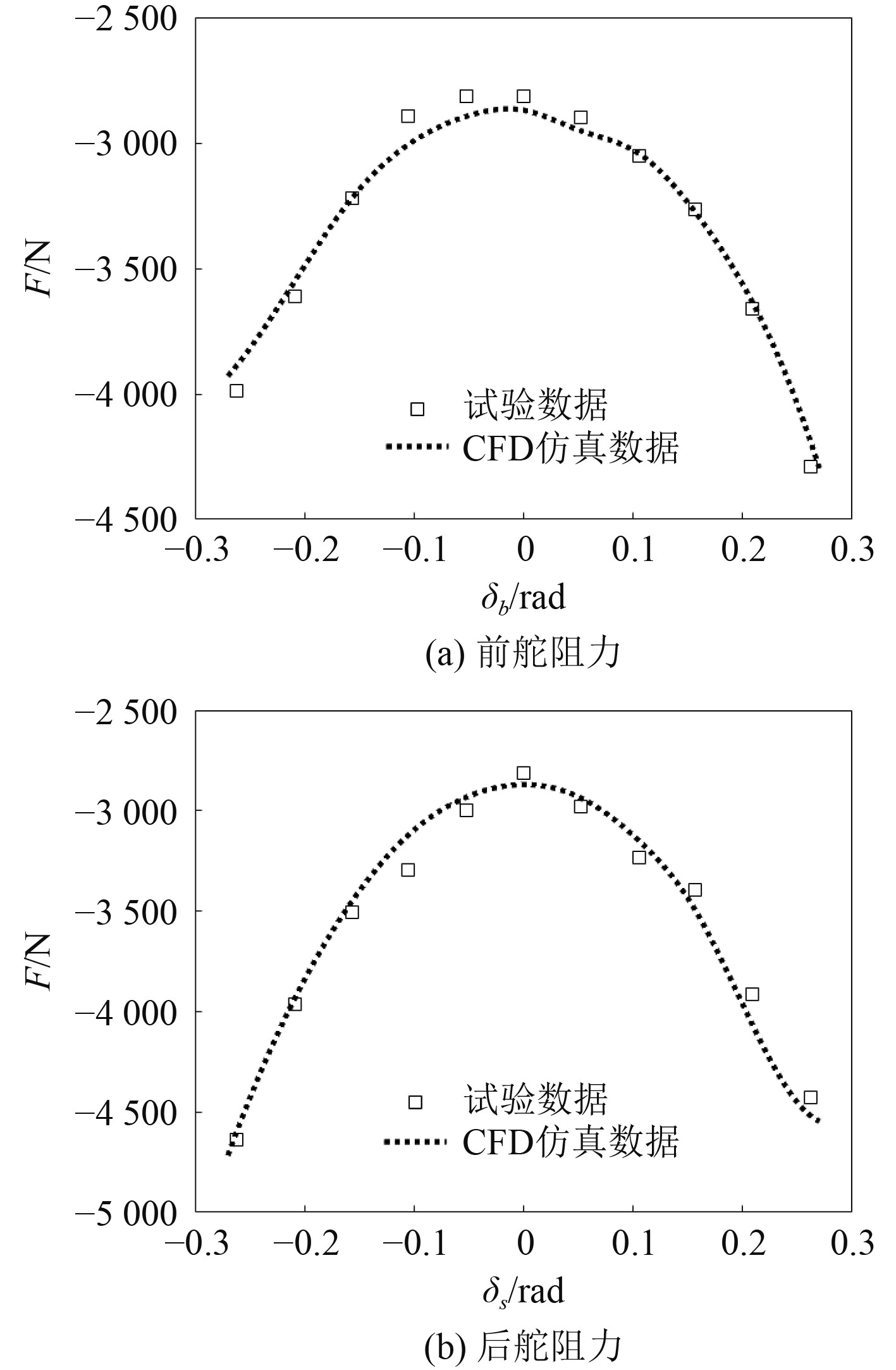
图 8 舵阻力系数曲线 Fig. 8 Rudder resistance coefficient curve

表 3 舵角流体动力系数 Tab. 3 Hydrodynamic coefficient of rudder angle

试验系数	数值	CFD系数	数值	误差/%
${X'}_{{\delta _b}{\delta _b}}^{EFD}$	–0.0255	${X'}_{{\delta _b}{\delta _b}}^{CFD}$	–0.0221	13.3
${X'}_{{\delta _s}{\delta _s}}^{EFD}$	–0.0335	${X'}_{{\delta _s}{\delta _s}}^{CFD}$	–0.0351	4.7
${Z'}_{{\delta _b}}^{EFD}$	–0.0444	${Z'}_{{\delta _b}}^{CFD}$	–0.0423	4.7
${Z'}_{{\delta _s}}^{EFD}$	–0.0667	${Z'}_{{\delta _s}}^{CFD}$	–0.0681	2
${M'}_{{\delta _b}}^{EFD}$	0.0288	${M'}_{{\delta _b}}^{CFD}$	0.0272	5.5
${M'}_{{\delta _s}}^{EFD}$	–0.0262	${M'}_{{\delta _s}}^{CFD}$	–0.0269	2.6

表 3 舵角流体动力系数 Tab.3 Hydrodynamic coefficient of rudder angle

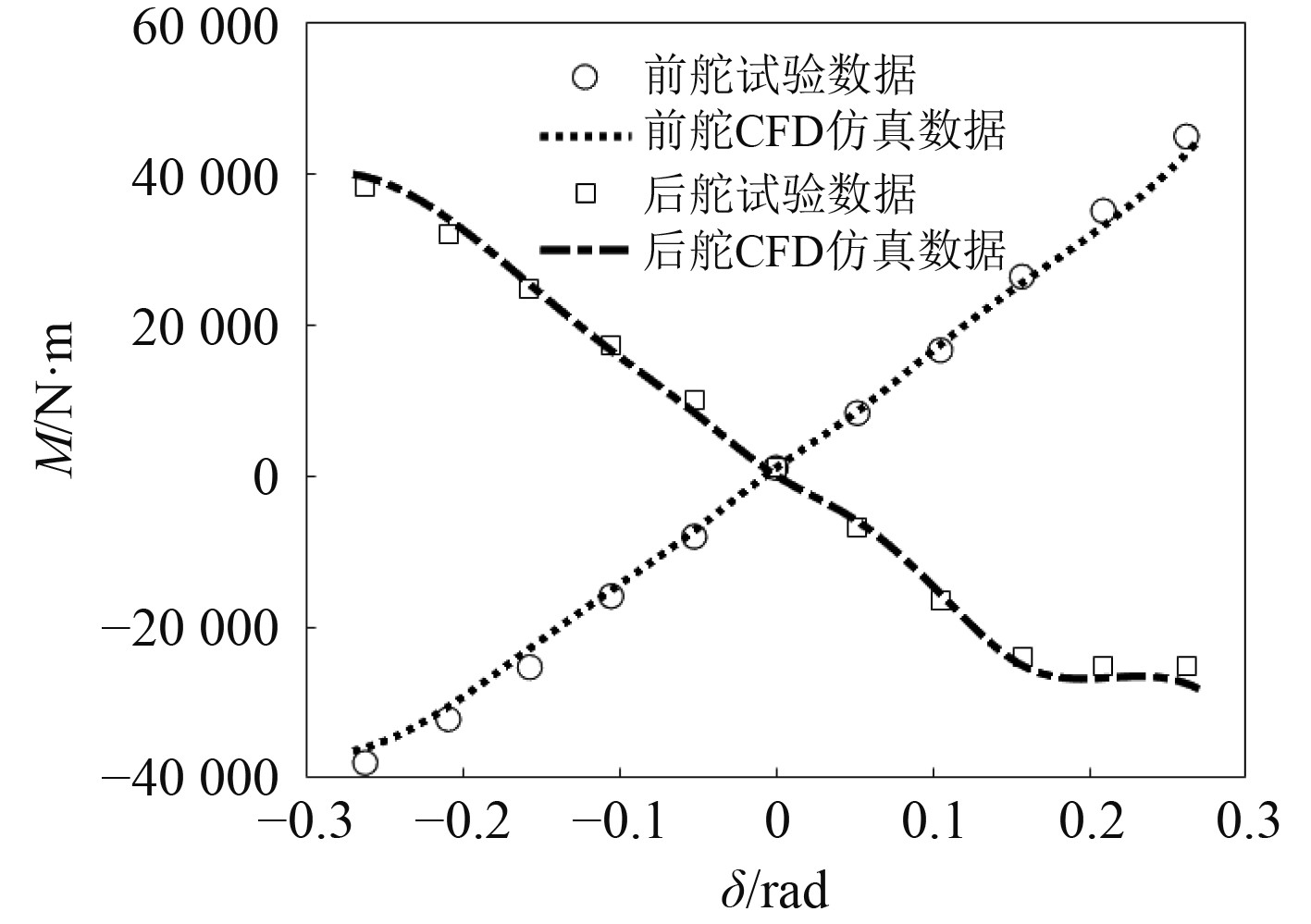
如图9和图10所示，前舵升力和力矩具有良好的线性，最大舵角15°时未发生舵效降低的现象或趋势。后舵的舵角9°以内变化趋势与前舵相近，升力数值大于前舵，打上舵角9°时开始出现舵效降低的现象，继续增加舵角升力增加不明显，该种现象主要原因在于前舵稍涡对后舵来流产生了影响，导致后舵失速角变小。对纵摇力矩起主要作用的是升力，后舵升力比前舵要大，但大舵下的纵摇力矩要小于前舵，表明在该种情况下后舵压力中心位置发生了偏移。在实际操纵过程中前舵在−15°～15°舵角范围内进行操舵，后舵在−9°～9°舵角范围内进行操舵，得到前、后舵无因次流体动力系数 $Z{'_{{\delta _b}}}$ ， $M{'_{{\delta _b}}}$ ， $Z{'_{{\delta _s}}}$ ， $M{'_{{\delta _s}}}$ 见表3。

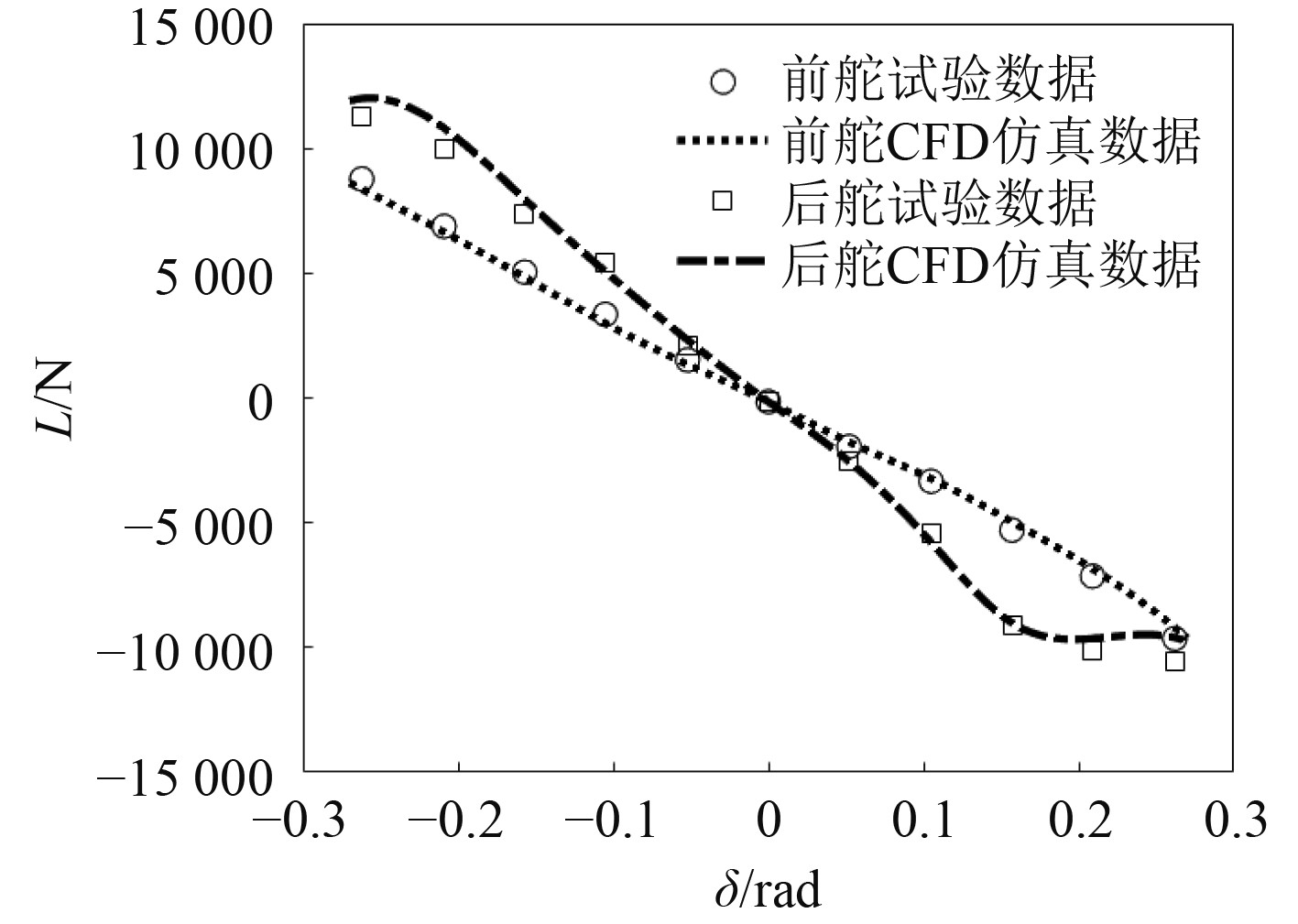
图 9 舵升力系数曲线 Fig. 9 Rudder lift coefficient curve

图 10 舵纵摇力矩系数曲线 Fig. 10 Rudder pitching moment coefficient curve

3.3.3 耦合系数

航行器受波浪影响会在埋首或抬首姿态情况下进行操舵，舵周期流场会受到航行器干扰，该种干扰表现为纵向耦合水动力。耦合水动力受航行器垂向速度和舵角的共同影响，升力可表示为：

$Z = {Z_0} + {Z_w}w + {Z_{w|w|}}w|w| + {Z_\delta }\delta + {Z_{w\delta }}w\delta 。$

(21)

通过改变航行器垂向速度和舵角，得到多组仿真数据，可表示为：

${Z}{ = }\left[ \begin{gathered} {Z_1} \\ {Z_2} \\ {Z_3} \\ { }. \\ { }. \\ { }. \\ {Z_n} \\ \end{gathered} \right] {X}{ = }\left[ \begin{gathered} {1 }{w_1}{ }w|w{|_1}{ }{\delta _1}{ }w{\delta _1} \\ {1 }{w_2}{ }w|w{|_2}{ }{\delta _2}{ }w{\delta _2} \\ {1 }{w_3}{ }w|w{|_3}{ }{\delta _3}{ }w{\delta _3} \\ {. }{. }{. }{. }{. } \\ {. }{. }{. }{. }{. } \\ {. }{. }{. }{. }{. } \\ {1 }{w_n}{ }w|w{|_n}{ }{\delta _n}{ }w{\delta _n} \\ \end{gathered} \right] {{Z}_{E}}{ = }\left[ \begin{gathered} {Z_0} \\ {Z_w} \\ {Z_{w|w|}} \\ { }{{Z}_\delta } \\ {Z_{w\delta }} \\ \end{gathered} \right] 。$

(22)

${{Z}_{E}}$ 的最小二估计量为 ${{(X'X)}^{{{ - 1}}}}{X'Z}$ ， ${Z}$ 的最小二乘估计量为 ${X(X'X}{{)}^{{\text{ - 1}}}}{X'Z}$ ，力矩的处理方式和力相同，可得到耦合系数 ${Z_{w\delta }}$ 和 ${M_{w\delta }}$ 。图11为升力和纵摇力矩拟合曲面，无因次化系数 $Z{'_{w\delta }}$ 和 $M{'_{w\delta }}$ 如表4所示。

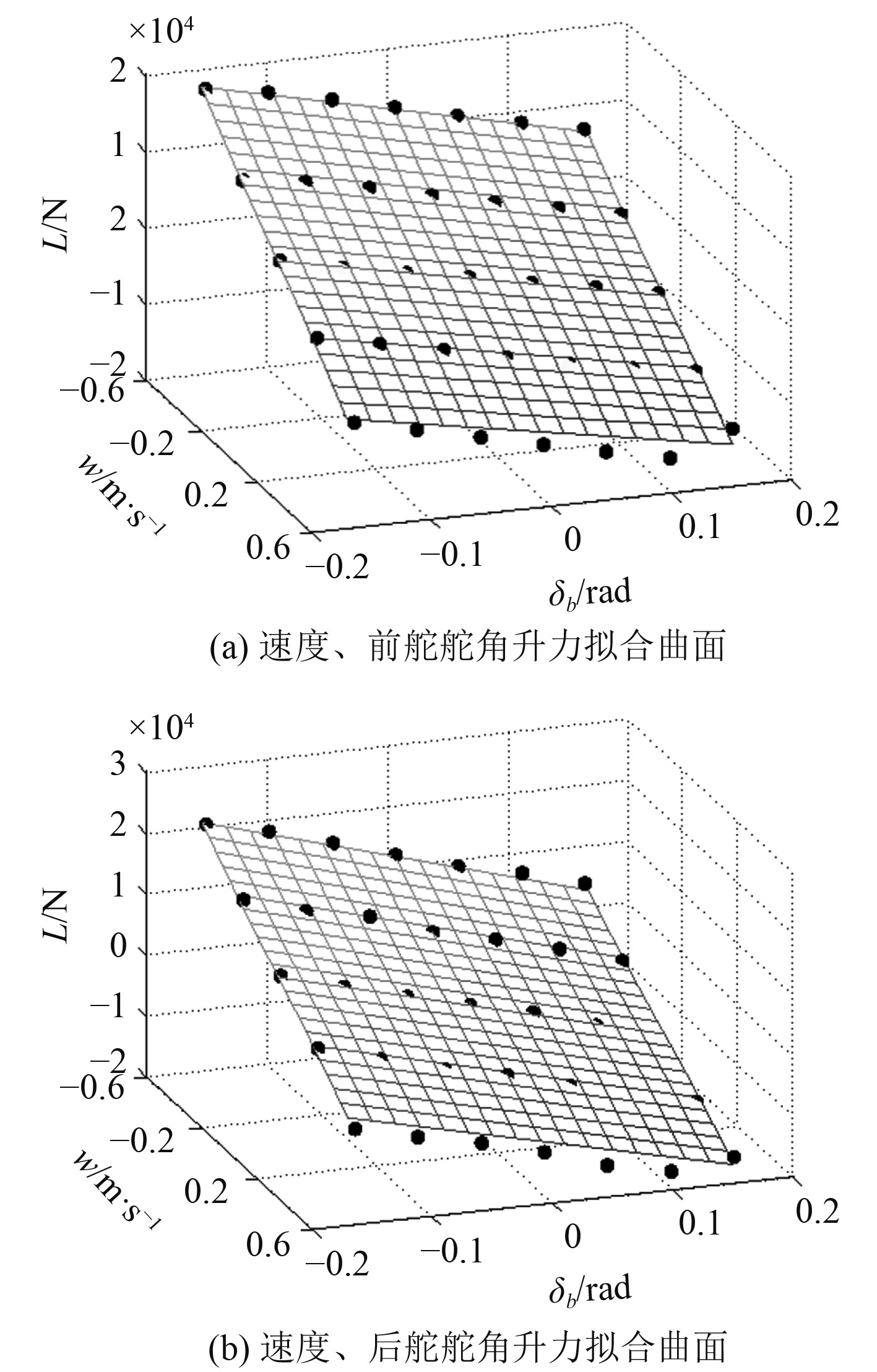
图 11 速度舵角升力拟合曲面 Fig. 11 Fitting surface of velocity and lift generated rudder

表 4 耦合流体动力系数 Tab. 4 Coupled hydrodynamic coefficient

CFD系数	数值
${Z'}_{w{\delta _b}}^{CFD}$	0.0516
${Z'}_{w{\delta _s}}^{CFD}$	–0.0177
${M'}_{w{\delta _b}}^{CFD}$	0.0704
${M'}_{w{\delta _s}}^{CFD}$	0.0255

表 4 耦合流体动力系数 Tab.4 Coupled hydrodynamic coefficient

可知，垂向速度的变化范围为–0.538～0.538 m/s，前、后舵角变化范围–0.157～0.157rad。耦合曲面与仿真数据拟合较好，满足线性拟合趋势。航行器垂向速度0.538 m/s，舵角0.157rad，前舵和后舵产生的升力皆降低，该工况对应的航行器攻角为6°，舵角为9°。上文前舵15°舵角未出现舵面升力降低的情况，表明前舵升力降低的主要原因为航行器攻角改变了周围流场的分布，对前舵产生影响。后舵升力降低的原因除了受前舵影响外可能和航行器攻角也有关，需结合流场进行进一步分析。

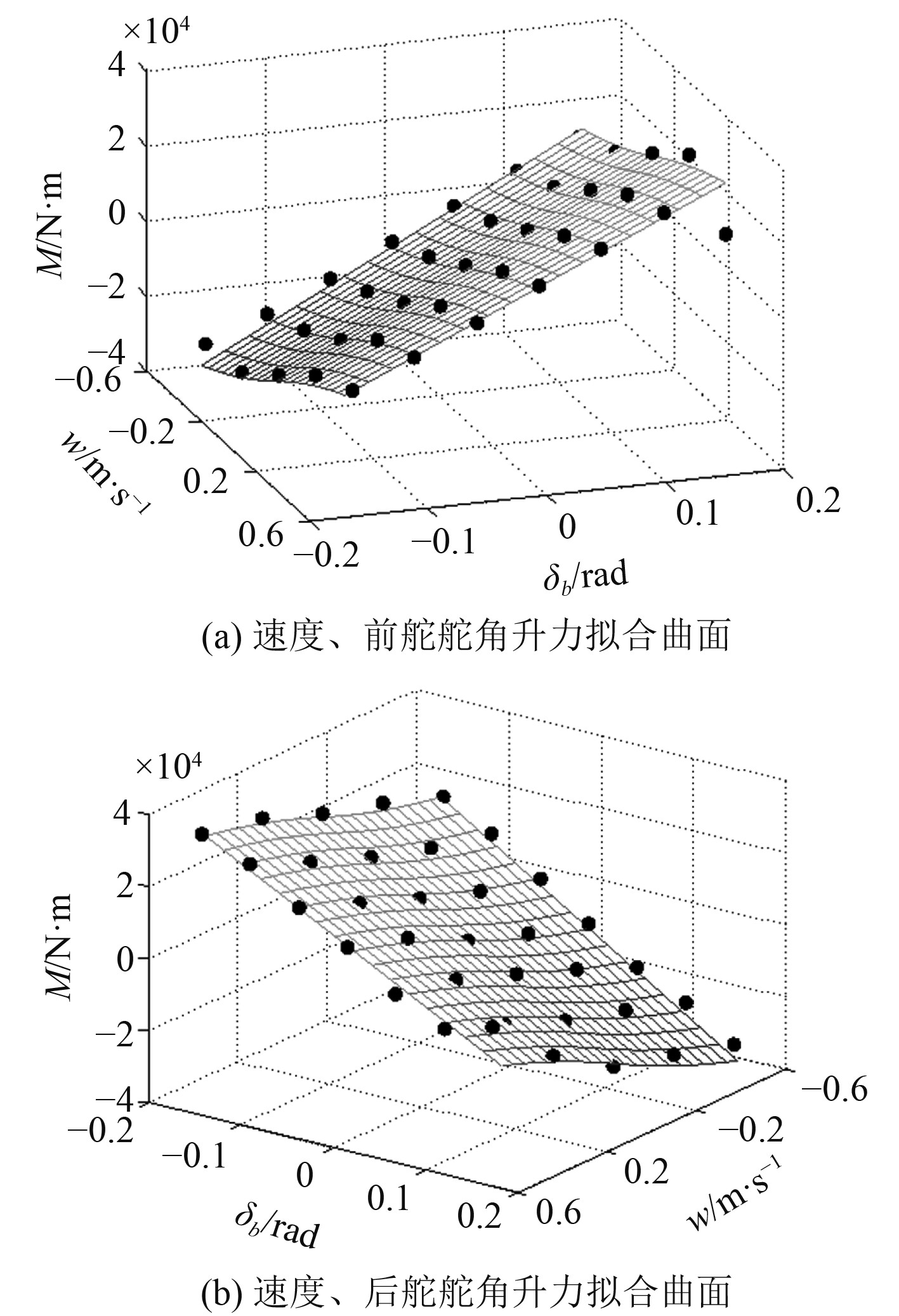
如图12所示，纵摇力矩拟合曲面与仿真数据拟合较好。与升力耦合曲面相似，航行器攻角为6°，舵角为9°，纵摇力矩数据点未落到曲面上，且误差较大，表明此时舵的调节效果降低，开始出现非线性变化规律，增加舵角甚至还会起到反作用。

图 12 速度舵角纵摇力矩拟合曲面 Fig. 12 Fitting surface of velocity and pitch moment about rudder

4 舵效降低原因分析

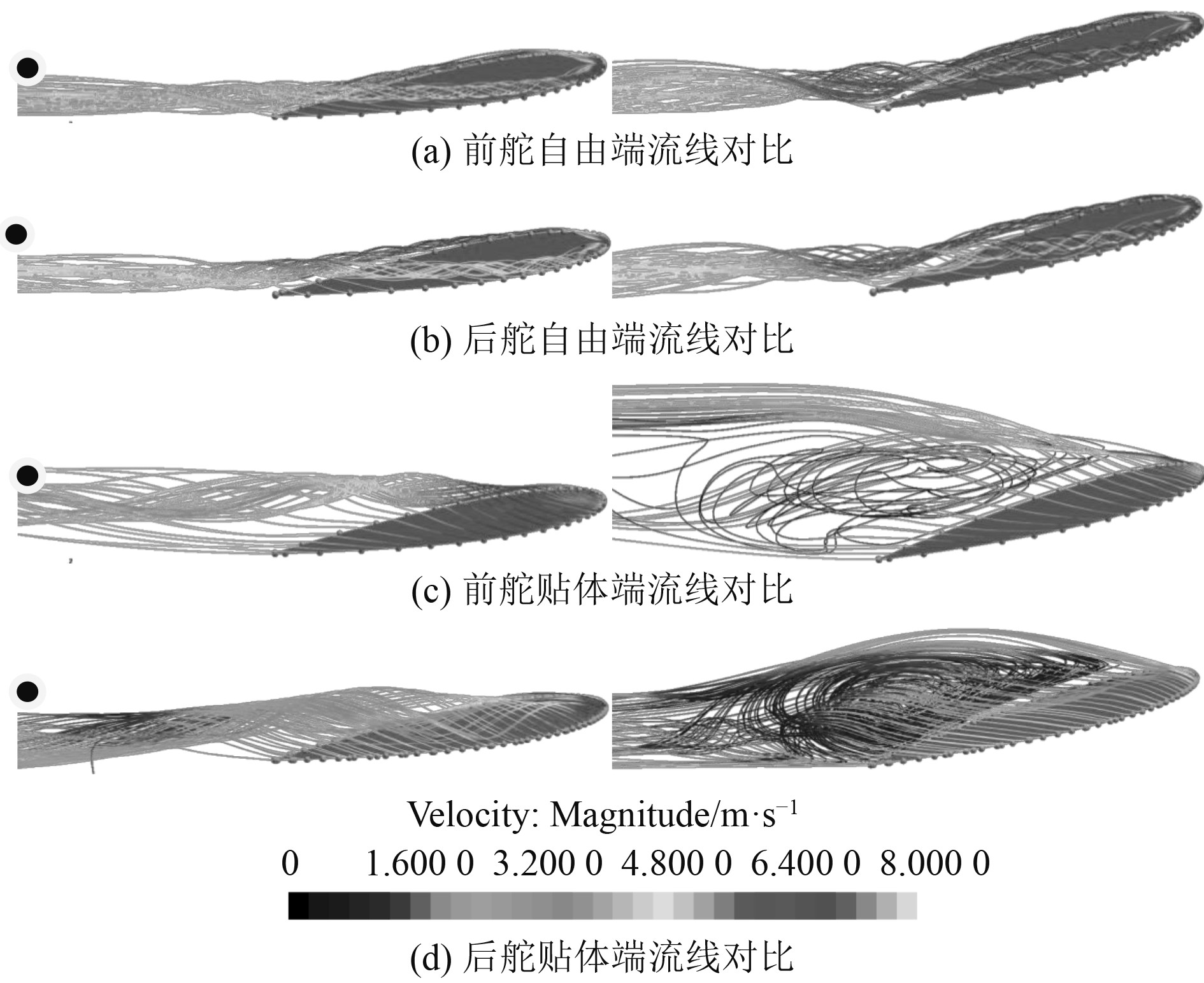
根据仿真结果，前、后舵在航行器有攻角情况下更易发生舵效降低的情况。为了研究该种现象产生的原因，对前、后舵周围流场进行分析。图13为航行器攻角0°和6°，前、后舵9°情况下流线分布图。为了更好描述，将靠近航行器主体的舵面称为贴体端，另一面为自由端，带•的图航行器攻角为0°。

图 13 前、后舵流线 Fig. 13 Streamlines of front and rear rudder

如图13(a)和图13(b)所示，自由端稍涡由压力面和吸力面两部分涡系组成，在舵板后缘汇聚。舵板前缘流线能够快速成型并向下迁移，靠近中后缘的流线会被稍涡捕获。航行器攻角增加了吸力面流线和稍涡脱落速度。

如图13(c)和图13(d)所示，贴体端稍涡主要由吸力面边界层分离产生，航行器的存在阻碍了压力面稍涡的形成，此时流体在压力的作用下流向上表面。随着航行器攻角的增加，前、后舵在舵面1/4以后位置形成直径与舵板弦长相当的表面涡，且后舵的涡更剧烈，这也是造成升力损失的主要原因。

结合前、后舵板表面极限流线进行进一步分析，舵面较小的是前舵，较大的是后舵。如图14所示，同一片舵中左侧为舵板压力面，右侧为舵板吸力面。两端稍涡使得极限流线发生偏转，且吸力面偏转更严重，表明吸力面受稍涡的影响更明显。由图15可以看出，在两端稍涡的影响下，极限流线偏转更严重，在舵板吸力面中间形成表面涡，表面涡与两端稍涡共同作用增加了吸力面压力。表明航行器攻角改变了周围流场环境，使得舵板失速角变小。

图 14 航行器0°攻角舵板极限流线 Fig. 14 Limit streamline of rudder plate at 0° attack angle of vehicle

图 15 航行器6°攻角舵板极限流线 Fig. 15 Limit streamline of rudder plate at 6° attack angle of vehicle

5 结　语

针对半潜航行器纵向水动力性能预报问题，通过数值方法开展了半潜航行器的纵向速度和舵角系数仿真计算，并与风洞试验结果进行对比验证；通过最小二乘法回归了速度、舵角耦合系数，分析了影响舵效的主要原因。得出主要结论如下：

1）CFD仿真结果与试验结果吻合较好，升力和纵摇力矩最大误差不超过6.5%，可满足工程应用的需要；

2）航行器无攻角情况下，后舵会受前舵影响，导致有效舵角范围变小，可通过增加前、后舵垂直方向距离进一步优化性能；

3）增加航行器攻角会影响前后舵板贴体端稍涡的形成，迫使稍涡向上偏移，两端稍涡迫使舵面流线发生偏移，在吸力面形成一个直径与舵板弦长相当的涡。

参考文献

[1]	MORI K, HOTTA T, EBIRA K, et al. A study on semi-submergible high speed ship with wings—Its resistance characteristics and possibility[J]. Journal of the Society of Naval Architects of Japan, 1988, 164: 74-81.
[2]	MORI K, DOI Y K. Numerical simulation of flows and motions of semi-submergible high speed ship with wings[J]. Transactions of the West-Japan Society of Naval Architects, 1991, 82: 41-52.
[3]	谈果戈. 双尾半潜无人艇近自由液面操纵性研究[D]. 哈尔滨: 哈尔滨工程大学, 2017. TAN G G. Study on the maneuverability of twin tail semi-submerged unmanned vehicle near free surface[D]. Harbin: Harbin Engineering University, 2017.
[4]	UENO M. Hydrodynamic derivatives and motion response of a submersible surface ship in unbounded water[J]. Ocean Engineering, 2010, 37: 879-890. DOI:10.1016/j.oceaneng.2010.03.004
[5]	HIRAYAMA Y, KONDO S, TAKAYAMA T, et al. Trial experiment on the submersible surface ship utilizing downward lift (Part 4): realization of continuous control process from surface, submergence to surface condition[J]. The Japan Society of Naval Architects and Ocean Engineers, 2007, 4: 143-144.
[6]	UENO M, TSUKADA Y, SAWADA H. A prototype of submersible surface ship and its hydrodynamic characteristics[J]. Ocean Engineering, 2011, 38: 1686-1695. DOI:10.1016/j.oceaneng.2011.08.002
[7]	CONG Huo, YI Zheng, XIAO Penggao. Free-running tests on a self-propelled submersible multi-state vehicle model[J]. Ocean Engineering, 2021, 236: 1-11.
[8]	董文才, 岳国强, 侯亚成, 等. 高速艇自由变深水动力试验研究[J]. 海军工程大学学报, 2016, 18(1): 57-62. DONG W C, YUE G Q, HOU Y C, et al. Experimental study on hydrodynamics of high-speed craft with freely varying draft[J]. Journal of Naval University of Engin Eering, 2016, 18(1): 57-62.
[9]	MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149
[10]	DENG R, LUO R, WU T, et al. Time-domin numerical research of the hydrodynamic characteristics of a trimaran in calm water and regular waves[J]. Ocean Engineering, 2019, 194: 1-13.
[11]	刘宗凯, 刘满红, 郭正阳, 等. 全附体潜航器螺旋桨桨叶损伤故障辨识机理[J]. 兵工学报, 2021, 4(12): 2710-2721. LIU Z K, LIU M H, GUO Z Y, et al. Identification Mechanisms for Damage Characteristics of Fully Appendage Submarine Propeller[J]. Acta Armamentarii, 2021, 4(12): 2710-2721. DOI:10.3969/j.issn.1000-1093.2021.12.019
[12]	ASNAAGHI A, SVENNBERG U, BENSOW R E. Evaluation of curvature correction methods for tip vortex prediction in SST K-Ω turbulence model framework[J]. International Journal of Heat and Fluid Flow, 2019, 75: 135-152. DOI:10.1016/j.ijheatfluidflow.2018.12.002
[13]	施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 2020.
[14]	LIU H, MA N, GU X C. CFD prediction of ship-bank interaction for KCS under extreme conditions[J] Journal of Marine Science and Technology, 2021, 26: 1062–1077.
[15]	HE T, FENG D, LIU L, et al. CFD simulation and experimental study on coupled motion response of ship with tank in beam waves[J]. Journal of Marine Science and Engineering. 2022, 10(113): 1-26.


舰船科学技术 2023, Vol. 45 Issue (5): 36-43 DOI: 10.3404/j.issn.1672-7649.2023.05.007	PDF