2. 上海海洋大学 工程学院,上海 201306
2. College of Engineering Science and Technology, Shanghai Ocean University, Shanghai 201306, China
深海空间站是在载人潜水器基础上发展起来的新一代居住型深海作业平台,在有限空间内集成生活起居、工作娱乐等各项功能,可长期在水下进行科学研究、海洋油气资源开采等。海洋油气资源主要有分布于800~3000 m深的富钴结壳、热液硫化物以及天然气水合物。深海空间站主体结构为大型耐压结构,壳体为站内工作人员创造安全舒适的生存空间,也为站内非耐压设备提供长期可靠的运行环境。现役大型耐压壳有柱形耐压壳、多球交接耐压壳,两者结构均为长柱结构,影响深海空间站转向性,且对缺陷较为敏感,影响深海空间站安全。
环形耐压壳周向尺寸分布均匀,空间利用率高,具有优越的使用性能,且对缺陷敏感性低,承载能力较强,是未来深海空间站优选结构[1]。Błachut[2]对2个低碳钢和1个不锈钢环形耐压壳进行压力测试,得到了壳体失稳载荷和失稳模式,表明环形耐压壳屈曲受材料塑性影响大。张建[3]将环形耐压壳与圆柱壳进行了等效比较,研究表明环形耐压壳相比其等效圆柱形耐压壳承载能力可提高29%;崔维成[4-5]提出一种加强肋环形耐压壳结构,研究了均布外压下加肋环形耐压壳和普通环形耐压壳的线性应力和非线性屈曲,推导出一个力学模型来设计水下加肋环形耐压壳。但是,上述环形耐压壳加工制造难度大、成本高。Wang[6]采用以直代曲的思想,将圆柱壳的圆截面设计成正多边形波纹截面结构,结果表明,当正多边形边数达到17时,波纹柱壳的承载能力为圆柱壳的97%。唐文献[7]也对波纹柱壳进行了试验研究,试验证明将圆柱壳改为波纹柱壳可以有效提高壳体屈曲载荷。
为此,本文尝试将这种波纹柱形结构的设计思想应用于环形耐压壳。在圆截面环形耐压壳基础上,提出了一种新型波纹截面环形耐压壳。研究波纹数对波纹截面环形耐压壳屈曲载荷的影响规律,优选出一种波纹截面环形耐压壳,并与圆环壳进行对比分析。
1 设计方案 1.1 现有深海空间站耐压壳简介NR-1深潜器是美国海军核电力驱动海洋工程潜艇,1960年海军上将H.G.Rickover将其设想为中间深度的海底探索深潜器。NR-1深潜器具有在海底进行油管勘测、地形勘探、搜寻预定目标物及打捞等功能。该深潜器的排水量为400 t,身长为41.8 m,单次下潜耐力可供13人居住25天。该深潜器主体大型耐压结构为圆柱形耐压壳,材料是高强度钢。由于圆柱壳承载能力相对于环形壳较弱,且对缺陷敏感,影响深潜器的安全,该深潜器最大下潜深度仅为910 m,相当于约10 MPa的水下压强。图1为美国NR-1深潜器示意图。

|
图 1 美国NR-1深潜器示意图 Fig. 1 Diagram of the NR-1 deep submersible of America |
10831型深潜器是俄罗斯研发的一艘核动力深海工作站,全长约70 m,艇宽7 m,满载排水量低于1000 t。其主体大型耐压结构为多球交接壳,相比于圆柱壳结构的NR-1深潜器在下潜深度方面有了很大提高,能在海底2500~3000 m进行地质勘测,最大下潜深度可达6000 m。该深潜器主要用于科研工作,具备深海钻探等技术,可获取大量深海地质样本及信息。图2为俄罗斯10831型深海空间站示意图。

|
图 2 俄罗斯10831型深海空间站 Fig. 2 Diagram of the 10831 deep-sea space station of Russia |
在圆截面环形耐压壳结构基础上,设计一种便于制造且可承受海底近20 MPa压强的新型波纹截面环形耐压壳。
建立圆截面环形耐压壳模型,横截面示意图如图3所示,旋转半径

|
图 3 环形耐压壳模型横截面示意图 Fig. 3 Diagram of cross section of toroidal pressure shell model |
根据耐压壳空间等体积原则建立若干个等效波纹截面环形耐压壳,波纹壳旋转半径和厚度均与圆截面环形耐压壳相同,其他参数如表1所示,波纹壳横截面示意图如图3所示。其中圆截面环形耐压壳体积计算公式如下:
|
|
表 1 波纹截面环形耐压壳参数 Tab.1 Parameters of toroidal pressure shell with corrugated cross section |
| $ {{V}}_{1}={\int }_{0}^{2{\pi }}2{\pi }R\times {\text{π}}\times {r}^{2}\mathrm{d}\theta 。$ | (1) |
将数值代入式(1)得圆环壳体积为
波纹数为6,8,10,12,14的波纹截面环形耐压壳体积公式分别如下:
| $ {V}_{2}={\int }_{0}^{2{\text{π}}}2{\text{π}}R\times1.5\sqrt{3}\times{a}^{2}\mathrm{d}\theta, $ | (2) |
| $ {V}_{3}={\int }_{0}^{2{\text{π}}}2{\text{π}}R\times(2+2\sqrt{2})\times{{a}}^{2}\mathrm{d}\theta ,$ | (3) |
| $ {V}_{4}={\int }_{0}^{2{\text{π}}}2{\text{π}}R\times2.5\mathrm{t}\mathrm{a}\mathrm{n}72°\times{a}^{2}\mathrm{d}\theta, $ | (4) |
| $ {V}_{5}={\int }_{0}^{2{\text{π}}}2{\text{π}}R\times3\mathrm{t}\mathrm{a}\mathrm{n}75°\times{a}^{2}\mathrm{d}\theta ,$ | (5) |
| $ {V}_{6}={\int }_{0}^{2{\text{π}}}2{\text{π}}R\times 15.335\times{a}^{2}\mathrm{d}\theta 。$ | (6) |
式中:R为环形耐压壳旋转半径;a为波纹壳横截面边长。通过以上公式可求得若干个波纹壳体积如表1所示,壳体之间体积相等。
由以上几何参数建立有限元模型如图4所示,根据CCS2013[8]耐压壳体极限强度非线性分析方法求得圆环壳承载能力为29.950 MPa,各个波纹截面环壳模型承载能力如图5所示。数值计算所用材料为马氏体镍钢C250,参数如下:密度

|
图 4 圆环壳与波纹截面环壳有限元模型 Fig. 4 Finite element model of toroidal shell and toroidal shell with corrugated cross section |
|
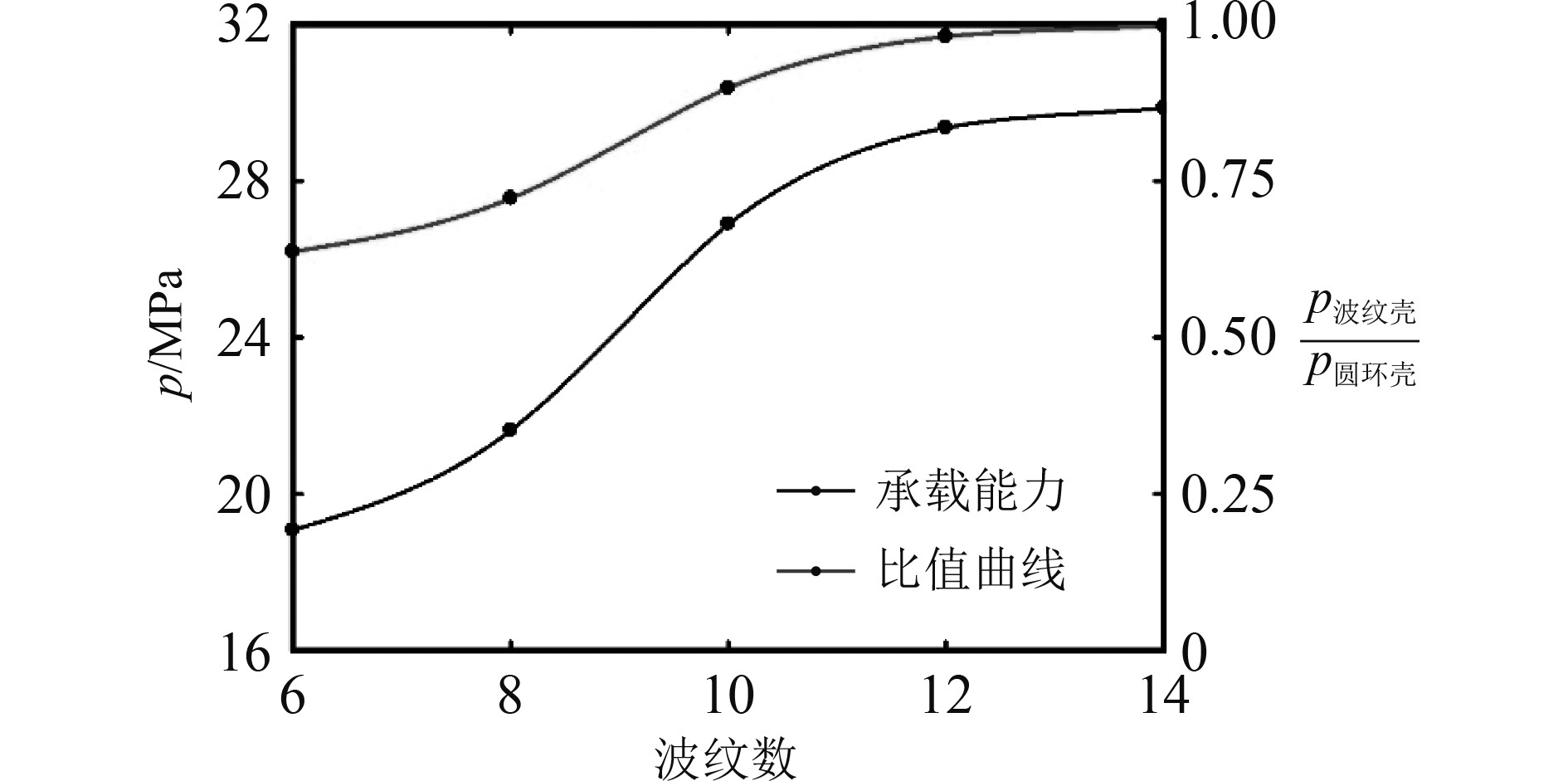
图 5 波纹截面环壳承载能力图 Fig. 5 Loading capacity diagram of toroidal shell with corrugated cross section |
计算过程采用了基于屈曲模态的几何初始缺陷分析方法,根据一阶模态导入初始缺陷的幅值大小为5 mm,单元类型为4边型壳单元,网格划分满足非线性求解收敛,网格数量见表1。有限元模型边界条件均为经典三点边界,该边界条件对称设置,既可以消除整体刚体位移,也不妨碍相对变性。增量求解方法采用了非线性弧长法。具体参数设置如下:
初始弧长增量为0.1,最大弧长增量为0.3,最小弧长增量为10−50,总弧长比例因子为1,最大增量步数为1000。
1.2.2 波纹截面环壳参数优选由图5可知,对于波纹截面环壳,随着波纹数的增加,其承载能力越来越接近于圆环壳,当波纹截面环壳的波纹数达到12时,其承载能力与圆环壳的承载能力比值为0.980,近乎相等,且与波纹数为14的环壳承载能力相差很小。对于波纹截面环壳,由于波纹数越多,相对加工工序越多,制造越麻烦,故在承载能力近乎相等的情况下考虑波纹截面环壳的相对加工简易程度,选取波纹数为12的环壳作为本次设计模型。
2 壳体性能分析 2.1 壳体强度分析由计算结果可得圆环壳与波纹数为12的波纹截面环壳失稳模式如图6所示,可知,波纹数为12的环壳与圆环壳失稳位置几乎相同,且与Błachut[2]前期进行的圆环壳模型试验研究失稳位置一致,圆环壳试验模型失稳位置如图7所示。
|
图 6 壳体失稳模式 Fig. 6 Instability mode of the Shell |
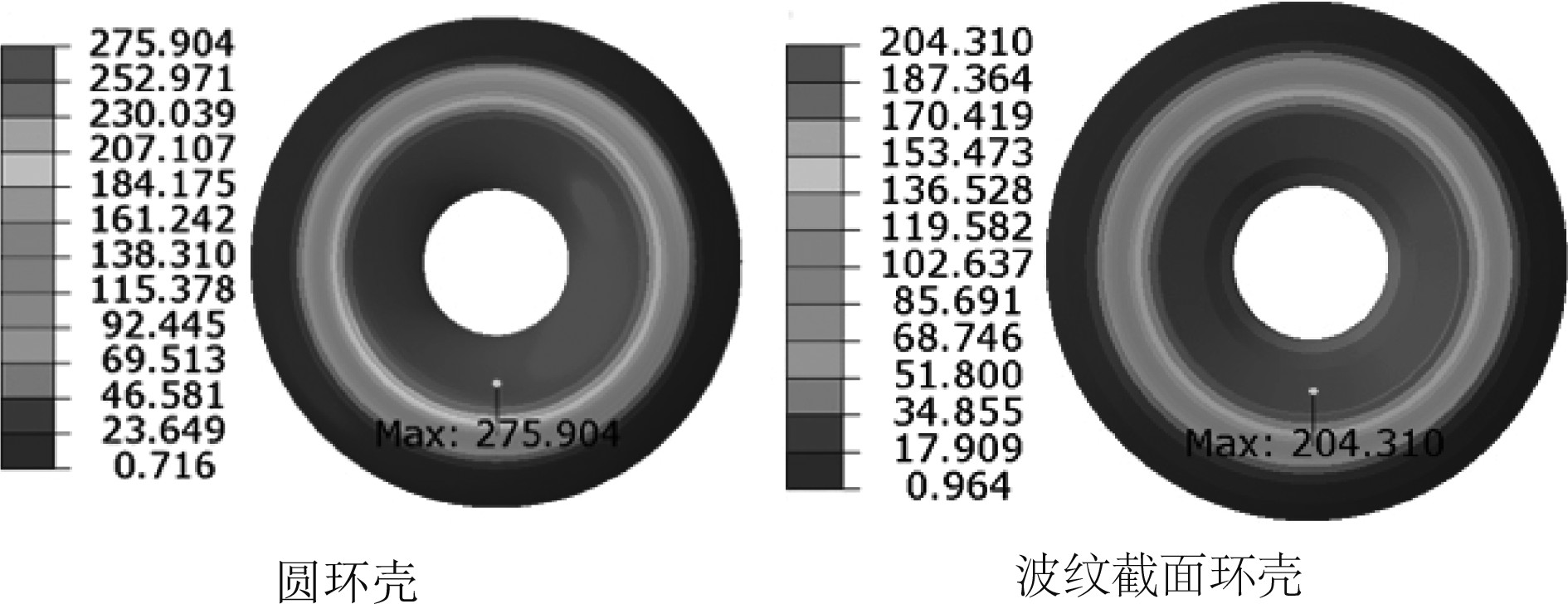
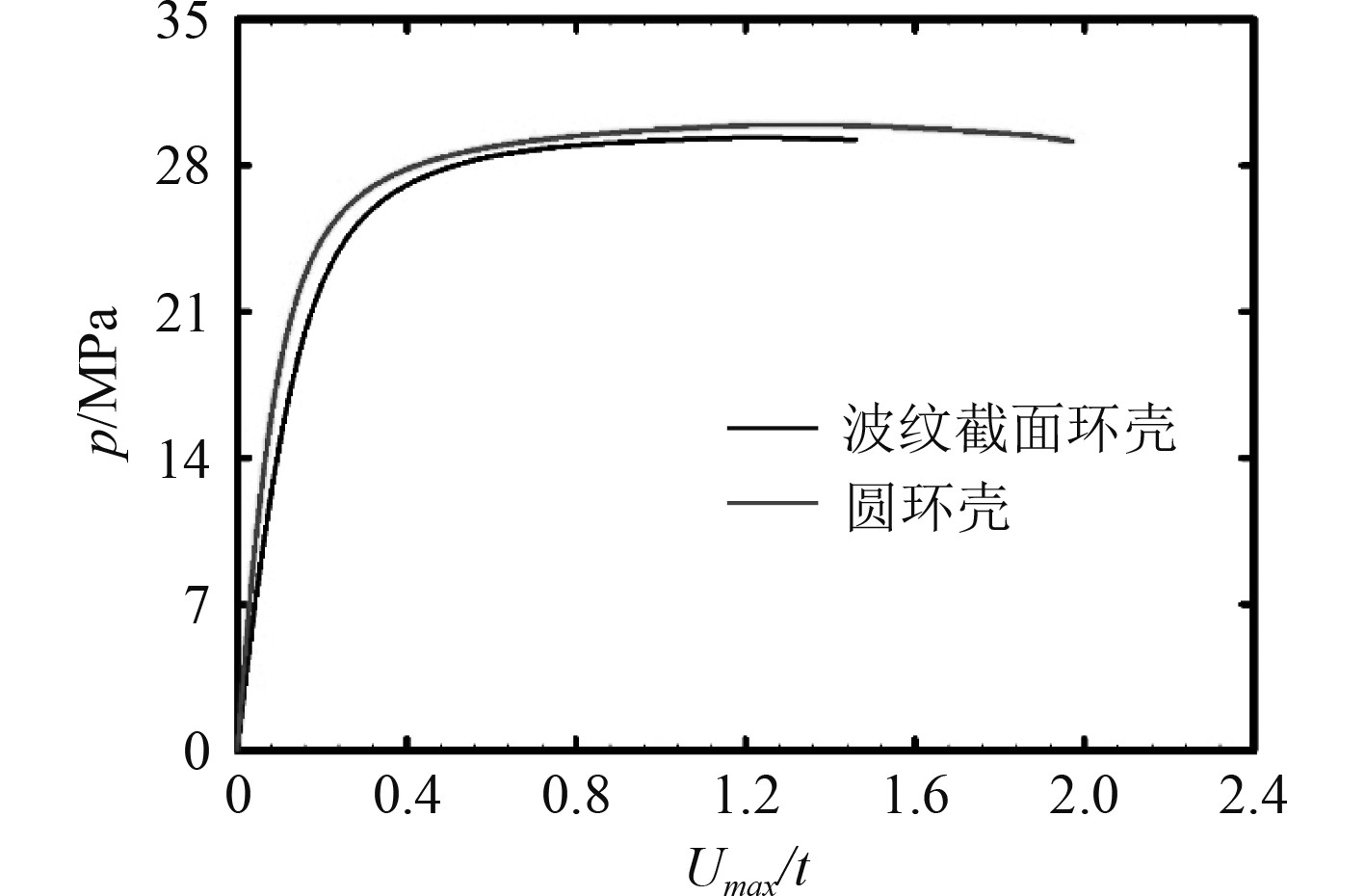
2种壳体的平衡路径如图8所示。图中横坐标为加载过程壳体变形最大处的位移量与厚度的比值,纵坐标为壳体承受的压力值。由平衡路径可知,波纹截面环壳计算过程收敛。曲线最高点即临界状态下对应的壳体应力分布情况如图9所示,应力最大值大于材料的屈服强度值,表明壳体失稳为强度破坏,发生了塑性变形。对比图7与图9可知,应力值最大处与位移变形最大处相同。综上可知,波纹截面环形耐压壳因其材料塑形、模态缺陷等因素,失稳形式表现为非线性弹塑性失稳。
|
图 8 壳体平衡路径 Fig. 8 The equilibrium path of the shell |

|
图 9 壳体临界状态应力分布 Fig. 9 Critical state stress distribution of the shell |
根据CCS2013[8] 耐压壳体极限强度非线性分析方法对载荷工况的要求,引入安全系数
为评价波纹截面环形耐压壳储备浮力的能力,引入浮力系数公式:
| $ \epsilon =\frac{V\rho }{{V}_{0}{\rho }_{0}}。$ | (7) |
其中:
波纹截面环形耐压壳材料体积公式如下:
| $ V=n\times a\times t\times 2{\text{π}}R,$ | (8) |
代入数值得
因实际情况波纹截面环形耐压壳全部淹没在水面以下,故排水体积等于壳体外轮廓体积,则由式(5)代入数值得
将以上数值代入浮力系数式(7)得
为评价耐压壳抗压性能,引入性能比公式[3]:
| $ \eta =\frac{PV}{W} 。$ | (9) |
其中:
该性能比系数大于不锈钢以及树脂材料制造的封头、球壳和蛋壳等多种壳体的性能比参数[3],故马氏体镍钢波纹截面环壳抗压性能优良。
3 结 语1)对于波纹截面环形耐压壳,当波纹数从6增加到14时,承载能力不断上升,且在波纹数为12时,波纹截面环壳承载能力高达圆环壳承载能力的98%。
2)优选波纹截面环形耐压壳周向为平面结构,空间利用率高,相比圆环壳加工制造简便,且便于深海空间站观察窗的开口以及各个单元设计,使用性能好。
3)优选波纹截面环形耐压壳失稳位置与圆环壳一致,应力最大处与失稳位置相同。由于材料塑形、模态缺陷等因素,失稳形式表现为非线性弹塑性失稳。
| [1] |
ROSS C T F. A conceptual design of an underwater vehicle[J]. Ocean Engineering, 2006, 33(16): 2087-2104. |
| [2] |
BłACHUT J. Collapse Tests on Externally Pressurized Toroids[J], J. Press. Vessel Technol. 125 (2003) 7092–7098.
|
| [3] |
ZHANG Jian, WANG Xin, TANG Wenxian, et al. Non-linear collapse behavior of externally pressurized resin toroidal and cylindrical shells: numerical and experimental studies[J]. Ships and Offshore Structures, 2020, 1-17. |
| [4] |
DU Qinghai, CUI Weicheng, ZHANG Bowen. Buckling characteristics of a circular toroidal shell with stiffened ribs[J]. Ocean Engineering, 2015, 108: 325-335. DOI:10.1016/j.oceaneng.2015.08.005 |
| [5] |
DU Qinghai, CUI Weicheng, WAN Zhengquan. Nonlinear finite element analysis of a toroidal shell with ring stiffed ribs[J]. OMAE2010-21088, 2010, 759-765. |
| [6] |
WANG C. Y. Buckling and postbuckling of segmented tubes under external pressure[J]. International Journal of Non-Linear Mechanics, 2005, 40: 551-556.ff. |
| [7] |
TANG Wen-xian, ZHANG Shan, ZHANG Jian, et al. Experimental study on the failure modes of circumferentially corrugated cylinders under external hydrostatic pressure[J]. Thin-Walled Structures, 2020, 156: 106988.1-8. |
| [8] |
Rules for the classification and construction of diving systems and submersibles[S]. China Classification Society (CCS), 2013.
|
| [9] |
杨青松, 胡勇, 姜旭, 等. 载人潜水器马氏体镍钢载人舱设计[J]. 船舶工程, 2018, 40(8): 72-76. |
 2023, Vol. 45
2023, Vol. 45

