相比常规全悬挂舵,半悬挂舵的结构形式由于在展向(舵高方向)中部附近通过挂舵臂提供了一个额外的支撑点,使得舵系梁的受力更加合理,可有效降低下舵杆处的剪力和弯矩,有利于控制舵杆直径,因而在大中型船舶的舵系设计上得到广泛应用。但是,由于挂舵臂固定于船体中线,对上半部分舵叶的来流起到整流作用,减小了来流攻角,使舵叶整体的升力系数曲线斜率下降,升力性能明显低于等展弦比的全悬挂舵[1-3],对船舶操纵性的影响是负面的。对于部分需要进江航行的船舶而言,因内河水域航道狭窄、交通繁忙,为了确保航行安全,必须具备良好的操纵性,如配备半悬挂舵,则易与操纵性需求形成矛盾。
在船型尺度确定的前提下,提高舵的升力是提升船舶操纵性的有效措施。本文对半悬挂舵的升力性能进行优化,改善配备半悬挂舵的进江船型的操纵性。
1 设计条件 1.1 方案设计以一型“曼谷型”集装箱船为优化设计目标船型。该船型服务于中国至东南亚航线,因需频繁进出长江、珠江和湄南河等内河狭窄航道,对操纵性有较高的要求。选取该船型已交付的同型船作为对标船型(以下简称“原船型”),原船型的舵系采用半悬挂舵(以下简称“原舵系”),舵叶翼型为NACA0021,厚度比为0.21,可动部分舵叶面积为26.88 m2,舵叶展弦比(含挂舵臂)为1.835。优化设计目标船型(以下简称“目标船型”)仍采用半悬挂舵(以下简称“优化舵系”),经过对外形的细微调整得到可动部分舵叶面积为26.99 m2,舵叶展弦比(含挂舵臂)为1.834,二者的侧投影几何特征可视为基本相同。舵系侧视图如图1所示。

|
图 1 舵系侧视图 Fig. 1 Side view of the rudder |
原船型和目标船型的船长、船宽、结构吃水均相同,舵设计航速均取19.5 kn。
1.2 计算条件对半悬挂舵的水动力计算及优化基于雷诺平均N-S方程(RANS)及计算流体力学(CFD)软件STAR-CCM+进行。由于半悬挂舵与挂舵臂之间的间隙范围大且特征尺度小,存在模型细节多、网格划分复杂及计算结果易发散等问题,以往的研究一般按舵平均宽度或相当展弦比将半悬挂舵重构为相似悬挂舵进行CFD分析[2]。为了准确模拟半悬挂舵的流动特性,本文采用精细化网格划分对包括挂舵臂在内的半悬挂舵进行直接建模和计算。
计算模型按照1∶3缩尺比建立,模型尺度雷诺数Re约7.05×106,高于文献[4]综述后建议的舵CFD分析的最小雷诺数6×106,一般认为在这一雷诺数下,尺度效应对舵的水动力系数已无实质影响。按雷诺数换算得到模型尺度的来流速度Vm为5.792 m/s。湍流模型采用Standard k-ε两方程模型,相关研究表明[5-6],Standard k-ε模型对单独舵升力性能的模拟与模型试验的综合匹配程度相对较高。计算域的长、宽、高取为约20c×12c×10c,其中c为计算模型的平均弦长。使用控制域对近壁面区域进行2层加密。使用壁面函数法处理近壁区流动,通过初始壁面无因次距离y+值控制边界层网格尺度,参考文献[2]和文献[7~8]的研究结果选取y+,实取y+约30~60。单个计算方案的网格总数约390万,大于文献[6]中网格无关性验证的最大数量网格方案。图2为模型周边的网格划分与过渡,图3为间隙区的网格划分。上述CFD计算条件的准确性已在其他类似研究中得到模型试验的验证[9]。

|
图 2 模型周边的网格划分与过渡 Fig. 2 Mesh division and transition near the model |
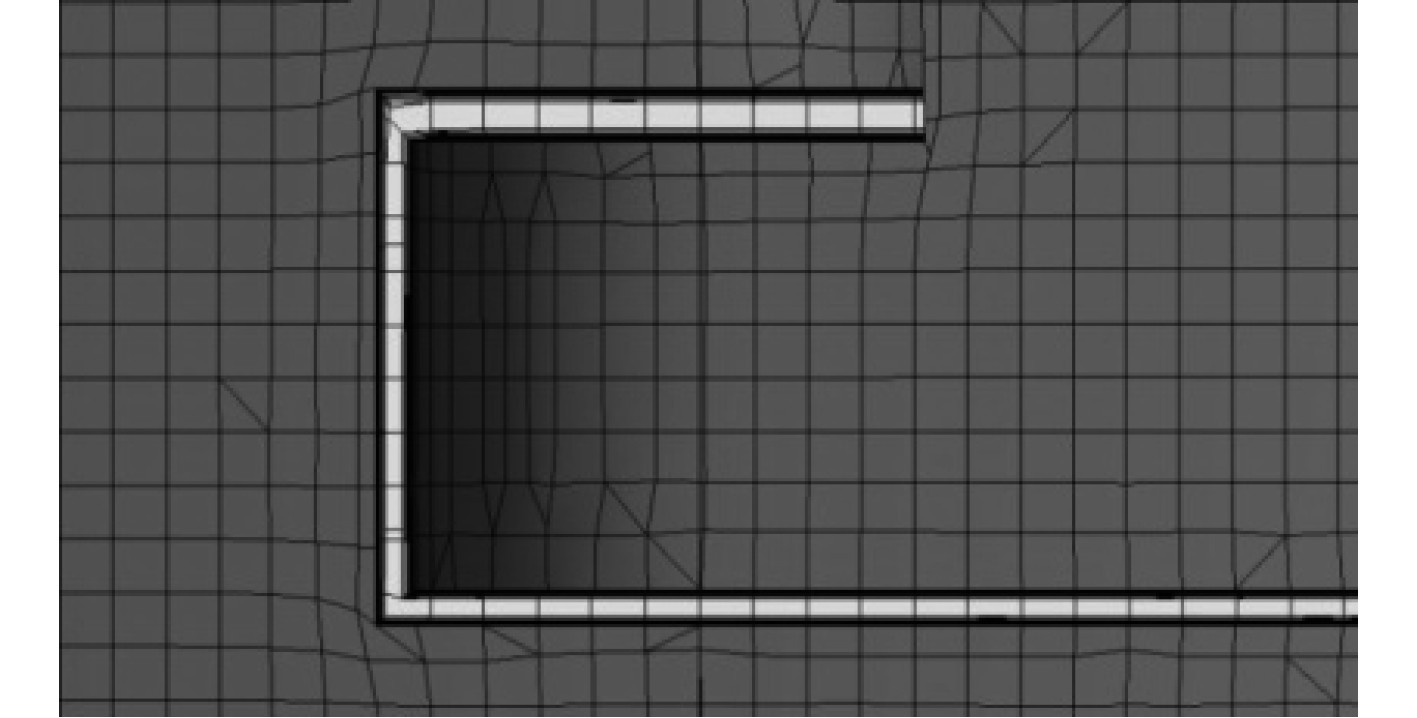
|
图 3 间隙区的网格划分 Fig. 3 Mesh division of the gap area |
基于上述计算条件求解各方案0~35°攻角范围的升力和阻力,得出升力系数和阻力系数,其中阻力计算结果为舵和挂舵臂组合体的阻力。
2 优化设计 2.1 翼型优化设计原舵系(方案0)采用的NACA0021翼型具有阻力较小、便于加工的优点,但缺点是升力系数较低。在不改变舵型和舵面积的前提下,为了使目标船型进出内河航道时具有更灵活的机动性,优化舵翼型的升力性能是有效的解决方案。
以NACA00翼型为基础,采用微凹翼型[10]的理念进行翼型优化设计,即通过使翼型去流段适当内凹,增大绕流速度环量,达到提高升力系数的目的。最大厚度位于距导边30%弦长的HSVA MP73微凹翼型已较多地应用于肥大船型的舵系设计[11-12],考虑到本船为高航速船型,半悬挂舵的空泡性能应予关注[13],按照前GL船级社的建议[14],将翼型的最大厚度位置由NACA00翼型的距导边30%弦长位置后移至距导边35%弦长位置,由此得到一种新的混合翼型A,如图4所示。采用厚度比为0.21的翼型A进行舵系设计,得到方案1。对方案0和方案1进行水动力计算,得到二者的升力系数CL0和CL1及阻力系数CD0和CD1计算结果及对比如表1所示。
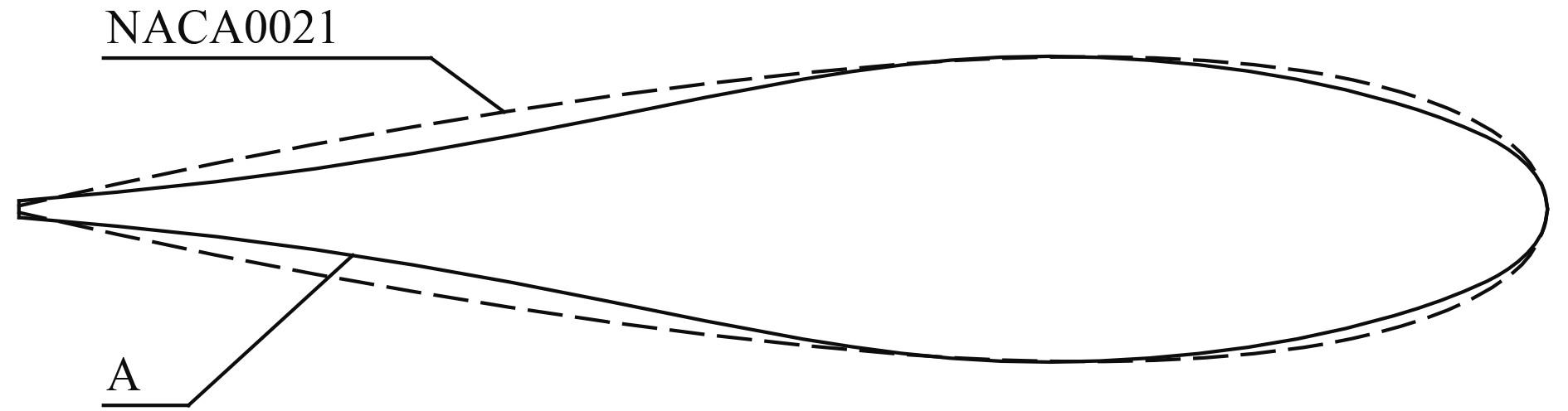
|
图 4 翼型A与NACA0021翼型剖面对比 Fig. 4 Comparison between the profile A and profile NACA0021 |
|
|
表 1 方案0和方案1升力系数、阻力系数计算结果及对比 Tab.1 Results and comparison of CL and CD between plan 0 and plan 1 |
表1所示结果表明:方案1的升力性能明显优于方案0,特别是20°常用攻角范围内升力系数增幅达20.1%(20°攻角)~37.3%(5°攻角);方案1的零攻角阻力系数较方案0增大了18.1%,按大中型运输船舶舵阻力通常约占船舶总阻力1%计,方案1将使船舶总阻力增加约0.18%,幅度较小。因此,采用翼型A进行半悬挂舵设计可以在微幅增加船舶阻力情况下有效提升舵的升力性能。
2.2 制流板优化设计在舵端部设置制流板,可以阻断小展弦比舵叶端部的横向绕流,增大弦向速度环量,从而提高舵的升力[10]。在一定范围内制流板的宽度越大,增升效果越明显,但舵的浸湿面积也随之增加,使得舵的摩擦阻力增加;另一方面,因制流板削弱了舵端部的三维效应和端部分离,可降低端部诱导阻力和分离阻力。因此理论上存在一种尺寸的制流板,使得因制流板增加的阻力和降低的阻力相互抵消,使制流板成为一定攻角范围内不产生额外阻力的纯增升装置。
以方案1为基础进行制流板设计及水动力计算,得到当制流板宽度超出舵叶端部轮廓150 mm时,零攻角阻力系数为0.0390,与方案1零攻角阻力系数0.0385基本持平,将此方案作为方案2,顶端和底端的制流板设计如图5所示。方案2的升力系数CL2、阻力系数CD2计算结果及与方案1、方案0的结果对比如表2所示。
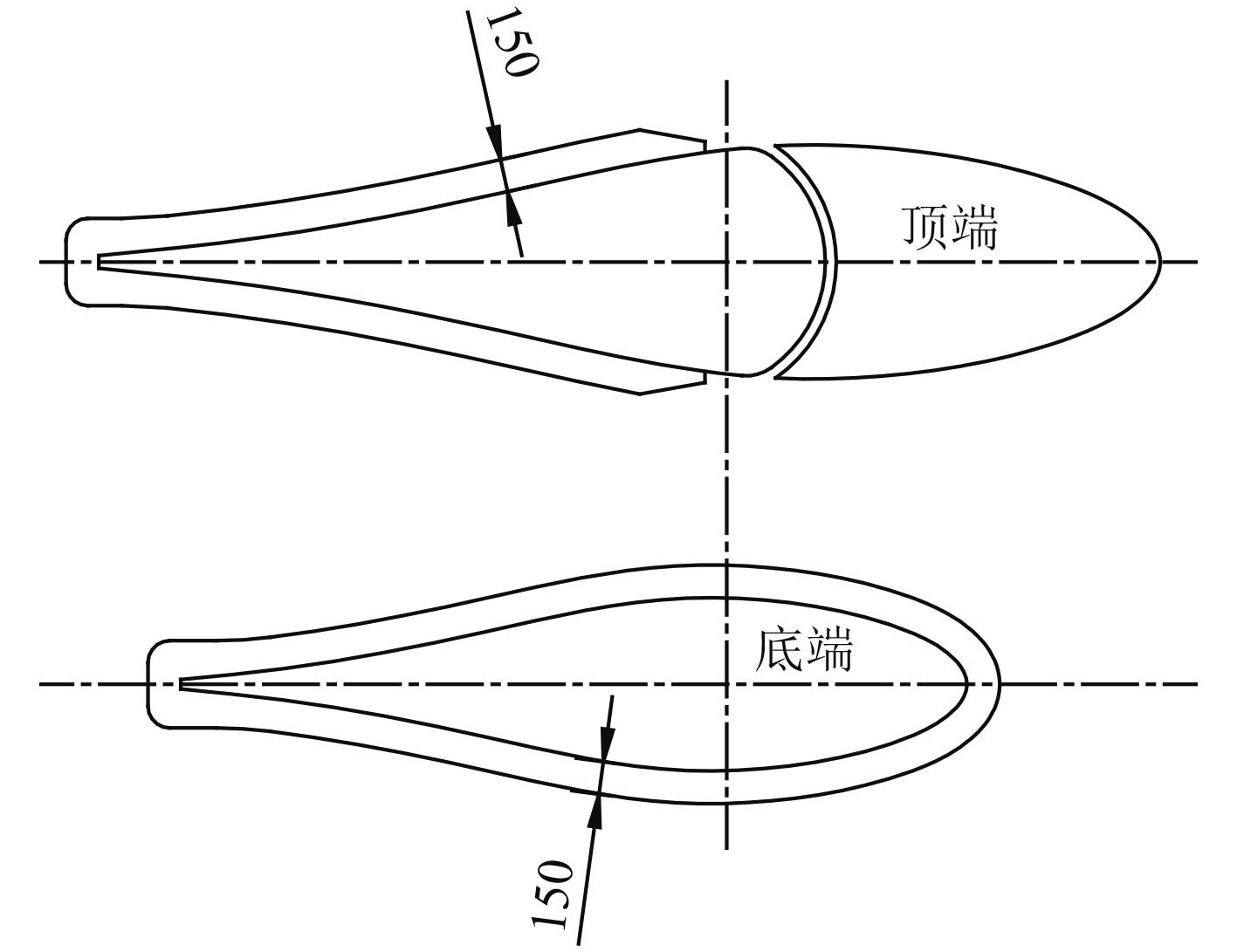
|
图 5 方案2顶端和底端的制流板设计 Fig. 5 Swash plate design at upper and lower ends of plan 2 |
|
|
表 2 方案2升力系数、阻力系数计算结果及对比 Tab.2 Results of CL and CD of plan 2 and comparison |
表2所示结果表明:增设如图5所示的制流板,在35°攻角范围内,方案2与无制流板的方案1阻力系数基本相当,对舵阻力无明显影响;在15°攻角范围内,方案2的升力系数较方案1有约5%左右的提高,有助于进一步提高舵在小攻角的升力性能。20°攻角及以后,方案2和方案1的升力系数基本持平。
2.3 随边直尾化设计随边线型对翼型升力系数有明显的影响,将随边线型设计为平直(即直尾),可加大舵面水流的偏折,增加绕流速度环量,起到提高升力的作用[10,15]。对翼型A距导边90%~100%弦长段进行优化设计,使得最后5%弦长的线型保持与中线平行,得到直尾翼型A1,如图6所示。在方案2的基础上,采用直尾翼型A1进行舵系设计,得到方案3。方案3的升力系数CL3、阻力系数CD3计算结果及与方案2、方案0的结果对比如表3所示。
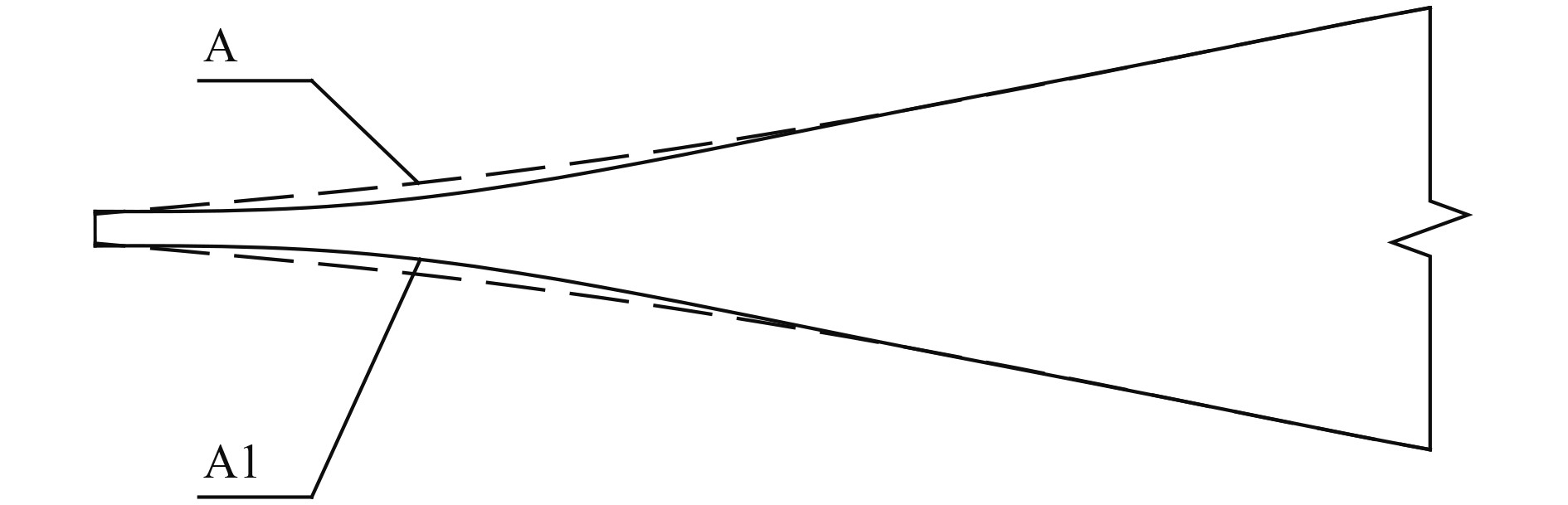
|
图 6 直尾翼型A1与翼型A随边区域剖面对比 Fig. 6 Comparison between the flat tail profile A1 and profile A near trailing edge |
|
|
表 3 方案3升力系数、阻力系数计算结果及对比 Tab.3 Results of CL and CD of plan 3 and comparison |
表3所示结果表明:采用随边直尾化设计后,在30°攻角范围内,方案3的升力系数较方案2有约2.1%(15°攻角)~5.9%(25°攻角)不等的进一步提高;方案3的零攻角阻力系数较方案2增大了7.4%,较方案0增大了28.5%,按大中型运输船舶舵阻力通常约占船舶总阻力1%计,方案3较方案0将使船舶总阻力增加约0.29%。
从方案0到方案3,舵的升力性能呈上升趋势,阻力性能呈下降趋势。方案3较方案0在20°常用攻角范围内的升力系数累计提高了24.1%(20°攻角)~52.5%(5°攻角),优化幅度十分可观。对一艘内河船舶[4]和一艘近海渡船[16]操舵频次的统计分析表明,前者绝大部分操舵舵角集中在−15°~+15°之间,后者超过90%的操舵舵角集中在−10°~+10°之间,因此小舵角升力性能的改善对于提高内河或进江船舶的操纵性是具有针对性和实用性的。需要说明的是,方案1~方案3在30°攻角之后都出现了失速现象,这主要是由翼型最大厚度位置后移引起的。实船上由于桨后尾流得到来自螺旋桨的能量补充,湍流度提高,实际的失速临界攻角更大。一般认为,35°攻角范围内的实际升力系数曲线可根据临界攻角之前的趋势外插得到[1]。
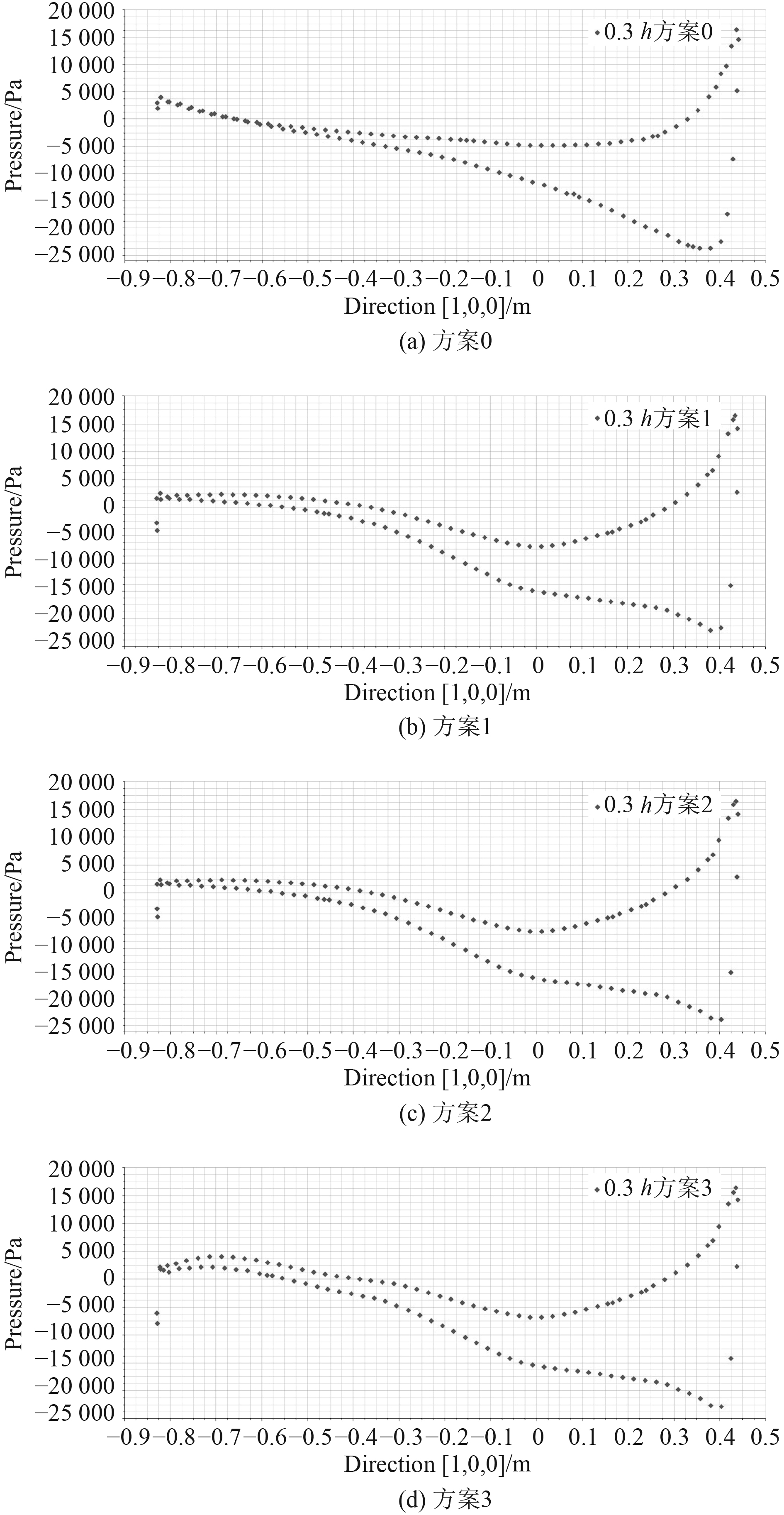
3 流场分析 3.1 舵面流动基于上述CFD计算结果,选取距舵底部0.3 h(h为舵高)的水平剖面为研究剖面,对4个方案10°攻角时的舵面压力分布进行对比分析。该剖面位于下部舵叶高度中点附近,受上部间隙流动和底端三维效应的影响相对较小,可相对准确地反映翼型的升力特性。方案0~方案3的0.3 h剖面压力分布曲线如图7所示。
|
图 7 10°攻角舵面压力分布曲线(0.3 h剖面) Fig. 7 Pressure distribution curve on rudder surface at 20°AoA (0.3 h section) |
由图7可知:10°攻角情况下,在0.3h剖面附近,方案1在舵杆中心线(即横坐标0位)以后的吸力面、压力面压差明显大于方案0,舵杆中心线以前的两面压差略大于方案0;方案2和方案1的压力分布趋势大致相同,但两面压差略大于方案1;随边直尾化设计进一步增大了方案3在随边附近的压差,其余舵面区域的压差也略微增大。这一流场细节与方案0~方案3升力性能逐步提升的宏观结果相匹配。同时值得注意的是,在不设制流板的情况下,图7中方案1的低压峰值小于方案0,说明翼型A的最大厚度位置相对于NACA00翼型后移5%弦长,起到了降低低压峰值的作用,对舵的空泡性能是有利的。
3.2 端部流动基于上述CFD计算结果,得到方案1、方案2在15°攻角时的舵面附近流线分布,如图8所示。

|
图 8 15°攻角时的舵面附近流线 Fig. 8 Stream lines near rudder surface at 15°AoA |
观察图8中的端部流线可以发现:相对于无制流板的方案1,方案2的制流板较好地约束了端部的弦向流动,抑制了横向绕流,弱化了上、下翼端涡,这是方案2在15°攻角范围内升力提高而阻力未明显增加的主要原因。图8同时也表明,由于挂舵臂及间隙的存在,挂舵臂后方的舵叶吸力面出现了较明显的流动分离,这是半悬挂舵升力性能不及全悬挂舵的主要原因之一。
4 实船应用3个优化方案中,方案2在方案1的基础上未付出阻力代价而提高了小攻角升力系数;方案3的升力系数较方案2虽然仍有小幅提高,但零攻角阻力系数增幅较大,升阻比收益较低。因此,方案2是3个方案最均衡和经济的选择,最终成为目标船型实际采用的半悬挂舵设计方案。
为了验证优化舵系对于船舶操纵性的影响,对原船型和目标船型的试航操纵性试验数据进行对比。二者的船舶尺度相同,试航工况、环境条件基本一致。
4.1 应舵性对比以IMO MSC.137(76)决议要求的2项应舵性指标—第一超越角和第二超越角作为衡量应舵性的标准,基于小舵角舵效的考虑,主要考察原船型和目标船型的10°/10°Z形试验结果,对比如表4所示。
|
|
表 4 原船型与目标船型10°/10°Z形试验结果对比 Tab.4 10°/10°zig-zag test comparison between original vessel and object vessel |
表4中:1St OS和2nd OS分别为第一超越角和第二超越角,T1和T2分别为从操舵起始点至达到第一超越角和第二超越角的时间。可见,目标船型的第一、第二超越角及达到各超越角的时间均小于原船型,表明目标船型在紧急避碰时具有更灵活快速的机动能力,一定程度验证了优化舵系在小舵角情况下的升力性能优势。
4.2 回转性对比以IMO MSC.137(76)决议要求的2项回转性指标——纵距和战术直径作为衡量回转性的标准,并通过分析试航操纵性试验数据得到原船型和目标船型的回转性指数K及其无因次量K’,对两型船的回转性进行对比。根据国际通行的右转应急避险原则,主要考察两型船的右满舵35°回转试验结果,对比如表5所示。
|
|
表 5 原船型与目标船型回转试验结果对比 Tab.5 Turning circle test comparison between original vessel and object vessel |
可以看出,目标船型的纵距和战术直径均低于原船型,目标船型的回转性指数K及其无因次量K'较原船型有一定幅度的提高,表明其回转性优于原船型。根据船舶操纵响应模型[17],舵的升力对K值具有直接影响,上述回转试验结果直观地验证了优化舵系因其具有更好的升力性能,对船舶回转性的提升作用。
5 结 语本文基于CFD方法,采用翼型优化设计、制流板优化设计、随边直尾化设计3种技术措施对一型“曼谷型”集装箱船的半悬挂舵系进行了升力性能优化,并经实船应用验证,得到如下结论:
1)采用微凹翼型、制流板和随边直尾化设计可显著提升半悬挂舵的升力性能。对于本文研究的舵系,在20°常用攻角范围内的升力系数较原舵系提升幅度累计达24.1%(20°攻角)~52.5%(5°攻角),有效改善了目标船型的操纵性。
2)采用微凹翼型和微凹翼型+随边直尾化设计将增加舵阻力。对于本文研究的舵系,二者的零攻角舵阻力较原舵系分别增加18.1%和28.5%。
3)微凹翼型和随边直尾化设计可增大舵叶两面的压差,从而提高升力;制流板可约束端部的弦向流动,抑制横向绕流,弱化上、下翼端涡,经过适当设计的制流板,在一定攻角范围内可提高升力而不明显增加阻力。
| [1] |
周昭明. 单桨船两种舵型的舵力和操纵效果的比较试验[J]. 船舶工程, 1981(3): 10-17. ZHOU Z M. Comparison test of rudder force and manoeuvring effect between two rudder types of single screw ship[J]. Ship Engineering, 1981(3): 10-17. |
| [2] |
周广礼, 董文才, 姚朝帮. 半悬挂舵敞水水动力性能数值计算方法研究[C]//船舶水动力学学术会议论文集, 2013: 38−40. ZHOU G L, DONG W C, YAO C B. Study on methods to evaluate hydrodynamic performance of semi-underhung rudder[C]// Proceedings of Ship Hydrodynamic, 2013: 38−40. |
| [3] |
林友红. 半悬挂舵的敞水水动力性能与舵力预估方法研究[J]. 舰船电子工程, 2015, 35(10): 142-147. DOI:10.3969/j.issn.1672-9730.2015.10.037 |
| [4] |
LIU J L, HEKKENBERG R. Sixty years of research on ship rudders: effects of design choices on rudder performance[J]. Ships and Offshore Structures, 2017, 12(4): 495-512. DOI:10.1080/17445302.2016.1178205 |
| [5] |
李邦华, 蒋曙晖, 赵耀中, 等. 不同湍流模型在高效舵水动力计算中的适用性分析[J]. 船海工程, 2019, 48(4): 21-23. DOI:10.3963/j.issn.1671-7953.2019.04.005 |
| [6] |
黎峰, 王亚磊, 蒋曙晖, 等. 随边扭曲舵的性能研究及应用[C]// 上海市船舶与海洋工程学会第五届青年科技论坛论文集, 2022: 77-88. LI F, WANG Y L, JIANG S H, et al. Study on performances and application of twisted-trailing edge rudder [C]//The 5th Forum of Youth Science & Technology SSNAME, 2022: 77-88. |
| [7] |
李邦华, 黎峰, 晋文菊, 等. 边界层网格尺度对高效舵水动力数值计算的影响[J]. 舰船科学技术, 2020, 42(2): 25-28. LI B H, LI F, JIN W J, et al. Research on impact of boundary layer grid scale in hydrodynamic performance computation of high effectiveness rudder[J]. Ship Science and Technology, 2020, 42(2): 25-28. |
| [8] |
LIU J L, HEKKENBERG R. 3D RANS simulations of shallow water effects on rudder hydrodynamics[C]//ICMT2016, Harbin 2016: 16−18.
|
| [9] |
李邦华, 孙海素, 郭振强, 等. 基于CFD的高效舵多方案优化设计[J]. 舰船科学技术, 2021, 43(10): 51-56. LI B H, SUN H S, GUO Z Q, et al. Multi-plan optimization design of high effectiveness rudder with the CFD Method[J]. Ship Science and Technology, 2021, 43(10): 51-56. |
| [10] |
黎峰, 胡红斌, 李邦华, 等. 高性能舵的发展及技术现状[J]. 中国舰船研究, 2020, 15(3): 61-74. LI F, HU H B, LI B H, et al. Developments and current technology status of high performance rudders[J]. Chinese Journal of Ship Research, 2020, 15(3): 61-74. |
| [11] |
黎峰, 孙高鹏, 林兆东. “绿色海豚”38 000 DWT散货船舵系设计[J]. 船舶设计通讯, 2016, (S1): 24−28.
|
| [12] |
晋文菊, 顾剑刚, 李邦华. 基于舵机能力验证要求的舵系优化设计[J]. 舰船科学技术, 2019, 41(9): 95-99. JIN W J, GU J G, LI B H. Optimization design of rudder unit based on requirements of steering gear capacity verification[J]. Ship Science and Technology, 2019, 41(9): 95-99. DOI:10.3404/j.issn.1672-7649.2019.09.018 |
| [13] |
LÜCKE T, STRECKWALL H. Cavitation research on a very large semi spade rudder[C]//Proceedings of First International Symposium on Marine Propulsors. Tronheim, Norway: International Symposium on Marine Propulsors, 2009.
|
| [14] |
GERMANISCHER LLOYD. Paper No. 05-1: Recommendations for Preventive Measures to Avoid or Minimize Rudder Cavitation [S]. GL Technical Publication.
|
| [15] |
欧礼坚, 马梓聪, 霍浩杰. 直尾舵的水动力性能分析研究[J]. 舰船科学技术, 2017, 39(3): 17-22. OU L J, MA Z C, HUO H J. Researches on hydrodynamic performances of tail plate rudder[J]. Ship Science and Technology, 2017, 39(3): 17-22. |
| [16] |
GREITSCH L, ELJARDT G, KRUEGER S. Operation condition aligned ship design and evaluation[C]//1st International Symposium on Marine propulsors, Trondheim, Norway, 2009.
|
| [17] |
吴秀恒, 张乐文, 王仁康. 船舶操纵性与耐波性[M]. 北京: 人民交通出版社.
|
 2023, Vol. 45
2023, Vol. 45
