2. 渤海造船厂集团有限公司,辽宁 葫芦岛 125000
2. Bohai Shipyard Group Co., Ltd., Huludao 125000, China
在流体介质中,任何引起压力波动的过程都会产生声波,包括气液界面的振动或脉动、作用在流体上的压力波动、流体的湍流运动等[1]。水下排气过程本质上属于气液两相流,流场内的压力波动与流动过程息息相关,众多研究已经表明,水下排气的频谱特性与排气流动特征有重要关联,因此,为研究水下排气的噪声特征,可结合图像学研究结论对其进行声学研究[2-4]。苗天丞[5]采用流动图像与噪声信号相结合的方法,研究了大孔径浸没式排气现象,分析了各频段噪声的主要来源,并将水下排气噪声分为三类:一是气体在管路中流动导致的单相流动噪声;二是离散气泡噪声;三是两相边界噪声。Manasseh等[6-7]采用流动图像和信号相结合方法,研究了单孔口气泡脱离过程,发现气泡脱离前的拉伸过程蓄积了表面张力能,脱离后气泡表面收缩释放出表面张力能激发气泡的体积脉动发声,气泡在脱离孔口后逐渐加速上浮,加速过程中被后续气泡追赶融合,发出比脱离时更高的声压。刘竞婷[8]分别采用流动图像和信号相结合方法,研究了单孔口气泡脱离过程,分析了孔口气泡脱离时噪声形成原因,分析认为排气管口气泡脱离瞬间气泡的收缩诱发临近液体侵入气泡底部,引起气泡体积振动导致发声。
受研究条件的限制,上述利用水箱进行水下排气噪声特性研究时气泡上浮时间短,导致各种流动现象的声频特征在时间轴上相互叠加,不便区别,并容易受设备噪声、气体流噪声等干扰。此外,上述研究主要是针对单个气泡或气泡串开展基础性的研究,对于处理工程中常见的气泡群噪声问题借鉴意义有限。一是因为气泡群内存在不同直径的气泡,其稳定上浮速度有差异,理论上存在底层大气泡追赶上层小气泡,引发气泡融合等复杂的流动现象,导致理论预测与实际测量结果的差异;二是气泡群整体呈现的声学特征与单个气泡或气泡串也不尽相同,理论上任意形状的声源,辐射场可通过小声源场叠加来计算[1],即气泡群的辐射声场可以通过单个气泡辐射声场叠加,但实际中气泡的声散射效应会耗散一部分声波,改变气泡群的声学特征。因此,有必要基于工程实际特点开展水下排气噪声特性的研究。
为尽可能避免单相流动噪声对试验结果的影响,本文试验中使用气瓶作为气源杜绝机械设备运转噪声,采用长度30 m的橡胶软管将上游阀门噪声隔离。为找出水下排气噪声的主要发生位置和噪声特性,将气泡运动各阶段的噪声区分开,充分利用气泡上浮速度趋于恒定且较慢的特性,将水下排气3个运动阶段在时间上充分隔离,再选取各时间段的噪声进行对比分析,并结合水下摄像对不同深度气泡直径分布特征进行研究,明确了各种噪声形成部位、噪声类型和频谱特征。
1 理论基础与试验装置 1.1 气泡上浮速度气泡稳定上浮时所受的力主要为浮力与粘滞阻力,气泡形成后浮力为定值,而气泡所受的粘滞阻力与速度的平方成正比,粘滞阻力增大到与浮力相等时气泡将保持匀速运动,因此得出不同直径气泡的平均上浮速度如下[9]:
| $ {V}_{b}=\sqrt{\dfrac{{\text{π} D}^{3}g}{3{C}_{d}{A}_{eff}}} ,$ | (1) |
| $ {C}_{d}=\left\{\begin{array}{l} 24/{Re}_{b},\;\; {Re}_{b} < 2 ,\\ 18.5/{Re}_{b}^{0.6},\;\; 2\leqslant {Re}_{b} < 500 ,\\ 0.44,\;\; 500\leqslant {Re}_{b} 。\end{array}\right. $ | (2) |
其中:Vb为气泡上浮平均速度;D为气泡直径;g为重力加速度;Cd为气泡阻力系数;Aeff为气泡有效截面;Reb为气泡上浮运动的雷诺数。
由于大气泡容易发生形变,其稳定上浮速度难以精确计算,根据张建生[10]对气泡上浮速度的研究,直径40 mm以下的气泡稳定上浮速度不超过0.5 m/s。因此,将试验装置由水箱改为水池,通过增加排气口入水深度,可大幅延长气泡上浮时间,为气泡各运动阶段提供充足的流动稳定和采样时间。
1.2 噪声源类型的判断依据水下排气过程中,气泡会经历形成、上浮和水面破碎3个显著的运动阶段,各阶段中气泡的动力学行为特征决定了水下压力波动特征,进而决定了水下排气的噪声特征。根据实验数据分析和定位噪声源后,如何判定噪声源的类型是一个重要的挑战。
根据噪声源的一般特性,脉动的体积或质量构成主要的简单声源,称为单极子,单极子是无方向性的,例如脉动的气泡。脉动力和刚体的振动产生偶极子,并有明显的指向性。流体的湍流运动和没有净作用力的变形产生四极子。单极子和偶极子只在流体界面上出现,四极子可在流体内部、远离流体界面出现。
在描述水中噪声源时,常采用FW-H形式的Lighthill方程声压进行描述:
| $ \dfrac{1}{{c}_{0}^{2}}\dfrac{{\partial }^{2}p}{\partial {t}^{2}}-{\nabla }^{2}p=\dfrac{\partial q}{\partial t}-\nabla \mathrm{f}+\dfrac{\partial {\tau }_{ij}}{\partial {x}_{i}\partial {x}_{j}} 。$ | (3) |
式中:c0为水中声速;p为声压;q为脉动质量;f为脉动力;τij为湍流应力张量。式(3)左边是传统波动方程的基本形式,右边第1项表征脉动体积声源,第2项表征脉动力的影响,第3项表征湍流应力的影响。
当只考虑脉动体积声源时,可由式(3)推导出单极子声压公式:
| $ p=\dfrac{{\rho }_{0}\ddot{V}}{4\text{π} r}=\dfrac{\dot{Q}}{4\text{π} r}=\dfrac{i\omega {\mathrm{Q}}_{0}}{4\text{π} r}{e}^{i\omega (t-r/{c}_{0})} 。$ | (4) |
式中:ρ0为脉动体的密度;V为脉动体的体积;r为声压测点与声源中心的距离;Q为脉动体的质量通量;ω=2πf为振动频率。
当只考虑脉动力的影响时,可由式(3)推导出偶极子声压公式:
| $ p=\dfrac{\dot{F}}{4\text{π} r{c}_{0}}\mathrm{cos}\theta 。$ | (5) |
式中:F为总脉动力;θ为力矢量与声压测点的方向夹角;cosθ项代表偶极子压力的指向性图。
对比式(4)和式(5)可知,单极子噪声的空间分布只与测点和声源的距离有关,而偶极子噪声的空间分布不仅与测点和声源的距离有关,还与测点和声源的方位有关。
除此,还可通过噪声幅值大小辅助判断噪声的类型。各类噪声的辐射效率计算公式[1]如下:
| $ \mathrm{\eta }=\dfrac{{\left({k}{a}\right)}^{2\mathrm{m}+1}}{\left(m+1\right){[1\cdot 3\cdot 5\cdots \left(2m-1\right)]}^{2}},$ | (6) |
| $ \mathrm{k}\mathrm{a}=\dfrac{\omega a}{{c}_{0}}=\left(\dfrac{\omega a}{U}\right)\left(\dfrac{U}{{c}_{0}}\right)=\left(\dfrac{\omega a}{U}\right)M 。$ | (7) |
式中:k为波数;a为特征尺度;m为多极子的阶,单极子m=0;偶极子m=1;四极子m=2;U为流速;
水中的流速通常远低于声速,M远小于1,根据式(6),当单极子存在时,总是起主要作用,没有单极子时偶极子才成为主要的,而四极子一般不重要。
因此,通过分析噪声发生的部位、幅值和指向性,可以为判断噪声的特征提供依据,为降噪设计提供指导。
1.3 气泡噪声特征频率与幅值气泡是典型的单极子声源,其辐射声压与气泡的体积变化率有关。早在1917年,Rayleigh就推导出不可压缩流场中理想球形气泡的运动方程,1933年,Minnaert研究毫米级管口气泡绝热振动问题时,推导出了计算气泡振动频率的Minnaert公式[11]。该公式实为Rayleigh公式的简化解,反映出气泡直径D与气泡特征频率f的关系。
| $ {f}=\dfrac{1}{\text{π} D}\sqrt{\dfrac{3\gamma {p}_{l}}{{\rho }_{l}}} 。$ | (8) |
式中:pl为液体压力;γ为气体的绝热指数;ρl为液体的密度。
将式(8)表示的气泡特征频率代入式(4),可以得出单个气泡噪声的声压为:
| $ p=\dfrac{\gamma {p}_{l}D}{r}{\dfrac{\Delta \mathrm{V}}{{V}_{0}}e}^{-(\eta /2)({\omega }_{0}t-kr)}。$ | (9) |
式中,η为气泡做阻尼振荡运动时的损失因子。式(9)表明,在其他因素相等时,峰值声压随气泡直径线性的增加。
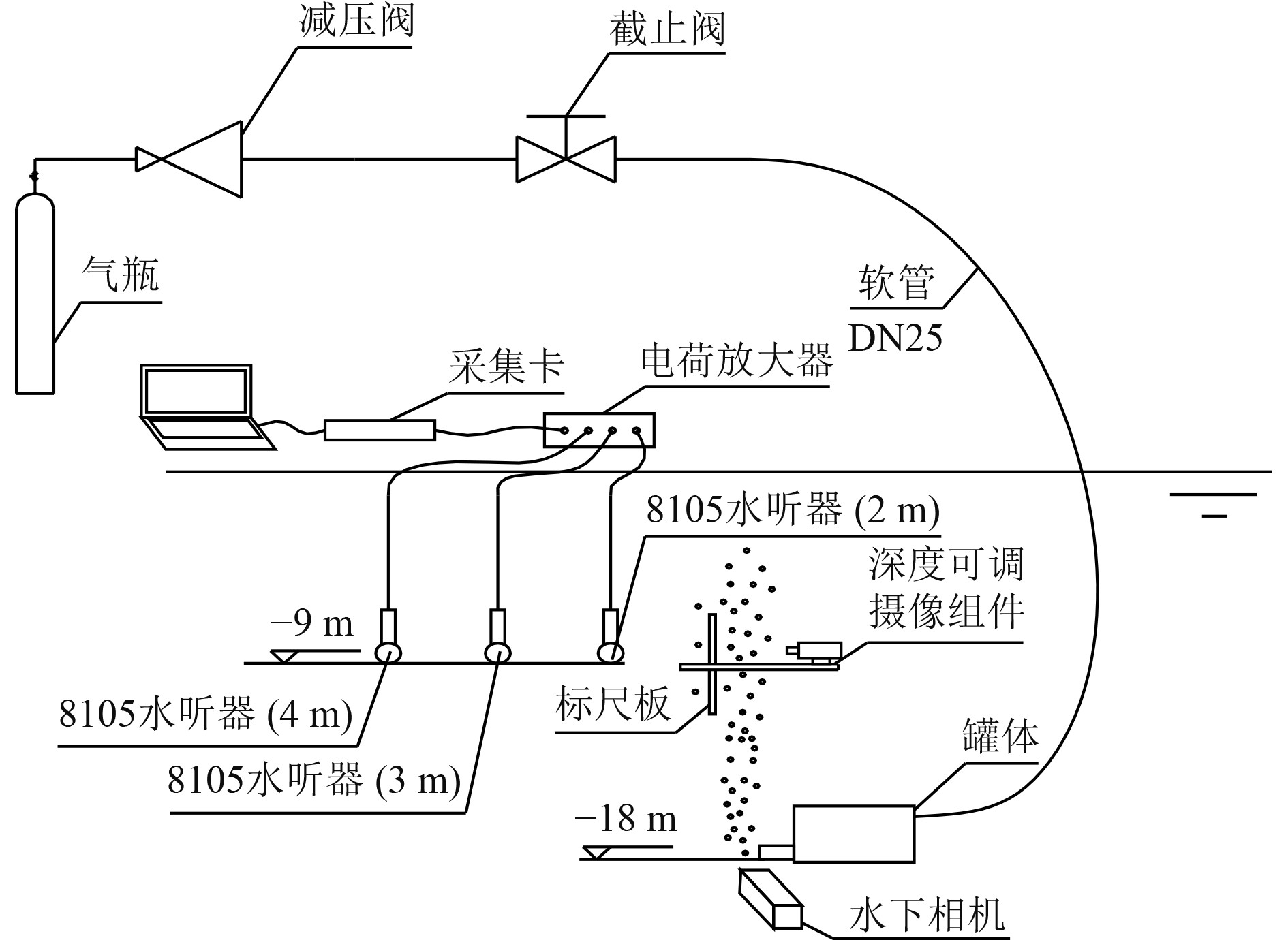
1.4 试验装置试验系统的原理见图1,主要由水听器组、气瓶、减压阀、截止阀、罐体、深度可调摄像组件等组成。罐体顶部装有进气软管,底部出口为直径40 mm钢管。噪声测试系统使用3部B&K8105型水听器,布置在水池深度中值面上,水平方向分别距罐体出口2 m,3 m,4 m。
|
图 1 试验系统原理图 Fig. 1 Schematic of experiment system |
通过水下相机观察和记录水下排气流动特征。固定在罐体出口附近的水下相机能够观测到水下排气过程中管口附近的流动特征。深度可调摄像组件的标尺板上刻有20 mm×20 mm的方格,还装有水下光源和水下相机,深度可调摄像组件可在竖直导轨做升降运动,对不同深度下气泡尺寸进行定深度观察和研究。
2 试验结果与分析 2.1 流场宏观观测结果试验属于大孔径水下排气,管口处排气流动模态介于气泡流向射流转换的过渡流状态。结合摄像结果、水听器测试结果和现场观测的近水面试验情况,整个过程可分为排水、排气、气泡上浮和气泡出水4个阶段。根据水听器测试结果,还可将排气阶段细分为初始排气阶段和稳定排气阶段。
图2(a)为初始排气瞬间,气体以射流形态进入水中,形成大量小气泡。罐内水全部排空后,出口排气流速迅速下降,如图2(b)所示。气流在浮力作用下迅速转向上浮,并在管口正上方形成数个大尺寸气泡,大气泡的上浮带动管口上方液体流动形成卷吸涡,随即破裂为大量小气泡。

|
图 2 排气出口流动形态 Fig. 2 Photos of underwater air flow |
在气泡上浮达到平衡速度后,毫米级的气泡基本不再出现合并或分裂,运动模式以振动和变形为主。厘米级的大气泡则还有可能在不稳定波的作用下分裂,与张建生[10]总结的规律相符。
气泡分2批涌出水面,首先是排气启动过程中产生的数个超大气泡,随后是直径不超过30 mm的细化气泡群。罐体出口处水深18 m,通过多次试验,证明小气泡群从池底上浮至水面历时约60 s,因此,将排气时间控制在25 s左右,保证排气噪声和气泡上浮噪声可以在时间维度上分离。
根据水下视频、噪声总级变化和目视情况,首批大气泡上浮历时38.3 s,大气泡上浮的平均速度为0.47 m/s,后续小气泡群上浮历时58.2 s,小气泡群上浮的平均速度为0.31 m/s,根据气泡直径与稳定上浮速度的关系[10]推断,大气泡直径约为50~200 mm,小气泡群内的气泡直径约为3~20 mm。
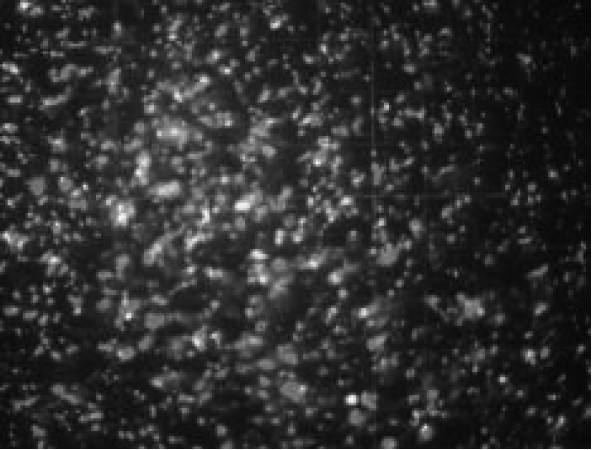
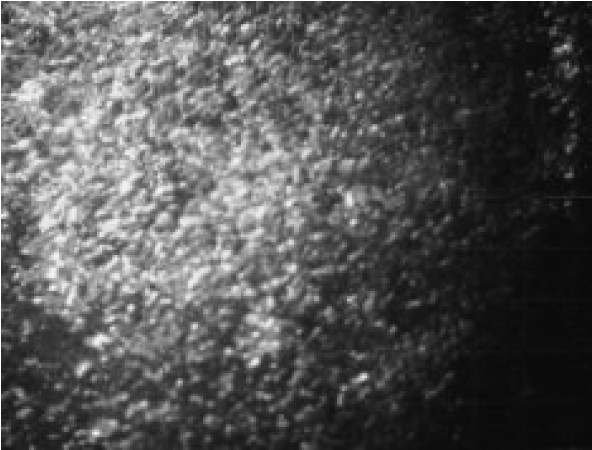
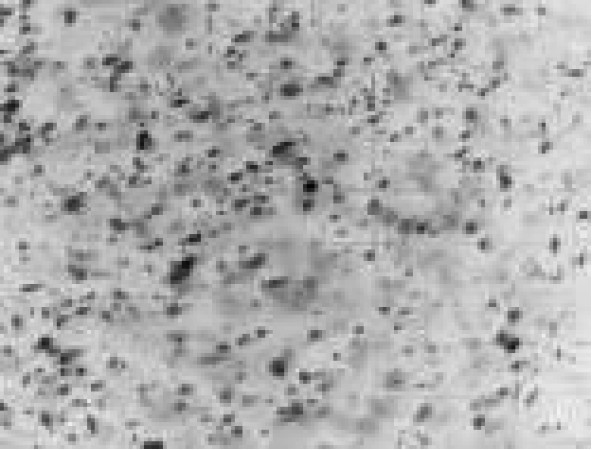
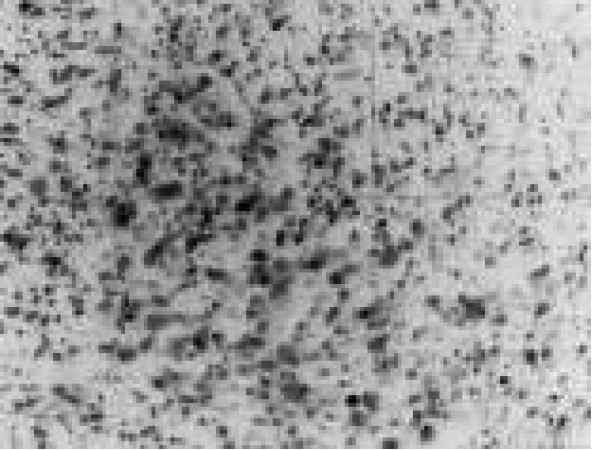
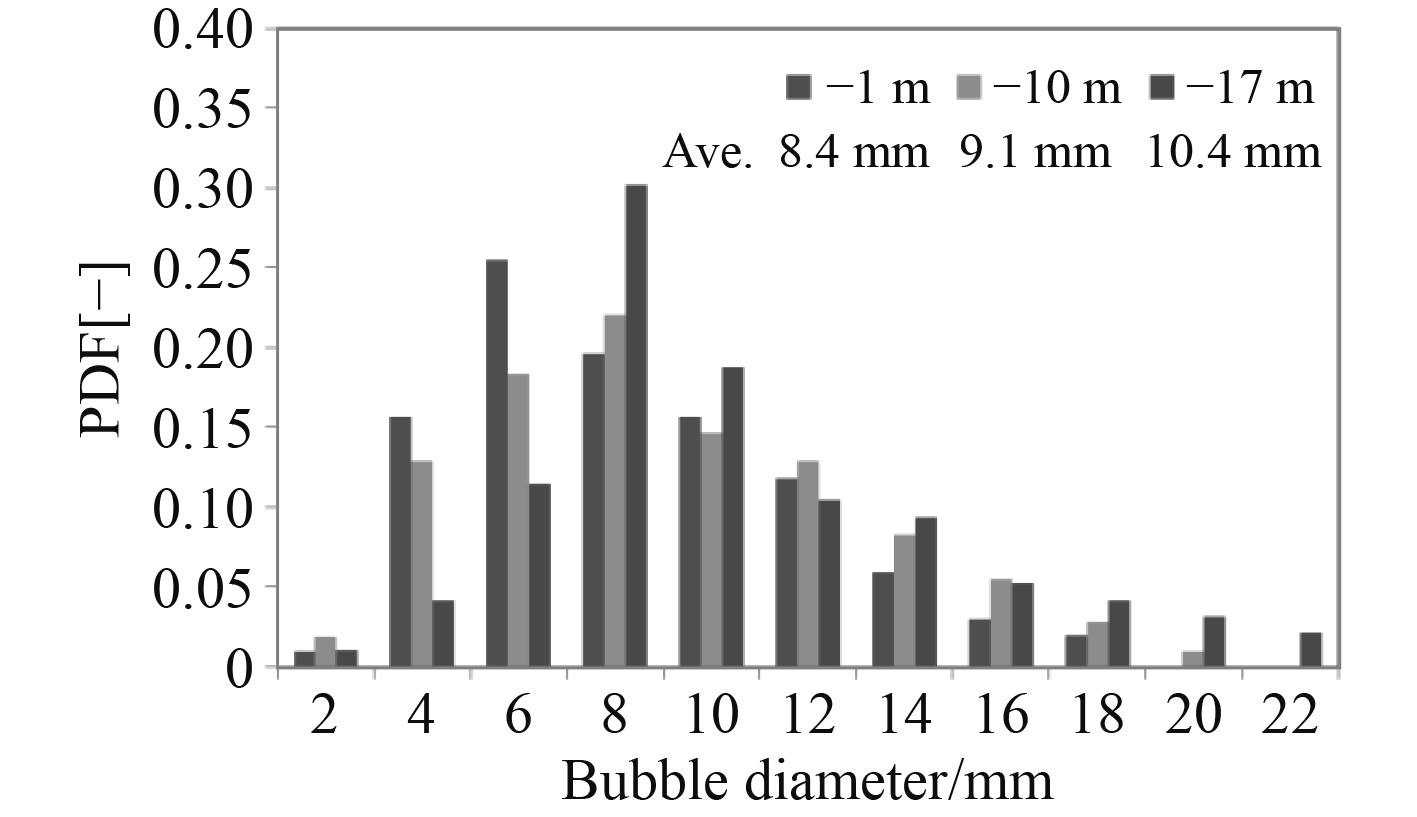
2.2 稳定排气过程气泡直径分布特性为了解稳定排气过程中气泡上浮至不同高度的直径分布特性,利用深度可调摄像组件对水下稳定排气产生的气泡群进行摄像。试验中观察到气泡上浮时的横向振荡和变形,拍摄的图像见表1。原图中气泡非常密集,随深度减小气泡的密集程度明显降低,但依然无法直接进行气泡直径的分析。为尽可能多地保留原始信息,将原始图像(I)进行取反(255-I),得出不同深度下气泡群的反色图像,鉴于反色图像中显示的气泡实际为反光部分,根据苗天丞[5]拍摄的单个大孔浸没式排气图像、Manassh[6-7]及刘竞婷[8]拍摄的单个小孔浸没式排气图像、Lesage[12]拍摄单孔口气泡脱离时刻的气泡图像,气泡反光部分尺寸约为气泡实际尺寸的1/3~1/4,因此,根据本文试验中拍摄照片的实际情况,取气泡尺寸为反色图像气泡直径统计值的3.5倍。据此测量得出−1 m,−10 m,−17 m的气泡直径分布如图3所示,不同深度下气泡直径均分布在3~22 mm范围内。
|
|
表 1 稳定排气水下摄像结果 Tab.1 Photos of air bubbles at steady flow stage |
|
图 3 稳定排气时不同深度气泡直径分布 Fig. 3 Air bubble diameter distribution at different depth |
稳定排气阶段,气泡上浮时的平均气泡直径随深度减小,说明气泡在上浮过程中存在气泡分裂趋势。此外,水下摄像得出的气泡直径与上文根据气泡上浮速度得出的气泡直径范围基本吻合。
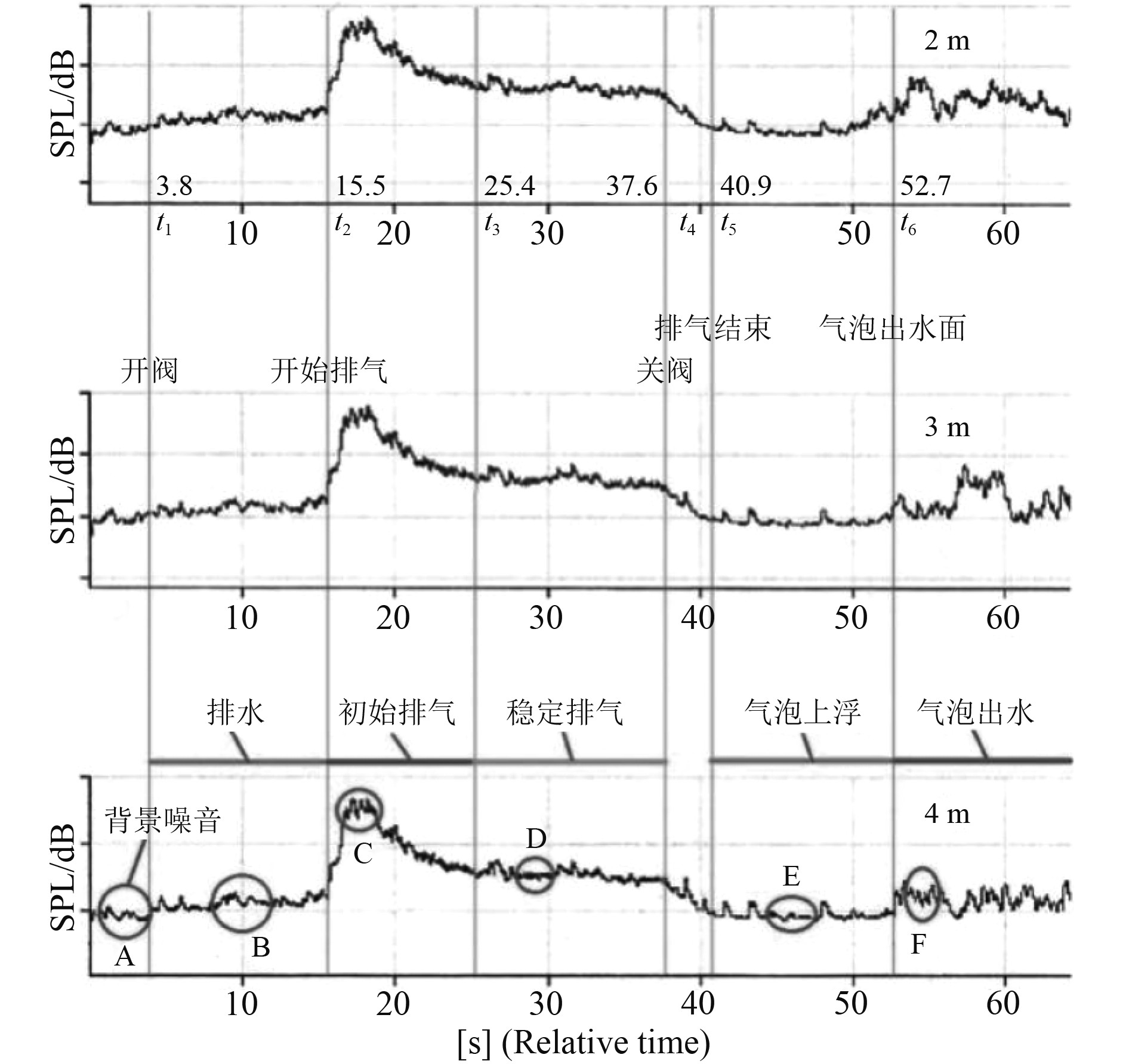
2.3 水下排气噪声总级试验结果3部水听器总声压级SPL时域曲线如图4所示。根据3部水听器数据并结合水下摄像记录视频,确定试验过程中主要时间节点为:3.8 s开阀供气,罐体排水,15.5 s水下排气开始,25.4 s排气稳定,37.6 s关阀,40.9 s排气结束,52.7 s首批大气泡浮出水面,75.5 s后续小气泡群浮出水面。
|
图 4 水下排气全程3部水听器的总声压级-时间曲线 Fig. 4 Sound pressure level measured by three different hydrophones |
对比3部水听器总声压级曲线的峰值出现时刻,可以看出气泡排出(15.5 s)前背景噪声具有较好的一致性,3部水听器的波形均能一一对应。
排水阶段,理论上只有液体流动引发的四极子噪声源,实测3部水听器的总噪声级变化平缓,略高于背景噪声,远低于排气噪声,符合式(6)预测结果,且3部水听器测试总声压级无明显差异,说明此时的辐射噪声无指向性。
初始排气阶段,因罐内液体排空,气体在管口处形成强烈的气泡射流,辐射噪声陡增,总声压级增量高达40 dB。在本阶段,3部水听器的总声压级曲线保持高度一致,说明此时辐射噪声无指向性,这与气泡形成时体积脉动辐射单极子噪声的特征吻合。
根据实测气泡上浮速度远低于声速,即M远小于1,代入式(6)可知,水下排气中单极子声源的辐射效率最高,对应的声压级也最大。邢允等[4]对本实验不同工况下的排水、排气噪声总级进行了对比研究,试验和仿真结果均证明排气噪声远高于排水噪声。
稳定排气阶段,噪声总级趋于稳定,比峰值低约20 dB,此时流动形态转变为鼓泡流,3部水听器的噪声总级接近,曲线形状和时序也保持高度一致,说明此时占主导地位的噪声源仍为各向同性声源。初始排气阶段,观察到少量超大尺寸的气泡的同时,也观察到总声压级峰值,与式(9)描述的单个气泡声压值规律相符。
气泡上浮阶段,3部水听器的噪声总级接近,说明此时辐射噪声无指向性。由于试验时深度足够大,在关阀时刻,尚无气泡浮出水面,在关阀至气泡浮出水面的时段只有气泡上浮噪声,实测总噪声级非常低,噪声总级与背景噪声一致,说明气泡上浮阶段的噪声可以忽略。这充分说明排气噪声主要在排气口附近发生,是气泡形成时体积脉动辐射的单极子噪声。
气泡出水阶段,排气噪声显著增加,且3部水听器总噪声级出现显著差异,说明此时的噪声指向性非常显著,偶极子噪声占主导地位。由式(3)可知,偶极子噪声由脉动力引发,且只发生在相界面[1],而气泡浮出水面后上浮速度突然归零,说明此时气泡受到一个瞬变的合外力,即由于气泡浮出水面,气泡所受浮力迅速衰减,气泡原本所处的浮力与液体拖曳力互相平衡的状态被打破形成瞬变的合外力,作用在气泡(气液相界面)上产生出偶极子噪声。此外,气泡破碎形成水滴再次溅落也会产生脉动力,引发偶极子噪声。
2.4 水下排气各阶段噪声频谱分析为进一步明确噪声来源和类型,取气泡形成阶段噪声总级较稳定的时段进行1/3倍频程频谱分析(CPB),见图4中A~F,得到水听器测量的频谱特征见图5,为便于比较,去除了背景噪声。
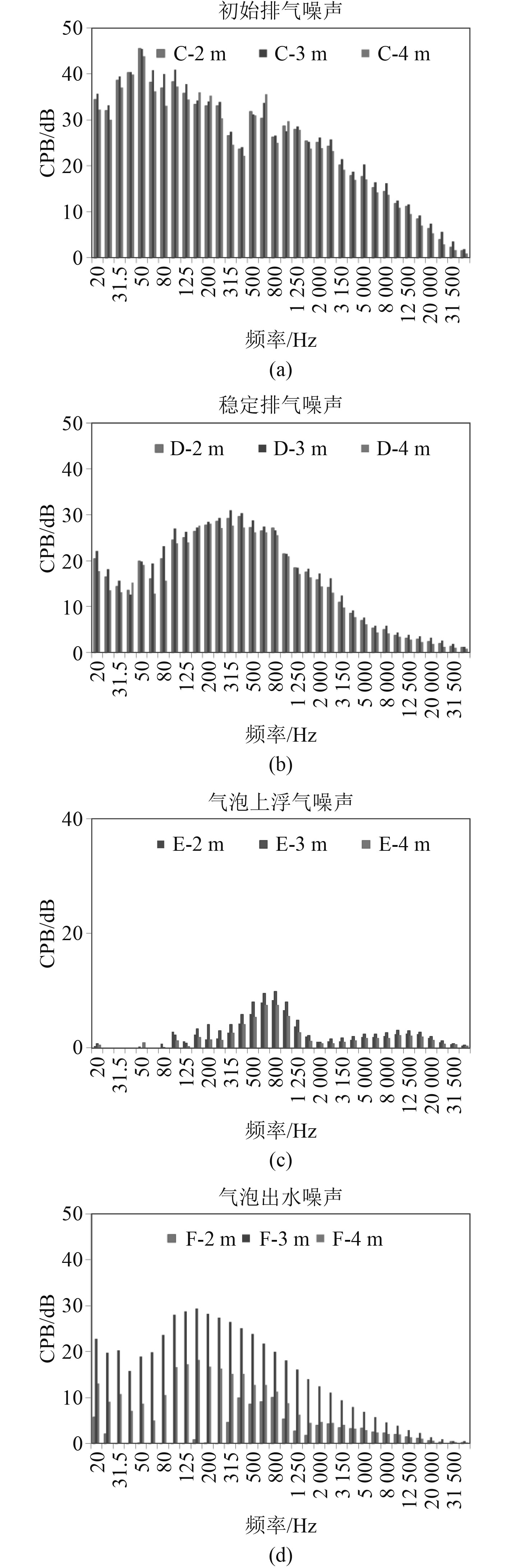
|
图 5 各阶段的噪声CPB分析 Fig. 5 Constant percentage bandwidth of each stage |
在初始排气阶段C,20~315 Hz的低频段辐射噪声占主导地位,对总噪声级影响最大,如图5(a)所示。50 Hz为最高峰值,采用式(5)计算出此时对应的气泡直径约120~150 mm,与通过气泡上浮速度推算出的气泡直径范围相符。315 Hz~20 kHz的中高频段辐射噪声占次要地位,形成另一个峰值,630 Hz频段为局部最大值,采用式(5)计算出对应的气泡直径约10~12 mm,与试验中观察到的气泡群尺寸范围相符。3部水听器测量的噪声频谱特性一致性良好,证明此时的辐射噪声细分频谱也无指向性。
在稳定排气阶段D(见图5(b)),3部水听器测量的噪声频谱特性一致性良好,证明此时的辐射噪声细分频谱无指向性。
在气泡上浮阶段E,尽管总噪声级已经与背景噪声一致,但是CPB分析中仍发现了与气泡直径高度相关的气泡噪声,如图5(c)所示。气泡噪声在315~1600 Hz频段内存在一个局部峰,最大值出现在800 Hz频段,对应的气泡直径分布范围为5.8~21 mm,与分析得出的气泡直径范围吻合,证明这就是气泡发出的噪声。
在气泡水面破碎阶段F,3部水听器测得噪声频谱也存在巨大差异(见图5(d)),说明偶极子噪声的频谱也存在各向异性。
3 结 语1)通过水下摄像获取了排气出口流动形态图像和流动形态转变时刻,计算出两类气泡的平均上浮速度和气泡平均直径范围;通过水下移动摄像获取了上浮路径不同深度的流动形态图像,得出不同深度下气泡直径的分布范围;通过气泡上浮过程中的频谱特征,推算出上浮气泡的直径范围。这3种方法得出的气泡平均直径分布范围基本重合,均为3~20 mm。
2)通过设置水听器阵列,获得不同位置处测量的声压总级曲线和频谱特征,证明水下排气过程中单极子辐射噪声占主导地位,并观察到气泡在水面破碎形成的噪声具有典型的指向性特征。
3)通过对水下排气图像、噪声总级和频谱的联合观察,获得不同流动阶段的声压总级曲线和频谱特征,证明水下排气噪声主要发生在排气管口附近,由气泡形成过程产生的辐射噪声占主导地位;其次是在水面由气泡破碎产生偶极子辐射噪声;气泡上浮过程的声压总级与背景噪声接近,是水下排气中可以忽略的噪声源。
| [1] |
罗斯. 水下噪声原理[M] 北京: 北京海洋出版社, 1983.
|
| [2] |
DEANE G B, CZERSKI H. A mechanism stimulating sound production from air bubbles released from a nozzle[J]. The Journal of the Acoustical Society of America, 2008, 123(6): 126-132. |
| [3] |
郝宗瑞, 王乐勤, 吴大转, 等. 水下气体喷射噪声特性研究[J]. 工程热物理学报, 2010, 31(9): 1492-1495. HAO Zongrui, WANG Leqin, WU Dazhuan, et al. Underwater noise characteristics of gas jet[J]. Journal of Engineering Thermophysics, 2010, 31(9): 1492-1495. |
| [4] |
邢允, 张凌, 胡秋旭, 等. 吹除过程中流动与噪声的数值模拟与实验验证[J]. 工程热物理学报, 2019, 40(8): 1799-1805. XING Yun, ZHANG Ling, HU Qiuxu, et al. Numerical simulation and experimental verification of flow and noise in blowing process[J]. Journal of Engineering Thermophysics, 2019, 40(8): 1799-1805. |
| [5] |
苗天丞. 浸没式排气的流动与声特性及其降噪方法研究 [D]. 杭州: 浙江大学, 2016.
|
| [6] |
RICHARD M, ANETA N, ANDREW O, et al. Anisotropy in the sound field generated by a bubble chain[J]. Journal of Sound and Vibration, 2004, 278: 807-823. DOI:10.1016/j.jsv.2003.10.015 |
| [7] |
RICHARD M, GUILLAUME R, FRÉDÉRIC R. Sound generation on bubble coalescence following detachment [J] International Journal of Multiphase Flow, 2008, 34 : 938−949
|
| [8] |
刘竞婷. 水下气体射流与气泡流声特性的数值模拟与实验研究[D]. 杭州: 浙江大学, 2018
|
| [9] |
谢建. 微小槽道内微孔壁面逸出气泡动力学行为及特性[D]. 重庆: 重庆大学, 2013.
|
| [10] |
张建生. 尾流的光学特性研究与测量[D]. 西安: 中国科学院西安光学精密机械研究所, 2001.
|
| [11] |
MINNAERT M. XVI. On musical air-bubbles and the sounds of running water[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1933, 16(104): 235-248. DOI:10.1080/14786443309462277 |
| [12] |
FRÉDÉRIC J. L, Francis marois experimental and numerical analysis of quasi-static bubble size and shape characteristics at detachment [J] International Journal of Heat and Mass Transfer, 2013, 64: 53−59
|
 2023, Vol. 45
2023, Vol. 45