水下航行器在工作时借助周围海水对航行器动力装置进行循环冷却,循环海水吸收设备产生的热量,温度升高,经由排放口排出,形成热射流尾迹。由于航行器在不断运动,形成的热射流尾迹往往存在时间长,不易消散,成为红外探测系统的识别目标。当前,国内外学者对于水下航行器热射流的形成、发展及衰减过程做了大量数值模拟和实验研究[1-7]。由于对热射流的实验研究不易进行,成本高昂,参数监测困难等,同时计算流体力学的兴起,通过软件仿真计算进行相关实验的模拟被越来越广泛运用。周哲等[8]研究了多种排放口形状及不同疏密程度的排列下冷却水热射流的换热效果和温度特性。张健等[9]对流动环境下水平热射流温度分布特性进行了相关研究,研究表明,椭圆形排放口更有利于冷却水的掺混换热及热量扩散。戴天奇等[10]研究了横流环境下的热射流浮升规律,分析得到了流速比和环境流速对热射流浮升轨迹和中心温度的影响规律。对于排放口的相关研究大多围绕排放孔形状对热射流的影响进行仿真研究,很少涉及排放口遮流罩对水下热射流温度扩散及衰减特性的研究。本文建立水下航行器冷却水排放的热射流模型,设计了圆形、椭圆形以及带有遮流罩结构的圆形和椭圆形的排放口模型,在Fluent软件平台上进行流场的仿真计算,研究对比了圆形和椭圆形排放口,以及有无遮流罩对热射流温度扩散及衰减的影响。结果表明,椭圆形排放口更有利于热射流的掺混换热,遮流罩能更好地降低热射流温度,有效地降低被红外探测的可能性,提升了水下航行器的热隐身性能。
1 物理模型及数学计算质量守恒方程
| $ \frac{\partial \rho}{\partial t }+\frac{\partial}{\partial x_i}(\rho u_i)=S_m \;。$ | (1) |
式中:源项
动量守恒方程
| $ \frac{\partial}{\partial t}\left(\rho u_{i}\right)+\frac{\partial}{\partial x_j}\left(\rho u_{i} u_{j}\right)=-\frac{\partial p}{\partial x_{i}}+\frac{\partial \tau_{ij}}{\partial x_j}+\rho g_{i}+F_{i} \;。$ | (2) |
式中:p为静压;
能量守恒方程
| $ \frac{\partial (\rho T)}{\partial t}+{\rm{div}}(\rho uT)={\rm{div}}\left(\frac{k}{c_p} {{\rm{gradT}}}\right)+S_{T}\;。$ | (3) |
式中:
连续性方程
| $ \frac{\partial \rho}{\partial t}+\frac{\partial (\rho u_i)}{\partial x_i}=0 \;。$ | (4) |
式中:
选择Realizable k-
湍动能k方程:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{\text{k}}}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k}{\kern 1pt} {\kern 1pt} + {G_b} - \rho \varepsilon \;,$ | (5) |
耗散率ε方程:
| $ \begin{split} \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\varepsilon } \right)}}{{\partial {x_j}}} =& \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _{{\varepsilon }}}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}S\varepsilon- \\ & \rho {{{C}}_{\text{2}}}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + {{{C}}_{{{1\varepsilon }}}}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} \;。\end{split} $ | (6) |
式中:
| $ \begin{split}&{C_1} = \max \left[ {0.43,\frac{1}{{\eta + 5}}} \right]\text{;} \eta {\text{ = }}S\frac{k}{\varepsilon } \text{;}S = \sqrt {2{S_{ij}}{S_{ij}}}\;;\\ &{C_{3\varepsilon }} = \tanh \left| {\frac{v}{u}} \right|\;。\end{split} $ | (7) |
式中:v为平行于重力矢量的速度分量;u为垂直于重力矢量的速度分量。
| $ {\mu _t} = \rho {C_\mu }\frac{{{k^2}}}{\varepsilon } \;。$ | (8) |
式中:
| $ {C_\mu } = \frac{1}{{{A_0} + {A_s}\dfrac{{k{U^*}}}{\varepsilon }}}\;。$ | (9) |
式中:
| $ {{\text{A}}_{\text{0}}} = 4.04\text{,} {A_s} = \sqrt 6 \cos \varphi \text{,}{U^*} \equiv \sqrt {{s_{ij}}{s_{ij}} + {{\tilde \varOmega }_{ij}}{{\tilde \varOmega }_{ij}}}\;,$ |
| $\begin{split}& \varphi =\frac{1}{3}{\cos ^{ - 1}}\left( {\sqrt 6 W} \right)\text{,}W = \frac{{{s_{ij}} + {s_{jk}} + {s_{ki}}}}{{{{\tilde s}^3}}}\text{,}\\ &W = \frac{{{s_{ij}} + {s_{jk}} + {s_{ki}}}}{{{{\tilde s}^3}}}\text{,}{s_{ij}} = \frac{1}{2}\left( {\frac{{\partial {u_j}}}{{\partial {x_i}}} + \frac{{\partial {u_i}}}{{\partial {x_j}}}} \right)\;。\end{split} $ |
式中,
Fluent软件计算求解流体相关问题时所采用的Simplec算法是基于有限体积法的求解方法。有限体积法从流体运动积分形式的守恒方程出发来建立离散方程,根据边界条件求解线性代数方程。计算中,考虑了重力加速度的存在,g为9.81 m/s2。将计算域海水密度随温度的变化拟合为四阶函数变化的曲线。计算过程中对各参数进行残差监测,当残差小于0.0001,能量参数残差小于10−7,可认为计算收敛。
图1为水下航行器排放口简化模型。航行器主体呈类椭圆体状,最大长度10 m,最大直径1 m。圆形排放口直径0.06 m;椭圆形排放口长轴半径0.09 m,短轴半径0.04 m;圆形遮流罩为1/4球面挡板;椭圆形遮流罩为1/4椭球面挡板,遮流罩厚度均为0.001 m。对于水下航行器的附体结构加以省略,仅保留航行器主体结构,便于计算。排放口中心位于航行器中心3.05 m正后方壳体上。

|
图 1 圆形、椭圆形、遮流罩结构下的圆形和椭圆形排放口模型 Fig. 1 Discharge outlet structural model of circular, elliptical, circular baffle and elliptical baffle |
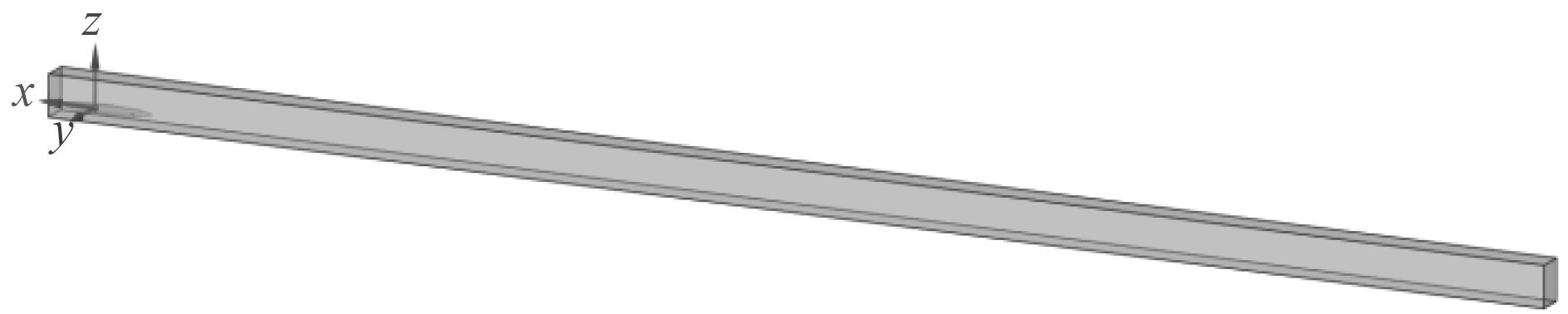
图2为计算域示意图,x轴负方向为水流流动方向,计算域长度为100 m;y轴方向计算域宽度为10 m,z轴方向计算域深度为10 m。航行器中心距水流入口面5 m,深度8 m,位于y轴中轴线上。
|
图 2 计算域示意图 Fig. 2 Schematic diagram of computing domain |
在完成物理模型的建立以及计算域的生成之后,依托Fluent Meshing处理手段对模型及计算域进行非结构性网格的划分,网格均采用四面体混合六面体网格结构,在排放口周围及水下热射流形成发展区域通过BOI方法进行局部网格加密,提高仿真计算精度。经网格无关性检验,每一排放口结构最终体网格数在150万左右,网格质量较好。若继续增加网格密度,对计算结果影响不大,计算时间大大增加。
2.2 边界条件计算域左侧水流入口边界条件为速度入口边界,水流入口速度v0=0.5 m/s,温度T0=293.15 K;计算域右侧水流出口边界条件为压力出口边界,水流温度也为T0=293.15 K。航行器排放口边界条件为速度入口边界,热射流初始速度v1=1.5 m/s,初始温度T1=333.15 K。其余边界条件均为无滑移壁面边界,近壁面区采用标准壁面函数法。
3 仿真计算结果对比 3.1 排放口形状对比将圆形排放口与椭圆形排放口仿真计算结果进行对比,2种排放口结构形状不同,其余计算条件,边界条件均一样,且2种排放口排水面积相同,排水流量相同。2种排放口水下热射流温度分布云图对比如图3所示。

|
图 3 圆形、椭圆形排放口热射流温度分布云图 Fig. 3 Temperature profile of hot jet discharging from circular and elliptical discharge outlet |
可以看出:不论是圆形排放口还是椭圆形排放口,热射流排出后在水体流动的作用下,均向流体运动方向扩散,呈长尾形。定义热射流温度衰减至300 K左右的扩散区域为排出的热射流核心温度衰减区域;椭圆形排放口的热射流核心温度衰减区域的水平长度短于圆形排放口的热射流核心温降区域的长度,说明椭圆形排放口对于热射流的掺混换热效果有所提升,加快了热射流的温度衰减速率。
热射流与水体掺混换热,使得局部水域温度升高,形成水体温升区域,选取热射流轨迹中心最高温度点,记录最高温度值。以排放口中心为坐标原点,热射流轨迹中心最高温度点距离排放口中心x轴水平距离(简称为水平距)为横坐标,温度值为纵坐标建立二维直角坐标系,可以得到航行器水下热射流温度衰减变化趋势。
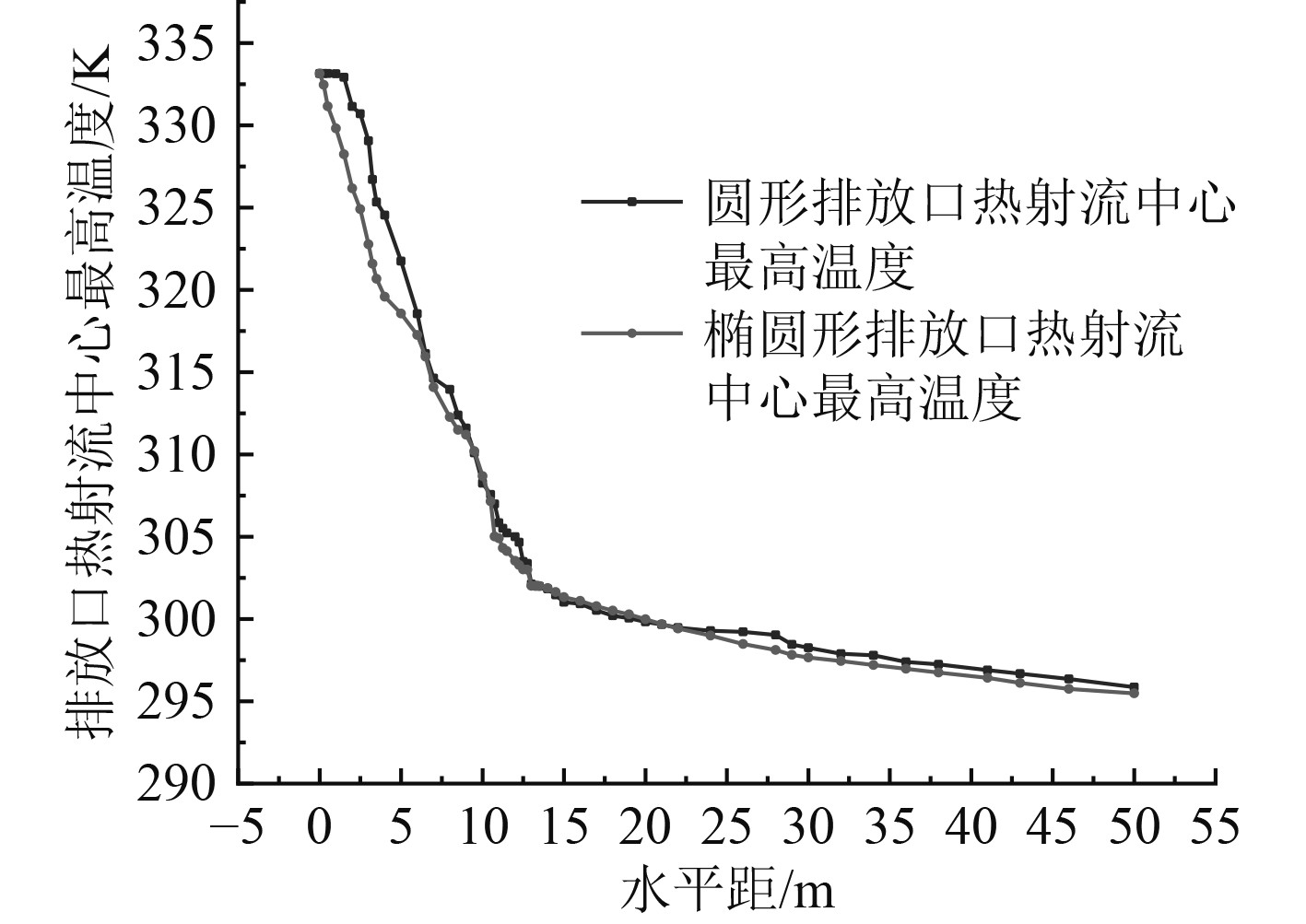
从图4结果分析可知,圆形排放口和椭圆形排放口作用下水下热射流温度衰减的变化趋势类似。靠近排放口中心区域热射流与环境水体掺混换热剧烈,温度下降也快,在远离排放口中心的热射流区域,温度下降越缓慢,变化不明显,与环境水体温差也较小,最终水下热射流的温度与环境水体一致。核心温度衰减区域的尾迹长度在15~20 m,但在降温的快慢程度上,椭圆形排放口优于圆形排放口,尤其是热射流中段区域,温度下降速率快于圆形排放口。椭圆形排放口热射流中心最高温度与圆形排放口热射流中心最高温度平均温差在1.184 K,在热射流前中段,平均温差在3.45 K,从降低热射流温度、提高与环境水体掺混换热效果上看,椭圆形排放口效果更好。从热射流后段温度衰减特性上看,椭圆形排放口热射流温度与环境水体温差更小。总体上看,椭圆形排放口更有利于热射流温度降低及衰减。
|
图 4 圆形、椭圆形排放口热射流中心最高温度衰减曲线 Fig. 4 Attenuation curve of maximum temperature in the center of hot jet discharging from circular and elliptical discharge ports |
对比圆形排放口和椭圆形排放口对形成水下热射流的温度衰减特性的作用效果,可以得到椭圆形排放口在提升水下热射流的温度衰减速率上效果更好,促进了水下热射流与环境水体的掺混换热。
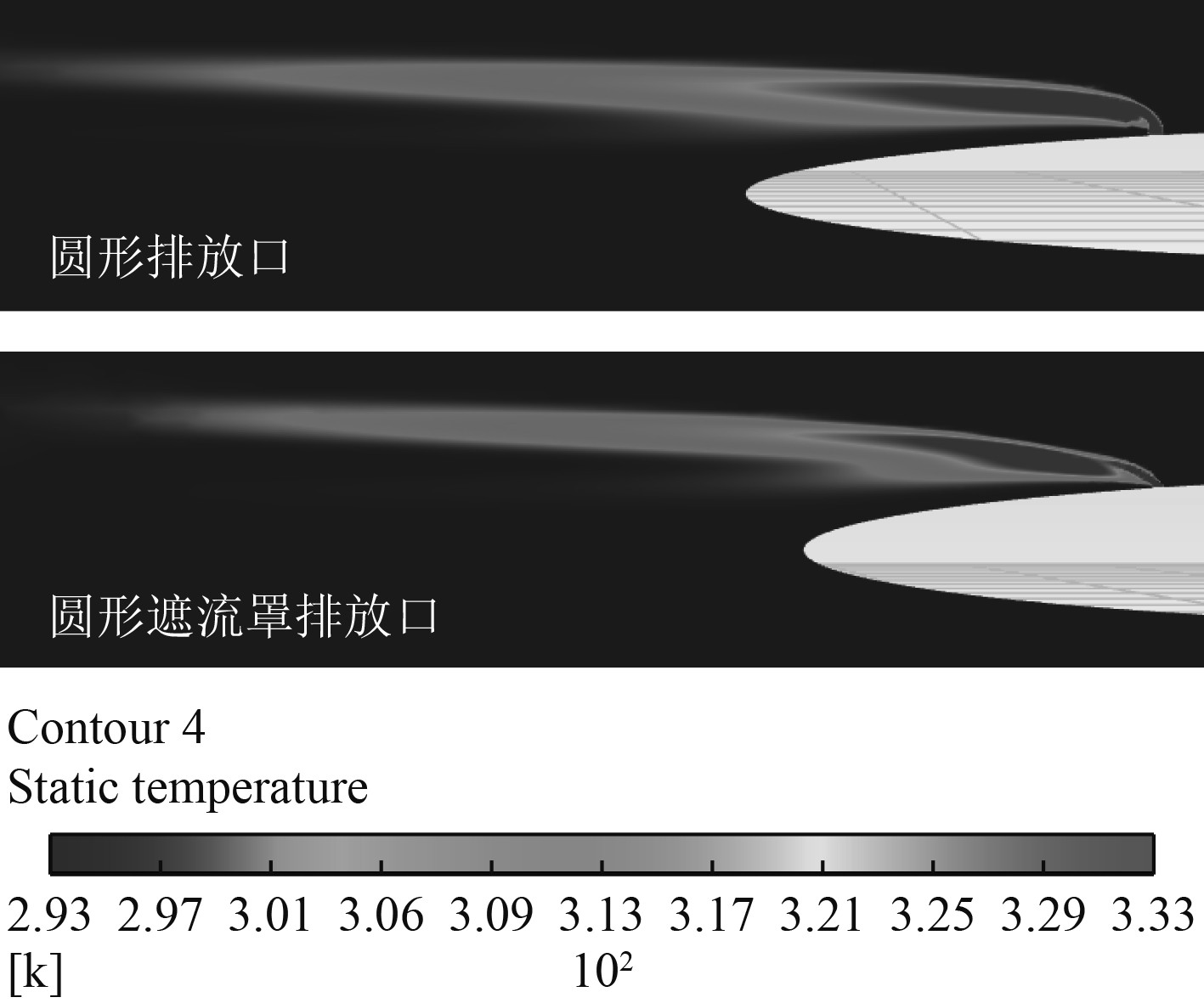
3.2 排放口有无遮流罩对比分别将圆形排放口和遮流罩作用下圆形排放口以及椭圆形排放口和遮流罩作用下椭圆形排放口进行两两对比,分析在一般状态下排放口以及有遮流罩状态下排放口对水下热射流的形成及衰减温度的影响效果。2组排放口水下热射流温度分布云图对比如图5和图6所示。
|
图 5 圆形、圆形遮流罩排放口热射流温度分布云图 Fig. 5 Temperature profile of hot jet discharging form circular and circular baffle discharge outlet |
|
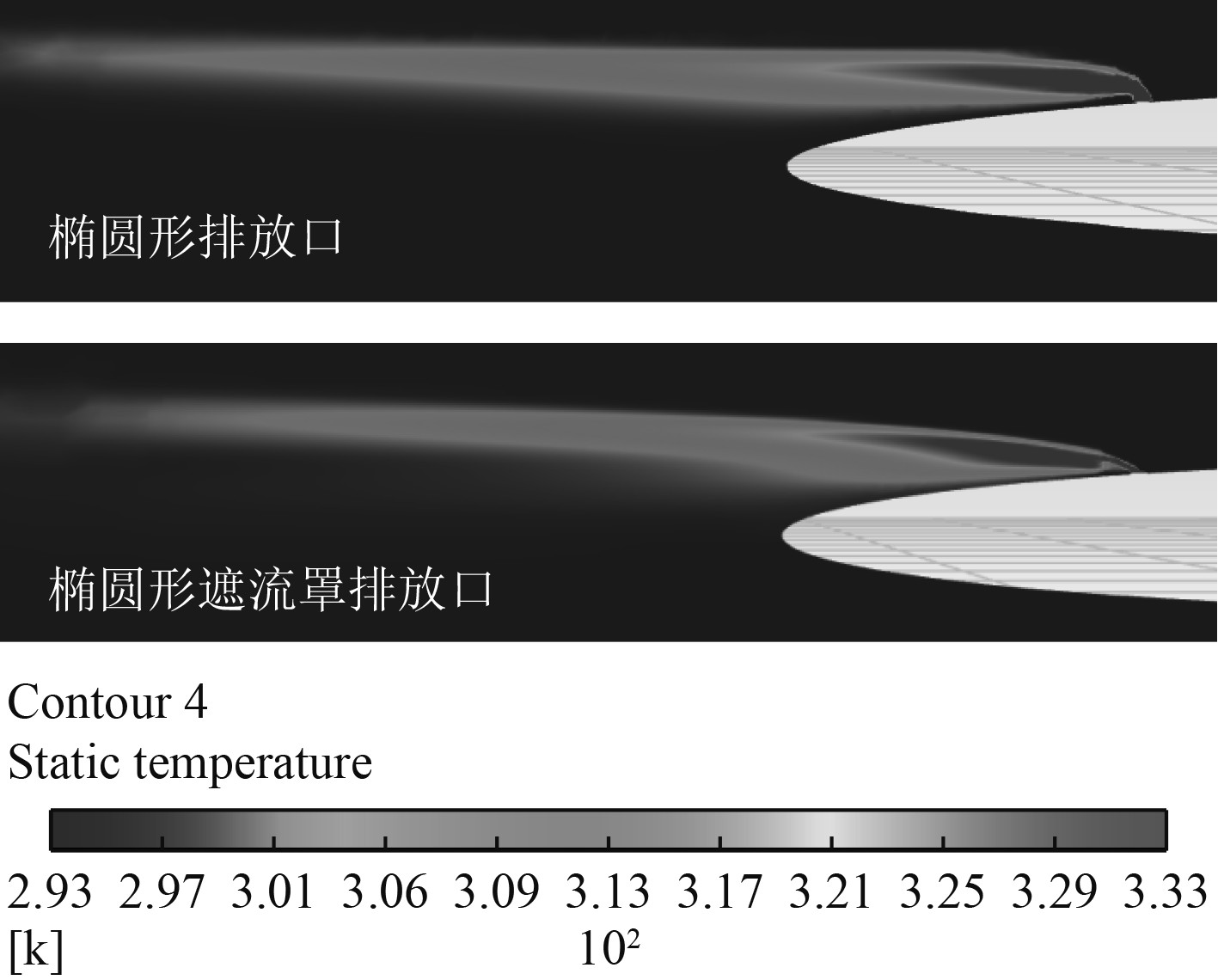
图 6 椭圆形、椭圆形遮流罩排放口热射流温度分布云图 Fig. 6 Temperature profile of hot jet discharging form elliptical and elliptical baffle discharge outlet |
由图5和图6可以看出,不论是圆形遮流罩还是椭圆形遮流罩,均对水下热射流有着束流整流的效果。在遮流罩作用下,排出的热射流流动更集中,热射流流迹与航行器壳体更贴近,体现出遮流罩对热射流的束流效果。另外,可以明显看出在热射流中段(核心温降区域),在遮流罩作用下,热射流温度扩散更好、更充分,热射流温度扩散纵向宽度也明显宽于无遮流罩作用下形成的热射流宽度,这说明在遮流罩作用下,热射流温度扩散更明显,温度衰减效果更好。同时,在总体上,有遮流罩作用下,水下排出热射流的长度略短于无遮流罩作用形成的水下排出热射流,说明在遮流罩作用下,热射流与环境水体掺混换热效果更好,热射流更快降至环境水体温度。同样对4类排放口水下热射流轨迹中心温度值两两进行数值分析,在同一坐标系下热射流温度衰减曲线如图7所示。
|
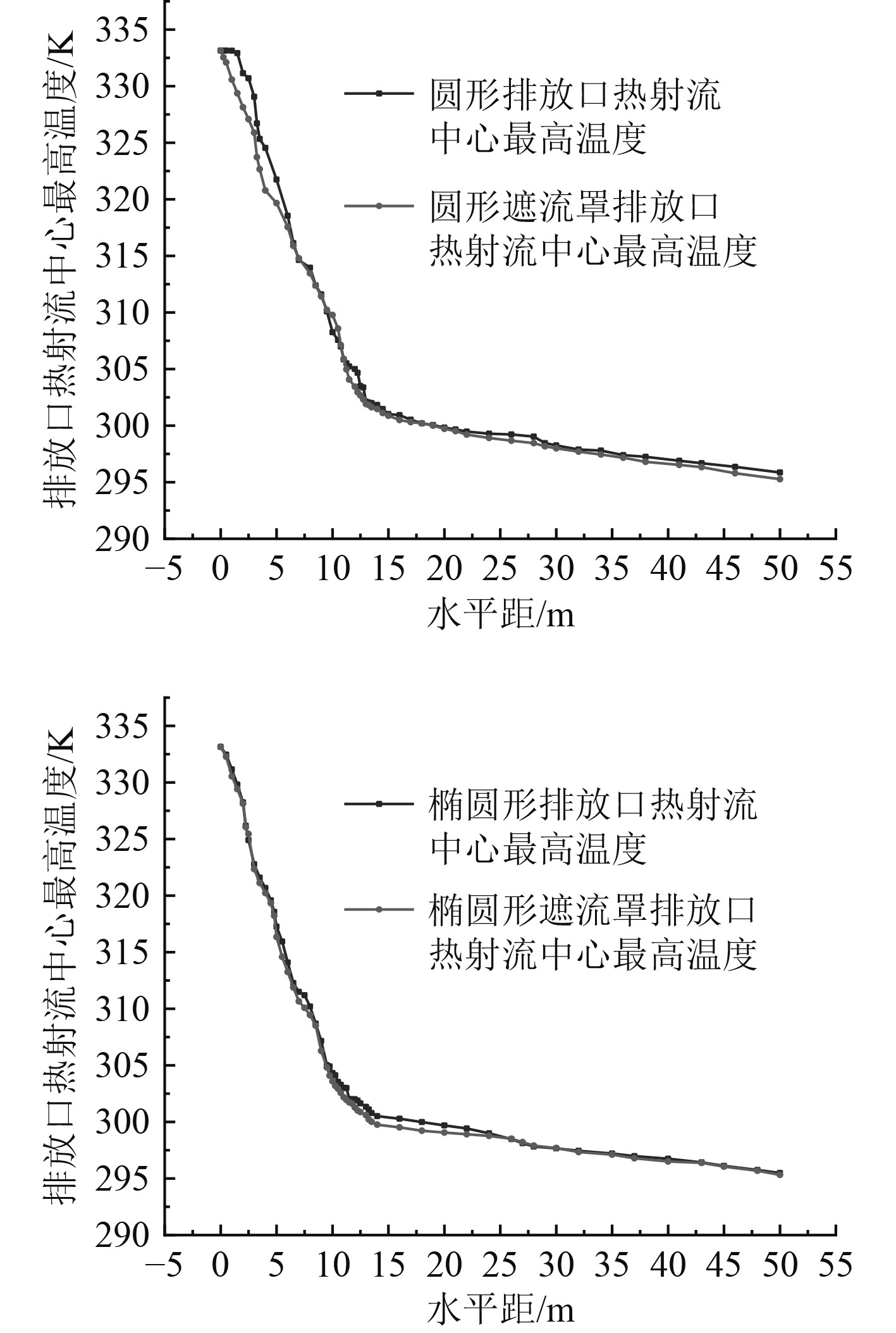
图 7 圆形、圆形遮流罩及椭圆形、椭圆形遮流罩排放口热射流中心最高温度衰减曲线 Fig. 7 Attenuation curve of maximum temperature in the center of hot jet discharging from circular、circular baffle and elliptical、elliptical baffle discharge ports |
对图中数据分析可知,在遮流罩作用下,圆形排放口排出热射流中心最高温度衰减与无遮流罩作用下排出热射流中心最高温度平均温差在0.778 K,核心温度衰减区域平均温差为1.956 K;椭圆形排放口排出热射流中心最高温度衰减与无遮流罩作用下排出热射流中心最高温度平均温差0.469 K,核心温度衰减区域平均温差1.433 K。圆形排放口平均温度衰减速率在−1.35 K/m,遮流罩作用下圆形排放口平均温度衰减速率−1.46 K/m;椭圆形排放口平均温度衰减速率−1.51 K/m,遮流罩作用下椭圆形排放口平均温度衰减速率−1.57 K/m。数据分析表明,在遮流罩作用下,水下热射流的温度衰减特性有所提升,热射流温度衰减更均匀,衰减速率更快,温度衰减下降更多。温度较高的排放冷却水与温度较低的环境水体掺混换热,在相同条件下,有遮流罩作用下的排放口形成热射流在距排放口中心水平距离一致的位置处,热射流中心最高温度与环境水体温差更小。
4 结 语在来流法的计算思路下,采用有限体积法,对4种不同结构的冷却水排放口(圆形排放口、椭圆形排放口、遮流罩结构下的圆形排放口、椭圆形排放口)进行仿真模拟,通过计算与分析得出如下结论:
1)4种排放口结构下的水下航行器排出热射流在环境水体中形成的温度升高区域均呈长尾形,并且热射流轨迹中心最高温度随着排出距离和排出时间的增加而降低,最终与环境水体温度一致。
2)与圆形排放口相比,椭圆形排放口对于水下航行器排出热射流的温度衰减以及与环境水体的掺混换热效果更好。由于椭圆形排放口出口截面狭长,在排放口面积相等的情况下,椭圆形排放口使得水下热射流在排出后更好地与环境流体混合,尤其是热射流形成的中后段,椭圆形排放口的结构有效降低了热射流与环境水体的温差,促进了热射流与环境水体的换热。
3)从圆形排放口和遮流罩结构下圆形排放口以及椭圆形排放口和遮流罩结构下椭圆形排放口的温度衰减曲线对比来看,遮流罩对水下热射流温度衰减特性有影响,尤其在形成热射流的中段,温度衰减效果较好,也较为明显。从热射流形成轨迹上看,在热射流排放口附近,遮流罩对水下热射流具有束流整流效果,更好地贴合水下航行器的运动状态,改善了由于热射流排出方向与水下航行器运动方向不一致造成的流体扰动,从而导致热射流与环境水体换热效果差的问题。在遮流罩作用下,水下航行器排出热射流温度也可更快衰减至环境水体温度,与环境水体温度趋于一致。
遮流罩结构促进了水下热射流与环境水体的掺混换热,提升了热射流温度衰减速率,减弱了热射流温度特征,从而达到增强水下航行器热隐身的目的。对水下航行器冷却水排放口结构进行优化设计,对抑制水下航行器排出热射流温度特性,提高水下航行器运动隐蔽性有着重要意义。
| [1] |
EL-AMIN Mohamed F, et al. Numerical simulation and analysis of confined turbulent buoyant jet with variable source [J]. Journal of Hydrodynamics, 2015, 27(6): 955–968 .
|
| [2] |
GERHARD H. JIRKA, Integral model for turbulent buoyant jets in unbounded stratifified flows [J]. Part I: Single Round Jet. Environmental Fluid Mechanics, 2004, 4: 1–56.
|
| [3] |
CHEN Yen-Lung, HSIAO Shih-Chun, Numerical modeling of a buoyant round jet under regular waves [J]. Ocean Engineering, 2018, 161: 154–167.
|
| [4] |
王平, 等, 基于动网格与来流法的潜艇热尾流浮升扩散规律对比研究 [J]. 工程热物理学报, 2020. 41(10): 2589–2595.
|
| [5] |
李大鹏, 张士诚, 舰艇尾流红外隐身技术的研究与进展[J]. 中外船舶科技, 2018(4): 13–28.
|
| [6] |
王兴茹, 潜艇尾流空间演化及流场特性仿真分析 [D], 哈尔滨: 哈尔滨工业大学. 74.
|
| [7] |
江传富, 等, 水下航行器热尾流浮升及分布研究 [J]. 激光与红外, 2005.12(7): 932–934.
|
| [8] |
周哲, 等, 基于CFD的潜艇排放口结构优化与仿真分析[J]. 舰船科学技术, 2020. 42(5): 66–70.
|
| [9] |
张健, 等, 流动环境中水平热射流温度分布特性研究 [J]. 华中科技大学学报(自然科学版), 2011. 39(8): 62–66.
|
| [10] |
戴天奇, 等, 横流环境中冷却水排放浮升规律[J]. 舰船科学技术, 2015. 37(4): 112–116. DAI Tian-qi, et al. Study of buoyant rule of cooling waterdischarged in cross flow[J]. Ship Science and Technology, 2005, 37(4): 112–116. |
 2023, Vol. 45
2023, Vol. 45
