2. 中国船舶科学研究中心,江苏 无锡 214082
2. China Ship Scientific Research Center, Wuxi 214082, China
操纵性是衡量潜艇综合性能优良的重要指标之一,良好的操纵性能是潜艇安全航行的重要保证[1-2]。潜艇操纵工况下绕流特性极为复杂,不但有主附体结合部和流水孔处各种形式涡的产生与演化,而且还涉及艇体、舵以及螺旋桨之间的复杂相互干扰,导致针对潜艇操纵性的研究具有很高的难度。早期研究主要依靠模型试验方式进行,对人力物力要求高而且试验设施复杂,难以在潜艇设计阶段进行广泛应用。
随着计算机技术的发展,计算流体动力学(computational fluid dynamics, CFD)方法在水下航行体操纵性预报中发挥越来越重要的作用。张楠等[3-5]提出了适用于水下航行器流场预报的数值方法,并开展了带自由液面、全附体模型的数值模拟。孙铭泽等[6]实现了全附体潜艇平面运动机构试验数值模拟,并将计算得到的水动力导数与试验值以及直线拖曳试验或回转试验的数值计算结果进行了对比验证。庞永杰[7]以椭球体为研究对象计算了其水动力导数,并通过与理论值进行对比验证了所采用数值方法的有效性。焦玉超等[8]对不同X形尾舵的潜艇绕流场进行了数值模拟,分析了X舵角度对潜艇性能的影响。翟朔等[9]对某潜艇模型的尾部水平操纵面分别进行了共翼型设计和非共翼型设计,并计算了2种操纵面产生的艇体水动力和尾流特征。
从目前已有研究可以看出,应用CFD方法开展潜艇操纵性能预报及评估已经成为领域内的趋势和研究热点。本文基于CFD平台STAR-CCM+对潜艇斜航工况下的操舵水动力及绕流场进行数值研究,以国际上广泛用于对比验证研究的SUBOFF潜艇模型为研究对象,分别应用雷诺平均(reynolds-averaged navier-stokes, RANS)与分离涡模拟(detached eddy simulation, DES)2种方法对潜艇不同舵角下的斜拖试验进行数值模拟,据此分析潜艇纵向力、横向力、转首力矩以及绕流场随舵角的变化规律,揭示潜艇操纵工况下水动力特性与绕流场间的内在联系,为水下航行体大舵角状态操纵性能预报和评估提供技术支持。
1 数值计算方法采用STAR-CCM+中的RANS与DES求解器开展相关数值计算工作,其中RANS方法和DES方法均采用剪切应力传输模型(shear stress transfer, SST)
| $ \left\{ \begin{gathered} \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}k} \right)}}{{\partial {x_j}}} = P - {\beta ^*}\rho \omega k + \\ \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _k}{\mu _t}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right],\\ \frac{{\partial \left( {\rho \omega } \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_j}\omega } \right)}}{{\partial {x_j}}} = \frac{{\rho \gamma }}{{{\mu _t}}}P - {\beta ^*}\rho {\omega ^2} + \\ \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + {\sigma _\omega }{\mu _t}} \right)\frac{{\partial \omega }}{{\partial {x_j}}}} \right] + 2\left( {1 - {F_1}} \right)\frac{{\rho {\sigma _{\omega 2}}}}{\omega }\frac{{\partial k}}{{\partial {x_j}}}\frac{{\partial \omega }}{{\partial {x_j}}} 。\end{gathered} \right. $ | (1) |
式中:
将RANS湍流模型中的长度尺度使用DES的长度尺度代替,就获得了基于该湍流模型的混合RANS/LES方法即DES方法。DES的长度尺度由RANS和LES的长度尺度以如下方式混合得到,即
| $ {l_{DES}} = \min \left( {{l_{RANS}},{l_{LES}}} \right),$ | (2) |
LES长度尺度由网格间距得到,即
| $ {l_{LES}} = {C_{DES}}\Delta ,$ | (3) |
式中,
RANS长度尺度为最近壁面距离,即
| $ {l_{RANS}} = \frac{{{k^{{1 \mathord{\left/ {\vphantom {1 2}} \right. } 2}}}}}{{{\beta ^*}\omega }} 。$ | (4) |
由DES模型的构造可知,当RANS长度尺度激活时,湍流模型为传统的RANS湍流模型,而当LES长度尺度激活时,湍流模型转换为经典的Smagorisnky亚格子模型,从而实现RANS和LES方法的转换。
2 数值计算设置 2.1 研究对象以美国DARPA潜艇模型SUBOFF-8为研究对象,该潜艇由裸艇、指挥台围壳及4个完全相同的尾翼(左右为升降舵,上下为方向舵)组成,主艇体总长Loa=4.356 m,垂线间长L=4.261 m,其中前体长1.016 m,平行中体长2.229 m,后体长1.111 m;艇体最大直径D=0.508 m;指挥台围壳长0.368 m,高0.205 m,上部有2∶1的椭圆形横截面的顶盖;4个相同的尾翼截面为NACA0020,呈十字布置在尾部,顶端弦长为0.152 m,详细几何特征由文献[11]提供,三维几何形状如图1所示。

|
图 1 SUBOFF几何模型 Fig. 1 Geometric model of SUBOFF |
计算工况具体参数如表1所示。考虑潜艇在漂角β=–4°、舵角0°~40°范围内的水动力性能,其中δ在0°~15°范围内数值计算结果可与Roddy[12]所做的公开实验数据进行对比,从而确定数值方法的可靠性。在STAR-CCM+中,漂角的处理方法是将SUBOFF以艇体质心所在的Z轴为旋转轴,进行逆时针旋转4°,其他保持不变。
|
|
表 1 工况设定 Tab.1 Setup of study condition |
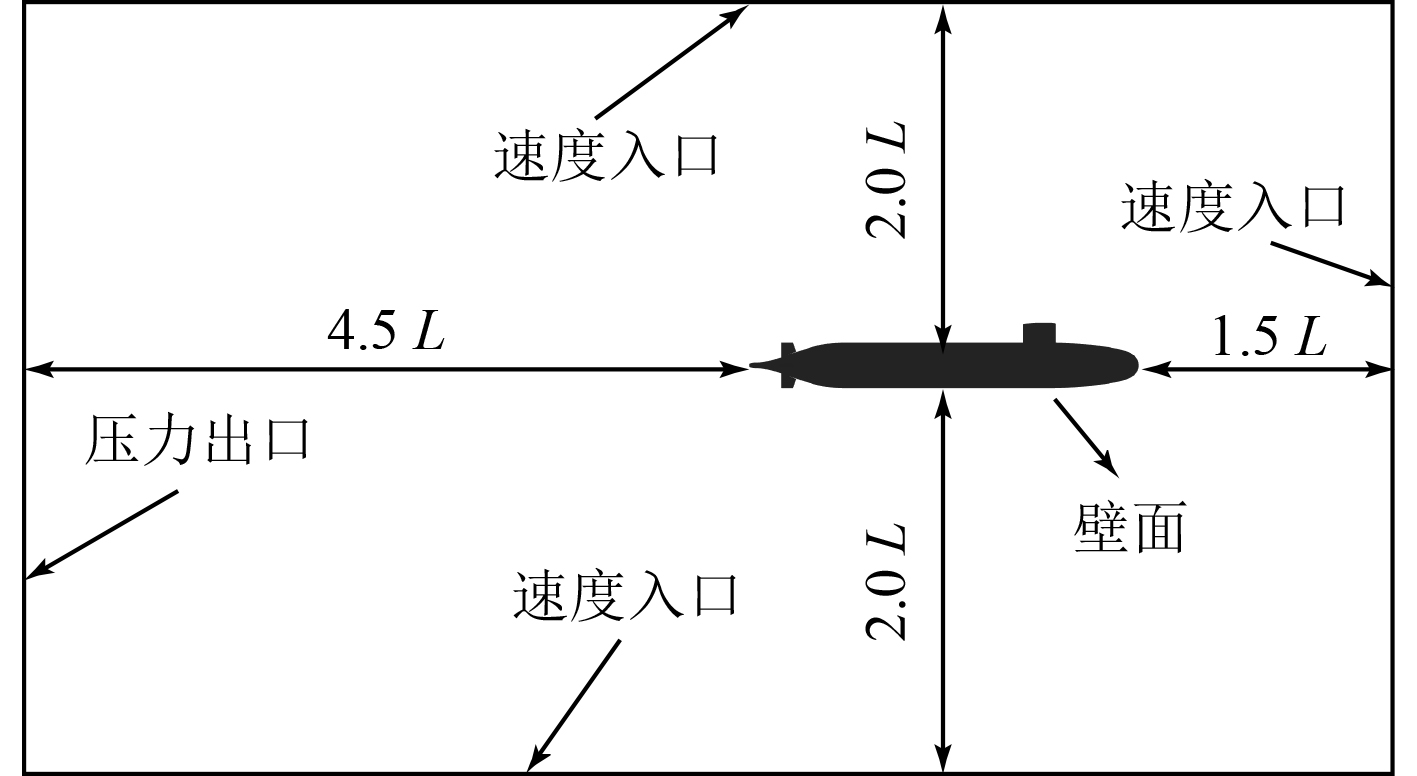
计算域总长为7倍艇长,首部距离进口1.5倍,尾部距离出口4.5倍,左右及上下边界距艇体均为2.0倍艇长。对于边界条件的设定,除计算域出流面采用压力出口条件以外,其他边界均采用速度入口条件,艇体所有表面采用无滑移壁面边界条件。计算域尺度及边界条件如图2所示。
|
图 2 计算域尺度及边界条件 Fig. 2 Dimensions and boundary conditions of the computational domain |
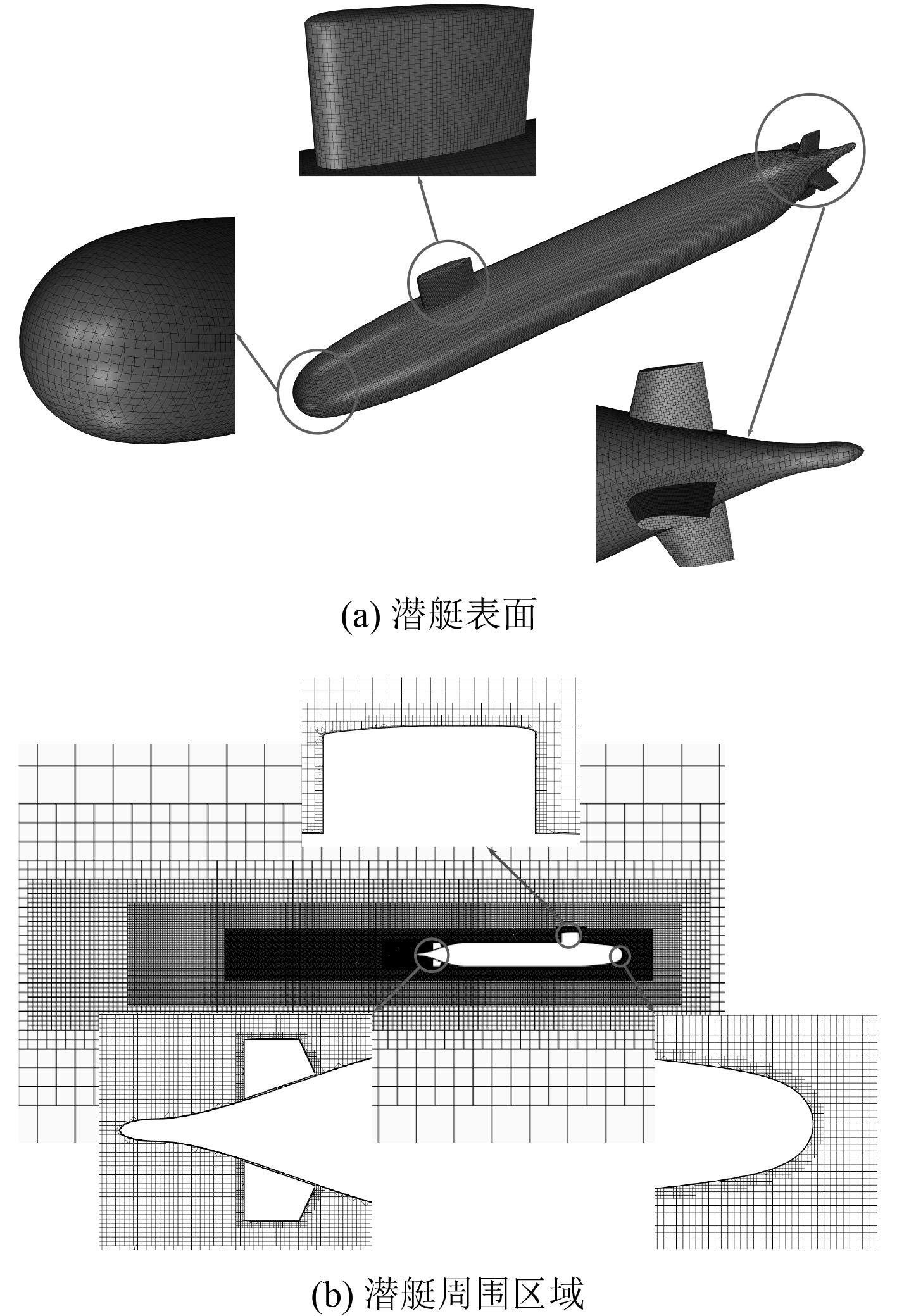
计算域采用STAR-CCM+中的切割体网格进行离散。切割体网格属于非结构网格,适用于具有复杂外形模型的网格划分。切割体网格在生成时可以通过控制体进行任意区域的网格加密,同时还可以对几何模型中的控制线、控制面进行线加密及面加密。为了保证潜艇附近的网格质量,对其表面进行了加密;通过使用切割体网格单元,在艇体附近及其尾流进行网格密化,从而更好地捕捉流动的细节,获得更准确的流场信息。同时,在近壁面生成棱柱层网格以便于边界层流动的求解。通过调整棱柱层网格的总厚度、层数及增长比率来控制近壁面第一层网格高度,使近壁面Y+值在30~60范围内。网格数量在500万左右,网格划分情况如图3所示。
|
图 3 计算域网格划分情况 Fig. 3 Gird generation in the computational domain |
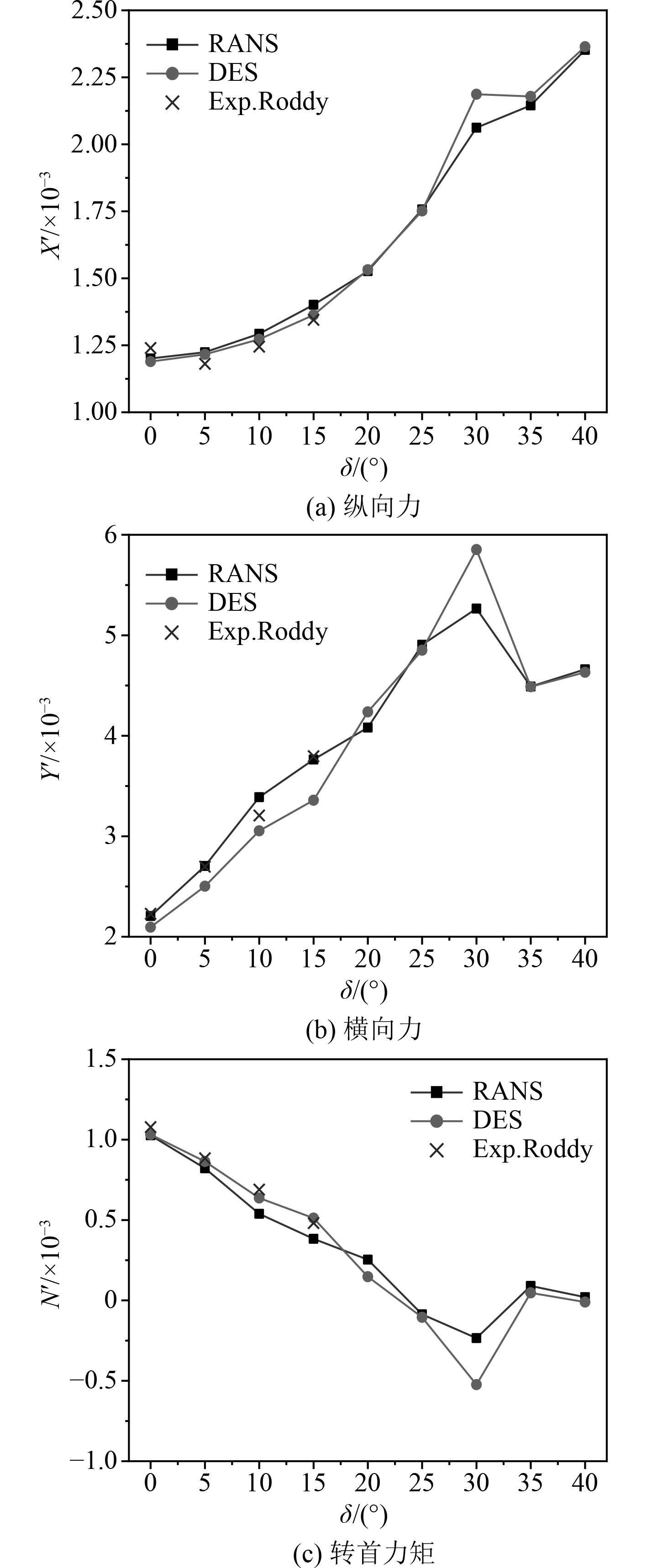
图4给出了RANS与DES方法获得的作用在潜艇上的纵向力X、横向力Y及转首力矩N。为了便于分析,均采用无因次形式表述:
|
图 4 数值结果与模型试验数据对比 Fig. 4 Comparison between the numerical results and the experimental data |
| $ X' = {X \mathord{\left/ {\vphantom {X {\left( {\frac{1}{2}\rho {V^2}{L^2}} \right)}}} \right. } {\left( {\frac{1}{2}\rho {V^2}{L^2}} \right)}} ,$ | (5) |
| $ Y' = {Y \mathord{\left/ {\vphantom {Y {\left( {\frac{1}{2}\rho {V^2}{L^2}} \right)}}} \right. } {\left( {\frac{1}{2}\rho {V^2}{L^2}} \right)}} ,$ | (6) |
| $ N' = {N \mathord{\left/ {\vphantom {N {\left( {\frac{1}{2}\rho {V^2}{L^3}} \right)}}} \right. } {\left( {\frac{1}{2}\rho {V^2}{L^3}} \right)}}。$ | (7) |
式中:ρ为流体密度;V为航行速度;L为潜艇总长。
相对X′而言,无论RANS还是DES对阻力的预报精度都在±3%以内;δ的变化会对阻力产生较大的影响,δ在0°~30°范围内,随着舵角的增大,艇体所受的阻力以抛物线的趋势增大;随着δ的进一步增大,RANS计算结果在30°~40°范围内基本呈线性增大,DES计算结果先有略微减小然后再增大。相对Y′而言,RANS计算结果与试验值的吻合程度略好于DES方法,RANS计算的误差均在10%以内,DES计算除了δ=15°时误差偏大,其余工况均在12%以内;δ在0°~30°范围内,DES与RANS计算得到的横向力随着舵角的增大而近似呈现线性增大;δ在30°~35°范围内,RANS及DES计算的横向力显著下降,发生了明显的舵失速现象;进一步增大舵角,艇体所受的横向力有微幅的增加,这表明舵效并未随舵角进一步增大而发生明显改善。相对于N′而言,DES计算在各工况下的计算精度均在±12%以内,而RANS方法在δ=10°和δ=15°计算误差较大,均超过20%;N′与Y′的变化规律保持基本一致。通过对水动力分析可知,就对比现有的公开试验数据而言,RANS方法在X′与Y′相关的计算精度比DES方法略好,但是DES方法对N′的计算精度明显优于RANS方法。
3.2 泄出涡系结构图5给出了由RANS及DES方法获得的不同舵角下艇尾区域的涡系结构,其中涡系结构采用Q准则等值面表示,并以无量纲纵向速度Ux/U0着色。可以看出,随着方向舵舵角的变化,艇尾区域涡系发展呈现出显著的差异。在小舵角(δ=10°)下,舵背风面主要以附着流为主,舵梢部有轻微涡泄出。随着舵角增大(δ=20°),方向舵附近产生的涡系结构明显增多。方向舵背风面靠近尾部区域开始产生泄出涡系。同时,由于偏转方向舵的阻滞效应,在艇身与方向舵的交汇处形成了明显的马蹄涡结构。随着舵角的进一步增大(δ=30°),舵背风面完全由泄出涡系覆盖,而且马蹄涡结构也更为显著。当舵角达到δ=40°时,舵背风面的泄出涡完全脱离舵表面发展,在下游形成了复杂的涡系结构,与舵失速状态相对应。通过对比可知,在小舵角工况下,RANS方法与DES方法得到的艇尾区域涡系结构差异不明显,随着舵角增大,二者的差异越发明显。特别是发生大规模流动分离的工况下,DES方法捕捉到的涡系结构更加精细。

|
图 5 不同舵角工况下的Q=100 s−2等值面图 Fig. 5 Iso-surface of Q=100 s−2 under different rudder angles |
图6给出了DES与RANS方法获得的舵叶中间位置处的舵附近流线分布。可知,在舵角δ=10°工况下,舵剖面附近流动主要以附着流为主,而且2种方法得到的流场没有明显的差异。在舵角δ=20°工况下,舵剖面背流面发生了明显的流动分离现象,其中RANS方法呈现出的流动分离更为明显,导致该区域的速度明显下降。在舵角δ=30°工况下,舵剖面的整个背流面均发生了流动分离,2种数值方法获得的流线分布差异也更加明显。RANS方法中背流面处的流动分离更加明显,而DES方法捕捉到的流动分离并未随舵角明显增强。另外,2种方法捕捉得到流场均在舵下游呈现出明显的低速区。在舵角δ=40°工况下,舵剖面背流面处的流动分离显著增强,对附近流场产生的扰动也十分明显,在下游形成了更为显著的低速区,这一流场特征与舵失速工况下的阻力增加及升力下降相对应。综上,DES方法在流场捕捉方面具有明显优势,能清晰地捕捉艇尾区域的复杂流场信息。

|
图 6 不同舵角工况下舵附近流线分布 Fig. 6 Streamlines around the rudder under different rudder angles |
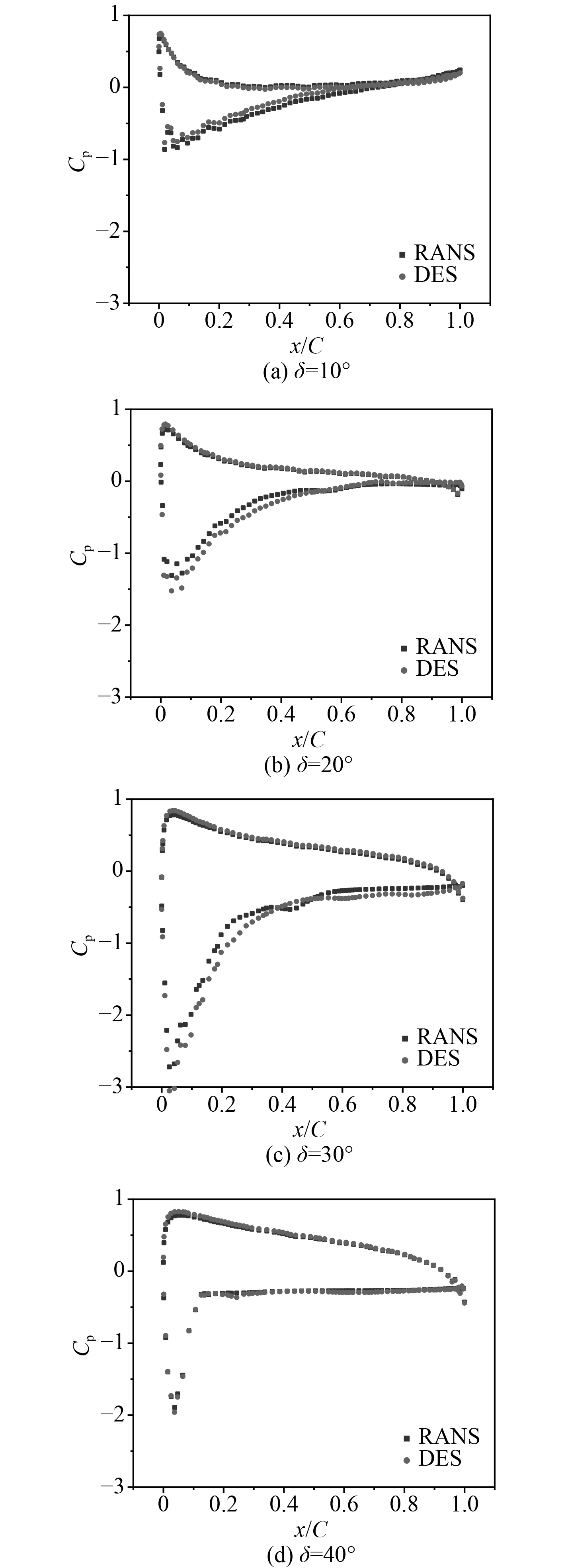
图7给出了RANS方法与DES方法获得的不同舵角工况下的舵剖面压力分布情况。压力采用无因次系数Cp表示,Cp=p/(0.5ρV2)。横坐标由无因次量x/C表示,坐标原点位于该舵前缘处,无因次量“1”表示舵尾缘。在舵角δ=10°工况下,舵剖面压力呈现出明显的吸力面和压力面,正压和负压的峰值均位于前缘附近,而且2种方法获得的压力分布较为一致。在舵角δ=20°工况下,DES方法得到的吸力面负压区较RANS方法更为显著,但整体分布差异很小。在舵角δ=30°工况下,吸力面负压区更为显著,同时发生流动分离的区域压力分布较为平缓。DES方法得到的吸力面负压区明显强于RANS方法,这也与该舵角工况下DES计算得到的舵横向力高于RANS计算结果相对应。在舵角δ=40°工况下,吸力面负压区峰值明显下降,而且发生流动分离的区域压力分布呈平直状,导致吸力面与压力面之间的压力差显著下降,这与舵发生失速导致的舵效下降相对应。总体而言,2种数值方法得到的压力分布差异相对较小,与潜艇操舵水动力性能的一般规律较为吻合。
|
图 7 不同舵角工况下舵剖面压力分布图 Fig. 7 Pressure distribution on the rudder section under different rudder angles |
本文针对潜艇斜航工况下的操舵水动力性能及绕流场进行数值模拟研究,主要得到以下结论:
1)潜艇斜航工况下的纵向力、横向力及转首力矩随着舵角的变化呈现复杂的变化规律,在潜艇操舵水动力预报精度方面DES方法整体上优于RANS方法;
2)DES方法对于潜艇操舵工况下艇尾区域的绕流场捕捉更为精细,在潜艇操纵工况下的水动力学机理探讨方面有明显的优势,在潜艇复杂操纵运动分析和性能评估方面具有很好的工程应用潜力。
| [1] |
周广礼, 欧勇鹏, 高霄鹏, 等. 潜艇操纵性预报研究现状与前景展望[J]. 中国造船, 2018, 59(3): 203-214. ZHOU Guang-li, OU Yong-peng, GAO Xiao-peng, et al. Progress and prospect of maneuverability prediction for submarine[J]. Shipbuilding of China, 2018, 59(3): 203-214. DOI:10.3969/j.issn.1000-4882.2018.03.021 |
| [2] |
林雄伟, 胡大斌, 戴余良. 潜艇非线性运动研究综述[J]. 船舶力学, 2013, 17(Z1): 187-195. LIN Xiong-wei, HU Da-bin, DAI Yu-liang. Overview on the research of submarine nonlinear motion[J]. Journal of Ship Mechanics, 2013, 17(Z1): 187-195. |
| [3] |
张楠, 沈泓萃, 姚惠之. 潜艇阻力与流场的数值模拟与验证及艇型的数值优化研究[J]. 船舶力学, 2005(1): 1-13. DOI:10.3969/j.issn.1007-7294.2005.01.001 |
| [4] |
张楠, 沈泓萃, 姚惠之. 用雷诺应力模型预报不同雷诺数下的潜艇绕流[J]. 船舶力学, 2009, 13(5): 688-696. ZHANG Nan, SHEN Hong-cui, YAO Hui-zhi. Prediction of flow around submarine at different Reynolds numbers with Reynolds stress model[J]. Journal of Ship Mechanics, 2009, 13(5): 688-696. DOI:10.3969/j.issn.1007-7294.2009.05.003 |
| [5] |
张楠, 张胜利, 沈泓萃, 等. 带自由液面的艇/桨干扰特性数值模拟与验证研究[J]. 水动力学研究与进展A辑, 2012, 27(1): 94-99. ZHANG Nan, ZHANG Sheng-li, SHEN Hong-cui, et al. Numerical simulation of hull/propeller interaction with free surface[J]. Journal of Hydrodynamics (A), 2012, 27(1): 94-99. DOI:10.3969/j.issn1000-4874.2012.01.014 |
| [6] |
孙铭泽, 王永生, 张志宏, 等. 基于网格变形技术的全附体潜艇操纵性计算[J]. 武汉理工大学学报(交通科学与工程版), 2013, 37(2): 420-424. SUN Mingze, WANG Yongsheng, ZHANG Zhihong, et al. Numerical Simulation of Submrine Maneuverability Basedon Deformation Technology[J]. Journal of Wuhan University of Technology (Transportation Science & Engieering), 2013, 37(2): 420-424. |
| [7] |
庞永杰, 杨路春, 李宏伟, 等. 潜体水动力导数的CFD计算方法研究[J]. 哈尔滨工程大学学报, 2009, 30(8): 903-908. PANG Yong-jie, YANG Lu-chun, LI Hong-fei, et al. Approaches for predicting hydrodynamic characteristics of submarine objects[J]. Journal of Harbin Engineering University, 2009, 30(8): 903-908. DOI:10.3969/j.issn.1006-7043.2009.08.010 |
| [8] |
焦玉超, 肖昌润. 潜艇X舵的布局优化[J]. 兵器装备工程学报, 2018, 39(3): 40-44+71. JIAO Yuchao, XIAO Changrun. Layout Optimization of Submarine X Rudder[J]. Journal of Ordnance Equipment Engineering, 2018, 39(3): 40-44+71. DOI:10.11809/bqzbgcxb2018.03.009 |
| [9] |
翟朔, 刘志华. 艇尾共翼型舵水动力和尾流场特征的数值计算研究[J]. 中国造船, 2019, 60(1): 109-119. ZHAI Shuo, LIU Zhihua. Numerical Research on Hydrodynamic Performance and Wake Flow of Conformal Rudder[J]. Ship Building of China, 2019, 60(1): 109-119. |
| [10] |
MENTER F R, KUNTZ M, LANGTRY R. Ten years of industrial experience with the SST turbulence model[J]. Turbulence, Heat and Mass Transfer, 2003(4): 625-632. |
| [11] |
GROVES N C, HUANG T T, CHANG M S. Geometric characteristics of DARPA suboff models: (DTRC Model Nos. 5470 and 5471)[R]. David Taylor Research Center, 1989.
|
| [12] |
RODDY R F. Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model (DTRC Model 5470) from captive-model experiments[R]. David Taylor Research Center Bethesda MD Ship Hydromechanics Department, 1990.
|
 2023, Vol. 45
2023, Vol. 45
