船舶在海面上航行过程中会遇到碰撞、搁浅等风险事故,这些事故一旦发生,船舶则很容易遭到损坏。船舶在海面上一旦产生事故,很难及时进行救援,这使得船舶在海面上的事故具有很大的危险性。因此对船舶应急物资运输调度进行系统性研究,对船舶应急物资的合理配备,降低船舶事故造成的损失有重要意义。本文借助计算机仿真验证技术,对船舶应急物资运输智能化联动调度体系进行研究,有助于推动船舶应急物资运输调动系统的构建。
1 船舶应急物资运输 1.1 船舶应急物资运输的影响因素船舶应急物资调度的主要目的是将相关船舶应急物资从其存储位置转移到船舶事故发生地点,这是一种物资空间转移过程。在船舶应急物资调度整个过程中会涉及到陆地运输和海上运输整个过程以及事故、集结、供应3个层面。针对海上突发事件的物资运输调度方案确定之后,距离事故点最近的救助机构则会将相关的装备和医疗物资迅速地发往海上的事故地点,并且在救援时间内及时地将救援物资运达目的地,确保救援工作的正常开展。由于船舶海上物资的调度存在弱经济性和时效性,这使得时间因素和经济因素成为制约船舶海上应急物资运输调度的主要因素。
在船舶海上应急物资运输调度网络中存在多供应点和反应基地,因此应急物资装备的运输速度和距离是最重要的影响因素,并且这2个属于时间因素。船舶在海面上的航行速度有绝对航行速度和相对航行速度2种。船舶的绝对航行速度又被称为实际航行速度,该速度是以海底为参考,并且考虑到了海风以及海流对海面上船舶航速产生的影响。以海水的流动为参考,属于船舶在海面上的相对航行速度,因此船舶在海面上的相对航行速度只考虑海风对船舶速度的影响。由此可以看出,船舶在海面上的实际航行速度是船舶的相对航行速度和水流速度的矢量和,并且船舶的速度、海风的速度以及洋流的速度均为矢量。在船舶海上应急物资运输调度的过程中,物资应急基地和海面船舶事故地点之间的距离一般采用经纬度进行衡量,并且为了确保速度参考系的一致性,需要对船舶在海面上的绝对速度进行求解。在对船舶的绝对速度进行求解过程中,假定船舶所在海面上的洋流和海风速度方向保持恒定。当应急物资运输船舶向海面上船舶事故点航行的时候,其绝对航行速度的计算公式为:
| $ V_S^{ \to l} = {V_S} + {V_w} \cdot \cos \beta + {V_{oc}} \cdot \cos \alpha \text{。} $ | (1) |
当应急物资运输船舶由海面上的船舶事故点向应急基地航行的时候,其绝对速度的计算公式为:
| $ V_S^{ \leftarrow l} = \left| { - {V_S} + {V_w} \cdot \cos \beta + {V_{oc}} \cdot \cos \alpha } \right|\text{。} $ | (2) |
应急物资运输飞行器的绝对速度是以大地为参考系的,即为对地速度,并且影响应急物资飞行器的主要因素为海面上的风速。应急物资救助飞行器向海面上事故点飞行的绝对速度计算公式为:
| $ V_p^{ \to l} = {V_p} + {V_w} \cdot \cos \beta \text{。} $ | (3) |
应急物资救助飞行器由海面船舶事故点向应急基地飞行的绝对速度计算公式为:
| $ V_p^{ \leftarrow l} = \left| { - {V_p} + {V_w} \cdot \cos \beta } \right|\text{。} $ | (4) |
在对应急物资运输调度策略规划的过程中,船舶事故点和应急基地之间的相对距离是该策略规划的重要因素之一。船舶事故点和应急基地之间的距离长短会直接影响应急物资在路上的运输时间。在实际船舶应急物资运输调度过程中,应急物资调度中心会使用AIS,GPS等设备获取精确的船舶事故点的坐标信息,然后进一步解算出距离。在进行两点之间距离的解算过程中,假设A坐标为(A1, A2),B坐标为(B1, B2),同时将0°经线看成是基准线,东经为正,西经为负,对A,B两点的坐标进行转换,转换之后A,B两点的坐标分别为(A11, A22)、(B11, B22),则AB两点间相隔的距离可以用式(5)进行计算,式中,a为维度差,b为经度差。
| $\begin{aligned}[b] & l = 2{\sin ^{ - 1}}\times\\ & \sqrt {{{\left( {\sin \frac{a}{2}} \right)}^2} + \cos \left( {B_{22}} \right)\cdot\cos \left( {A_{22}} \right)\cdot \left( {\sin \frac{b}{2}} \right)} \cdot 6378.137 \text{。} \end{aligned} $ | (5) |
假设船舶事故海域的船员需要得到紧急救援,并且船舶遇险船员人数为X1,则此时的救援时间最紧,需要在最短的时间内将遇险人员救出,因此救援的第一阶段结束的标志为最后一名船员被救出,并且这时候救援时间为T1。设应急物资调度成本为C,第二阶段救援开始时间为T2,应急基地到海面事故点的距离为li,应急物资的运输调运的绝对速度为V→l ik。每台运输装备从应急基地往返事故地点一次为一个应急物资调度小周期,并且经过n个应急物资调度小周期之后,完成第一阶段的救援任务,其目标函数可以表示为:
| $ \left\{ {\begin{array}{*{20}{c}} {{T_1} = \max \left( {t_1^n,t_2^n,...,t_i^n} \right)} \text{,}\\ {t_i^n = \min \left( {t_{i1}^n,t_{i2}^n,...,t_{ik}^n} \right)} \text{。} \end{array}} \right. $ | (6) |
式(6)显示了第一阶段救援需要的最短时间,其中
| $ t_{ik}^n = t_{ik}^m = m \cdot \frac{l}{{V_{ik}^{ \to l}}} + \left( {m - 1} \right) \cdot \frac{l}{{V_{ik}^{ \leftarrow l}}}\text{。} $ | (7) |
假设第n个应急物资调度小周期的货运运输量用qn来表示,经过n−1个应急物资调度小周期之后,剩余的待救援人数为
| $ q_{ik}^n = \min \left( {{Q_{ik}},X_1^{n - 1}} \right)\text{。} $ | (8) |
船舶应急物资运到海上船舶事故地点之后,需要在事故地点停留一段时间,并进行救援工作,等到消耗型物资消耗完之后,则由下一班次的应急物资运输船舶提供,以确保应急物资能够持续供应。应急物资运输调度的成本主要在于应急基地的位置、运输装备的船舶以及装备停留的时间,因此第二阶段的目标函数可以用式(9)表示。式中,Cij的计算方法如式(10)所示,平均成本的计算公式如式(11)和式(12)所示。
| $ C = \min \left( {{C_{11}} + {C_{12}} + ... + {C_{ij}}} \right)\text{,} $ | (9) |
| $ {C_{ij}} = \sum\nolimits_{{x_{ik}}}^{{x_{ij}}} {q_{ij}^{{x_{ij}}}{c_{ij}} + \sum\nolimits_{{x_{ik}}}^{{x_{ij}}} {\frac{{q_{ij}^{{x_{ij}}}}}{{{V_S}}}} } \cdot c_{ij}^S\text{,} $ | (10) |
| $ \bar C_{ij}^{m - k} = \frac{{c_{ij}^0 + {c_{in}} + q_{ij}^{m - k}{c_{ij}}}}{{q_{ij}^{m - k}}}\text{,} $ | (11) |
| $ {C_{in}} = \frac{{q_{ij}^{m - k}}}{{{V_s}}} \cdot {c_{ij}}\text{。} $ | (12) |
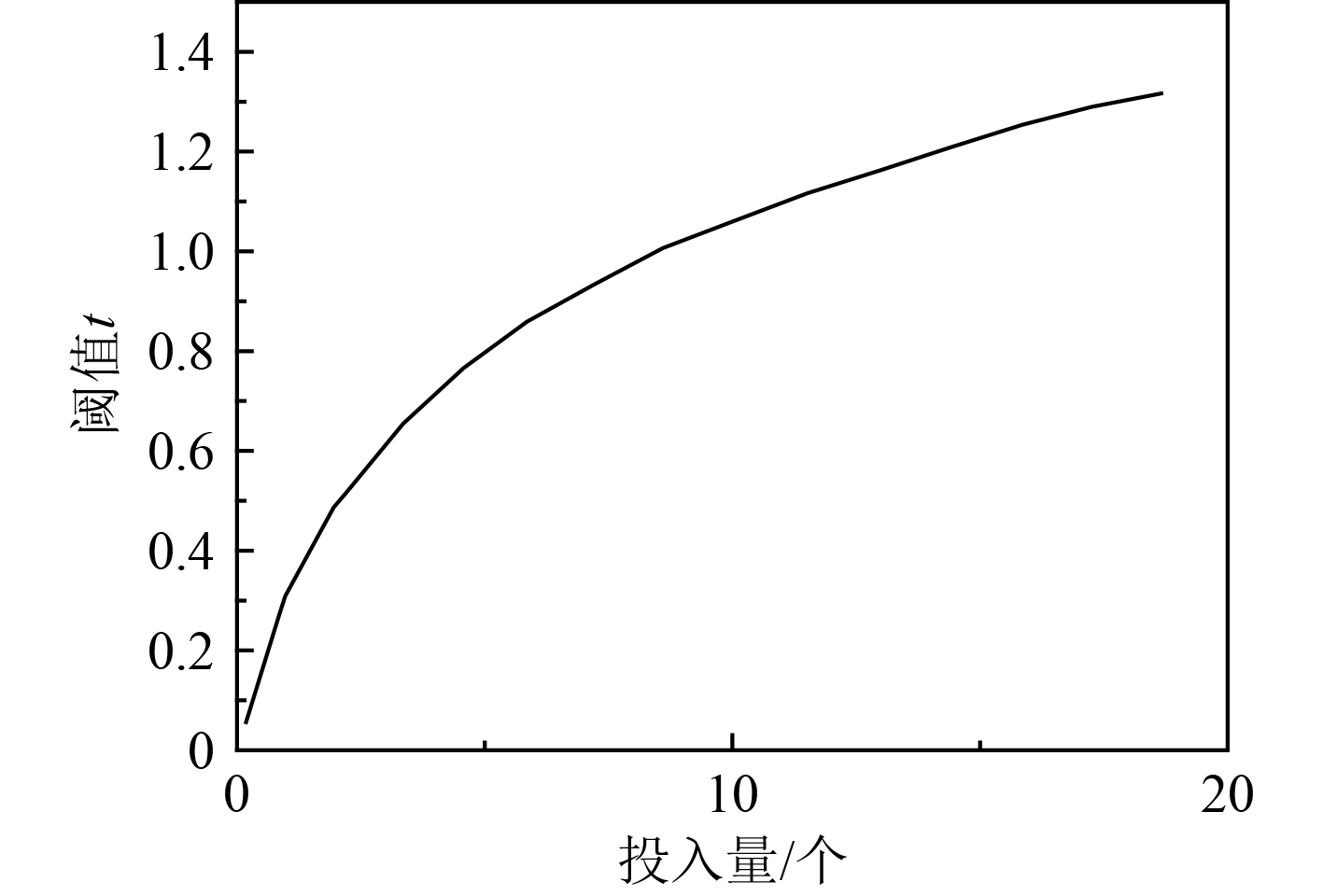
本文研究的船舶应急物资并不只是针对某一种物资,因此研究方法具备通用性。由于海面上船舶事故的实际数据获取相对比较难,因此基于船舶应急物资运输模型进行分析,同时对船舶应急物资运输模型中的部分变量以及函数进行合理假设。实际船舶应急物资的配备量在不同的救援阶段中,其阈值的边际贡献呈现递减现象,即船舶事故救援刚开始的时候,物资供应数据对系统阈值的边际贡献比较大,但是随着应急物资投入量的不断增加,其边际效用不断降低,最终使得经济性很差。应急物资投入量和阈值之间的关系,如图1所示。
|
图 1 应急物资投入量和阈值之间的关系 Fig. 1 Relationship between emergency material input and threshold |
可以看出,应急物资投入量和阈值之间的关系与对数函数十分类似,考虑到实际的应急物资投入量和阈值之间的函数关系复杂且很难获得,并且不同的船舶应急物资,其投入量和系统阈值之间的函数关系也不一样。为了降低计算难度,用3段对数函数描述应急物资投入量和阈值之间的关系,公式为:
| $ {f_1}\left( {{x_1}} \right) = {\log _8}\left( {{x_1} + 1} \right),{x_1} \geqslant 0 \text{,} $ | (13) |
| $ {f_2}\left( {{x_2}} \right) = {\log _{12}}\left( {{x_2} + 1} \right),{x_2} \geqslant 0\text{,} $ | (14) |
| $ {f_3}\left( {{x_3}} \right) = {\log _{15}}\left( {{x_3} + 1} \right),{x_3} \geqslant 0\text{。} $ | (15) |
船舶应急物资运输过程中的损失函数也是一个十分复杂的问题,为了能够更好地分析船舶应急物资运输,本文需要对损失函数进行假设。假设损失函数是线性的,其描述公式为:
| $ D = f\left( {{e_4}} \right) = 10\cdot{e_4}\text{。} $ | (16) |
陆地上通常使用三角模糊数处理应急物资运输调度问题,本文将三角模糊数应用到海面上船舶应急物资调度中,并进行去模糊化处理,以便可以处理不确定环境中的应急物资运输调度问题,并构造出应急物资运输调运所费时间最少的模型。假设存在三角模糊数A,其隶属度可以表示为:
| ${u_A} = \left\{ {\begin{array}{*{20}{l}} {\dfrac{{x - a}}{{b - a}},}&{a \leqslant x \leqslant b,}\\ {\dfrac{{x - c}}{{b - c}},}&{b \leqslant x \leqslant c,}\\ 0,&{{\rm{others }}}。\end{array}} \right.$ | (17) |
当属性的数值比较高时,则a,b,c可以选择较大的数;当属性的数值比较低时,则a,b,c可以选择较小的数;当a,b,c相等时,A则是非模糊数。假设UAL的逆函数为GAL;UAR的逆函数为GAR,则模糊数A的左右期望值的计算方式,分别如式(18)和式(19)所示,则模糊数的整体期望数值的计算方法如式(20)所示。
| $ {I_L}\left( A \right) = \int_0^1 {{G_{AL}}\left( y \right){\rm{d}}y} \text{,} $ | (18) |
| $ {I_R}\left( A \right) = \int_0^1 {{G_{AR}}\left( y \right)}{\rm{ d}}y\text{,} $ | (19) |
| $ {I_T}\left( A \right) = \frac{{{I_L}\left( A \right) + {I_R}\left( A \right)}}{2}\text{。} $ | (20) |
本文进行船舶应急物资联动调度仿真过程中,假定本次参与应急物资运输调度的仓库有4个,分别为S1,S2,S3和S4,并且需要救援的地点有2个,分别为D1和D2。2个救援地点距离4个应急物资运输调度仓库的距离如表1所示。每个应急物资运输调度仓库配有A类和B类2种类型的运输调度船舶,并且A类运输船舶的运载量为300 t,航行速度为8 kn;B类船舶的运载量为100 t,航行速度为20 kn。
|
|
表 1 应急仓库距离事故点的距离 Tab.1 Distance from emergency warehouse to accident point |
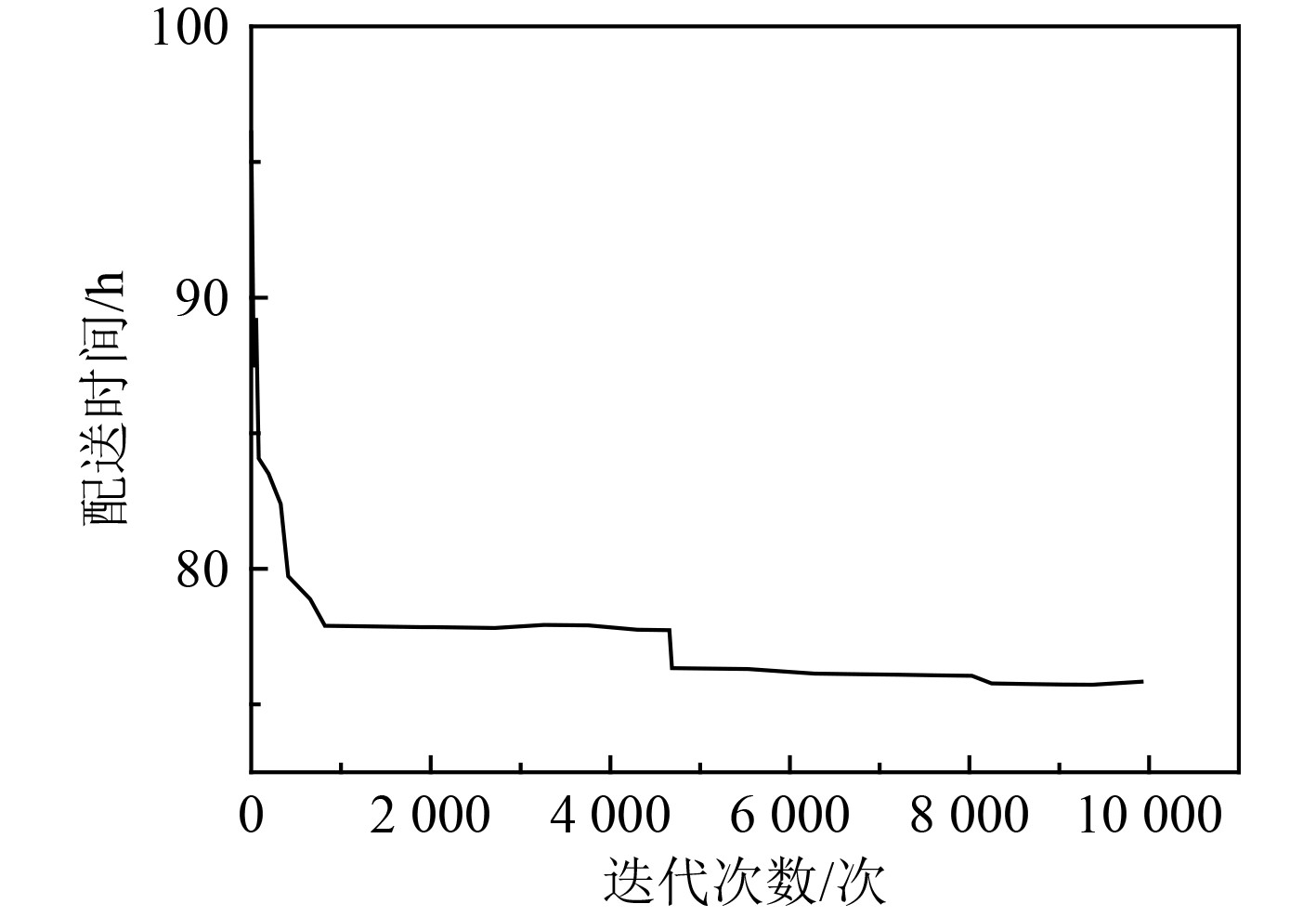
作为启发算法的一种,遗传算法在进行求解的过程中,无法得出最优的全局解。为了能够避开这种局部最优解,使用多次求解并选择最优的解的方法,以避免产生局部最优的情况。完成该算法的设计之后,然后对算法进行运算,配送时间和迭代次数之间的关系如图2所示。
|
图 2 配送时间和迭代次数之间的关系 Fig. 2 Relationship between delivery time and iterations |
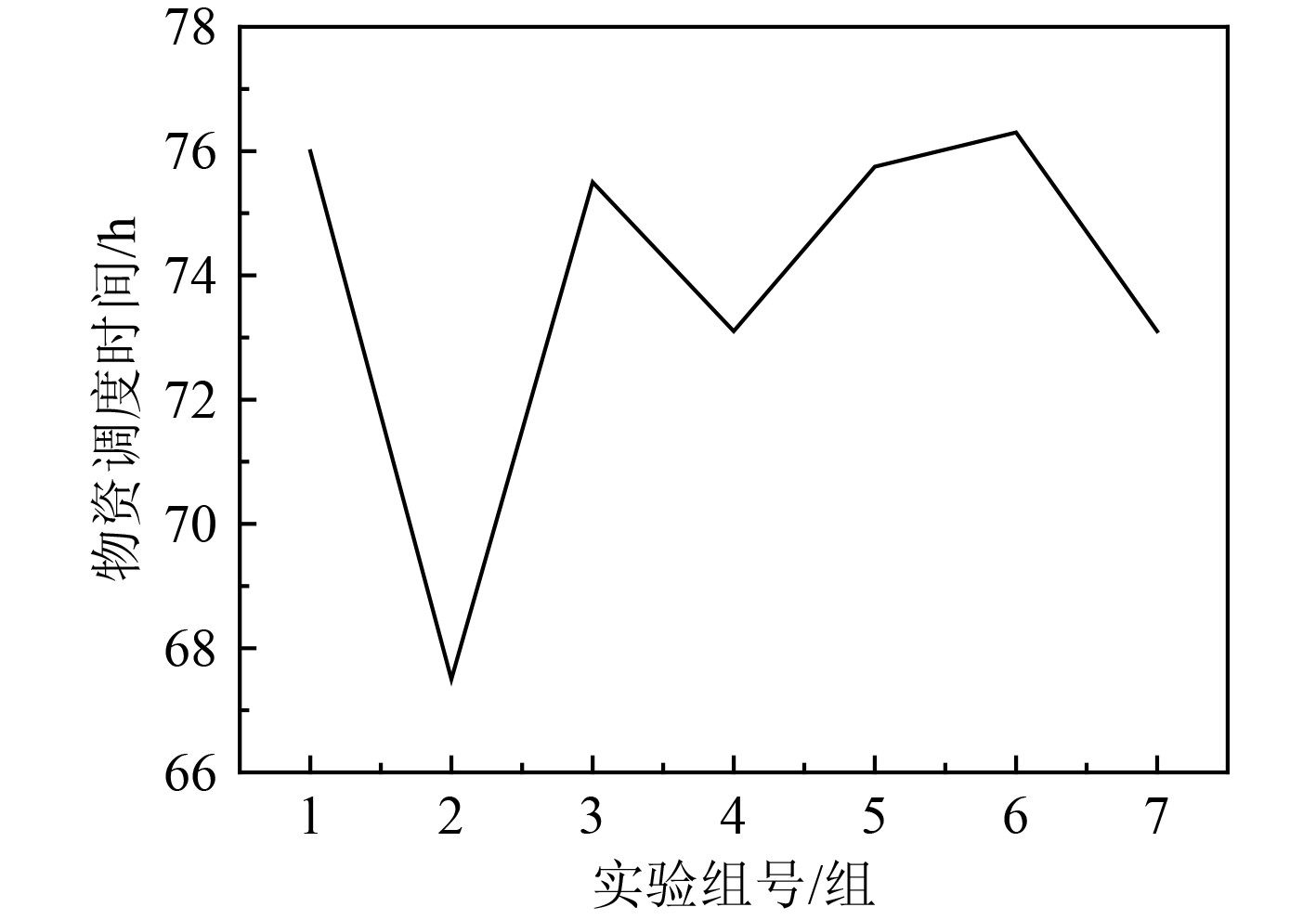
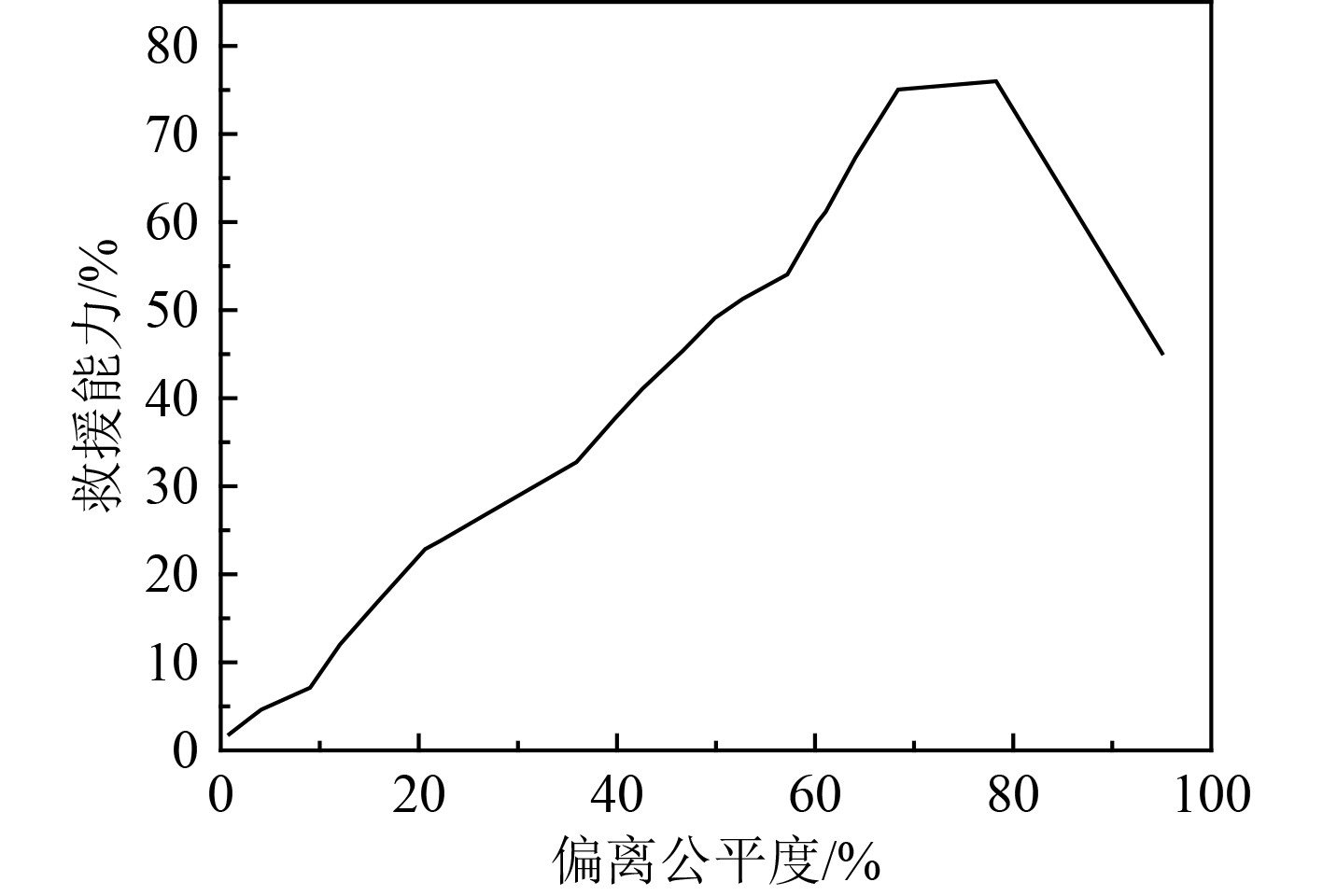
将遗传算法的迭代次数固定为10000次,在多次解算的过程中,得到了7次的解算结果,如图3所示。可以看出,7次迭代结果中,最短的应急物资运输调度时间为67.5 h,图4为应急救援能力和偏离公平度之间的关系。
|
图 3 不同实验组号下的物资调度时间 Fig. 3 Material scheduling time under different experimental group numbers |
|
图 4 应急救援能力和偏离公平度之间的关系 Fig. 4 Relationship between emergency rescue capability and deviation from fairness |
随着国家社会对船舶应急物资的重视,船舶应急物资运输调度配置系统不断得到完善,这使得海面上船舶事故所产生的损失不断地降低。本文对船舶应急物资配置调度方法进行研究,对降低船舶事故产生的损失有实际指导意义。
| [1] |
李松, 陈莹珍, 李海伟, 等. 大型海上船舶溢油事故应急物资联动调度优化研究[J]. 水道港口, 2019(40): 735-741. DOI:10.3969/j.issn.1005-8443.2019.06.018 |
| [2] |
苏鑫, 刘桂云, 王慈云. 基于超网络理论的海上溢油事故应急物资区域调度[J]. 中国航海, 2020(43): 110-115. DOI:10.3969/j.issn.1000-4653.2020.04.019 |
| [3] |
李攀, 周兆军, 孙晓叶, 等. 基于强化学习的应急物资动态模型配送算法优化[J]. 科学技术与工程, 2022(22): 1107-1116. DOI:10.3969/j.issn.1671-1815.2022.03.032 |
| [4] |
王军, 陈金晶, 陆永样. 基于贪婪算法的水上应急物资协同调度优化方法[J]. 安全与环境学报, 2013(13): 254-258. |
| [5] |
陈金晶. 基于调度优先权的海上多物资应急调度方法[J]. 浙江海洋学院学报, 2014(33): 377-381. |
| [6] |
栾志玲. 基于物联网的海上应急物资运输路径优化仿真[J]. 舰船科学技术, 2019, 41(14): 202-204. |
| [7] |
王军, 陈金晶, 陆永样, 等. 基于需求连的海上应急物资协同调度方法研究[J]. 计算机应用研究, 2013(30): 1727-1730. |
| [8] |
张聆晔, 吕靖, 梁孝, 等. 考虑多事故点的海上重大事故应急物资优化调度[J]. 系统工程, 2021(39): 103-114. |
| [9] |
杜坤, 王堃. 面向重大灾害的船舶应急物流运输线路规划方法[J]. 舰船科学技术, 2021, 43(4): 208-210. |
| [10] |
吴凤媛. 智能网络下船舶海上应急物流路径规划方法[J]. 舰船科学技术, 2018(40): 172-174. |
 2023, Vol. 45
2023, Vol. 45
