船舶控制系统必须控制好航向使船行驶在一条线上,尽可能地减少燃油消耗,航行中保持船速稳定并不困难,但能否使之灵活地转向则至关重要,保持航向也就是航线稳定,是保证航行安全、经济合理地完成各种任务的一个主要因素[1-3]。当在预定的路线上碰到障碍物或者其他船舶时,或经由受限航道进出港,便要求在适当的时候,将航速、方向进行调整,即船舶需要机动能力强。稳定性与操纵性是体现船舶航行性能最主要的指标。本文介绍船舶导航设备中主要应用的几种船舵控制系统,其中以导航系统最为普遍,即船舶的自动导航系统。本文在总结已有研究成果基础上建立一种新的数学模型,即基于神经网络与模糊逻辑相结合的自适应控制方法。船舶自动舵机控制技术与控制理论发展有重大关联,由于可以很方便地应用于各种不同类型和大小的船上,因此得到了广泛应用。这种模型的特点是:构造简单、易于利用标准试验资料建立模型。由于它不需要对舵信号做任何处理,因而可以实现较高精度的控制效果,因此船用航向调节器多采用Nomoto模式。这些不确定性会引起船舶运动参数变化而使控制系统不稳定或产生较大误差,考虑船舶水力的非线性问题,和航行时受海浪、海流和其他因素的影响,航向控制是不确定的,从而使船舶操纵问题成为一种非线性问题。现在的反馈线性化法比传统的泰勒推广法有显著的提高,在此基础上,采用线性控制理论对其进行分析与设计。当系统的实际工作状况与选定的均衡状态相差较大时,将产生较大的误差,但在线性化处理中,不能忽视高阶的非线性。这样,可以保证线性化处理过程中的精确性,然后就可以在全部区域进行线性化处理[4-5]。非线性系统需要满足一定的条件,比如差分配对,以实现准确的反馈线性化,从而限制精确的反馈线性。
1 船舶航向控制系统与数学模型在20世纪20年代,美国、德国先后研制出了首代无人驾驶自动驾驶仪器,但因技术上的局限性,其控制精度不高,仅适用于精度不高的教学。20世纪50年代,由于电子与伺服系统的发展与应用,第二代无人驾驶仪-PID舵机的问世,使其控制精度得到了极大改善。当船速、水深、风、浪、流等因素发生改变时,必须对其进行人工调节。20世纪60、70年代,将自适应控制技术引入到船舶的航向控制中,从而产生了自适应舵机。瑞典的J. Astrom等在海洋中做了一次实际的船舶试验,实践证明,这种转向器在海洋环境中仍能工作,适应能力强。从20世纪80年代开始,专家控制、模糊控制、神经网络控制等技术在船舶的航行控制中得到了广泛应用。
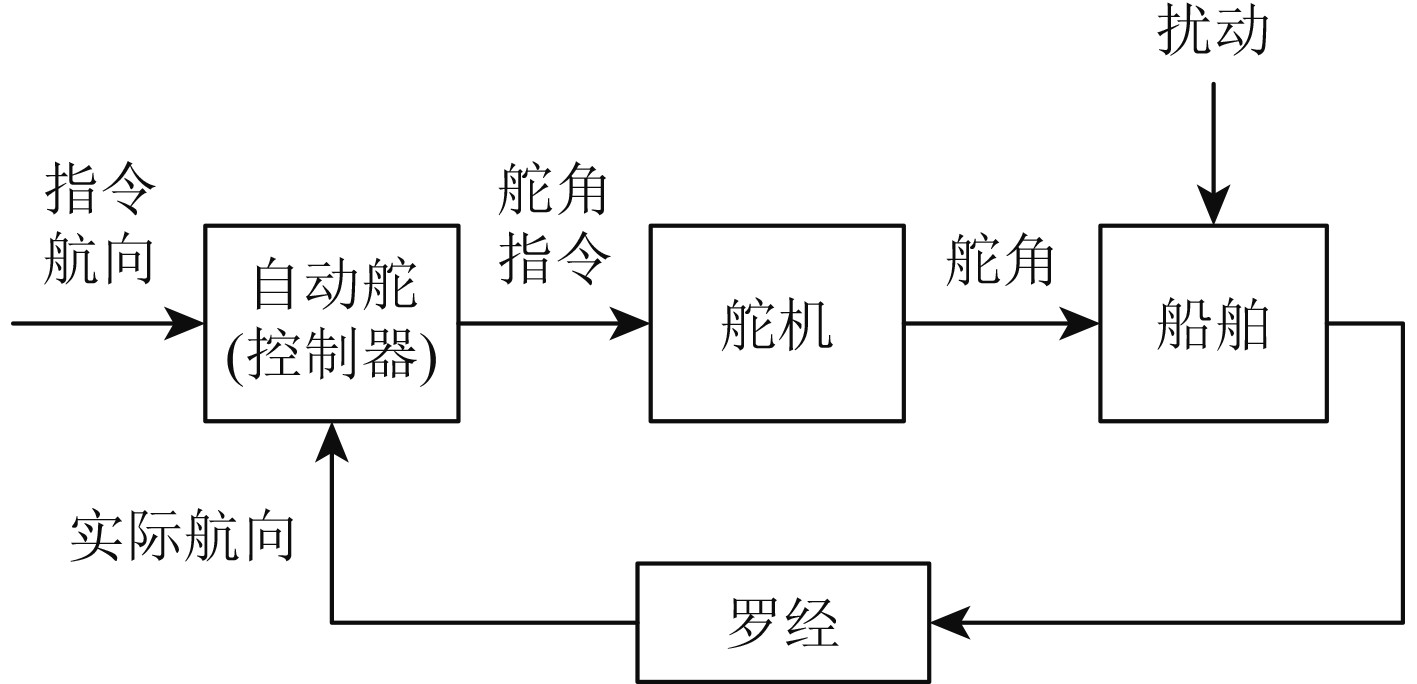
1.1 船舶航向控制原理船舶航向控制的主要任务是方向导向与方向追踪,舵机是用于操纵船舶航行方向的常用设备,船在地图上显示了它的方向,船舶的航向一般用罗盘来测定。当控制器收到船舶的航向控制指令后,控制器会在经过一定的运算后,给出相应的舵角指令。如图1所示,舵机根据输入的舵角指令来调整船舵角度,由于舵机的作用,轮船改变航向有一个完整的流程周期。
|
图 1 船舶航向控制 Fig. 1 Ship heading control |
在船舶航向控制器的归一化数学模式设计过程中,可采用一阶线性化数学模型对船舶航向控制系统进行描述:
| $ \dfrac{{{{r}}\left( {{s}} \right)}}{{\delta \left( {{s}} \right)}} = \dfrac{K}{{\left( {1 + {T_{}}{\text{s}}} \right)}} \text{,} $ |
即
| $ T{{r}} + {{r}} = K\delta \text{。} $ |
式中:r为摇摆速度;δ为舵角;T为时间常量;K为舵面增益。由于船舶的体积和水力的非线性,所以用H(r)代替方程中的 r,用于描述船舶的非线性操作性能,即
| $ H\left( {{r}} \right) = \alpha {{{r}}^3} + {{r}} {。} $ |
式中,α为逆推-系数。由式中的H(r)代之,从而获得对应的逆推-非线性船舶运动模型:
| $ T{{r}} + \alpha {{{r}}^{{3}}} + {{r}} = K\delta {。} $ |
设Ψ为船舶航向,通过归一化分析可以得到如下的方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {\psi = {{r}}},\\ {{{r}} = -\dfrac{{{1}}}{{{T}}}\left( {{{r}} + \alpha {{{r}}^3}} \right) + \dfrac{K}{T}\delta } 。\end{array}} \right. $ |
同时,由于船舶在海上航行时经常受到风、浪、电等外界因素的影响,所以航向控制是一个不确定的模型。
| $ \left\{ {\begin{array}{*{20}{l}} {\psi = {{r}}} ,\\ {{{r}} = - \dfrac{{{1}}}{{{T}}}\left( {{{r}} + \alpha {{{r}}^3}} \right) + \dfrac{K}{T}\delta + \Delta } 。\end{array}} \right. $ |
一般情况下,Δ外部扰动是有界的,这里假定它的边界是不可知的:
| $ \left| \Delta \right| \leqslant {{p}} \text{,} $ |
其中,p为未知的常数。
2 船舶航向控制法 2.1 李雅普诺夫稳定性1892年,俄罗斯李雅普诺夫运用状态矢量描述法,建立了一种可用于单一变量、常数、线性系统、多变量、时变的方法,李雅普诺夫理论在多个稳定概念的基础上,给出了2种评价系统稳定性的方法:一是利用微分方程对系统的稳定性进行评价,即李雅普诺夫法或间接法;二是采用李雅普诺夫函数对整个航向控制系统的稳定性进行分析,也就是所谓的直接法。间接方法的使用受限于有限元方法,因为需要求解微分方程,且不便于求解。由于直接方法无需求解系统的微分方程,使得系统的稳定性分析变得十分容易,因而被广泛采用。
在经典力学中,随着时间的推移,系统的能量会随着时间的推移而逐渐衰减,最终会达到一个平衡。李雅普诺夫认为,可以建立一种与系统状态、时间有关的虚能函数,也就是李雅普诺夫函数。李雅普诺夫方程是一类具有标量性质的数学模型,如果能量始终大于0,那么它就是一个正定的函数,利用李雅普诺夫方程导出了能量衰减的公式。第2种方法是利用李雅普诺夫函数,不需要求解系统的状态方程,就可以直接估计出平衡状态的稳定性。
2.2 控制器的结构设计根据系统的指标要求,假设存在状态变量x1=ψ,x2=r;选择状态变量x=x1−r;可以用严格的反馈格式来表示,利用输出与输入控制参量的关联性,可以得到:
| $ \begin{gathered} {{{x}}_{{1}}} = {{{x}}_{{2}}} ,\\ {{{x}}_{{2}}} = - \dfrac{1}{T}\left( {{{{x}}_1} + \alpha {{{x}}_{{2}}}^3} \right) + \dfrac{K}{T}{{u}} + \Delta ,\\ {{y}} = {{{x}}_{{1}}}。\\ \end{gathered} $ |
步骤1 可以假设系统的初始船舶航向为x0,由于收到外部干扰,所以实际会产生一定的误差值为
| $ {{{z}}_{{1}}} = {{{x}}_1} - {{{x}}_0} {,} $ |
可以进一步假设系统存在虚拟控制量x2,则
| $ {{{z}}_{}} = {{{x}}_2} - \varphi {\left( {{{{z}}_{{1}}}\times{{{z}}_2}} \right)_{}} {,} $ |
其中,z2为一个新的状态变量。
| $ \begin{gathered} {{{z}}_{{2}}} = {{{x}}_2} - {\phi _{}}= \\ - \dfrac{1}{T}\left( {{{{x}}_2} + \alpha {{{x}}_2}^3} \right) + \dfrac{K}{T}{{u}} - \phi + \Delta = \\ - \dfrac{1}{T}\left( {{{{x}}_2} + \alpha {{{x}}_2}^3} \right) + {{{c}}_1}{{{z}}_1} + \dfrac{K}{T}{{u}} + \Delta。\\ \end{gathered} $ |
定义Lyapunov函数:
| $ {{V}}_{{2}}\left({{z}}_{1}{,}{{z}}_{{2}}\right)=\dfrac{1}{2}{{z}}_{1}^{2}+\dfrac{1}{2}{{z}}_{2}^{2} {,} $ |
可得:
| $\begin{aligned}[b] {{{V}}_{{2}}} =& {{{V}}_{\text{1}}} + {z_2} \cdot \left[ { - \dfrac{1}{T}\left( {{x_2} + \alpha x_2^3} \right) + \dfrac{K}{T}u + {c_1}{z_1}} \right] =\\ &{{{V}}_{\text{1}}} + {z_2} \cdot \left[ { - \dfrac{1}{T}\left( {{x_2} + \alpha x_2^3} \right) + \dfrac{K}{T}u + {c_1}{x_2}} \right] \text{。} \end{aligned} $ |
步骤2 引入一个非线性的阻尼项,以补偿方程中的不确定性。
| $ {{u}} = - \dfrac{T}{K} \left[ {{{{z}}_1} + \left[ {{{{c}}_{{1}}}^{} - \dfrac{1}{T}} \right] \cdot {{{x}}_2} - \dfrac{\alpha }{T} \cdot {{x}}_2^3 + \left( {{{{c}}_2} + {{k}}} \right) \cdot {{{z}}_2}} \right] 。$ |
式中,k>0为设计的参数。
3 非线性船舶航向控制律设计 3.1 船舶自适应非线性航向保持控制律设计为了满足以后的设计要求,采用如下2种状态变量x1=Ψ,x2=Ψ',而变量u=δ。由于船在不同的水深下,航速会发生变化,故将模型中的参数用T,K,α等作为不确定的常数,从而使方程的状态空间形式能满足以后的设计要求,令控制变量u=8。由于水深、船舶装载和速度的改变,使船舶的操纵运动模式参数发生改变,故将模型参数T,K,α看作是一个未知的常量,可以用以下的状态空间公式表示:
| $ \begin{array}{l}\stackrel{\cdot }{{x}}={{x}}_{2},\\ \stackrel{\cdot }{{{x}}_{{2}}}={\theta }_{0}{u}+{\displaystyle \sum _{{j}=1}^{2}{\theta }_{{j}}{\varphi }_{2{,}{j}}\left({{x}}_{2}\right)}。\end{array} $ |
式中:θ0=K/T,即所谓的增益,当船舶的直线运动稳定时,T>0;如果直线运动时船舶的稳定性不足,那么方程中的不确定性控制增益θ0则会变得更加不确定,那么,航线控制系统就变成一个不确定常量的非线性系统。其控制目的是通过对舰船进行状态反馈的自适应控制,使船舶航向Ψ保持在指令航向上。
3.2 船舶自适应鲁棒非线性航向跟踪控制律设计考虑到波浪干扰,设计一种新的鲁棒自适应非线性跟踪模型为:
| $ \begin{array}{l}\stackrel{\cdot }{{x}}={{x}}_{2},\\ \stackrel{\cdot }{{{x}}_{{2}}}={\theta }_{0}{u}+{\displaystyle \sum _{{j}=1}^{2}{\theta }_{{j}}{\varphi }_{2{,}{j}}\left({{x}}_{2}\right)}+{w}。\end{array}$ |
式中,w可以被认为是海浪引起的扰动项。这样,船舶的实际航向函数为:
| $ {\psi _{{d}}} = \dfrac{{\omega _{{n}}^2}}{{{{{s}}^2} + 2\xi {\omega _{{n}}}{{s}} + \omega _{{n}}^2}}{\psi _{{r}}} {。} $ |
式中:ξ与
本文以航行中的货船为研究对象,对其进行航向控制系统的设计,介绍一种新型的微机控制系统,并对其进行仿真。船长126 m,宽度20.8 m,吃水8.0 m,方差0.681,舵叶面积18.8 m2,排水量14278 m3。建立数学模型,并模拟计算不同风速、风向条件下的影响,并对其动力学特性和规律进行研究。当速度为7.5 kn时,诺尔班船舶的非线性运动模式具有K=0.42 s−1,T=216.73 s,o=30的参数。在此基础上,结合船舶的实际航行状况,设计一种基于模糊逻辑的船舶航向控制系统。将船舶航向控制器的设计参数设定为:c1=0,cz=0.5,λ=0.5,n=0.6。
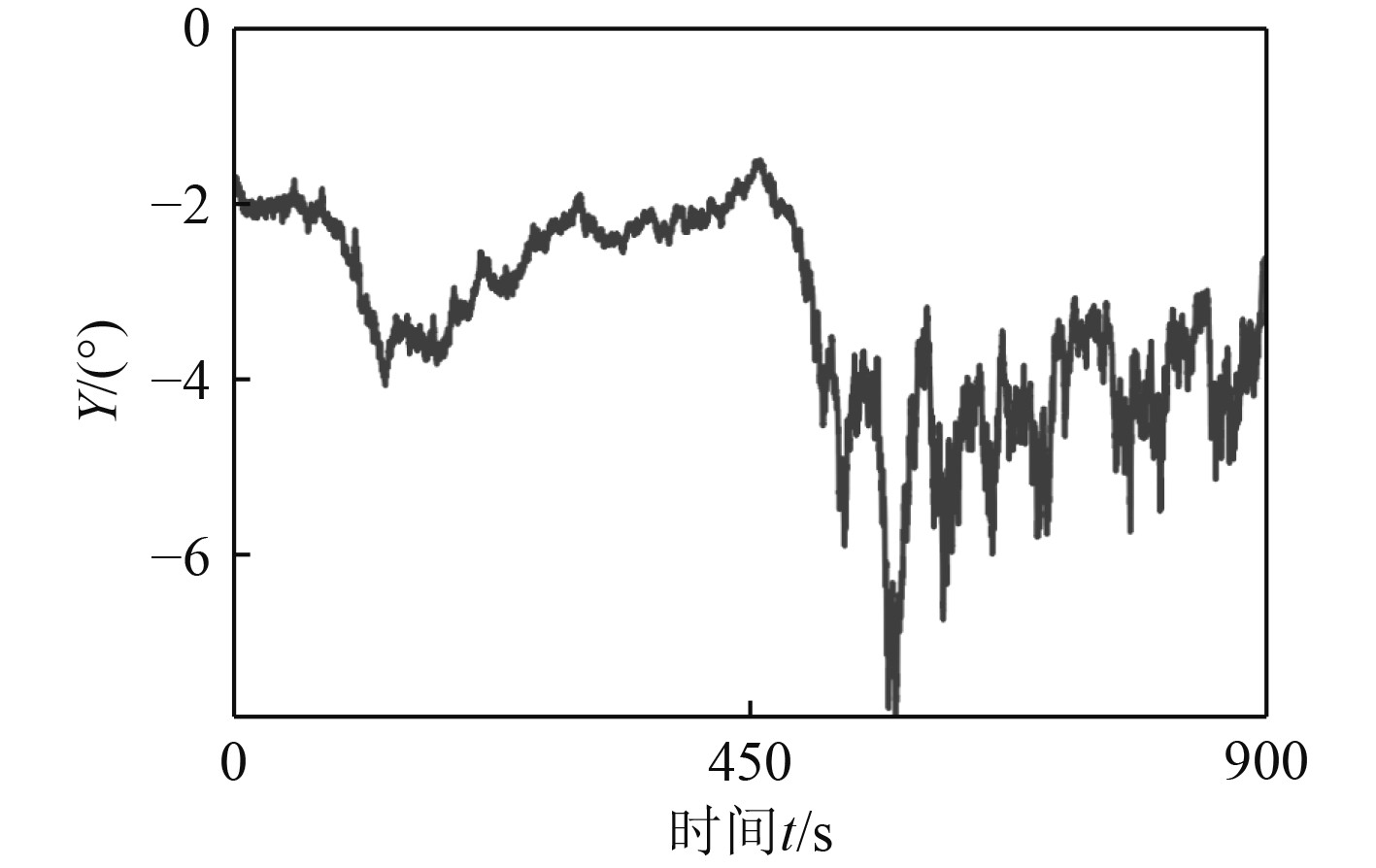
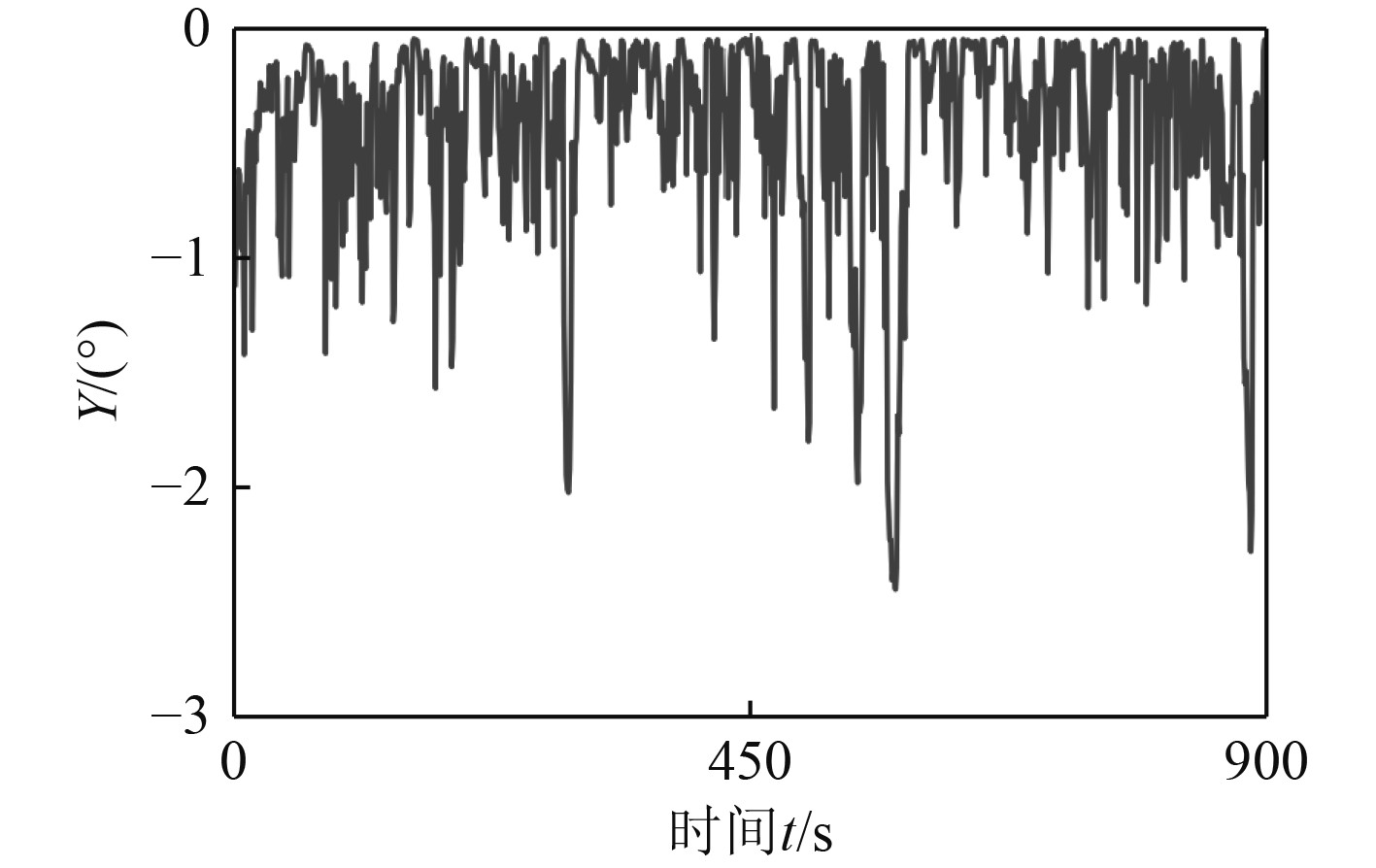
控制舵角δ的变化曲线如图2所示,航向角ψ的变化曲线如图3所示。利用该模型对某大型货轮进行仿真,得出在不同输入条件下,舵面倾角、速度的变化规律,并在各个工况点处调整相应的舵角分布。结果表明:采用积分控制器,舵面的摆动范围可控制在−0.005°~+0.005°,该方法明显降低了舵面的转向角,同时也显示了该方法的有效性。另外,本文还分析了转向角速度、转角变化对系统稳定性和能量消耗的影响。从模拟和调试的程序可以看出,积分系数的取值对舵角的影响比较大,随着外部输入量的减小,舵角的尖峰减小,而舵角的起伏也变得更大;随着外部干扰入射量的增大,舵面的尖峰增大,舵角的起伏增大,使其变得更加平稳。
|
图 2 控制舵角δ的变化曲线 Fig. 2 Change curve of control rudder angle δ |
|
图 3 航向角ψ的变化曲线 Fig. 3 Change curve of the heading angle ψ |
本文以一种新的逆推法为基础,建立一种新的非线性航向控制方法。采用非线性阻尼方法,考虑风、浪、海流等因素的影响,建立一种非线性的船舶航行控制系统。利用Lyapunov函数,证明该方法能保证闭环系统的最终一致边界。因为所引进的积分项是角偏移和角速度积分,其实质是角和比例的积分,通过积分控制可以消除偏移,使系统的性能得到改善。
| [1] |
张凯, 李铁山, 秦奇, 等. 神经网络和二阶滑模算法在船舶航向控制中的应用[J]. 中国水运(下半月), 2016,16(11): 24–26.
|
| [2] |
伊戈, 刘忠, 张建强, 等. 基于改进终端滑模控制的USV航向跟踪控制方法[J]. 电光与控制, 2020, 27(10): 12-16+21. |
| [3] |
曹斌, 苏珂, 原帅, 等. 基于微分代数神经网络的含新能源区域电网端口动态特性学习方法[J]. 中国电力: 1–7 [2023-01-30].
|
| [4] |
白鹤, 赵明侠, 袁一如, 等. 基于GA-BP神经网络算法的FDM 3D打印制件拉伸性能预测[J]. 塑料工业, 2022, 50(9): 192-197. |
| [5] |
安顺, 何燕, 王龙金. 基于反步自适应控制算法的船舶航向控制方法[J]. 机电设备, 2020, 37(6): 65-69. DOI:10.16443/j.cnki.31-1420.2020.06.014 |
 2023, Vol. 45
2023, Vol. 45
