2. 中科院南京天文仪器研制中心,江苏 南京 210018;
3. 中科院南京天文仪器有限公司,江苏 南京 210018
2. CAS Nanjing Astronomical Instruments Research Center, Nanjing 210018, China;
3. CAS Nanjing Astronomical Instruments Co. Ltd., Nanjing 210018, China
在海洋监测中,由于红外遥感器可以在夜间工作,因此是一种全天候的遥感监测方法。由于受到海洋环境条件的制约,红外遥感技术在海洋监测中受到一定的限制,云、雾等环境对红外遥感的影响很大,因此,研发能够对其几何参数和成像质量实现集成化、高效率、高精度检测的设备成为当务之急。可见光的空间分辨率比较高,因此可见光能够在更小尺度上对目标进行观测。此外可见光获取的图像信息更加直观,不需要复杂的计算就可以对目标进行定位[1-3]。本文基于C#设计船舶光学载荷参数测试系统,对采集的数据进行实时分析计算得到所需结果,对船舶光学成像系统的发展有积极促进作用。
1 海面动态目标光学特性分析 1.1 船舶海面几何建模海面上的弱小船舶目标以及船舶航行所产生的尾迹目标是两类海面弱小动态目标,在对这两类目标进行可见光探测过程中,必须要得到该弱小动态目标和海面背景的直观表达,这使得在对这两类目标进行探测以及探测系统设计的过程中需要对海面进行几何建模,并对不同光照以及大气下的光学散射特性进行分析。在对海面进行光照散射以及成像特性进行研究的过程中,必须掌握海面的几何特性,海面的几何特性主要包括海面的高低起伏以及功率谱等。本文采用海谱法对海面进行几何建模,即是对海面形状以及相关参数进行解析的过程。作为一种功率谱,海谱是一种用来描述海面的方法。将描述海面起伏高度变化的函数进行傅里叶变换得到海谱,因此海谱是一种描述粗糙面的统计量,表示海浪的能量在不同波频下的分布情况。在对海浪进行二维模型的构造过程中,不但要考虑海浪的能量,还需要考虑海风以及海面的各向异性,同时添加海浪的方向数学模型,并和海谱相融合,最后得到海浪谱。功率谱可以用下式表示[4]:
| $ \int_0^\infty {S\left( \omega \right)} {\rm{d}}\omega = \int_0^\infty {S\left( k \right){\rm{d}}k = {\sigma ^2}} \text{。} $ | (1) |
通过代入方向角θ,可以将方向函数引入到数学模型当中,如下式:
| $ k = \left( {k\cos \theta ,k\sin \theta } \right) = \left( {{k_x},{k_y}} \right)\text{。} $ | (2) |
对功率谱函数进行积分计算,则可以得到海浪的能量,同时考虑到方向函数产生的影响,则可以得到转换关系如下式:
| $ S\left( {\omega ,\theta } \right){\rm{d}}\omega {\rm{d}}\theta = S\left( {k,\theta } \right)k{\rm{d}}k{\rm{d}}\theta = S\left( {{k_x},{k_y}} \right){\rm{d}}{k_x}{\rm{d}}{k_y}\text{。} $ | (3) |
忽略海浪和海浪之间的非线性作用之后,k和ω之间的转换关系可以表示为:
| $ {\omega ^2} = \tau k\left( {1 + \frac{{{k^2}}}{{k_m^2}}} \right)\text{。} $ | (4) |
式中,τ为海水张力。对式(3)中的各个方向进行积分计算,则可以得到下式:
| $ S\left( \omega \right) = \int_0^{2\text{π} } {S\left( {\omega ,\theta } \right){\rm{d}}\theta } \text{,} $ | (5) |
| $ S\left( k \right) = \int_0^{2{\text π} } {S\left( {k,\theta } \right)} {\rm{d}}\theta \text{,} $ | (6) |
| $ S\left( {{k_x}} \right) = \int_0^\infty {S\left( {{k_x},{k_y}} \right){\rm{d}}{k_y}} \text{。} $ | (7) |
式中:S(ω)为海浪能量随频率ω变化情况;S(k)为海浪能量随波数k的变化情况;S(kx)为在x方向上海浪能量随波数变化情况。作为一个经验式的海浪谱模型,Neumann海浪谱模型可以用来描述不断变化的海浪信息。Neumann海浪谱模型通过检测海面上单个波的高度以及周期,并将所有的海浪波进行叠加,则最终可以获得海浪谱的数学模型,如下式:
| $ S\left( \omega \right) = C\frac{\text{π} }{{2{\omega ^6}}}{e^{ - \frac{{2{g^2}}}{{{\omega ^2}U_{7.5}^2}}}}\text{。} $ | (8) |
式中:C=3.05;U7.5为海面上方7.5 m处的海风速度。频谱的频率和周期分别如下式:
| $ {\omega _p} = \sqrt {\frac{2}{3}} \frac{g}{{{U_{7.5}}}}\text{,} $ | (9) |
| $ {T_p} = \sqrt 6 {\text π} \frac{{{U_{7.5}}}}{g}。$ | (10) |
图1给出在海面上方7.5 m处,海风速度为16 m/s和12 m/s情况下的Neumann海浪谱曲线波形。可以看出,随着海面风速的提升,海面波浪的高度也会升高,并且波峰朝着低频区域移动。
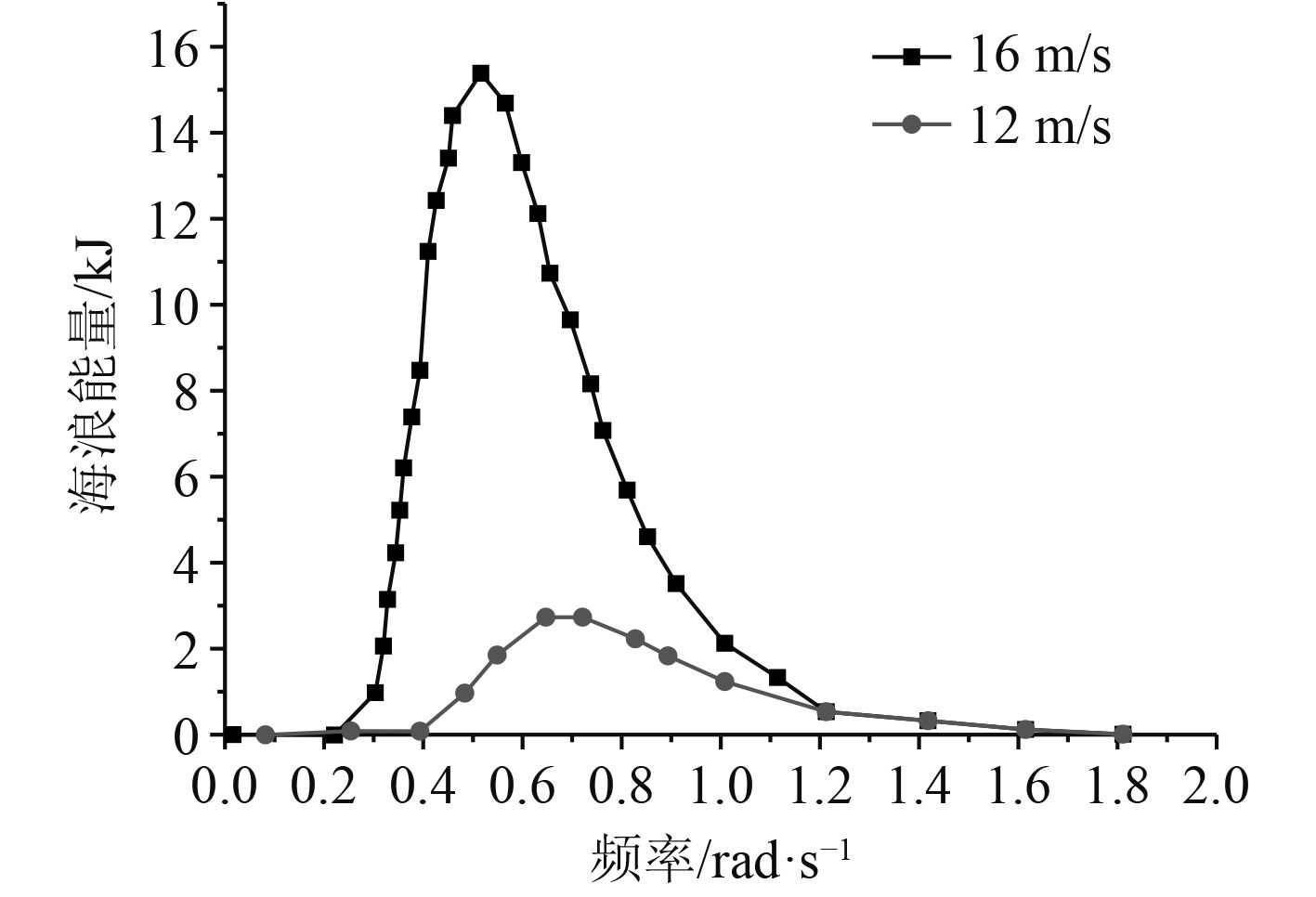
|
图 1 波浪能量随频率的变化情况曲线 Fig. 1 Curve of wave energy changing with frequency |
船舶在航行过程中会产生相应的波纹信息,这种波纹信息被称作尾迹,并且这种尾迹能够在数千米的海面上维持几小时。尾迹的出现给船舶的目标探测提供了一种新的方法,海面上的尾迹信息在船舶海面目标探测中发挥的作用越来越重要。由于尾迹呈一种波浪状态,这导致海面上的尾迹信息处于暗弱的、不显著的状态,因此在实际检测过程中不易察觉。
表面波、湍流以及内波是3种常见的船舶尾迹目标。V型状态的Bragg波和臂型状态的Kelvin波是2种最常见的表面波尾迹。在布拉格作用下张角<10o的表面波为Bragg波;由倾斜和水动力产生的张角约39o的表面波为Kelvin尾迹。考虑到船舶Kelvin尾迹特性比较清晰,因此本文对Kelvin尾迹模型进行构建。在对Kelvin模型进行构建的过程中,可以以点源扰动模型为基础进行理论解析。将船只假设成一个理想的点源,然后使用格林函数分析法对点源进行分析,接着基于一定的边界条件对波高以及海水表面速度进行求解,求解出每个点的航迹模式之后,最终可以得到Kelvin尾迹模型。本文假设船舶沿着x轴的负方向行驶,并且船舶的速度为v,则船舶在航行过程中产生的Kelvin尾迹的波高可以表示为:
| $ \zeta \left( {x,y} \right) = {Re} \int_{ - \tfrac{\text{π} }{2}}^{\tfrac{\text{π} }{2}} {F\left( \theta \right)} {e^{ - i{k_0}{{\sec }^2}\theta \left( {x\cos \theta - y\sin \theta } \right)}}{\rm{d}}\theta \text{。} $ | (11) |
式中,F(θ)为船舶的特征参数。该特征参数和水流强度以及船体倾斜度成正比,其计算方法如下式:
| $ F\left( \theta \right) = \frac{{2{k_0}}}{\text{π} }{\sec ^3}\theta \iint {\frac{{\partial Z\left( {x,z} \right)}}{{\partial x}}{e^{{k_0}\left( {x\sec \theta + z{{\sec }^2}\theta } \right)}}}{\rm{d}}x{\rm{d}}z\text{,} $ | (12) |
式中,Z(x,z)为船舶坐标以及吃水深度的函数,其表示方式如下式:
| $ Z\left( {x,z} \right) = \left\{ {\begin{array}{*{20}{c}} {b\left( {1 - \dfrac{{{x^2}}}{{{l^2}}}} \right)}&{ - d \leqslant z \leqslant 0} \\ 0&{z < - d} \end{array}} \right.。$ | (13) |
不同船速下波浪高度的变化曲线如图2所示。

|
图 2 海面波浪高度的变化曲线 Fig. 2 Variation curve of sea wave height |
光谱响应校准方法可以分成绝对和相对2种,相对光谱响应率是将待测的辐射响应映射到一个已知的标准光谱探测器上,这种方法比较简单,因此不需要知道实际的辐射强度。但是绝对光谱响应率需要先对光谱测试系统进行校准,然后构建出辐射强度和像元灰度值之间的对应关系[6]。假设探测器检测到的光的波长为λ,那么在λ±∆λ波段内的像元响应可以通过下式获得:
| $ S\left( \lambda \right) = \int_{\lambda - \Delta \lambda }^{\lambda + \Delta \lambda } {\frac{{\text{π} \lambda {A_d}}}{{4{F^2}hc}}} \eta \left( \lambda \right){\tau _0}\left( \lambda \right){T_e}L\left( \lambda \right){\rm{d}}\lambda \text{。} $ | (14) |
式中:L(λ)为辐射亮度;Te为积分常量。可以看出,在恒定的积分时间以及λ的窄带范围之内,光照的辐射强度决定了光谱的响应度,并且光照的辐射强度和光谱响应度成正比例关系[7-8]。
光学成像系统通常利用调制传递函数进行分析,光学成像系统的调制度和目标物体调制度的比为MTF,同时随着目标物体空间频率的增加,MTF数值会随之降低。本文假定光学成像系统是线性不变的,并且光学系统导致的模糊一致,同时光学成像系统的响应也是线性的,因此调制传递函数可以定义成扩散函数的模,通过调制传递函数可以对光学成像系统目标空间频率的重建能力进行判断,其计算方法如下式:
| $ MT{F_{opt}}\left( \xi \right) = \frac{2}{\text{π} }\left[ {{{\cos }^{ - 1}}\left( {\frac{{\xi \lambda }}{D}} \right) - \frac{{\xi \lambda }}{D}\sqrt {1 - {{\left( {\frac{{\xi \lambda }}{D}} \right)}^2}} } \right]\text{。} $ | (15) |
光学成像系统除了可以显示目标物体的空间信息之外,还能够反映目标物体光学辐射的分布信息,图像的灰度值之间的差异即是因为目标物体辐射能量值的不同,因此光学图像本身也反映出了物体的温差特性,物体的温差特性是光学成像系统十分重要的特性。根据物体的温差特性可以对目标物体进行检测、识别等操作。本文基于最小可分辨温差以及噪声等效温差2种特性对光学成像系统的温度分辨能力进行分析,最小可分辨温差(MRTD)和噪声等效温差(NETD)的解算方法如下式:
| $MRTD = \dfrac{{\sqrt 2 {{\text π}^2}}}{8}\dfrac{{SN{R_D} \cdot NETD}}{{MTF(\xi )}}{\left( {\dfrac{{{f_T}\beta \Delta {f_{{\rm{{\rm{eye}} }}}}}}{{{t_e}{f_p}\varepsilon \Delta \xi }}} \right)^{1/2}},$ | (16) |
| $ NETD = \frac{{4{F^2} \cdot {\sigma _{total}}}}{{{A_d}{\tau _0}}}{\left( {\int_{{\lambda _1}}^{{\lambda _2}} {\frac{{\partial M\left( {\lambda ,{T_b}} \right)}}{{\partial T}}R\left( \lambda \right){\rm{d}}\lambda } } \right)^{ - 1}}\text{。} $ | (17) |
光学载荷参数是评价光学成像系统性能的重要参数,是光学成像系统检测的重要内容。传统的主观参数测试方法由于测试时间长、成本高,渐渐地被客观测试方法取代。视频法和光度法是2种常用的客观观测方法,但是这2种方法的计算都很复杂并且成本也高。本文针对光学成像系统基于C#设计一种客观的光学参数测试系统。C#是目前使用广泛的一种面向对象的编程语言,使用C#可以非常快速地构建系统界面以及内核算法,大幅度节约设计人员的开发时间。
测试过程中,首先使用待测光学系统进行图像数据的采集,然后基于C#构建出LeNet结构的CNN神经网络系统,接着使用LeNet经典网络对待测光学系统采集到的原始图像数据集进行训练,最终获得参数的测试结果。
光学系统的相对光谱响应率主要是针对光学系统的探测器,可以对光学系统探测器的光谱响应能力进行评价,本文在3~5 μm波长区间内对光学成像系统的探测器进行测试。从图3可以看出,该光学成像系统探测器的光谱响应率的峰值在波长4.5 μm处。
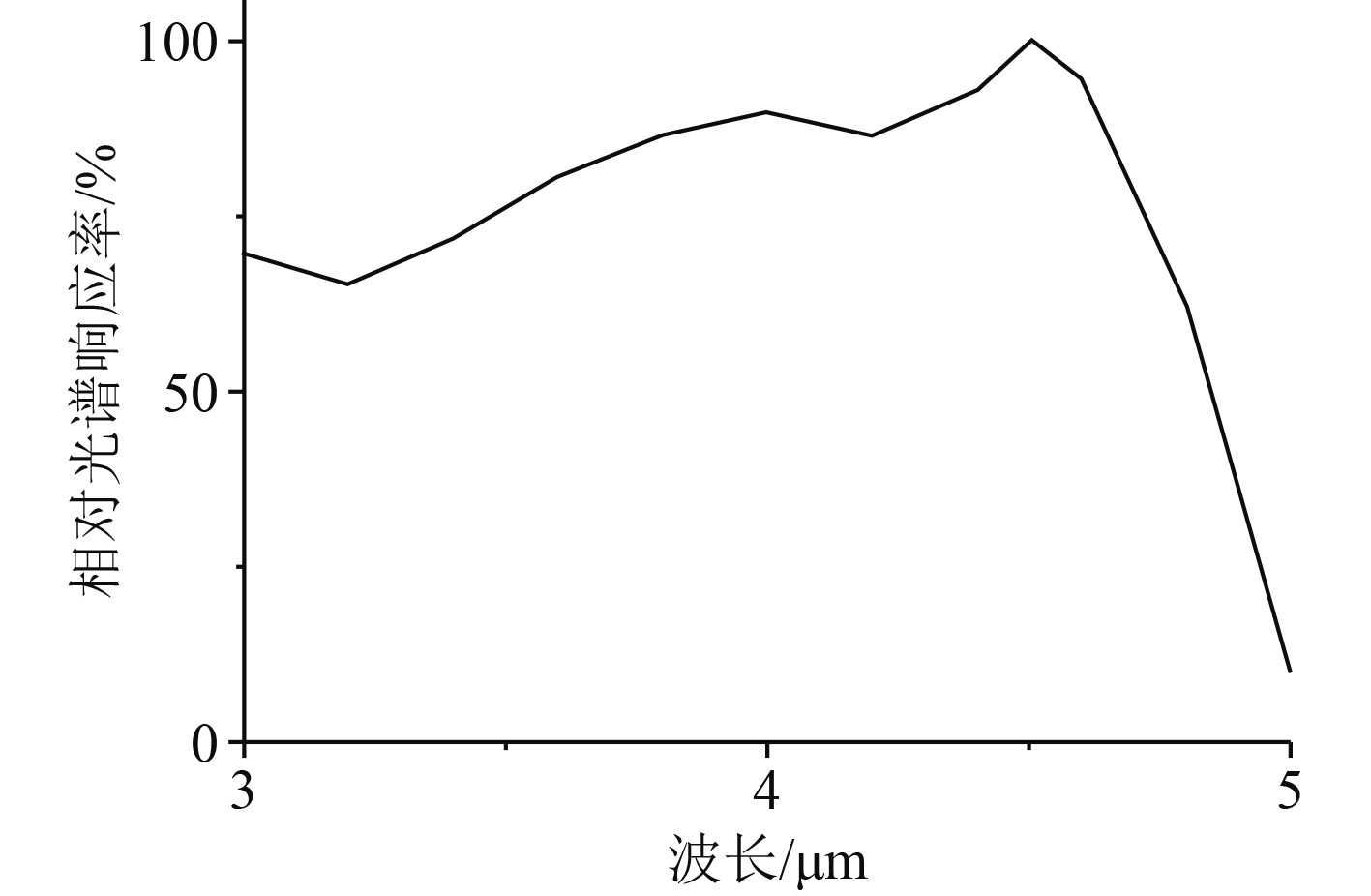
|
图 3 相对光谱响应率随波长的变化曲线 Fig. 3 Curve of relative spectral responsivity with wavelength |
光学成像系统的MTF值是光学成像系统空间分辨能力的评价指标。本文用于测试的红外机芯的的像元间距为17 μm,焦距为34 mm,奈奎斯特频率为29l p/mm,MTF值在不同频率下的测试情况如图4所示。
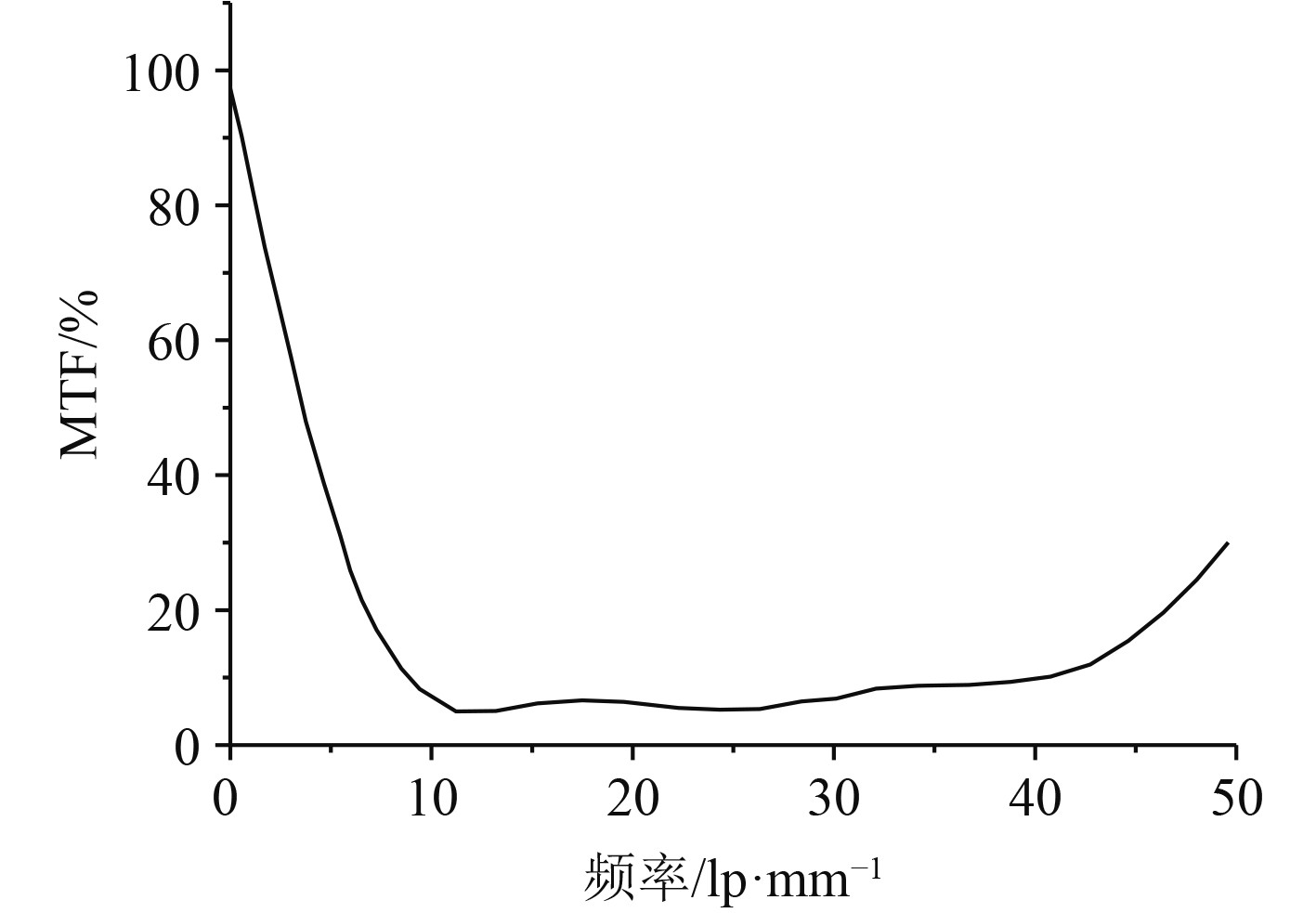
|
图 4 MTF的值随频率的变化情况 Fig. 4 Change of MTF value with frequency |
MRTD参数是用来反映光学成像系统的空间以及温度分辨率的,本文采用基于C#的主观测试方法,测试得到的MRTD和空间频率之间拟合曲线如图5所示。可以看出,MRTD的数值会随着空间频率的变大而增大,由于探测器的采样频率被机芯的像元限制了,因此最终会出现一个截止频率。
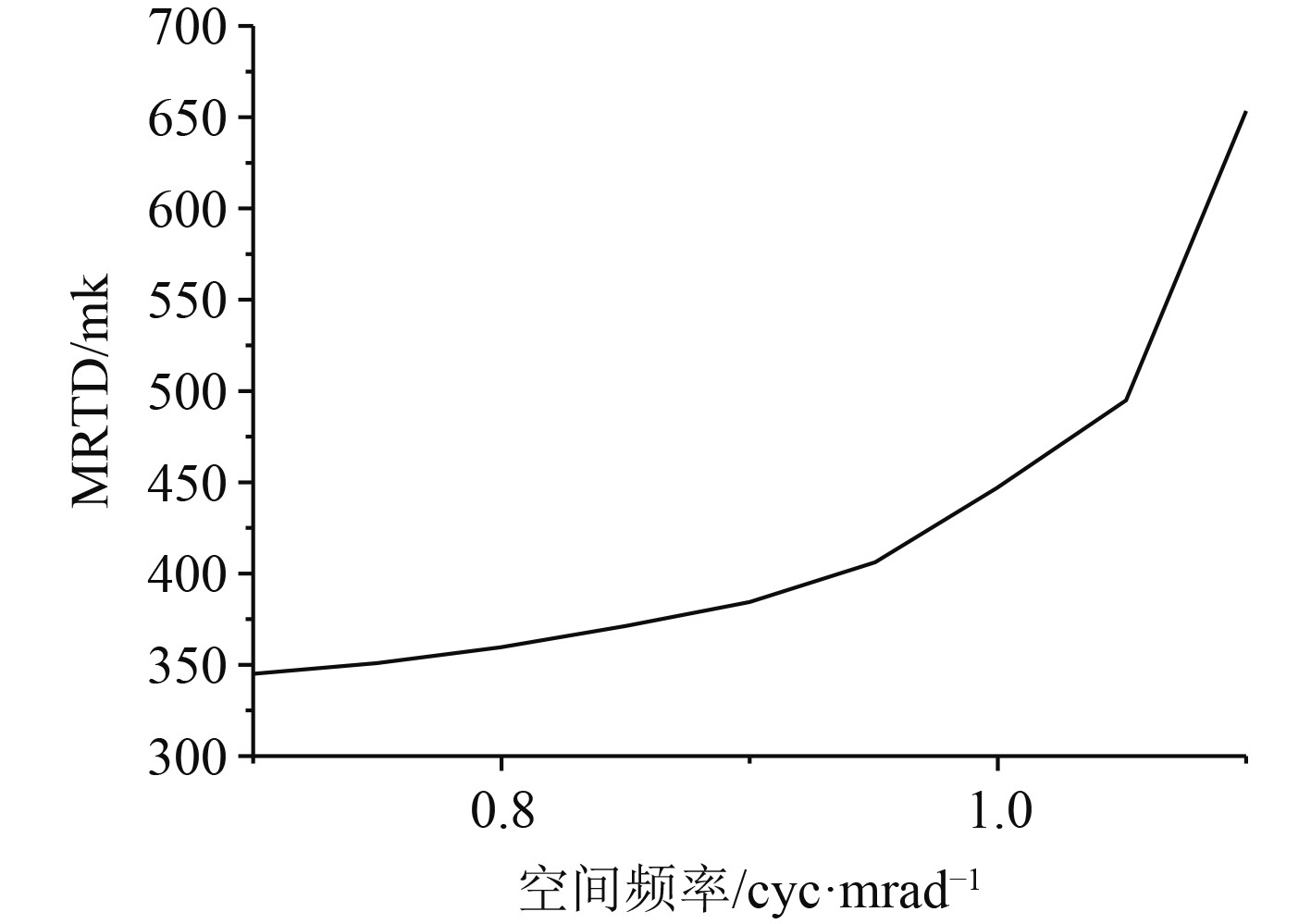
|
图 5 MRTD和空间频率之间的曲线关系 Fig. 5 Curve relationship between MRTD and spatial frequency |
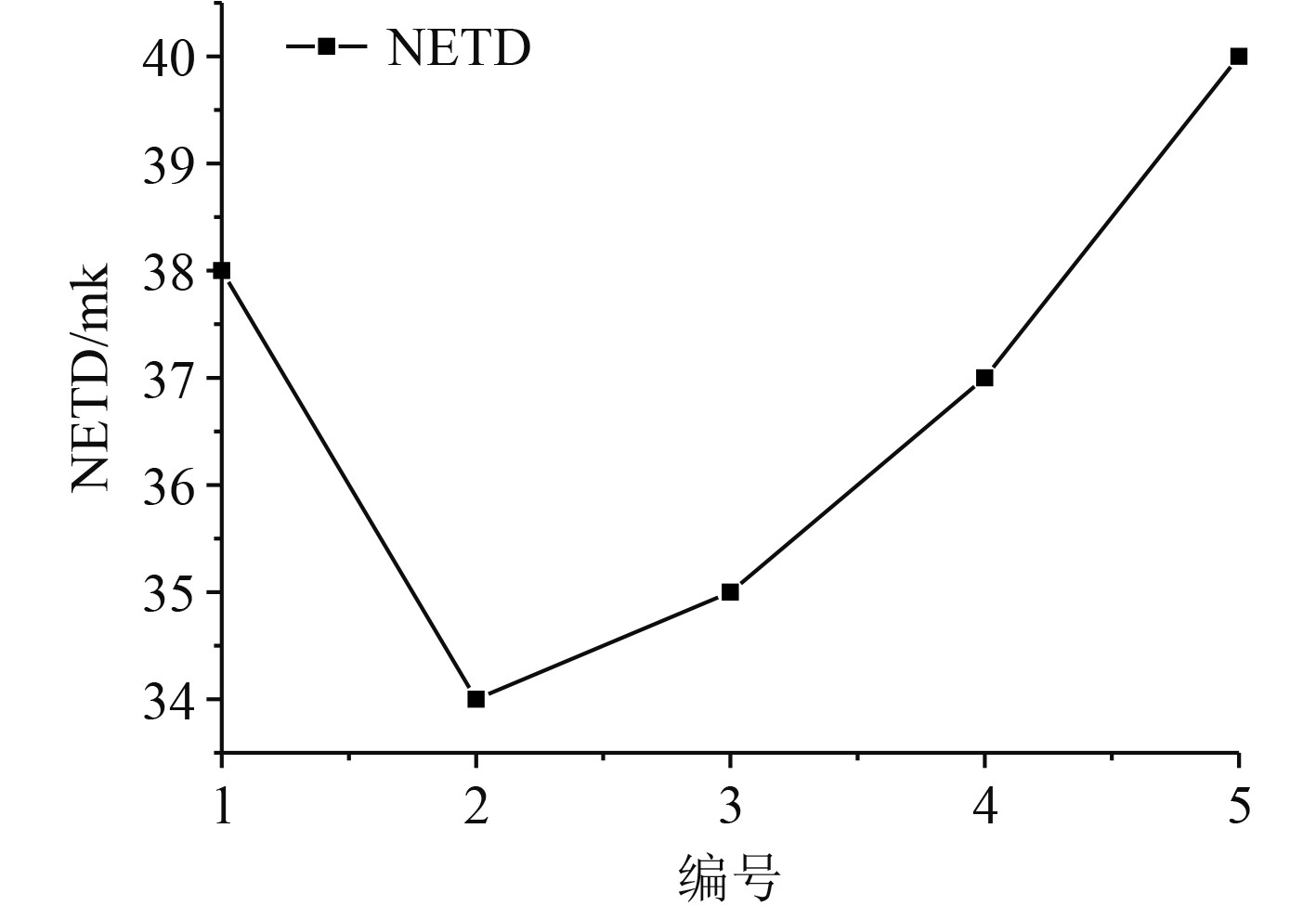
采用本文提出的测试方法对机芯的NETD参数进行测试,测试过程中将半圆靶图当作目标靶,对5款机芯样本的NETD参数进行测试,测试结果如图6所示。光学成像系统的NETD参数主要是衡量光学成像系统的灵敏度,体现了生成图像过程中噪声的影响水平。由于NETD没有考虑到人眼的视觉效应,同时也无法对图像空间的分辨能力进行判断,因此存在一定的局限性。
|
图 6 不同机芯的NETD测试结果 Fig. 6 NETD test results of different movements |
船舶光学成像系统的设计和生产都需要相关的系统参数体现该成像系统的性能,以便能够指导光学成像系统的设计及其质量控制,尤其是在海洋环境中对光学载荷参数的校准,基于光学载荷的高光谱的特征,对光学成像参数进行精确的检测,确保光学成像系统采集到的光谱信息的有效性以及准确性对光学成像系统有重要意义。本文基于C#设计了船舶光学载荷参数测试系统,对船舶光学成像系统的发展有推动作用。
| [1] |
张可立, 丁振宇, 高杰. 海洋一号C/D卫星全球船舶自动识别系统设计与应用[J]. 航天器工程, 2019(28): 26-31. ZHANG Ke-li, DING Zhen-yu, GAO Jie. Design and application of AIS on HY-1C/D Statellite[J]. Spacecraft engineering, 2019(28): 26-31. |
| [2] |
张晔, 樊午洋, 化青龙, 等. 基于三维模型的SAR舰船仿真与运动状态识别[J]. 指挥信息系统与设计, 2020(11): 89-95. |
| [3] |
郭春雨, 郐云飞, 韩阳, 等. 舰船流场实验测试技术研究进展[J]. 中国舰船研究, 2022(17): 103-115. GUO Chun-yu, KUAI Yun-fei, HAN Yang, et al. Review of research on ship flow field measurement technology[J]. chinese journal of ship research, 2022(17): 103-115. |
| [4] |
孙远翔, 田俊宏. 近场水下爆炸载荷及舰船结构动态响应研究综述[J]. 舰船科学技术, 2019(41): 1-8. SUN Yuan-xiang, TIAN Jun-hong. Review of near-field underwater explosion load and ship structure dynamic response[J]. Ship science and techonogy, 2019(41): 1-8. |
| [5] |
赵凯旋, 车腊梅, 彭超, 等. 空间光学载荷低温部件地面气体保护系统设计[J]. 航天器环境工程, 2017(34): 560-565. |
| [6] |
徐思华, 于新辰. 面向航天快速发射的光学载荷设计与制造[J]. 光学精密工程, 2021(29): 513-523. |
| [7] |
潘俏, 朱嘉诚, 杨子江, 等. 星载高光谱碳监测光学载荷的研究进展[J]. 航天返回与遥感, 2021(42): 34-44. |
| [8] |
崔阳, 陈雪笛, 姚小松, 等. 遥感微纳卫星载荷平台高精度标定技术研究[J]. 南京航空航天大学学报, 2022(54): 499-507. |
 2023, Vol. 45
2023, Vol. 45
