0 引　言

水下波达方向估计是水下阵列数据处理的主要任务，相比于空间波达估计，水下声环境更为复杂。近年来，随着科技的发展，人类水下活动急剧增多导致水下噪声水平上升，同时潜艇和水面船舰的制造工艺提升，使得目标信号强度减弱，进一步降低水下信噪比。如何在低信噪比条件下，快速高效的进行方位估计是水下阵列信号处理的核心任务。

相比于标量水下阵列，矢量水下阵列不仅能获取声压单通道信息，在空间共点同步拾取声场的振速信息。因而矢量水听器成为水下声呐技术中一个快速发展的新方向^[1]。在矢量阵列信号处理领域，传统波束形成算法面临着瑞利限的分辨率限制^[2]。基于子空间和特征分解算法的提出解决了分辨率限制，形成了包括MUSIC在内多种子空间类DOA估计方法^[3]，具有较好的估计性能。但是基于子空间和特征分解算法面临着矢量水听器声压与振速通道接收噪声功率不一致的问题^[4]，随着信噪比逐渐减小，信号子空间与噪声子空间的划分变得逐渐困难，算法性能急剧下降。同时信号空间分解计算复杂，不能满足DOA估计快速性要求。

随着深度学习的快速发展，多种类型的神经网络被应用于水下DOA估计^[5-8]。相比于传统DOA估计算法，在神经网络中，不用考虑对水声阵列采集数据进一步处理，而是将DOA估计看作数据分类问题。神经网络的应用克服了对阵列模型误差敏感，低信噪比下效果不佳等问题，同时训练生成的网络模型，能够实现DOA的实时估计^[9]。卷积神经网络在DOA估计中的应用已取得良好效果，但由于池化层丢失部分位置信息，同时神经元输出采用标量形式导致细节特征提取不充分，需要大数据样本才能更好提取详细特征。

本文采用Hinton等于2017年提出的胶囊网络模型^[10]，其核心思想是将神经网络中输出形式由标量输出变为矢量输出，舍弃池化层结构，保留网络中的位置特征信息，从而实现更好的特征提取效果。采用胶囊神经网络作为训练模型，利用胶囊神经网络基于矢量特征输出特性，证明了在不同信噪比噪声环境下，胶囊网络DOA估计性能优于传统子空间类算法和卷积神经网络模型。

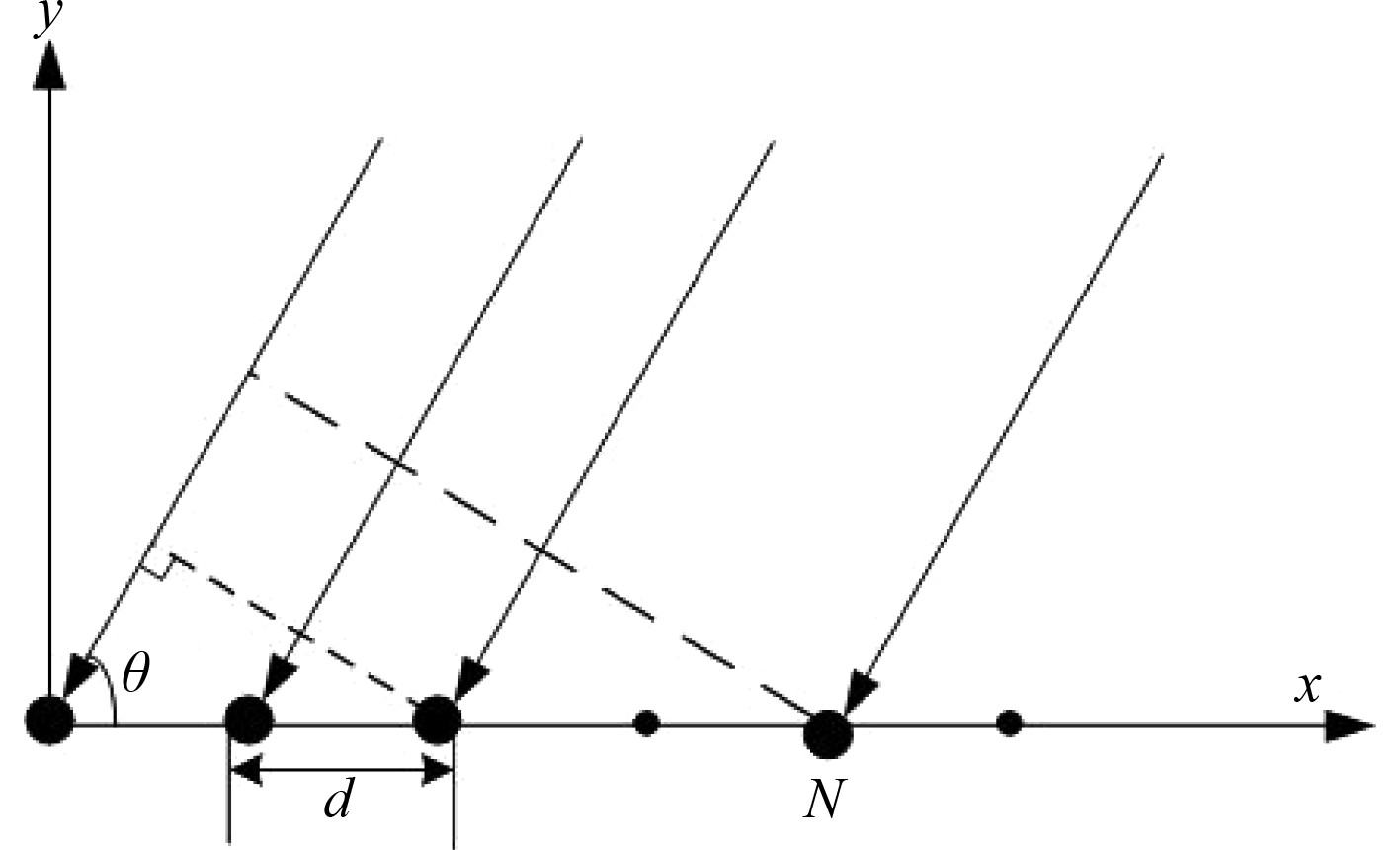
1 矢量水听器阵列基本原理 1.1 矢量水听器阵列模型

如图1所示，在二维平面情况下，建立一个含有N个矢量阵元的均匀线阵，相邻阵元间距为半波长 $ d = \lambda /2 $ 。在远场条件下，以位于坐标系原点的阵元1为参考阵元，假设有一个波长为 $ \lambda $ 的窄带入射信号，入射水平方位角为 $ \theta $ 。理想情况下省略时间因子和波阻抗，则矢量线阵接收到1个声压通道信息P和2个相互正交的振速分量 $ {v_x} $ 和 $ {v_y} $ ，可以表示为：

$ \left\{ \begin{gathered} p = x(t), \\ {v_x} = x(t)\cos \theta, \\ {v_y} = x(t)\sin \theta 。\\ \end{gathered} \right. $

(1)

式中， $ x(t) $ 为该平面波波形。由单个矢量阵元的单位幅度响应可定义：

$ h(\theta ) = {\left[ {1{\text{ cos}}\theta {\text{ sin}}\theta } \right]^{\rm{T}}}, $

(2)

矢量线阵的空间相位延迟向量表达为：

$\begin{split} {a_p}(\theta ) =& \left[ 1,{e^{j(2{\text{π}} /\lambda )d\cos (\theta )}},{e^{j2(2{\text{π}} /\lambda )d\cos (\theta )}} ,\cdots,\right.\\ &\left.e^{j(N - 1)(2{\text{π}} /\lambda )d\cos (\theta )} \right]^{\rm{T}}, \end{split}$

(3)

则矢量水听器阵列导向矢量为:

$ a(\theta ) = {a_p}(\theta ) \otimes h(\theta )。$

(4)

式中， $ \otimes $ 表示为Kronecker积。在J次快拍下，这个远场窄带信号入射到均匀矢量线阵的输出数据为：

$ X = AS + N。$

(5)

式中： $ X $ 为 $ 3N \times J $ 维数据矩阵，表示矢量水听器对该信号J次快拍下的输出向量； $ A = a(\theta ) $ 为 $ 3N \times 1 $ 维阵列流型； $ S = \left[ {{x_1}(t){\text{ }}...{\text{ }}{x_J}(t)} \right] $ 是 $ 1 \times J $ 维信号矩阵； $ N = \left[ {{n_1}(t){\text{ }}...{\text{ }}{n_J}(t)} \right] $ 是 $ 3N \times J $ 维高斯噪声矩阵。矢量阵列输出数据的协方差矩阵可以表示为：

$ {R_x} = {\rm{E}}\left[ {X{X^{\rm{H}}}} \right]。$

(6)

式中， ${(·)}^{{\rm{H}}}$ 和 ${\rm{E}}[·]$ 表示为共轭转置和数学期望。

1.2 阵列数据分析与处理

在传统子空间分类算法中可以将 $ {R_x} $ 看作是由信号子空间 $ {U_S} $ 和噪声子空间 $ {U_N} $ 构成：

$ {R_x} = {U_S}{\Lambda _S}U_S^H + {U_N}{\Lambda _N}U_N^H。$

(7)

式中： $ {U_S} $ 代表信号子空间； $ {U_N} $ 代表噪声子空间， $ {\Lambda _S} $ ； $ {\Lambda _N} $ 代表着对应的特征值对角矩阵。在理想的条件下，信号子空间与噪声子空间是相互正交的，所以信号的阵列流型与噪声子空间也是相互正交，即

$ {A^{\rm{H}}}(\theta ){U_N} = 0。$

(8)

Schmidt利用这个特性构造了经典MUSIC算法空间谱：

$ {P_{music}} = \frac{1}{{{A^{\rm{H}}}(\theta ){U_N}U_N^{\rm{H}}A(\theta )}}。$

(9)

仿真实验中由于声波包含幅值与相位角两部分信息，所得到的 $ {R_x} $ 矩阵存在复数数值。由于神经网络训练过程中不能处理复值数据，不能将 $ {R_x} $ 直接作为数据输入。需要对 $ {R_x} $ 进行相应数学处理。已知 $ {R_x} = {Re} \left\{ {{R_x}} \right\} + {Im} \left\{ {{R_x}} \right\}i $ ，常见方式为将 $ {R_x} $ 分为实虚部两部分，令

$ \left\{ \begin{gathered} Q = {{\rm{Re}}} \left\{ {{R_x}} \right\}, \\ P = {{\rm{Im}}} \left\{ {{R_x}} \right\}。\\ \end{gathered} \right. $

(10)

式中： $ \mathrm{Re}\{·\} $ 表示复数实部， $ \mathrm{Im}\{·\} $ 表示复数虚部。将 $ {R_x} $ 的实虚部 $ Q,P $ 看作2个独立实值矩阵作为数据输入。实虚部分离法可视作将协方差矩阵分为2个维度数据并行输入神经网络，已在卷积神经网络中取得了良好效果。但实虚部分离法削弱了相位与幅值间关联，考虑到声波信息中幅值相位相互关联，采用幅值相位角法进行数据变换输入。已知对任意复数有：

$ {R_x} = \left| {{R_x}} \right|(\cos \theta + i\sin \theta ) ，$

(11)

式中： $ |·| $ 表示复数的模； $ \theta = \arctan \left(\dfrac{{{Im} {R_x}}}{{{Re} {R_x}}}\right) $ 。可将数据输入变换为模长与相位角矩阵 $ \left( {\left| {{R_x}} \right|,\theta } \right) $ ，其中：

$ \left\{ \begin{gathered} \left| {{R_x}} \right| = \sqrt {{Q^2} + {P^2}}, \\ \theta = \arctan \left(\frac{P}{Q}\right)。\\ \end{gathered} \right. $

(12)

通过将数据变换为幅值与相位角输入，最大限度保留幅值与相位角的相关性，使得网络更好地提取相关位置信息特征，进一步提升模型性能。

2 胶囊神经网络

2017年，Hinton等提出了胶囊网络概念。核心思想为采用动态路由方式，将神经元标量输入输出变为向量输入输出。相比于传统神经网络，向量输出的胶囊网络，具有更丰富的特征表达能力。

在胶囊网络中，由不同神经元组成的胶囊包含多个特征信息，从而拥有包含空间方向位置等多特征提取能力。胶囊网络结构如图2所示。

其主要结构包括，卷积特征提取层，主胶囊层，数字胶囊层。卷积层主要功能在于通过卷积运算提取输入数据中的特征，输出特征图。主胶囊层是由卷积层产生的特征图经过卷积操作后，将生成的标量转化为所需要的向量胶囊结构。数字胶囊层与卷积神经网络中全连接层相似，但不再是由神经元求和后以标量形式输出，而是改造为胶囊结构进行分类输出。通过输出的向量模大小进行分类，以模值最大的向量作为输出类别。

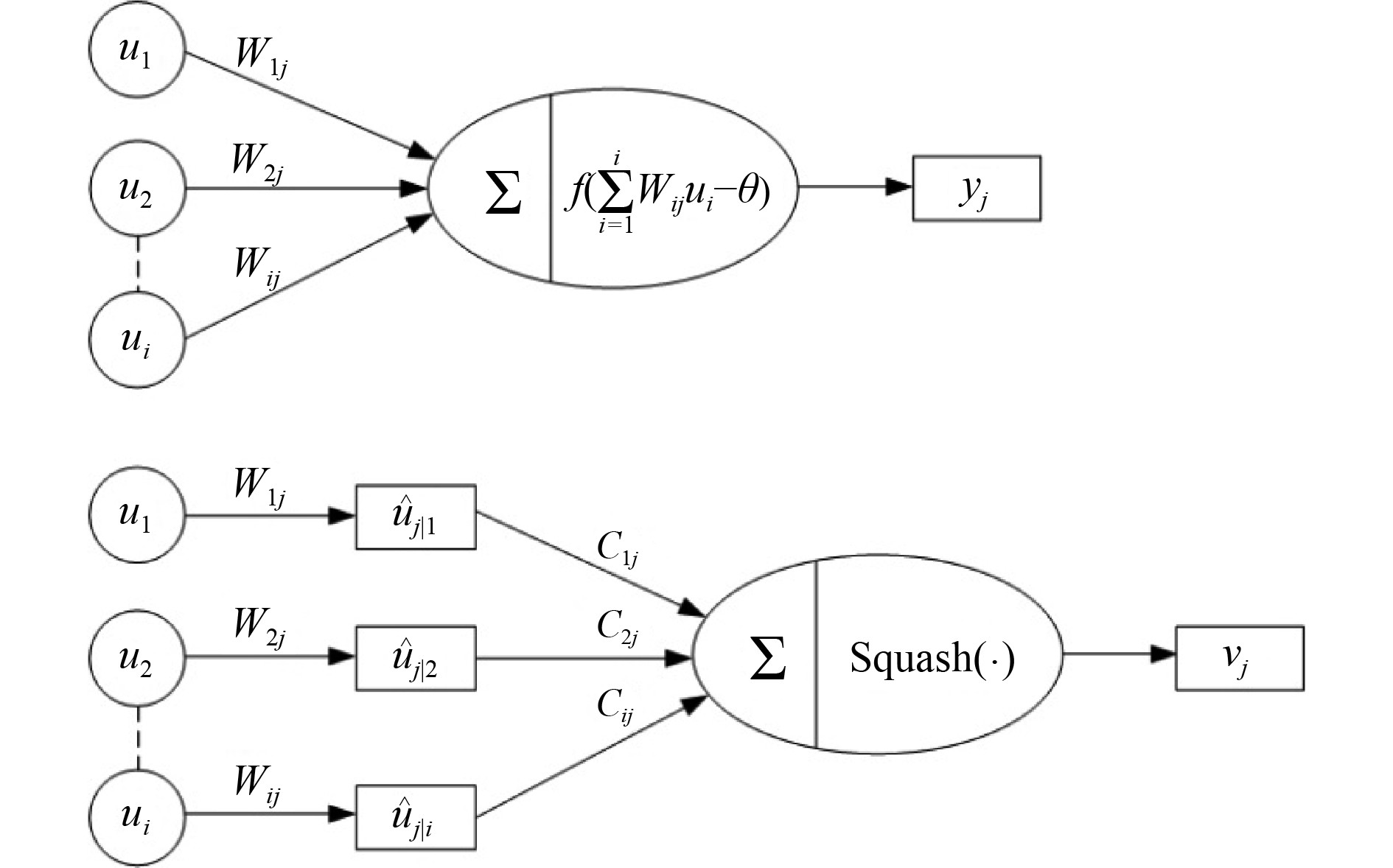
胶囊网络动态路由算法与卷积神经网络激活方式对比如图3所示。其算法过程如下：

1）初始化， $ l $ 层胶囊 $ i $ 到 $ l + 1 $ 层胶囊 $ j $ 的特征传递系数为 $ {b_{ij}} \leftarrow 0 $ 。

2）在胶囊网络中引入新的胶囊权重耦合系数 $ {c_{ij}} $ ，由动态softmax方式获取，具体公式为：

$ {c_{ij}} = \frac{{\exp ({b_{ij}})}}{{\displaystyle\sum {_k\exp ({b_{ik}})} }}。$

(13)

3）上层胶囊特征 $ {u_i} $ 传递至下层胶囊，得到下层胶囊特征 $ {s_j} $ ，公式为：

$ {s_j} = {\sum {_i{c_{ij}}\mathop u\limits^ \wedge } _{j|i}}，$

(14)

式中， $ {\mathop u\limits^ \wedge _{j|i}} = {W_{ij}}{u_i} $ 。与神经网络相似， $ {W_{ij}} $ 为权重矩阵，由误差反向传播更新。

4）胶囊的输出向量的长度来表示某些特征的概率大小。因此，使用一个非线性的“Squashing”函数保证上层胶囊进行特征压缩得到下层特征，公式为：

$ {v_j} = \frac{{{{\left\| {{s_j}} \right\|}^2}}}{{1 + {{\left\| {{s_j}} \right\|}^2}}}\frac{{{s_j}}}{{\left\| {{s_j}} \right\|}}。$

(15)

实践发现权值1改为0.5，可以将模长接近0的向量放大输出，加强了特征提取能力。

5）动态迭代更新 $ l $ 层胶囊 $ i $ 到 $ l + 1 $ 层胶囊 $ j $ 的特征传递系数，其公式为：

$ {b_{ij}} \leftarrow {b_{ij}} + {\mathop u\limits^ \wedge _{j|i}}{v_j}。$

(16)

胶囊网络中损失函数采用类似支持向量机算法中的边缘损失函数，其具体公式为：

$ \begin{split} {L_k} =& {T_k} \cdot (\max {(0,{m^ + } - \left\| {{v_k}} \right\|)^2} + \lambda \cdot\\ &(1 - {T_k}) \cdot \max {(0,\left\| {{v_k}} \right\| - {m^ - })^2}。\end{split} $

(17)

式中： $ k $ 为分类数； $ {T_k} $ 为分类的指示函数 (存在为 1，不存在为 0)； $ {m^ + } = 0.9 $ 为上界，代表着若数据分类后输出属于第 $ k $ 类中，则其对应数字胶囊输出向量的模长至少>0.9，反之则若数据分类输出不属于第 $ k $ 类中，则胶囊输出的是一个很短的向量，其模长<0.1； $ \lambda $ 为比例系数，调整两者比重，本文取 $ \lambda = 0.5 $ 。总损失是所有数字胶囊损失之和。

3 仿真实验与性能分析 3.1 数据处理和预处理

为验证本文所提胶囊网络算法的性能，进行数值仿真。考虑到增强算法结果对比以及水下阵列布放难度，采用阵元数较少的均匀线阵。该线阵由3个矢量水听器组成，阵元间距为半波长，信号源搜索范围为 $ \left[ { - 90^\circ , + 90^\circ } \right] $ ,每隔 $ 1^\circ $ 取一个样本，快拍数为500，对每个角度进行1000次Monte-Carlo仿真实验。以信噪比为0 dB时为例，仿真得到181000个大小为9×9的二维协方差矩阵。将数据进行幅值相位处理，以对应入射角度为标签，得到训练所需要的训练集数据 $ \left( {\left| {{R_x}} \right|,\theta } \right) $ 。

3.2 网络模型对比和相关参数

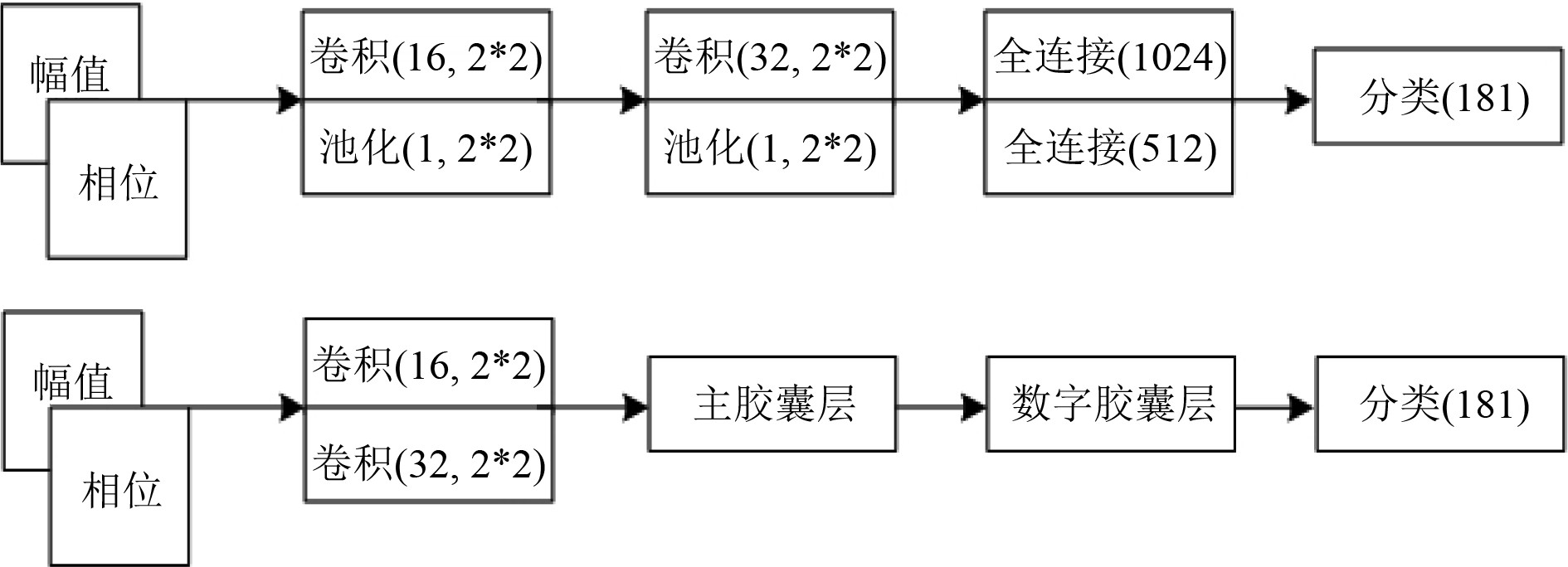
实验中，采用卷积神经网络与胶囊神经网络进行仿真对比。为了保证实验结果准确性，2个网络中卷积核相同，步长为1，模型均采用Relu激活函数，优化方法为Adam，学习率为率为0.001，训练过程中单次数据读入量为32，最大迭代次数设置为50。卷积神经网络与胶囊网络具体结构如图4所示。

3.3 数值结果与性能分析

相邻阵元间距为半波长 $ d = \lambda /2 $ ，假设有一个角度为 $ \theta $ ，波长为 $ \lambda $ 的窄带入射信号下得到信噪比为−5 dB，0 dB，5 dB，10 dB，15 dB的5组样本数据。将样本按照9∶1的比例随机划分为训练集核验证集。

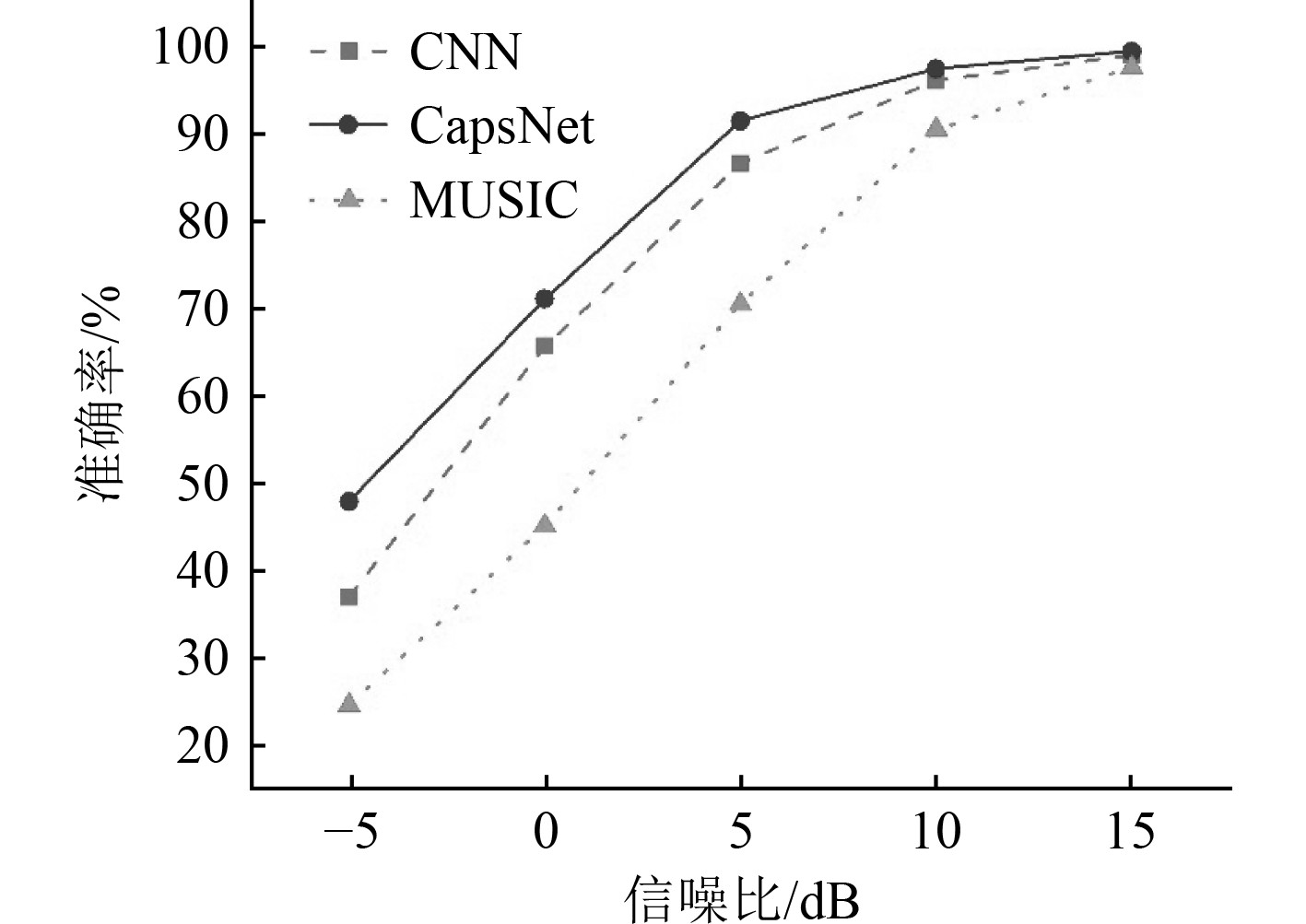
图5为MUSIC，CNN，CapsNet等3种算法在不同信噪比条件下的准确率。可以看出，由于存在噪声条件影响，3种方法不同程度的受到影响。其中，传统子空间分解所受影响最大，MUSIC算法的DOA估计效果较差。卷积神经网络具有一定抗噪效果，较MUSIC算法准确率有一定提升。胶囊网络在低信噪比条件下，DOA估计效果优于卷积神经网络。证明胶囊网络通过动态路由方式，有效地进行了多特征提取，加强了的网络分类能力。

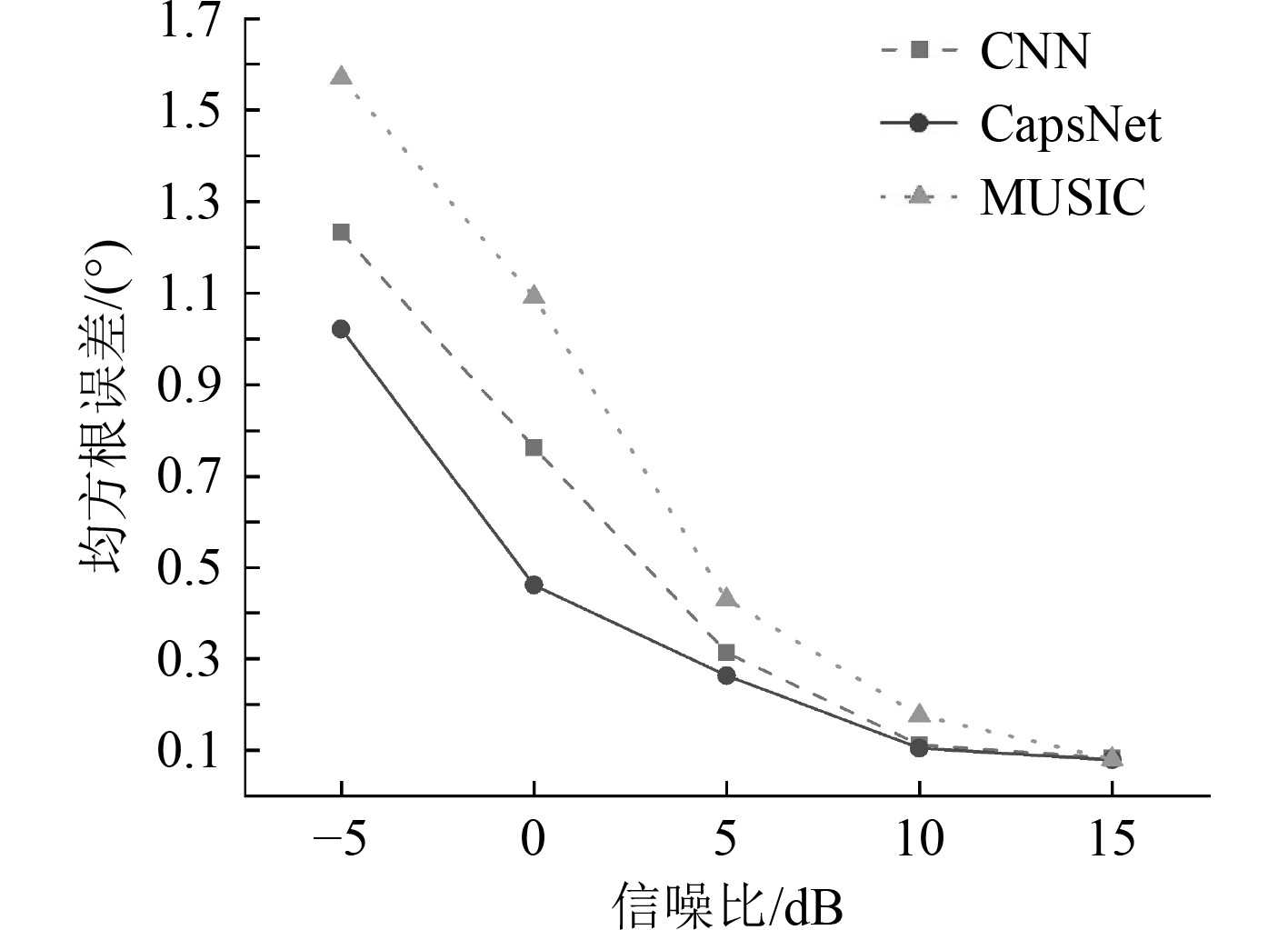
图6为几种算法的估计角度均方根误差统计，其公式为：

$ {\text{RMSE = }}\sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{(({y^*}^{(i)}) - {y^{(i)}})}^2}} }。$

(18)

式中： $ y $ 为真实波达角度； $ {y^*} $ 为估计的波达角度； $ m $ 代表需要估计的数据个数。均方根误差统计可以较好的反应出算法的精度和稳定性。可以看出，胶囊网络算法分辨率总体优于卷积神经网络和MUSIC算法，且随着信噪比降低，算法性能优势更加明显。高信噪比情况下，3种算法均能提供较好的分辨能力。总体来说，胶囊网络在广泛的信噪比范围下具有比其他算法更加稳定算法精度与分辨能力。

表1为快拍数为500时，各算法单次估计角度的消耗时长。运行时长为测试1000所取平均时间。由表1可知单次估计时，使用网络模型估计时长低于子空间类算法20倍左右。卷积神经网络与胶囊网络消耗时长相差较小。综上，胶囊网络在保证算法估计性能同时在运行时间上有着明显优势。

4 结　语

本文提出了一种基于胶囊网络的水下波达估计算法。结合矢量水下均匀阵列仿真实验，对比不同信噪比环境下胶囊网络，多重空间分类法与卷积神经网络3种方法的方位估计准确率与稳定性能。实验结果表明，低信噪比环境下，各算法预测均受严重影响。相比较其他算法，胶囊网络所拥有向量动态路由方式，降低了噪声影响同时加强了特征能力提取能力，使得在低信噪比环境下，方位估计模型准确率与稳定性能均有较大提升，同时满足DOA估计的快速性要求。考虑到本文使用信号均为单个信源，如何利用胶囊网络进行多信源方位估计将是下一步工作中心。