0 引　言

舰船是海上作战中最主要的武器平台，舰船在应用过程中，各个分区电网互相联通共同协作，为舰船提供稳定电源供应^[1]。当前电网技术不断提升，舰船电网也随之升级和扩容，这也为舰船电网维护带来了一定难度。而舰船电网重构则是舰船电网稳定运行的基础，尤其是舰船电网出现故障时，其电网受到较大的冲击，形成大扰动状态^[2]，此时通过对该电网进行重构，可迅速恢复舰船电力供应。目前有很多学者研究舰船电网重构技术，吴建旭等^[3]提出多目标配电网重构方法，该方法通过对电网负荷进行削峰填谷处理后，使用以欧式距离为基础的聚类算法对舰船电网进行分段，在通过对不同舰船电网分段内进行自适应和声搜索后，实现舰船电网重构。苏丽等^[4]提出船舶微电网重构方法，该方法通过构建舰船电网重构目标函数后，依据双重混合机制求解舰船电网重构目标函数，实现舰船电网重构。上述2种方法虽然均可实现舰船电网重构，但二者在实际应用过程中，均存在舰船电网重构及时性差，重构后的舰船电网运行不够稳定等问题，因此上述2种方法应用效果不佳。多目标差分进化算法属于群体差异的启发式随机搜索算法，其可通过启发式搜索策略实现目标优化求解，该优化算法具备较好的全局性和收敛性^[5]。本文以该算法为基础，研究大扰动状态下基于多目标差分进化算法的舰船电网重构方法，为舰船电力系统保护提供一种有效手段。

1 多目标差分进化算法舰船电网重构 1.1 大扰动状态冲击规律分析及能量计算

由于舰船电网分区较多，每个区之间电流进行互联时，形成一定规模的交流同步电网，当电流发生冲突时，会导致舰船电网产生区域大扰动，造成舰船电网区域故障或瘫痪，严重威胁舰船安全。 $ n $ 表示舰船电网内发电设备数量，在舰船电网发生扰动时，第 $ b $ 个发电设备被分配的功率计算公式为：

$ \Delta {P_b} = {K_{Sim}} \cdot \frac{{\Delta P}}{{\displaystyle\sum\limits_{b = 1}^n {{K_{Sim}}} }} 。$

(1)

式中： $ \Delta {P_b} $ 表示第 $ b $ 个发电设备被分配的功率； $ \Delta P $ 表示 $ n $ 个发电设备的总功率；K_sim表示发电设备节点和扰动节点之间的同步系数。可知，舰船电网发电设备输出功率与其节点和扰动节点之间的同步系数成正相关关系。

当舰船电网处于大扰动状态时，电网内联络线的有功功率变化顺序和变化幅值，可呈现当前舰船电网大扰动冲击过程。令舰船电网大扰动时，电网线路暂态势能为0，则该线路在大扰动冲击后，其暂态势能计算公式如下：

$ {V_p} = \frac{{{\rm{d}}{\theta _k}}}{{{\rm{d}}t}}{\rm{d}}t \cdot \int_{{t_s}}^t {({P_k} - P_k^s)}。$

(2)

式中：V_p表示大扰动冲击后舰船电网暂态势能；t_s表示大扰动发生时刻；P_k表示舰船电网有功潮流； $ P_k^s $ 表示大扰动状态时，舰船电网稳态有功潮流； $ {\theta _k} $ 表示线路电压相角差值； $ t $ 表示时刻； $ d $ 表示求导表达式。

利用公式(2)即可得到舰船电网在大扰动状态下的电网能量。

1.2 舰船电网重构模型构建

以舰船电网在大扰动状态下的电网能量为基础，从负荷恢复度指标、开关操作代价等多个角度建立舰船电网重构模型，其详细过程如下：

舰船电网分为一级、二级和三级负荷，分别由 $ {L_{g1}} $ ， $ {L_{g2}} $ ， $ {L_{g3}} $ 表示舰船电网一级、二级和三级负荷，则舰船电网负荷恢复度指标目标函数 $ {Q_L} $ 表达式如下：

$ {Q_L} = \left( {{\lambda _1} + {\lambda _2} + {\lambda _3}} \right)\left( {\sum\limits_{i \in {L_{g1}}} {{x_i}{I_i}} + \sum\limits_{j \in {L_{g2}}} {{x_j}{I_j}} + \sum\limits_{k \in {L_{g3}}} {{x_k}{I_k}} } \right)。$

(3)

式中： $ {\lambda _1} $ ， $ {\lambda _2} $ ， $ {\lambda _3} $ 分别表示舰船电网负荷等级权系数； $ i $ ， $ j $ ， $ k $ 分别表示其对应电网负荷等级内的节点； $ I $ 表示对应电网负荷等级电流； $ x $ 表示对应电网等级投切状态。

舰船电网内的开关操作代价是衡量电网重构可操作性和恢复速度的主要指标，B_G，B_M，B_A表示对应开关动作次数，Q_C表示舰船电网开关操作代价指标，其目标函数如下：

$ {Q_C} = {O_G}{B_G} + {O_M}{B_M} + {O_A}{B_A} 。$

(4)

式中：O_G，O_m，O_A表示电网不同类型开关的操作代价权重系数。

由联络线路容量裕度Q_M表示舰船电网重构后的稳定指标，其目标函数如下：

$ {Q_M} = \min \left\{ {\left( {{H_{i,rated}} - {H_i}} \right)\frac{1}{{{H_{i,rated}}}}\left| {i \in \left[ {1,2, \cdots ,{N_M}} \right]} \right.} \right\} ，$

(5)

式中：N_M为舰船电网联络线路总数；H_i，H_i,rated分别为舰船电网联络线路损耗和额定线损。

电网负荷分配不均匀也是衡量舰船电网重构指标之一，其可描述舰船电网重构的承载能力和均衡性。电网负荷分配不均匀Q_p目标函数为：

$ {Q_p} = \sum\limits_{i = 1}^{{N_D}} {I_i^2} \cdot \frac{1}{{{{\left(\displaystyle\sum\limits_{j = 1}^{{N_L}} {{I_{Lj}}} \right)}^2}}} 。$

(6)

式中：I_Lj表示负荷 $ j $ 的电流；N_L表示舰船电网负荷总数。

在重构舰船电网时，需充分考虑电网内部发电设备自身负载情况，建立舰船电网重构发电设备负载率Q_G目标函数如下：

$ {Q_G} = \min \left\{ {{H_i}\frac{1}{{{H_{i,rated}}}}\left| {i \in \left[ {1,2, \cdots ,{N_G}} \right]} \right.} \right\}，$

(7)

式中，N_G表示舰船电网内部发电设备最低负载率。

以舰船电网在大扰动状态下的电网能量为基础，由式(3)~式(7)，组成舰船电网重构模型 $ E $ ，表达式如下：

$ Q = \left( {{Q_L} + {Q_C} + {Q_M} + {Q_P} + {Q_G}} \right){V_p}。$

(8)

设置舰船电网重构模型约束条件如下：

$ \left\{ \begin{gathered} {x_{i1}} + {x_{i2}} \leqslant 1，\\ {I_i} \leqslant {I_{i,rated}}。\\ \end{gathered} \right. $

(9)

式中：x_i1，x_i2表示转换开关常规和备用供电路径的工作状态，其是电网负荷供电约束； $ {I_i} \leqslant {I_{i,rated}} $ 为电流约束，即当前电路电流不得高于最大电流限值。

1.3 基于多目标差分进化算法的模型优化求解

多目标差分进化算法是竞争生存策略在试验种群和原始种群中通过竞争生成新一代种群的寻优方法，使用该方法依据舰船电网重构模型约束条件求解该模型后，得到舰船电网重构结果。 $ \varphi $ 表示舰船电网重构的种群代，对该种群代舰船电网重构模型解的目标向量 $ {R_{i,\varphi }} $ 进行变异操作，得到其变异向量 $ {y_{i,\varphi + 1}} $ ，表达式如下：

$ {y_{i,\varphi + 1}} = {R_{r1,\varphi }} + \psi ({R_{r2,\varphi }} - {R_{r3,\varphi }})。$

(10)

式中： $ {R_{r1,\varphi }} $ 表示父代基向量； $ ({R_{r2,\varphi }} - {R_{r3,\varphi }}) $ 表示父代差分向量； $ \psi $ 表示缩放因子。

对舰船电网重构模型解的目标向量 $ {R_{i,\varphi }} $ 进行交叉操作，得到其交叉向量 $ {R_{ij,\varphi + 1}} $ ，公式如下：

$ {z_{ij,\varphi + 1}} = \left\{ \begin{gathered} {y_{ij,\varphi + 1}}\mathop {}\limits^{} ，ran{d_j} \leqslant \alpha，\\ {R_{ij,\varphi }}\mathop {}\limits^{}，ran{d_j} > \alpha。\\ \end{gathered} \right. $

(11)

式中： $ \alpha $ 表示交叉概率； $ ran{d_j} $ 表示任意常数； $ {R_{ij,\varphi }} $ 表示交叉和变异操作后的目标向量； $ {y_{ij,\varphi + 1}} $ 表示经过一轮交叉和变异后的变异向量。

利用式(10)和式(11)对第 $ \varphi $ 代种群进行交叉变异操作时，设置临时种群 $ P* $ ，在临时种群内选择试验个体z_i，以交叉和变异方式令其与父代个体u_i进行竞争。当试验个体约束支配父代个体时，则将试验个体归入临时种群内，反之，将父代个体归于临时种群内。通过不断重复上述步骤，选择最好的N_P个个体生成新父代种群，该父代种群即为舰船电网重构结果。

2 实验分析

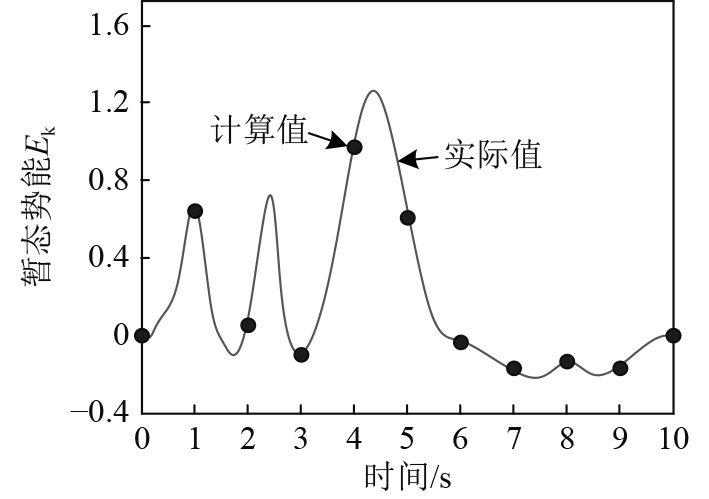
以某远洋船作为实验对象，该船总长为158.24 m，宽为18.5 m，排水量约为1.655×10⁴ t。该船电网分为主电网、应急电网、照明电网以及弱电电网。使用本文方法对该船电网在大扰动状态下进行重构，并分析本文方法的应用效果。在电网大扰动冲击状态下，使用本文方法计算电网的暂态势能，结果如图1所示。分析可知，本文方法舰船电网暂态势能的计算值在不同时间节点时，结果均与其实际值曲线重合。表明本文方法计算大扰动状态下，舰船电网暂态势能结果精准。

以该船配电系统10台设备作为实验对象，在大扰动状态下，使用本文方法对该船电网进行重构，结果如表1所示。分析可知，电网在受到大扰动冲击时，其配电系统10台设备开关大多数为断开状态，说明此时电网出现故障，无法正常运行。而使用本文方法对该舰船电网进行重构后，其配电系统10台设备仅1台为断开状态，其余设备开关均为闭合状态。说明本文方法可有效在舰船电网处于大扰动状态时，对其进行重构，应用效果较为显著。

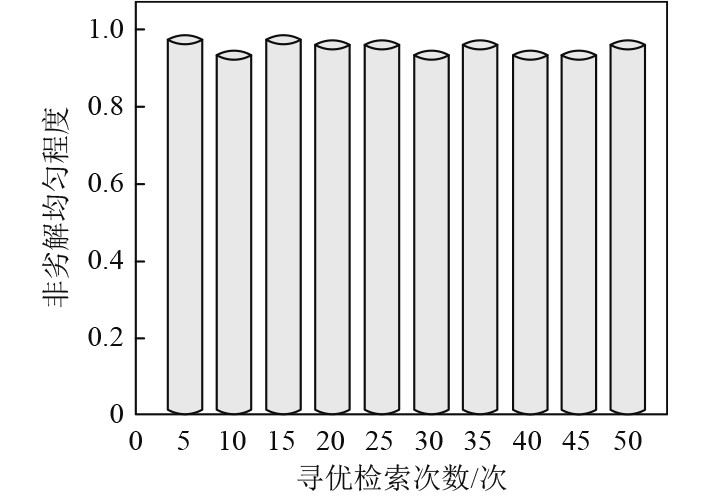
以多目标差分算法求解舰船电网重构模型时的非劣解分布的均匀程度作为衡量指标，测试本文方法重构舰船电网的精度，结果如图2所示。分析可知，使用多目标差分算法求解舰船电网重构模型时，其输出的非劣解均匀程度随着寻优检索次数的增加呈现波动趋势，但其波动起伏不大，均匀程度数值始终在0.95左右波动。上述结果表明，本文方法使用多目标差分算法求解舰船电网重构模型输出结果较为精准，可有效对舰船电网进行重构。

3 结　语

本文研究大扰动状态下基于多目标差分进化算法的舰船电网重构方法，使用多目标差分进化算法求解舰船电网重构有效解，使舰船电网重构结果为最佳结果。经过实验验证，本文方法计算大扰动状态下的舰船电网暂态势能精度较高，可有效对舰船电网进行重构，且其求解舰船电网重构模型时的非劣解分布均匀程度较高，具备较好的应用效果。