2. 船舶振动噪声重点实验室,湖北 武汉 430033
2. National Key Lab on Ship Vibration and Noise, Wuhan 430033, China
目前液压控制技术广泛应用于各个工业领域,根据采用的流量控制元件,液压系统可分为泵控系统和阀控系统。阀控系统应用最为广泛,但该系统存在节流损失,特别是控制具有负负载工况的作动器,节流损失更大;而泵控系统直接控制液压泵的转向和排量来控制作动器的速度[1]。由于非对称液压缸具有占用空间小、输出力大等优点,目前约80%的液压系统使用非对称液压缸,且多为阀控或开式泵控系统[2]。基于非对称液压缸的闭式电液作动器(简称“非对称式电液作动器”)两腔有效作用面积不同,导致两腔进出口的流量与泵进出油口的流量不对等。因此对于闭式泵控非对称电液作动器,必须在系统中增加补油回路,这是闭式泵控非对称电液作动器必须要解决的问题[3]。
补偿不对等流量的方法有多种,主要包括增加补油泵、使用补油阀以及应用一些新型元件设计如非对称泵[4]、单出杆对称式液压缸[5-6]等,但都存在各自的缺点。使用补油泵会增大作动器体积,不利于集成化;非对称泵主要改进泵的配流原理,使泵的流量比与非对称液压缸的面积比匹配,但由于液压系统存在泄漏、制作误差等因素,导致液压泵的排量比很难与非对称液压缸的活塞面积比理想匹配[7];单出杆对称式液压缸目前在国外应用较多,但其价格昂贵、结构复杂,在国内尚未得到广泛应用,可靠性有待考证。
目前,对非对称式电液作动器的单泵解决方案主要是采用液控单向阀或者低压梭阀来补偿不对称流量,但这2种解决方案的共同问题是系统存在压力和速度振荡,导致稳定性差[8-9]。针对非对称电液作动器的速度和压力振荡问题,本文提出一种新的作动器液压原理,将低压梭阀和2个液控换向阀的组合与蓄能器相连,高压时系统多余的液压油通过低压梭阀流向蓄能器,低压时系统多余的液压油通过2个串联的常开式液控换向阀流向蓄能器;补油时,蓄能器通过单向阀进行补油。利用AMEsim仿真平台搭建作动器模型,对其动态特性进行仿真研究。结果表明,本文提出的作动器架构在负载换向时不存在速度和压力振荡,具有良好的稳定性。
1 作动器液压原理设计 1.1 速度振荡产生原因如图1所示,根据负载和运动速度的不同,可以将
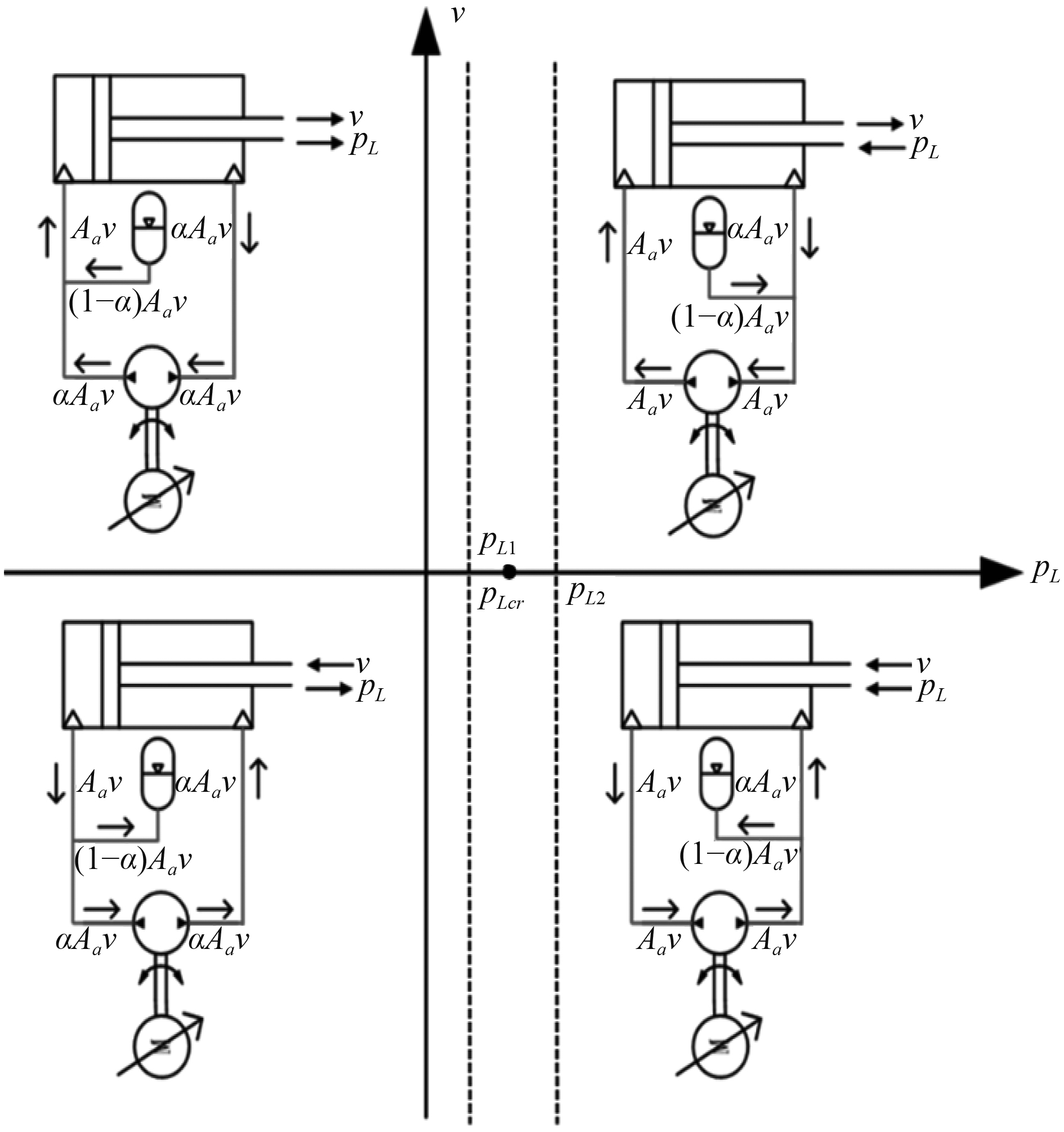
|
图 1 临界区域划分 Fig. 1 Critical area division |
| $ {p_{Lcr}} = {p_a} - \alpha {p_b} = (1 - \alpha ){p_S} $ | (1) |
式中:
以低压梭阀为例,当蓄能器与有杆腔相连时,液压缸2个腔室的压力满足:
| $ {p}_{a}-{p}_{b}>{p}_{op}, $ | (2) |
| $ {p_b} = {p_S} ,$ | (3) |
式中:
根据液压缸的受力平衡,推导出临界区域的上限为:
| $ {p_{L2}} = {p_a} - \alpha {p_b} \approx ({p_S} + {p_{op}}) - \alpha {p_S} = {p_{Lcr}} + {p_{op}}, $ | (4) |
同理,临界区域的下限为:
| $ {p_{L1}} = {p_a} - \alpha {p_b} \approx {p_S} - \alpha ({p_S} + {p_{op}}) = {p_{Lcr}} - \alpha {p_{op}} 。$ | (5) |
当
假定液压泵的泄漏与2个油口之间的压差成正比,则非对称式液压缸两腔的流量连续性方程为:
| $ {D_p}\omega - {A_a}v - {H_e}{p_a} - {H_i}({p_a} - {p_b}) - {Q_{a \to c}} = {C_a}{\dot p_a}, $ | (6) |
| $ \alpha {A_a}v - {D_p}\omega - {H_e}{p_b} + {H_i}({p_a} - {p_b}) - {Q_{b \to c}} = {C_b}{\dot p_b}。$ | (7) |
式中:
为研究临界负载附近的动态特性,取
在临界负载附近,
| $ {v_{eq}} = - \frac{{{H_e}({p_{aeq}} + {p_{beq}})}}{{A(1 - \alpha )}} 。$ | (8) |
式中:
当梭阀关闭时,此时蓄能器和液压缸两腔之间没有任何流量交换。根据式(8)可以看出,当系统泄漏系数一定时,作动器的速度与液压缸两腔的压力之和正相关,压力波动越大,速度波动就越大,该式将通过仿真得到证明。针对闭式系统低压梭阀关闭,系统多余流量无法及时流向蓄能器,目前多数研究人员通过增加系统的泄漏来避免系统的速度和压力振荡。本文提出采用2个液控换向阀来充当泄漏,解决小负载工况下低压梭阀关闭系统多余流量无法补偿的问题。
1.2 作动器原理与组成图2为非对称式电液作动器液压原理图,系统采用伺服电机和定排量泵取代以往系统所使用的电液伺服阀和变排量液压泵。作动器具体工作原理为:控制器根据液压缸反馈的实时位移以及液压缸两腔的压力信号与给定指令对比输出控制信号,调节伺服电机的转速和转向。伺服电机通过联轴器,带动双向定量泵运行。伺服电机转速不同,液压泵出口流量不同,实现调速控制;伺服电机转向不同,液压泵输出流量方向不同,实现换向控制。
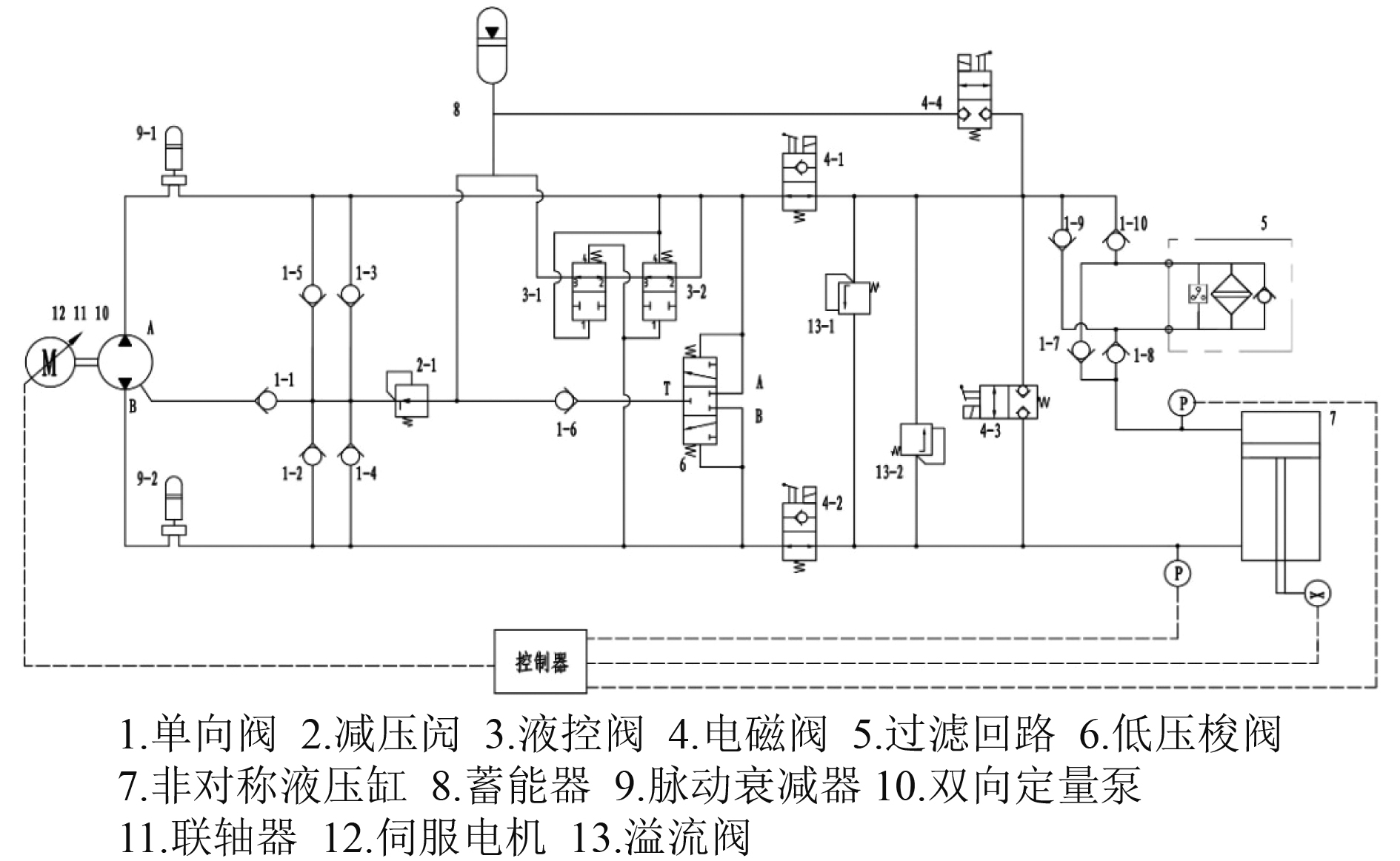
|
图 2 作动器液压原理图 Fig. 2 Hydraulic schematic diagram of actuator |
油路中电磁阀等元件仅作为系统的辅助元件,主油路上的电磁阀4-1和4-2实现泵源的隔离;过滤回路5用于过滤油液杂质,保持系统的油液清洁度;并联的溢流阀13-1和13-2用于高压情况下的溢流保护,防止因系统压力过高而造成过载现象;电磁阀4-3和4-4实现液压缸的旁通,一旦作动器发生故障,打开电磁阀即可实现液压缸自由动作,方便检修;液压泵出口的脉动衰减器9-1和9-2主要用于衰减系统宽频带上的压力脉动,达到降低作动器引起的结构振动效果。
系统采用低压梭阀6和2个液控换向阀3-1和3-2解决非对称式电液作动器的速度和压力波动问题。当活塞杆伸出时,此时蓄能器通过单向阀1-3和1-5或者1-2和1-4向系统中补充不对等流量。当活塞杆缩回时,有2种工况:当系统处于大负载工况时,系统压差较大,低压梭阀开启,液压缸活塞杆缩回所产生的多余流量经低压梭阀流入蓄能器;当系统处于小负载工况时,系统压差较小,低压梭阀阀芯处于中位,此时2个串联的常开式液控换向阀3-1和3-2开启,而活塞杆缩回所产生的多余流量经2个液控换向阀流入蓄能器。
1.3 工作特性分析液压泵的工作正方向定义和四象限工作模式如图3和图4所示。假定液压缸活塞杆伸出的方向为正方向,液压泵的工作压力为
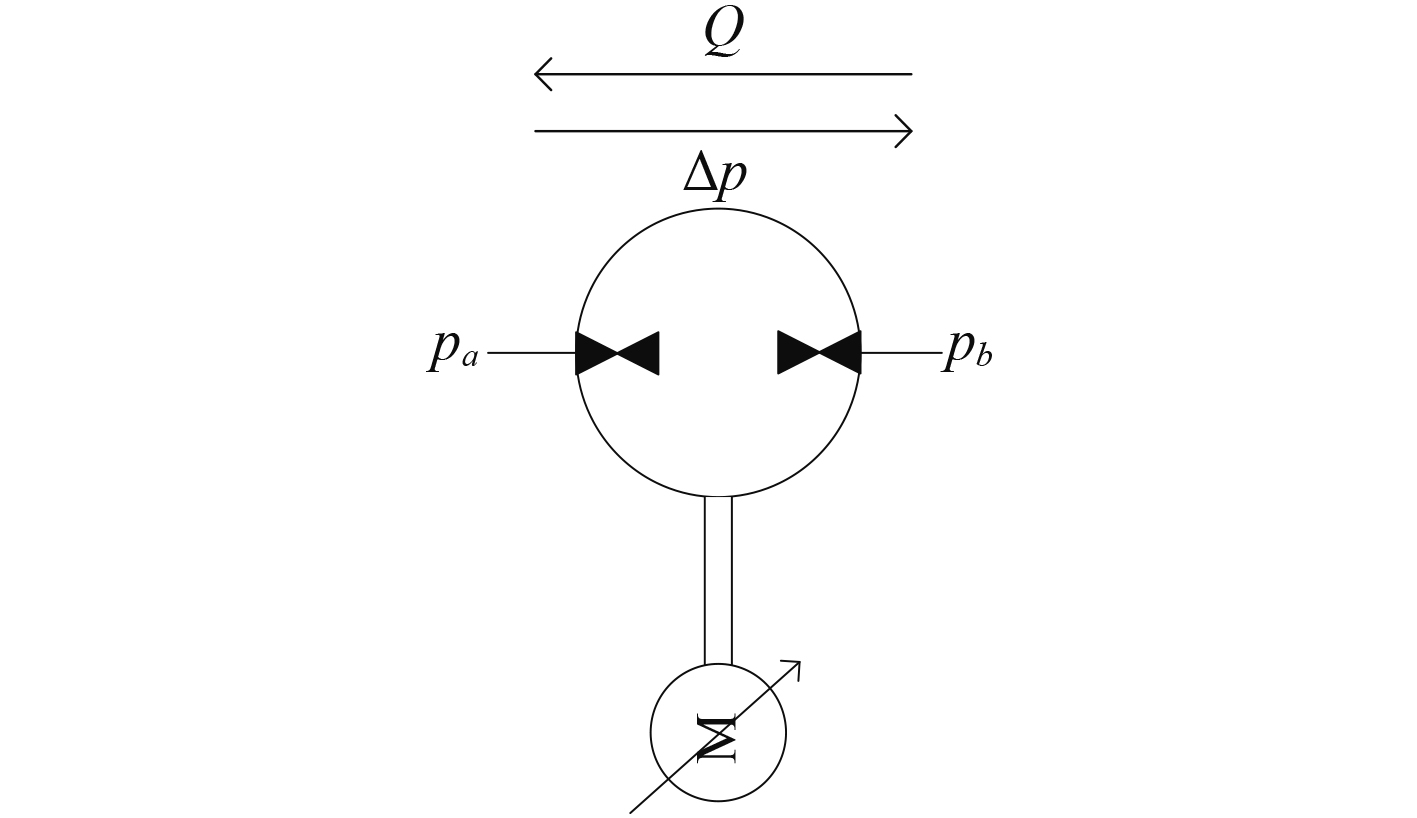
|
图 3 正方向定义图 Fig. 3 Positive direction definition map |

|
图 4 四象限工作模式 Fig. 4 Four-quadrant working mode |
当
当活塞杆正向伸出时,液压油的流向为顺时针方向(B端口→液压泵→A端口),此时有2种工况:
1)
2)
当活塞杆反向缩回时,液压油的流向为逆时针方向(A端口→液压泵→B端口),此时同样有2种工况:
1)
2)
由于本文采用的液控换向阀以及低压梭阀均为非标准件,因此首先需要用AMEsim中的HCD库分别建立阀门的模型。根据液控换向阀和低压梭阀的结构图,分别建立其HCD模型如图5和图6所示。
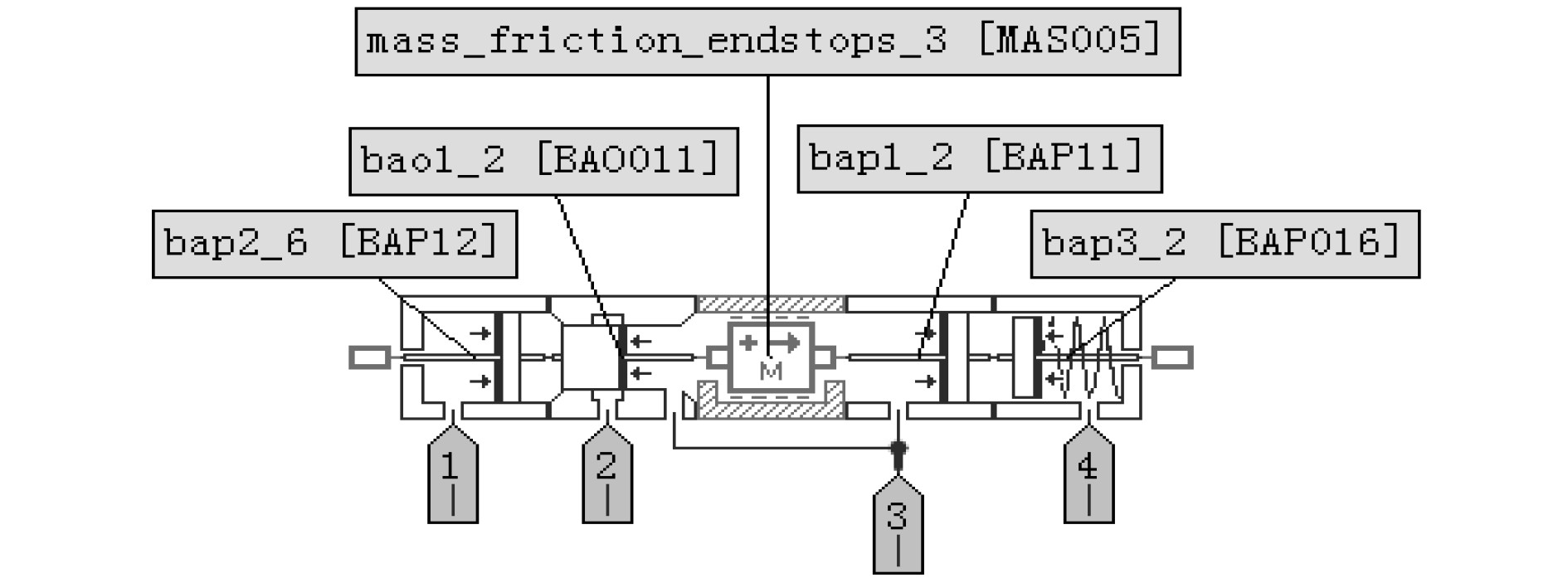
|
图 5 液控换向阀HCD模型图 Fig. 5 HCD model diagram of hydraulic control valve |

|
图 6 低压梭阀HCD模型图 Fig. 6 HCD model diagram of low pressure shuttle valve |
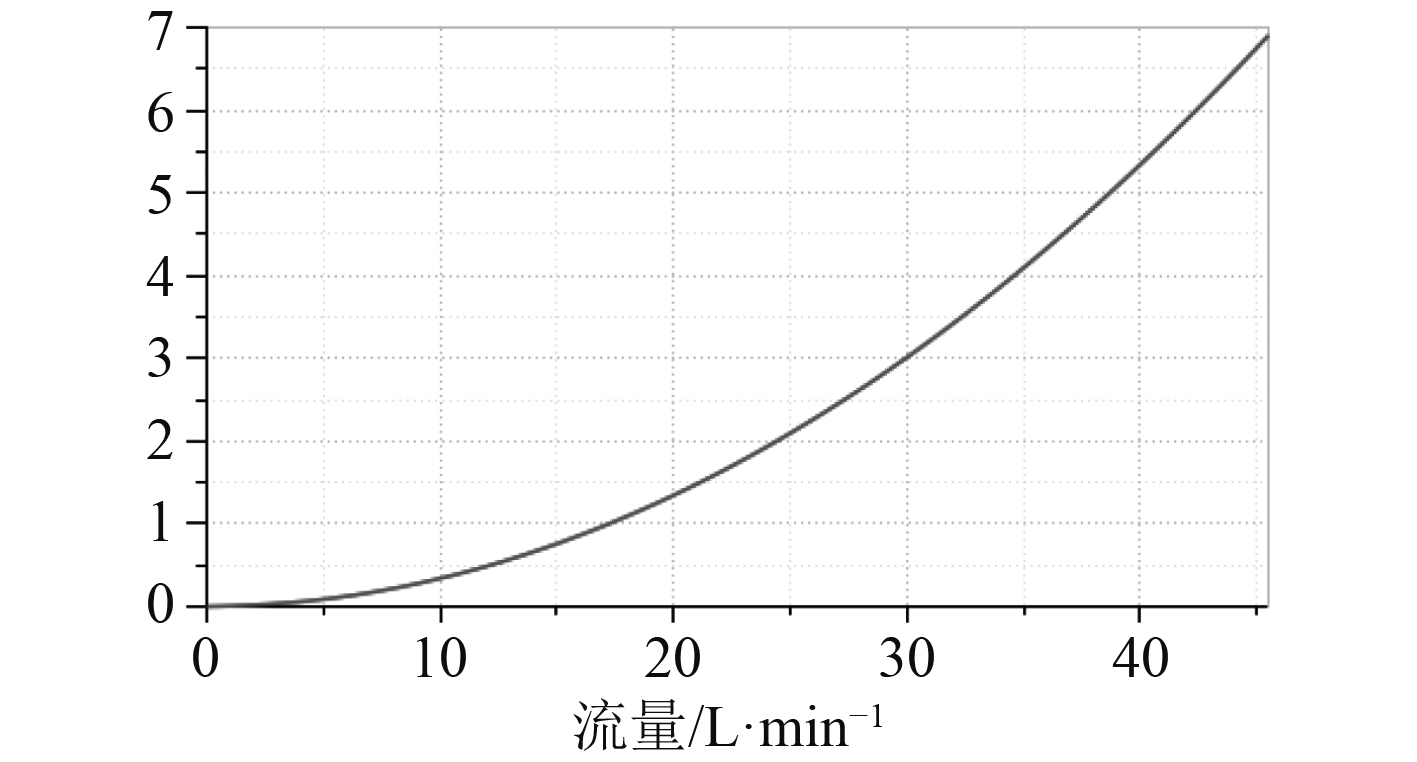
对阀门性能进行仿真,并与阀门的性能选型曲线进行对比,以验证阀门模型的正确性。图7和图8分别为液控换向阀的性能选型曲线和仿真曲线[12],图9和图10分别为低压梭阀的性能选型曲线和仿真曲线[13]。对比可知,液控换向阀和低压梭阀的性能仿真曲线和选型曲线一致,阀门的HCD模型正确。

|
图 7 液控换向阀性能选型曲线 Fig. 7 Performance selection curve of hydraulic control directional valve |
|
图 8 液控换向阀性能仿真曲线 Fig. 8 Performance simulation curve of hydraulic control directional valve |

|
图 9 低压梭阀性能选型曲线 Fig. 9 Performance selection curve of low pressure shuttle valve |

|
图 10 低压梭阀性能仿真曲线 Fig. 10 Performance simulation curve of low pressure shuttle valve |
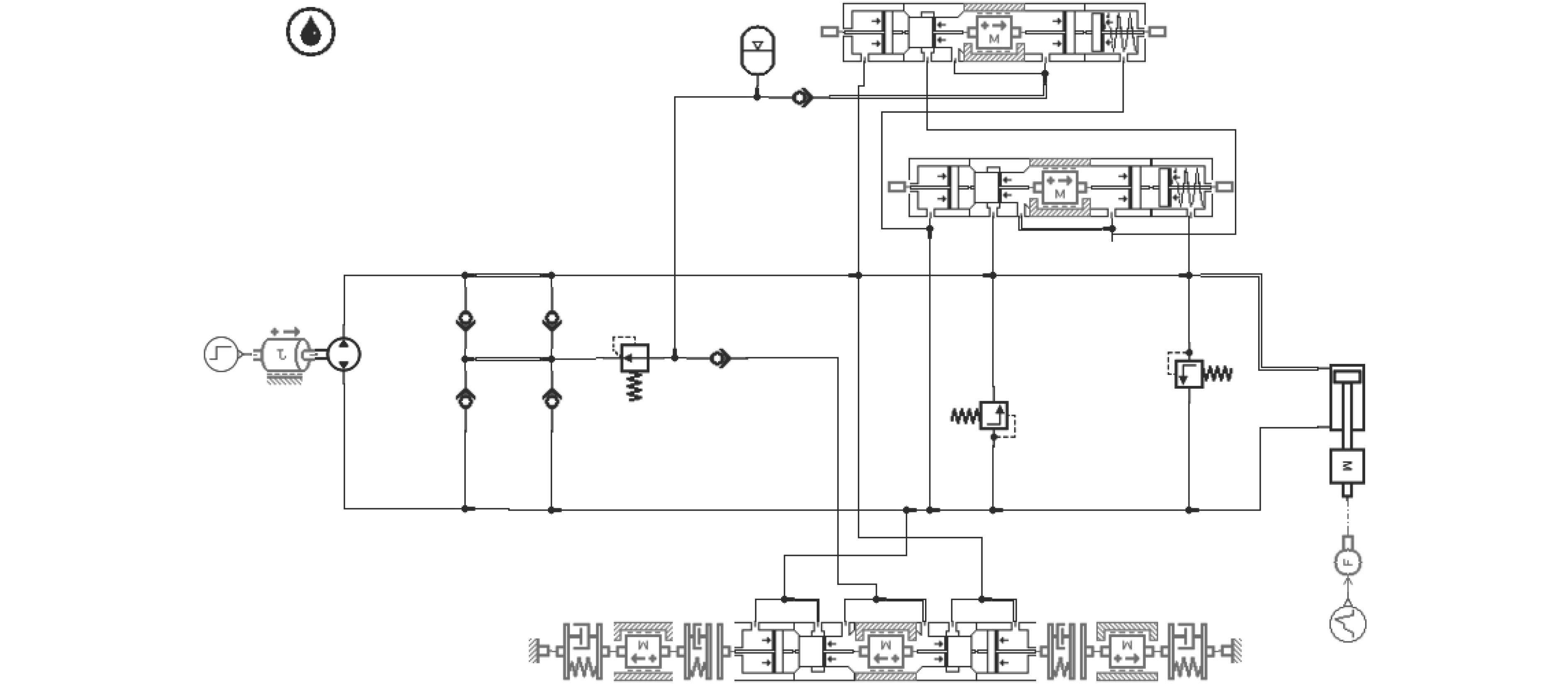
作动器其他元件均为标准件,采用AMEsim模型库中相应的模型。其次根据作动器系统的控制原理图,搭建非对称式电液作动器的AMEsim模型。在草图模式下,将所有的子模型按照作动器系统连接起来,构成如图11所示的仿真模型。
|
图 11 作动器AMEsim仿真模型 Fig. 11 AMEsim simulation model of actuator |
根据作动器的四象限工况特性分析可知,作动器活塞杆伸出时,蓄能器通过单向阀向系统补油,而活塞杆缩回时,蓄能器则需要通过低压梭阀及时吸收系统的多余流量。只有当作动器运行在第三、第四象限之间切换工况时,系统油路变化大,低压梭阀会出现关闭的时刻。为研究低压梭阀关闭时系统的稳定性,在活塞杆缩回过程中改变负载力方向,观察系统的速度和压力是否出现波动现象。
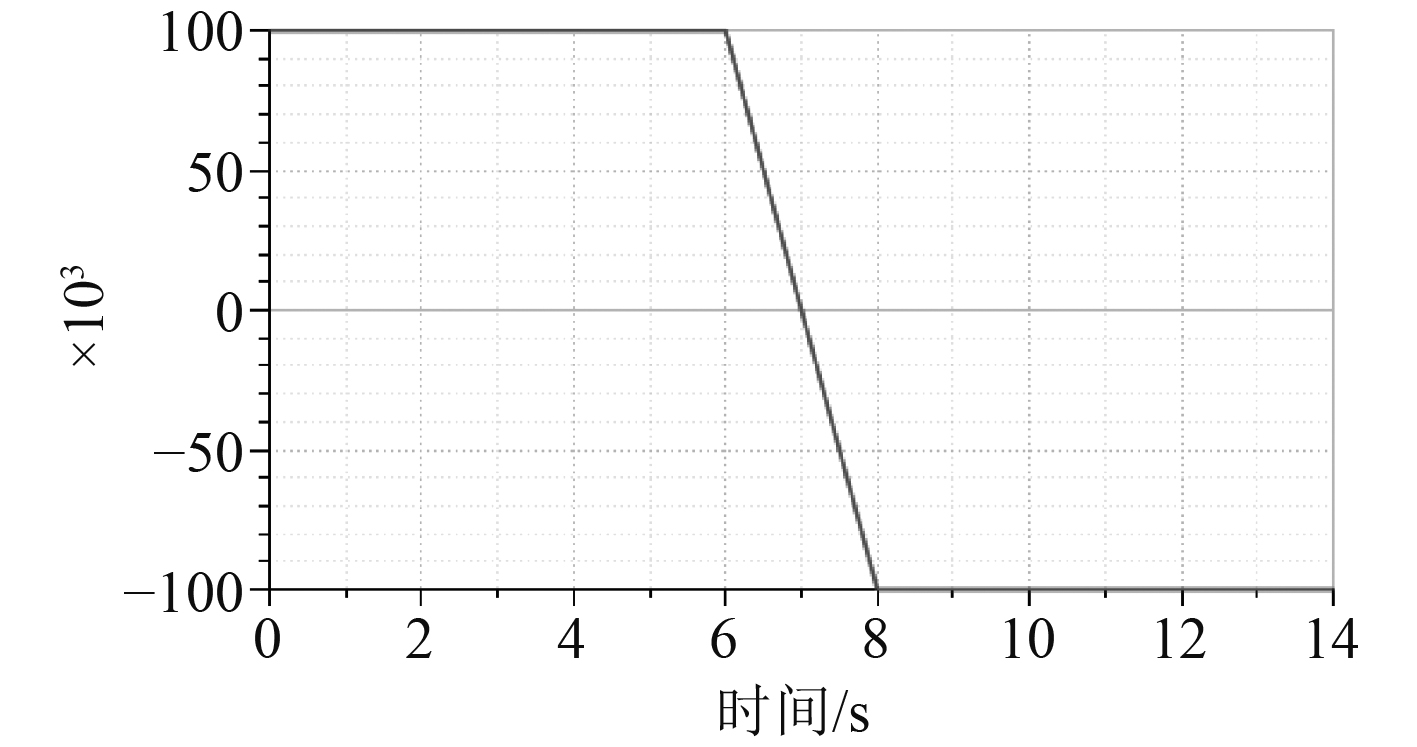
保持伺服电机反向旋转、转速为1 500 r/min不变,如图12所示。在活塞杆伸出的过程中改变负载力的方向,使作动器完成第三、第四象限工况的切换。
|
图 12 外界负载力变化曲线 Fig. 12 Variation curve of external load force |
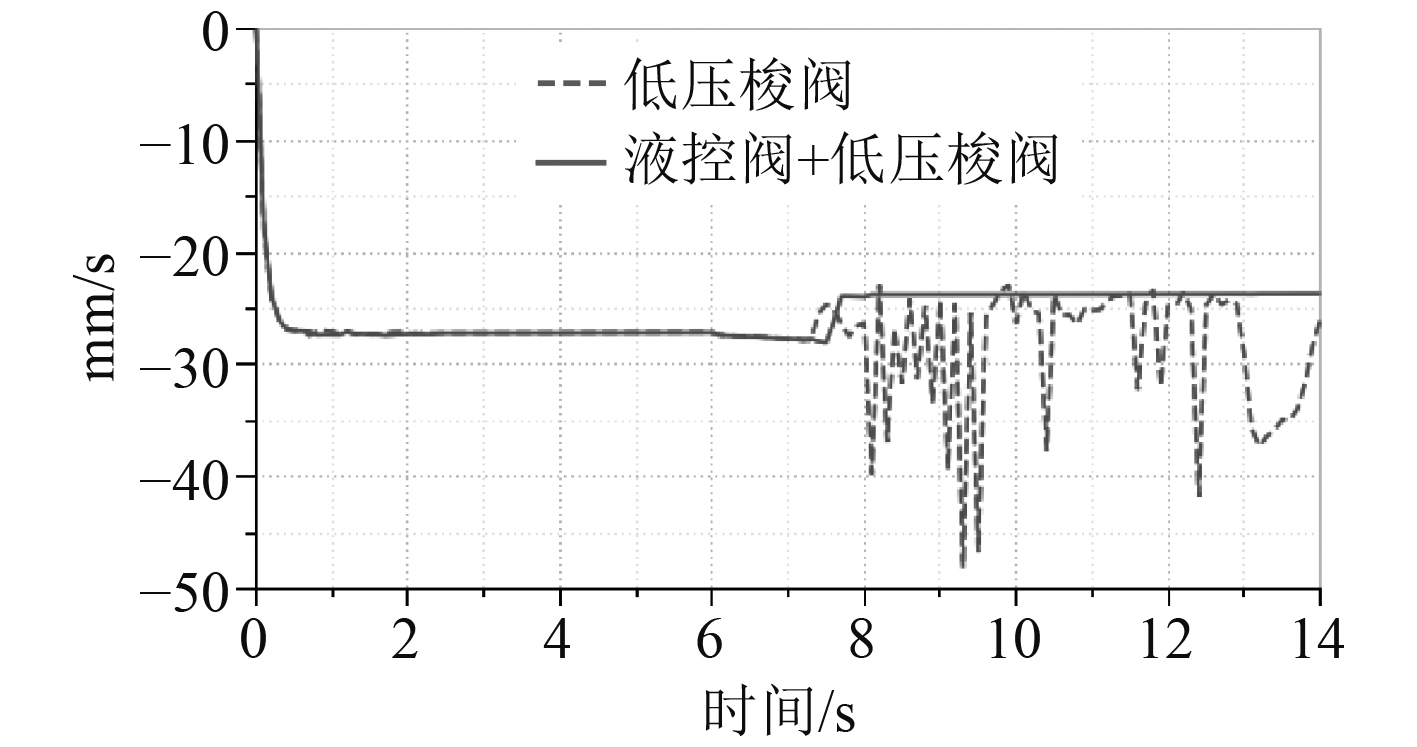
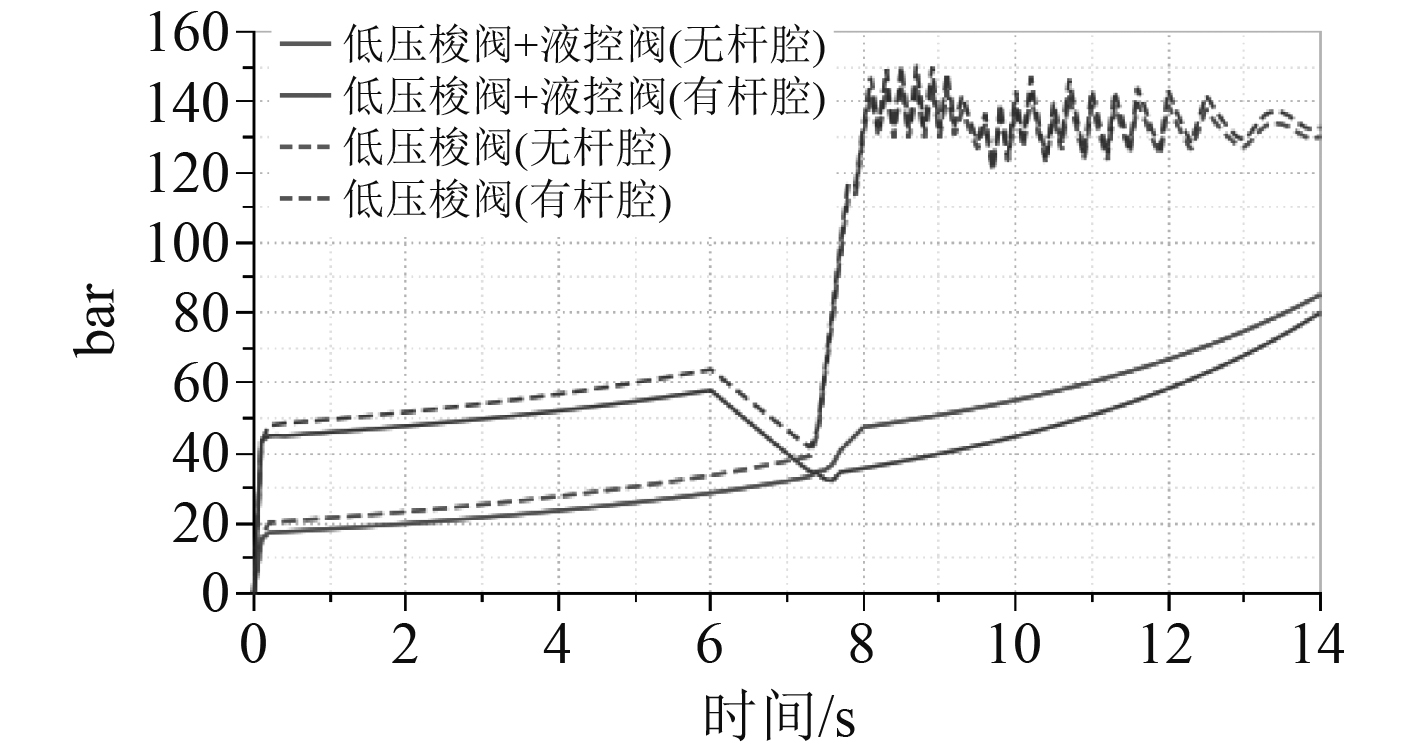
图13和14分别为采用低压梭阀和液控换向阀的作动器与只采用低压梭阀的作动器工作时液压缸活塞杆速度和压力的变化曲线。可以看出:在7 s以前,作动器工作在第三象限,活塞杆缩回,负载力做负功,有杆腔为高压腔,液压缸两腔压力逐渐增大;在7~14 s,作动器工作在第四象限,活塞杆缩回,负载力做正功。
|
图 13 速度变化曲线 Fig. 13 Speed change curve |
|
图 14 液压缸压力变化曲线 Fig. 14 Variation curves of hydraulic cylinder pressure |
作动器工况由第三象限向第四象限切换即负载改变方向时,仅采用低压梭阀的作动器两腔压力存在较大的压力和速度振荡,系统不稳定。作动器由第三象限向第四象限切换时,液压泵从液压缸的无杆腔吸油,向有杆腔供油,此时低压梭阀处于关闭状态,由于两腔的活塞面积不同,蓄能器无法吸收活塞杆缩回产生的不对称流量,系统憋压,导致系统处于失控状态。
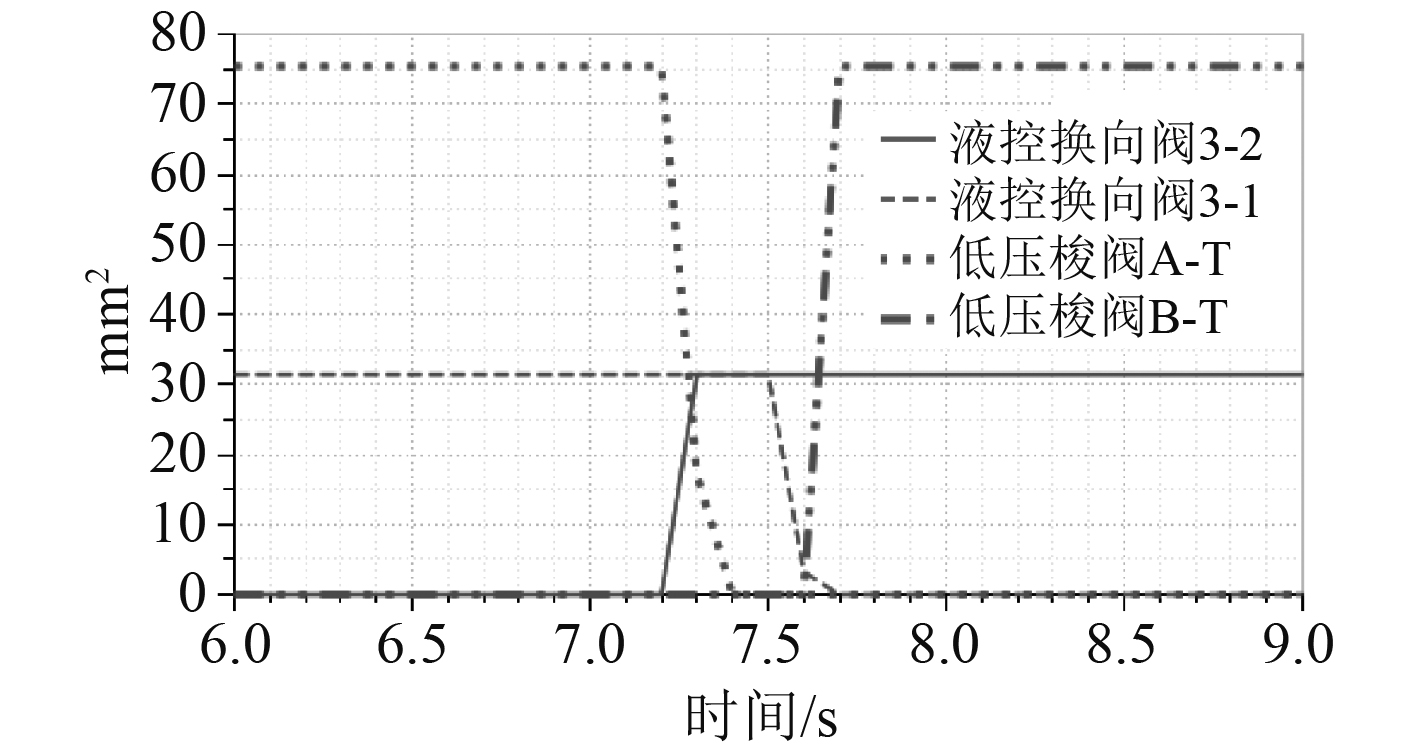
采用低压梭阀和液控换向阀的作动器在负载改变方向时,系统未出现速度和压力波动,稳定性良好。图15和图16为阀门的流量和流通面积变化曲线。当系统的压差小于低压梭阀的换向压力即小负载工况时,低压梭阀关闭,流量为0,2个液控阀同时打开,活塞杆缩回产生的多余流量及时流向蓄能器,因此本文提出的提出采用2个液控换向阀补偿小负载工况下的多余流量能够解决非对称电液作动器的速度和压力波动问题。

|
图 15 阀门流量变化曲线 Fig. 15 Variation curves of valve flow |
|
图 16 阀门流通面积变化曲线 Fig. 16 Variation curves of valve flow area |
本文针对非对称电液作动器存在的流量不对等带来的速度和压力波动问题展开研究,对闭式单泵控非对称液压缸的补油回路进行改进,提出采用2个液控换向阀补偿小负载工况下的多余流量,并利用AMEsim仿真平台搭建作动器模型,对其动态特性进行仿真研究。结果表明,与仅采用低压梭阀的单泵控非对称液压缸系统相比,本文提出的作动器架构在负载换向时不存在速度和压力波动,具有良好的稳定性。
| [1] |
权龙. 泵控缸电液技术研究现状、存在问题及创新解决方案[J]. 机械工程学报, 2008, 44(11): 87-92. |
| [2] |
QUAN Z, LONG Q, ZHANG J. Review of energy efficient direct pump controlled cylinder electro-hydraulic technology[J]. Renewable and Sustainable Energy Reviews, 2014, 35: 336–346.
|
| [3] |
王波, 李运华, 赵斌, 等. 泵控非对称液压缸系统能效特性对比研究[J]. 液压与气动, 2018(10): 8-14. DOI:10.11832/j.issn.1000-4858.2018.10.002 |
| [4] |
张晓刚, 权龙, 杨阳, 等. 并联型三配流窗口轴向柱塞泵特性理论分析及试验研究[J]. 机械工程学报, 2011, 47(14): 151-157. |
| [5] |
蒋志昌. 液压参数对称的单活塞杆伺服液压缸[J]. 液压与气动, 2008(8): 75-76. DOI:10.3969/j.issn.1000-4858.2008.08.027 |
| [6] |
于安才, 李阳, 王超光, 等. 直驱式单出杆对称液压促动器电液伺服系统研究[J]. 液压与气动, 2017(2): 27-32. DOI:10.11832/j.issn.1000-4858.2017.02.006 |
| [7] |
程冬宏, 高有山, 弓旭峰, 等. 基于流量匹配的泵控挖掘机动臂能耗特性分析[J]. 机床与液压, 2019, 47(21): 155-159. |
| [8] |
ÇALSKAN H, BALKAN T, PLATIN B E. A complete analysis for pump controlled single rod actuators[C]// In Proceedings of the 10th International Fluid Power Conference, Dresden, Germany, 2016: 119–132.
|
| [9] |
KILIC E, DOLEN M, CALISKAN H, et al. Pressure prediction on a variable-speed pump controlled hydraulic system using structured recurrent neural networks[J]. Control Engineering Practice, 2014, 26, 51–71.
|
| [10] |
王留根. FAST新型液压促动器的研制及性能分析[D]. 秦皇岛: 燕山大学, 2020.
|
| [11] |
王成宾. 伺服变量泵和泵控差动缸系统理论分析及静动态特性研究[D]. 太原: 太原理工大学, 2014.
|
| [12] |
海德福斯. Valves - Directional Controls - Piloted Directional Valve/PD10-45/Piloted Directional Valve. [EB/OL]. https://www.hydraforce.com/zh/products/valves/directional–controls/pd10-45/.
|
| [13] |
SUN. 直动式, 低压侧, 3位, 梭阀. [EB/OL]https://www.sunhydraulics.com/zh/model/DSCL.
|
 2023, Vol. 45
2023, Vol. 45

