随着“碳中和”和“碳达峰”概念的提出,电力驱动已成为时代发展的主流方向。在船舶电力推进这样的大功率负载驱动领域,单台电机受限于功率、体积等因素,已经无法满足使用需求[1-2]。解决这一问题,常用的方法有2种方法:一是采用多相电机代替传统三相电机[3],二是采用2台或者多台电机协同工作[4]。采用双电机共轴驱动,可以在降低系统转动惯量和体积的同时增大输出转矩[5]。而多相感应电机,具有转矩脉动低、电机损耗小、电机极限容量大、能量密度高、容错性好等一系列优点,适合于对可靠性要求较高的推进领域[6]。共轴双电机系统的难点在于如何解决负载均衡和双机协调控制问题。文献[7]在主从控制和交叉耦合的基础上,加入了“差矩反馈”环节,解决了功率平衡问题,提高了电机功率平衡精度,改善了动态性能。靳运莘等[8]构建了基于主从结构的共轴双无刷直流电机仿真模型,验证了主从控制结构下系统具有良好的稳定性。耿强等[9]针对硬连接电机磨损后造成转矩不平衡问题,提出了转矩均衡控制策略,大幅降低了单台电机过载的风险。上述文献对于共轴电机的研究,集中在共轴双机输出均衡上,研究对象以三相电机和直流电机为主[10-12],同时对于故障后的双机负载分配研究较少。
为解决共轴双机驱动系统中的快速跟踪响应问题和故障状态下的功率分配问题,本文从双Y移30°异步电机数学模型入手,通过坐标变换,构建出两相旋转坐标系下的电机数学模型,并利用S函数进行共轴双机系统仿真建模。在单电机矢量控制基础上,研究六相双电机共轴驱动系统主从控制策略。为验证该驱动系统正常工况下的跟踪性能和故障工况下的容错性能,进行了仿真实验分析。仿真结果对于多相电机共轴驱动系统的研究有一定参考作用。
1 共轴双六相异步电机模型 1.1 六相电机物理结构模型六相电机按相绕组位置安排分为对称分布和不对称分布,本文选用的电机为双Y移30°异步电机,采用不对称分布。该电机模型有2套三相绕组,分别记为ABC和XYZ,2套三相绕组之间中性点隔离,相位差为30°[13-14],其绕组分布结构如图1(a)所示。
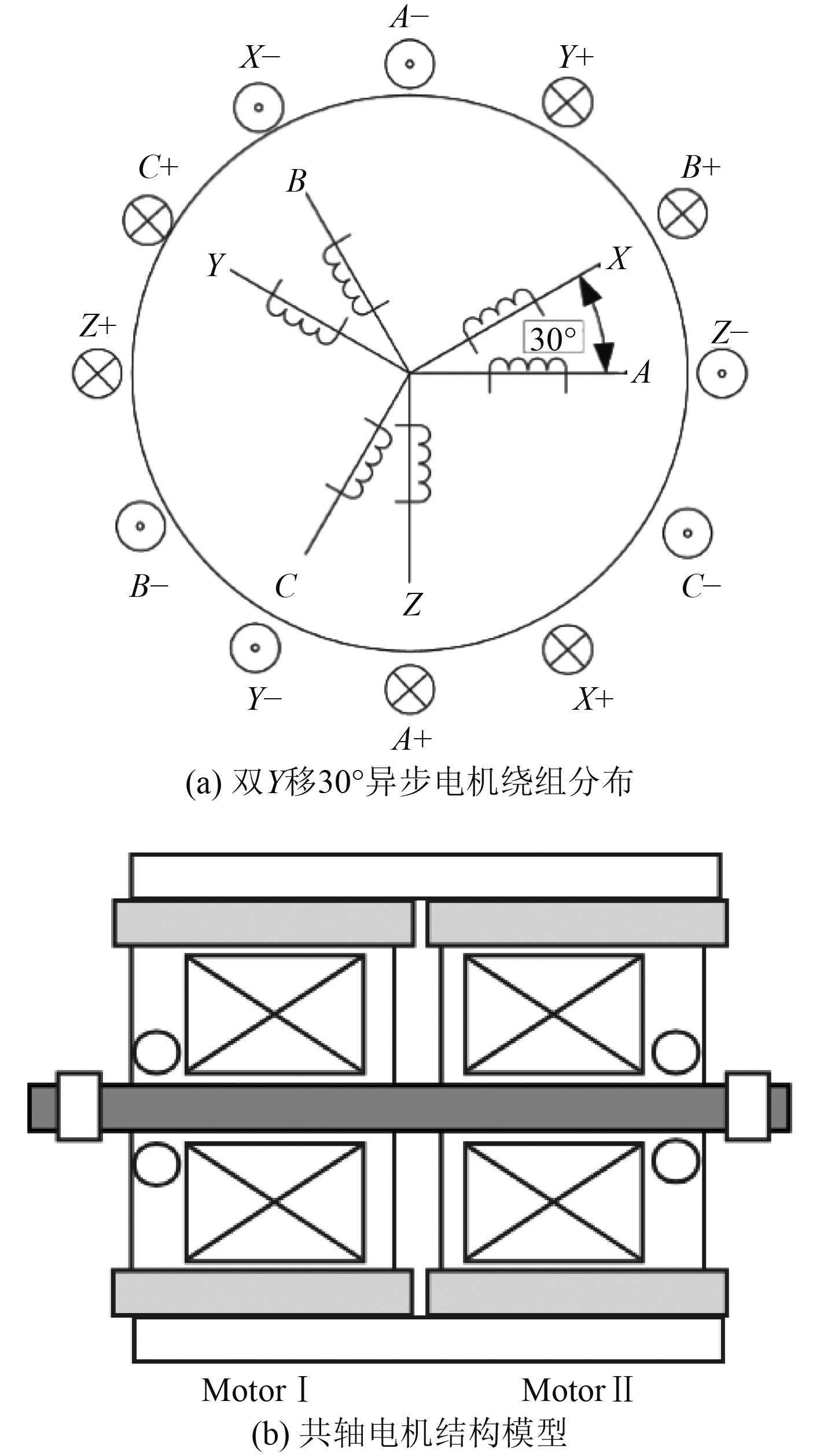
|
图 1 物理结构 Fig. 1 Physical structure |
共轴双电机的特点是2个独立电机同轴安装,电机I和II在电路和磁路上互相独立,转速上强制相同,运行过程中互为备份,其结构如图1(b)所示。
1.2 六相电机坐标变换六相电机在自然坐标系下是一个多变量耦合的非线性系统,很难直接进行分析。为降低分析难度,在磁势和功率不变2个约束条件下,采用线性变换进行坐标变换是必要的[15-18]。坐标变换时,通常假设绕组按正弦分布,气隙均匀,且忽略磁饱和、铁心损耗。
根据绕组磁动势的关系得出:
| $\begin{aligned}[b] {F_\alpha } = &{F_A} + {F_X}\cos \left( {\text{π} /6} \right) + {F_B}\cos \left( {4\text{π} /6} \right) +\\ & {F_Y}\cos \left( {5\text{π} /6} \right) + {F_C}\cos \left( {8\text{π} /6} \right), \\ {F_\beta } =& {F_X}\sin \left( {\text{π} /6} \right) + {F_B}\sin \left( {4\text{π} /6} \right) + {F_Y}\sin \left( {5\text{π} /6} \right) + \\ & {F_C}\sin \left( {8\text{π} /6} \right) - {F_Z}\sin \left( {9\text{π} /6} \right), \end{aligned}$ | (1) |
式中,
| $\begin{aligned}[b] & \left( {\begin{array}{*{20}{c}} {{F_\alpha }} \\ {{F_\beta }} \end{array}} \right) = \frac{1}{2}\left( {\begin{array}{*{20}{c}} 2&{\sqrt 3 }&{ - 1}&{ - \sqrt 3 }&{ - 1}&0 \\ 0&1&{\sqrt 3 }&1&{ - \sqrt 3 }&{ - 2} \end{array}} \right)\times \\ & {\left( {\begin{array}{*{20}{c}} {{F_A}}&{{F_X}}&{{F_B}}&{{F_Y}}&{{F_C}}&{{F_Z}} \end{array}} \right)^{\rm{T}}}。\end{aligned}$ | (2) |
六相静止坐标系与两相静止坐标系之间的变换关系如图2(a)所示。
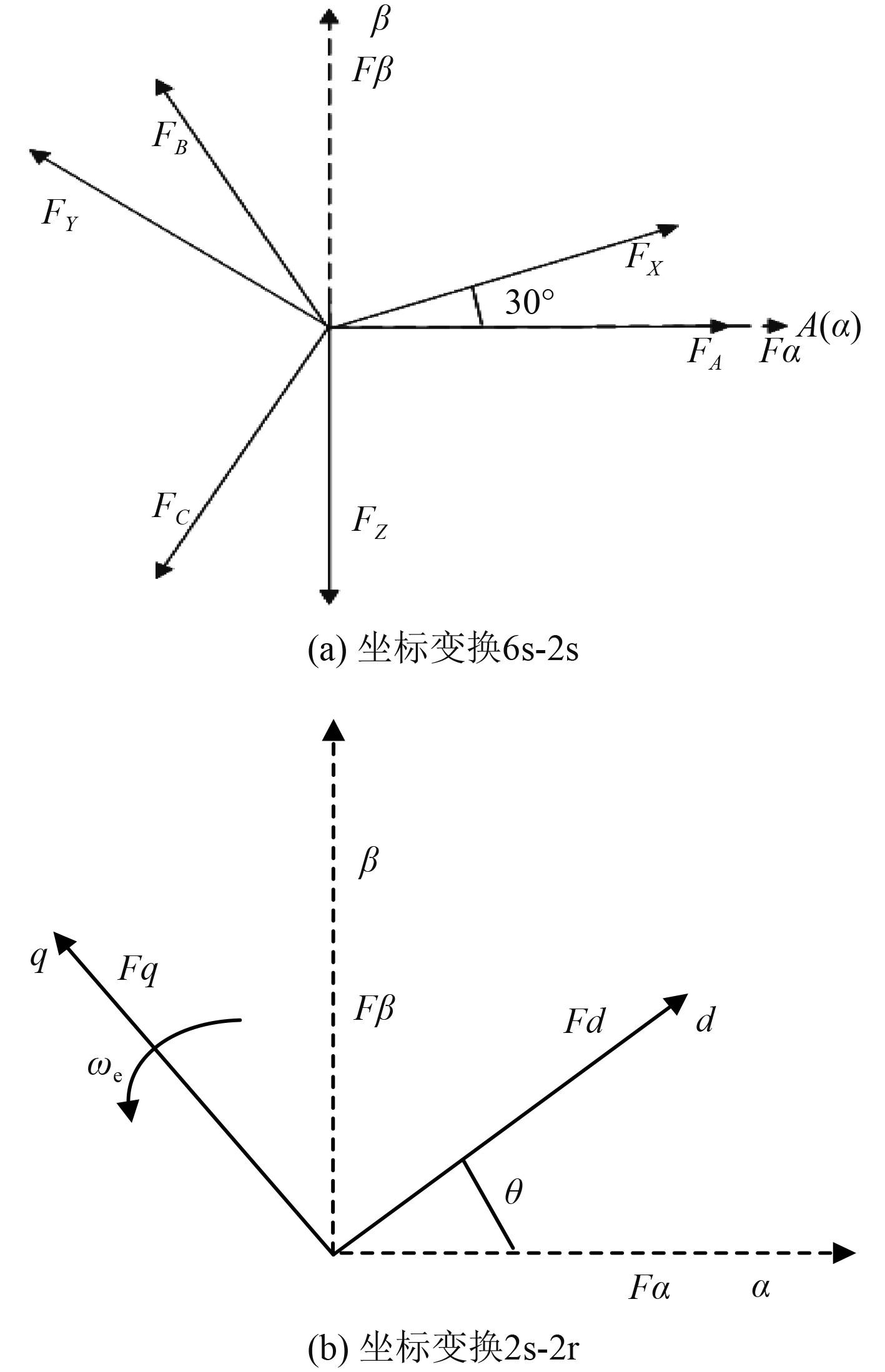
|
图 2 坐标系之间转换 Fig. 2 Transformation between coordinate systems |
为将变换矩阵正交化,添加4个不涉及机电能量转化的零序正交分量,变换矩阵:
| $ {C_{6{\text{s}}/2s}} = \frac{1}{{2\sqrt 3 }}\left( {\begin{array}{*{20}{c}} 2&{\sqrt 3 }&{ - 1}&{ - \sqrt 3 }&{ - 1}&0 \\ 0&1&{\sqrt 3 }&1&{ - \sqrt 3 }&{ - 2} \\ 2&{ - \sqrt 3 }&{ - 1}&{\sqrt 3 }&{ - 1}&0 \\ 0&1&{ - \sqrt 3 }&1&{\sqrt 3 }&{ - 2} \\ 2&0&2&0&2&0 \\ 0&2&0&2&0&2 \end{array}} \right)。$ | (3) |
为将静止坐标系下的绕组等效成直流电机的2个绕组,构建两相dq(MT)旋转坐标系,两坐标系的转换关系如图2(b)所示。
变换矩阵:
| $ {C_{2{\text{s}}/2r}} = \left( {\begin{array}{*{20}{c}} {\cos \theta }&{\sin \theta }&{{o_4}} \\ { - \sin \theta }&{\cos \theta }&{{o_4}} \\ {{o_4}}&{{o_4}}&{{E_4}} \end{array}} \right)。$ | (4) |
根据各矩阵间的关系可得:
| $ \begin{aligned}[b] & {C_{6{{s}}/2{{r}}}} = {C_{6{{s}}/2s}}.{C_{2{{s}}/2r}}, \\ & {C_{2{{r/}}6{{s}}}} = {C_{6{{s}}/2{{r}}}}^{ - 1} = {C_{6{{s}}/2{{r}}}}^{\rm{T}} 。\end{aligned} $ | (5) |
式中:下标
通过坐标变换,可实现六相电机的数学模型在自然坐标系下与两相旋转坐标系下的互相转换,简化分析过程。
1.3 基于S函数的双机共轴系统模型双电机共轴系统每台电机受独立逆变器控制,因此系统的电压、磁链可看做2个独立的个体,而系统的转矩、运动因共轴连接,可看做整体进行分析。通过建立dq坐标系下的状态方程,用Matlab中S函数编程,可实现对异步电机的准确描述[19-20]。
在dq旋转坐标系下,异步电机的电压方程为:
| $ \begin{aligned}[b] & {{{u}}_{{{sd}}}} = {R_s}{{{i}}_{sd}} + p{\psi _{sd}} - {\psi _{sq}}{\omega _s}, \\ & {{{u}}_{{{sq}}}} = {R_s}{{{i}}_{sq}} + p{\psi _{sq}} + {\psi _{sd}}{\omega _s}, \\ & {{{u}}_{{{rd}}}} = {R_r}{{{i}}_{rd}} + p{\psi _{rd}} - {\psi _{rq}}{\omega _{sl}}, \\ & {{{u}}_{{{rq}}}} = {R_r}{{{i}}_{rq}} + p{\psi _{rq}} + {\psi _{rd}}{\omega _{sl}}。\end{aligned} $ | (6) |
定子、转子磁链方程为:
| $ \begin{aligned}[b] & {\psi _{sd}} = {L_{s{\text{d}}}}{i_{sd}} + {L_{md}}{i_{rd}},\\ & {\psi _{sq}} = {L_{sd}}{i_{sq}} + {L_{md}}{i_{rq}},\\ & {\psi _{rd}} = {L_{rd}}{i_{rd}} + {L_{md}}{i_{sd}},\\ & {\psi _{rq}} = {L_{rd}}{i_{rq}} + {L_{md}}{i_{sq}}。\end{aligned} $ | (7) |
式中:
将式(7)代入式(6),按照有无微分算子分开整理,可得方程:
| $ \begin{aligned}[b] & \left( {\begin{array}{*{20}{c}} {{{u}_{{sd}}}} \\ {{{u}_{{sq}}}} \\ {{{u}_{{rd}}}} \\ {{{u}_{{rq}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{R_s}}&{ - {\omega _s}{L_{sd}}}&0&{ - {\omega _s}{L_{md}}} \\ {{\omega _s}{L_{sd}}}&{{R_s}}&{{\omega _s}{L_{md}}}&0 \\ 0&{ - {\omega _{sl}}{L_{md}}}&{{R_r}}&{ - {\omega _{sl}}{L_{rd}}} \\ {{\omega _{sl}}{L_{{\text{m}}d}}}&0&{{\omega _{sl}}{L_{{\text{r}}d}}}&{{R_r}} \end{array}} \right)\times\\ & \left( {\begin{array}{*{20}{c}} {{i_{sd}}} \\ {{i_{sq}}} \\ {{i_{rd}}} \\ {{i_{r{\text{q}}}}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{L_{sd}}}&0&{{L_{md}}}&0 \\ 0&{{L_{sd}}}&0&{{L_{md}}} \\ {{L_{md}}}&0&{{L_{rd}}}&0 \\ 0&{{L_{md}}}&0&{{L_{rd}}} \end{array}} \right)\times p\left( {\begin{array}{*{20}{c}} {{i_{sd}}} \\ {{i_{sq}}} \\ {{i_{rd}}} \\ {{i_{r{\text{q}}}}} \end{array}} \right), \end{aligned}$ | (8) |
对于笼型异步电机,转子电压为0,即urd= urq= 0,将式(3)化为状态方程标准形式:
| $ x = {\left( {\begin{array}{*{20}{c}} {{i_{sd}}}&{{i_{sq}}}&{{i_{rd}}}&{{i_{rq}}} \end{array}} \right)^{\rm{T}}}\quad u = {\left( {\begin{array}{*{20}{c}} {{u_{sd}}}&{{u_{sq}}}&{{u_{rd}}}&{{u_{rq}}} \end{array}} \right)^{\rm{T}}} $ |
| $\begin{aligned}[b] & A = - {\left( {\begin{array}{*{20}{c}} {{L_{sd}}}&0&{{L_{md}}}&0 \\ 0&{{L_{sd}}}&0&{{L_{md}}} \\ {{L_{md}}}&0&{{L_{rd}}}&0 \\ 0&{{L_{md}}}&0&{{L_{rd}}} \end{array}} \right)^{ - 1}}\times \\ & \left( {\begin{array}{*{20}{c}} {{R_s}}&{ - {\omega _s}{L_{sd}}}&0&{ - {\omega _s}{L_{md}}} \\ {{\omega _s}{L_{sd}}}&{{R_s}}&{{\omega _s}{L_{md}}}&0 \\ 0&{ - {\omega _{sl}}{L_{md}}}&{{R_r}}&{ - {\omega _{sl}}{L_{rd}}} \\ {{\omega _{sl}}{L_{{\text{m}}d}}}&0&{{\omega _{sl}}{L_{{\text{r}}d}}}&{{R_r}} \end{array}} \right), \quad \\ & B = {\left( {\begin{array}{*{20}{c}} {{L_{sd}}}&0&{{L_{md}}}&0 \\ 0&{{L_{sd}}}&0&{{L_{md}}} \\ {{L_{md}}}&0&{{L_{rd}}}&0 \\ 0&{{L_{md}}}&0&{{L_{rd}}} \end{array}} \right)^{ - 1}}, \end{aligned}$ |
转矩方程为:
| $ {T}_{\text{e}}={n}_{p}{L}_{md}\left( {{i}_{sq}{i}_{rd}-{i}_{sd}{i}_{rq}} \right), $ | (9) |
运动方程为:
| $ {T_{{\text{e1}}}} + {T_{{\text{e2}}}} - {T_L} = \frac{J}{{{{n}_p}}}.\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}}。$ | (10) |
式中:
采用S函数对异步电机进行建模,根据状态方程式进行函数编程,建立异步电机模型,选择输入向量为
为简化控制流程,对单电机采用矢量控制策略,基于电机数学模型的坐标变换,解耦出励磁电流和转矩电流,建立转速外环、电流内环的双闭环控制系统,实现稳定转速和控制转矩的目的。
为实现双机控制系统中的快速跟踪响应和同步控制,双机驱动系统选用主从控制结构,其原理是将主电机的输出作为从电机输入参考值,可实现从电机对主电机的跟踪,具有结构简单、控制灵活、抗扰动性好等优点。本文共轴双机控制系统,因两电机转速强制相同,依据转矩方程式(11)和运动方程式(12),计算出共轴系统输出转速,与参考值比较产生误差,经过转速调节器(ASR)生成主电机参考转矩电流;将主电机的实际输出转矩电流作为从电机的输入参考值,实现从机对主机的转矩跟踪;将两电机电流分别进行PI控制生成dq轴电压,经过S函数,输出六相电流、电磁转矩和转速,实现双机同步控制。
为实现双机功率灵活分配,确保故障情况下电机不过载,设置了主从跟踪系数K[21]。通过改变K值,控制主从电机的输出比例。由功率
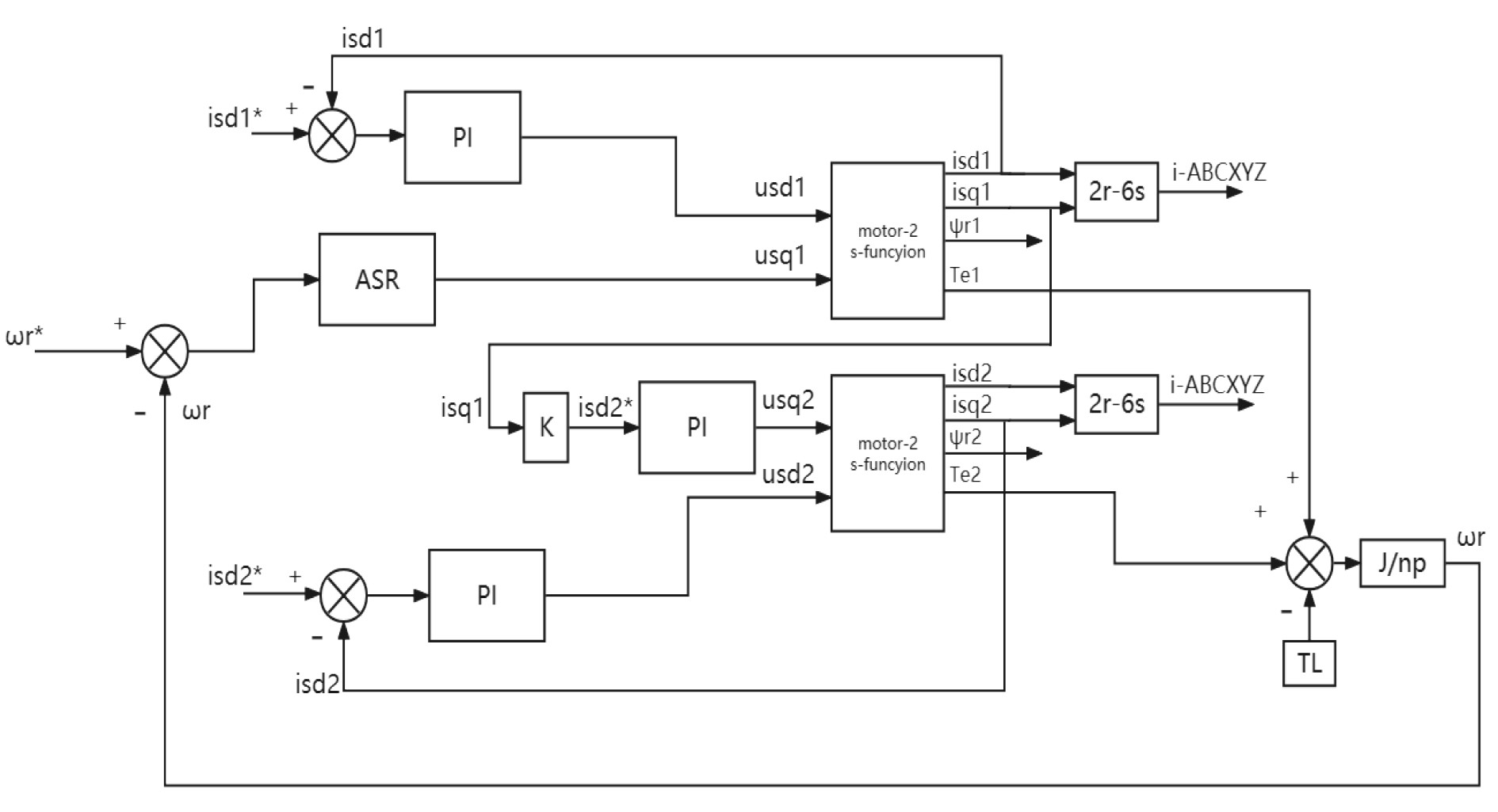
|
图 3 双机主从控制原理图 Fig. 3 Master/slave control schematic diagram of dual machines |
为验证共轴双机控制系统正常工作时稳定性能和故障时的容错性能,对系统进行仿真实验。
3.1 双机控制系统同步性能仿真分析为检验双机主从控制结构下的同步性能及抗负载扰动能力,进行仿真验证。系统空载起动,给定转速
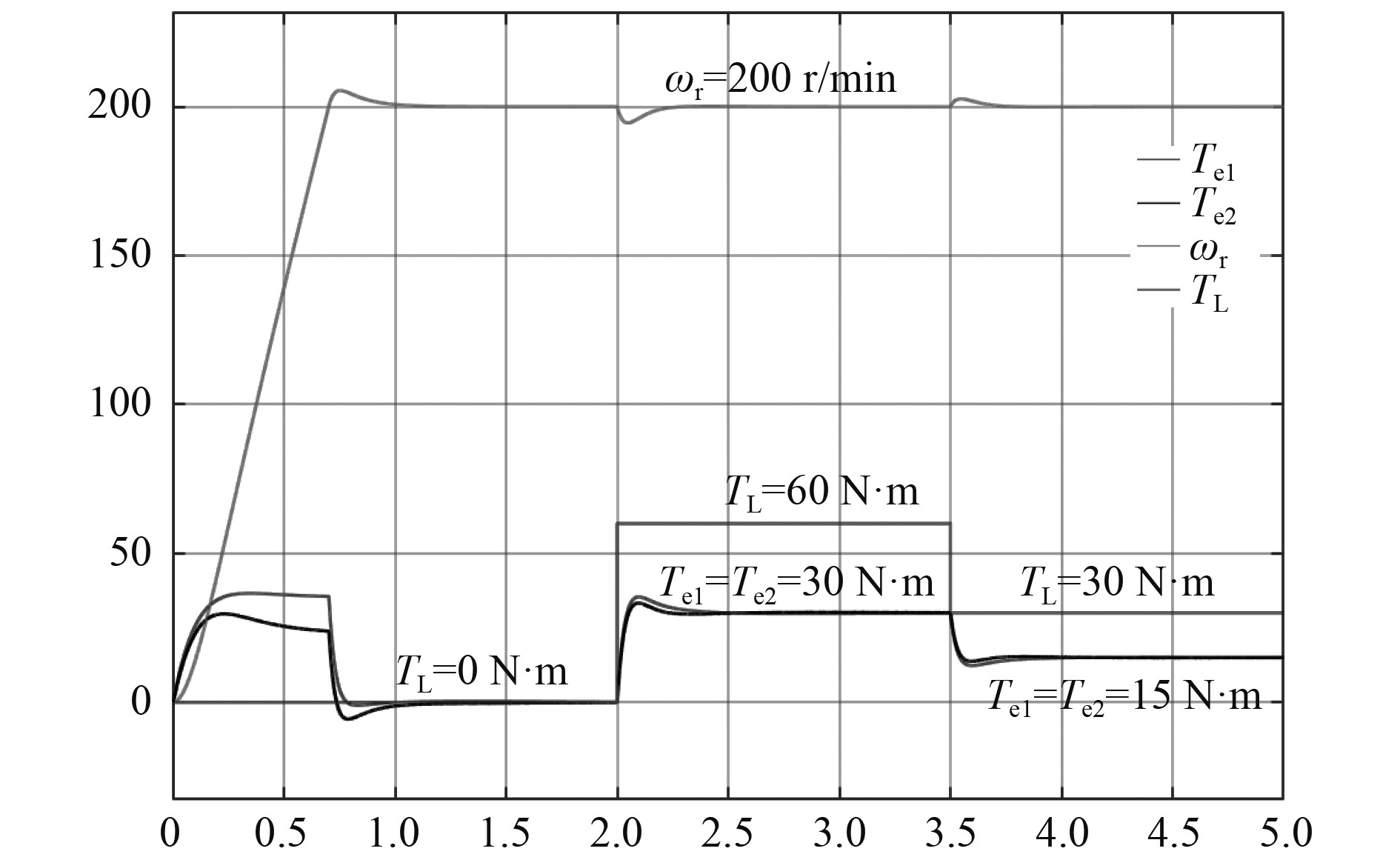
|
图 4 系统转速、转矩变换曲线 Fig. 4 Transformation curves of system speed and torque |
可以看出,在空载启动阶段,转速由0上升至稳定耗时0.9 s,启动速度较快,超调量较小,启动曲线较为理想,电磁转矩随着转速上升而升高,转速达到给定值后,电磁转矩下降至0;2 s加负载后,转速出现小幅度下降后迅速恢复至给定值,3.5 s卸负载后,转速略有上升后恢复,期间随着负载转矩的变化,电磁转矩能迅速响应,使电机处于新的平衡状态。在电机的启动、加载、卸载过程中,系统运行过程平稳,波动量低于5%,抗负载扰动能力较好。电机I作为主电机响应速度较快,电机II作为从电机,跟踪主电机信号略有滞后,因此其超调量较小,整体运行更为稳定,符合主从结构的特点。系统整体显示出良好的同步性能。从图5的电流曲线可以看出,系统运行过程中,主电机和从电机电流波形较为稳定,基本一致。由图6(c)和图6(d)看出,从电机电流追踪主电机,幅值略小于主电机,响应上存在延迟,两者相位存在一个固定差值,与理论分析和转矩特性一致。
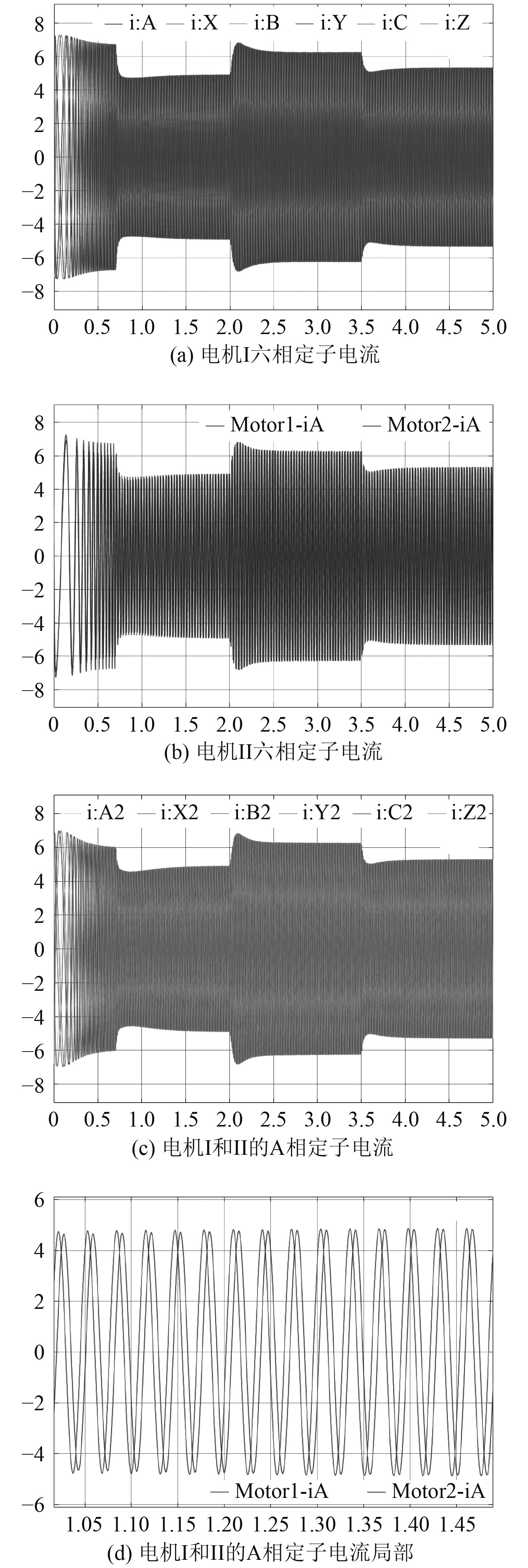
|
图 5 定子电流相应曲线 Fig. 5 Corresponding curve of stator current |
双Y移30°异步电机有2套三相绕组,在出现故障导致缺失一套绕组后,另一套绕组可以保持电机继续工作,相当于切换为三相电机状态,具有良好的容错性。故障条件下,为防止故障电机过载,保持系统运行稳定性,可根据现存正常绕组套数,重新配置各电机的输出比例,保证每套绕组输出均衡。
当从电机缺失一套负载,系统工作时,主从电机现存绕组数为2∶1,为保证从电机绕组电流不过载,主从电机输出转矩应调整为2∶1。通过改变模型K值为0.5,可以将负载按照2∶1分配给主从电机,保证各套绕组输出均衡。系统转矩变化曲线如图6(a)所示。
当主电机缺失一套负载,系统工作时,主从电机现存绕组数为1∶2,为保证从电机绕组电流不过载,主从电机输出转矩应调整为1∶2。通过改变模型K值为2,可以将负载按照1∶2分配给主从电机,保证各套绕组输出均衡。系统转矩变化曲线如图6(b)所示。
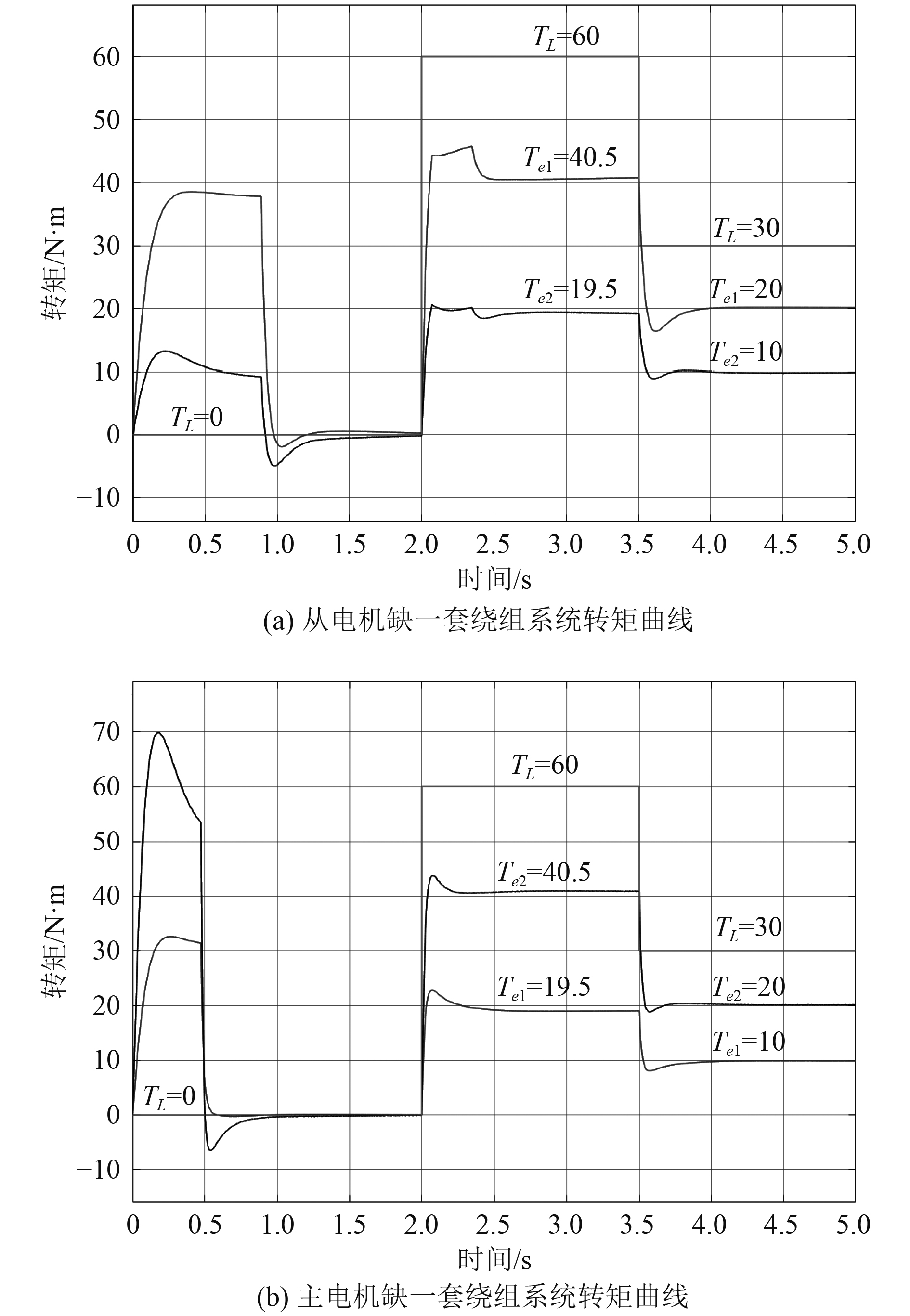
|
图 6 系统负载转矩和电磁转矩变换曲线 Fig. 6 System load torque and electromagnetic torque transformation curves |
根据仿真分析可知,共轴系统缺失绕组后,可根据现存正常工作绕组套数改变主从跟踪系数K,调整主从电机输出功率比,使电机在缺失一套绕组后仍能正常工作,且能保证正常工作的绕组输出均衡,确保了故障电机不过载,保证了系统故障下的稳定运行。
仿真结果与理论分析一致,验证了主从控制策略下的共轴双六相电机驱动系统具有良好的稳定性能和抗负载扰动性。因主从控制策略固有特性限制,从机响应存在一定滞后,但总体性能较为稳定,响应速度较快。故障条件下,系统可根据现存绕组套数,改变主从跟踪系数K,实现灵活控制主从电机的输出比重,保证了故障电机不过载,证明了模型的正确性。
4 结 语本文以六相双电机驱动系统为研究对象,根据双Y移60°六相异步电机的结构特点,采用S函数建立了两相旋转坐标系下的电机仿真模型;在单电机矢量控制基础上,构建出主从结构下的双机共轴驱动系统模型并进行仿真实验。实验结果表明:主从控制结构下的双电机共轴驱动系统在正常工作状态下,具有良好的跟踪性和抗扰动性;在缺失绕组故障情况下,能改变主从跟踪系数,实现主从电机功率合理分配的目的,确保故障电机不过载,保证了系统的稳定性。
| [1] |
肖雄, 王浩丞, 武玉娟, 等. 基于双滑模估计的主从结构共轴双电机模型预测直接转矩控制无速度传感器控制策略[J]. 电工技术学报, 2021, 36(5): 1014-1026. |
| [2] |
张超, 裴延涛. 基于矢量控制的同轴串联双电机负载平衡系统[J]. 电工电气, 2010(2): 33-34+53. |
| [3] |
孟超, 欧阳红林, 刘伟候, 等. 双Y移30°永磁同步电机的空间矢量调制[J]. 中国电机工程学报, 2010, 30(3): 90-98. |
| [4] |
叶宇豪, 彭飞, 黄允凯. 多电机同步运动控制技术综述[J]. 电工技术学报, 2021. |
| [5] |
LIN Faa-Jeng, CHOU Po-Huan, CHEN Chin-Sheng, et al. DSP-based cross-coupled synchronous control for dual linear motors via intelligent complementary sliding mode control[J]. IEEE Transactions on Industry Electronics, 2012, 59(2): 1061-1073. DOI:10.1109/TIE.2011.2157286 |
| [6] |
郭新华, 郭保甲, 颜冰钧, 等. 双Y移30°六相异步电机弱磁控制算法研究[J]. 控制工程, 2015, 22(1): 180-184. |
| [7] |
毕如林, 褚建新, 张兆恒. 基于矢量控制的双电机硬联结负载功率平衡[J]. 计算机仿真, 2013, 30(4): 353-355+364. |
| [8] |
靳运莘, 徐永向, 王骞, 等. 基于主从控制结构的多电机转矩均衡控制研究[J]. 微电机, 2016, 49(8): 58-61. |
| [9] |
耿强, 单长帅, 刘涛, 等. 双电机刚性齿轮传动系统转矩均衡控制[J]. 电工技术学报, 2017, 32(15): 17-26. |
| [10] |
BOGIATZIDIS I, SAFACAS A, MITRONIKAS E, et al. A novel control strategy applicable for a dual AC drive with common mechanical load[J]. IEEE Transactions on Industry Applications, 2012. |
| [11] |
MENGONI M, TANI A, ZARRI L, et al. Position control of a multi-motor drive based on series-connected five-phase tubular PM actuators[J]. IEEE Transactions on Industry Applications, 2013. |
| [12] |
陈光团, 周扬忠. 六相串联三相双永磁同步电机预测型直接转矩控制研究[J]. 中国电机工程学报, 2018, 38(15): 4526-4536. |
| [13] |
张伟伟, 肖飞, 乔鸣忠, 等. 六相双Y移30°异步电机调速设计与仿真[J]. 海军工程大学报, 2017, 29(2): 22-26. |
| [14] |
ABJADI NR. Sliding-mode control of a six-phase series/parallel connected two induction motors drive[J]. Isa Transactions, 2014. |
| [15] |
朱军, 阮江军, 陈嘉福. 十五相异步电机建模及稳态仿真研究[J]. 电机与控制学报, 2017, 21(9): 8-14. |
| [16] |
黄守道, 王铭, 钱鋆, 等. 双Y移30度六相PMSM的空间矢量控制[J]. 控制工程, 2011, 18(2): 202-205+243. |
| [17] |
王贤明, 程晗, 何露, 等. 六相双Y30°绕组感应电机建模与控制技术研究[J]. 舰船科学技术, 2020, 42(15): 140-144. |
| [18] |
刘陵顺, 张少一, 刘华菘. 双 Y 移 30° PMSM 两电机串联系统的谐波效应[J]. 电机与控制学报, 2014, 18(7): 72-78. LIU Lingshun, ZHANG Shaoyi, LIU Huasong. Harmonic effects of double Y shift 30° PMSM two-motor series-connected system[J]. Electric Machines and Control, 2014, 18(7): 72-78. |
| [19] |
周晓华, 张银, 潘盛辉, 等. 异步电机S函数建模及矢量控制仿真实验设计[J]. 实验技术与管理, 2018, 35(1): 120-124. |
| [20] |
蔡卓剑, 赵荣祥, 汪槱生, 等. 一种多相异步电机的通用数学模型[J]. 中国电机工程学报, 2015, 35(15): 3929-3938. |
| [21] |
王琛琛, 齐龙, 苟立峰, 等. 基于无速度传感器的异步电机并联加权矢量控制[J]. 电工技术学报, 2015, 30(10): 131-137+156. |
 2023, Vol. 45
2023, Vol. 45

