2. 浙江理工大学 机械与自动控制学院,浙江 杭州 310018
2. College of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China
并联出水问题来源于水下弹道导弹的齐射出水、水下枪炮多管并射形成弹幕拦截或攻击低空飞行目标等海战背景,具有很强的工程应用价值。当采用并联发射方式潜射导弹/射弹时,可以显著地增加武器的突防概率和毁伤效果。并联出水过程中不仅涉及了流体介质的突变,气相、固体、液相的三相耦合流动,还存在航行体之间的流场彼此干扰,导致航行体的流场和运动特性非常复杂。
导弹/射弹以较高速度水下发射时,其表面发生空化形成空泡,空泡的演化过程及形态关系到水下航行体的受力情况,进而影响到航行体的弹道特性。因此,空泡演化特性的研究一直是该领域的研究重点。在国外,Logvinovich等[1]提出的空泡截面独立膨胀原理,可用于计算空泡的形状。Savchenko等[2]提出了计算超空泡轮廓的半经验公式。Waugh等[3]通过实验研究了发射角度和空泡对导弹出水姿态的扰动影响,给出了出水空泡的形态。Nguyen等[4]利用数值模拟方法研究了射弹匀速出水过程的超空泡流动,给出了射弹出水过程的阻力变化和超空泡形态。在国内,贾会霞等[5,6]利用高速摄像技术开展了超空泡射弹出水的实验研究,获得了出水过程中空泡的演化过程和射弹的速度变化,给出了不同模型和参数下超空泡出水形态尺寸的变化规律。施红辉等[7]采用实验和数值模拟相结合的方法研究了超空泡射弹出水的现象,分析了射弹头部形状对射弹运动、自由面破碎、超空泡形状的影响。别庆等[8]基于Mixture多相流模型,采用动网格技术和6DOF技术建立了潜射导弹水下运动模型,获得了变速状态下导弹的空泡特性。鲁传敬等[9]基于多相流模型,采用动网格技术数值模拟了细长体出水过程。魏海鹏等[10]比较了不同多相流模型在航行体出水过程中对流体界面捕获、压力计算方面的差异,给出了VOF模型和Mixture模型的适用范围。颜开等[11]对出水空泡的行为进行了很多数值计算,给出了空泡周围速度场和压力场的变化规律。Zhang等[12]数值模拟了出水空泡溃灭的过程,获得了出水速度对空泡形态及溃灭压力的影响。陈瑛等[13]利用大涡模拟的数值方法对导弹出水过程中空泡脱离和溃灭进行了研究。
针对并联出水问题,Mnasri等[14]利用VOF模型和动网格技术进行了双圆柱体低速并联出水的二维数值模拟,分析了出水过程中自由面的变形以及流场的相互干扰。卢佳兴等[15]进行了回转体齐射出水实验,分析了回转体间的流体动力干扰和艇速对其影响。毕凤阳等[16]建立了多细长体水下齐射多相流动与多体运动耦合数值模拟的计算模型,分析了典型工况下的齐射扰动特性。
综上所述,现有的研究主要集中在单航行体出水过程的空泡演化、流体动力以及弹道特性等,但对高速航行体并联出水的超空泡流动特性研究还偏少。本文基于VOF多相流模型,引入Schnerr-Sauer空化模型、SST
采用VOF多相流模型描述水、水蒸汽、空气构成的多相流动系统,该模型将三相当作密度可变的单一介质的混合相来处理,各相共享同一压力差和速度场。混合相的连续性方程和动量方程分别为:
| $ \frac{{\partial {\rho _{\text{m}}}}}{{\partial t}} + \frac{{\partial \left( {{\rho _{\text{m}}}{u_i}} \right)}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \begin{split}\frac{{\partial \left( {{\rho _{\text{m}}}{u_j}} \right)}}{{\partial t}} + \frac{{\partial \left( {{\rho _{\text{m}}}{u_i}{u_j}} \right)}}{{\partial {x_i}}} = & - \frac{{\partial P}}{{\partial {x_j}}} + \frac{\partial }{{\partial {x_i}}}\left[ {\mu _{\text{m}}}\left( \frac{{\partial {u_i}}}{{\partial {x_j}}} +\right.\right.\\ & \left.\left.\frac{{\partial {u_j}}}{{\partial {x_i}}} \right) \right] +{\rho _{\text{m}}}{g_i} + {F_i}。\end{split} $ | (2) |
式中:
采用SST
| $ \frac{\partial }{{\partial t}}({\alpha _{\text{v}}}{\rho _{\text{v}}}) + \nabla \cdot ({\alpha _{\text{v}}}{\rho _{\text{v}}}\overrightarrow {{v_{\text{v}}}} ) = {R_e} - {R_c}, $ | (3) |
| $ {R_e} = \frac{{{\rho _{\text{v}}}{\rho _{\text{l}}}}}{{{\rho _{\text{m}}}}}{\alpha _{\text{v}}}\left( {1 - {\alpha _{\text{v}}}} \right)\frac{3}{{{\Re _B}}}\sqrt {\frac{2}{3}\left( {\frac{{{P_{\text{v}}} - P}}{{{\rho _{\text{l}}}}}} \right)} ,{P_{\text{v}}} > P, $ | (4) |
| $ {R_c} = \frac{{{\rho _{\text{v}}}{\rho _{\text{l}}}}}{{{\rho _{\text{m}}}}}{\alpha _{\text{v}}}\left( {1 - {\alpha _{\text{v}}}} \right)\frac{3}{{{\Re _B}}}\sqrt {\frac{2}{3}\left( {\frac{{P - {P_{\text{v}}}}}{{{\rho _{\text{l}}}}}} \right)} ,{P_{\text{v}}} < P 。$ | (5) |
式中:
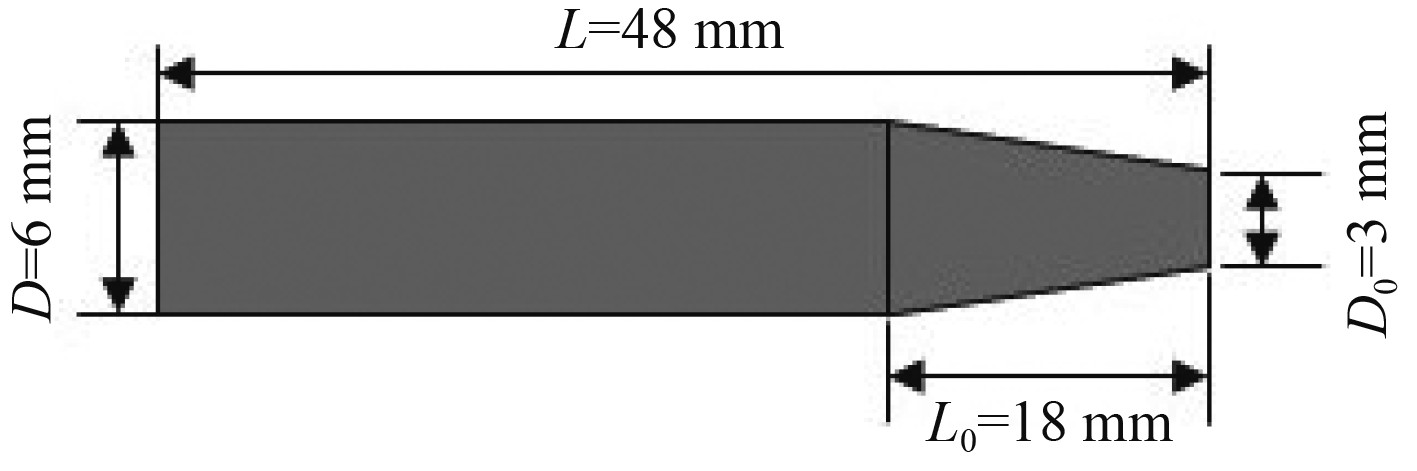
数值模型中采用的航行体模型为截锥型射弹,如图1所示。该弹由1个圆台和1个圆柱组成,质量为2.98 g,圆柱段直径D=6 mm,锥段长L0=18 mm,射弹全长L=48 mm,空化器直径D0=3 mm。
|
图 1 几何模型示意图 Fig. 1 Schematic diagram of geometric model |
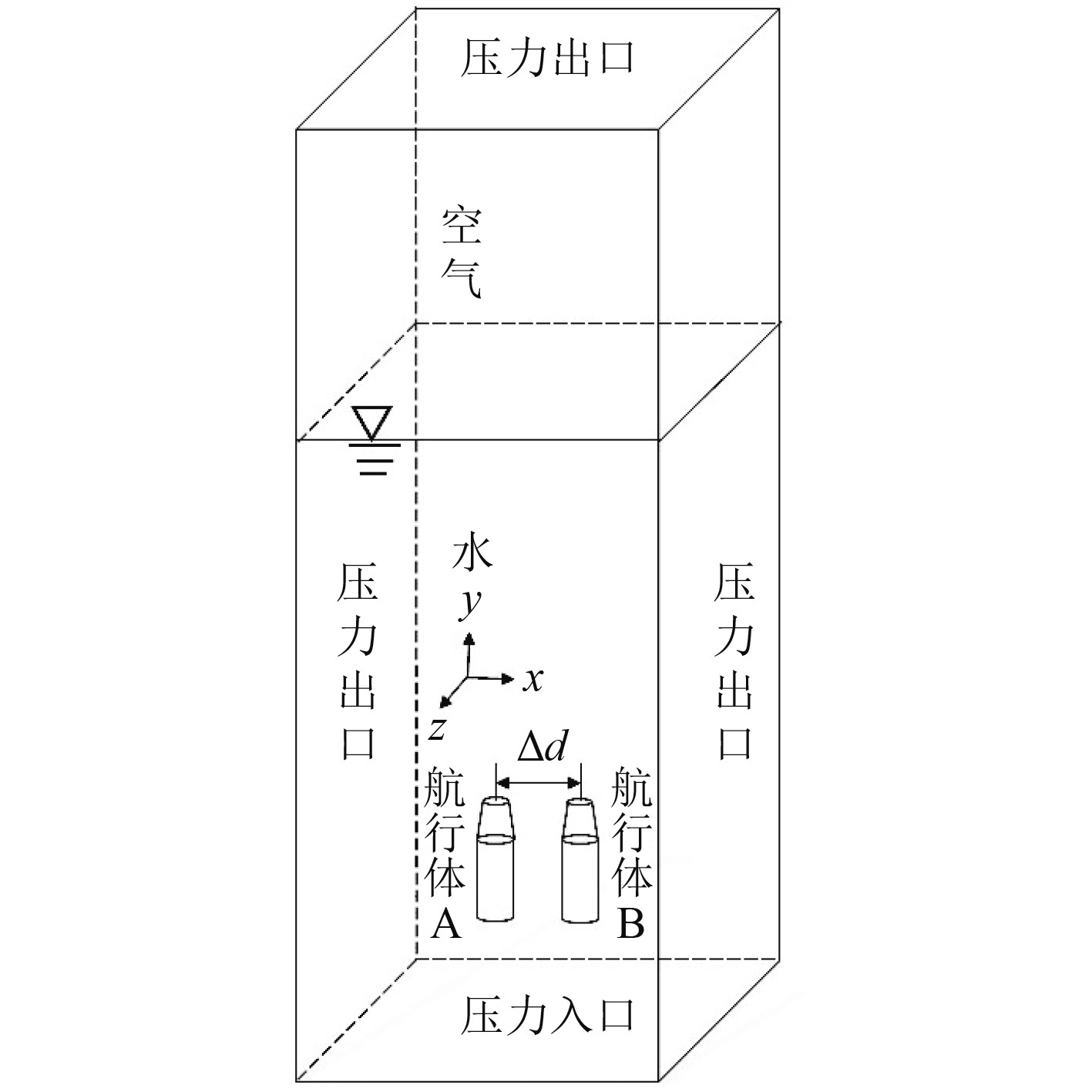
计算域和边界条件设置如图2所示,计算域为长方体,高780 mm,长210 mm,宽120 mm。计算域的底部为压力入口,计算域的侧面和上部为压力出口,采用用户自定义场函数定义边界面上的压力。空气域高300 mm,水域高480 mm,航行体头部距离自由液面的高为400 mm,航行体A和航行体B的表面均设定为无滑移壁面。上述计算模型中压力与速度耦合的求解采用Coupled算法,压力场和空间离散采用PRESTO!格式,体积率离散采用Modified HRIC。定义两航行体轴线之间的距离为并联间距△d。航行体的质心在y方向的位移为纵向位移Sy,在y方向的速度为纵向速度Vy,取竖直向上为正,定义航行体无量纲纵向位移
|
图 2 计算域及边界条件设置 Fig. 2 Computational domain and boundary condition setting |
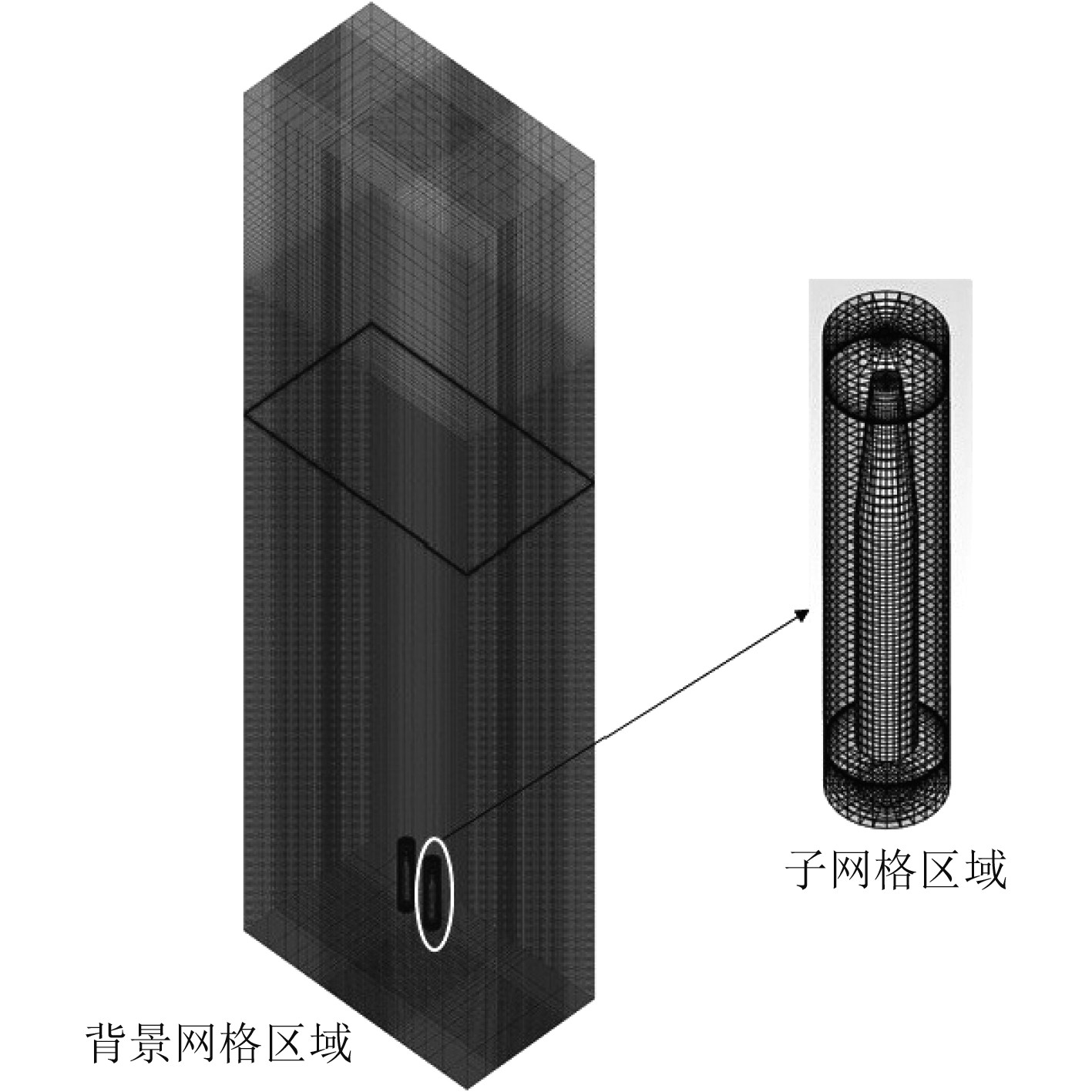
在数值模拟中重叠网格技术是研究流场中多物体运动最为直接有效的方法之一,因此本文选择重叠网格技术实现2个航行体并联出水的数值模拟。计算区域分为背景网格区域和子网格区域,由于航行体A和航行体B分别独立运动,因此需要划分2个子网格区域。图3为计算域的网格划分示意图,均采用结构化网格进行划分,全计算域的网格总数约为216.5万。背景网格区域中的航行体运动区域和自由液面附近进行局部加密,以便精确捕捉空泡界面和自由液面的变形,外部背景区域网格较疏,加快收敛速度。2个子网格区域大小相同,均为包裹航行体的圆柱,其长度为10D,直径为2D,并且采用相同的网格划分方式,对航行体壁面附近区域进行网格加密。计算中,航行体的运动通过6DOF刚体运动模型求解。
|
图 3 网格划分示意图 Fig. 3 Schematic diagram of meshing |
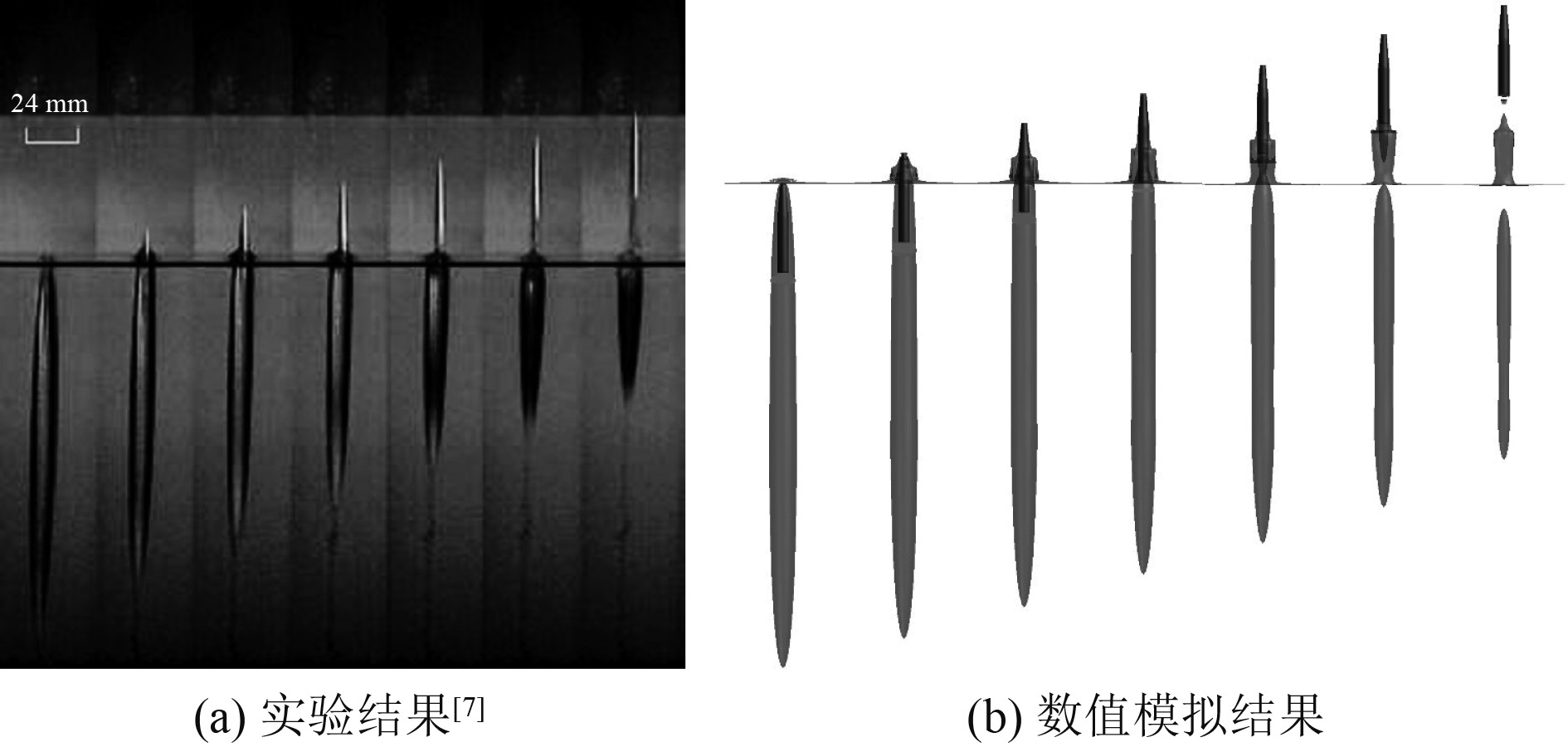
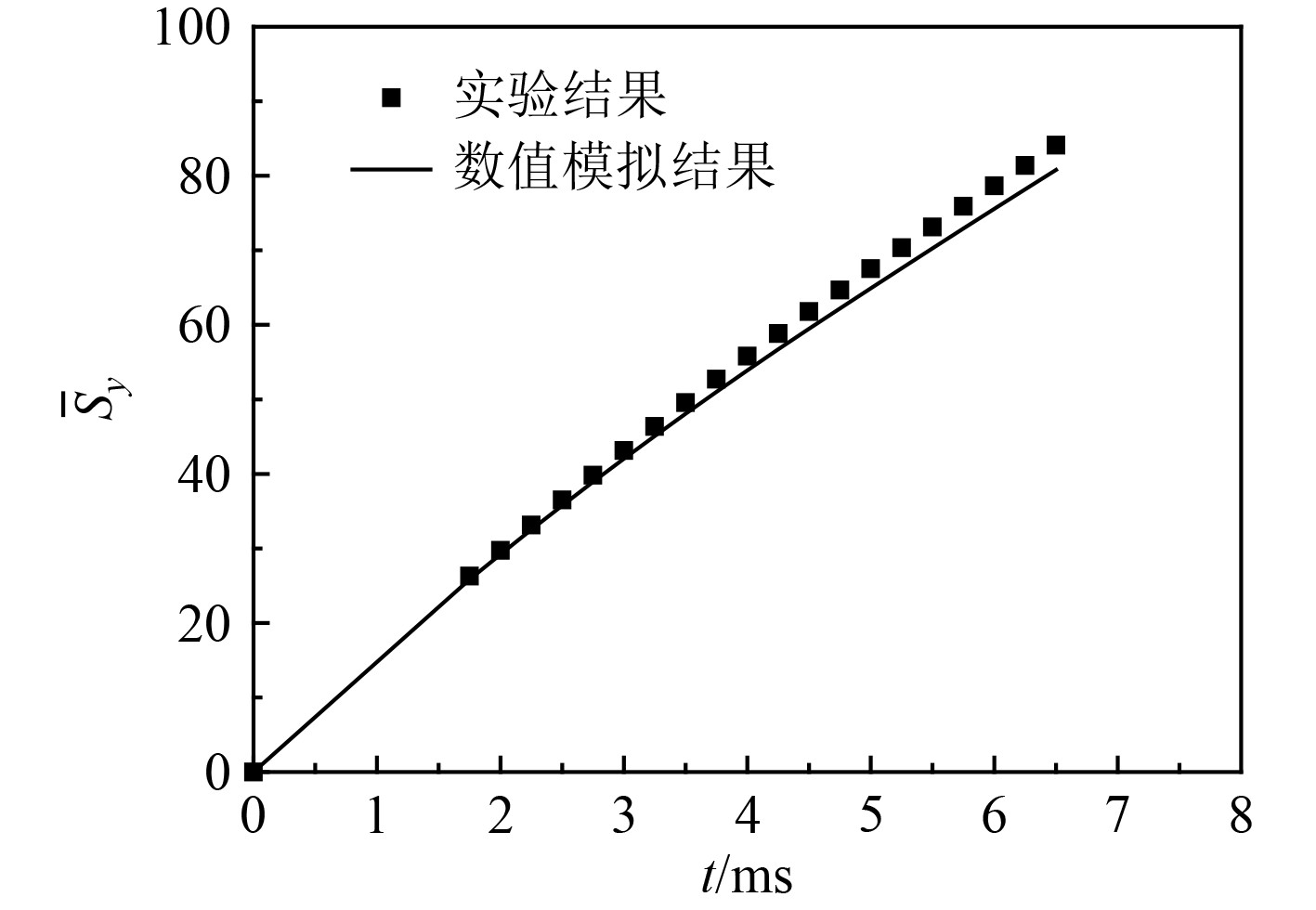
根据文献[7]中射弹模型2的实验数据,对水下超空泡射弹出水进行数值方法验证。图4给出了出水超空泡演化过程的实验和数值模拟结果,相邻图片的时间间隔为Δt=0.25 ms。通过对比可以发现,数值模拟较好地模拟出了实验中的出水超空泡演化过程。为了进一步验证数值模拟方法有效性,将射弹的无量纲纵向位移的数值结果与实验数据进行对比,如图5所示。可以看出,射弹无量纲纵向位移的数值结果与实验数据具有较好的一致性,最大误差约为3.9%。通过上述比较验证了本文数值模拟方法的有效性。
|
图 4
射弹出水超空泡的演化过程对比(Δt=0.25 ms)
Fig. 4
Comparisons of water-exit supercavity evolutions of the projectile between numerical simulation and experiment (
|
|
图 5 关于射弹无量纲纵向位移的数值模拟和实验结果[7]对比 Fig. 5 Comparisons of dimensionless longitudinal displacements of the projectile between numerical simulation and experiment |
本文以单航行体出水为参照工况,考虑并联间距为2D,3D,4D,5D四种工况,分别对不同工况开展数值模拟研究,计算工况如表1所示。表中VA0,VB0,V0分别为航行体A、航行体B、单航行体出水时的初速度,方向为竖直向上。
|
|
表 1 计算工况表 Tab.1 Numerical simulation cases |
图6(a)给出了航行体单独出水过程的超空泡演化过程。可以看出,航行体在水下运动至出水过程中经历了形成自然超空泡、超空泡随动、超空泡局部溃灭等。在水下运动阶段,由于航行体的运动速度较高,导致航行体肩部位置的压力降低到水的饱和蒸汽压以下,此时液相水会不断汽化形成空泡,随着空泡不断的发展形成超空泡,超空泡的形状为细长的椭球体,航行体被包裹在超空泡内部,只有头部沾湿,如图6(a)中t=1 ms所示。随着航行体继续向上运动,超空泡跟随航行体向上运动。航行体穿越水面时,被航行体带入空气中的空泡在大气压力的作用下发生溃灭,如图6(a)t=2.8 ms所示。由于航行体出水速度较高,水面以下的空泡来不及随航行体出水而被剥离在自由液面以下,如图6(a)中 t=3 ms所示。当航行体完全进入空气之后,出现了向上运动的水的喷溅,如图6(a)中 t=3.4 ms所示。6(b)给出了并联间距△d = 4D 时,航行体并联出水过程中超空泡演化过程。为了便于分析,以t=2 ms的图像为例,定义2个航行体相隔较近的一侧为内侧,相隔较远的一侧为外侧。可以看出,2个航行体都各自形成了超空泡,航行体被包裹在超空泡内部。由于受到相邻航行体的限制,超空泡内侧的扩张受到了抑制,而超空泡的外侧自由扩展,导致双航行体超空泡外侧轮廓的曲率要大于内侧轮廓,形成了一对非对称超空泡,但双超空泡形态在空间上呈现出较好的镜面对称特征,如图6(b)中 t = 1~1.8 ms 所示。随着双航行体继续向上运动,超空泡继续发展,其直径和长度增加。在穿越水面阶段,并联出水与单独出水相似,出现水面以上的空泡溃灭、还未溃灭的空泡被自由液面阻隔等行为,如图6(b)t=2.6~3 ms所示。另外还可以看出,超空泡的后半段以并联航行体的中轴线为基准相互靠拢。在双航行体完全出水后,喷溅的水花是不对称的,外侧喷溅高度大于内侧,如图6(b)中 t = 3.4 ms所示。

|
图 6 单独出水和并联出水的超空泡演化 Fig. 6 Supercavity evolutions of the single vehicle exiting water and two vehicles exiting water in parallel |
图7为t=2 ms时,不同并联间距下的出水超空泡形态对比。可以看出,随着航行体并联间距的减小,超空泡尾部向内侧扩张的程度逐渐增加。当并联间距△d为2D和3D时,双超空泡尾部壁面融合形成“U”形空泡,而△d为3D和4D的工况没有出现双超空泡的尾部融合。其原因主要是由于随着双航行体内侧流体域变小,该区域接受双航行体传递动能的水流体减少,引起每个流体质点获得的动能平均值增加,根据伯努利定理,内侧区域的平均压力必然降低,增强了超空泡向内侧扩张的速度,从而导致双空泡在内侧壁面发生了融合。

|
图 7 t=2 ms时,不同并联间距的出水超空泡形态对比 Fig. 7 Comparisons of the shape of supercavitation with different parallel distances when t = 2 ms |
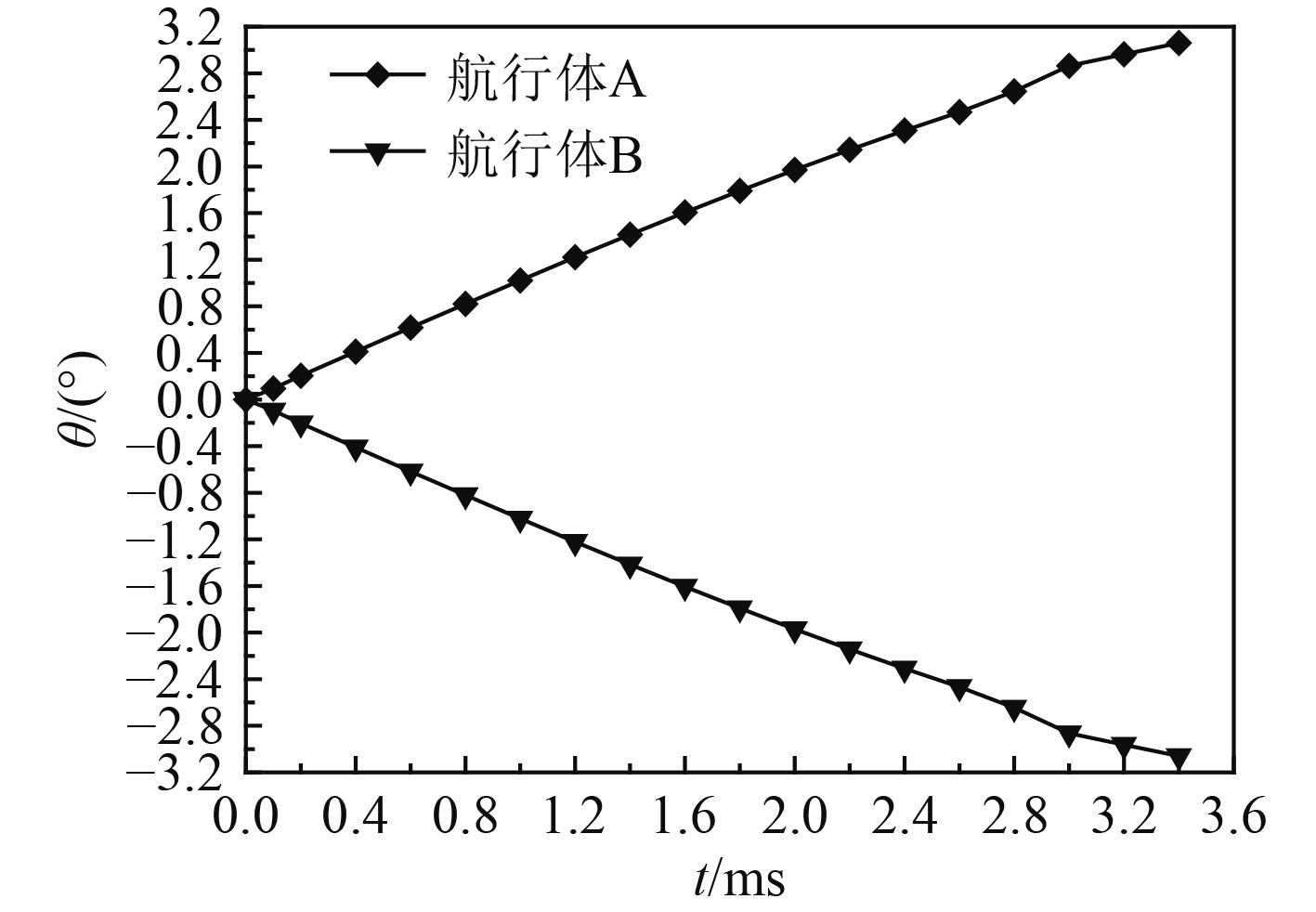
定义航行体的偏航角θ为当前航行体轴线与y轴的夹角,逆时针旋转方向为偏航角的正方向。图8给出了并联间距△d = 4 D时,双航行体偏航角随时间变化的曲线。从图中可知,并联出水时,航行体A向外侧进行偏转,航行体B向另一外侧进行偏转,即2个航行体的运动向着两者头部远离、尾部靠近的方向偏转,从整体上看航行体A和航线体B的偏转运动表现为良好的对称性。航行体偏转的原因主要是航行体诱导的超空泡沿轴线不对称,导致航行体受到了不对称的水动力。在此种工况下,随着航行体运动时间的增加,偏航角也越来越大,在时间为3.4 ms时,偏航角达到了3.06°。
|
图 8 并联间距△d = 4D时,双航行体的偏航角随时间变化 Fig. 8 Variations of yaw angle of two vehicles with time when parallel distance △d = 4D |
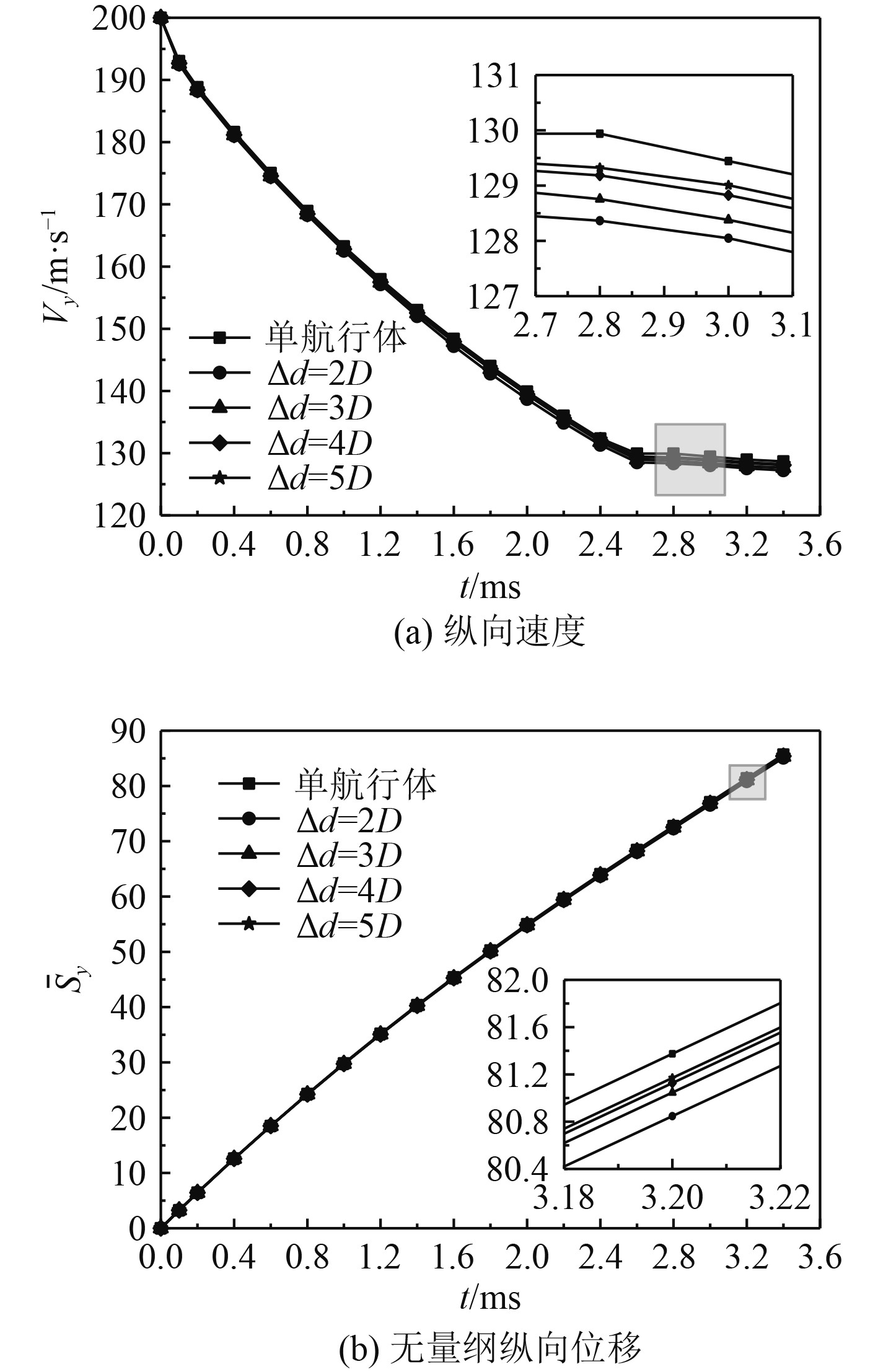
鉴于两航行体运动的对称性,将基于航行体A进行并联出水过程的运动分析。图9给出了不同工况下航行体的纵向位移、纵向速度随时间的变化。可以看出:5种工况下航行体的速度变化趋势相似,在运动初始阶段,航行体的速度衰减很快,这是由于超空泡尚未形成,受到水的阻力较大;随着航行体产生稳定的超空泡,减小了受到的水的阻力,速度衰减趋势逐渐变缓;2.6 ms之后,航行体的速度衰减变得很小,原因为2.6 ms时,航行体开始穿越水面进入空气中,在穿越过程中,航行体头部进入空气中,尾部在空泡中,头部流体介质由液相水变成气相,密度突变,从而导致航行体受到的压差阻力变得很小,当航行体完全进入空气中,航行体只受到量级较小的空气阻力。通过对比纵向速度和无量纲纵向位移的放大图可以发现,虽然各工况下航行体纵向速度和无量纲纵向位移相差较小,但是仍有区别。对于并联出水,随着并联间距的减小,航行体的纵向速度衰减略微增快,无量纲纵向位移变小。航行体单独出水的纵向速度和纵向无量纲位移大于并联出水的,这表明并联出水对超空泡航行体的减阻产生不利影响。
|
图 9 不同工况下航行体无量纲纵向位移、纵向速度随时间的变化 Fig. 9 Variations of dimensionless longitudinal displacement and longitudinal velocity of vehicle with time under different cases |
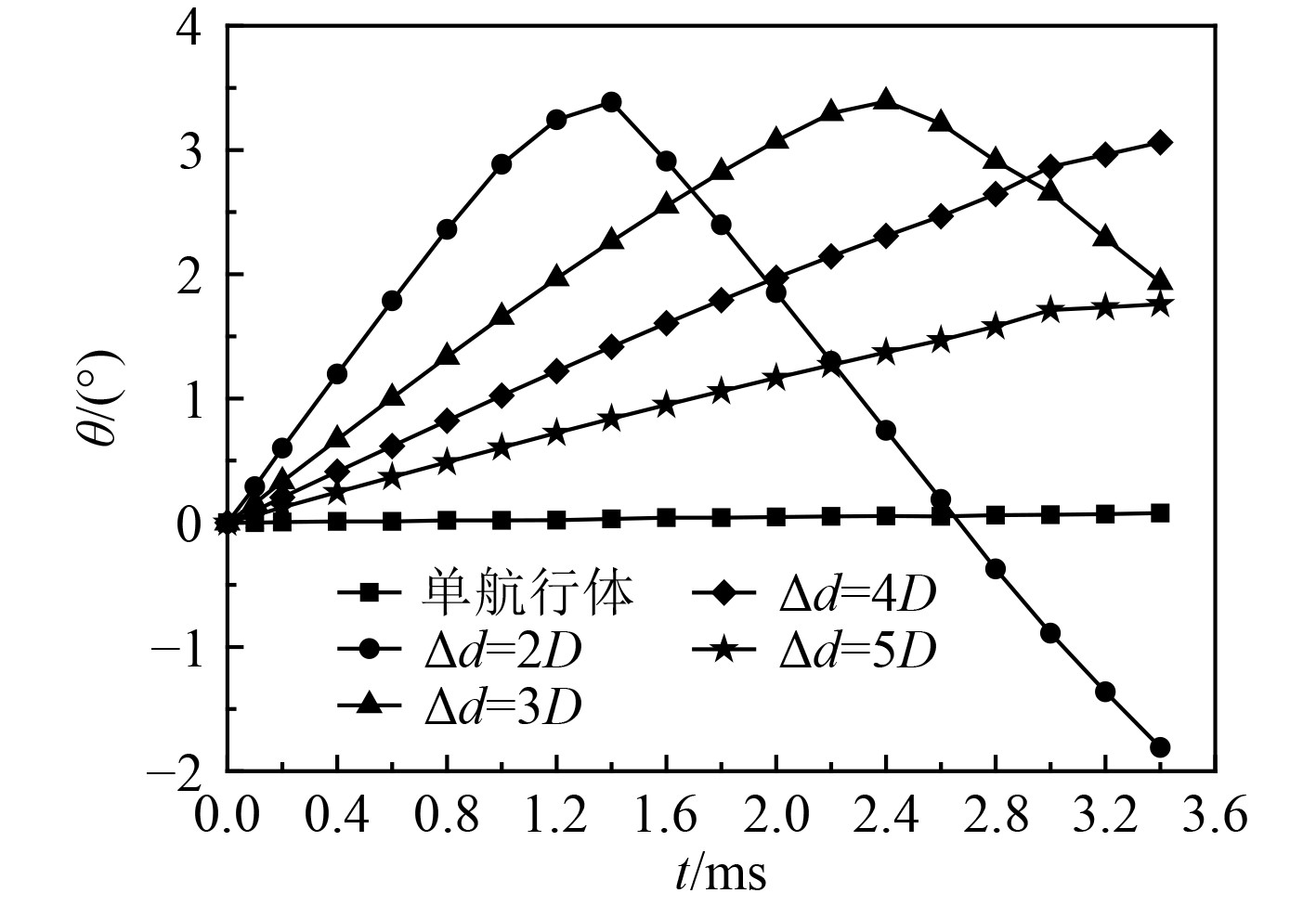
图10为不同工况下航行体出水过程的偏航角变化。从图中可知,航行体单独出水时,航行体几乎没有发生偏转,偏航角的变化近似为 0°附近的一条直线。对于并联出水,并联间距△d为2D和3D时,航行体的偏航角随时间的增加先增加后减小,其原因为航行体向外侧偏转,当偏航角达到某一临界值时,本文工况条件下约为3.4°,航行体的尾部刺穿超空泡内测壁面沾湿,产生了横向沾湿面作用的均布力,均布力产生向内侧的偏转力矩,此力矩大于航行体受到的向外侧偏转的力矩,因此航行体开始向内侧偏转,对应偏航角减小。△d为4D和5D时,随着并联间距的增大,航行体受到相邻航行体流场干扰的影响减弱,航行体向外侧的偏航角减小,一直到航行体完全出水时偏航角还没有达到临界值,所以航行体只发生了向外侧偏转。因此为确保航行体出水弹道的稳定性,需要合理控制并联间距。
|
图 10 不同工况下航行体出水的偏航角变化 Fig. 10 Variations of the yaw angle of vehicles exiting water under different cases |
本文采用数值模拟方法对高速航行体并联出水问题进行研究,获得主要结论如下:
1)并联出水过程中,航行体周围流场彼此发生干扰,出水超空泡内侧扩张受到抑制,导致超空泡外侧轮廓的曲率要大于内侧轮廓。而且当并联间距较小时,2个出水超空泡的尾部发生融合。
2)相比航行体单独出水,并联出水过程中航行体的纵向速度衰减较快,使航行体的减阻性能小幅下降。
3)航行体并联出水受到不对称的水动力作用,航行体的弹道发生偏转,当并联间距较小时,航行体先发生向外侧偏转之后转向内侧偏转,当并联间距较大时,航行体只发生向外侧的偏转。
| [1] |
LOGVINOVICH G V. Some problems of supercavitating flows [C] //Proceedings of NATO-AGARD, Ukraine: NAS-IHM, 1997: 36–44.
|
| [2] |
SAVCHENKO Y N, VLASENKO Y D, SEMENENKO V N, et al. Experimental Studies of High-Speed Cavitated Flows[J]. International Journal of Fluid Mechanics Research, 1999, 26(3): 365-374. DOI:10.1615/InterJFluidMechRes.v26.i3.80 |
| [3] |
WAUGH J G , STUBSTAD G W. Water-exit behavior of missiles part 1. preliminary studies[R]. Naval Ordnance Test Station China Lakeca, Califomia, 1961.
|
| [4] |
NGUYEN V T, HA C T, PARK W G. Multiphase flow simulation of water-entry and-exit of axisymmetric bodies[C] //ASME International Mechanical Engineering Congress and Exposition, California: American Society of Mechanical Engineers, 2013.
|
| [5] |
贾会霞, 施红辉, 胡俊辉, 等. 潜射超空泡射弹出水的流体力学现象的实验研究[J]. 船舶力学, 2017, 21(7): 814-820. JIA H X, SHI H H, HU J H, et al. Experiments on water exit phenomenon of underwater launched projectiles with a supercavity[J]. Journal of Ship Mechanics, 2017, 21(7): 814-820. |
| [6] |
贾会霞, 胡俊辉, 施红辉, 等. 出水超空泡的形状与弗劳德数影响的实验研究[J]. 西安交通大学学报, 2015, 49(3): 67-73. |
| [7] |
SHI H H, ZHOU D H, LU L W, et al. On the water exit of supercavitating projectiles with different head shapes[J]. Shock Waves, 2021, 31(6): 597-607. DOI:10.1007/s00193-021-01025-7 |
| [8] |
别庆, 吕卫民, 袁书生, 等. 潜射导弹垂直发射非定常空泡仿真研究[J]. 舰船科学技术, 2015, 37(S1): 185-189. BIE Q, LU W M, YUAN S S, et al. The simulation study of unsteady cavitations in vertical launchina of a submarine launched missile[J]. Ship Science and Technology, 2015, 37(S1): 185-189. |
| [9] |
CAO J, LU C J, CHEN Y, et al. Research on the base cavity of a sub-launched projectile[J]. Journal of Hydrodynamics, 2012, 24(2): 244-249. DOI:10.1016/S1001-6058(11)60240-0 |
| [10] |
魏海鹏, 符松. 不同多相流模型在航行体出水流场数值模拟中的应用[J]. 振动与冲击, 2015, 34(4): 48-52. |
| [11] |
刘志勇, 颜开, 王宝寿. 潜射导弹尾空泡从生成到拉断过程的数值模拟[J]. 船舶力学, 2005, 9(1): 43-40. |
| [12] |
ZHANG J, YOU T Q, HE Q K, et al. Numerical analysis of cavitation flow during vertical water exit of underwater vehicles[J]. Advanced Materials Research, 2011, 201: 2780-2784. |
| [13] |
CHEN Y, GONG Z X, LI J, et al. Numerical investigation on the regime of cavitation shedding and collapse during the water-exit of submerged projectile[J]. Journal of Engineering, 2020, 142(1): 011403. |
| [14] |
MNASRI C, HAFSIA Z, OMRI M, et al. A moving grid model for simulation of free surface behavior induced by horizontal cylinders exit and entry[J]. Engineering Applications of Computational Fluid Mechanics, 2010, 4(2): 260-275. DOI:10.1080/19942060.2010.11015315 |
| [15] |
卢佳兴, 王聪, 魏英杰, 等. 回转体齐射出水过程空泡演化规律与弹道特性实验研究[J]. 兵工学报, 2019, 40(6): 1226-1234. |
| [16] |
毕凤阳, 卢丙举, 赵世平, 等. 水下齐射扰动特性[J]. 航空动力学报, 2020, 35(7): 1345-1352. |
| [17] |
MENTER F R. Two-equation eddy-viscosity transport turbulence model for engineering applications[J]. AIAA Journal, 1994, 32(8): 1598-1605. DOI:10.2514/3.12149 |
 2023, Vol. 45
2023, Vol. 45
