0 引　言

伴随着经济全球化时代潮流，国际海洋运输业务覆盖面积逐渐扩大，加强海上运输船舶安全管理和航迹监测是国际海洋运输行业重点关注目标。由于海上水域状况复杂，船舶航行周期也较长^[1-2]，为避免船舶在复杂水域出现航线偏离，发生触礁或船舶海上交通事故，精准预测船舶航线意义重大。有很多学者研究船舶航线预测方法，鄢博冉等^[3]利用AIS系统采集船舶航行状态数据，采用卡尔曼循环网络去除船舶航行状态数据中所含的噪声，再利用滑动窗口加窗方法建立船舶航行状态方程，用该状态方程输出船舶航迹数据点，将船舶航迹数据点按照时间顺序连接后，得到船舶航迹。王余宽等^[4]以船舶相邻航迹点船位特征变化趋势数据为基础，使用差值算法填补船位特征变化趋势数据，将其输入到长短记忆神经网络中，利用该神经网络输出船舶航迹预测结果。上述2种方法虽均可实现船舶航迹预测，但前者受滑动窗加窗算法参数选取具备主观性影响，其输出船舶航迹预测结果不佳。后者则受长短记忆神经网络迭代影响，容易陷入局部极值情况，输出船舶航迹预测偏差数值较大。高阶微分方程是导数未知且高于一阶的微分方程，该方程可挖掘动态观测样本，依据动态观测样本规律，挖掘样本关联或者预测样本走向，高阶微分方程被应用在识别、监测、预测等多个领域^[5-6]。本文以高阶微分方程为基础，研究基于高阶常微分方程的复杂水域船舶航迹精准预测方法，为船舶安全航行提供保障。

1 复杂水域船舶航迹精准预测方法具体设计 1.1 基于AIS的船舶航行行为动态观测样本采集

AIS系统也称为船舶自动识别系统，每艘船舶上均配备AIS系统，该系统由通信机、GPS定位仪等多个设备组成，可获得船舶船位、航速、航向等船舶航行行为数据，利用AIS系统采集船舶航行行为动态观测样本。船舶航行行为观测样本为：

$Ship=\left\{\lambda \text{，}\phi \text{，}V\text{，}{R}_{1},{R}_{2}\right\}。$

(1)

式中：Ship表示船舶航行行为预测样本； $\lambda$ ， $\varphi$ 为船舶航行时的经度和纬度； $V$ 为船舶当前航行速度；R₁，R₂为船舶的航首向和对地航向。

利用式(1)获得时间段船舶航行行为观测样本后，构建船舶航行动态观测样本集为：

${\boldsymbol{G}} = (g({t_0}),g({t_1}), \cdots , g({t_{n - 1}}))。$

其中： $n$ 为船舶航行动态观测样本个数；t_i为时刻；g()表示观测样本中元素。

1.2 高阶常微分方程船舶航迹预测模型构建

以船舶航行动态观测样本集 ${\boldsymbol{G}} = (g({t_0}),g({t_1}), \cdots , g({t_{n - 1}}))$ 作为基础，利用常微分方程建立该船舶航行动态观测样本集规律挖掘模型，其表达式如下：

$y = f(g({t_0}),g({t_1}), \cdots ,g({t_{n - 1}}))。$

(2)

式中： $u$ 表示船舶航行动态观测样本集规律，该规律即为船舶轨迹坐标点；f表示船舶航行动态观测样本集规律挖掘模型。

利用高阶常数微分方程对船舶航行动态观测样本集进行外推，外推步数为 $n$ ，可对 $n$ 个时刻的船舶航行动态观测样本进行预测。但由于船舶在航行过程中，其航线虽然是直线状态，遇见船舶躲避和暗礁躲避时，航线会发生变化，所以船舶航行动态观测样本具备非线性特征。使用常微分函数建立的船舶航行动态观测样本集规律挖掘模型无法充分呈现船舶航行动态观测样本之间的规律，在此仅以式(1)描述船舶航行动态观测样本之间的特性，利用高阶常微分方程实现复杂水域船舶航迹精准预测，详细过程如下：

在船舶航行动态观测样本集 $G = (g({t_0}),g({t_1}), \cdots ,$ $g({t_{n - 1}}))$ 中存在 $n$ 个样本，则该观测样本集的规模为 $n$ ，进行阶差分近似处理，其表达式为：

$M = \left[ \begin{gathered} g({t_0})\mathop {}\limits^{} g'({t_0})\mathop {}\limits^{} \cdots {g^{(m)}}({t_0}) \\ g({t_1})\mathop {}\limits^{} g'({t_1})\mathop {}\limits^{} \cdots {g^{(m)}}({t_1}) \\ \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \mathop {}\limits^{} \vdots \\ g({t_{n - 1}})\mathop {}\limits^{} g'({t_{n - 1}})\mathop {}\limits^{} \cdots {g^{(m)}}({t_{n - 1}}) \\ \end{gathered} \right] 。$

(3)

式中， $M$ 表示阶差分近似处理后的船舶航行动态观测样本集矩阵，该矩阵维度为 $n \times m$ 。

使用高阶常微分对矩阵 $M$ 中元素进行建模，得到船舶航行动态观测样本集 $G = (g({t_0}),g({t_1}), \cdots ,g({t_{n - 1}}))$ 的高阶微分方程航迹预测模型，其表达式为：

$\frac{{{{\rm{d}}^m}G*}}{{{\rm{d}}{t^m}}} = f(t,g(t),g'(t), \cdots ,{g^{(m - 1)}}(t)) 。$

(4)

式中： ${\rm{d}}t$ 表示高阶微分方程表达式， $t$ 表示自变量； $G*$ 表示高阶微分后的船舶航行动态观测样本集。

设置式(4)约束条件如下：

$\min \left\{ {\left\| {G* - G} \right\|} \right\} = \sqrt {\sum\limits_{i = 0}^n {{g^{*(m)}}({t_i})} } - \sqrt {\sum\limits_{i = 0}^n {{g^{(m)}}({t_i})} }，$

(5)

式中， ${g^{*(m)}}({t_i})$ 为高阶微分后的船舶航行动态观测样本集 $G*$ 中的元素。

当式(4)结果满足式(5)条件时，令 $\left\| Q \right\| = \dfrac{{{{\rm{d}}^m}G*}}{{{\rm{d}}{t^m}}}$ ，则式(4)左边可改写为：

$\left\| Q \right\| = \sqrt {\sum\limits_{i = 0}^{n - 1} {q_i^2} }。$

(6)

式中，q_i表示高阶常微分后的船舶航行动态观测样本集中第 $i$ 个样本高阶常微分结果。

将式(6)代入式(4)，并对式(4)进行求解，即可得到船舶航迹精准预测值。但直接求解高阶常微分方程过程较为复杂，在此使用四阶龙格-库塔方法，将式(4)转换成若干个一阶常微分方程，再对其进行求解。式(4)转换成常一阶方程表达式如下：

$(g(t),g'(t), \cdots ,{g^{(m - 1)}}(t)) = ({u_1}(t),{u_2}(t), \cdots ,{u_n}(t)) 。$

(7)

式中， ${u_i}(t)$ 表示船舶航迹精准预测值。

将式(7)右边转换成方程组，其表达式为：

$\left\{ \begin{gathered} u_1'(t) = {u_2}(t)，\\ u_2'(t) = {u_3}(t)，\\ \vdots \\ u_n'(t) = f(t,{u_1}(t),{u_2}(t), \cdots ,{u_n}(t)) 。\\ \end{gathered} \right.$

(8)

式中， $u_i'(t)$ 为 ${u_i}(t)$ 的转换方程表达形式。式(8)的初始值为^[7]：

${u_0}(t) = f({u_1}({t_0}),{u_2}({t_0}), \cdots ,{u_n}({t_0})) 。$

(9)

通过求解式(8)并经过多次迭代后，得到该方程的一组预测值 $U$ ，其表达式为：

$U = ({u_1}(t + 1),{u_1}(t + 2), \cdots ,{u_n}(t + m)) 。$

(10)

式(10)中预测值对应的船舶航行动态观测样本为：

$\tilde G = (g(t + 1),g(t + 2), \cdots ,g(t + m)) 。$

(11)

通过上述步骤得到船舶航行动态观测样本的轨迹精准预测值，但该值为独立坐标点，在此使用最小二乘法对船舶航行动态观测样本预测值轨迹精准预测值进行拟合，得到复杂水域船舶航迹曲线。

为使得到的复杂水域船舶航迹足够精准，使用最小二乘法拟合船舶航行动态观测样本预测值进行3次拟合，则第 $k$ 次拟合船舶航迹预测值时，得到船舶航迹曲线的表达式为：

${H_k} = \min \sum\limits_{i = 1}^k {\left[ {{{\hat f}_k}{{({x_{ki}})}^2}} \right]} - \sum\limits_{i = 1}^k {\left[ {{{\hat f}_k}{{({y_{ki}})}^2}} \right]} 。$

(12)

式中：H_k表示第k次拟合后的船舶航迹曲线；k表示拟合次数；x_ki表示第 $k$ 次拟合时，第 $i$ 个船舶航迹预测值的横坐标， ${\hat f_k}({x_{ki}})$ 表示的拟合值；y_ki表示船舶实际航向时的坐标量测值。

通过式(12)即可得到复杂水域船舶航迹精准预测曲线。

2 实验结果与分析

以某运输船作为实验对象，该船长期执行远洋运输，其航行里程数值较大，航期较长，且其穿越海洋洋流流经区域以及海域较为狭窄的海峡。从该船的AIS系统中采集其航行数据样本并建立数据集，其中样本数量为4426个。使用本文方法对该船在复杂水域航行时的航迹进行精准预测，分析本文方法实际应用效果。

首先使用本文方法采集该船舶航行行为动态数据样本，采集结果如表1所示。分析可知，本文方法可有效采集该船舶航行的不同时刻航行速度、航首向、对地航向等船舶航行行为动态数据样本，为后续精准预测船舶轨迹提供数据支撑。

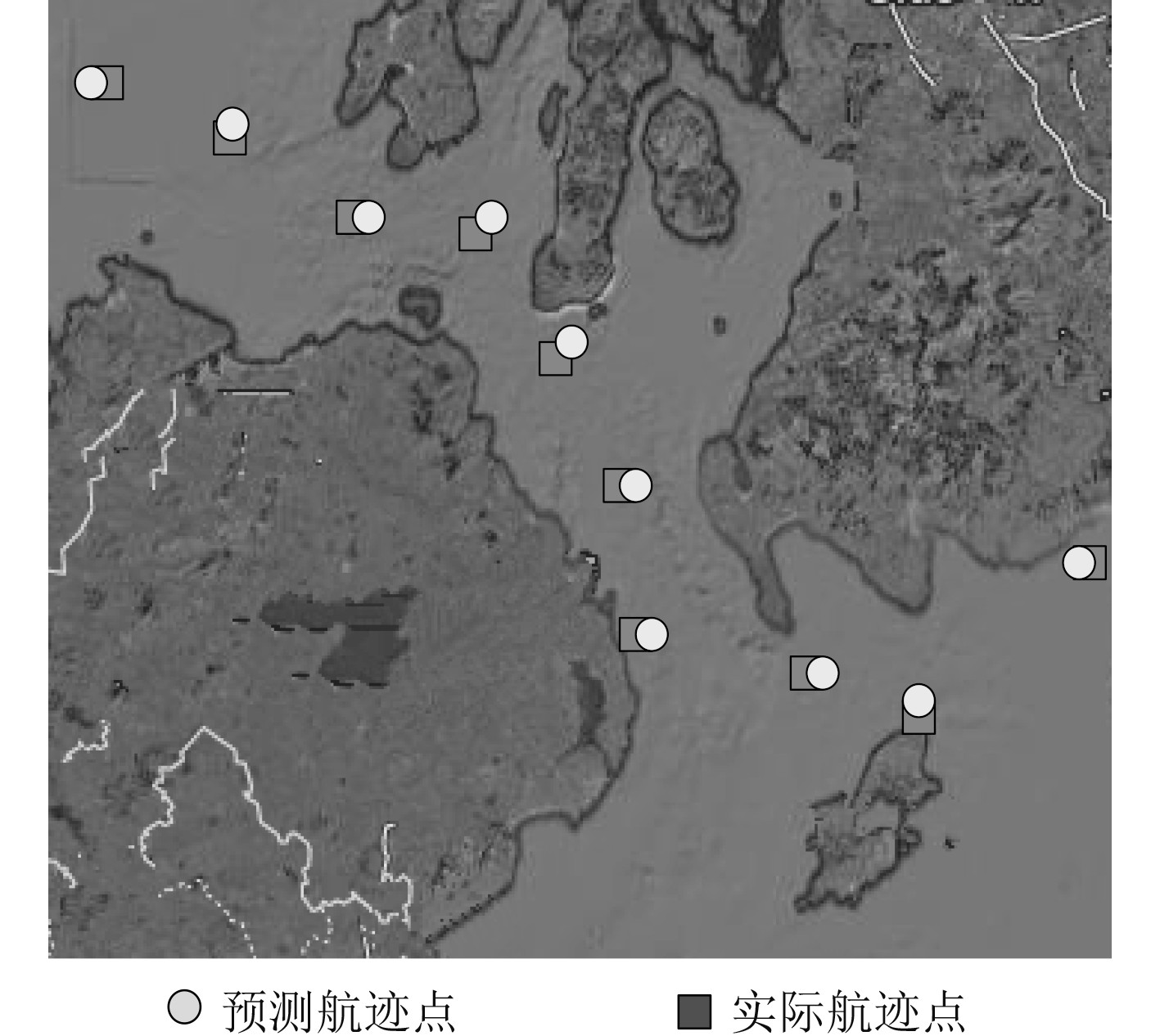
使用本文方法预测该船舶在复杂水域某次航行时的航迹预测值，预测结果如图1所示。分析可知，使用本文方法预测的复杂水域船舶航迹时，预测航迹点与该船舶实际航迹点位置完全吻合，说明本文方法可精准获得船舶航迹点，也从侧面说明本文方法预测的船舶航迹曲线能力较强。

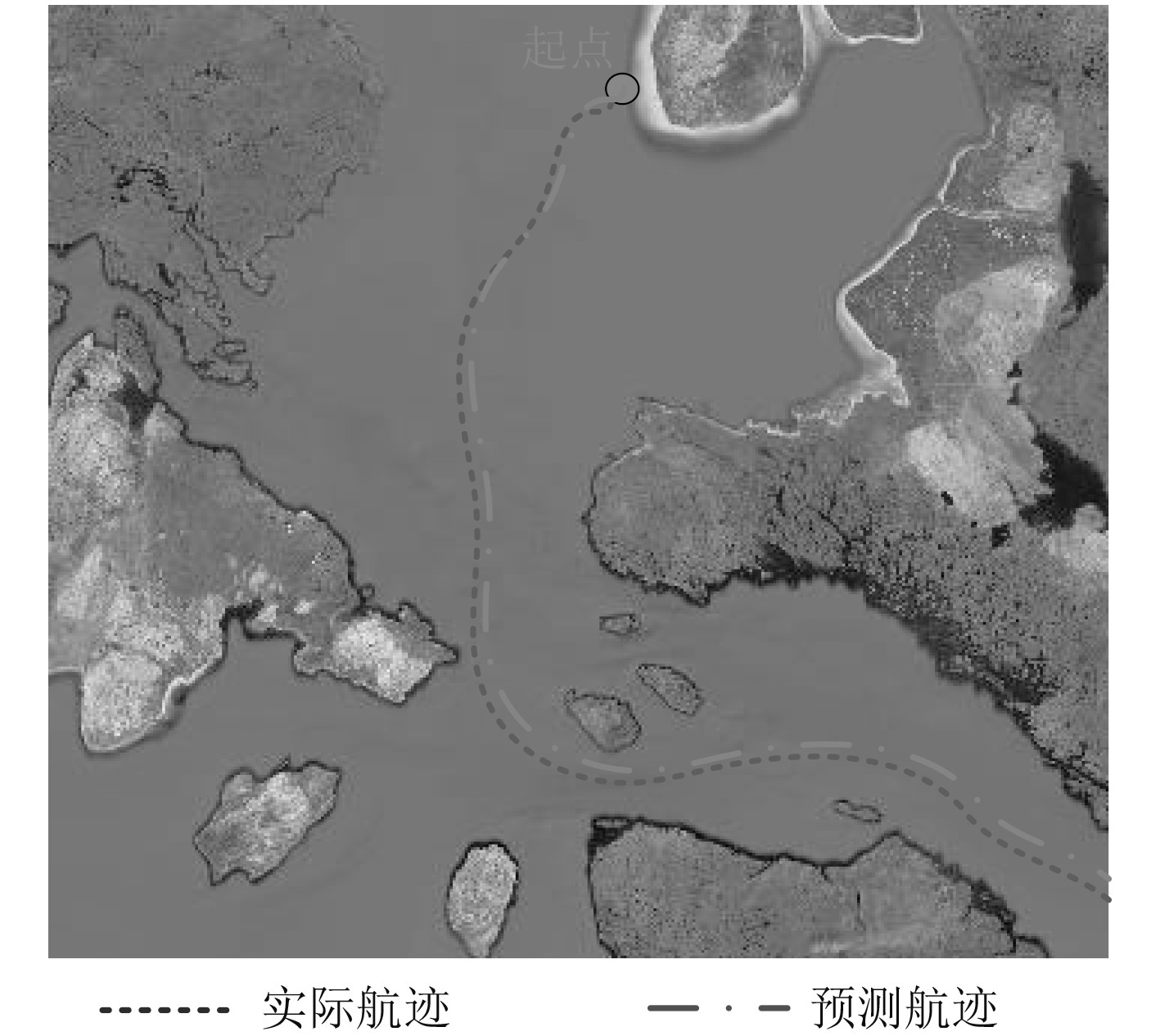
以该船某次在复杂水域航行时的动态航行数据作为实验对象，使用本文方法预测该船舶的航迹点预测值后，再对其进行拟合处理得到该船航迹曲线，结果如图2所示。分析可知，该船从起点出发后，其穿越海峡和礁石，然后向东方航行，其航迹呈现弧状。而使用本文方法预测该航迹后，得到的该船航迹曲线与其实际航迹曲线重合，说明本文方法不仅可有效预测船舶在复杂水域航行航迹，其预测的结果也足够精准。

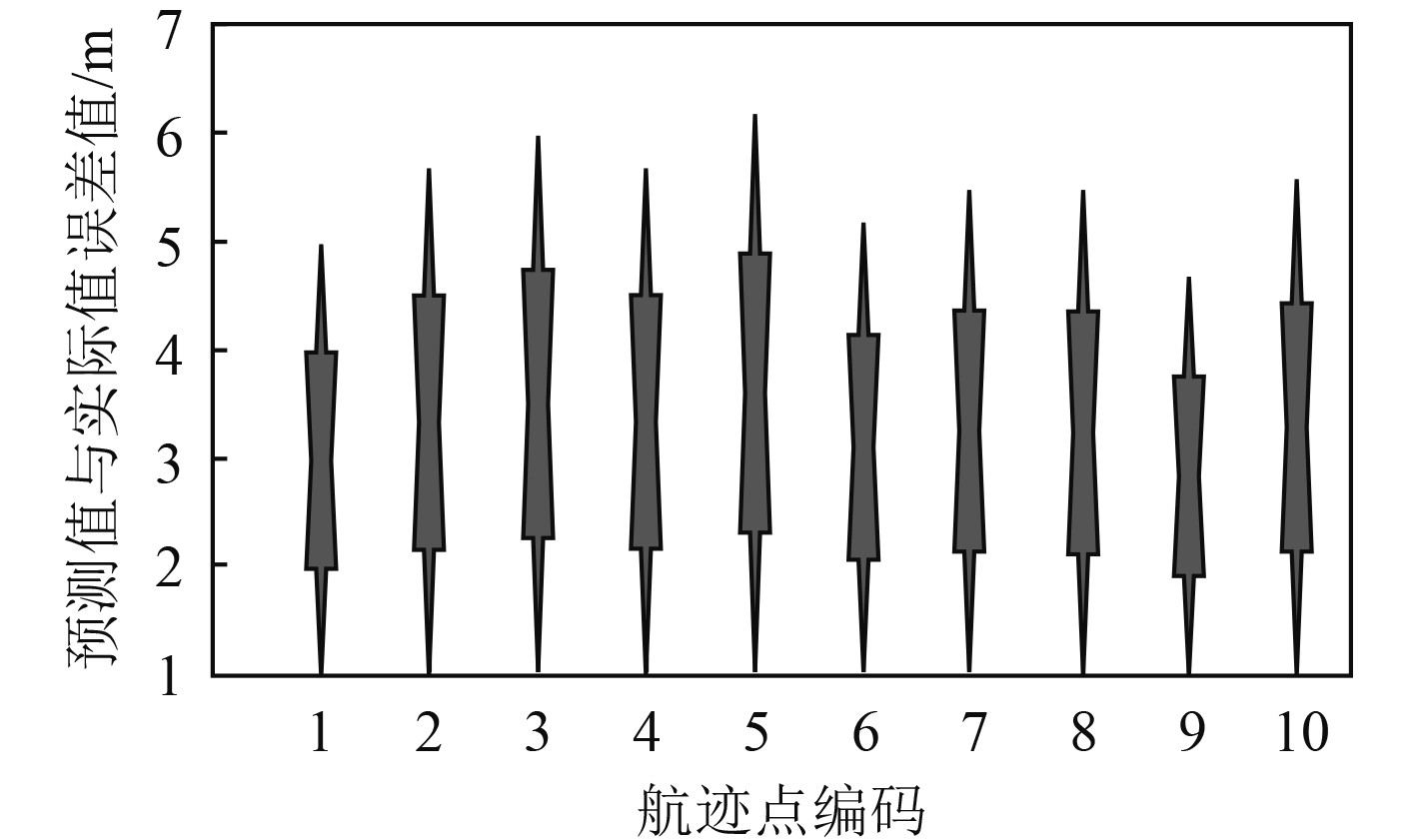
以10个船舶航迹点预测值作为实验对象，通过计算船舶航迹点预测值和实际值之间的欧式距离方式，得到预测值和实际值之间的误差，以该误差呈现本文方法预测船舶航迹精度，并设置误差阈值为10 m。测试结果如图3所示。分析可知，本文预测的船舶航迹点与实际点偏差始终在4.5～6.1 m左右波动，该数值远低于较预设的阈值，该结果说明本文方法预测复杂水域船舶航迹精度较高，应用性较强。

3 结　论

本文提出基于高阶常微分方程的复杂水域船舶航迹精准预测方法，并对该方法进行了实际验证。从验证结果得知，本文方法在预测航迹点、拟合航迹曲线以及预测船舶在复杂水域航行是的航迹精度方面能力均较强，未来可应用在船舶导航、避障等多个领域。