0 引　言

船舶碰撞属于较为严重的海洋事故。碰撞后，既会破坏船舶结构，还会污染海水^[1]，导致船舶航行安全受到影响，以及船员生命安全受到威胁^[2]。为降低船舶碰撞导致的严重后果，研究船舶碰撞载荷数值计算方法，为设计抗撞性能更佳的船舶结构^[3]提供参考。刘俊杰等^[4]通过瞬态动力学分析程序，对船舶碰撞载荷实施数值模拟，经过实验分析认为碰撞位置与浮冰尺度均会对船舶碰撞载荷产生影响。童宗鹏等^[5]利用有限元耦合方法，数值模拟分析船舶碰撞载荷，经过实验分析得知：冰层越厚，碰撞载荷越大，当冰层厚度为1.6 m时，船舶不会出现裂纹扩散情况，破坏面积较小。但这2种方法的数值模拟稳定性均较差，无法为船舶碰撞载荷分析提供稳定可靠的数据支持。精细积分法通过添加对偶变量，降阶处理动力学方程，通过指数函数的精细算法，求解降阶后的动力学方程，获取精准的计算结果^[6-8]。精细积分法计算准确性高、稳定性强，在线性与非线性动力分析中均有较优的应用效果。为此，研究应用精细积分的船舶碰撞载荷数值计算方法，提升载荷数值计算稳定性。

1 被撞船舶结构参数

为分析船舶碰撞载荷情况，选择3种不同质量的船舶作为试验对象，被撞船舶的具体结构参数如表1所示。

在3种不同类型的船舶外部均安装一个防护装置，用于提升船舶的防撞性能，防护装置内包含橡胶、泡沫铝与钢壳3层材料，利用精细积分法计算不同泡沫铝与橡胶厚度时碰撞载荷数值，分析不同泡沫铝与橡胶厚度时的防撞性能。

以质量为15000 t的船舶为例，不同防护装置方案如表2所示。

1.1 船舶碰撞的运动方程建立

针对碰撞过程，依据船舶基本参数，建立碰撞的运动方程，公式如下：

$ S\ddot x\left( t \right) + C\dot x\left( t \right) + Kx\left( t \right) = Df\left( t \right) 。$

(1)

式中：x(t)为被撞船舶的广义位移向量； $ t $ 为时间； $ \dot x\left( t \right) $ ， $ \ddot x\left( t \right) $ 分别为 $ x\left( t \right) $ 的一阶、二阶微分； $ S $ 为被撞船舶质量阵； $ K $ 为刚度阵； $ D $ 为载荷分布矩阵； $ f\left( t \right) $ 为船舶碰撞载荷向量； $ C $ 为阻尼阵。

1.2 基于精细积分的船舶碰撞载荷数值计算

为便于计算，对式（1）展开降阶，并添加对偶向量 $ p $ ，令其表达式为 $ p = S\dot x\left( t \right) + \dfrac{{Cx\left( t \right)}}{2} $ ，对 $ p $ 的表达式展开转换，得到：

$ \dot x\left( t \right) = - \frac{{{S^{ - 1}}Cx\left( t \right)}}{2} + {M^{ - 1}}p。$

(2)

微分处理 $ p $ 的表达式，并将式（2）代入式（1），得到：

$ \dot p = \left( {\frac{{C{M^{ - 1}}C}}{4}} \right)x\left( t \right) - \frac{{C{M^{ - 1}}p}}{2} - Df\left( t \right)，$

(3)

其中， $ \dot p $ 为 $ p $ 的一阶微分。

整理式（2）与式（3），得到：

$ \dot Z = GZ\left( t \right) + Bf\left( t \right)。$

(4)

其中： $ Z\left( t \right) = \left\{ \begin{gathered} x\left( t \right) \\ \dot x\left( t \right) \\ \end{gathered} \right\} $ 为被撞船舶的状态向量； $G = \left[ \begin{array}{ll} 0& I \\ - {S^{ - 1}}K& - {S^{ - 1}}C \end{array} \right]$ ； $ B = \left[ \begin{gathered} \mathop {}\nolimits_{} 0 \\ {M^{ - 1}}D \\ \end{gathered} \right] $ 为被撞船舶矩阵； $ I $ 为被撞船舶的直接矩阵。

式（4）属于碰撞问题的状态传递方程，式（4）的一般解为：

$ Z\left( t \right) = {e^{\left( {Gt} \right)}}Z\left( 0 \right) + \int_0^t {{e^{G\left( {t - \tau } \right)}}Bf\left( \tau \right){\rm{d}}\tau }。$

(5)

其中： $ Z\left( 0 \right) $ 为被撞船舶初始条件； $ \tau $ 为时延。

离散碰撞载荷，获取步长为 $ \Delta t $ 的时间间隔，令随机时刻为 $ k\Delta t $ ，则 $ {t_{k + 1}} = {t_k} + \Delta t $ 。其中，时间间隔编号为 $ k $ ，因此：

$ \begin{split} & Z\left( {{t_k}} \right) = {e^{\left( {G{t_k}} \right)}}Z\left( 0 \right) + \int_0^{{t_k}} {{e^{G\left( {{t_k} - \tau } \right)}}} Bf\left( \tau \right){\rm{d}}\tau，\\ & Z\left( {{t_{k + 1}}} \right) = {e^{\left( {G\Delta t} \right)}}Z\left( {{t_k}} \right) + \int_{{t_k}}^{{t_{k + 1}}} {{e^{G\left( {{t_{k + 1}} - \tau } \right)}}} Bf\left( \tau \right){\rm{d}}\tau 。\end{split} $

(6)

令指数矩阵是 $ R\left( {\Delta t} \right) = {e^{\left( {G\Delta t} \right)}} $ ，则

$ \begin{split} Z\left( {{t_{k + 1}}} \right) =& R\left( {\Delta t} \right)Z\left( {{t_k}} \right) + \int_{{t_k}}^{{t_{k + 1}}} {{e^{G\left( {{t_{k + 1}} - \tau } \right)}}Bf\left( \tau \right){\rm{d}}\tau } = \\ & R\left( {\Delta t} \right) \cdot \left( Z\left( {{t_k}} \right) + {G^{ - 1}}\left( {Bf\left( {{t_k}} \right)} \right) + {G^{ - 1}} \times \right.\\ &\left.\frac{{Bf\left( {{t_{k + 1}}} \right) - Bf\left( {{t_k}} \right)}}{{\Delta t}} \right)- \\ & {G^{ - 1}}\left( {{G^{ - 1}}\frac{{Bf\left( {{t_{k + 1}}} \right) - Bf\left( {{t_k}} \right)}}{{\Delta t}} + Bf\left( {{t_{k + 1}}} \right)} \right)。\\ \end{split} $

(7)

$ R\left( {\Delta t} \right) $ 的求解公式如下：

$ R\left( {\Delta t} \right) = {e^{G\Delta t}} = {\left( {{e^{G\frac{{\Delta t}}{{{2^N}}}}}} \right)^{{2^N}}} = {\left( {{e^{G\tau }}} \right)^{{2^N}}} 。$

(8)

其中： $ N $ 为时间间隔数量； $ \tau = \dfrac{{\Delta t}}{{{2^N}}} $ 。

展开 $ R\left( {\Delta t} \right) $ 获取其泰勒级数，公式如下：

$ \begin{split} & R\left( \tau \right) = {e^{G\tau }} = I + {R_a} ，\\ &{R_a} = G\tau + \frac{{{{\left( {G\tau } \right)}^2}}}{{2!}} + \frac{{{{\left( {G\tau } \right)}^3}}}{{3!}} + \cdots + \frac{{{{\left( {G\tau } \right)}^l}}}{{l!}}。\end{split} $

(9)

其中， $ l $ 为截断阶数。

为提升船舶碰撞载荷数值计算精度，变更 $ {R_a} $ 的计算公式为：

$ {\left( {{R_a}} \right)_{i + 1}} = 2{\left( {{R_a}} \right)_i} + {\left( {{R_a}} \right)_i} \times {\left( {{R_a}} \right)_i} ，$

(10)

其中，时间间隔编号为 $ i = 1,2, \cdots ,N $ 。

通过式（10）可获取 $ {\left( {{R_a}} \right)_N} $ ，因此：

$ R\left( {\Delta t} \right) = I + {\left( {{R_a}} \right)_N}。$

(11)

通过式（11）可计算获取 $ R $ ，将其代入式（7）可得到被撞船舶的状态向量 $ Z\left( t \right) $ ，在式（4）内代入 $ Z\left( t \right) $ ，便可获取船舶碰撞载荷向量 $ f\left( t \right) $ ，完成船舶碰撞载荷数值计算。

2 试验分析 2.1 不同航行速度时船舶碰撞载荷数值计算结果

以被撞船舶质是15000 t，碰撞角度60°，防护装置方案1为例，利用精细积分法，计算不同被撞船舶航行速度时，横纵方向上船舶的碰撞载荷数值，分析船舶的防撞性能，计算结果如图1所示。

根据图1（a）可知，随着被撞船舶速度的提升，在垂直方向上，首个碰撞载荷峰值越来越小，第二个碰撞载荷峰值越来越大；根据图1（b）可知，在水平方向，被撞船速度越快，碰撞载荷的数值越大。综合分析可知，被撞船速度越快，碰撞载荷数值越大，船舶外壳破裂速度也随之加快。

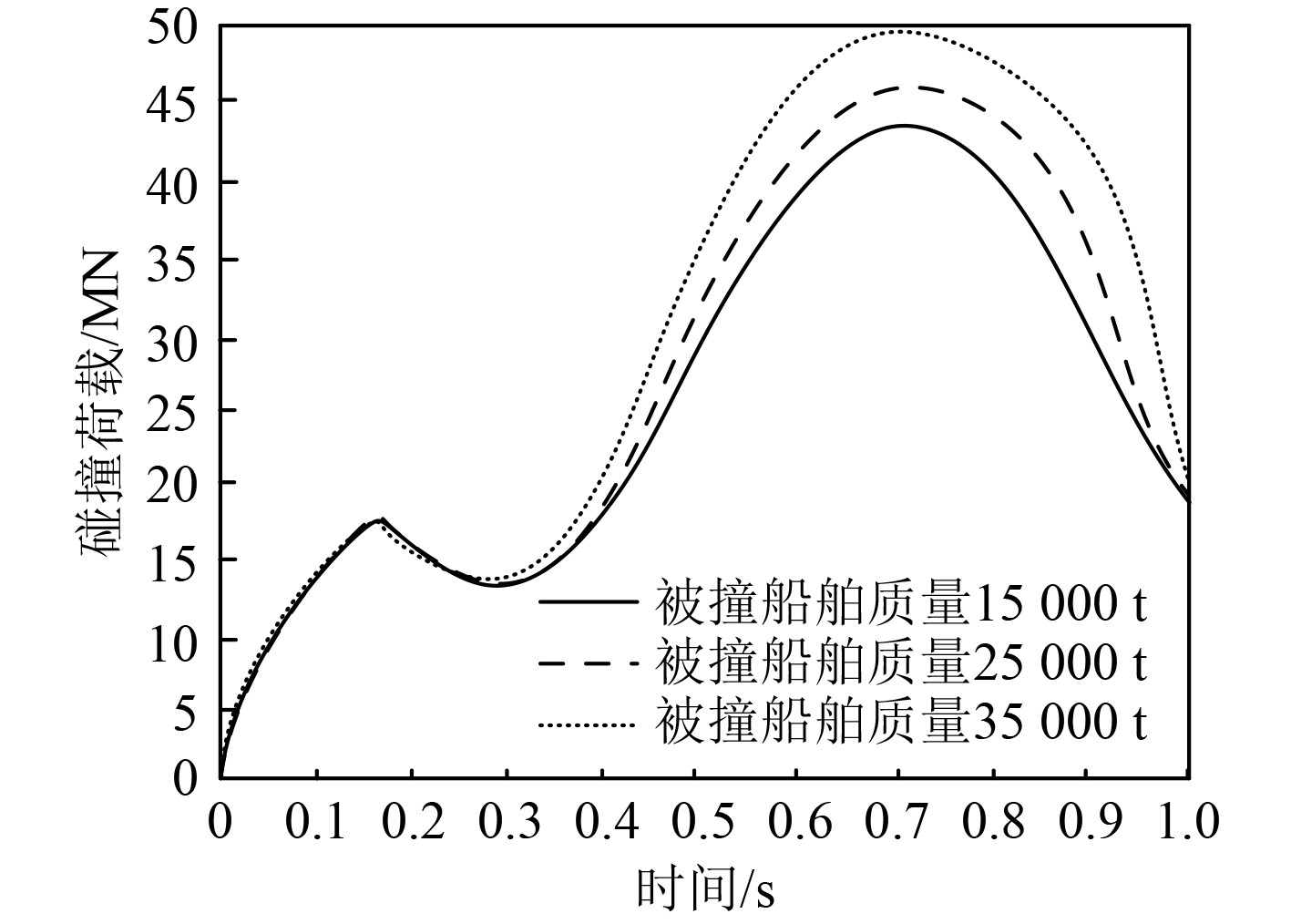
2.2 不同船舶质量时碰撞载荷数值计算结果

以被撞船舶航行速度1 m/s，碰撞角度60°，防护装置方案1为例，利用精细积分法，计算不同被撞船舶质量时的碰撞载荷数值，分析船舶的防撞性能。因为碰撞载荷在垂直方向上的变化较为明显，所以后续试验仅分析不同被撞船舶质量时，垂直方向上的碰撞载荷数值，计算结果如图2所示。

可知，随着被撞船舶质量的提升，碰撞前期，3种类型被撞船舶质量的载荷数值相差较小，当时间超过0.4 s左右时，3种类型被撞船舶质量的载荷数值差距开始变大，被撞船舶质量越大，碰撞载荷数值越大。试验证明：碰撞前期，不同被撞船舶质量时的碰撞载荷数值非常接近，碰撞后期，不同被撞船舶质量时的碰撞载荷数值间的差距不断变大，被撞船舶质量越大，碰撞载荷数值越大。

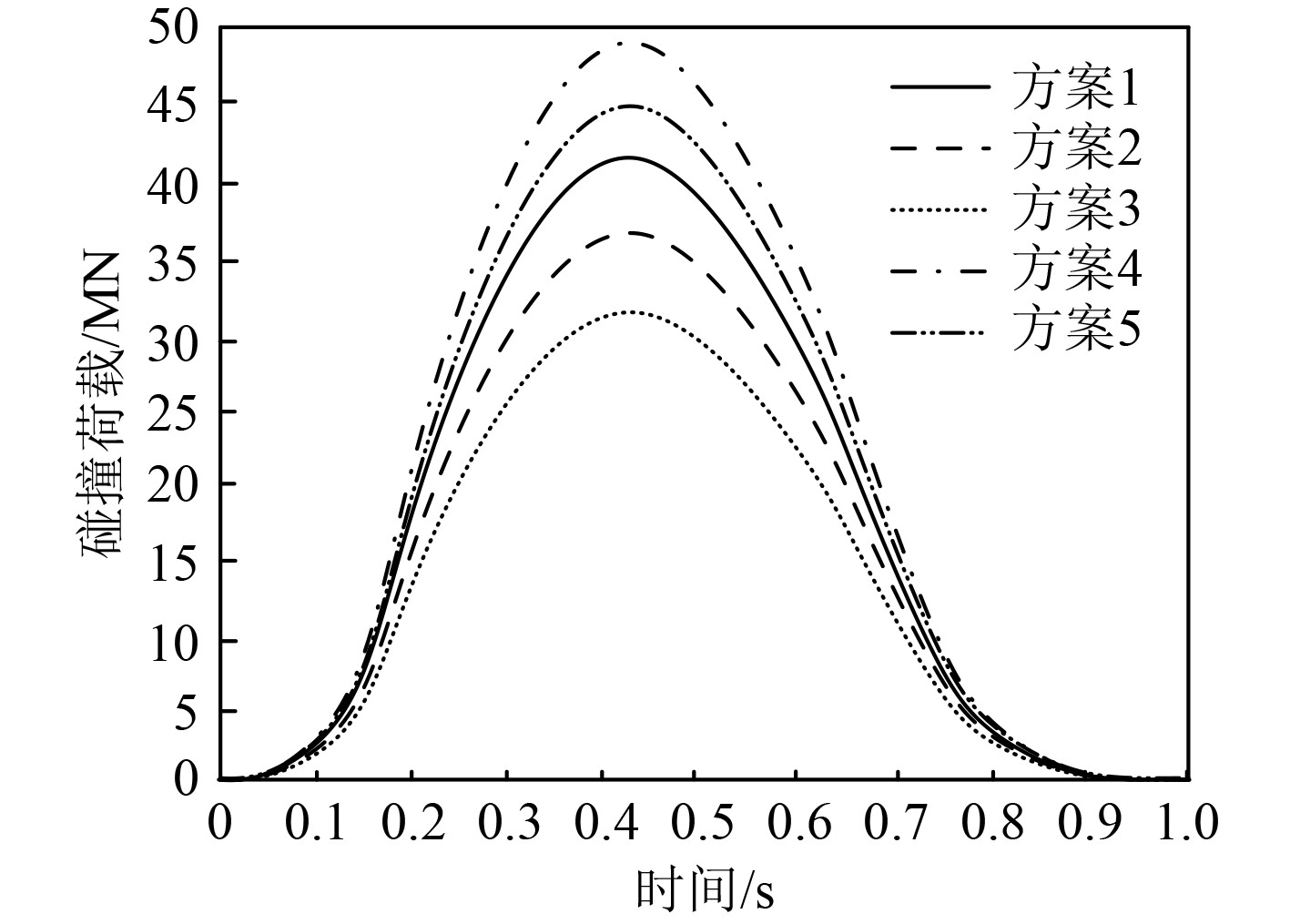
2.3 不同防护装置方案时船舶碰撞载荷数值计算结果

以被撞船舶质量15000 t，被撞船舶航行速度1 m/s，碰撞角度60°为例，利用精细积分法，计算不同防护装置方案时船舶可承受的碰撞载荷数值，分析船舶的防撞性能，计算结果如图3所示。

可知：当碰撞时间在0.4 s左右时，不同防护装置方案下，船舶碰撞载荷均达到峰值；当橡胶厚度一致时，泡沫铝越厚，船舶可承受碰撞载荷数值越大；当泡沫铝厚度一致时，橡胶厚度越厚，船舶可承受碰撞载荷数值越大；船舶碰撞载荷数值的最大值是方案4，即泡沫铝厚度为3 m与橡胶厚度为3 m时的防护装置抗撞性能最佳。试验证明，随着泡沫铝厚度与橡胶厚度的增加，船舶碰撞载荷数值越来越大，船舶防护装置的防撞性能越佳。

3 结　语

船舶航行速度不断提升，导致船舶航行过程中出现碰撞事故的概率也不断增加。为避免碰撞破坏船舶结构，影响其航行的安全性，研究应用精细积分的船舶碰撞载荷数值计算方法。研究结果表明：船舶航行速度与船舶质量，均会影响船舶碰撞载荷数值；提升被撞船舶航行速度与质量，均会提升船舶碰撞载荷数值，加快船舶外壳破裂速度。