0 引　言

船舶设计开发过程中，高速性、耐波性是重要的参数特性。耐波性是指船舶在波浪条件恶劣的环境下航行时是否稳定，是否能避免出现横摇幅度过大导致的倾覆问题，尤其对于高速型船舶来说，速度的增加使波浪阻力特性更加显著，船体的稳定性更差。传统的船舶耐波性设计以船模测试为主，这种方式的周期长、消耗成本高。近年来，随着计算流体动力学技术的发展，结合流体特性仿真的船舶耐波性优化成为一种趋势。

本文首先介绍波浪理论，通过建立船舶在波浪中的动力学模型，研究船舶的波浪增阻特性，最后结合流体力学仿真软件Fluent进行了船舶不同型线的波浪增阻特性仿真。本文研究对于提升高速船舶的流体动力学设计有一定指导意义。

1 波浪理论

船舶航行阻力包括风阻、波浪阻力等，其中波浪阻力是船舶航行阻力的主要来源，且随着船舶航行速度提升，波浪增阻效应更加明显。波浪增阻是船舶失速的主要原因，会造成船舶动力系统的能量损失。试验数据显示，波浪增阻导致的船舶动力损耗可达20%，因此，研究高速船舶在波浪中的增阻特性，改善船舶的型线设计，对于提高船舶能量利用率，降低能耗有重要作用。

波浪理论是指从波浪的产生、特性描述、建模等方面详细描述波浪的理论，波浪是自由液面在外界的扰动下离开原来的平衡位置，在重力、干扰力和惯性力的作用下，液面不断做往复运动。波浪可以分为规则波和不规则波2种，典型的不规则波包括海中的涌浪等，规则波具有一定的幅值和频率周期性。

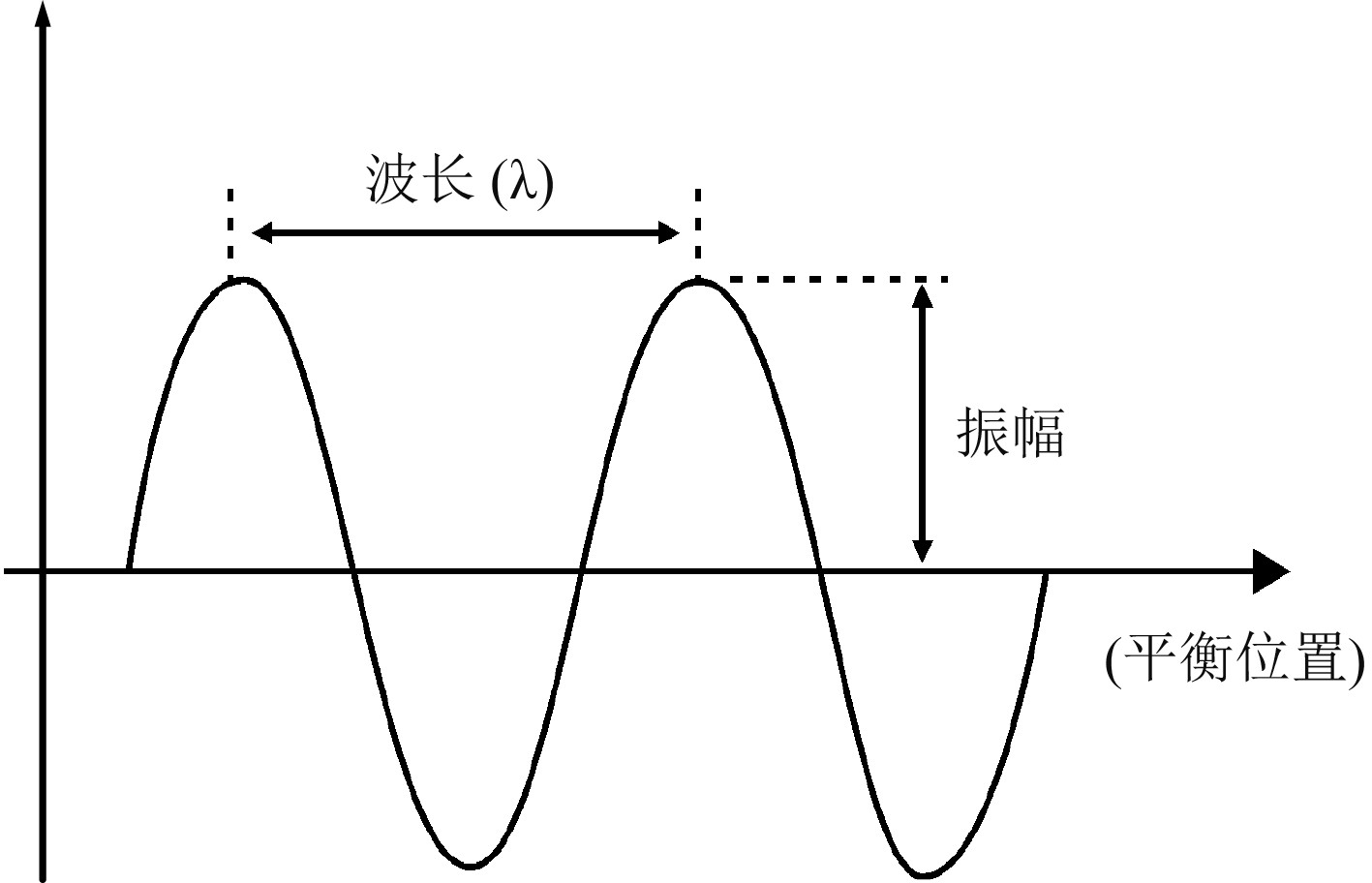
本文在进行船舶波浪增阻特性时只考虑规则波，规则波的特性曲线如图1所示。

根据规则波的特性曲线，可以建立海浪特性模型为：

$\xi (t) = \sum\limits_{i = 1}^n {{\xi _0}(t)\cos ({w_0}t + \varphi )} 。$

式中： ${\xi _0}(t)$ 为波浪幅值； ${w_0}$ 为规则波的角速度； $\varphi$ 为波浪的初始相位^[1]。

定义波浪的能谱密度公式^[2]如下：

$\eta ({\omega _0}) = \frac{{{k_1}}}{{{\omega _0}^3}}\exp (\frac{{ - {k_2}}}{{{\omega _0}^4}}) 。$

其中： ${k_1}$ ，k₂均为能谱密度系数， ${k_1} = 7.9 \times {10^{ - 3}}{g^2}$ ， ${k_2} = \dfrac{{3.09}}{{{h_0}^2}}$ ； ${h_0}$ 为波浪的义波高。

根据规则波的分布特性，对波浪特性模型进行简化，可得波面方程如下式：

$\eta {\text{ = }}{\varphi _0}\cos \left( {kx - {w_0}t} \right) \text{，}$

其中， ${\varphi _0}$ 为周期内的最大振幅。根据波面方程可得波浪在u/w两个方向分量的速度场方程为：

$\begin{gathered} u=\frac{{\text π} }{2}{\varphi _0}{\theta ^{kt}}\cos \left( {kx - {w_0}t} \right), \\ w = \frac{1}{2}{\varphi _0}{\theta ^{kt}}\sin \left( {kx - {w_0}t} \right)。\\ \end{gathered}$

式中， ${\theta ^{kt}}$ 为波浪的速度势。

2 高速船舶的波浪增阻特性建模与计算 2.1 切片理论

在船舶流体动力学仿真和计算领域，如船舶水动力特性计算、型线优化等，目前常用的计算方法是切片理论，这种理论与微积分思想基本一致，是将船舶等效为一个细长体，细长体的截面特性与船舶剖面一致，将细长体在轴向上划分为无数个切片，先对每一个切片的流体动力学特性进行分析，然后沿船舶长度方向进行积分，最终获得整船的水动力特性。

在建立船舶的切片模型时，将切片细化率 ${r_0}$ 定为 $\sqrt 2$ ，定义3种切片长度 ${S_1},{S_2},{S_3}$ ，定义切片模型的收敛率^[3] $\kappa$ 为：

$\begin{split} &\kappa = \frac{{{\tau _1}}}{{{\tau _2}}} ,\\ & {\tau _1} = {S_1} - {S_2}, \\ & {\tau _2} = {S_2} - {S_3}。\end{split}$

当 $\kappa$ 满足 $0 < \kappa < 1$ 时，切片精度符合要求，本文采用的收敛率为：

${\kappa _o} = \frac{{{\varepsilon _1}}}{{{\varepsilon _2}}} = \frac{{0.000086}}{{0.000127}} = 0.677 。$

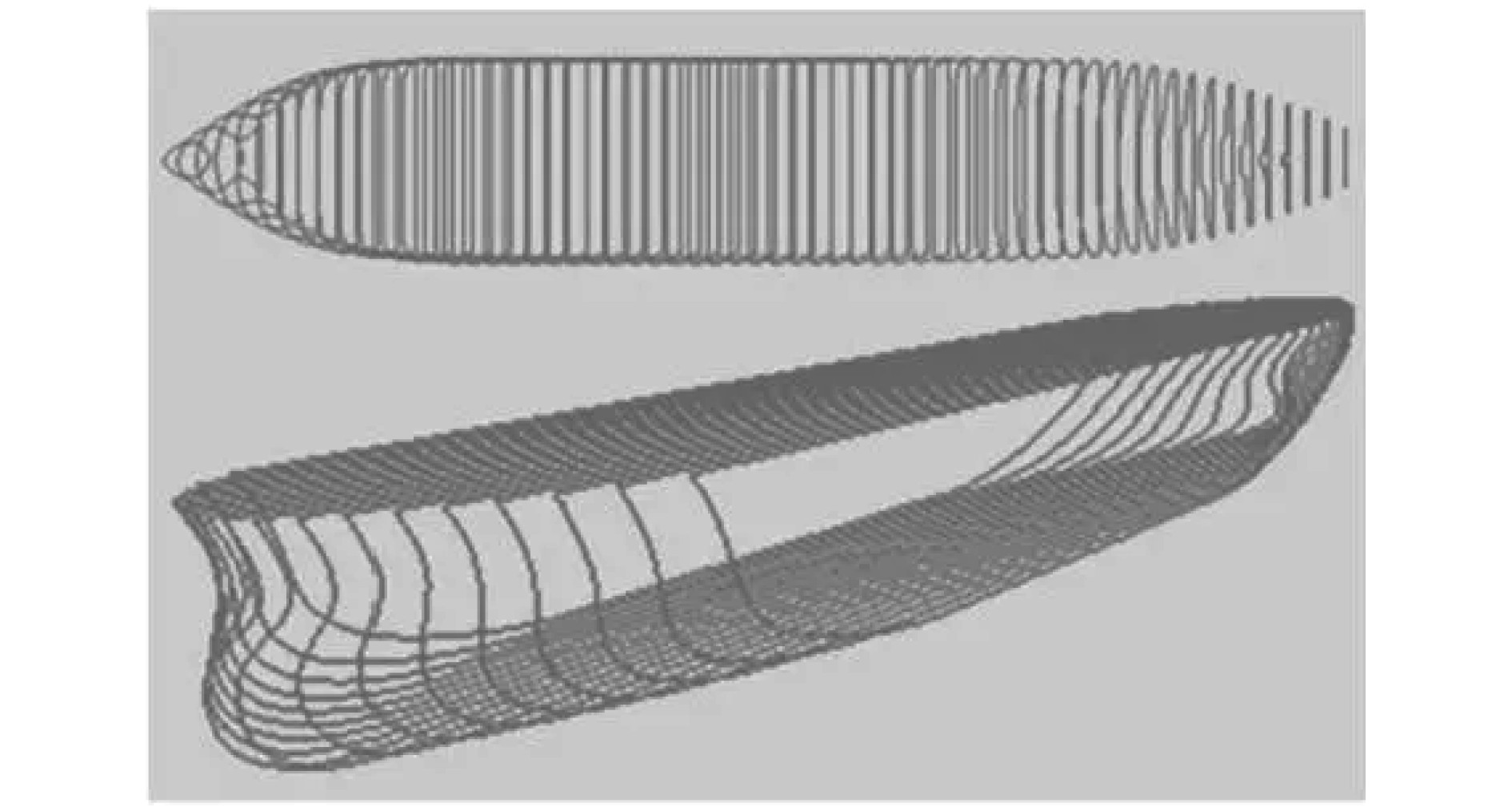
船舶切片模型示意图如图2所示。

2.2 基于切片理论的船舶波浪增阻特性建模

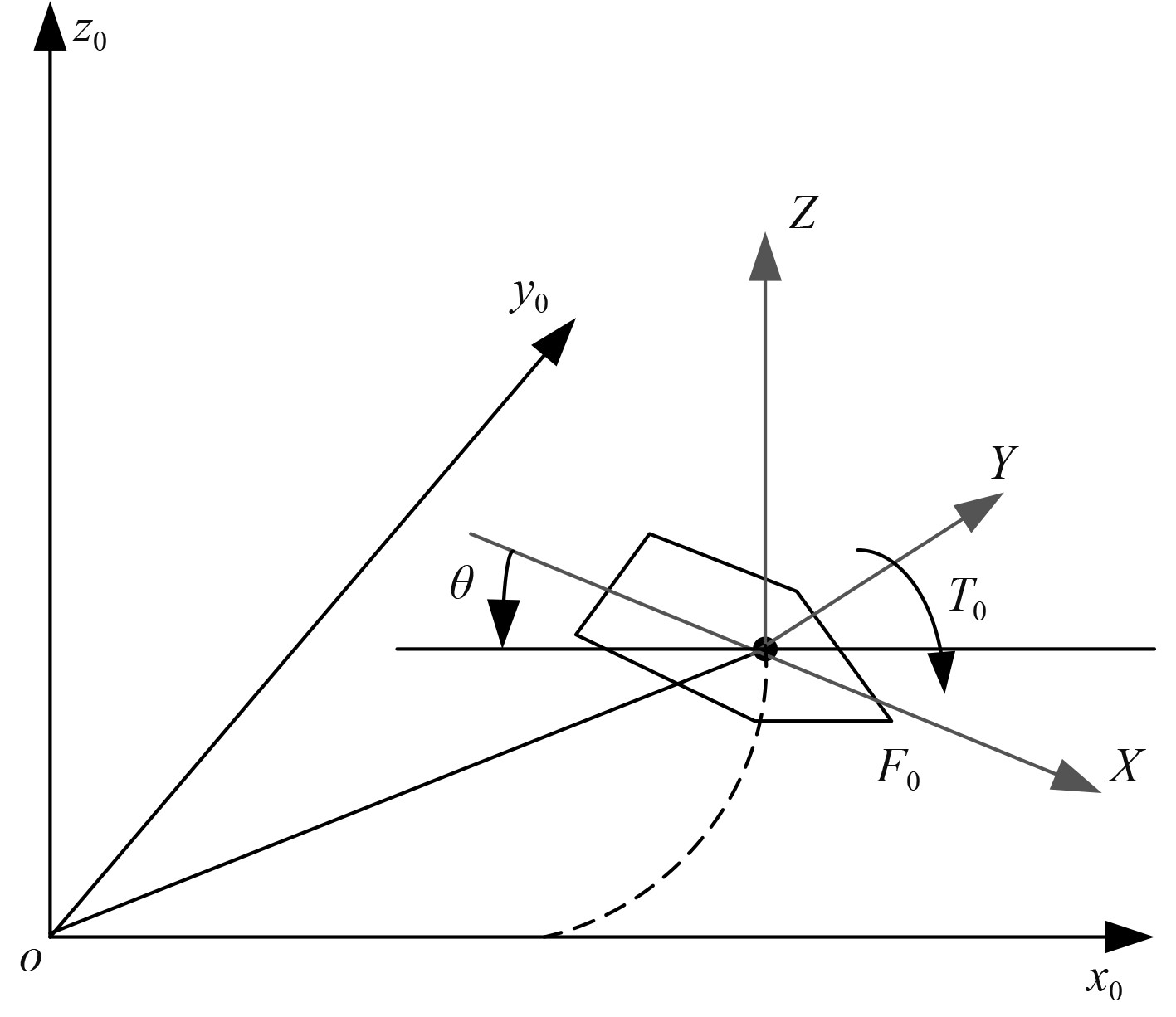
由于船舶在波浪中的阻力特性与船舶升沉运动、吃水深度、纵摇运动特性相关，因此为了研究船舶的波浪增阻特性，必须要建立描述船舶波浪中运动的坐标系，如图3所示。

结合图3所示的船舶运动坐标系，建立船舶的运动学方程为：

$\frac{F}{M} = \frac{{\rm{d}}}{{{\rm{d}}t}}f\left[ {x,y,z} \right] \text{，}$

其中：x = x(t)，y = y(t)，z = z(t)，分别为沿x₀，y₀，z₀三个方向的速度分量；M为船舶重量。

船舶在波浪条件下的动力学方程如下式：

$\left\{ {\begin{array}{*{20}{c}} {\left( {{J_{}} + \Delta {J_{}}} \right)w + 2\kappa w + \dfrac{1}{2}h\theta = {T_0}}, \\ {M\dfrac{{{\rm{d}}{{\vec u}_i}}}{{{\rm{d}}t}}\sin \theta + M\dfrac{{{\rm{d}}{{\vec u}_i}}}{{{\rm{d}}t}}\cos \theta = {F_0}} 。\end{array}} \right.$

式中： $J$ ， $\Delta J$ 分别为船舶的转动惯量和附加转动惯量； $\kappa$ 为阻尼系数； $\theta$ 为航向角度； $h$ 为吃水深度； $\vec u$ 为船舶的速度矢量； ${T_0}$ 为波浪对船舶产生的倾覆力矩； ${F_0}$ 为波浪对船舶产生的作用力； $w$ 为伴流系数。

根据高速型船舶的特性，在计算高速船的波浪增阻时，选择伴流系数为：

$w = 0.55{C_P} - 0.23 \text{，}$

整流系数为：

$\gamma = 1.635 - 1.956{C_P}^2 \text{，}$

式中， ${C_P}$ 为波浪粘度系数。

计算得到高速船舶的波浪增阻特性方程如下式：

${K_l} = {J_{}}{\left( {\frac{{\text{π}} }{2}D - 1} \right)^2}{\rho _0}\gamma \frac{w}{{{B_0}}}\left\{ {\left( {0.63 + 0.0569{C_P}\frac{{{L_0}}}{{{B_0}}}} \right)} \right\} 。$

式中： ${L_0}$ 为长度； ${B_0}$ 为宽度。

3 高速船舶的波浪增阻特性及型线优化仿真 3.1 结合高速船舶波浪增阻特性的船型优化流程

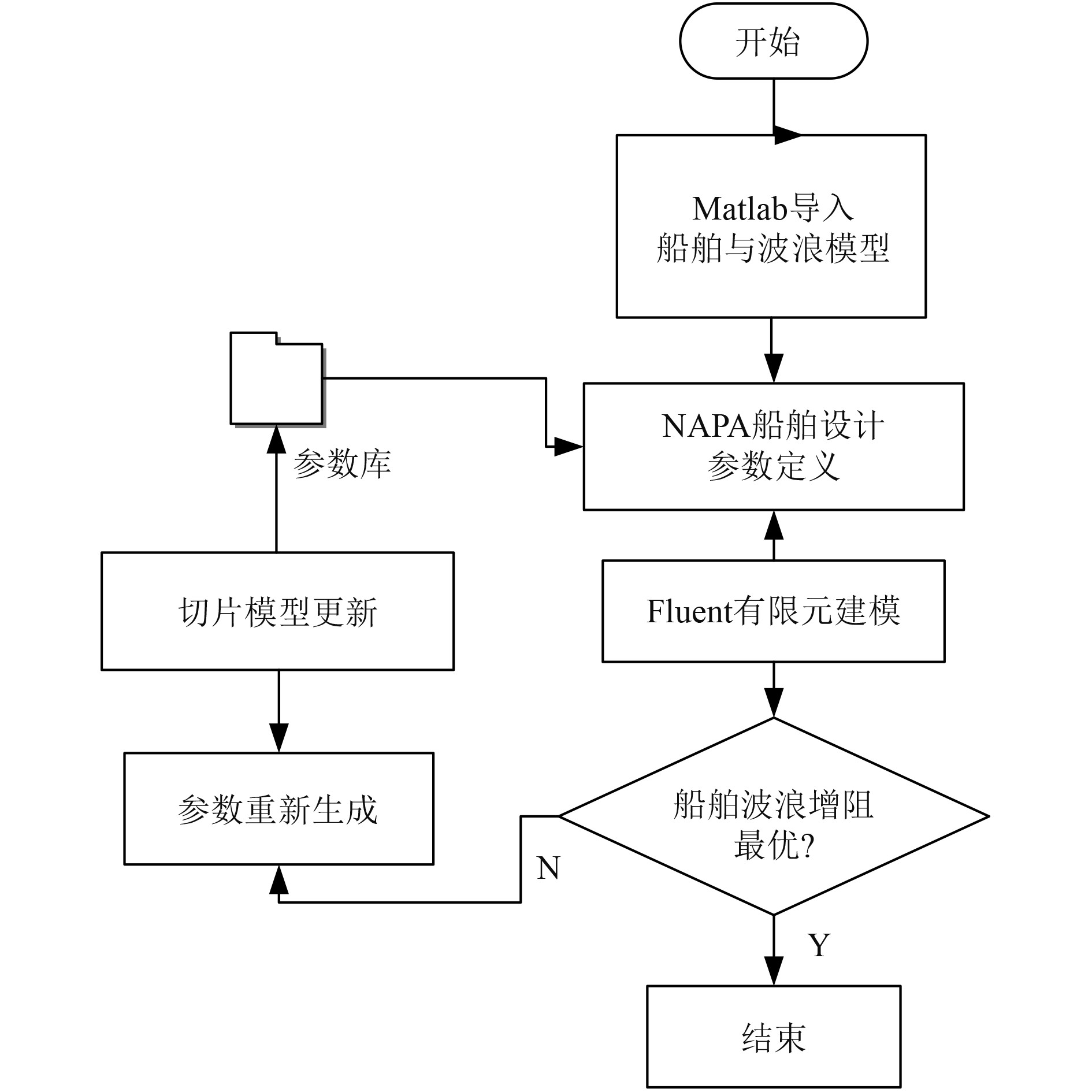
针对船舶的波浪增阻特性进行船型优化，结合Matlab平台建立船舶运动学和动力学模型，导入规则波模型，通过船舶设计软件NAPA建立船舶的切片模型，结合Fluent^[4]流体力学有限元仿真软件，进行船舶的优化设计。设定初始航速和初始波浪振幅，通过仿真船舶波浪增阻的大小进行船型的优化。结合波浪增阻特性的船型优化流程如图4所示。

3.2 高速船舶波浪增阻特性的有限元建模及仿真

基于Fluent的有限元仿真可以较准确的获取船舶波浪阻力，Fluent是计算流体力学CFD技术的重要应用软件，结合Fluent建立船舶不同型线的有限元模型，完成波浪增阻的仿真和船型的优化。

依据某型号高速船舶进行有限元仿真，部分参数如表1所示。

仿真过程中Fluent计算域的建立是关键环节，计算域的网格密度、网格质量直接决定了仿真的精确程度。本文在建立仿真计算域时，选择计算域的长度应为8倍船长 ${L_0}$ ，宽度为5倍船宽 ${B_0}$ ，采用分块划分的网格划分方法，船体与波浪接触区域的有限元网格采用四面体网格，其他较规则区域的网格采用六面体网格。

图5为基于Fluent建立的高速船计算域有限元模型。

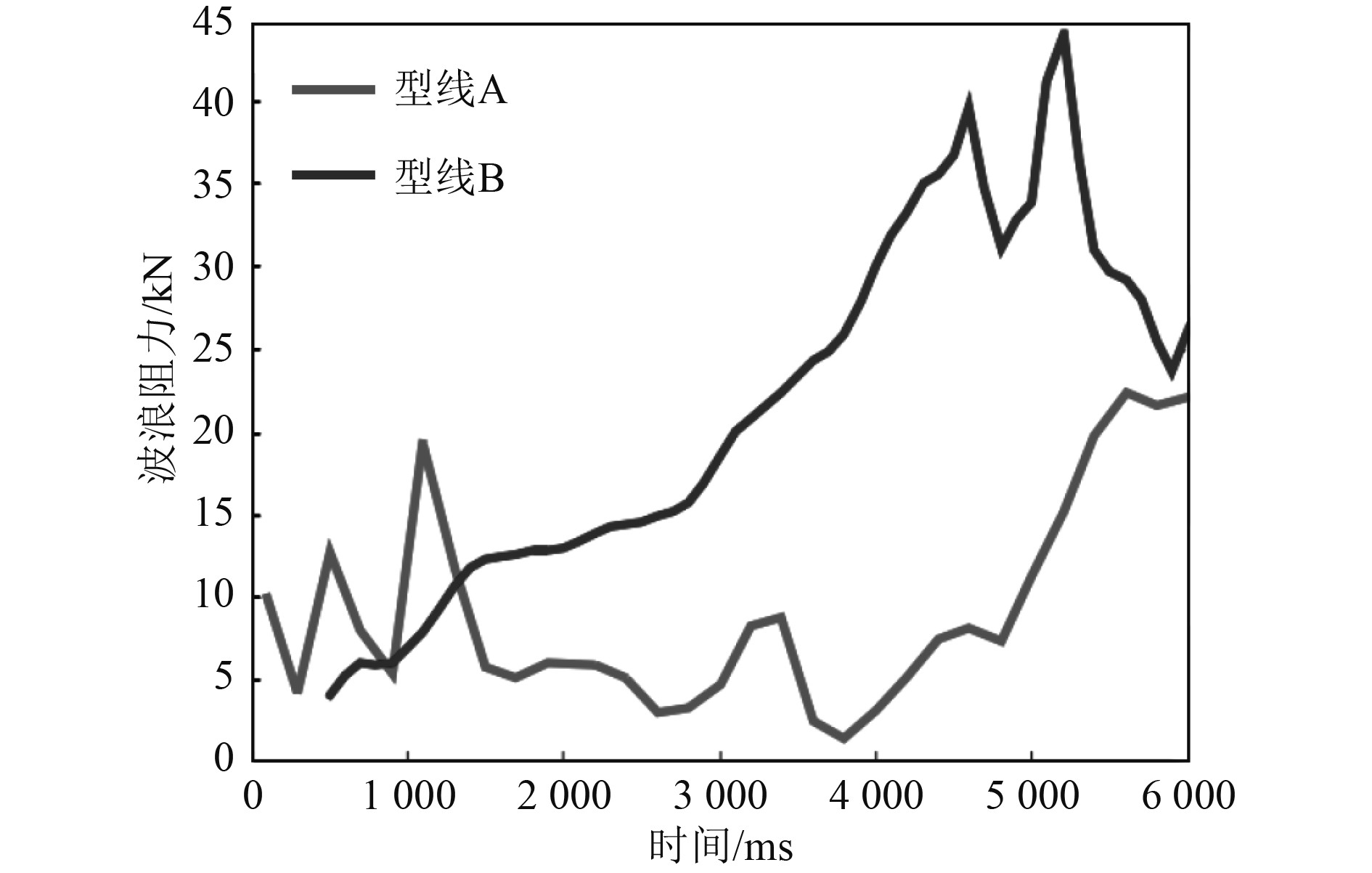
本文共仿真了2种不同的高速船剖切面型线，型线A采用指数函数拟合，型线B采用Bezier曲线拟合，得到2种设计剖面型线的波浪阻力仿真结果如图6所示。

4 结　语

船舶的耐波性是重要的设计参数，针对船舶在波浪中的增阻特性，本文建立波浪与船舶的运动学模型，结合Matlab和Fluent软件进行了不同船型设计的优化仿真。