0 引　言

因船舶设计周期短，且在详细设计阶段需完成船舶舱室噪声预报，虽在前期设计阶段可采用经验公式^[1]对舱室噪声进行预报，但其预报值过于保守，故只能作为定性判断而不能定量分析。在详细设计阶段对噪声超标舱室采取降噪优化设计比建造完成后再采取降噪补救措施可节约成本2.5倍左右，因此在详细设计阶段如何快速有效解决易出现的舱室噪声超标问题迫在眉睫。

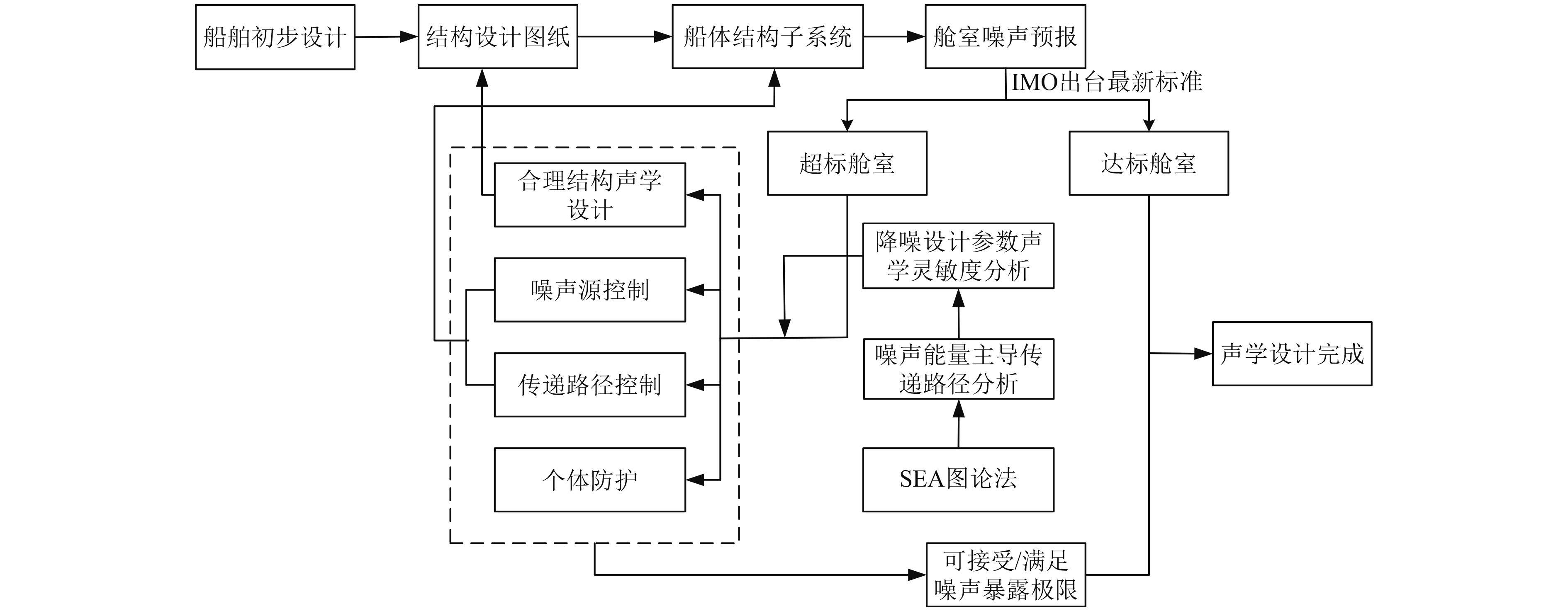
通常船舶舱室噪声设计分为舱室噪声水平数值预报和降噪设计2个阶段。中高频段噪声是舱室噪声的主导分量，统计能量分析^[2-4]（SEA）被广泛应用于船舶舱室噪声预报阶段。在全船总体布局确定的情况下，根据图纸建立SEA子系统模型，对船舶舱室噪声水平进行数值预报，舱室噪声控制流程图如图1所示。而降噪设计是船舶舱室噪声设计的难点之一。降噪设计应基于科学性、先进性、经济性三大原则^[5]综合考虑以确定最优降噪方案。科学性是指从噪声的产生机理出发明确噪声源特性以制定相应减振降噪措施；先进性是指制定降噪措施应在工程应用具有可实施性，且不影响其原有设备的技术指标性能；经济性是指采取的降噪措施需充分考虑经济成本问题，而不是将其噪声控制的越低越好。为快速有效解决详细设计阶段易出现的舱室噪声超标问题，本文依据噪声控制原理，以振动噪声传递路径为切入点，引入SEA图论法，对振动噪声能量的主导传递路径展开降噪设计的声学灵敏度分析，并结合降噪优化设计的三大原则对降噪方案进行评价以选最优方案。

采用SEA图论法结合振动噪声能量的主导传递路径对2层平板声腔结构降噪设计参数展开声学灵敏度分析，给出降噪设计指导性建议，为船舶舱室噪声降噪设计提供理论支撑。同时以某VLCC船声学设计实例，采用SEA图论法结合其噪声超标舱室的能量输入谱，确定其噪声主导传递路径的灵敏度，优化降噪方案并结合评价指标对其展开评价，成功将最优降噪方案应用于实船（预报值与实测值吻合良好）。可见，基于SEA图论法的船舶舱室噪声的降噪优化设计具有可行性，为降噪声学指标的定量优化设计提供参考。

1 SEA框架下的图论法

文献[6]将SEA模型中一系列相邻的损耗因子矩阵与图论法中图的数据结构相类比，发展提出SEA图论法。通过赋予SEA模型中相邻损耗因子矩阵不同权重，可得到统计能量模型中噪声能量的多条传导路径。在SEA模型中寻找最大能量传递路径实际等效于图论法中最短路径的寻求问题。对船舶舱室进行降噪设计，首先需知噪声超标舱室的主要噪声来源与其多条主要噪声能量传导路径，即等效于图论法中K则最短路径^[5]问题。

1.1 SEA法传递路径基础理论

Craik^[8-9]提出从有声源子系统（a source subsystem）的能量传递到目标考核舱室（a target subsystem）的第N条传递路径，其中经过N-1个子系统的损耗因子贡献度为：

$ {P}_{s12\cdots t}=\prod _{i=0}^{N-1}\frac{{\zeta }_{ii+1}}{{\zeta }_{i+1}} 。$

(1)

式中： $ {\zeta }_{ij} $ 表示子系统 $ i $ 和子系统 $ {j} $ 之间的耦合损耗因子； $ {\mathrm{\zeta }}_{i}={\zeta }_{id}+\displaystyle\sum _{j}{\zeta }_{ij} $ 表示子系统 $ i $ 的总损耗因子；其中 $ {\zeta }_{id} $ 为子系统 $ i $ 的内损耗因子； $ i=0 $ 代表源子系统， $ i=N $ 代表目标子系统。

式（1）为源子系统通过传递路径 $ {P}_{s12\cdots t} $ 传递到目标子系统的能量传递率，其传递的总能量为 $ {P}_{s12\cdots t}{E}_{s} $ ^[8]。在SEA模型中关心的仅仅是声源舱室到目标舱室的前几条噪声能量的主要传导路径，即文献[8]中的前K则最短路径。为研究不同传递路径传递能量的贡献度，根据Neumann级数对SEA系统矩阵进行展开。假设标准SEA的损耗因子矩阵为H，则SEA法中求解方程为 $ \mathit{H}\mathit{E}={\mathit{E}}^{0} $ ，其相关参数定义如下：

$ H_{ij}={\zeta }_{ji}(2{\delta }_{ij}-1) ，$

(2)

$ {\mathrm{\delta }}_{ij}=\left\{\begin{array}{c}0,i\ne j，\\ 1,i=j，\end{array}\right. $

(3)

$ {\mathrm{\zeta }}_{ii}\equiv {\zeta }_{i} ，$

(4)

$ {\boldsymbol{E}}^{0}= {\boldsymbol{W}}\omega。$

(5)

式中： $ \mathrm{\omega } $ 为计算频带的中心圆频率； $ \mathit{W} $ 为外部向系统输入的功率向量；E为各子系统的能量。

由文献[8,10]将 $ \mathit{E} $ 表达为：

$ \mathit{E}={\left(\mathit{I}-\mathit{S}\right)}^{-1}{\mathit{E}}^{0}=\left(\sum _{K=0}^{\infty }{\mathit{S}}^{k}\right){\mathit{E}}^{0}=(\mathit{I}+\mathit{S}+{\mathit{S}}^{2}+\cdots ){\mathit{E}}^{0}。$

(6)

式中： $ {\mathit{E}}^{0} $ 重新定义为 $ {\mathit{E}}_{i}^{0}={\mathit{E}}_{i}^{0}/{\zeta }_{i} $ ； $ {\mathit{S}}_{ij}=({\zeta }_{ji}/{\zeta }_{i})(1-{\delta }_{ij}) $ 。

1.2 SEA图论法描述

式（6）展开的级数虽不能直接解决传递路径排序问题，但能将SEA法与图论法关联在一起。定义SEA有向图 $ {G}_{SEA}=\left({U}_{SEA},{E}_{SEA}\right) $ ，其中N个节点数代表SEA模型中子系统数目， $ \left\{{u}_{1},{u}_{2},\cdots ,{u}_{N}\right\}\in {U}_{SEA} $ ； $ {N}_{E} $ 条边 $ \left({u}_{i},{u}_{j}\right)\in {E}_{SEA}\subset {U}_{SEA}\times {U}_{SEA} $ 表示SEA子系统的连接，规定 $ \left({u}_{i},{u}_{j}\right) $ 为从 $ {u}_{i} $ 到 $ {u}_{j} $ ， $ {u}_{i} $ 表示终点， $ {u}_{j} $ 表示起点，将周边节点 $ {u}_{i} $ 与节点连接的边定义为集合 $ {\mathrm{\varepsilon }}_{i} $ ， $ {\mathrm{\varepsilon }}_{i}={\varepsilon }_{i}^{+}\cup {\varepsilon }_{i}^{-} $ ，其中 $ ({u}_{j},{u}_{i})\in {\mathrm{\varepsilon }}_{i}^{+} $ , $ ({u}_{i},{u}_{j})\in {\mathrm{\epsilon }}_{i}^{-} $ 。取式（6）的矩阵 $ \mathit{S} $ 作为有向图 $ {G}_{SEA} $ 的相邻矩阵，将矩阵 $ \mathit{S} $ 定义为 $ {E}_{SEA} $ 各边的加权值，具体定义为：

$ {\mathrm{S}}_{ij}=\left\{\begin{array}{c}\dfrac{{\zeta }_{ji}}{{\zeta }_{i}},{\rm{if}}({u}_{i},{u}_{j})\in {E}_{SEA}，\\ 0,{\rm{if}}({u}_{i},{u}_{j})\notin {E}_{SEA}。\end{array}\right. $

(7)

通过第 $ n $ 条传递路径 $ {p}_{ij}^{n} $ 定义其边权值为：

$ w\left({p}_{ij}^{n}\right)=\prod _{m=0}^{n-1}{w}_{{h}_{m}{h}_{m+1}}=\prod _{m=0}^{n-1}\frac{{\zeta }_{{h}_{m}{h}_{m+1}}}{{\zeta }_{{h}_{m+1}}}\equiv \prod _{p}{w}_{ij}=w\left({p}_{ij}\right) 。$

(8)

式中： $ {h}_{0}=i,{h}_{n}=j $ 。

假设 $ {p}_{ij} $ 表示节点 $ {u}_{i} $ 到 $ {u}_{j} $ 的传递路径， $ {q}_{jl} $ 表示节点 $ {u}_{j} $ 到 $ {u}_{l} $ 的传递路径，那么用 $ {p}_{ij}\circ {q}_{jl} $ 表示从节点 $ {u}_{i} $ 到 $ {u}_{l} $ 的传递路径，且同时满足下式：

$ w\left({p}_{ij}\circ {\mathrm{q}}_{jl}\right) = w\left({p}_{ij}\right)w\left({q}_{jl}\right) = \prod _{p}{w}_{ij}\prod _{q}{w}_{jl} = \prod _{p+q}{w}_{il} 。$

(9)

在统计能量分析模型中，对于任意2个子系统 $ s $ 和 $ t $ ，前K则噪声能量主导传递路径可描述为： $ P_{st,K}= \{{p}_{st,1},{p}_{st,2},\cdots ,{p}_{st,K}\}\subseteq {P}_{st} $ ， $ {p}_{st,k} $ 总是先一步于 $ {p}_{st,k+1} $ 找到，其中需要满足以下条件^[4]：

$ \left\{\begin{array}{l} w\left({p}_{st,k}\right)\geqslant w\left({p}_{st,k+1}\right),\forall k\{\mathrm{1,2},\cdots ,K-1\}，\\ w\left({p}_{st,k}\right)\geqslant w\left({q}_{st}\right),\forall {q}_{st}\in {P}_{st}-{P}_{st,K}，\\ {p}_{st,k} > 0。\end{array}\right. $

(10)

对于式（10）问题的实现，可采用文献[6]中MPS算法或文献[11]中Dijkstra去边算法。

2 基于SEA图论法的船舶舱室噪声主导传递路径及灵敏度分析 2.1 基于SEA图论法传递路径的舱室降噪设计灵敏度分析方法

一般而言，基于SEA图论法主导传递路径对舱室降噪设计参数进行灵敏度分析，首先要采用数值预报方法对舱室进行噪声预报，获得其舱室的相关声学量，建立舱室声学量的目标函数，通过在其主要传递路径上采取减振降噪措施，并对降噪设计参数进行微小改变，重新计算后分析其微小变化引起声学目标函数的变化。从而根据声学灵敏度的大小确定对声学目标函数影响较大的设计参数，通常降噪设计中只需对声学灵敏度大的参数进行降噪处理，此种方法能够高效确定降噪方案。对于大型复杂工程结构，基于SEA图论法确定其噪声主导传递路径，可有效避免声学灵敏度分析的大规模计算，只需在其主要噪声传递路径上的结构进行声学设计参数的灵敏度分析，相对而言在很大程度上减少了计算工作量。在噪声主传递路径上定义其声学灵敏度参数^[12]为：

$ \frac{\partial p}{\partial IL}=\frac{{p}_{1}-{p}_{2}}{IL} 。$

(11)

式中： $ {p}_{1} $ 表示未采取降噪措施的目标舱室的噪声总声级； $ {p}_{2} $ 表示在噪声主导传递路径上的舱室某个舱壁表面或某几个舱壁表面上采取降噪措施后的噪声总声级；IL表示采取降噪措施后所引起的物理参数变化（如吸声材料的吸声量、隔声板的隔声量等）。声学灵敏度能够客观反映出降噪方案设计中物理参数与目标声学量的相互关系。

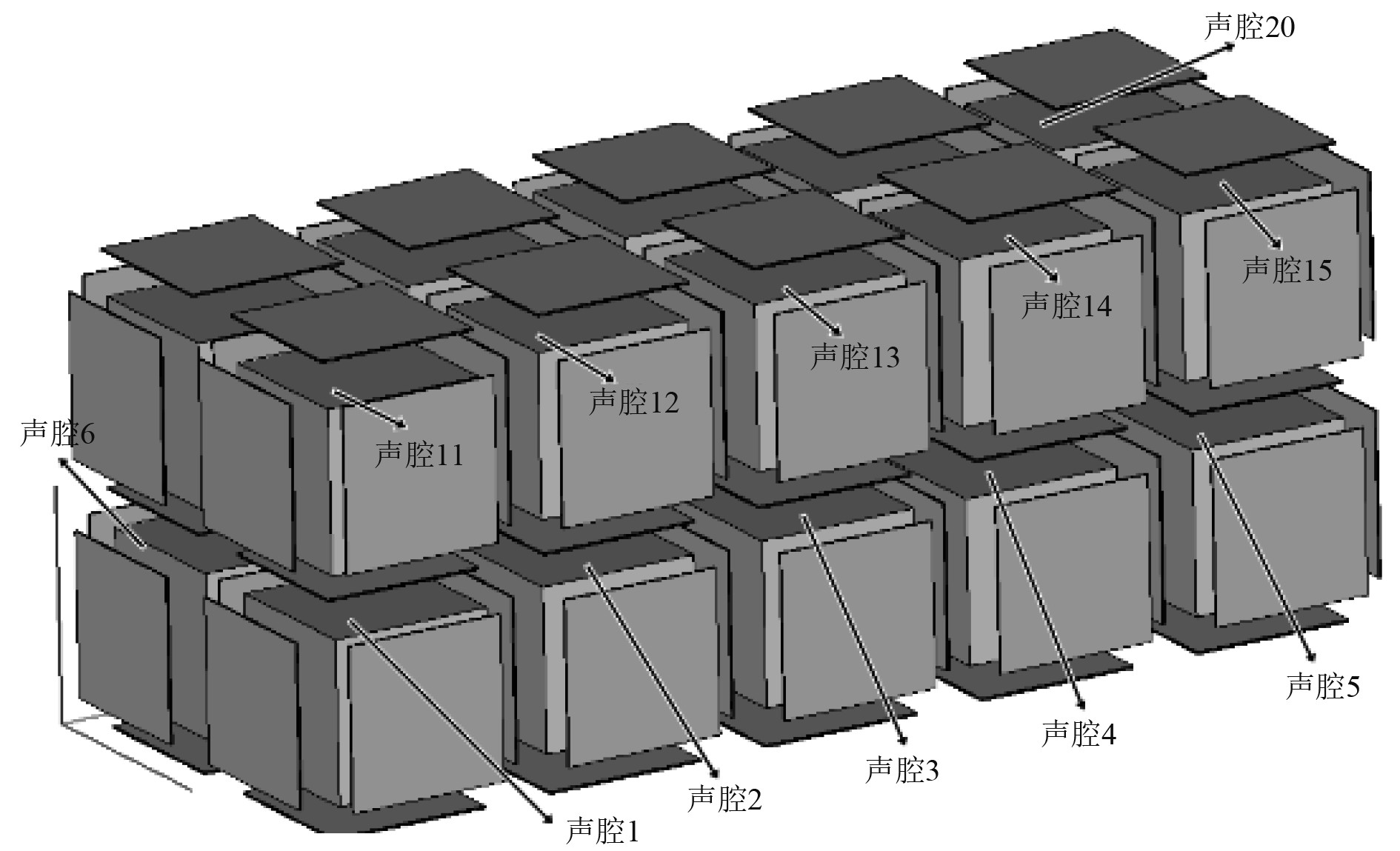
以2层平板声腔结构为研究对象，基于SEA图论法确定其噪声主导传递路径，在传递路径上进行降噪设计灵敏度分析。图2为2层平板声腔结构示意图，声腔为边长为1 m的立方体，平板和声腔的内损耗因子都取为1%，在声腔1加载噪声源，声压为109 dB（参考声压为 $ 2\times {10}^{-5}\;\mathrm{P}\mathrm{a} $ ），计算频段范围取为800 Hz~8 kHz，图3为从第1个声腔到第20个声腔的前2条噪声能量的主导传递路径。

经数值计算得到该SEA模型的损耗因子矩阵，确定从声源子系统声腔1到目标子系统声腔20的前2条主导噪声传递路径为：1）1→2→3→4→5→15→20；2）1→2→3→4→5→10→20。由于图2中模型具有对称性，因此图3中的前2条噪声能量的主导传递路径具有相同的边权值（损耗因子贡献度）。在基于SEA图论法得到声腔1到声腔20的前2条噪声主导传递路径的基础上，对目标舱室20进行舱室降噪设计参数灵敏度分析，为船舶降噪设计提供参考。

通过定义噪声能量主传递路径经过的舱室为重点路径舱室，利用指定在全频段隔声量为10 dB的隔声板对重点路径舱室进行降噪设计处理，研究声腔1中噪声源至目标舱室声腔20的主导传递路径对隔声板隔声量的灵敏度分析。在重点路径舱室间主导噪声传递路径上敷设10 dB隔声量的隔声板后，噪声能量主导传递路径上声学灵敏度为：

$ \frac{\partial p}{\partial IL}=\frac{{p}_{1}-{p}_{2}}{10} 。$

(12)

对目标舱室进行降噪设计可采取2种降噪方案：1）在重点路径舱室局部结构敷设隔声板；2）对重点路径舱室进行整体降噪处理。根据式（12）分别对2种降噪方案进行声学灵敏度分析，具体结果如表1和表2所示。

表1中j→k表示在舱室j和舱室k的直接能量传递路径上采取降噪措施。

由表1和表2对比可发现，噪声主导传递路径上中间路径舱室的声学灵敏度基本一致，而在噪声源处的舱室和目标舱室处的声学灵敏度相对大很多。随着噪声源舱室和目标舱室距离越远，噪声能量的传递路径也会越多，由此可判断出：在大型复杂船舶结构中，随着甲板层数的增多，噪声能量的传递路径也会更为错综复杂，对其中某个中间路径舱室进行降噪处理无法对所有传递路径产生综合决定性影响，但在靠近目标舱室的舱室或相邻甲板舱室的降噪设计参数的声学灵敏度再次升高表明各条主要噪声传递路径所携带的能量都通过这类舱室或此层甲板向目标舱室进行能量集聚。表2中的数据表明，对目标舱室（舱室20）采取整舱降噪处理的声学灵敏度远大于其他降噪措施。由此可知，对目标舱室采取隔声降噪措施是最有用的方法。

根据表1和表2计算的声学灵敏度表，对船舶舱室降噪设计提供指导性意见：1）应优先考虑对噪声源所处舱室和目标舱室采取减振降噪处理，原因在于二者分别对应噪声主导传递路径的起点处和终点处，且声学灵敏度值都为最大值。若舱室噪声声压总声级超过噪声限值较多时，首先应在目标舱室中采取整体降噪措施，再考虑对噪声源所处舱室采取声学降噪措施，如隔声罩、消声器、阻尼减振及隔振系统等；2）对噪声超标舱室噪声主要传递路径进行分析，确定噪声源舱室到目标舱室的前几条主要噪声能量传递路径，并对其进行声学灵敏度分析。根据声学灵敏度分析结果，对声学灵敏度较为敏感的重点路径舱室采取减振降噪措施，对传递路径上的声学灵敏度不敏感的中间舱室可不作声学降噪处理。这样不仅节省了声学设计成本，也达到了舱室降噪的目的。

2.2 降噪方案评价指标

在制定噪声控制措施方案时，需综合考虑空船重量、稳性、可执行性、占用舱室空间等问题，但最重要的是对经济成本的考虑。因此，降噪方案一般是综合运用多种噪声控制措施。对降噪方案的经济性进行评价，可量化其评价指标，具体为：

$ {C}_{p}={\beta }_{1i}+{\beta }_{2j}+{\beta }_{3k}+{\beta }_{4l}+{\beta }_{5m}+A ，$

(13)

$ C=\mathrm{m}\mathrm{i}\mathrm{n}\left({C}_{p}\right) 。$

(14)

其中： $ C $ 为所有降噪方案中的最低成本； $ {{C}}_{p} $ 为第p套降噪方案的花费成本； $ i=\mathrm{1,2},3 $ 依次为舱室空间布置设计成本、声学结构设计成本、建造增加成本； $ j=\mathrm{1,2},3 $ 依次为加设隔声罩、隔振器、消声器的成本； $ k=1, 2,3 $ 依次为贴设声学材料成本、施工花费、损失空间； $ l=1 $ 为整船重量变化增加的损失； $ m=1 $ 为舱室个体防护听力保护器花费成本； $ A $ 为额外其他增加的成本。

3 声学设计案例分析

根据统计能量分析法（SEA法）对某VLCC船进行舱室噪声分析并确定其噪声超标舱室。对VLCC船噪声超标舱室，根据其噪声能量的主导传递路径，结合降噪设计指导意见制定降噪方案，最后根据降噪方案评价指标对降噪方案进行评价，选取最优降噪方案。

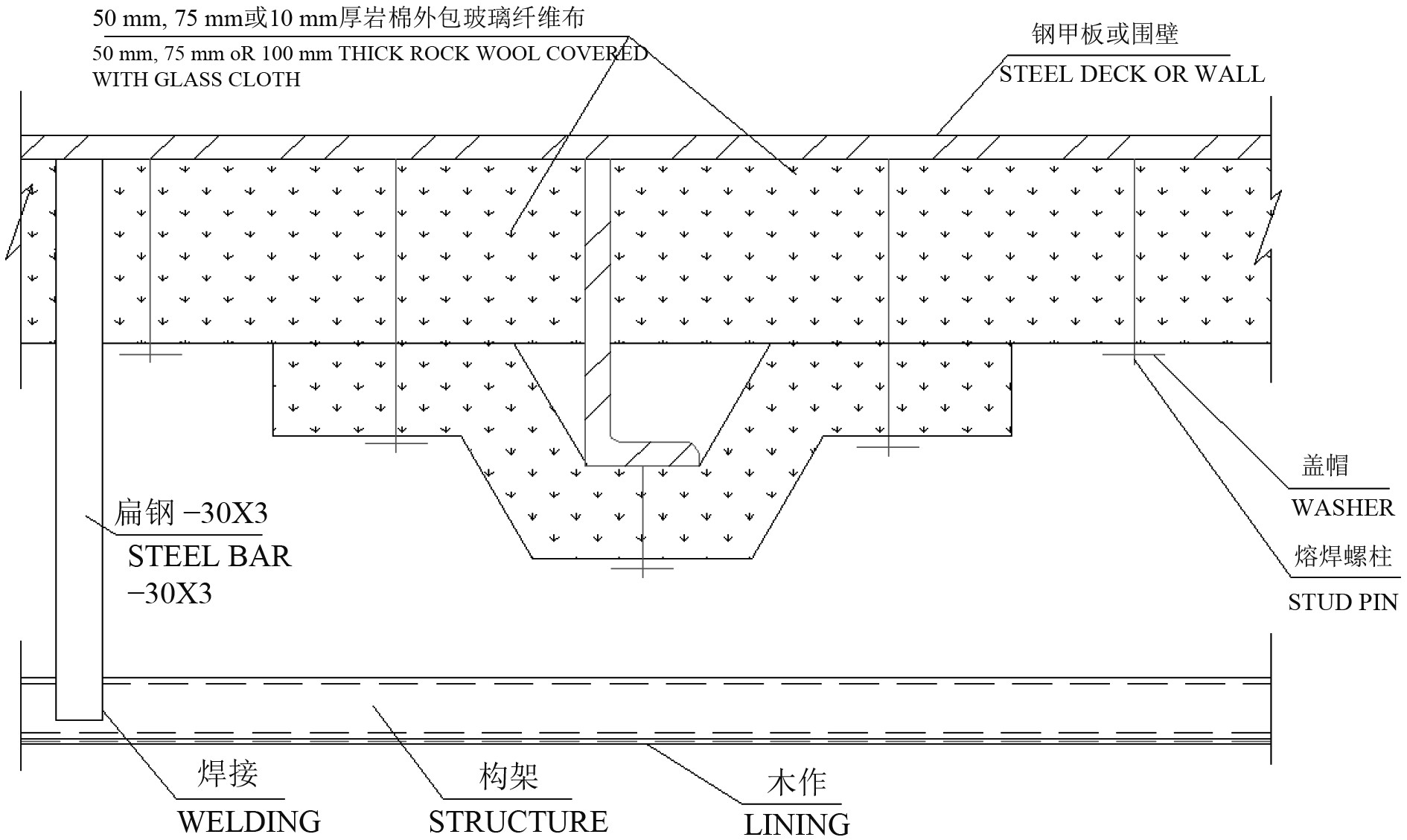
绝大部分舱室的木作衬板通常采用复合岩棉板。以岩棉为例，绝缘布置材料典型安装节点示意图如图4所示。

该VLCC船采用的岩棉的容重为100 kg/m³，不同厚度的岩棉吸声系数如表3所示。

该VLCC船的木作衬板及天花板，有25 mm复合岩棉板和50 mm复合岩棉板，两型复合岩棉板的隔声性能参数如表4所示。

3.1 某VLCC噪声超标舱室降噪方案

以某VLCC噪声超标舱室主甲板医务室为例，首先确定该舱室的主导输入能量及主导传递路径，进而提出降噪指导性意见对其主导传递路径舱室制定噪声控制方案，使其舱室噪声水平降低，满足规范要求。

3.1.1 噪声超标舱室的噪声主导传递路径确定

1）主甲板医务室能量输入谱确定

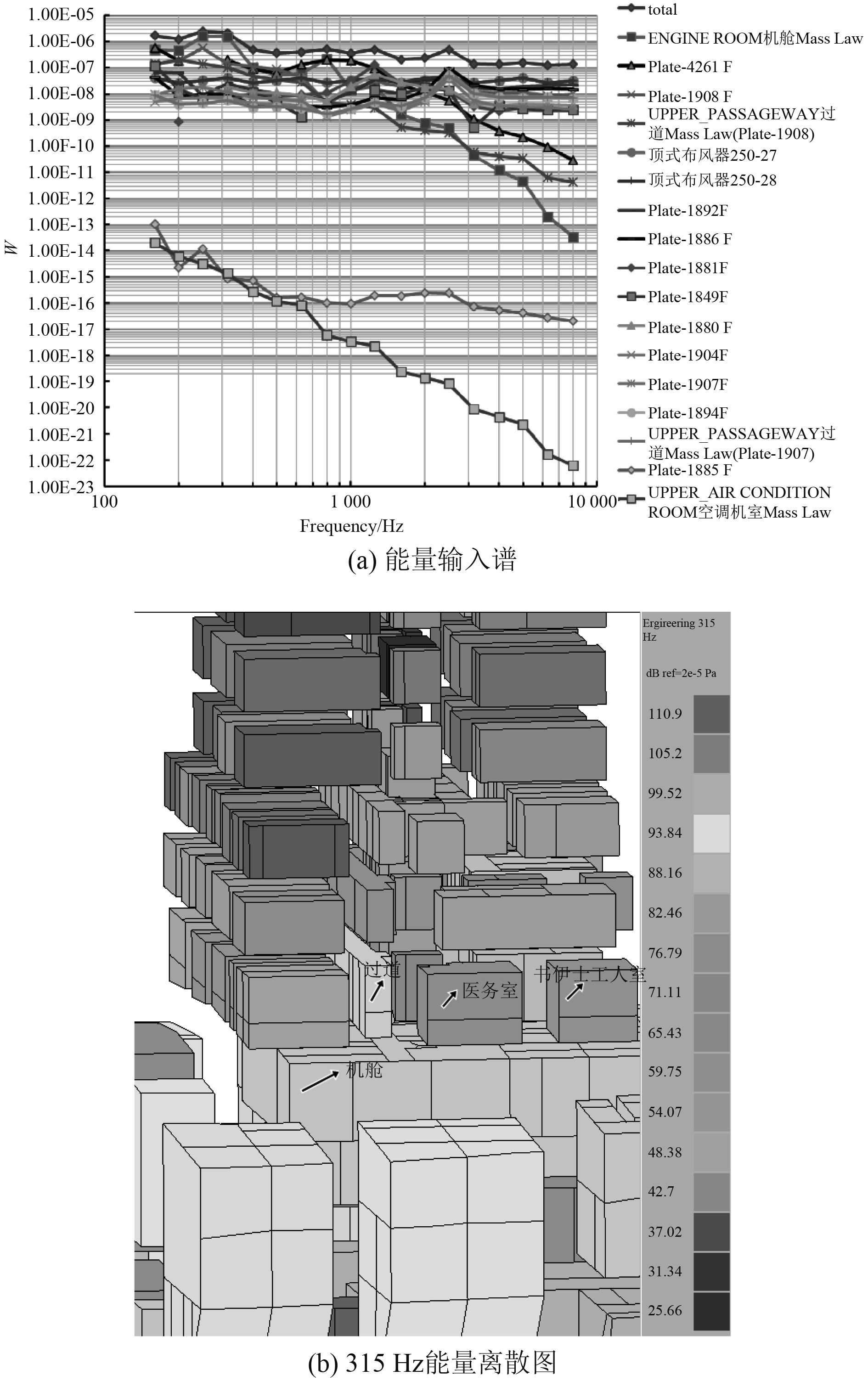
医务室位于主甲板左舷一侧，其噪声预报值为63.2 dB(A)，超出其规范限值8.2 dB(A)。主甲板医务室的能量输入如图5所示。

可知，对主甲板医务室声腔能量输入贡献较大的子系统有：机舱、板-4261（医务室地板）、板-1908（医务室前壁板）、板-1892（医务室后壁板）。由SEA图论法分析可知主甲板医务室噪声能量的主导传递路径为：1）机舱-医务室地板-医务室；2）机舱-过道-医务室前壁板-医务室；3）机舱-苏伊士工人室-医务室后壁板-医务室。经分析确定，主甲板医务室舱室噪声成分中空气噪声与结构噪声的构成比重相当。

3.2 超标舱室降噪方案及评价

25 mm隔声复合岩棉板和50 mm高隔声复合岩棉板是船上常用的声学材料，从降噪效果考虑，选用50 mm高隔声复合岩棉板作为其主要降噪声学材料。

1）降噪方案1

根据舱室噪声成分构成比重和降噪指导性建议，在噪声超标舱室声学灵敏度值较大的噪声主导传递路径上采取吸声或隔声、阻尼减振等措施，制定降噪方案如表5所示。

2）降噪方案2

按照噪声超标舱室的噪声能量输入谱，确定超标舱室的主要噪声能量来源，同时根据降噪设计建议，对目标舱室进行整体降噪处理，制定如表6所示的降噪方案。

3）方案评价

由表7可知，方案2比方案1降噪效果要显著；但方案1消耗的吸声、隔声、阻尼材料较方案2少1倍左右，舱室空间损失较小，且施工相对简单易行。因此，从可实施性、节省空间、经济性综合考虑，方案1为最优降噪方案。

3.3 误差分析

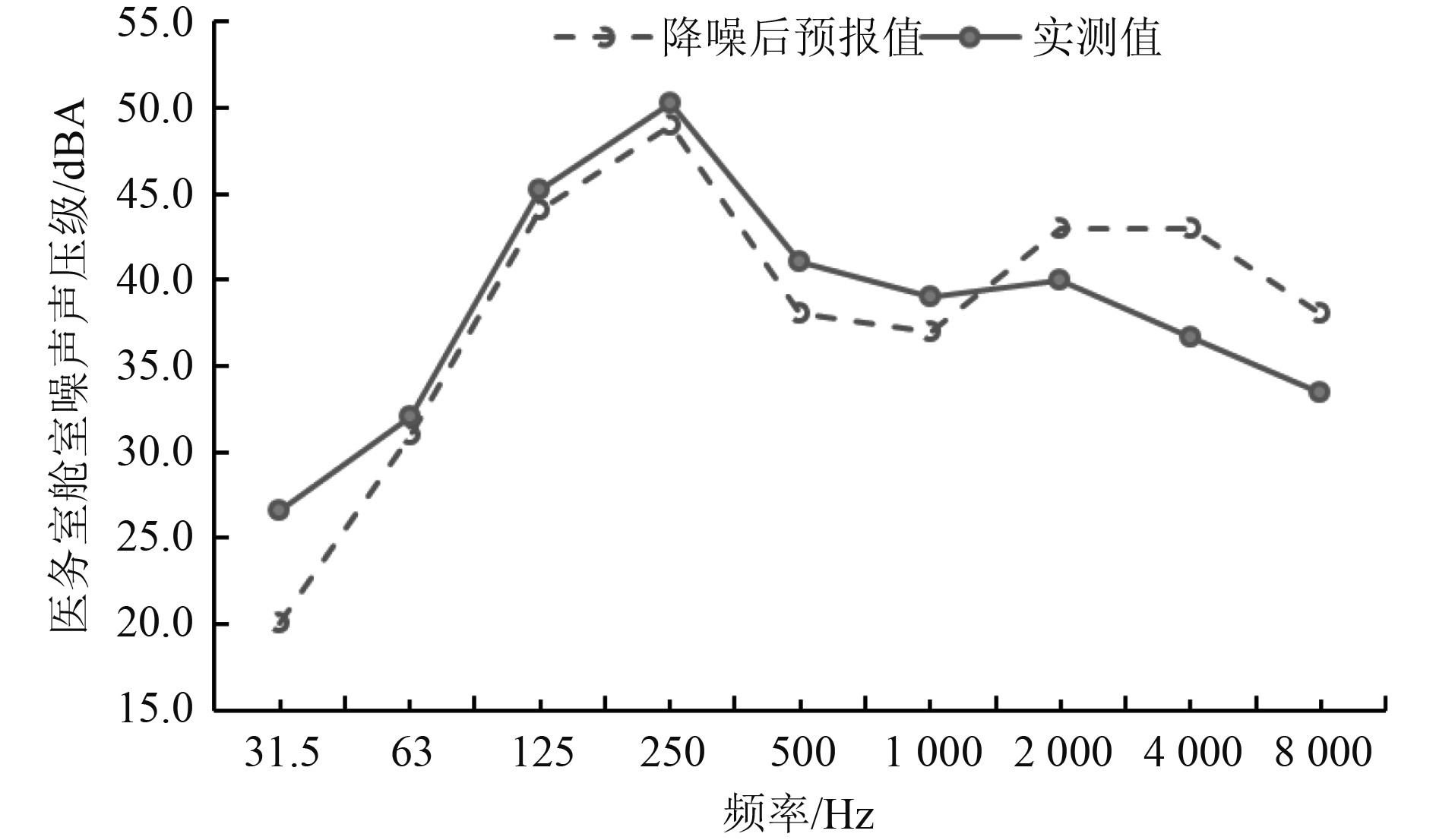
将采取方案1降噪措施后的医务室的舱室噪声预报值与实测值对比如表8所示。SEA法预报值与实测值图谱预报结果对比如图6所示。

由表8可知：1）基于SEA图论法传递路径确定的舱室降噪设计方案是可行的，并能满足工程实用精度的要求；2）实测值比预报值偏高，原因可能在于测量条件或开孔处缝隙等。

4 结　语

针对详细设计阶段易出现的船舶舱室噪声超标问题，依据噪声控制原理，以振动噪声传递路径为切入点，引入SEA图论法，结合振动噪声能量的主导传递路径对2层平板声腔结构降噪设计参数展开声学灵敏度分析，给出降噪设计指导性建议，为船舶舱室降噪设计提供理论支撑；以某VLCC船声学设计实例，采用SEA图论法结合其噪声超标舱室的能量输入谱，确定其噪声主导传递路径的灵敏度，结合评价指标选取最优降噪方案，成功应用于实船，预报值与实测值吻合良好。可见，基于SEA图论法的船舶舱室噪声的降噪优化设计具有可行性，为降噪声学指标的定量优化设计提供参考。