海流能作为海洋能源之一,储量约为50×109 kW[1]。参考风力发电装置设计原理,利用流体流经结构引发结构振动进行发电,使得海流能发电领域的运用获得更多关注。
密歇根大学可再生能源实验室[2]设计并制造流致振动低流速海流发电装置,在振子上固定皮带条,随着振子运动,皮带条带动电机旋转产生感应电压,这套装置具有高能量密度与低启动流速的特点。Lobo[3]在涡激振动基础上加入了直线电机,组成VIV(vortex induced vibrations)系统,该系统通过改变质量比与雷诺数分析对振子振幅、发电效率的影响。Hai Sun[4]通过对发电机的功率以及效率建模,提出一种能够准确计算多振子流致振动耦合功率以及效率的方法,并运用实验去验证计算方法的准确性。谭俊哲[5]制作了直线发电机发电装置,将直线发电机与流致振动捕能装置相结合,通过实验方法得到发电机在0.5 m/s流速下的发电功率为0.075 W。李莉[6]利用柔性轻质圆管在水流中产生涡激振动,在柔性管中添入双压电片悬臂梁进行发电,根据数学建模得到的响应曲线计算出发电的最大电压为2.431 V。已有成果多是基于金属弹簧提供弹性回复力进行流致振动研究。考虑到金属弹簧使用寿命短,需定期跟换等缺点,白旭等[7-8]提出了具有磁边界的涡激振动装置,将磁力引入到流致振动发电装置中进行研究。Masoumi[9]研究了磁悬浮排斥式的波浪能收集装置,并且建立Duffing方程以计算不同外激力作用下的振幅响应,根据法拉第定律估算出系统的输出电压与频率。
目前对于磁悬浮支撑的流致振动研究仍然较少,本文针对磁悬浮流致振动捕能装置利用等效磁荷法计算出永磁体间磁力大小与磁体间间距关系,设定永磁弹簧中磁体排列方式以及最大压缩量,得到永磁弹簧的磁力在不同位移下的磁力值,通过最小二乘法计算出磁力与位移的函数,将函数代入到流固耦合计算模型中,计算出磁悬浮支撑的单圆柱振子流致振动的振动响应并加以分析。
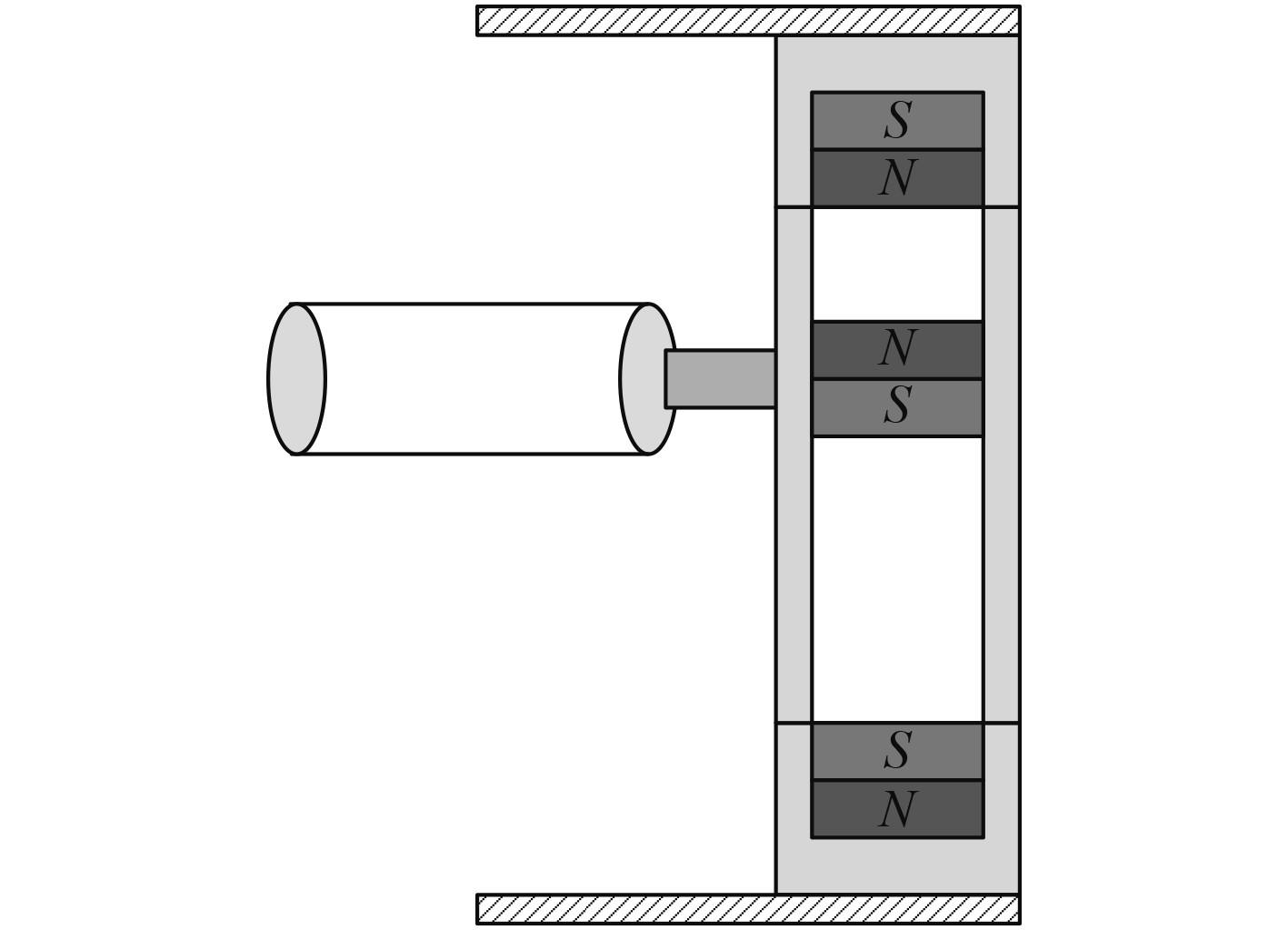
1 磁悬浮支撑振子流致振动物理模型圆柱振子在来流作用下发生流致振动,利用磁弹簧代替金属弹簧给振子提供回复力,其物理模型如图1所示。单圆柱振子在来流作用下产生流致振动发生位移,振子两端的永磁体随着振子运动偏离平衡位置,导轨两端永磁体对振子端部永磁体产生反向作用力促使振子回到平衡位置,振子在水流力、弹性回复力以及系统自身阻尼力作用下产生往复运动。其受力模型如图2所示。
|
图 1 磁悬浮的单圆柱刚性振子流致振动装置原理图 Fig. 1 Schematic diagram of flow induced vibration device of magnetic suspension single cylinder rigid vibrator |

|
图 2 磁悬浮的单圆柱刚性振子流致振动装置受力模型 Fig. 2 Force model diagram of flow induced vibration device of magnetic suspension single cylinder rigid vibrator |
磁悬浮支撑流致振动装置得弹性回复力主要由永磁弹簧提供,由图1可以看出,永磁弹簧主要由3块永磁体构成,可分为中间永磁体与端部永磁体,端部永磁体固定在导轨的两端,中间永磁体连接着导轨并固定在振子上,跟随振子沿着导轨运动。中间永磁体在运动过程中受到2块端部永磁体对它的作用力,分别求出端部永磁体对中间永磁体的磁力并进行矢量求和即可得到振子在振动过程中受到磁弹簧的回复力,本文主要使用等效磁荷法对磁力进行求解。
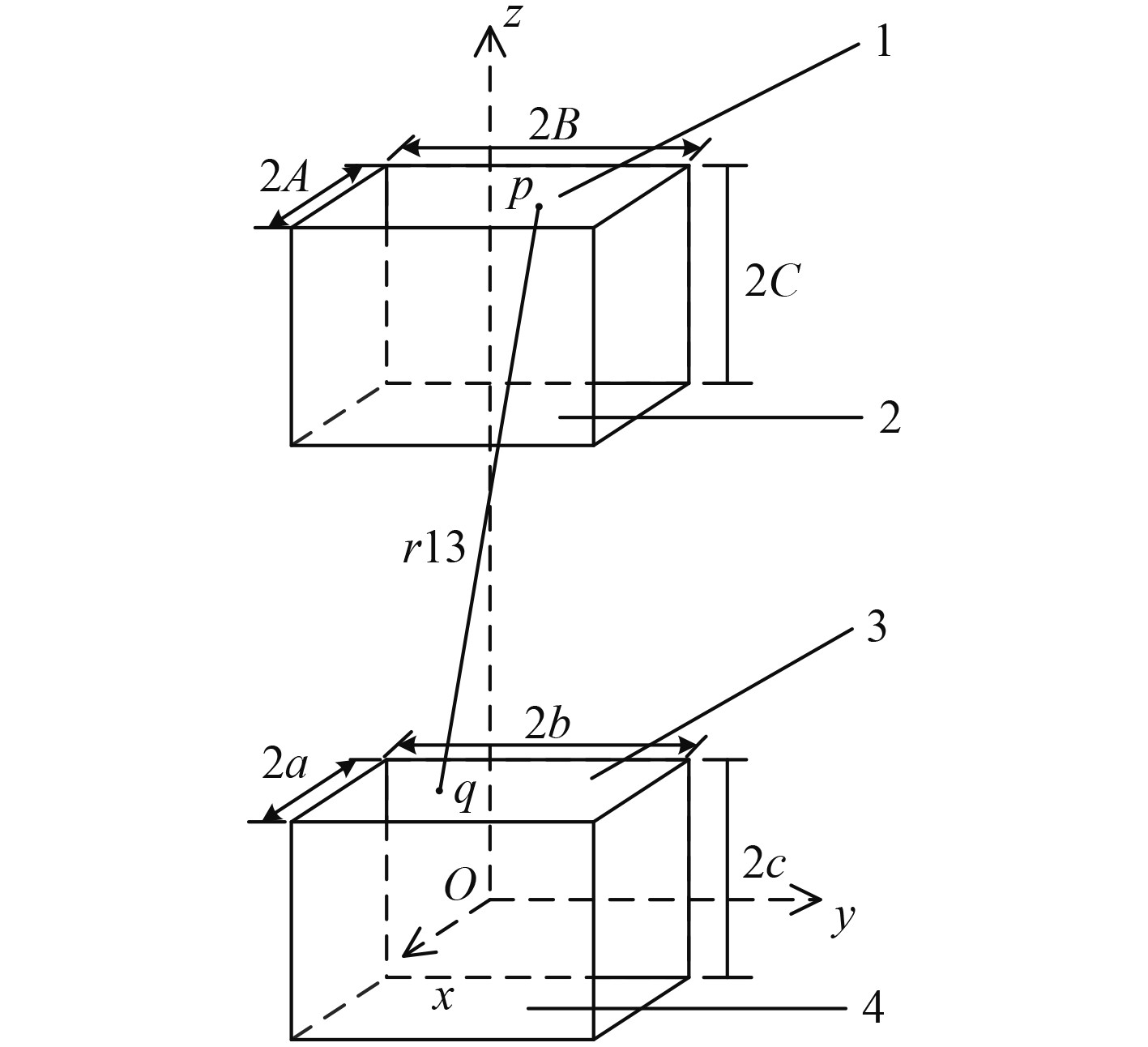
2.1 等效磁荷法计算2块永磁体的几何尺寸分别为2A,2B,2C以及2a,2b,2c,2块永磁体间的距离即面2和面3间距为
|
图 3 永磁体磁力求解模型 Fig. 3 Permanent magnet magnetic force solution model |
永磁体的充磁方式为沿z轴方向充磁,2块永磁体的极性相反。根据等效磁荷法[10],设面1上的一点p(x1,y1,2C+h+c),面3上一点q(x2,y2,c),
| $ {\rm{d}}{M_p} = {\sigma _1}{\rm{d}}{x_1}{\rm{d}}{y_1}, $ | (1) |
| $ {\rm{d}}{M_q} = {\sigma _2}{\rm{d}}{x_2}{\rm{d}}{y_2}。$ | (2) |
式中:σ1,σ2分别为面1与面3的磁荷面密度。
根据文献[11]中给出的永磁材料的磁化关系可知,磁荷面密度与剩磁感应强度的关系为:
| $ \left\{ \begin{gathered} {\sigma _1} = {B_{r1}}, \\ {\sigma _2} = {B_{r2}}。\\ \end{gathered} \right. $ | (3) |
根据式(1)与式(2)可推出点p对点q的作用力矢量为:
| $ {\rm{d}}{{\boldsymbol{F}}_{13}} = \frac{1}{{4 \text{π} {\mu _0}}}\frac{{{B_{r1}}{B_{r2}}{\rm{d}}{x_1}{\rm{d}}{x_2}{\rm{d}}{y_1}{\rm{d}}{y_2}}}{{{r_{13}}^3}}{{\boldsymbol{r}}_{13}}。$ | (4) |
通过矢量力dF13可以求出点q点对点p在z方向上的分量为:
| $ {\rm{d}}{F}_{13}={\rm{d}}{{\boldsymbol{F}}}_{13}\cdot{\boldsymbol{k}}=\frac{1}{4 \text{π} {\mu }_{0}}\frac{{B}_{r1}{B}_{r2}{\rm{d}}{x}_{1}{\rm{d}}{x}_{2}{\rm{d}}{y}_{1}{\rm{d}}{y}_{2}}{{\left|{{\boldsymbol{r}}}_{13}\right|}^{3}}{{\boldsymbol{r}}}_{13}\cdot{\boldsymbol{k}}。$ | (5) |
式中,k为
| $ \left| {\boldsymbol{k}} \right| = \frac{{2C + h}}{{\left| {{{\boldsymbol{r}}_{13}}} \right|}} 。$ | (6) |
由点q与点p的坐标可以求出:
| $ \left| {{{\boldsymbol{r}}_{13}}} \right| = {[{({x_2} - {x_1})^2} + {({y_2} - {y_1})^2} + {(2C + h)^2}]^{\frac{1}{2}}}。$ | (7) |
通过对dF13的积分可得出面3对面1的作用力为:
| $ {F_{13}} = \frac{{{B_{r1}}{B_{r2}}\left( {2C + h} \right)}}{{4{\text{π}} {\mu _0}}}\int_{ - a}^a {} \int_{ - b}^b {} \int_{ - A}^A {\int_{ - B}^B {} } \frac{1}{{{{\left| {{{\boldsymbol{r}}_{13}}} \right|}^3}}}{\rm{d}}{x_1}{\rm{d}}{x_2}{\rm{d}}{y_1}{\rm{d}}{y_2} 。$ | (8) |
同理可以求出F23,F14,F24,根据4个面之间的力F13,F23,F14,F24以及磁面极性即可得出2块磁体间的斥力为:
| $ {F_{mag}} = - {F_{13}} + {F_{23}} - {F_{24}} + {F_{14}} 。$ | (9) |
永磁弹簧的磁力主要受永磁体的材料、规格、永磁弹簧的最大压缩量影响,本文主要研究永磁体的规格对磁力的影响,数值计算的材料属性与最大压缩量如表1所示。根据设定参数构建不同规格永磁体的永磁弹簧模型,并根据等效磁荷法算出永磁弹簧在随振子位移过程中受到磁力如图4所示。永磁弹簧的磁力曲线呈非线性增长,中间永磁体在平衡位置时的磁力变化趋势较平缓,当中间永磁体靠近两端时,磁力迅速增加。根据力与位移的关系使用最小二乘法进行多项式拟合即可得到力与位移的函数关系。
|
|
表 1 永磁体参数 Tab.1 Parameters of permanent magnet |

|
图 4 不同规格永磁弹簧磁力与位移的关系 Fig. 4 Relationship between magnetic force and displacement of permanent magnet springs of different specifications |
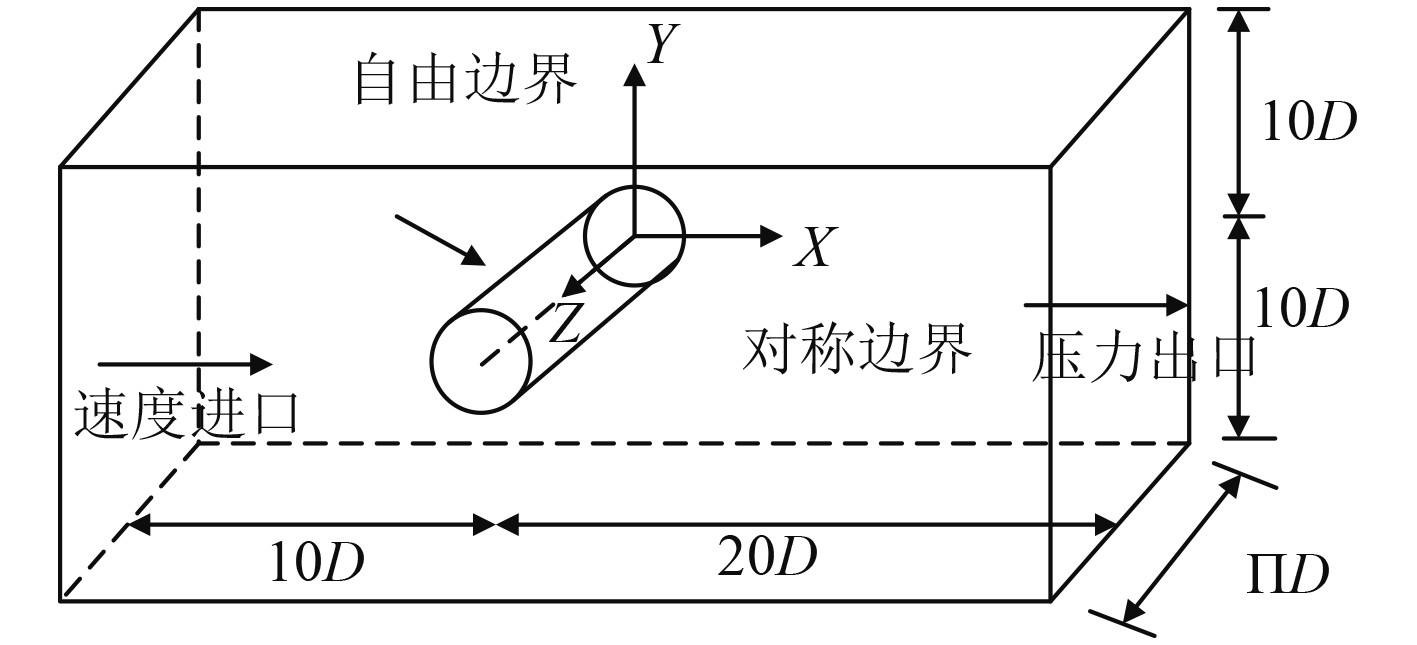
圆柱振子的流固耦合计算模型如图5所示。整体采用柱形计算域,计算域上下边界为自由滑移表面(free slip wall),计算域的前后边界为对称边界(symmetry),计算域入口采用速度进口(velocity inlet),计算域出口为压力出口边界(pressure outlet),圆柱表面是无滑移壁面(no slip wall)。
|
图 5 计算域及边界条件示意图 Fig. 5 Schematic diagram of calculation domain and boundary conditions |
为了保证计算结果的准确性,根据H.Lee[13]在高阻尼比实验中的模型为基础,具体参数如表2所示。为了保证振子在计算时的三维特性[15],振子的长度等比例缩小了3.27倍,相对应的振子的质量、刚度、阻尼力也同比例缩小,刚度为2.3的拟合结果,系统阻尼为文献[13]中的系统阻尼。
|
|
表 2 振子具体参数 Tab.2 Specific parameters of vibrator |
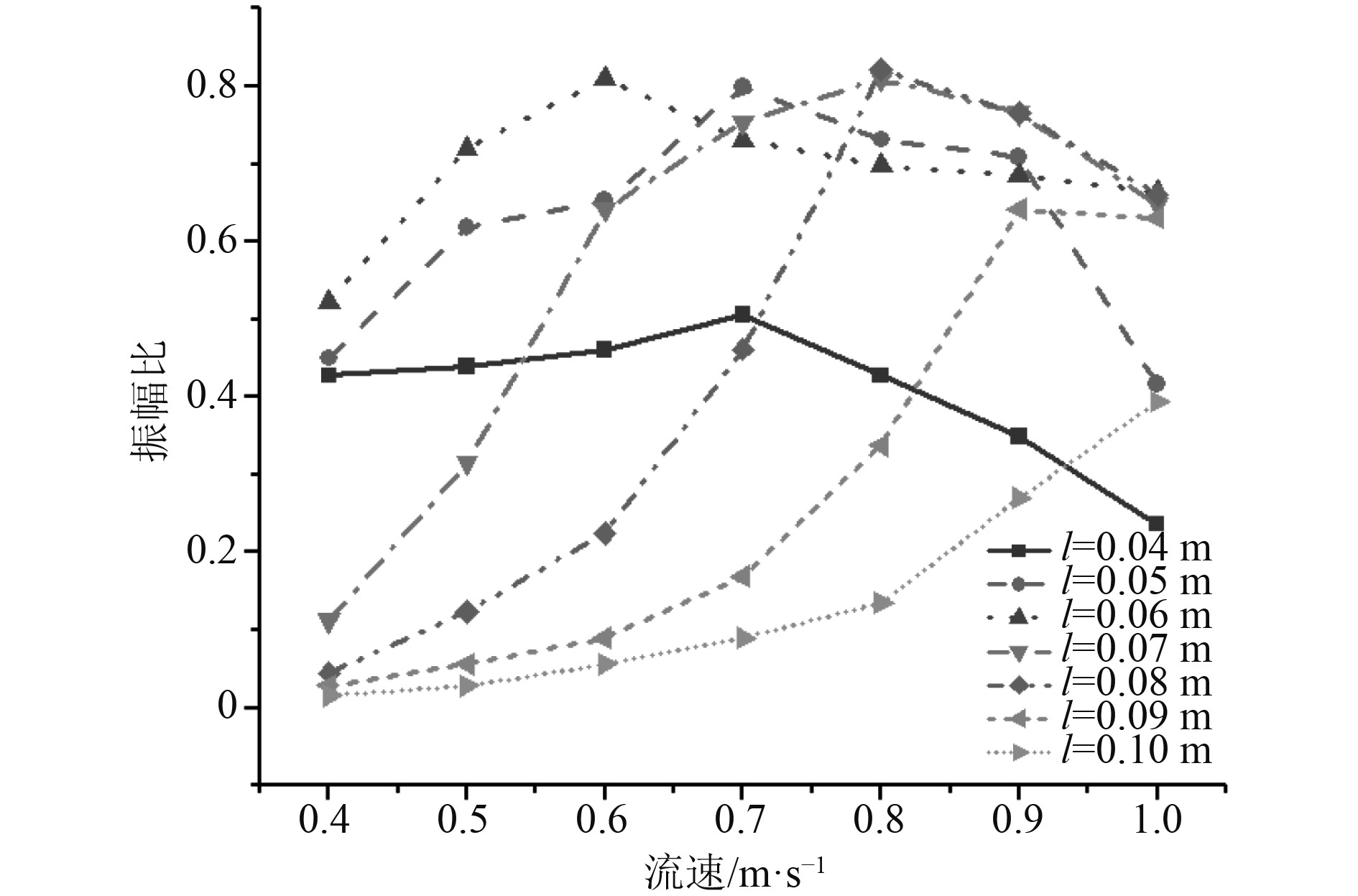
图6为不同流速下振子的振幅比。可以看出:0.04~0.06 m永磁体振子的起振流速都较低,在计算流速区间内的振幅比变化相对平稳,在0.6~0.7 m/s区间内达到最大值,最大振幅比接近0.8。0.07~0.1 m永磁体振子的起振流速较高;随着流速增长0.07 m,0.08 m永磁体振子的振幅比增量较大,最大振幅比在0.8左右;0.09 m永磁体振子的振幅比增量较小,最大振幅比在0.64左右;0.1 m永磁体振子在整个流速区间上的振幅比都很低,最大振幅比为0.39。比较不同规格永磁体的最大振幅比可以看出,永磁弹簧振子的流致振动过程中存在上限振幅比。这主要是由永磁弹簧的磁力增长呈非线性关系造成的,当振子位移振幅比较大时,永磁体间斥力增大幅度增加,振子向端部运动过程中受到的磁力迅速增大,抑制了振子振幅的增加,根据本文计算结果可以看出最大压缩量1.2D的永磁弹簧流致振动临界振幅比在0.8左右,这是振子在运动过程中能达到的最大振幅比。
|
图 6 不同流速下振幅比随永磁体规格变化曲线 Fig. 6 Variation curve of amplitude ratio with permanent magnet specification at different flow rates |
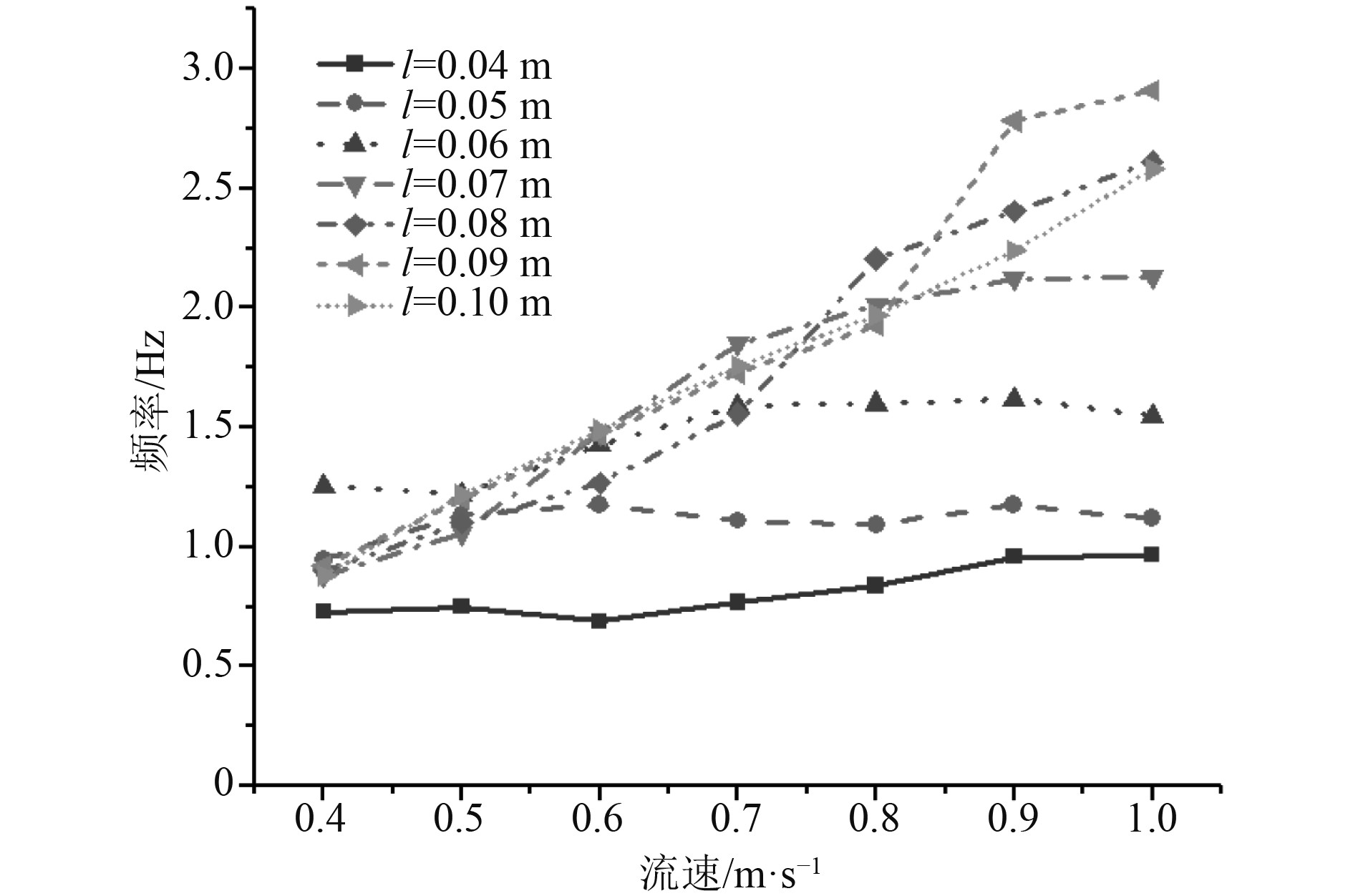
由图7可以看出,在整个流速区间内,振子振动频率随着流速增加而增加,增长趋势的快慢主要受永磁体规格影响。在0.4~0.6 m/s流速区间内,振子的振动频率相差不大,随着流速增加,振子的振动频率随着永磁体规格的增加先增加再减小,0.04 m永磁体振子的振动频率增幅最小,0.09 m永磁体振子的振动频率增幅最大。
|
图 7 不同流速下频率随永磁体规格变化曲线 Fig. 7 Variation curve of frequency with permanent magnet specification at different flow rates |
本文基于等效磁荷法对永磁体间的磁力进行拟合并构建永磁弹簧模型,得到不同规格永磁弹簧的磁力位移函数,并将函数代入到STAR-CCM+中进行单圆柱振子流致振动求解,得到以下结论:
1) 0.06 m永磁体振子在整个流速区间上的平均振幅比较大,频率相对稳定,平均频率能达到1.5 Hz,能够适应流速在0.4~1 m/s的变化的流场。
2)0.07 m和0.08 m永磁体振子在0.8~1 m/s流速范围内能够达到临界振幅比,频率能够达到0.06 m永磁体振子的2倍,如果流场的流速能够稳定在0.8~1.0 m/s范围内,0.07 m和0.08 m永磁体振子能够获得更多的能量。
3)磁悬浮支撑流致振动装置有上限振幅,当振子运动幅度较大时,永磁弹簧会对振子的振动频率起到抑制作用,1.2D压缩量的永磁弹簧的上限振幅比在0.8左右。
| [1] |
马冬娜. 海洋能发电现状分析[J]. 科技资讯, 2015, 13(20): 224-225. DOI:10.16661/j.cnki.1672-3791.2015.20.012 |
| [2] |
BERNITSAS MICHAEL M, RAGHAVAN KAMALDEV, BEN SIMON Y, et al. A new concept in generation of clean and renewable energy from fluid flow[J]. Journal of Offshore Mechanics and Arctic Engineering, 2008, 130(4): 10−24.
|
| [3] |
LOBO V , MAINSAH N , BANERJEE A , et al. Design feasibility of a vortex induced vibration based hydro-kinetic energy harvesting system[C]// IEEE Green Technologies Conference. IEEE, 2011.
|
| [4] |
WU W, SUN H, LV B, et al. Modelling of a hydrokinetic energy converter for flow-induced vibration based on experimental data[J]. Ocean Engineering, 2018, 155(5): 392–410.
|
| [5] |
谭俊哲, 王保振, 王树杰, 等. 直线发电机在流致振动潮流能发电装置中的应用研究[J]. 太阳能学报, 2020, 41(9): 9−14.
|
| [6] |
李莉, 葛占岭, 安然然, 等. 一种涡致振动压电发电结构的仿真与实验分析[J]. 通信电源技术, 2017, 34(6): 21-25. DOI:10.19399/j.cnki.tpt.2017.06.008 |
| [7] |
白旭, 乐智斌. 一种具有磁边界的涡激振动发电装置[P]. 江苏省: CN109286300B, 2020-08-25.
|
| [8] |
白旭, 罗小芳, 乐智斌. 一种随振幅转换的磁边界涡激振动发电装置[P]. 江苏省: CN109378934B, 2020-08-25.
|
| [9] |
MASOUMI M, WANG Y. Repulsive magnetic levitation-based ocean wave energy harvester with variable resonance: Modeling, simulation and experiment[J]. Journal of Sound & Vibration, 2016, 381: 192-205. |
| [10] |
张钢, 张坚, 张海龙, 等. 基于等效磁荷法用蒙特卡洛法计算永磁轴承磁力[J]. 轴承, 2013(10): 1-4. DOI:10.3969/j.issn.1000-3762.2013.10.001 |
| [11] |
赵凯华, 陈熙谋. 电磁学[M]. 北京: 人民教育出版社, 1979.
|
| [12] |
LEE J H, BERNITSAS M M. High-damping, high-reynolds VIV tests for energy harnessing using the VIVACE converter[J]. Ocean Engineering, 2011, 38(16): 1697-1712. DOI:10.1016/j.oceaneng.2011.06.007 |
| [13] |
贾晓荷. 单圆柱及双圆柱绕流的大涡模拟[D]. 上海: 上海交通大学, 2008.
|
 2023, Vol. 45
2023, Vol. 45

