舰炮伺服系统是舰炮武器系统的重要组成部分,其主要作用是根据系统指令控制电机转速,从而实现对舰炮位置的控制,同时伺服系统的低速稳定性直接影响武器系统的跟踪射击精度。舰炮在以较低的速度运动时,非线性摩擦力会导致伺服系统出现速度爬行等问题[1-2]。为了消除摩擦力的不良影响,弥补传统控制策略的不足,提高伺服系统的低速稳定性,有必要对摩擦现象和系统控制策略进行研究。
摩擦模型分为静态和动态摩擦模型,静态模型结构简单、易于工程实现,但不能满足高精度伺服系统的需要[3-4]。LuGre摩擦模型能够准确地描述摩擦过程中各种复杂的动静态特性,但其不能反映内、外部条件变化带来的影响[5-6]。由于舰炮伺服系统的运动部件处于舱室外,环境温度变化范围大,且随着时间积累存在一定的机械磨损和润滑状态变化,由此可以看出舰炮伺服系统的摩擦力矩是一个非线性、时变的物理量,需要对原有摩擦模型进行改进才能建立一个相对准确的摩擦模型。
自抗扰控制技术不依赖系统准确的数学模型,同时又把现代控制理论中状态观测的思想引入其中,对系统内外部扰动进行观测、补偿,具有较强的鲁棒性。目前,自抗扰控制技术在舰炮伺服控制领域已经有一些研究应用,并取得了较好的控制效果。但自抗扰控制器参数整定复杂,不利用工程应用[7-8]。线性自抗扰控制控制参数少、实现简单,但还没有针对变摩擦负载下舰炮伺服系统线性自抗扰控制策略的相关应用研究。
本文首先对某型舰炮伺服系统进行分析和建模,并基于LuGer模型和舰炮伺服系统的摩擦力特点,引入摩擦系数来表达摩擦力的变化趋势,然后设计一种模型参考线性自抗扰控制器(MLADRC),并引入前馈补偿组成复合控制器以提高控制精度,最后对系统进行了仿真验证。
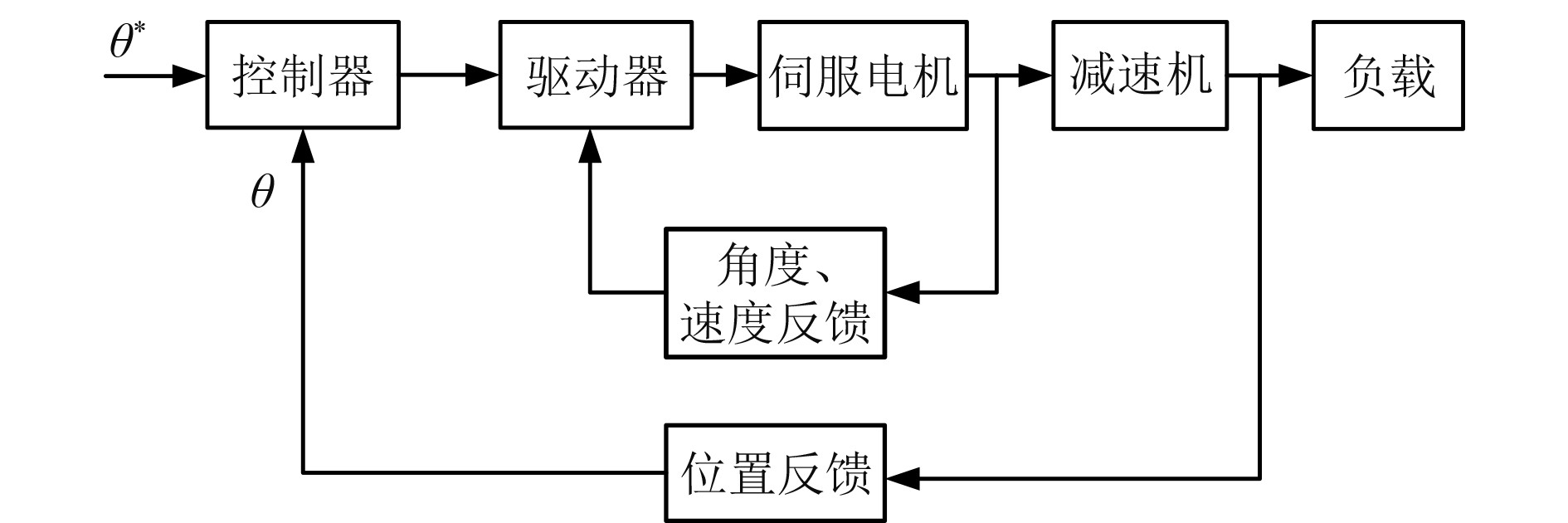
1 舰炮伺服系统设计 1.1 伺服系统组成及原理舰炮伺服系统主要由控制器、驱动器、位置反馈器件、伺服电机、减速机和负载组成,其组成框图如图1所示。为保证伺服系统的自主可控,各部件均选用国产基础产品完成设计。
|
图 1 舰炮伺服系统控制框图 Fig. 1 Control block diagram of naval gun servo system |
舰炮伺服系统采用经典的三闭环控制结构。其中,控制器用于实时接收控制指令,采集舰炮位置信息,经内部运算处理,输出速度指令到驱动器,完成外环位置控制。驱动器接收到速度指令后,采集电机速度、角度和电流信息,采用PI控制算法实现速度环和电流环的闭环控制。
1.2 伺服系统建模某型舰炮伺服系统中使用的是永磁同步电机,为了便于分析建模,不考虑磁路饱和磁滞损耗,且认为磁场正弦分布,在dq坐标系,定子电流分量id=0,从而得到电机的数学模型:
电压方程
| $ {u_q} = {R_s}{i_q} + {L_q}\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}} + {\omega _r}{\psi _f},$ | (1) |
电磁转矩方程
| $ {T_e} = \frac{3}{2}p{\psi _f}{i_q} = {K_t}{i_q},$ | (2) |
机械运动方程:
| $ {T_e} - {T_L} - {T_f} = J\frac{{{\rm{d}}{\omega _m}}}{{{\rm{d}}t}} 。$ | (3) |
式中:
速度环和电流环的结构框图如图2所示。

|
图 2 速度环和电流环结构图 Fig. 2 Block diagram of speed loop and current loop |
电流环闭环传递函数可以简化为:
| $ {G_I}(s) = \frac{{1/\alpha }}{{{T_I}s + 1}},$ | (4) |
速度环闭环传递函数可以简化为:
| $ {G_\omega }(s) = \frac{{1/\beta }}{{{T_I}{T_m}{s^2} + {T_m}s + 1}}。$ | (5) |
式中:
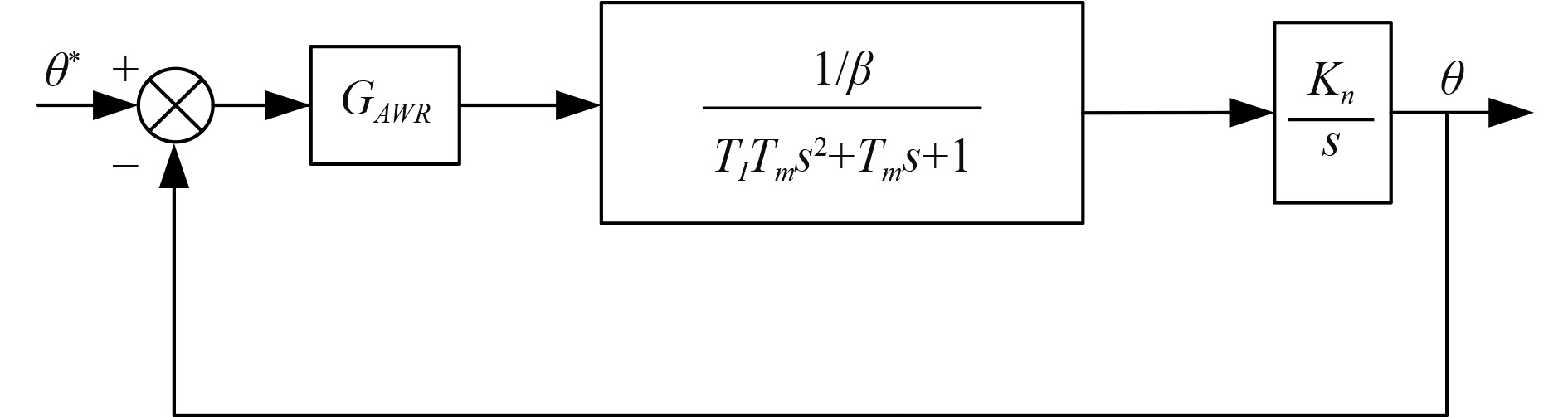
位置环的结构框图如图3所示。
|
图 3 位置环结构图 Fig. 3 Block diagram of position loop |
为了更好控制位置环节,需要对速度环进行数学处理。为简化处理可以将速度环等效成一个一阶惯性环节[9],速度环传递函数可以简化为:
| $ {G_\omega }(s) = \frac{{{K_p}}}{{{T_p}s + 1}},$ | (6) |
被控对象的开环传递函数可以简化为:
| $ {G_p}(s) = \frac{{{K_p}{K_n}}}{{s({T_p}s + 1)}} 。$ | (7) |
式中:
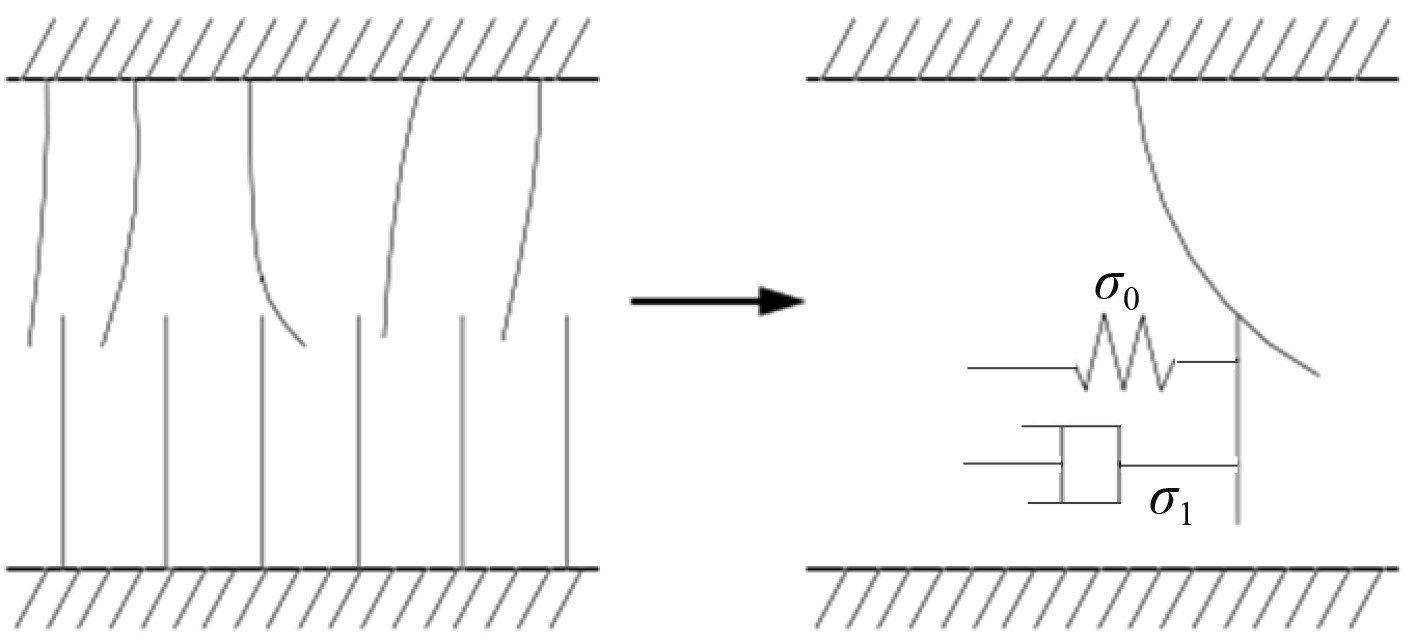
1995年法国学者Canudas对Dahl模型进行了扩展,采用鬓毛模型思想提出了LuGre模型。该模型认为在两摩擦表面之间有随机分布的鬓毛接触,当受到外部切向力时,弹性鬓毛会发生形变,产生相应大小的摩擦力,当鬓毛变形增大时会产生滑动现象[6,10],如图4所示。
|
图 4 Lugre模型简图 Fig. 4 The sketch of Lugre model |
Lugre摩擦模型的数学表达式为:
| $ \frac{{{\rm{d}}z}}{{{\rm{d}}t}} = w - \frac{{\left| w \right|}}{{g(w)}}z,$ | (8) |
| $ {\sigma _0}g(w) = {T_c} + \left( {{T_s} - {T_c}} \right){e^{ - {{\left( {\frac{w}{{{w_s}}}} \right)}^2}}} ,$ | (9) |
| $ {T_f} = {\sigma _0}z + {\sigma _1}\frac{{{\rm{d}}z}}{{{\rm{d}}t}} + {\sigma _2}w 。$ | (10) |
式中:z为鬓毛的变形量;
考虑到舰炮伺服系统的环境温度、润滑状态、机械磨损等因素都是随时间变化的,故引入摩擦系数
| $ {T_f} = \lambda \left( {{\sigma _0}z + {\sigma _1}\frac{{{\rm{d}}z}}{{{\rm{d}}t}} + {\sigma _2}w} \right) ,$ | (11) |
当伺服系统稳态运行时,鬓毛变形量不变,此时修正LuGre模型为:
| $ {T_f} = \lambda \left[ {\left( {{T_c} + \left( {{T_s} - {T_c}} \right){e^{ - {{\left( {\frac{w}{{{w_s}}}} \right)}^2}}}} \right){{\rm{sgn}}} (w) + {\sigma _2}w} \right]。$ | (12) |
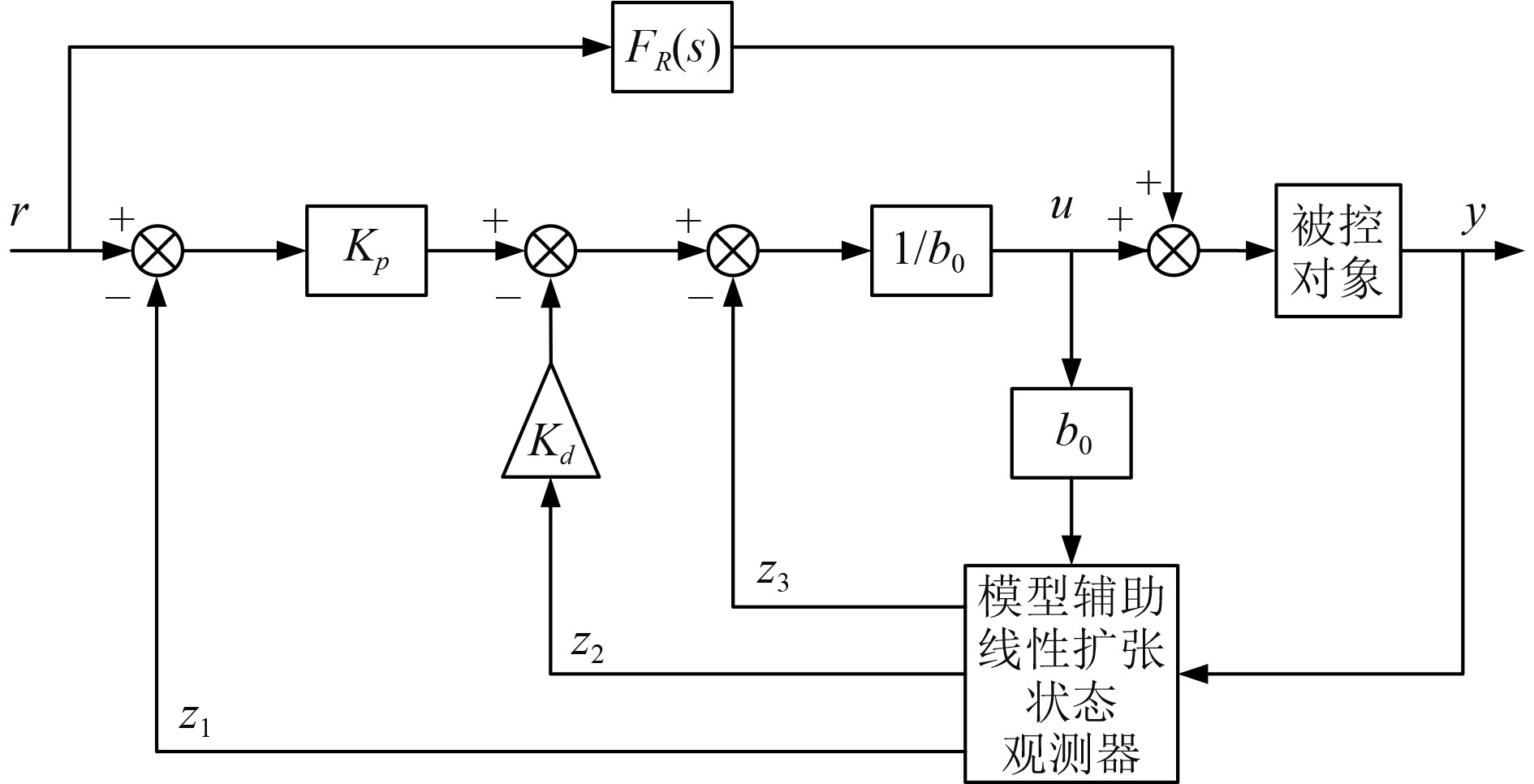
得到伺服系统的部分模型信息后,可以将这些信息加入到线性状态观测器(linear extended state observer, LESO)中,以降低LESO的带宽,提高系统的控制效果[11]。由于单纯的自抗扰控制器会使系统在跟踪快速变化的信号时产生稳态误差,故引入前馈来消除稳态误差,前馈模型参考线性自抗扰控制器结构如图5所示。
|
图 5 前馈模型参考线性自抗扰控制器结构图 Fig. 5 Block diagram of feedforward MLADRC |
由式(7)可知,系统可以简化为二级系统,用微分表示为:
| $ \stackrel{··}{y}=-{a}_{1}\stackrel{·}{y}-{a}_{0}y+w+bu 。$ | (13) |
式中:u和y分别为系统的输入和输出信号;w为未知扰动;
| $ \stackrel{··}{y}=-{a}_{1}\stackrel{·}{y}-{a}_{0}y+w+(b-{b}_{0})u+{b}_{0}u,$ | (14) |
实际的未知总扰动为:
| $ {f'} = w + (b - {b_0})u,$ | (15) |
未知总扰动与已知对象信息的总和为:
| $ f=-{a}_{1}\dot{y}-{a}_{0}y+w+(b-{b}_{0})u。$ | (16) |
选状态变量
| $ \left\{\begin{array}{l}\dot{x}=Ax+Bu+E\stackrel{·}{f},\\ y=Cx。\end{array}\right. $ | (17) |
式中:
模型辅助线性扩张状态观测器(LESO)为:
| $ \left\{\begin{array}{l}\dot{z}=(A-LC)z+[BL]{u}_{c},\\ {y}_{c}=z。\end{array} \right.$ | (18) |
式中:
使用极点配置法求出增益矩阵的各状态量:
| $ \left\{ \begin{gathered} {L_1} = 3{w_0} - {a_1},\\ {L_2} = 3{w_0}^2 - 3{a_1}{w_0} - {a_0} + {a_1}^2 ,\\ {L_3} = {w_0}^3 - 3{a_1}{w_0}^2 + 3({a_1}^2 - {a_0}){w_0} + 2{a_0}{a_1} - {a_1}^3。\\ \end{gathered} \right. $ | (19) |
式中,
因为状态观测器可以实时估计并补偿内外部扰动,所以可以省去传统PID控制中为了消除静差的积分器,故线性状态误差反馈控制率(linear state error feedback, LSEF)可以进一步简化为PD组合。
| $ {u_0} = {k_p}\left( {r - {z_1}} \right) - {k_d}{z_2},$ | (20) |
根据线性自抗扰的参数整定方法[12],确定比例和微分系数:
| $ {k_p} = {\omega _c}^2,{k_d} = 2{\omega _c}。$ | (21) |
式中:
根据不变性原理,当
为验证带前馈的模型参考线性自抗扰控制器性能,搭建舰炮伺服系统仿真模型。设置仿真参数为:永磁同步电机额定转速
当方位伺服系统摩擦系数
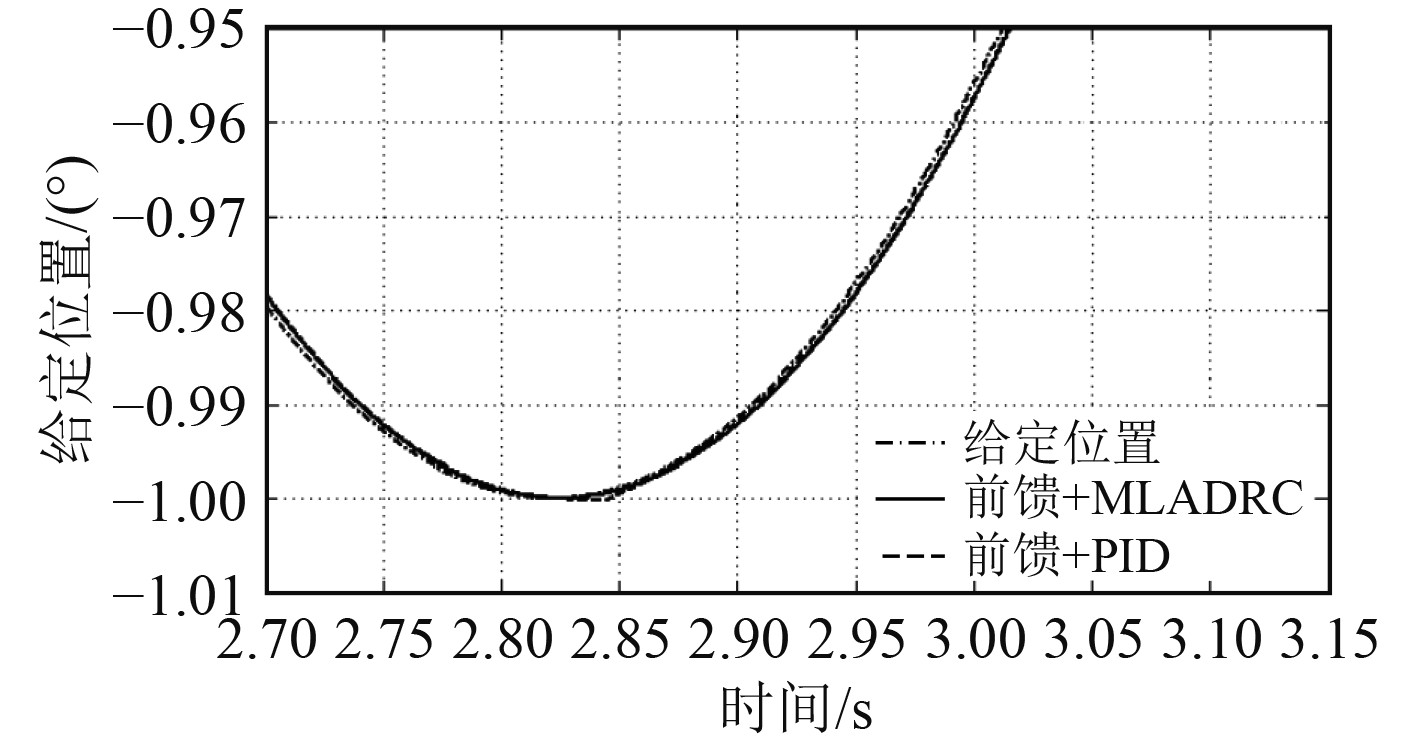
|
图 6 实验跟踪曲线(摩擦系数为1) Fig. 6 Tracking curve of experiment |
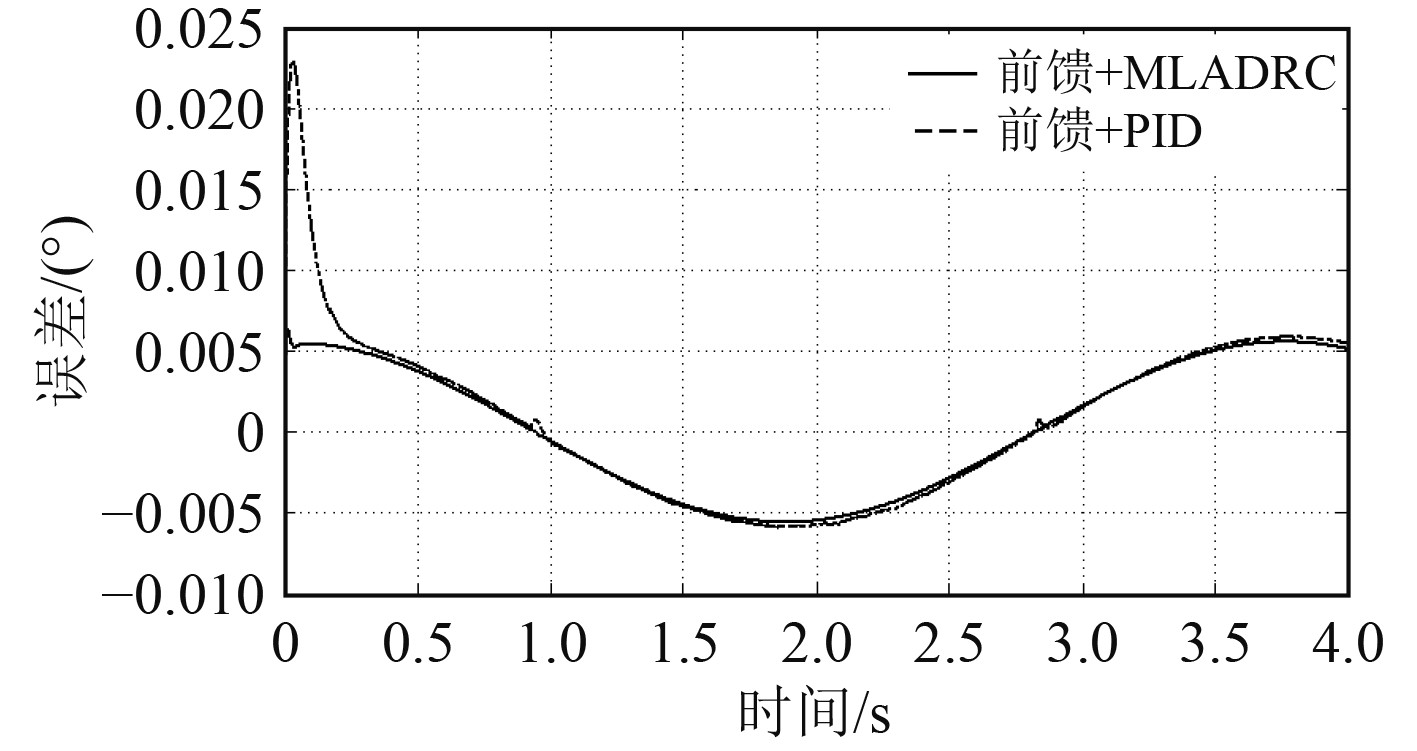
|
图 7 实验跟踪误差曲线(摩擦系数为1) Fig. 7 Tracking error curve of experiment |
当方位伺服系统摩擦系数
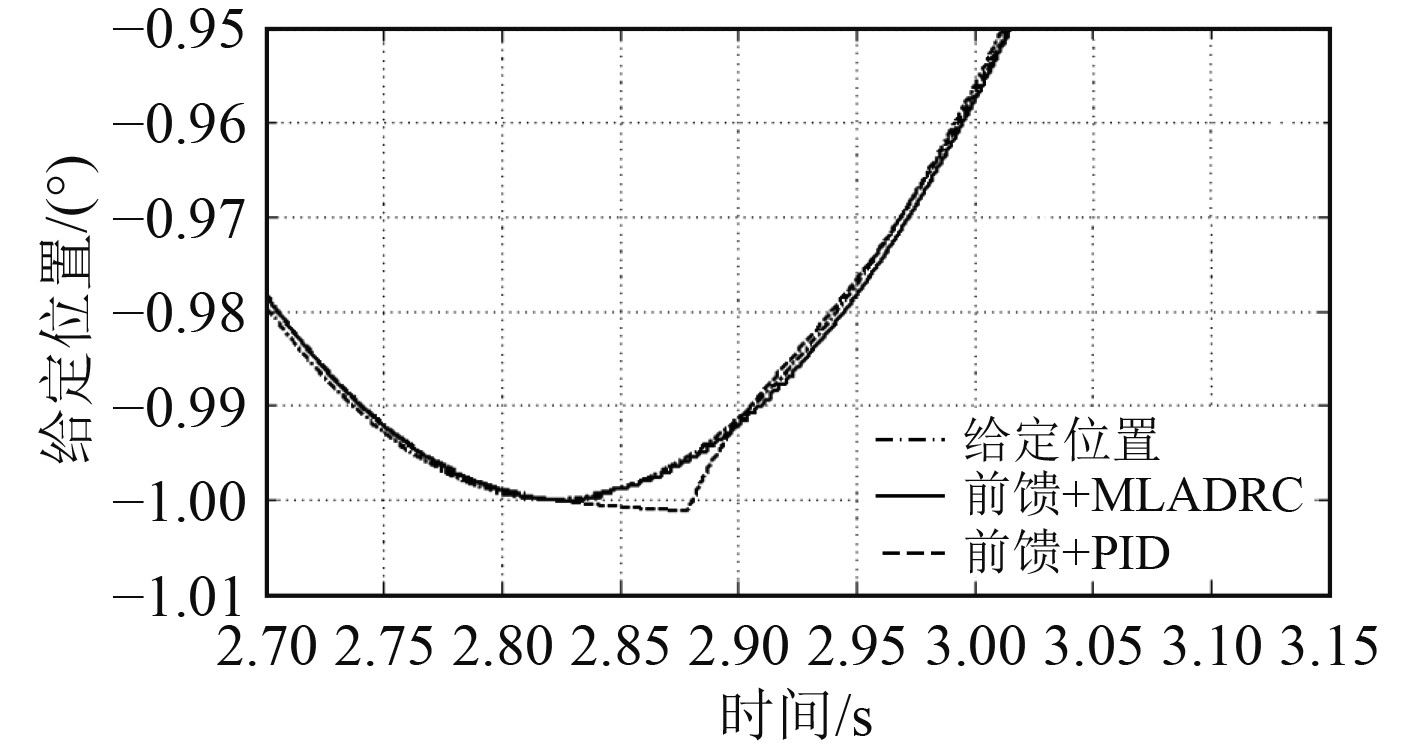
|
图 8 实验跟踪曲线(摩擦系数为6) Fig. 8 Tracking curve of experiment |

|
图 9 实验跟踪误差曲线(摩擦系数为6) Fig. 9 Tracking error curve of experiment |
在舰炮伺服系统中,非线性、时变摩擦力严重影响系统的动静态性能,需要设计对应的补偿策略消除其干扰。首先对舰炮伺服系统进行数学分析,并利用改进的LuGre 摩擦模型对非线性、时变摩擦力进行了描述;然后提出一种基于前馈补偿和模型参考线性自抗扰控制的复合控制器,最后通过仿真实验与传统的前馈PID控制器进行对比。结果表明,在不同的摩擦系数下新设计的复合控制器可以有效避免爬行等低速不稳定现象,同时启动误差相比前馈PID控制也大幅减小70%以上,可有效提高系统的控制精度。
| [1] |
吴宇航, 崔敏. 摩擦力矩对舰炮随动系统低速平稳性的影响[J]. 火力与指挥控制, 2011, 36(7): 85-87. WU Y H, CUI M. Research on friction moment influencing naval gun servo system’s low speed stability[J]. Fire Control & Command Control, 2011, 36(7): 85-87. DOI:10.3969/j.issn.1002-0640.2011.07.024 |
| [2] |
赵远征, 陈延伟, 程守虎. 基于Stribeck模型的舰炮伺服系统摩擦力矩补偿[J]. 兵工自动化, 2016, 35(5): 59-62. ZHAO Y Z, CHEN Y W, CHENG S H. Friction compensation in naval gun servo systems based on stribeck model[J]. Ordnance Industry Automation, 2016, 35(5): 59-62. DOI:10.7690/bgzdh.2016.05.016 |
| [3] |
周金柱, 段宝岩, 黄进. LuGre摩擦模型对伺服系统的影响与补偿[J]. 控制理论与应用, 2008, 25(6): 990-994. ZHOU JZ, DUAN B Y, HUANG J. Effect and compensation for servo systems using LuGre friction model[J]. Control Theory & Applications, 2008, 25(6): 990-994. |
| [4] |
谭文斌. 伺服系统摩擦与温度变化干扰的建模及补偿研究[D]. 天津: 天津大学, 2011.
|
| [5] |
向红标, 谭文斌, 李醒飞, 等. 基于LuGre模型的自适应摩擦补偿[J]. 机械工程学报, 2012, 48(17): 70-74. XIANG H B TAN W B LI X F, et al. Adaptive friction compensation based on LuGre model[J]. Journal of Mechanical Engineering, 2012, 48(17): 70-74. DOI:10.3901/JME.2012.12.070 |
| [6] |
刘国平, 机械系统中的摩擦模型及仿真[D]. 西安: 西安理工大学. 2007.
|
| [7] |
韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. HAN J Q. Auto disturbances rejection controller and its applications[J]. Control and Decision, 1998, 13(1): 19-23. DOI:10.3321/j.issn:1001-0920.1998.01.005 |
| [8] |
庞金锋. 基于自抗扰控制技术的舰炮随动控制系统[J]. 机电产品开发与创新, 2019, 32(6): 74-77. PANG J F. Naval gun servo system based on auto disturbance rejection control technology[J]. Development & Innovation of Machinery & Electrical Product, 2019, 32(6): 74-77. DOI:10.3969/j.issn.1002-6673.2019.06.023 |
| [9] |
郑印. 升降滚床伺服控制系统研究[D]. 长春工业大学, 2020.
|
| [10] |
薛进学, 郭清远, 张丰收. 基于LuGre摩擦模型前馈补偿的模糊PID控制系统设计[J]. 现代制造工程, 2020, 20(1), 136–142. XUE J X, GUO Q Y, ZHANG F S. Design of fuzzy PID control system based on feedforward compensationof the LuGre friction model[J], Modern Manufacturing Engineering, 2020, 20(1), 136–142. |
| [11] |
张敏捷, 杨雷, 侯砚泽, 等. 线性自抗扰控制器的噪声抑制改进研究[J]. 宇航学报, 2019, 40(7): 803-810. ZHANG J M, YANG L, HOU Y Z, et al. Improved linear active disturbance rejection controller with denoising performance[J]. Journal of Stronautics, 2019, 40(7): 803-810. DOI:10.3873/j.issn.1000-1328.2019.07.009 |
| [12] |
GAO Z Q. Scaling and bandwidth paramet erization based controller tuning[C]//Proceeding of the 2003 American Control Conference, Denver, 2003, 4989–4996.
|
 2023, Vol. 45
2023, Vol. 45
