0 引　言

船舶交通密度是海上交通工程中的重要研究内容，船舶交通密度需要考虑海上船舶的交通行为^[1-3]。船舶交通密度不仅需要考虑某艘船舶的运动行为状态，更需要考虑研究海域内全部船舶的航行状态。船舶交通密度的计算目的是及时发现影响海上交通安全的因素，通过船舶交通密度计算，搜寻解决海上交通问题的相关措施以及办法。船舶交通密度需要收集船舶航行轨迹数据，处理所搜集的船舶航行轨迹数据^[4]，精确了解海上船舶航行的交通状况、交通规律以及航行特征。AIS设备是采集船舶航行轨迹数据的重要设备，AIS设备可以实现船舶航行轨迹数据的全天候以及高频度交换。利用AIS设备采集船舶航行轨迹数据，数据量过大，影响数据的应用性能，船舶航行轨迹数据的高效处理极为重要。

目前已有众多学者针对船舶交通密度进行研究。张黎翔等^[5]针对船舶轨迹AIS数据的缺陷数据进行修复，利用修复后数据分析船舶交通密度。该方法通过分析AIS数据中的加速度、经纬度以及船舶航向数据，判定船舶轨迹数据，对轨迹异常点进行修复，提升船舶交通密度的计算精度。林信海等^[6]将多约束二维排样方法应用于船舶最大密度布列中，该方法针对船舶最大密度布列设置相关约束条件，构建距离约束的数学模型，选取启发式靠边定位算法解决边界约束问题，完成船舶的最大密度布列。以上研究方法虽然可以计算船舶交通密度，但是存在无法依据船舶航行轨迹，更新船舶交通密度的问题。

针对以上研究方法存在的问题，本文提出依据轨迹数据的船舶交通密度计算方法，对船舶轨迹数据进行聚类处理，计算船舶交通密度。海域管理人员可以根据船舶交通密度，高效制定海上交通的船舶航行规划。

1 船舶交通密度计算方法 1.1 基于均匀参数化的船舶轨迹数据重采样

利用AIS设备采集船舶航行轨迹数据，所采集的航行轨迹数据由离散数据点的时间序列组成。航行轨迹数据包括航行时间、航行实时位置、航行速度、航行角度等信息。利用AIS设备采集的航行轨迹数据包含大量冗余数据点，为了降低航行轨迹数据的冗余性，满足轨迹数据聚类的需求，对航行轨迹数据进行重采样处理。利用均匀参数化方法，对航行轨迹数据进行重采样处理。设某船舶航行轨迹包含 $n$ 个轨迹点(p₁,p₂,..,p_n)，轨迹点数据p_i=(x_i,y_i)中的x_i与y_i分别为轨迹点经度以及纬度。

利用累加弦长方法，将船舶航行轨迹数据参数化处理至[0,1]区间。通过haversine公式衡量2个船舶轨迹点间的距离，轨迹点 $i - 1$ 与轨迹点 $i$ 间的距离为 $l\left( {{x_{i - 1}},{y_{i - 1}},{x_i},{y_i}} \right)$ 。船舶航行轨迹数据的均匀参数化表达式如下：

${\phi _i} = {\phi _{i - 1}} + \frac{{l\left( {{x_{i - 1}},{y_{i - 1}},{x_i},{y_i}} \right)}}{{\sum\limits_{j = 2}^n {l\left( {{x_{j - 1}},{y_{j - 1}},{x_j},{y_j}} \right)} }}。$

(1)

式中： ${\phi _i}$ 为第 $i$ 个船舶航行轨迹点 ${p_i}$ 在[0,1]区间对应的参数值， ${\phi _1} = 0$ ， ${\phi _n} = 1$ 。

设船舶航行轨迹数据的重采样点数量为 $v$ 。在[0,1]区间内，均匀选取 $v$ 个采样点，采样点的首位以及终位为0与1。对船舶航行轨迹数据重采样时，不改变航行轨迹数据的首个轨迹点以及最终轨迹点。保留首个以及最终轨迹点的情况下，搜寻船舶轨迹重采样点的区间 $\left[ {{\phi _{i - 1}},{\phi _i}} \right]$ ，在该区间内搜寻重采样轨迹点前后的原始船舶轨迹点。通过以上过程完成船舶航行轨迹数据的重采样，完成重采样获取的船舶航行轨迹数据用 $\left( {{q_1},{q_2}, \cdots ,{q_v}} \right)$ 表示，其中p₁=q₁，p_n=q_v。

1.2 基于DBSCAN的船舶航行轨迹数据聚类

根据船舶航行轨迹数据变化，将完成重采样获取的船舶航行轨迹数据 $\left( {{q_1},{q_2}, \cdots ,{q_u}} \right)$ ，划分为静止轨迹数据点以及移动轨迹数据点，分别对应船舶停泊区以及船舶航行区。选取基于密度的DBSCAN聚类算法，根据各船舶航行轨迹数据点的欧式距离，通过 $\varepsilon$ 邻域计算静止轨迹数据点的邻域。利用DBSCAN聚类算法对移动轨迹数据点聚类时，不仅需要考虑数据点间的欧式距离，还要根据船舶航行方向以及航行速度的相似性对船舶轨迹数据聚类。利用船舶航行轨迹数据聚类结果，体现船舶航行的轨迹模式。

为了降低船舶航行轨迹数据聚类的运算量，针对船舶移动轨迹数据点，引入重心向量 $Z$ ，提取船舶航行轨迹数据的聚类特征。 $Z = \left\{ {A,B,C,D,E} \right\}$ 表示航行轨迹数据聚类的重心向量，重心向量是航行轨迹数据聚类的特征提取结果，利用重心向量将航行轨迹数据划分为多个类别，每个类别可以包含多个重心向量。重心向量 $Z$ 中的 $A$ 与 $B$ 分别为平均航向以及平均航速； $C$ 与 $D$ 分别为船行轨迹的经度与纬度； $E$ 为航行轨迹数据的中值距离。获取船舶航行轨迹数据聚类的重心向量过程如下：

1）计算航行轨迹数据聚类平均方向 $A'$ ；

2）依据 $A'$ 方向，对航行轨迹数据内的全部轨迹点聚类处理；

3）利用以上过程划分航行轨迹数据网格，生成各网格的重心向量。

设航行轨迹数据随机网格中，包含航行轨迹点数量为 $k$ ，F_i为第 $i$ 个轨迹点，该网格的重心向量计算公式如下：

$A = \sum\limits_{i = 1}^k {{F_i}} A'/k ，$

(2)

$B$ ， $C$ 与 $D$ 的聚类过程与式(2)相同。

$E = \sum\limits_{i = 1}^k {E'{F_i}} \left( {C',D'} \right)/k，$

(3)

利用抽样集表示通过随机采样方式生成的点集，依据采样半径 $u$ 以及停止区域面积 $area$ 确定抽样集内样本数量 $m$ 。针对船舶静止轨迹数据点，生成抽样集过程如下：

1）搜寻全部静止轨迹数据集在聚类空间中的边界点，计算停止区域面积。依据给定的聚类抽样半径 $u$ ，计算抽样点数量 $m$ 的计算公式如下：

$m = \overline {area/\text{π} {u^2}}。$

(4)

2）在数据集内随机抽取抽样点，计算抽样集内的全部已抽样数据点与抽样点的距离，当距离计算结果大于抽样半径 $u$ 时，将该抽样点加入抽样集中，否则重新抽取抽样点。

3）重复以上过程，直至抽样集合中的数据样本点数量为 $m$ ，完成船舶航行轨迹数据聚类。

1.3 基于多维密度的船舶交通密度计算

将航行轨迹数据聚类结果用数据集表示为： $R = \left\{ {{r_1},{r_2}, \cdots ,{r_n}} \right\}$ ，描述船舶在固定时间段的航行路径点r_i，路径点坐标处于网格g_i区域内。依据航行轨迹数据聚类结果，利用多维密度方法，计算船舶交通密度。集合 $R$ 内的数据点，可以组成1个或多个船舶航行路段，各航行路段可能航行1到多个网格。航行路段信息包括航行起点以及终点的全部信息，o₁与o₂表示航行起点与终点的属性值。 $\Delta C$ 与 $\Delta D$ 分别表示船舶经过某航段的经度以及纬度变化， $\Delta T$ 表示航行该航段的时间变化。网格g₀中，包含航行起点与终点时，AIS设备采集的船舶航行轨迹数据处于连续发送状态，视该时间段船舶不存在跨网格航行情况，判定该船舶为低速航行或停泊状态。计算此种情况的船舶交通密度时，根据船舶航行的起点以及终点的属性值，确定AIS信息发送增量表达式如下：

${g_0}\left( {S,W,T} \right) = \left\{ {\begin{array}{*{20}{l}} {{S_{i + 1}} = {S_i} + {o_1} + {o_2}} ，\\ {{W_{i + 1}} = {W_i} + 1} ，\\ {{T_{i + 1}} = {T_i} + \Delta T} 。\end{array}} \right.$

(5)

式中： $S$ 与 $W$ 分别为网格中AIS轨迹数据的信息发送总数以及经过的船舶总数量； $T$ 为网格中船舶经过的总时间。

当船舶航行起点以及终点位于g₀与g_n+1两个不同的网格内时，依据网格的位置坐标，以及轨迹数据穿过网格的信息，计算船舶交通密度的差异特征。船舶从起点至终点的航行过程，可以视为匀速直线运动，差异网格内船舶航行时间的增量，用当前网格内行驶长度占船舶航行总路段的比例体现。根据船舶航行路段、海域划分网格的位置关系，将船舶交通密度计算划分为以下2种情况：

1）航行路段不存在水平方向位移时，航行起点、终点与经度线平行，此时不存在直线斜率。起点以及终点在网格g₀与g_n+1外，船舶经过其他网格时间相同，此时船舶交通密度如下：

${g_i}\left( {W,T} \right) = \left\{ {\begin{array}{*{20}{l}} {{W_{i + 1}} = {W_i} + 1} ，\\ {{T_{i + 1}} = {T_i} + \dfrac{{\Delta T\left| {{r_{i + 1}}\left( C \right) - {r_i}\left( C \right)} \right|}}{{\Delta C}}} 。\end{array}} \right.$

(6)

式中：r_i+1(C)与r_i(C)分别为航行路径点r_i与r_i+1的经度。

2）航行路段在水平方向以及垂直方向均存在位移时，航行起点、终点与网格的经度线和纬度线均存在交点，此时船舶的航行线段存在斜率。通过计算投影长度和交点代替线段长度与交点求解问题，降低船舶交通密度计算复杂度。将航行路段对应的线段，投影至X轴方向，随机2个投影点的距离与船舶所在经度、纬度之比，即该网格内船舶航行时间占航行路段总时间之比。此时船舶交通密度计算公式如下：

${g_i}\left( {W,T} \right) = \left\{ {\begin{array}{*{20}{l}} {{W_{i + 1}} = {W_i} + 1} ，\\ {{T_{i + 1}} = {T_i} + \dfrac{{\Delta T\left| {{r_{i + 1}}\left( D \right) - {r_i}\left( D \right)} \right|}}{{\Delta D}}} 。\end{array}} \right.$

(7)

式中，r_i+1(D)与r_i(D)分别表示航行路径点r_i与r_i+1的纬度。

聚类获取的航行轨迹数据作为船舶交通密度计算的输入，将完成更新的船舶交通密度作为输出。遍历待计算船舶交通密度海域的全部船舶航行路段，获取固定海域内，船舶经过总数 $W$ 、经过总时间 $T$ 、航行轨迹数据发送总数 $S$ 等交通密度特征值。利用交通密度计算结果，体现固定海域内的船舶活动情况。

2 仿真测试

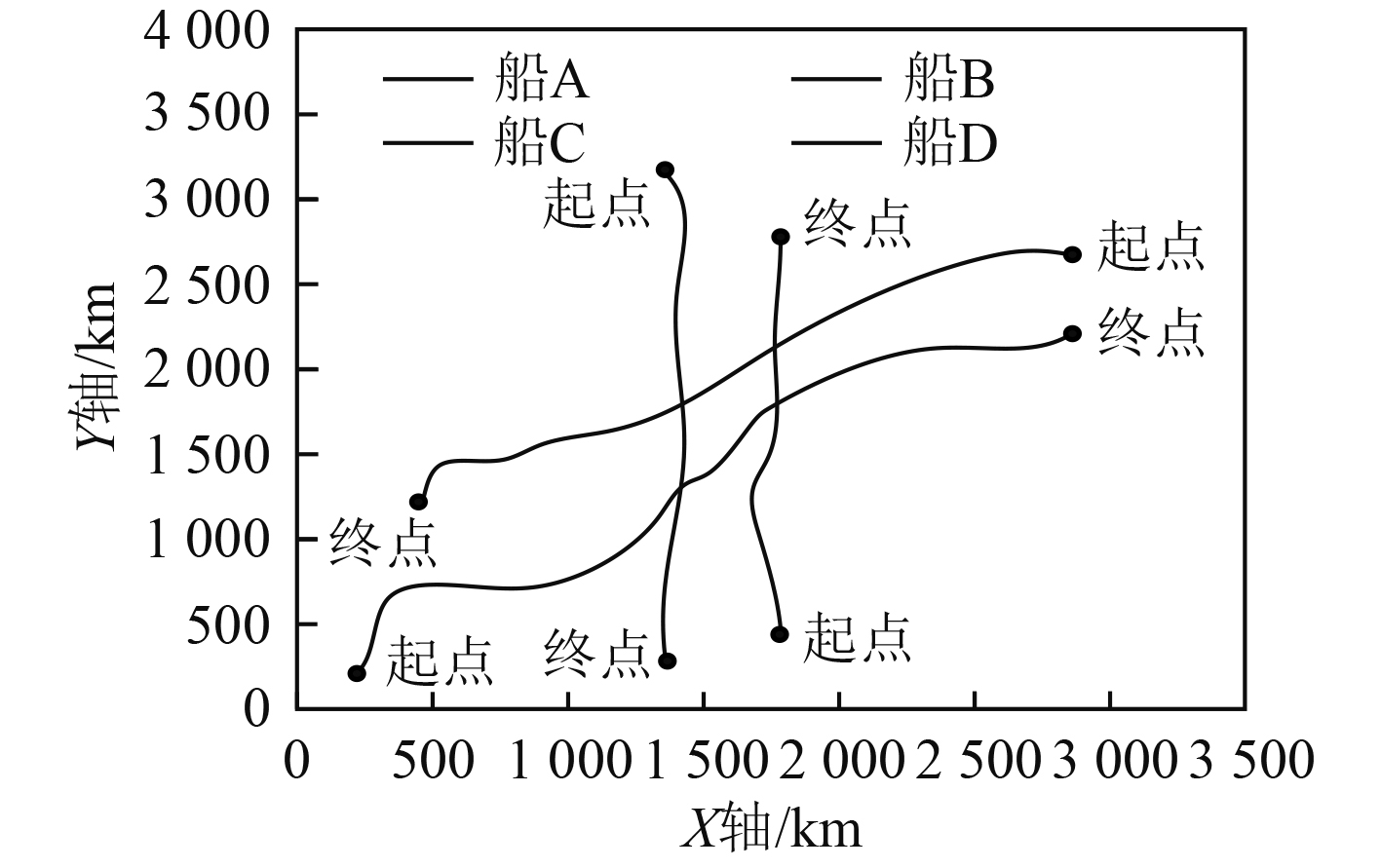
选取某海事公司的监管海域作为研究对象。海事公司管理人员根据船舶交通密度计算结果，规划船舶航行状态。利用AIS设备采集研究海域的船舶航行轨迹数据，随机选取其中10艘船舶的航行轨迹数据采集结果如表1所示。通过表1实验结果可以看出，利用AIS设备可以有效采集船舶航行的轨迹数据，为船舶交通密度计算提供有效的数据基础。对AIS设备采集的船舶航行轨迹数据进行聚类处理，获取其中4艘船舶的行驶轨迹如图1所示。可以看出，采用本文方法可以实现海量船舶航行轨迹数据的有效聚类。本文方法通过船舶航行轨迹数据的聚类，获取固定时间段内船舶在研究海域的航行轨迹，将所获取的航行轨迹作为船舶交通密度计算的基础。

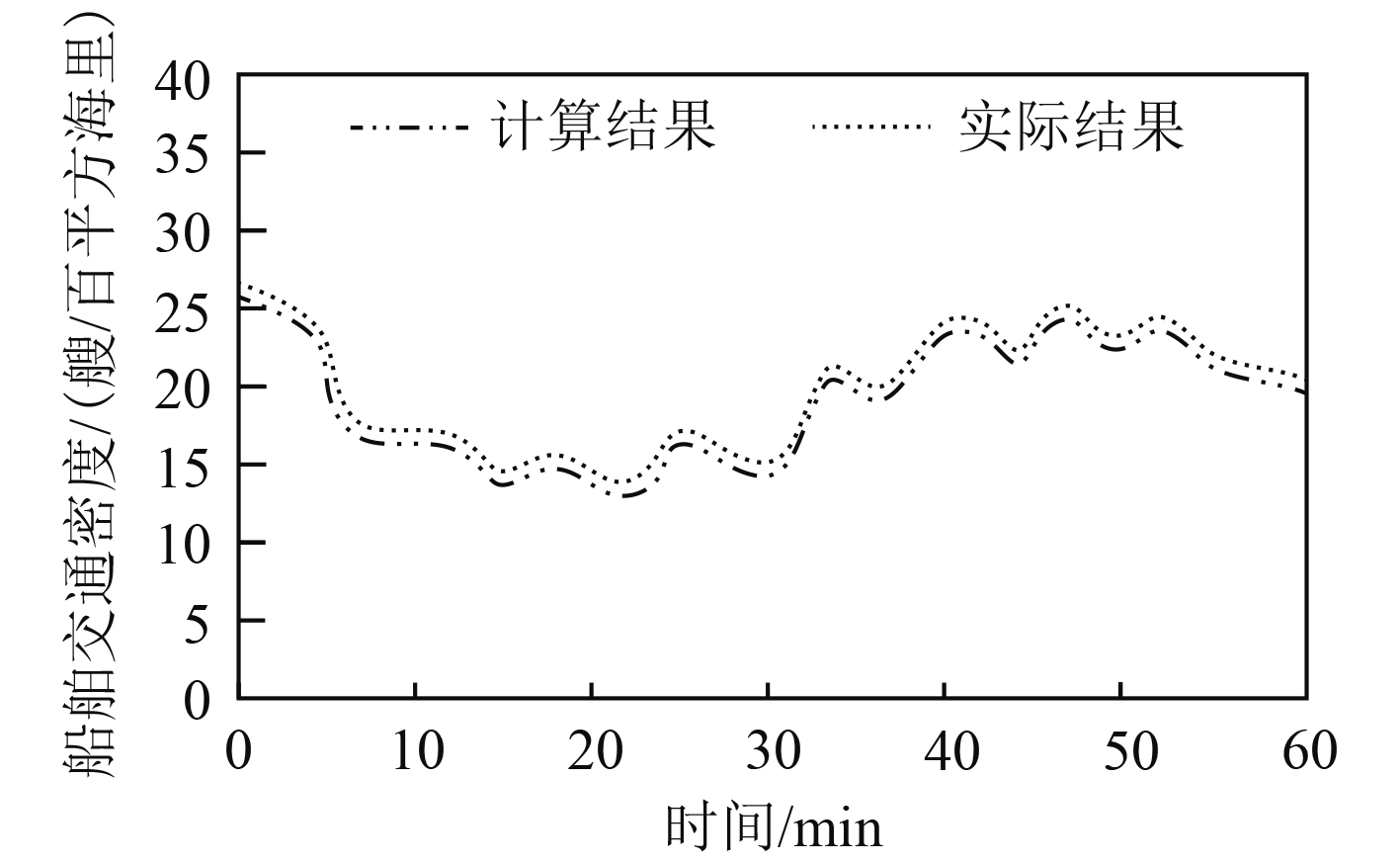
采用本文方法计算海域于2020年9月6日10-11时60 min内的船舶交通密度。结果如图2所示。可以看出，采用本文方法计算的船舶交通密度与实际船舶交通密度曲线相差极小，验证本文方法具有较高的船舶交通密度计算精度，可以为研究海域的管理人员提供精准的船舶交通密度计算结果。本文方法的船舶交通密度计算结果可以为船舶航行规划提供有效支撑。

3 结　语

依据船舶航行的轨迹数据，计算船舶交通密度，满足船舶交通密度计算的高效性、可靠性以及实时性需求。利用聚类算法处理海量船舶航行轨迹数据，具有速率快的优势。实验结果验证，该算法可以有效计算研究海域的船舶交通密度，以及船舶航行的时空分布特征。将船舶轨迹数据聚类结果作为船舶交通密度的计算依据，该方法可以应用于研究海域的船舶航行规划中，具有较高的实用性。