随着世界各国对潜艇装备技术认识的不断充分,潜艇成为战略威慑的中坚力量[1-3]。可以预见的是随着AIP动力系统、降噪隐身技术、水下探测技术的持续发展,新型信息系统的不断投入使用,潜艇将在未来海战中发挥无可替代的作用[4-6]。与此同时,潜艇面对的威胁也呈现多样化的局面[7],特别是以美国P-3C为代表的防控体系成为最主要的反潜手段[8]。针对航空磁探带来的威胁,对抗方式可以分为主动和被动2种。主动对抗是指潜艇主动采取正面应对的方式对抗反潜兵力,戚学文等[9]对无人潜航器集群对潜防御进行介绍及仿真分析。孙明太等[10]和高学强等[11]对潜艇发射防空导弹等被动对抗手段进行详细的介绍,但从实践结果来看,采取以上方法时,很容易发生对时机产生误判等情况,成功率很低,不足30%。
而给潜艇配备诱饵是有效的对抗方式之一[12]。诱饵技术是指以诱饵为载体,模拟潜艇的声磁信号的尺度特征,且具备长时间机动性,混淆敌方的视听跟踪,以达到迷惑敌军兵力,提高我方舰艇生存几率的一种对抗方式[13]。因作战对抗灵活、诱骗效果佳等特点,其逐渐成为各国海军对抗武器发展的重点。汪晓雨等[14]对两电极式磁源结构的诱饵进行研究,从量级上对潜艇空中磁场进行了模拟。
随着航空磁探技术不断的进步,对于诱饵的性能要求越来越高,但目前的诱饵设计技术仅能实现战术上的对抗,作为战役型诱饵存在着存储能源不足等问题,这造成了诱饵在战役层面上不能长时间做对抗使用。王冲霄等[15]针对诱饵的流体阻力运用多学科优化的方法对水下拖缆进行优化,从诱饵布置上一定程度解决了减小能源损耗的问题。刘忠乐等[16]对诱饵组合磁源结构进行分析,提出“单(多)磁体加后置两电极”式组合磁源方案,利用遗传算法进行仿真研究,对比证明单磁体式组合磁源结构能减小磁模拟损耗的能源。
针对能源利用问题,在提出“航行体(兼磁体)加单电极前置的两电极”式磁源结构的基础上,对比研究磁体表面完全导电和完全绝缘2种理想情况下组合磁源的空中磁场分布情况,仿真和试验结果均表明,相同尺度下,将磁体表面设计成绝缘状态,磁场强度明显增大,能有效实现能源的高效利用。
1 “航行体加单电极前置的两电极”式组合磁源空中磁场分布图1为“航行体加单电极前置的两电极”式组合磁源结构示意图,定端电极B以环电极的形式固定在航行体头部,而动端电极A由电缆连接固定在外形为回转体(兼磁体)的航行体上。
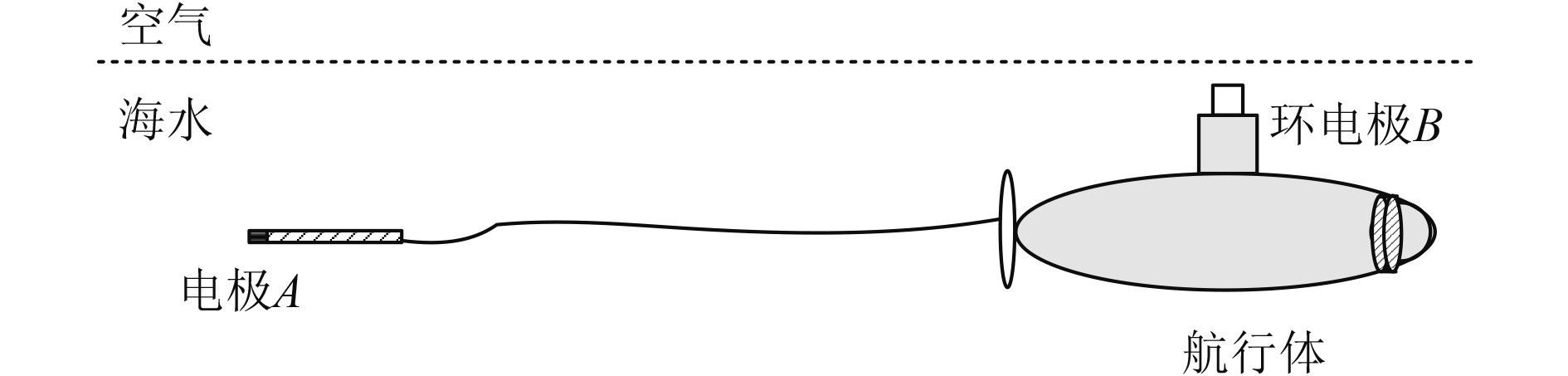
|
图 1 组合磁源结构示意图 Fig. 1 Schematic diagram of combined magnetic source structure |
为计算方便,在上述假设的基础上再对该磁源结构作出如下等效简化:
理想情况下,航行体表面是完全导电的,即意味着航行体内部电源电流会从航行体表面流入海水,产生分流电流磁场。由此可以得出航行体在生磁回路中既可以充当一段长度为长轴的导线,又可以是一段长度为长轴的线电极。此时的环电极B因为附着在导电航行体的表面,远小于整个大型自航式诱饵的尺度,也就等效于一点电极附着在一段线电极上,可忽略其存在。
以电极A右端与航行体头部距离的中点在海平面的投影为坐标原点,x轴正向为电流I的方向,z轴竖直向下,三轴满足右手螺旋法则,将磁源模型置于如图2所示的同一坐标系中。P(x,y,z)为空中任意一点,磁源定深为d,海水深h,电极A左端距离航行体尾部的距离为L1。航行体的长轴为L0=2a,短轴为2b。
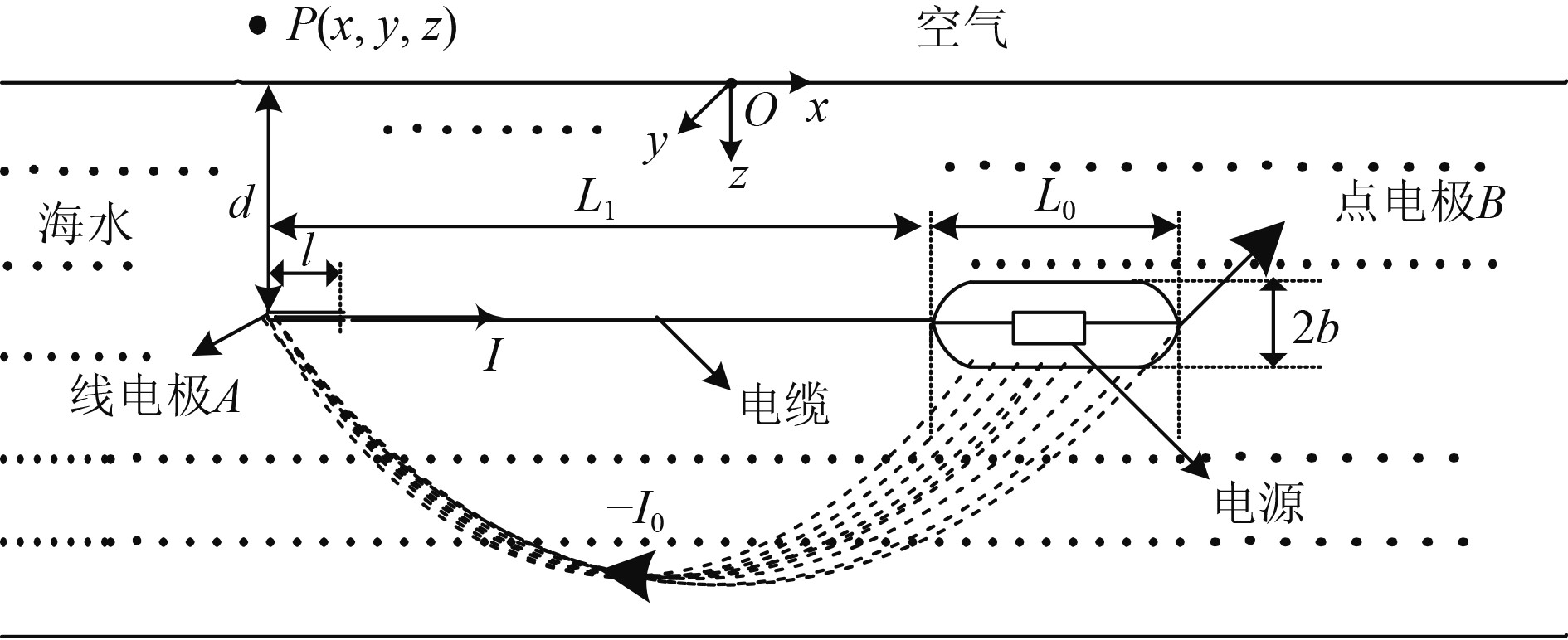
|
图 2 航行体导电状态下组合磁源模型 Fig. 2 Combined magnetic source model under the conduction state of the vehicle |
在理想状态下,“导电体加单电极前置的两电极”式组合磁源的空中磁场由以下部分的分磁场组成:
1)长度为L1+L0-l的有限长载流直导线的空中磁场;
2)长度为l的线电极A的线电极线电流空中磁场;
3)长度为l的线电极A的线电极分流电流空中磁场;
4)长度为L0的线电极的线电流空中磁场;
5)长度为L0的线电极的分流电流空中磁场;
6)沿航行体长轴为L0=2a均匀磁化的旋转椭球体的空中磁场。
长度为L1+L0-l的有限长载流直导线在空中任意一点P的磁场分布为:
| $ \left\{\begin{array}{l}{H}_{x1}=0,\\ {H}_{y1}=-\dfrac{I}{4\text{π} }\cdot\dfrac{z-d}{{y}^{2}+{\left(z-d\right)}^{2}}\times \\ \qquad\quad \left[\dfrac{0.5{L}_{1}+0.5{L}_{0}-0.5l+x}{\sqrt{{\left(0.5{L}_{1}+0.5{L}_{0}-0.5l+x\right)}^{2}+{y}^{2}+{\left(z-d\right)}^{2}}}+\right.\\ \qquad\quad \left.\dfrac{0.5{L}_{1}+0.5{L}_{0}-0.5l-x}{\sqrt{{\left(0.5{L}_{1}+0.5{L}_{0}-0.5l-x\right)}^{2}+{y}^{2}+{\left(z-d\right)}^{2}}}\right],\\ {H}_{z1}=-\dfrac{I}{4\text{π} }\cdot\dfrac{y}{{y}^{2}+{\left(z-d\right)}^{2}}\times\\ \qquad\quad\left[\dfrac{0.5{L}_{1}+0.5{L}_{0}-0.5l+x}{\sqrt{{\left(0.5{L}_{1}+0.5{L}_{0}-0.5l+x\right)}^{2}+{y}^{2}+{\left(z-d\right)}^{2}}}+\right.\\ \qquad\quad\left.\dfrac{0.5{L}_{1}+0.5{L}_{0}-0.5l-x}{\sqrt{{\left(0.5{L}_{1}+0.5{L}_{0}-0.5l-x\right)}^{2}+{y}^{2}+{\left(z-d\right)}^{2}}}\right]。\end{array}\right. $ | (1) |
线电极A上的线电流是沿电流方向(即x轴正向)从其最左端开始衰减,起始点坐标为 ,则动端电极A的线电流在空中任意一点P的磁场分布为:
| ${\left\{ \begin{gathered} {H_{x2}} = 0 ,\\ {H_{y2}} = - \dfrac{{I\left( {z - d} \right)}}{{4\text{π} \sinh \dfrac{l}{\lambda }}}\int_0^l \times \\ \qquad {\dfrac{{\sinh \dfrac{{l - \xi }}{\lambda }}}{{{{\left( {\sqrt {{{\left( {x + 0.5{L_1} + 0.5{L_0} + 0.5l + \xi } \right)}^2} + {y^2} + {{(z - d)}^2}} } \right)}^3}}}} {\rm{d}}\xi ,\\ {H_{y2}} = \dfrac{{Iy}}{{4\text{π} \sinh \dfrac{l}{\lambda }}}\int_0^l\times \\ \qquad {\dfrac{{\sinh \dfrac{{l - \xi }}{\lambda }}}{{{{\left( {\sqrt {{{\left( {x + 0.5{L_1} + 0.5{L_0} + 0.5l + \xi } \right)}^2} + {y^2} + {{(z - d)}^2}} } \right)}^3}}}} {\rm{d}}\xi 。\\ \end{gathered} \right. }$ | (2) |
长度为l的线电极A的线电极分流电流在空中任意一点P的磁场分布为:
| $ {\left\{ \begin{gathered} {H_{x3}} = - \dfrac{1}{{4\text{π} }} \cdot \dfrac{I}{{\lambda \sinh \dfrac{l}{\lambda }}}\int_0^l {\dfrac{y}{{r_3^2}}} \times \\ \qquad\quad \left(1 + \dfrac{{z - d}}{{\sqrt {r_3^2 + {{(z - d)}^2}} }}\right)\cosh \dfrac{{l - \xi }}{\lambda }{\rm{d}}\xi ,\\ {H_{y3}} = \dfrac{1}{{4\text{π} }} \cdot \dfrac{I}{{\lambda \sinh \dfrac{l}{\lambda }}}\int_0^l {\dfrac{{x + 0.5{L_1} + 0.5{L_0} + 0.5l + \xi }}{{r_3^2}}}\times \\ \qquad\quad \left(1 + \dfrac{{z - d}}{{\sqrt {r_3^2 + {{(z - d)}^2}} }}\right)\cosh \dfrac{{l - \xi }}{\lambda }{\rm{d}}\xi ,\\ {H_{z3}} = 0 。\\ \end{gathered} \right.} $ | (3) |
其中,
航行体段看作长度为L0的线电极,电极上的线电流是沿电流方向(即x轴正向)从其最右端开始衰减,起始点坐标为
| $\left\{ \begin{split} {H_{x4}} =& 0 ,\\ {H_{y4}} =& \dfrac{{I(z - d)}}{{4\text{π} \sinh \dfrac{{{L_0}}}{\lambda }}}\int_0^{{L_0}} {\dfrac{{\sinh \dfrac{{{L_0} - \xi }}{\lambda }}}{{{{\left( {\sqrt {{{\left( {x - 0.5{L_1} - 0.5{L_0} + 0.5l + \xi } \right)}^2} + {y^2} + {{(z - d)}^2}} } \right)}^3}}}} {\rm{d}}\xi,\\ {H_{z4}} =& - \dfrac{{Iy}}{{4\text{π} \sinh \dfrac{{{L_0}}}{\lambda }}}\int_0^{{L_0}} {\dfrac{{\sinh \dfrac{{{L_0} - \xi }}{\lambda }}}{{{{\left( {\sqrt {{{\left( {x - 0.5{L_1} - 0.5{L_0} + 0.5l + \xi } \right)}^2} + {y^2} + {{(z - d)}^2}} } \right)}^3}}}} {\rm{d}}\xi 。\end{split} \right. $ | (4) |
长度为L0的线电极分流电流在空中任意一点P的磁场分布为:
| $ \left\{\begin{split}{H}_{x5}=&\dfrac{1}{4\text{π} }\times \dfrac{I}{\lambda \mathrm{sinh}\dfrac{L{}_{0}}{\lambda }}\displaystyle {\int }_{0}^{{L}_{0}}\times\\ &\dfrac{y}{{r}_{5A}^{2}}\left(1+\dfrac{z-d}{\sqrt{{r}_{5A}^{2}+{\left(z-d\right)}^{2}}}\right)\mathrm{cosh}\dfrac{{L}_{0}-\xi }{\lambda }{\rm{d}}\xi ,\\ {H}_{y5}=&\dfrac{1}{4\text{π} }\times \dfrac{I}{\lambda \mathrm{sinh}\dfrac{L{}_{0}}{\lambda }}\displaystyle {\int }_{0}^{{L}_{0}}\dfrac{x-0.5{L}_{1}-0.5{L}_{0}+0.5l+\xi }{{r}_{5A}^{2}}\times\\ &\left(1+\dfrac{z-d}{\sqrt{{r}_{5A}^{2}+{\left(z-d\right)}^{2}}}\right)\mathrm{cosh}\dfrac{{L}_{0}-\xi }{\lambda }{\rm{d}}\xi ,\\ {H}_{z5}=&0。\end{split}\right. $ | (5) |
其中,
航行体的磁场建模将其等效为沿长轴均匀磁化的旋转椭球体模型,其长轴为L0=2a,短轴为2b,那么半焦距
| $ \left[ {\begin{array}{*{20}{c}} {{H_{xt}}} \\ {{H_{yt}}} \\ {{H_{zt}}} \end{array}} \right] = \left[ \begin{gathered} {A_x} \\ {B_x} \\ {C_x} \\ \end{gathered} \right] \times {m_x} ,$ | (6) |
式中,mx为航行体被磁化后的轴向磁矩。其中:
| $ \left\{ \begin{array}{l} {A_x} = - \dfrac{3}{{4\text{π} }}\left( {\dfrac{1}{{2{K^3}}}\ln \dfrac{{{a_n} + K}}{{{a_n} - K}} - \dfrac{{{a_n}}}{{{K^2}t}}} \right),{B_x} = \dfrac{{3{x^,}y}}{{4\text{π} {a_n}b_n^2t}},\\ Cx = \dfrac{{3{x^,}{z^,}}}{{4\text{π} {a_n}b_n^2t}},\\ t = \sqrt {{{\left( {{x^{,2}} + {y^2} + {z^{,2}} + {K^2}} \right)}^2} - 4{K^2}{x^{,2}}} ,\\ {x'} = x - 0.5\left( {{L_1} - l} \right);{z^,} = z - d ,\\ {a_n} = \sqrt {\dfrac{1}{2}\left( {{x^{,2}} + {y^2} + {z^{,2}} + {K^2} + t} \right)} ;{b_n} = \sqrt {a_n^2 - {K^2}} 。\end{array} \right. $ |
综上所述,“导电航行体加单电极前置的两电极”式组合磁源在空中任意一点P(z<0)的磁场强度为:
| $ \left\{\begin{array}{l}{H}_{x导电}={H}_{x1}+{H}_{x2}+{H}_{x3}+{H}_{x4}+{H}_{x5}+{H}_{xt},\\ {H}_{y导电}={H}_{y1}+{H}_{y2}+{H}_{y3}+{H}_{y4}+{H}_{y5}+{H}_{\text{yt}},\\ {H}_{z导电}={H}_{z1}+{H}_{z2}+{H}_{z3}+{H}_{z4}+{H}_{z5}+{H}_{z}{}_{t}。\end{array} \right.$ | (7) |
此时环电极B仍等效于一个点电极,而航行体在回路中只充当一段长度为长轴的导线,如图3所示。
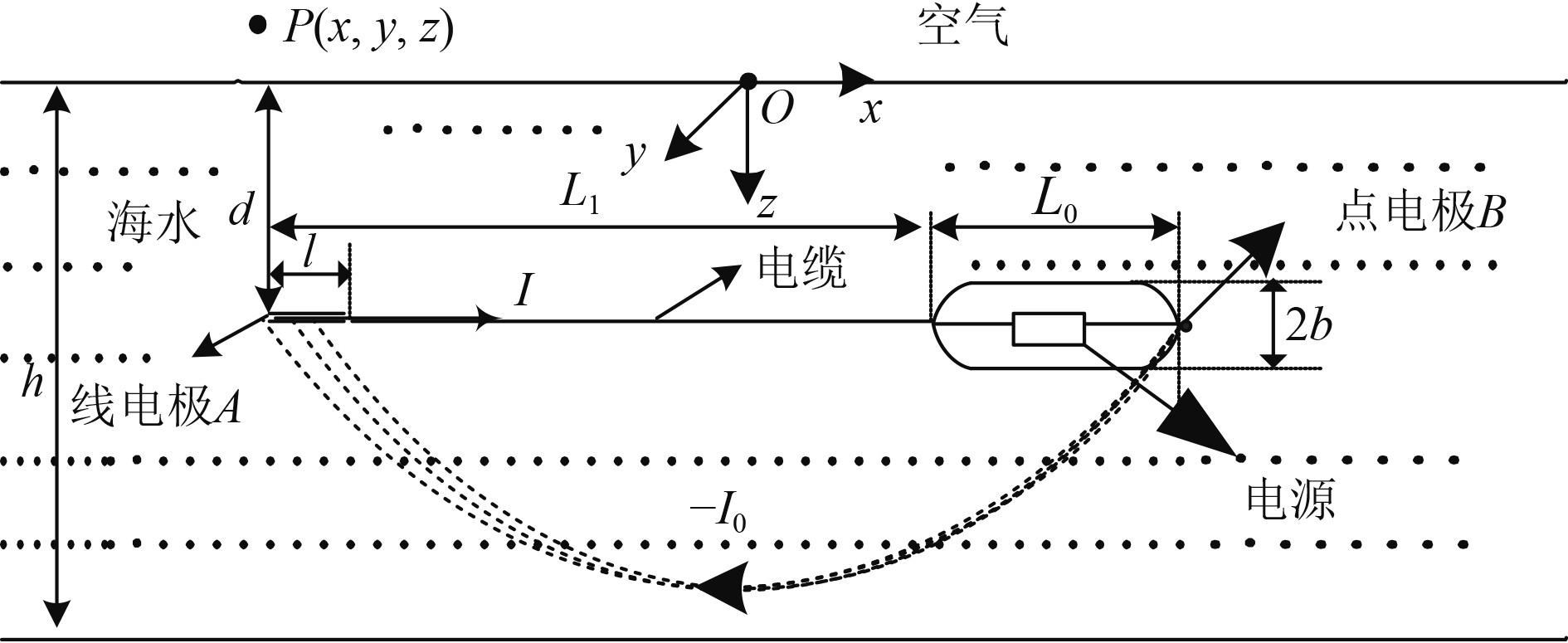
|
图 3 航行体绝缘状态下组合磁源模型 Fig. 3 Model of combinedga magnetic source in the insulated state of the vehicle |
在理想状态下,“绝缘体加单电极前置的两电极”式组合磁源的空中磁场由式(1)、式(2)、式(3)、式(5)、式(6)及点电极B分流电流的空中磁场组成。
单点电极B的坐标为
| $ \left\{ \begin{gathered} {H_{x6}} = \frac{{Iy}}{{4\text{π} r_6^2}}\left[1 + \frac{{z - d}}{{\sqrt {r_6^2 + {{\left( {z - d} \right)}^2}} }}\right],\\ {H_{z6}} = - \frac{{I(x - 0.5{L_1} - 0.5{L_0} + 0.5l)}}{{4\text{π} r_6^2}}\left[1 + \frac{{z - d}}{{\sqrt {r_6^2 + {{\left( {z - d} \right)}^2}} }}\right] ,\\ {H_{z6}} = 0 。\\ \end{gathered} \right. $ | (8) |
其中,
综上所述,则“绝缘航行体加单电极前置的两电极”式组合磁源在空中任意点P(z<0)的磁场强度为:
| $ \left\{\begin{array}{l}{H}_{x绝缘}={H}_{x1}+{H}_{x2}+{H}_{x3}+{H}_{x6}+{H}_{xt} ,\\ {H}_{y绝缘}={H}_{y1}+{H}_{y2}+{H}_{y3}+{H}_{y6}+{H}_{\text{yt}} ,\\ {H}_{z绝缘}={H}_{z1}+{H}_{z2}+{H}_{z3}+{H}_{z6}+{H}_{z}{}_{t} 。\end{array} \right.$ | (9) |
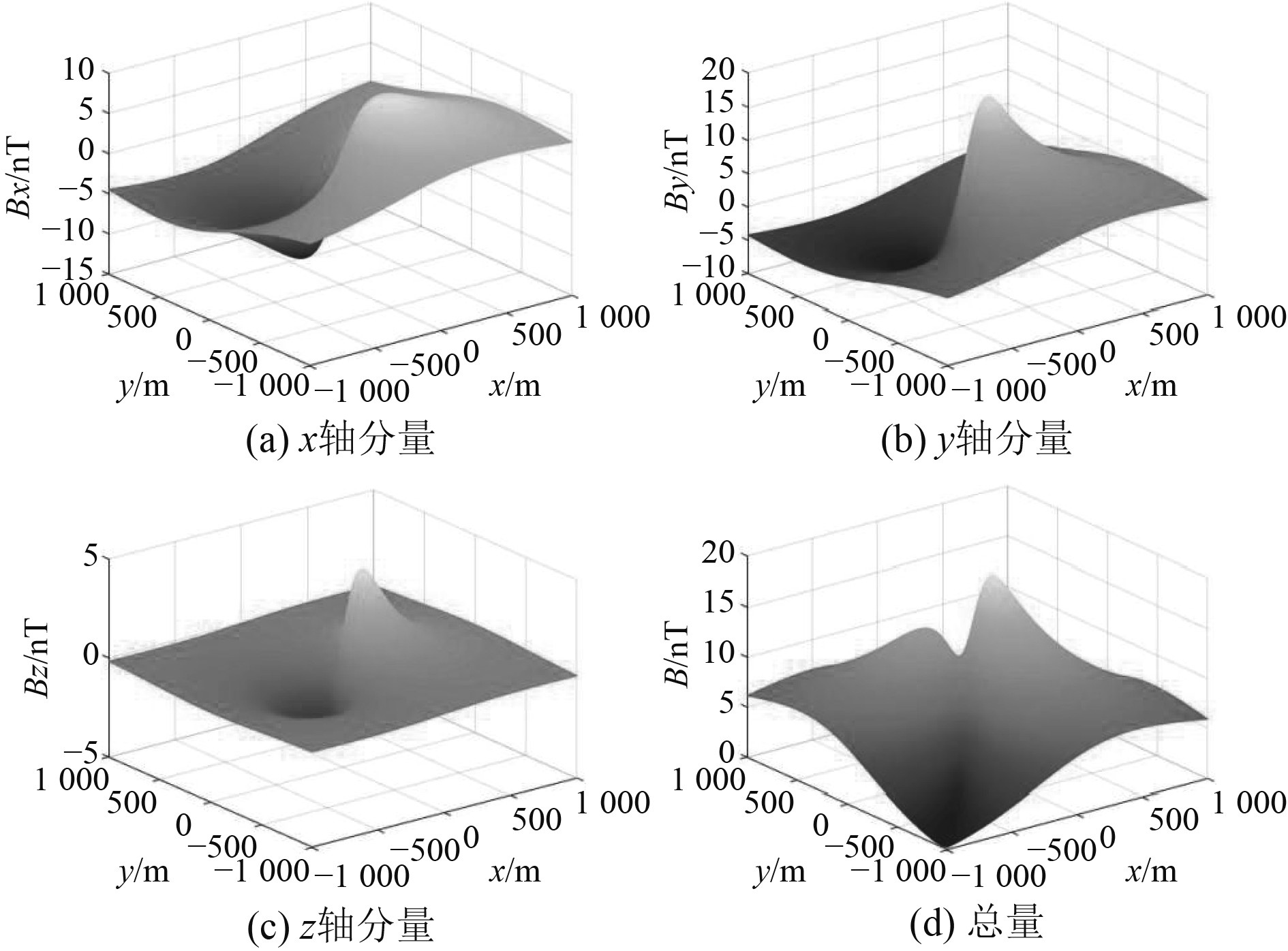
取电极长度l=2 m,通电电流I=50 A,海水典型深度h=100 m;L1=90 m,常规定深d=10 m;L0=2a=9 m,短轴2b=1.3 m。对组合磁源距离海平面(z=0 m)200 m处的空中磁场进行仿真,分别得到航行体表面完全导电和完全绝缘2种状态下的组合磁源空中磁场分布如图4和图5所示。
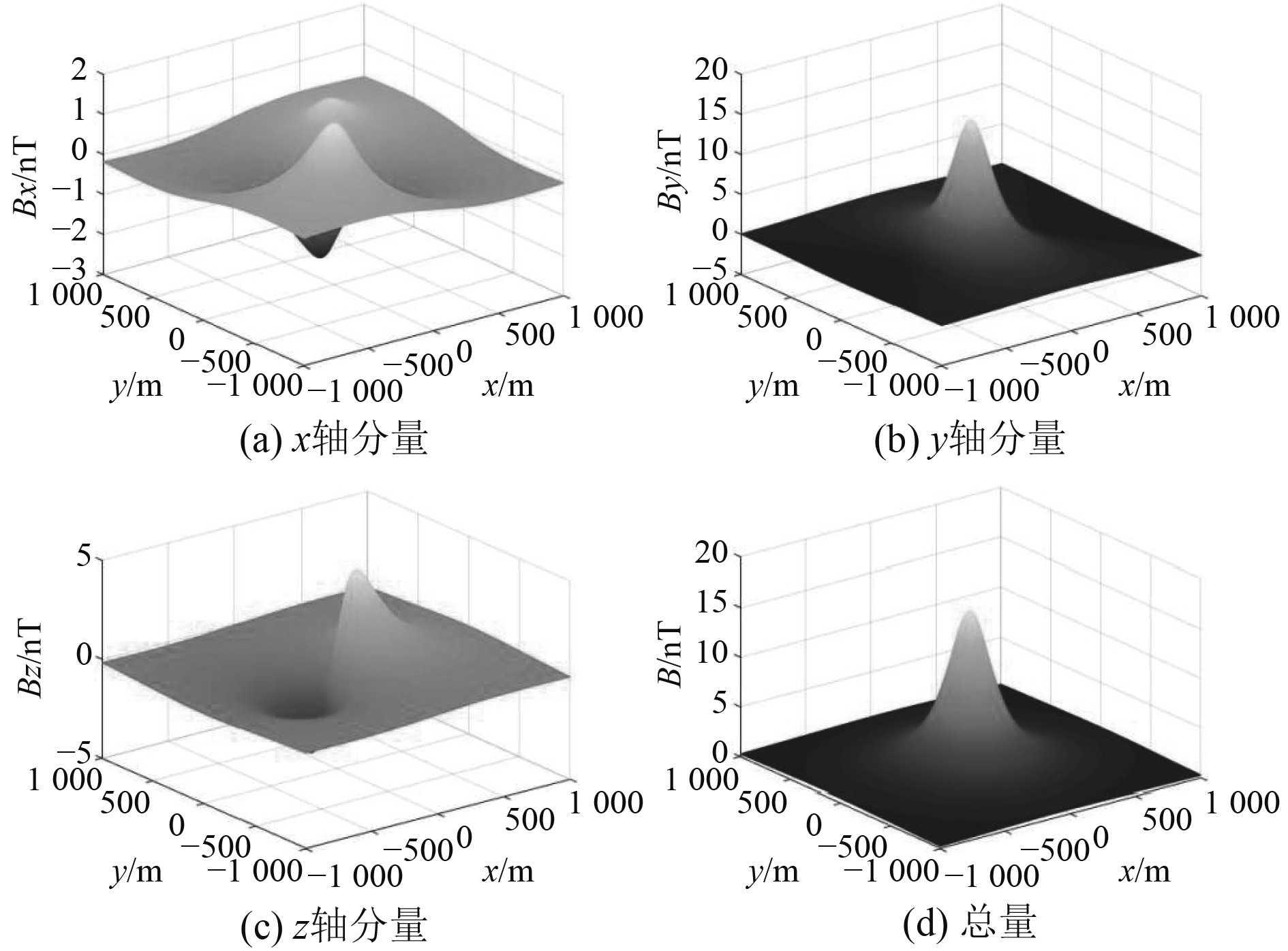
|
图 4 航行体导电状态下组合磁源空中磁场分布 Fig. 4 Distribution of magnetic field in the air by combined magnetic source under the conduction state of the vehicle |
|
图 5 航行体绝缘状态下组合磁源空中磁场分布 Fig. 5 Distribution of magnetic field in the air by combined magnetic source under the insulation state of the vehicle |
在相同条件及尺度下对“航行体加后置两电极”组合磁源空中磁场进行仿真,与电极前置下2种状态组合磁源的最大磁感应强度对比如表1所示。
|
|
表 1 不同组合磁源在空中200 m处磁感应强度最大值 Tab.1 The maximum magnetic induction intensity of different combinations of magnetic sources at 200 m in the air |
由图4、图5和表1可知:基于现有的“航行体加后置两电极”式组合磁源结构提出将靠近航行体的一端电极前置于航行体头部后,组合磁源空中磁场强度明显增大,且航行体绝缘状态下组合式磁源的磁场分布宽度要比导电状态下的磁场分布大,最大磁场强度在总量上大约提高了33% 。这说明“航行体加单电极前置的两电极”是较优的磁源结构,把航行体设计成绝缘体比导电体要好,有利于磁场强度的增大。即使在使用过程中受海水腐蚀等影响造成航行体外壳处于半导电半绝缘状态,组合磁源的空中磁场强度仍然比后置两电极式组合磁源的空中磁场强度要大。
3 试验验证试验在无磁环境下的盐水池进行,水池长宽高分别为8 m×5 m×1.3 m,水深0.8 m,含盐度大约为25%。水池上方有无磁材料建造的移动导轨,无磁导轨可以实现二维平面的移动。采用自主研发的三轴磁传感器,将其固定在无磁导轨上。航行体内装有的螺线管式磁源长0.135 m,直径0.05 m,缠绕线圈260匝。电缆用铜电线,电阻为0.00461
试验采用固定模型,移动传感器的方法以实现模型相对运动的方式测量空间磁场分布情况。将模型固定在无磁材料做成的模型架上,使模型中心点与水池中心点重合在同一平面,距离水面的距离为0.15 m,距离传感器的高度为1.0 m。
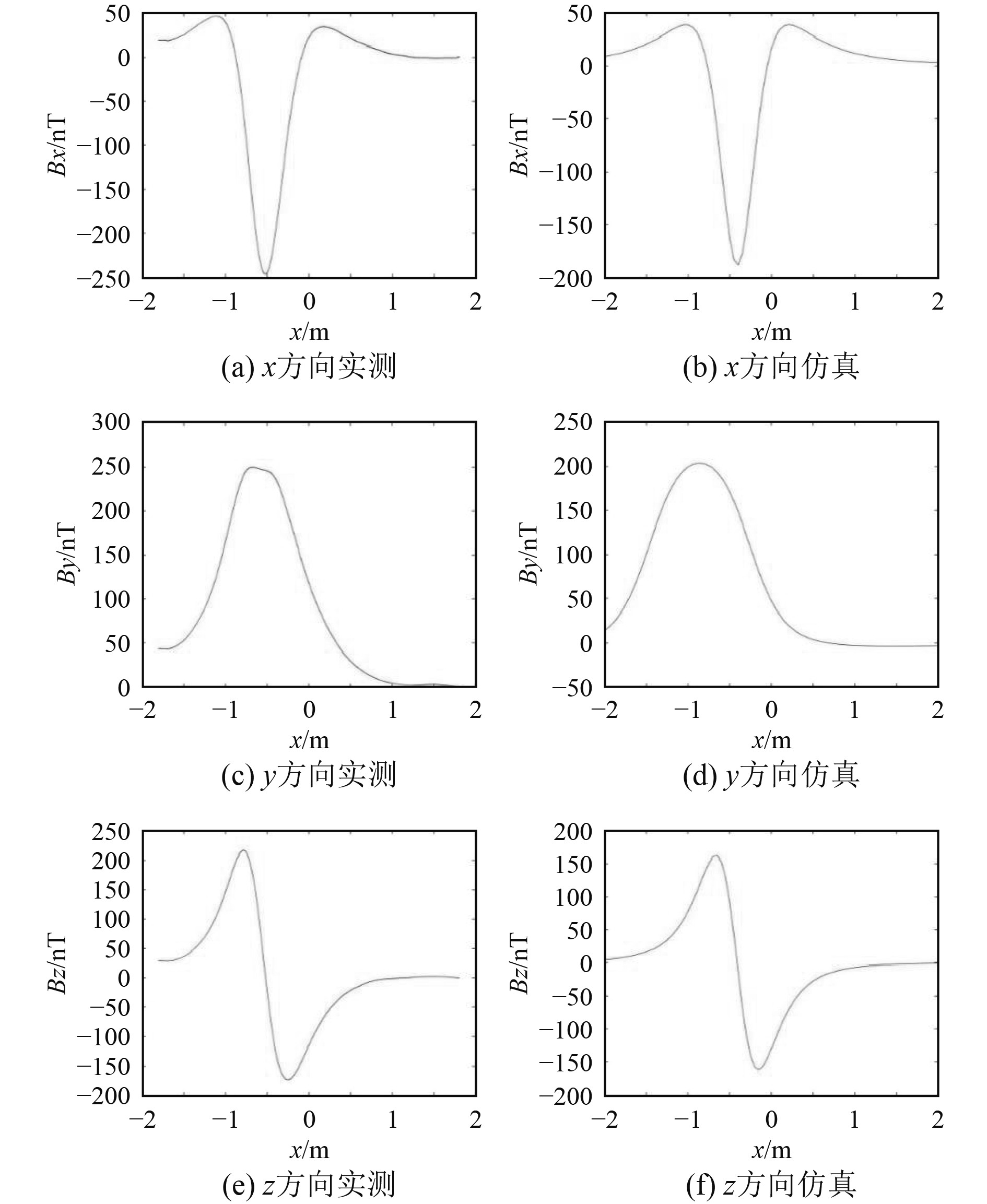
“导电航行体+单电极前置的两电极”实测数据与仿真数据对比如图6所示。
|
图 6 导电航行体组合式磁源磁场处理 Fig. 6 Conductive voyage body combined magnetic source magnetic field processing |
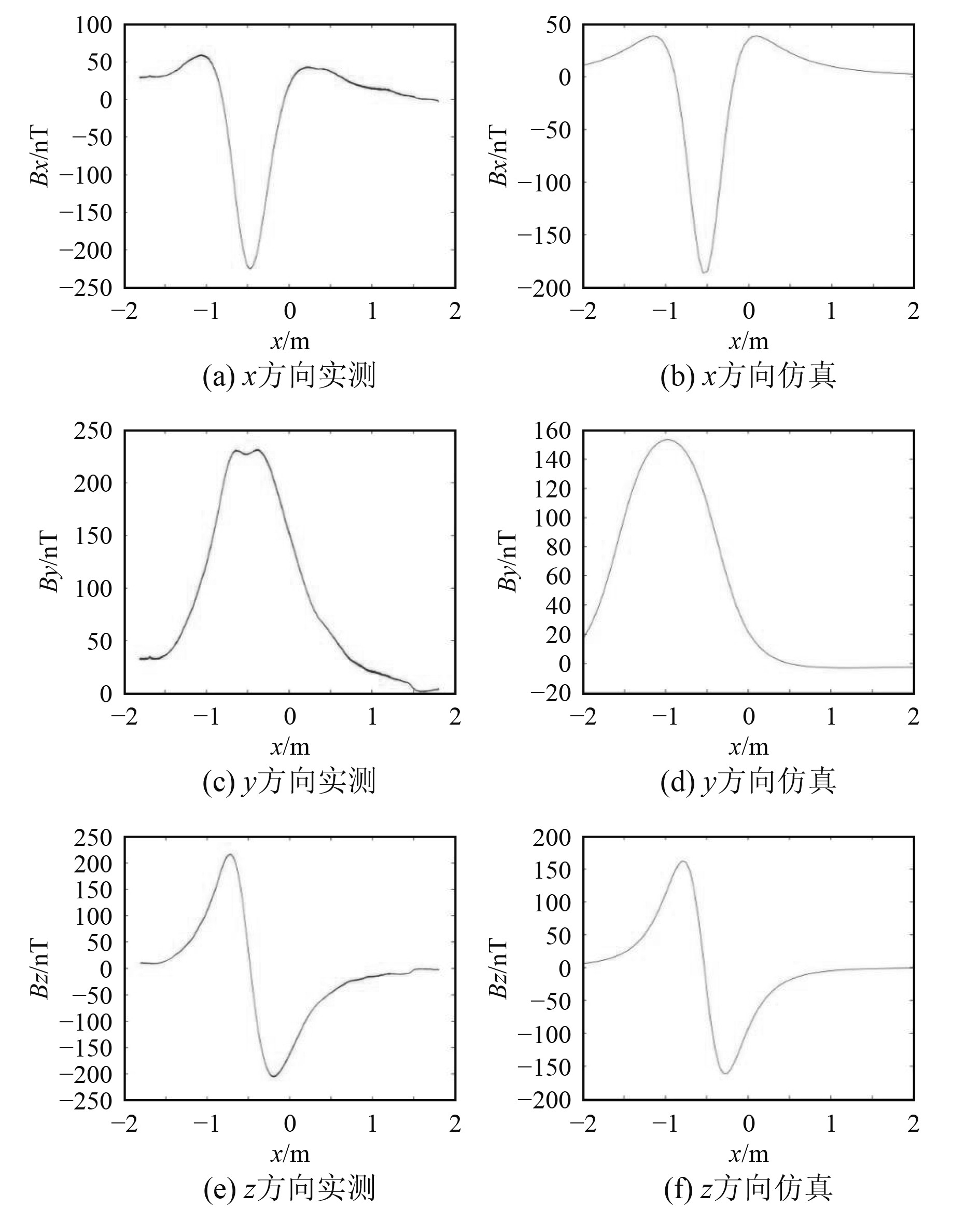
“绝缘航行体+单电极前置的两电极”方案实测数据与仿真数据对比如图7所示。
|
图 7 绝缘航行体组合式磁源磁场处理 Fig. 7 Insulated voyage body combined magnetic source magnetic field processing |
由图6和图7可知,2种状态下组合磁源的磁场实测和仿真数值在各分量方向上的分布规律基本一致,量值也相差不大。2种实物模型的磁场测量值均比仿真值大,且实测曲线在测量点开始和结束的位置相对不平滑。虽然受限于试验条件及客观因素干扰,但将实测数据与仿真数据对比,也可看出模型的试验结果与仿真值的变化趋势与量级相吻合,且航行体处于绝缘状态下的磁场强度更大。
4 结 语本文针对目前诱饵能源利用问题,在提出“单电极前置的两电极”式组合磁源结构基础上,针对航行体(兼磁体)表面导电性进行对比研究,分别建立了航行体表面完全导电和完全绝缘2种状态下的空中磁场分布模型,仿真和试验结果均表明:“航行体加单电极前置的两电极”是较优的磁源结构;将航行体表面设计成绝缘,能有效实现磁场强度增大,实现能源的高效利用。
| [1] |
刘晓伟, 马宇, 李筠, 等. 2020年国外潜艇装备发展综述[J]. 飞航导弹, 2021(1): 47-54. LIU Xiaowei, MA Yu, LI Jun, et al. Overview of the development of foreign submarine equipment in 2020[J]. Flying Missile, 2021(1): 47-54. DOI:10.16338/j.issn.1009-1319.20200853 |
| [2] |
Modern maritime security kockums A26 [R]. 2014.8. SAAB.
|
| [3] |
郭维, 杨清轩, 苏强. 国外弹道导弹核潜艇发展趋势研究[J]. 舰船科学技术, 2015, 37(7): 233-237. GUO Wei, YANG Qing-xuan, SU Qiang. Research on the development trend of foreign ballistic missile nuclear submarines[J]. Ship Science and Technology, 2015, 37(7): 233-237. DOI:10.3404/j.issn.1672-7649.2015.07.055 |
| [4] |
李红军, 王海珍. 世界海军装备技术新近发展[J]. 现代军事, 2016(6): 78-82. LI Hong-jun, WANG Hai-zhen. The recent development of world naval equipment and technology[J]. Modern Military, 2016(6): 78-82. |
| [5] |
DAVID KELLY. Submarine requirements forthe global war on terrorism [C]//RUSI Defence Systems Autumn 2006.
|
| [6] |
TIM WHITTEN. Achieving the goal of a submarine modular mission payload system[J]. UDT 2011(Europe).
|
| [7] |
林玉琛. 潜艇面临的威胁及潜空导弹[J]. 现代防御技术, 2005(1): 19-27. LIN Yuchen. The threats faced by submarines and submarine-to-air missiles[J]. Modern Defense Technology, 2005(1): 19-27. DOI:10.3969/j.issn.1009-086X.2005.01.005 |
| [8] |
宋海凌, 吴新宏. 国外舰载防空体系与武器发展趋势[J]. 现代防御技术, 2011, 39(1): 33-36+53. SONG Hai-ling, WU Xin-hong. The development trend offoreign shipborne air defense systems and weapons[J]. Modern Defense Technology, 2011, 39(1): 33-36+53. DOI:10.3969/j.issn.1009-086x.2011.01.006 |
| [9] |
戚学文, 夏青峰, 王相. 水面舰艇反潜防御中无人潜航器兵力需求研究[J]. 现代防御技术, 2021, 49(3): 30-37+46. QI Xue-wen, XIA Qing-feng, WANG Xiang. Study on the demand for unmanned submarine forces in surface warship anti-submarine defense[J]. Modern Defense Technology, 2021, 49(3): 30-37+46. DOI:10.3969/j.issn.1009-086x.2021.03.004 |
| [10] |
孙明太, 刘海光, 吴杰, 等. 潜艇对抗反潜巡逻机作战方法综述[J]. 电光与控制, 2015, 22(6): 1-5. SUN Ming-tai, LIU Hai-guang, WU Jie , et al. Overview of submarine combat methods against anti-submarinepatrol aircraft[J]. Electro-Optics and Control, 2015, 22(6): 1-5. DOI:10.3969/j.issn.1671-637X.2015.06.001 |
| [11] |
高学强, 杨日杰, 杨春英. 潜艇规避对主动声纳浮标作战效能影响研究[J]. 系统工程与电子技术, 2008(2): 300-303. GAO Xue-qiang, YANG Ri-jie, YANG Chun-ying. Study on the influence of submarine evasion on the combat effectiveness of active sonar buoy[J]. System Engineering and Electronic Technology, 2008(2): 300-303. DOI:10.3321/j.issn:1001-506X.2008.02.026 |
| [12] |
孙明太. 航空反潜装备[M]. 北京: 国防工业出版社, 2012: 161–243.
|
| [13] |
李杰, 毛启明, 崔国平. 水下精确制导武器对抗技术发展现状与趋势[J]. 现代防御技术, 2018, 46(4): 73-78+138. LI Jie, Mao Qi-ming, CUI Guo-ping. Development status and trend of countermeasure technology for underwater precision guided weapons[J]. Modern Defense Technology, 2018, 46(4): 73-78+138. DOI:10.3969/j.issn.1009-086x.2018.04.012 |
| [14] |
汪晓雨, 刘忠乐. 基于小型运动载体的潜艇磁诱饵磁场产生方法[J]. 水雷战与舰船防护, 2006(4): 18-21. WANG Xiao-yu, LIU Zhong-le. Magnetic field generation method of submarine magnetic decoy based on small moving carrier[J]. Mine Warfare and Ship Protection, 2006(4): 18-21. |
| [15] |
王冲霄, 刘忠乐, 文无敌, 等. 水下拖缆稳态运动的多目标优化研究[J]. 兵器装备工程学报, 2020, 41(4): 244-248. WANG Chong-xiao, LIU Zhong-le, WEN Wu-di, et al. Multi-objective optimization researchon steady-state motion of underwater streamer[J]. Chinese Journal of Ordnance Equipment Engineering, 2020, 41(4): 244-248. DOI:10.11809/bqzbgcxb2020.04.046 |
| [16] |
刘忠乐, 石剑, 文无敌, 等. 模拟潜艇磁场的组合式磁源[J]. 航空学报, 2017, 38(12): 1-11. LIU Zhong-le, SHI Jian, WEN Wu-di, et al. Combined magnetic source for simulating submarine magnetic field[J]. Acta Aeronautica Sinica, 2017, 38(12): 1-11. DOI:10.7527/S1000-6893.2017.321240 |
 2023, Vol. 45
2023, Vol. 45
