2. 中国人民解放军92697部队,海南 陵水 572400
2. The 92697 Unit of PLA, Lingshui 572400, China
对于潜航器的水声目标被动定位技术而言,声场的空间采样受限于水听器阵列的尺寸,而水听器阵列尺寸受制于载体尺寸。国内外学者对基于小孔径基阵的水声目标定位展开了一系列研究。Touze等[1]采用模式滤波实现了单个水听器的声源定位;李焜等[2]结合时域最小二乘方法,实现了单阵元声源匹配被动定位;王晋晋等[3]的研究指出,利用Rake接收机对水声信道的匹配特性,可以实现单阵元对脉冲声源的匹配场定位;王良等[4]给出了一种基于压缩感知的优化匹配处理会聚区判别方法;李晓曼等[5]利用简正波匹配的原理实现了浅海中宽带脉冲声源的被动测距。上述小孔径基阵被动定位多是借助宽带信号,以频域的多频点数据来弥补小孔径采样的不足。
频域多频点数据可弥补小孔径采样不足,那么空域和时域上的数据能否扩展孔径实现目标被动定位呢?本文基于这种假设,提出一种基于等效单阵元多空间采样点数据时空联合处理的目标被动定位方法。该方法针对补偿过程中目标线谱频率未知的情况,利用广义波束形成——匹配场技术,采用距离、深度、频率三维搜索的算法给出了空域、时域联合的数据补偿矩阵,合成大孔径基阵,实现目标被动定位。
1 运动声源声场及补偿矩阵 1.1 移动声源声场模型Hawker曾提出了一种解决声源运动对基阵各水听器接收到的声场影响的方法,其是从简正波的解入手,考虑多普勒效应以及运动声源位移对声信号幅度和相位的影响,其模型为[6]:
| $ {p_n}(t) \approx \frac{{iQ\sqrt {2\text{π} } {e^{ - i{\omega _0}t - i\text{π} /4}}}}{{\sqrt {{r_n}(t)} }}\sum\limits_{j = 1}^J {{Z_j}({z_s})} {Z_j}(z\left( t \right))\frac{{{e^{ik_{rj}^0{r_n}(t){\beta _j}(\theta (t))}}}}{{\sqrt {k_{rj}^0} }} 。$ | (1) |
式中:
连续空间变深采样获取的数据在时域上时间不同步,需进行相位补偿。将
| $ {{\boldsymbol{S}}_{\boldsymbol{n}}}(f) = \left[ {\begin{array}{*{20}{c}} {{x_{n1}}}&{{x_{n2}}}& \cdots &{{x_{nM}}} \end{array}} \right] ,$ | (2) |
总采样过程包含
| $ {\boldsymbol{Z}} = \left[ {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1M}}} \\ {{x_{21}}}&{{x_{22}}}&{}&{{x_{2M}}} \\ \vdots &{}& \ddots & \vdots \\ {{x_{N1}}}&{{x_{N2}}}& \cdots &{{x_{NM}}} \end{array}} \right] ,$ | (3) |
频域快拍矩阵Z的补偿矩阵B为:
| $ \begin{split}{\boldsymbol{B}} = &\left[ {\begin{array}{*{20}{c}} {\frac{{P_{{A_1}}^{}}}{{P_{{A_1}}^ * }}{e^{\left[ {{{j2\text{π} T(N - 1)(K - 1){f_s}} / K}} \right]}}}\\ {}&{\frac{{P_{{A_2}}^{}}}{{P_{{A_2}}^ * }}{e^{\left[ {{{j2\text{π} T(N - 2)(K - 1){f_s}} / K}} \right]}}} \\ {}&{} \\ {}&{} \end{array}} \right. \\ &\left. {\begin{array}{*{20}{c}} {}&{} \\ {}&{} \\ \ddots &{} \\ {}&{\frac{{P_{{A_N}}^{}}}{{P_{{A_N}}^ * }}{e^{\left[ {{{j2\text{π} T(N - N)(K - 1){f_s}} / K}} \right]}}} \end{array}} \right] ,\end{split}$ | (4) |
式中:B为对角矩阵;N为对角线元素个数。
对矩阵Z进行补偿可以得到:
| $ {{{{\boldsymbol{Z}}}}^*} = {{{\boldsymbol{BZ}}}} = \left[ {\begin{array}{*{20}{c}} {x_{_{11}}^*}&{x_{_{12}}^*}& \cdots &{x_{_{1M}}^*} \\ {x_{_{21}}^*}&{x_{_{22}}^*}&{}&{x_{_{2M}}^*} \\ \vdots &{}& \ddots & \vdots \\ {x_{_{N1}}^*}&{x_{_{N2}}^*}& \cdots &{x_{_{NM}}^*} \end{array}} \right] ,$ | (5) |
补偿后的快拍矩阵Z*进行了时间对齐,矩阵中第m列用Vm表示,则合成垂直阵m号线谱测量场为:
| $ K_m^* = V_m^*V_m^{*H},m = 1 \cdots M 。$ | (6) |
上述不同合成阵元间的时间对齐补偿是基于目标真实频率构建的补偿矩阵,但实际运动中目标线谱的真实频率往往难以获取,需要改进算法解决线谱真实频率模糊情况下各合成阵元数据间的相位补偿问题。
若式(4)中,用以时延差相位补偿的频率为
| $\begin{split}& [ \exp \left( {{{j2\text{π} T\left( {N - 1} \right)\left( {{f_T} + \Delta f} \right)}/N}} \right) \cdots \\ &\qquad \exp \left( {{{j2\text{π} T\left( {N - N} \right)\left( {{f_T} + \Delta f} \right)} / N}} \right) ] \end{split}。$ | (7) |
可以看出,实际上频率f只需满足
对真实频率为

|
图 1 目标距离、深度、频率搜索示意图 Fig. 1 Target distance, depth and frequency search |
以一定细分频率间隔分别对N个等效阵元数据进行时间对齐的相位补偿,若频率搜索点数为J,则可以得到J组补偿后的测量场。假定目标位置点
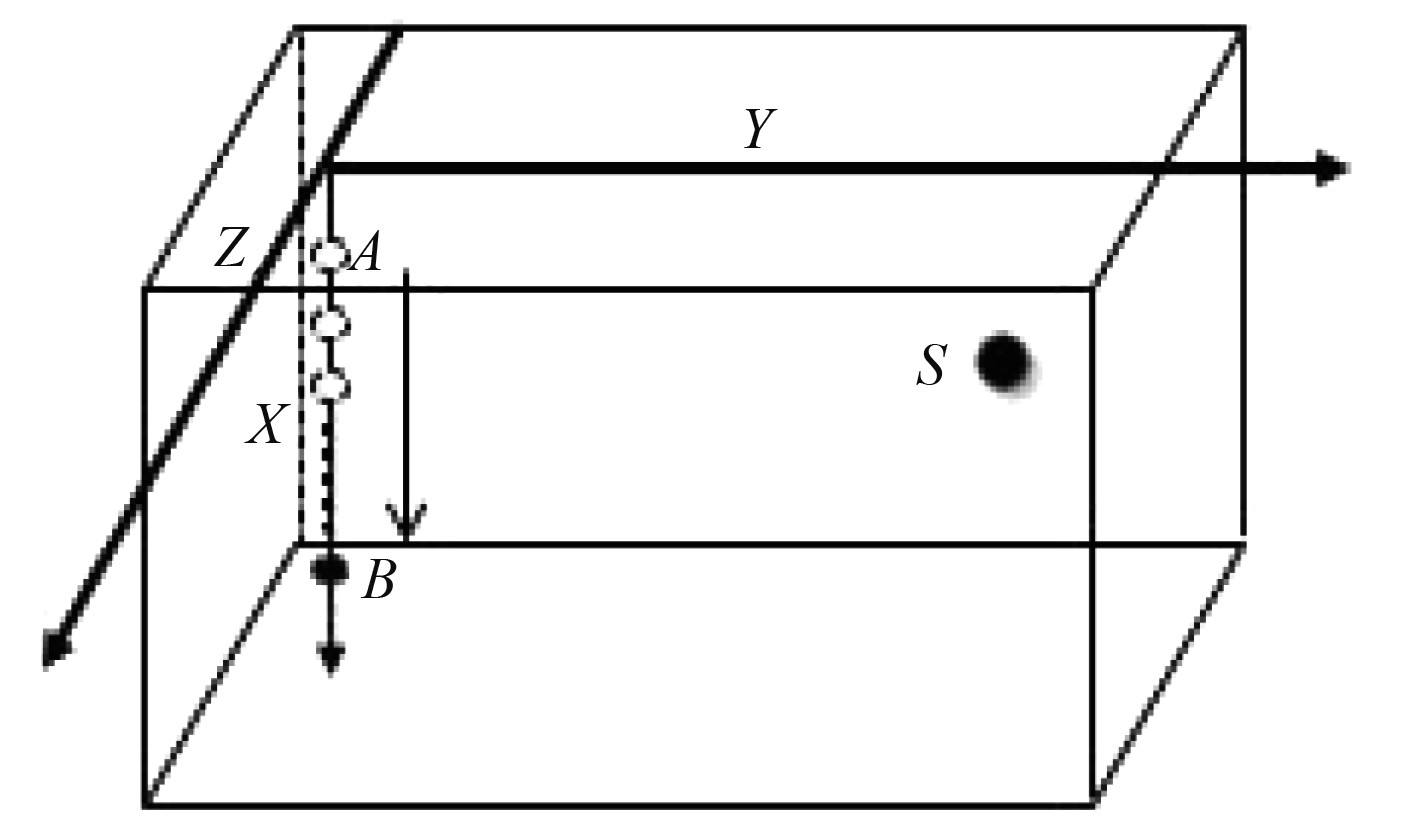
试验于消声水池展开,水池尺寸为21 m×6 m×7 m,水面未铺设消声材料,选取一种相对简单的态势,建立如图2所示的坐标系。声源为频率3 kHz的连续单频正弦信号,静止于S点,坐标为(2.5 m, 8 m, 0),单水听器初始位置位于坐标系原点A,以速度v=0.125 m/s匀速下放至池底B点,有效采集数据时长56 s,根据测算水池为均匀层,声速约为1459.4 m/s,其中1次数据采集结果如图3所示。
|
图 2 水池试验示意图 Fig. 2 Schematic diagram of pool test |
|
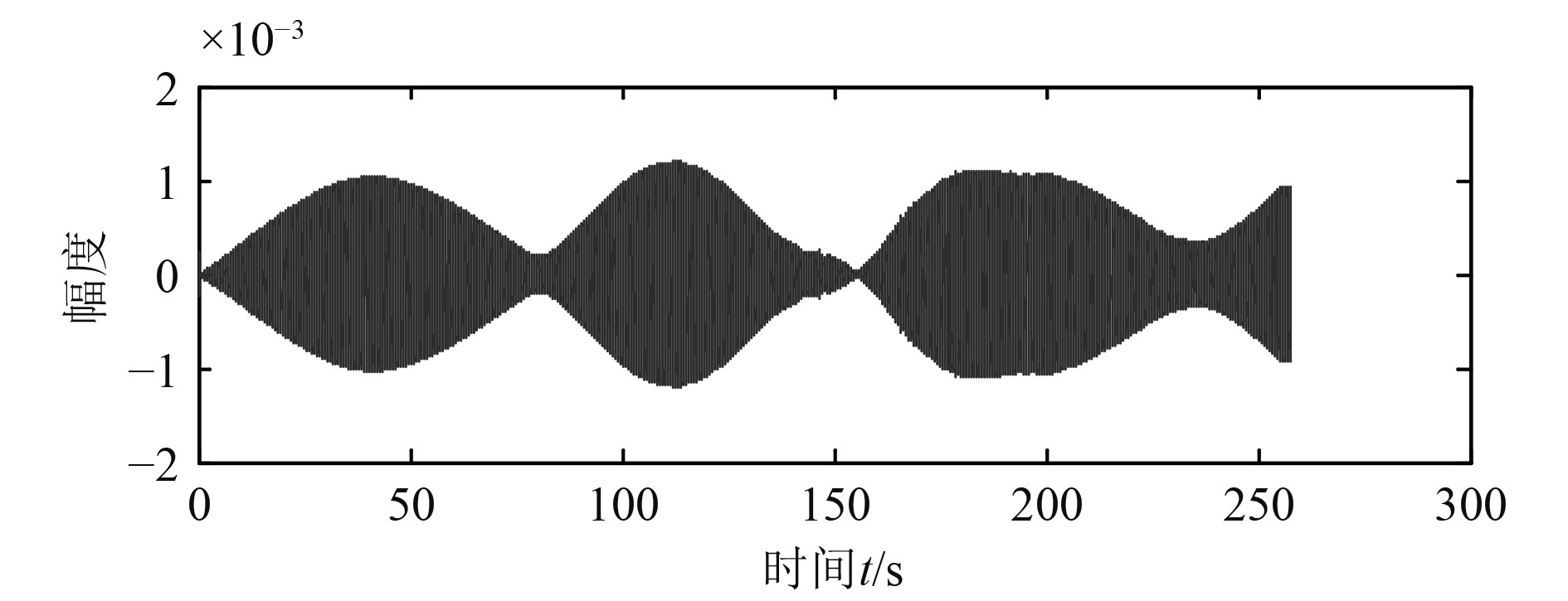
图 3 水池试验滤波后单次信号采集结果 Fig. 3 Single signal acquisition result after filtering in pool test |
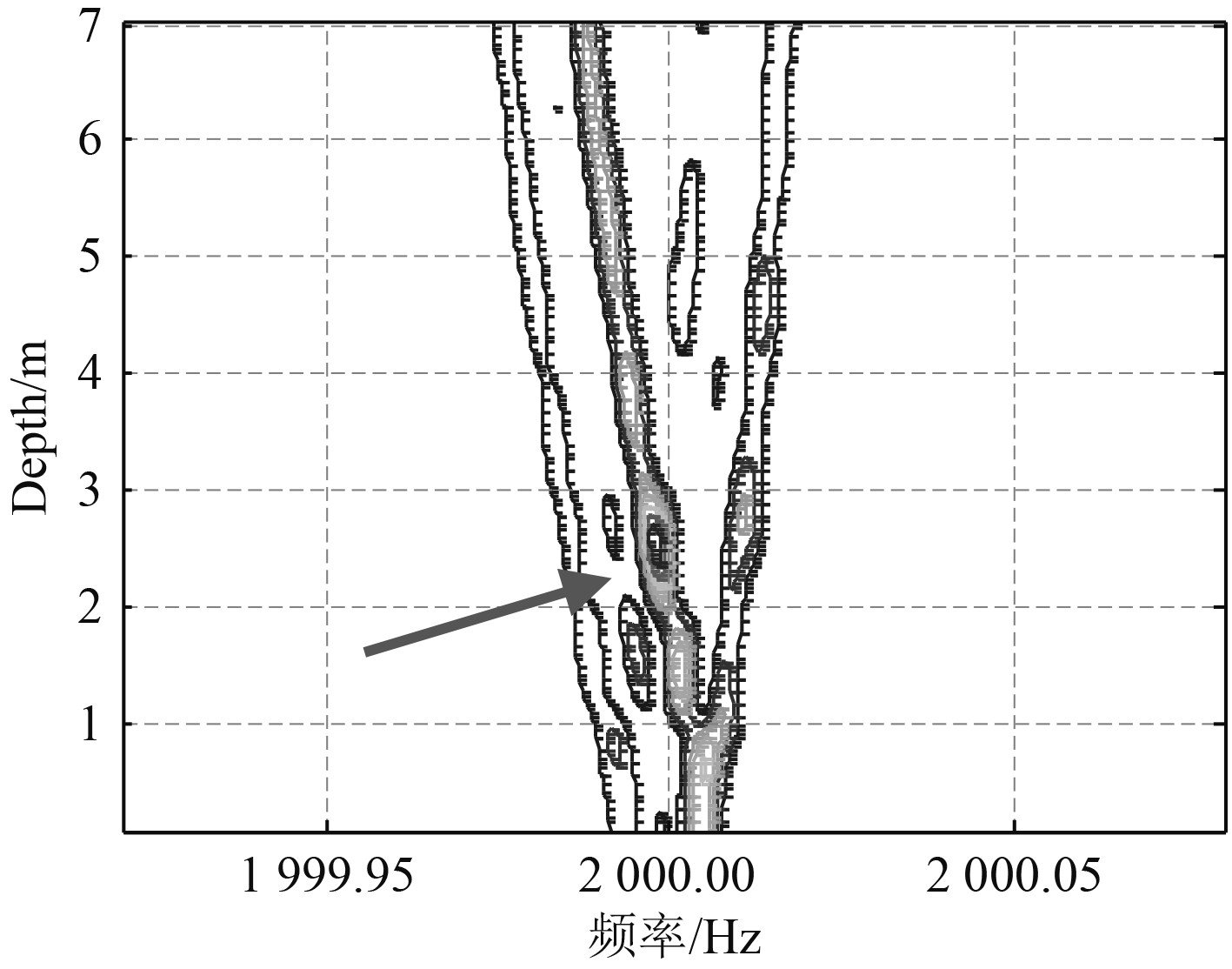
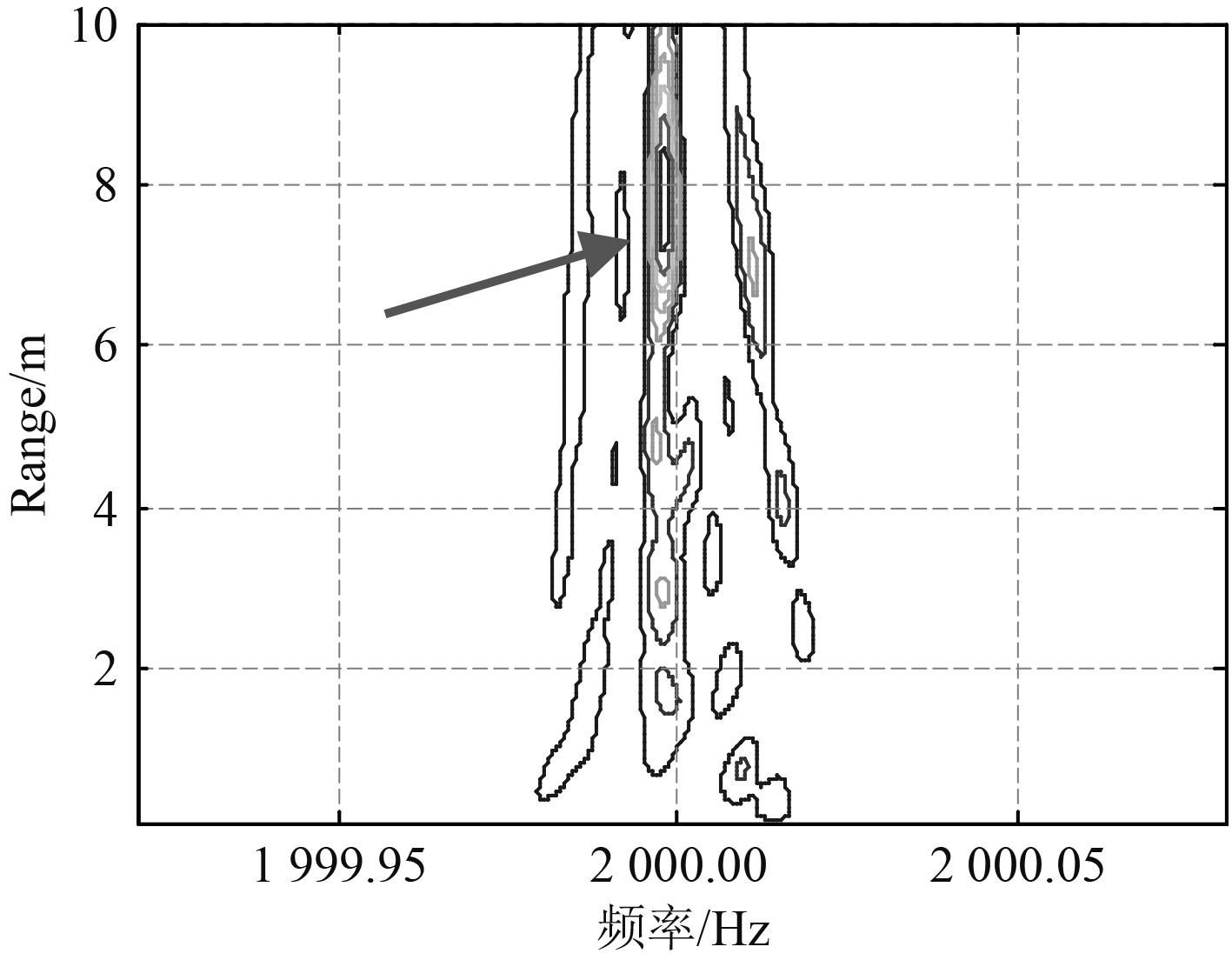
将图3所示信号进行SFFT处理,并以一定频率间隔构建补偿矩阵进行三维搜索。图4为深度、频率搜索切片等值线图,图5为距离、频率搜索切片等值线图,图6为最终定位的声源模糊度图。搜索得到的声源距离和深度为(7.929 m,2.548 m),与实际声源距离存在0.071 m偏差,深度存在0.048 m偏差定位结果较准确。
|
图 4 水池试验深度、频率搜索切片等值线图 Fig. 4 Depth and frequency search slice contour map in pool test |
|
图 5 水池试验距离、频率搜索切片等值线图 Fig. 5 Range and frequency search slice contour map in pool test |

|
图 6 水池试验补偿频率对应的定位模糊面 Fig. 6 Positioning surface corresponding to compensation frequency |
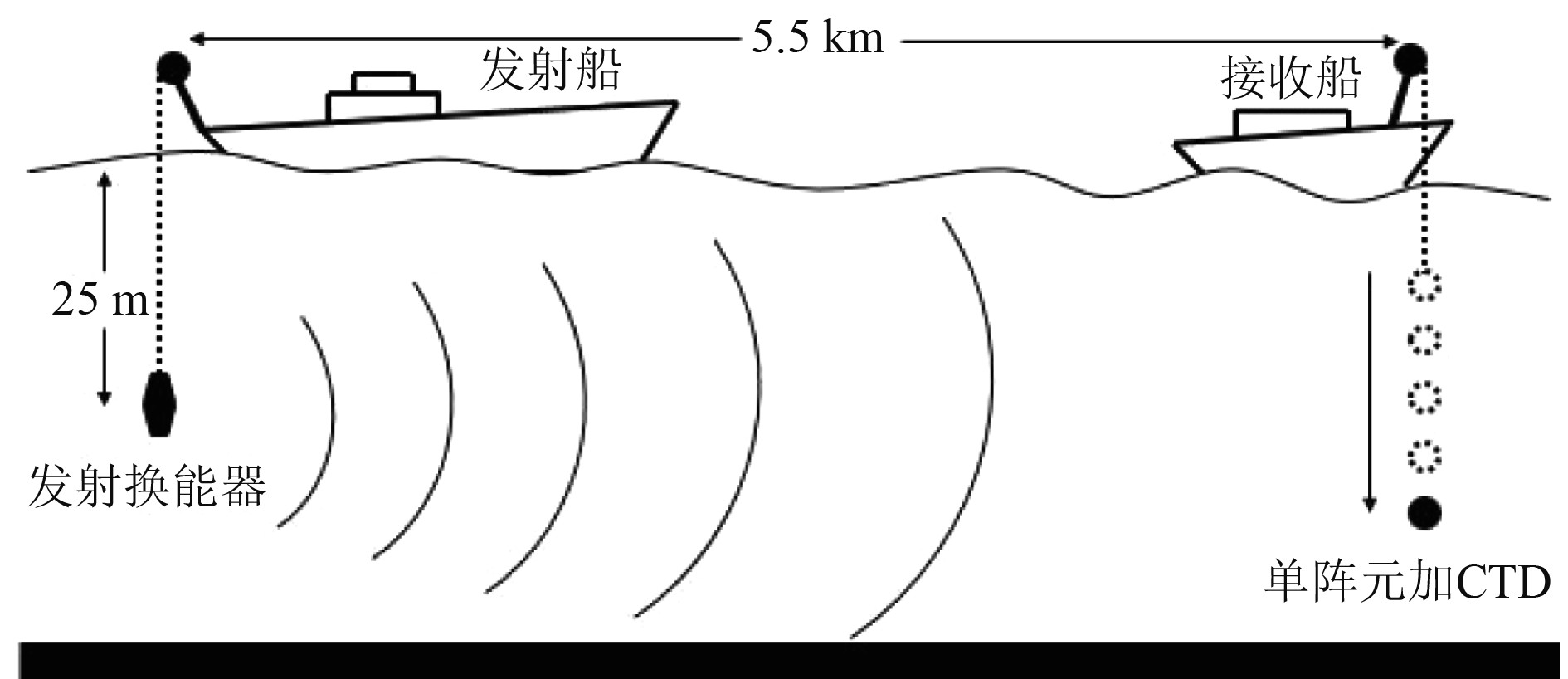
如图7所示,声源发射船与接收船分别锚定,直线距离5.5 km。声源发射船通过船尾吊车吊放发射换能器,发射换能器深度25 m。CTD固定于单水听器上,并通过接收船侧边吊车吊放,在单水听器及发射换能器下部分别配重。单次信号采集过程中,单水听器由海面匀速下放至近海底,停留10 s后提升至海面,在这个过程中,多通道记录设备开机对声源产生的声场进行采样。
|
图 7 海试示意图 Fig. 7 Schematic diagram of sea test |
进行多组吊放,试验数据获得较好的定位效果,给出其中2组结果。
1)第1组,声源频率1 kHz,距离5.5 km,单水听器由47.12 m匀速提升至0.18 m。
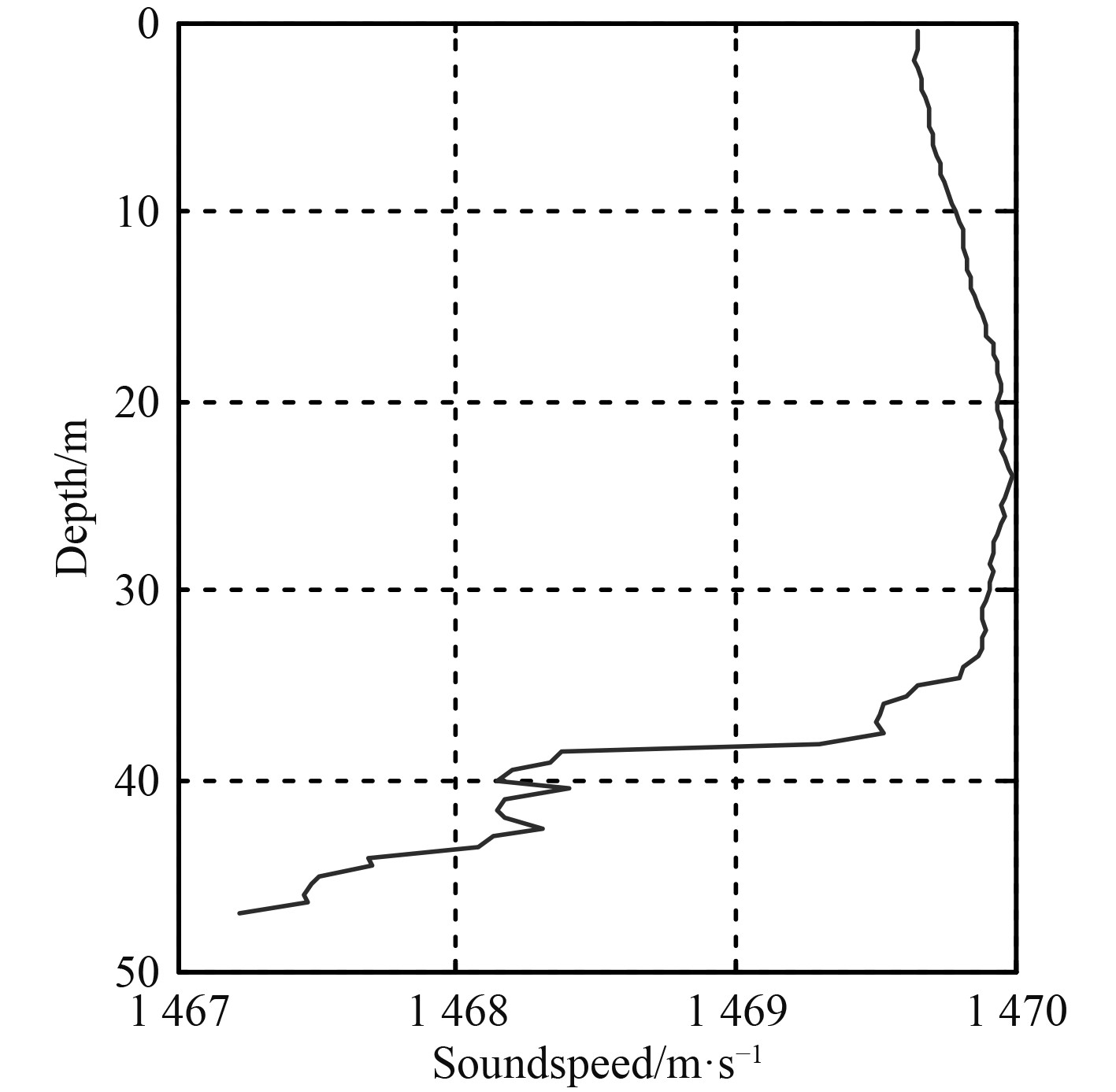
CTD采样的声速剖面如图8所示。海底沉积层为黏土,声速为1543 m/s,密度为1.485 kg/m3,吸收系数
|
图 8 海上试验声速分布 Fig. 8 Sound velocity distribution in sea test |
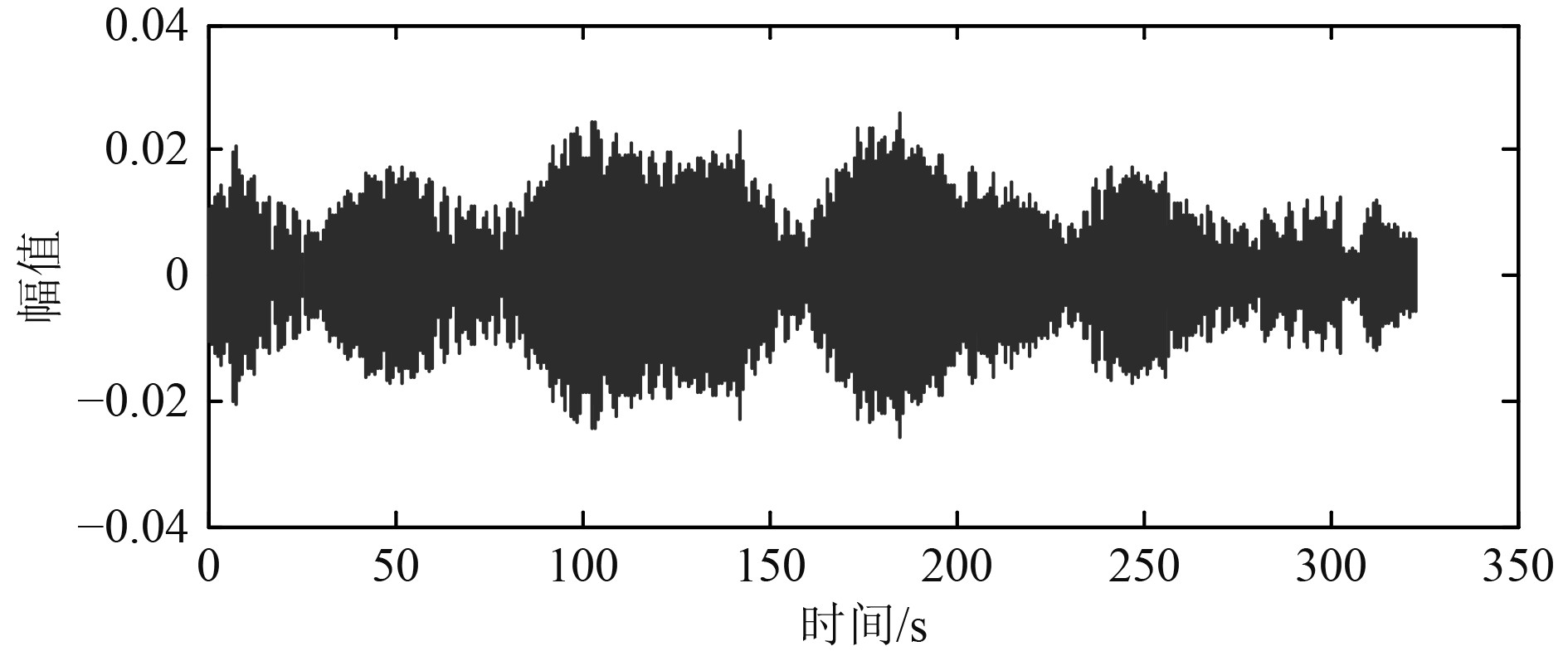
将第1组获取的信号降采样并滤波后得到的接收信号如图9所示。
|
图 9 第1组降采样滤波后的采样信号 Fig. 9 Group 1 sampling signal after downsampling and filtering |
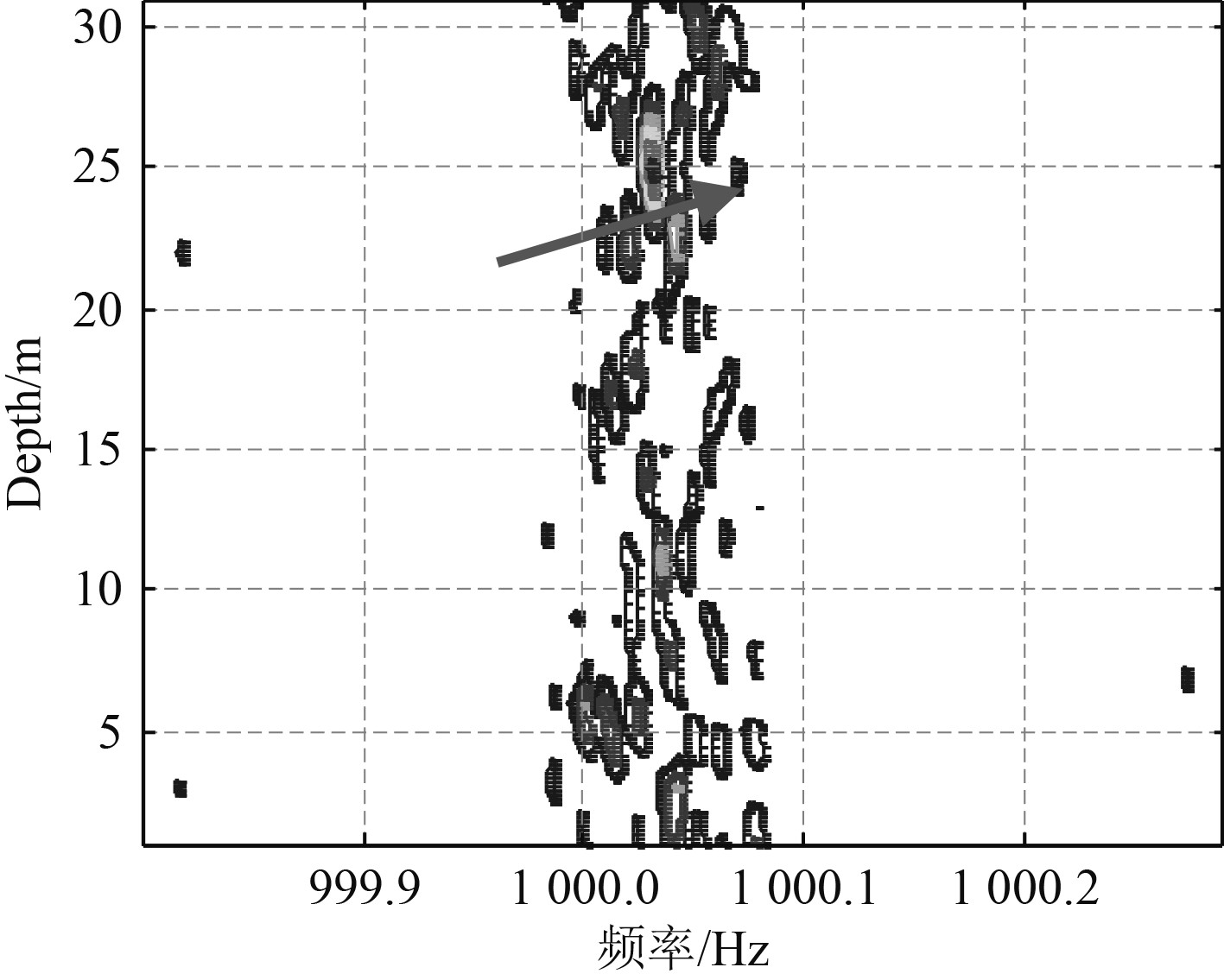
将图9所示信号进行SFFT处理,并以一定频率间隔构建补偿矩阵进行三维搜索,图10为深度、频率搜索切片等值线图,图11为距离、频率搜索切片等值线图,图12为第1组补偿频率对应的定位模糊面。搜索得到的目标距离和深度为(5950 m,25.5 m),与实际声源距离存在495 m偏差,深度存在0.5 m偏差,定位结果较准确。
|
图 10 第1组深度、频率搜索切片等值线图 Fig. 10 Group 1 depth and frequency search slice contour map |

|
图 11 第1组距离、频率搜索切片等值线图 Fig. 11 Group 1 range and frequency search slice contour map |
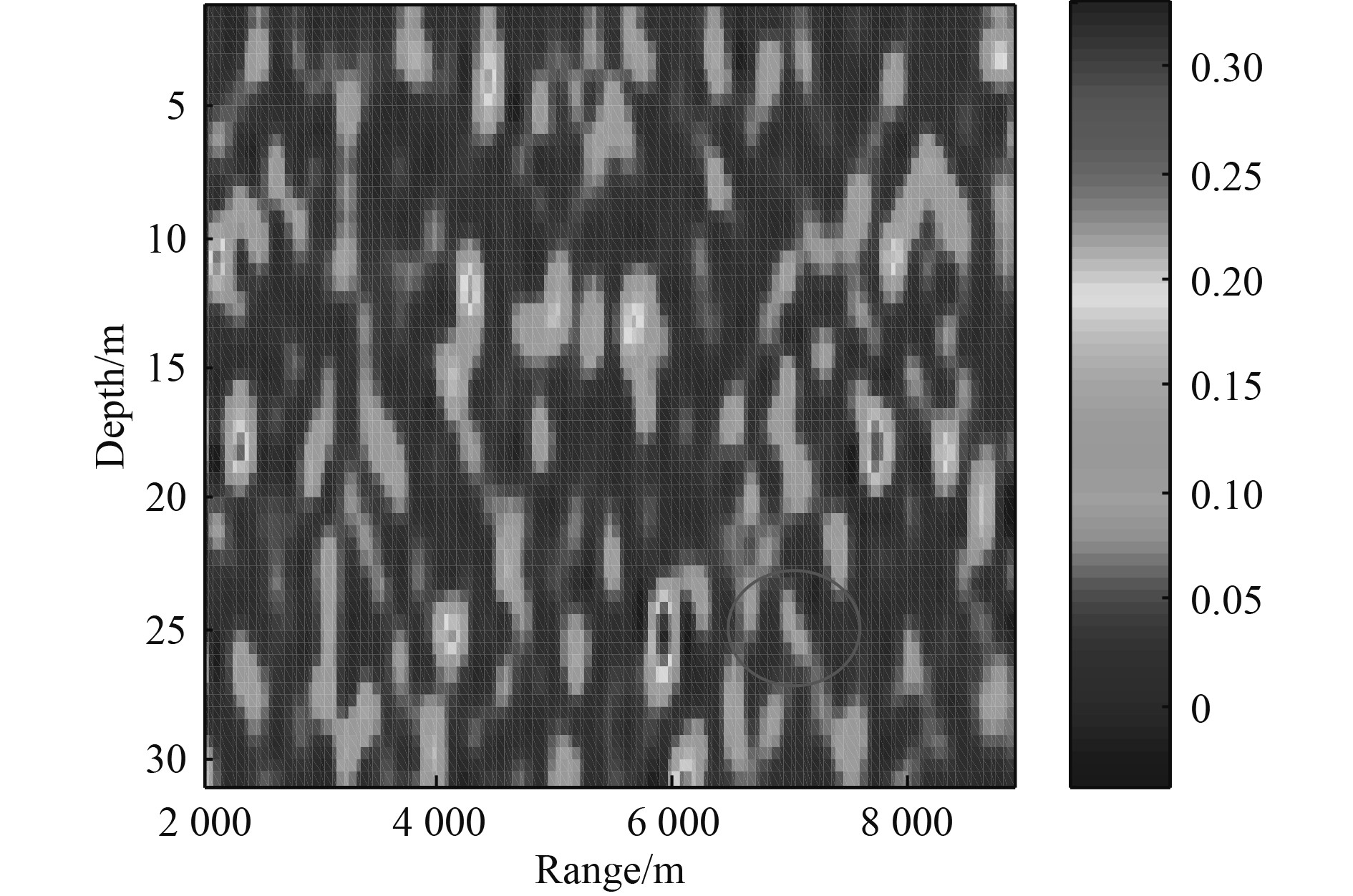
|
图 12 第1组补偿频率对应的定位模糊面 Fig. 12 Group 1 positioning fuzzy surface |
2)第2组,声源频率、距离不变,单水听器由10.1 m处匀速下放至42.07 m,与第1组采用相同声速剖面。第2组最终定位模糊度面如图13所示。搜索得到目标距离和深度为(6150 m,26.5 m),考虑到实际海况、环境参数失配以及接收船自噪声的影响,搜索定位误差在合理范围。
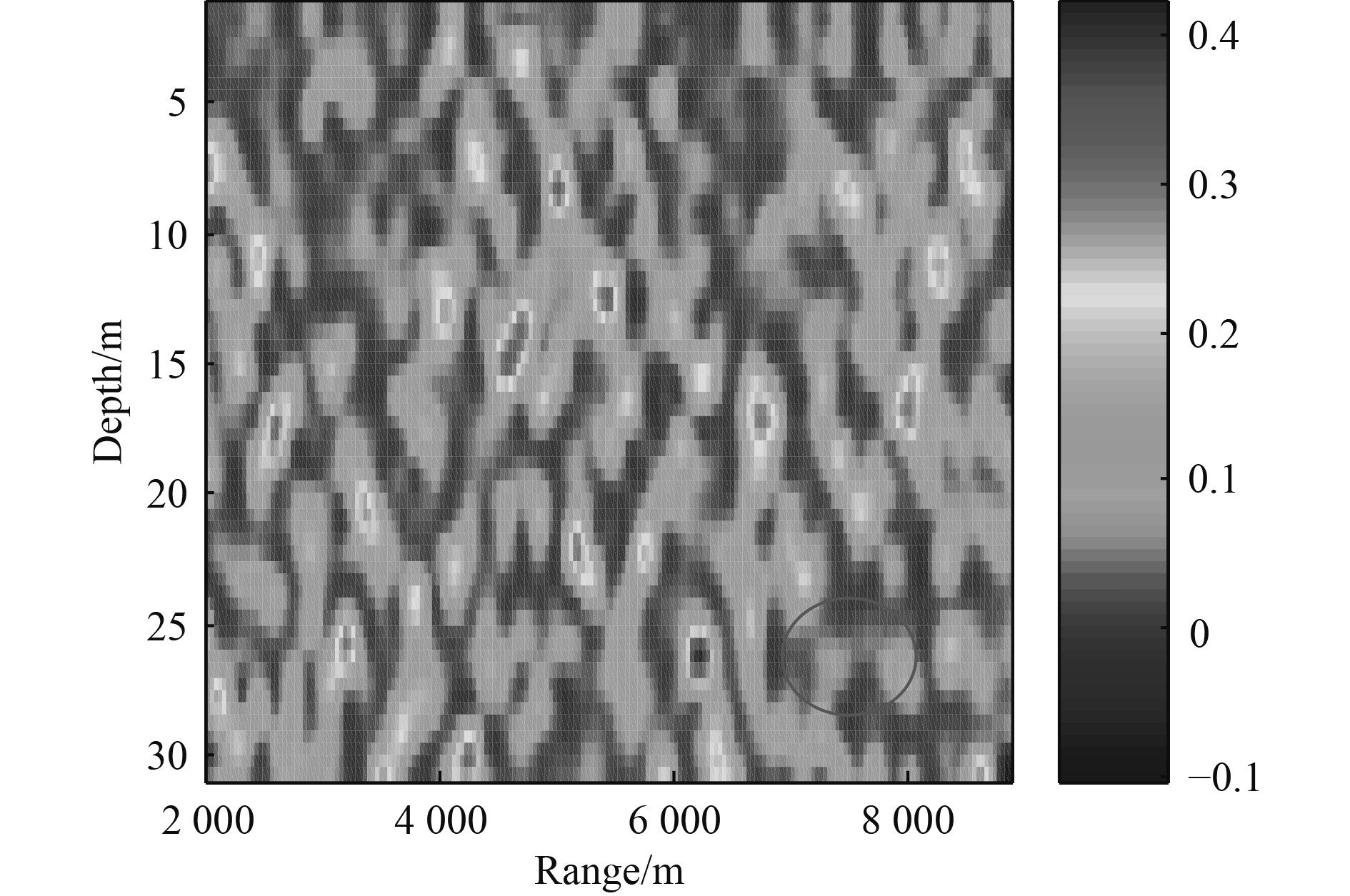
|
图 13 第2组补偿频率对应的定位模糊面 Fig. 13 Group 2 positioning fuzzy surface |
本文研究一种基于等效单阵元垂直合成孔径的水声目标被动定位方法。该方法利用距离、深度、频率三维搜索算法构建补偿矩阵,对连续变深采样得到的等效单阵元截断信号进行相位补偿,构建距离、深度、频率的三维数据场,估计目标真实位置,最后通过水池试验及海上试验验证了方法的有效性。该方法为水下潜航器目标被动定位提供了一种新思路,但方法中由于采用了广义波束形成——匹配场,因此对声场时变、空变、环境失配等比较敏感,实际使用具有一定限制。
| [1] |
TOUZE G L, TORRAS J, NICOLAS B, et al. Source localization on a single hydrophone[C]// Oceans IEEE, 2009.
|
| [2] |
李焜, 方世良, 安良. 非合作水声脉冲信号的单阵元匹配场定位研究[J]. 电子与信息学报, 2012, 34(11): 2541-2547. LI K, FANG S L, AN L. Research on single element matched field location of non cooperative underwater acoustic pulse signal[J]. Journal of Electronics and Information, 2012, 34(11): 2541-2547. |
| [3] |
王晋晋. 基于声传播模型的信道模拟与应用[D]. 哈尔滨: 哈尔滨工程大学, 2012. WANG J J. Channel simulation and application based on acoustic propagation model [D]. Harbin Engineering University, 2012. |
| [4] |
王良, 高大治, 王宁, 等. 一种宽带噪声信号的深海会聚区判别方法[J]. 中国科学: 物理学 力学 天文学, 2016, 46(9): 7–8. WANG L, GAO D Z, WANG N, et al. A discrimination method for deep sea convergence area of broadband noise signal [J] Chinese Science: Physics, mechanics and Astronomy, 2016, 46(9): 7–8. |
| [5] |
李晓曼, 张明辉, 张海刚, 等. 一种基于简正波匹配的浅海波导中宽带脉冲声源的被动测距方法[J]. 物理学报, 2017, 66(9): 203-218. LI X M, ZHANG M H, ZHANG H G, et al. A passive ranging method of broadband pulsed sound source in shallow water waveguide based on normal mode matching[J]. Journal of Physics, 2017, 66(9): 203-218. |
| [6] |
HAWKER K E. A normal mode theory of acoustic doppler effects in the oceanic waveguide[J]. The Journal of the Acoustical Society of America, 1979, 65(3): 675-681. DOI:10.1121/1.382478 |
 2023, Vol. 45
2023, Vol. 45
