在水声通信中,多普勒效应主要是由发射机和接收机之间存在相对运动引起的[1]。声波的传播速度约1500 m/s,对于高速移动平台而言,严重的多普勒效应会导致接收信号在频域发生选择性扩展和频谱偏移,同时在时域上产生扩展或压缩现象[1-2],影响对接收码元的准确判决和进一步的解调。因此,估计和补偿多普勒效应引起的频率偏移对于高速移动平台水声通信系统至关重要。
目前,针对低速移动平台的多普勒估计与补偿技术研究较多,而适用于高速移动平台的多普勒估计和补偿技术研究较少。针对高速运动条件下的多普勒估计与补偿技术,岳玲等[3]利用具有多普勒不变特性的HFM信号和对多普勒频移敏感的单频脉冲信号,提出了一种适用于低信噪比条件下收发双方存在高速运动时的多普勒频移估计与补偿方法。该方法同时具备接收信号捕获与同步的功能,但鲁棒性较差。Han X等[4]将移动水声通信中的多普勒估计与补偿分为3个阶段:首先通过LFM信号估计主要多普勒因子;再对数据进行重采样补偿后,通过被动时反技术削弱多径;然后通过判决反馈均衡进一步减小码间干扰与多普勒效应对通信结果的影响,但是该算法的计算复杂度较高。Li Y等[5]提出一种采用共轭Zadoff-Chu(ZC)序列进行多普勒因子估计与定时同步方法。该方法通过共轭ZC序列的相关峰差异估计多普勒扩展因子,同时完成定时同步,但是该算法需要在共轭ZC序列对前后添加循环前缀和循环后缀,导致同步信号的持续时间较长,降低了数据利用率。Wang K等[6]提出了时域连续发射升降扫HFM信号作为帧前导信号的多普勒因子估计方法,但没有给出多普勒补偿后的通信系统性能情况,且该方法仍然存在前导信号持续时间较长的问题,同样导致数据利用率降低。
为克服以上多普勒估计算法的不足,本文在分析多普勒效应对水声通信信号影响的基础上,利用HFM信号对多普勒频移的不敏感特性,提出一种基于时域叠加上扫和下扫HFM信号作为前导信号的帧同步方法,并通过线性插值的方法进行多普勒因子补偿。通过计算机仿真分析,验证了该方法在实测水声信道中对收发两端存在高速相对运动条件下水声通信的有效性。
1 多普勒效应对通信信号的影响假定水声通信中的发射机和接收机分别处于点
| $ d = \sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2} + {{\left( {{z_1} - {z_2}} \right)}^2}},$ | (1) |
因此,水声信号从发射机到接收机的传播时延可以写为
| $ \tau = \frac{d}{c} ,$ | (2) |
式中,
假定发射机和接收机的移动速度分别为
| $ \Delta v = \sqrt {{{\left( {{v_{x1}} - {v_{x2}}} \right)}^2} + {{\left( {{v_{y1}} - {v_{y2}}} \right)}^2} + {{\left( {{v_{z1}} - {v_{z2}}} \right)}^2}},$ | (3) |
多普勒因子定义为收发两端相对径向运动速度与声速之比,即
| $ \alpha = \frac{{\Delta v}}{c}。$ | (4) |
当通信双方相向移动时,
水声通信信号作为一种宽带信号,多普勒效应将宽带信号中的每个频率分量转变为不同的量,因此应将其建模为信号波形的扩展或压缩[2],即
| $ r(t) = s\left( {(1 + \alpha )t} \right),$ | (5) |
式中,
在离散时间系统中,式(5)可以被写为
| $ r\left[ {n{T_s}} \right] = s\left[ {n(1 + \alpha ){T_s}} \right]。$ | (6) |
式中:
对于频率为
| $ f = {f_0}(1 + \alpha )。$ | (7) |
在多普勒效应的影响下,水声通信信号会发生时间展宽或压缩,将导致符号同步误差累计。以运动速度为15 m/s的水下航行器为例,其时间的伸展或压缩为
上扫频HFM信号的复数形式[7]表示为:
| $ {S_{HFM}}(t) = \exp \left[ {j\frac{{2{\text{π}} }}{\gamma }\ln \left( {1 + \gamma {f_{\min }}t} \right)} \right] ,$ | (8) |
式中:
其瞬时频率为:
| $ {f_{HFM}}(t) = \frac{{{f_{\min }}}}{{1 + \gamma t{f_{\min }}}},$ | (9) |
当存在多普勒效应时,HFM信号的瞬时频率改变为:
| $ {f_{DOP}}(t) = \frac{{D{f_{\min }}}}{{1 + D\gamma {f_{\min }}t}}。$ | (10) |
比较式(9)和式(10),可以发现存在一个时延差
| $ {f_{DOP}}(t - {\tau _0}) = {f_{HFM}}(t) $ | (11) |
且
| $ {\tau _0} = - \frac{\alpha }{{\gamma f(1 + \alpha )}} $ | (12) |
由此可见,通过解算时延
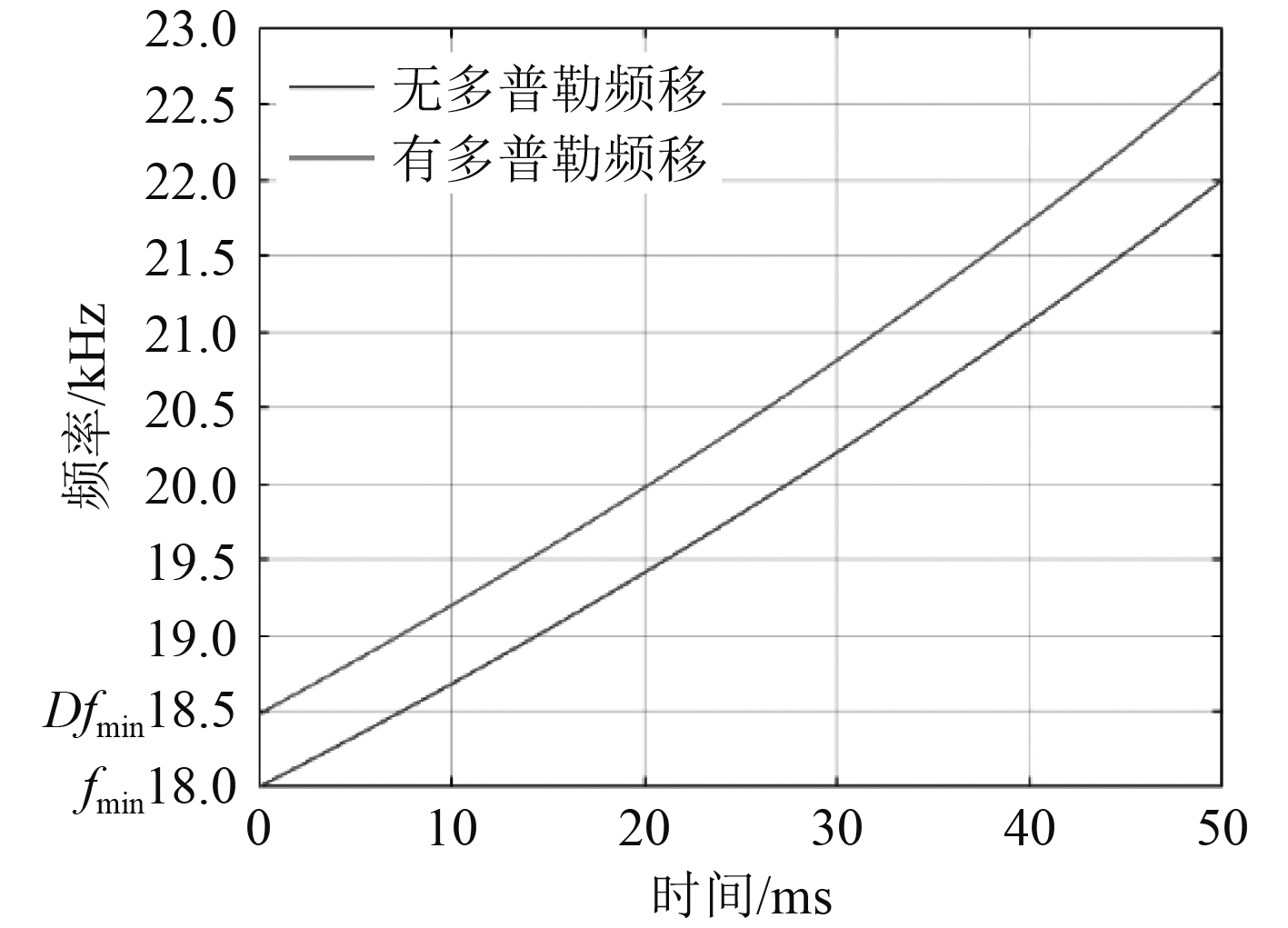
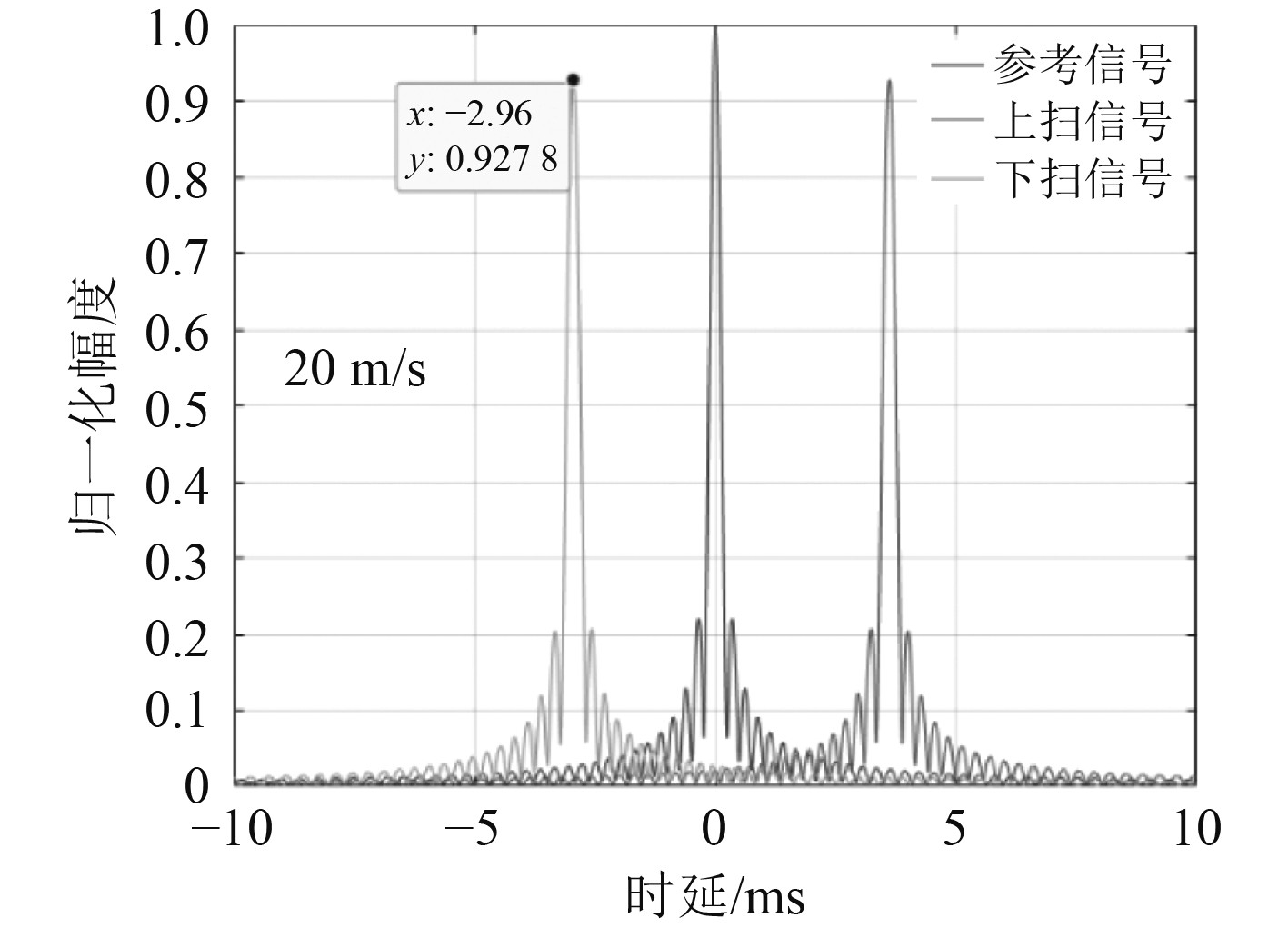
图1给出了收发端相对运动速度为0和40 m/s时HFM信号瞬时频率的变化情况,图2仿真给出了收发端相对运动速度为20 m/s时,利用副本相关处理方法分别对上扫频和下扫频HFM时延
|
图 1 存在多普勒效应时上扫HFM信号瞬时频率变化 Fig. 1 Instantaneous frequency change of up-sweep HFM signal with Doppler effect |
|
图 2 HFM信号的相关输出 Fig. 2 The correlation output of HFM signal |
从图1可以看出,HFM信号具有多普勒不变性,信号仅发生频移,调制频率未发生变化。由图2可见,收发两端在20 m/s相对运动条件下,接收信号仍然与本地保存信号存在很好的相关性,归一化相关峰值可以达到约0.93。同时可见,由2个HFM信号分别相关处理得到的时延差,可以进一步解算和估计得到相对运动速度为20.036 m/s,这与仿真设定的收发两端相对运动速度一致。因此,HFM信号可以应用于水下高速移动通信信号的多普勒精确估计。
3 高速移动水声通信的多普勒因子估计与补偿方法 3.1 帧结构设计高速移动水声通信中,图3(a)所示的发射帧结构是传统的多普勒因子估计算法,该算法存在帧同步信号持续时间较长的问题。

|
图 3 发射帧结构 Fig. 3 The structure of transmitted frame |
为克服该缺点,将时域叠加的上扫频和下扫频HFM信号作为帧前导信号,发射帧结构如图3(b)所示。其中
假设发射帧中
在接收端,设置2个并行相关器对接收信号进行拷贝相关处理。具体而言,对接收信号中的

|
图 4 多普勒因子估计结构图 Fig. 4 The structure of Doppler factor estimation |
如图4所示,2个并行相关器分别输出上扫频和下扫频HFM信号的相关峰偏移量
| $ {\tau _1} = \arg \mathop {\max }\limits_\tau \int_0^T r (t + \tau ){s_{HF{M^ + }}}(t){\rm{d}}t = \frac{{ - \alpha T{f_{\max }}}}{{({f_{\min }} - {f_{\max }})(1 + \alpha )}},$ | (13) |
| $ {\tau _2} = \arg \mathop {\max }\limits_\tau \int_0^T r (t + \tau ){s_{HF{M^-}}}(t){\rm{d}}t = \frac{{\alpha T{f_{\min }}}}{{({f_{\min }} - {f_{\max }})(1 + \alpha )}}。$ | (14) |
式中,
由式(13)和(14)可得,两个相关峰之间的差值可以表示为:
| $ \Delta \tau = {\tau _1} - {\tau _2} = \frac{{\alpha T({f_{\min }} + {f_{\max }})}}{{({f_{\max }} - {f_{\min }})(1 + \alpha )}},$ | (15) |
因此,多普勒因子
| $ \hat \alpha = \frac{{\Delta \tau ({f_{\max }} - {f_{\min }})}}{{T({f_{\max }} + {f_{\min }}) - \Delta \tau ({f_{\max }} - {f_{\min }})}} 。$ | (16) |
分析式(16)可知,多普勒因子
估计得到多普勒因子
| $\begin{split} \hat s\left[ {n{T_s}} \right] =& r\left[ {\frac{n}{{1 + \hat \alpha }}{T_s}} \right] = \left( {m + 1 - \frac{n}{{1 + \hat \alpha }}} \right)r\left[ {m{T_s}} \right] + \\ &\left( {\frac{n}{{1 + \hat \alpha }} - m} \right)r\left[ {(m + 1){T_s}} \right]\end{split} $ | (17) |
式中:
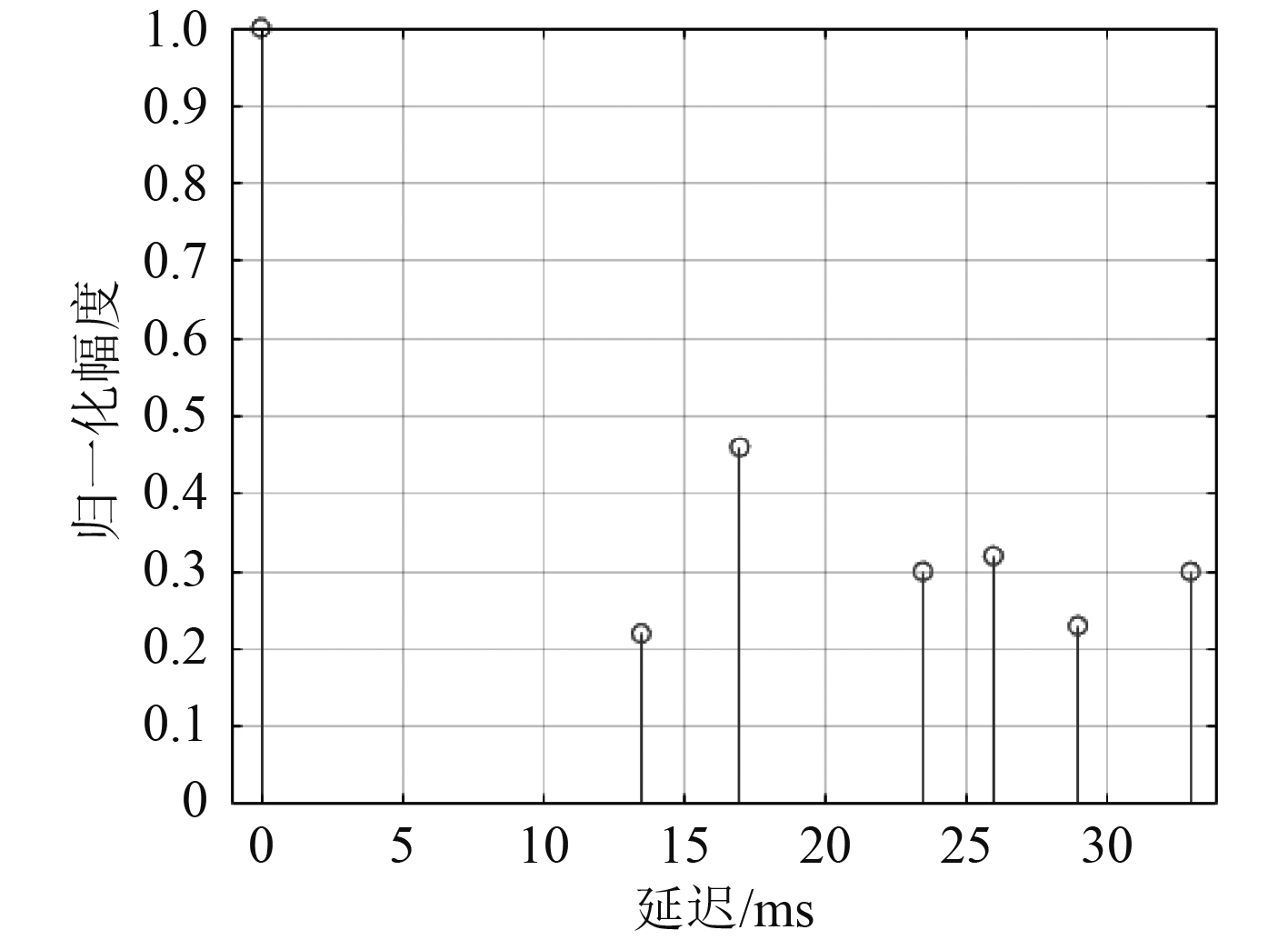
针对实测水声多径信道条件下高速移动节点水声通信的典型应用场景,利用时域叠加上扫频和下扫频HFM信号作为前导信号,进行计算机仿真。仿真时,上扫频和下扫频HFM信号的起始频率
|
图 5 信道冲激响应 Fig. 5 Normalized channel impulse response |
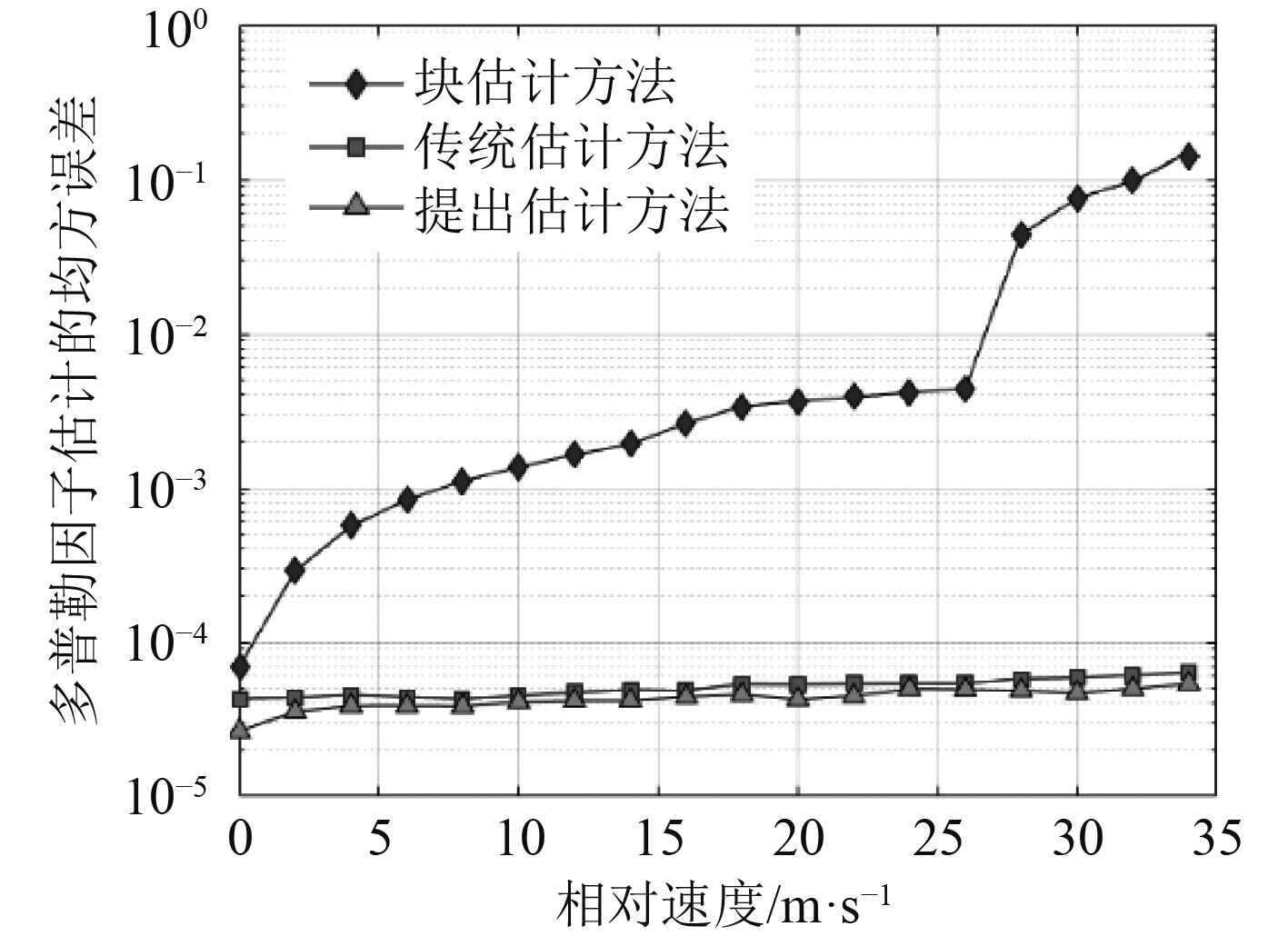
为了进行对比分析,首先给出相同信道条件下LFM块估计算法、图3(a)所示帧结构的传统估计算法以及本文估计算法的估计性能,3种估计算法的信号参数设置与HFM信号一致,多普勒因子估计结果的均方误差如图6所示。可以看出,随着收发端相对运动速度增大,LFM块估计方法的估计误差逐渐上升,导致水声通信系统性能迅速恶化,而传统估计算法和所提估计算法的估计性能基本不随相对运动速度变化,均适合于高多普勒水声通信系统,且本文估计算法可以提高发射帧的数据利用率。
|
图 6 3种多普勒因子估计方法的性能对比 Fig. 6 Performances comparison of three Doppler factor estimation methods |
为了深入研究,进一步仿真分析信号类型对于所提多普勒因子估计算法性能的影响。分别采用LFM和HFM两种不同信号在相同信道条件下对多普勒因子进行了仿真估计,仿真结果如图7所示,同时仿真对比不同持续时间和带宽的HFM信号对所提算法的性能影响,仿真结果如图8和图9所示。

|
图 7 信号类型对多普勒因子估计性能影响 Fig. 7 Influence of signal type on Doppler factor estimation performance |
|
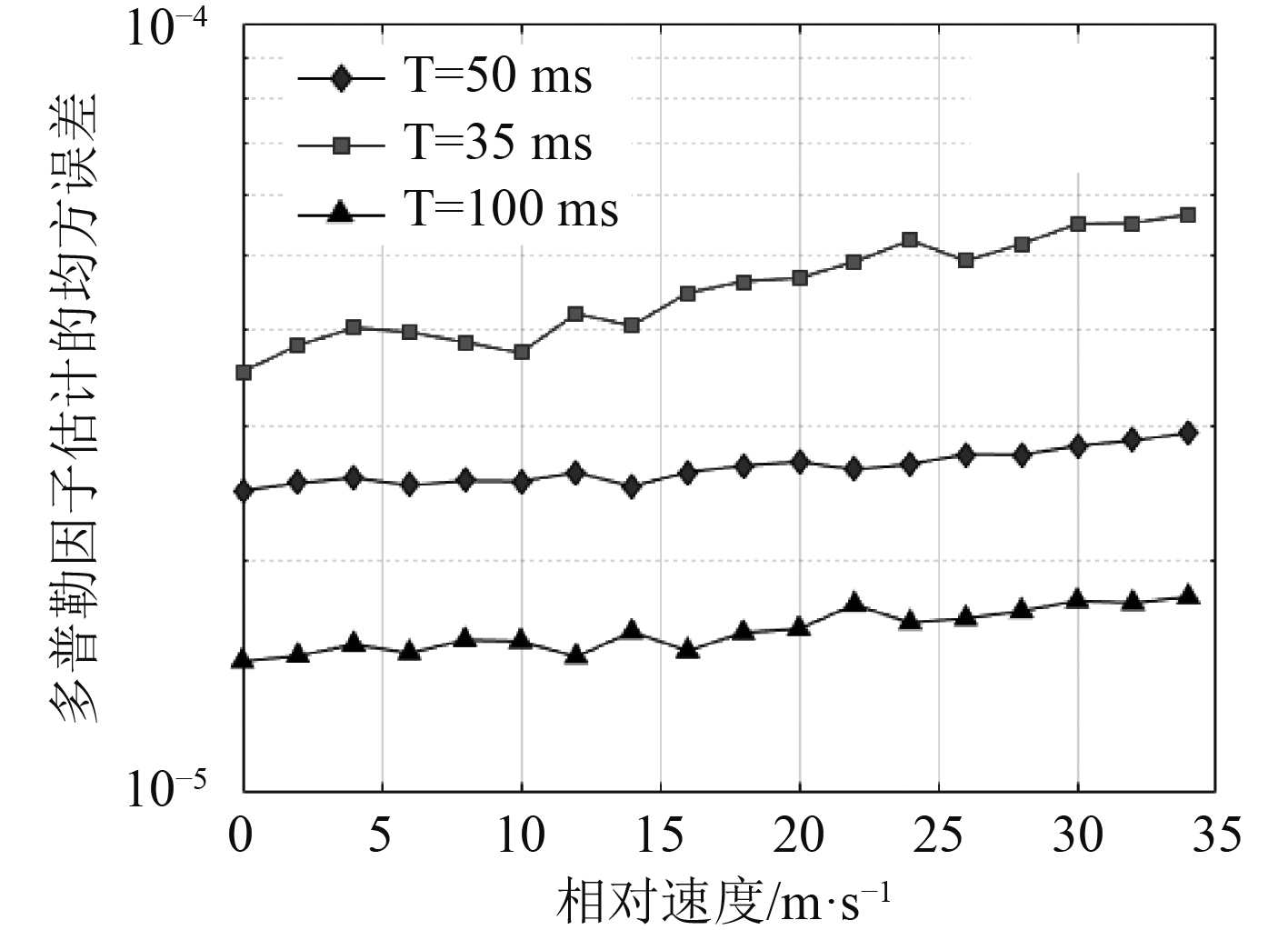
图 8 信号持续时间对多普勒因子估计性能影响 Fig. 8 Influence of signal duration on Doppler factor estimation performance |

|
图 9 信号带宽对多普勒因子估计性能影响 Fig. 9 Influence of signal bandwidth on Doppler factor estimation performance |
从图7可以看出,随着收发端相对运动速度增大,LFM信号估计误差呈近似直线上升,而HFM信号估计性能基本不随相对运动速度变化,可见HFM信号更适合于高多普勒水声通信系统。
对比分析图8和图9可知,前导信号持续时间越长、带宽越宽,则多普勒因子的估计均方误差越小,估计性能越好。
图10为不同信噪比情况下的多普勒因子估计性能仿真。可以看出,该多普勒估计算法在−10 dB和−15 dB时均具有良好的性能,但是在−20 dB时不具有优良性能。

|
图 10 信噪比对多普勒因子估计性能影响 Fig. 10 Influence of SNR on Doppler factor estimation performance |
为了验证本文方法在实际水声通信系统应用中的有效性,选用典型的DBPSK水声通信系统,进行不同条件下的计算机仿真。
假设收发两端相对运动速度36 kn,分别对无多普勒补偿、利用LFM信号进行多普勒估计与补偿、利用HFM信号进行多普勒估计与补偿3种情况下的通信误码率情况进行统计分析,结果如图11所示。

|
图 11 HFM和LFM信号的误码率 Fig. 11 Bit error ratio with HFM and LFM signals |
由图11可知,在实测多途水声信道中,收发两端运动速度为36 kn情况下,采用LFM信号作为同步信号已无法获得理想的误码率性能,但基于HFM信号同步方法仍可以提供良好的误码率性能,实现可靠通信。
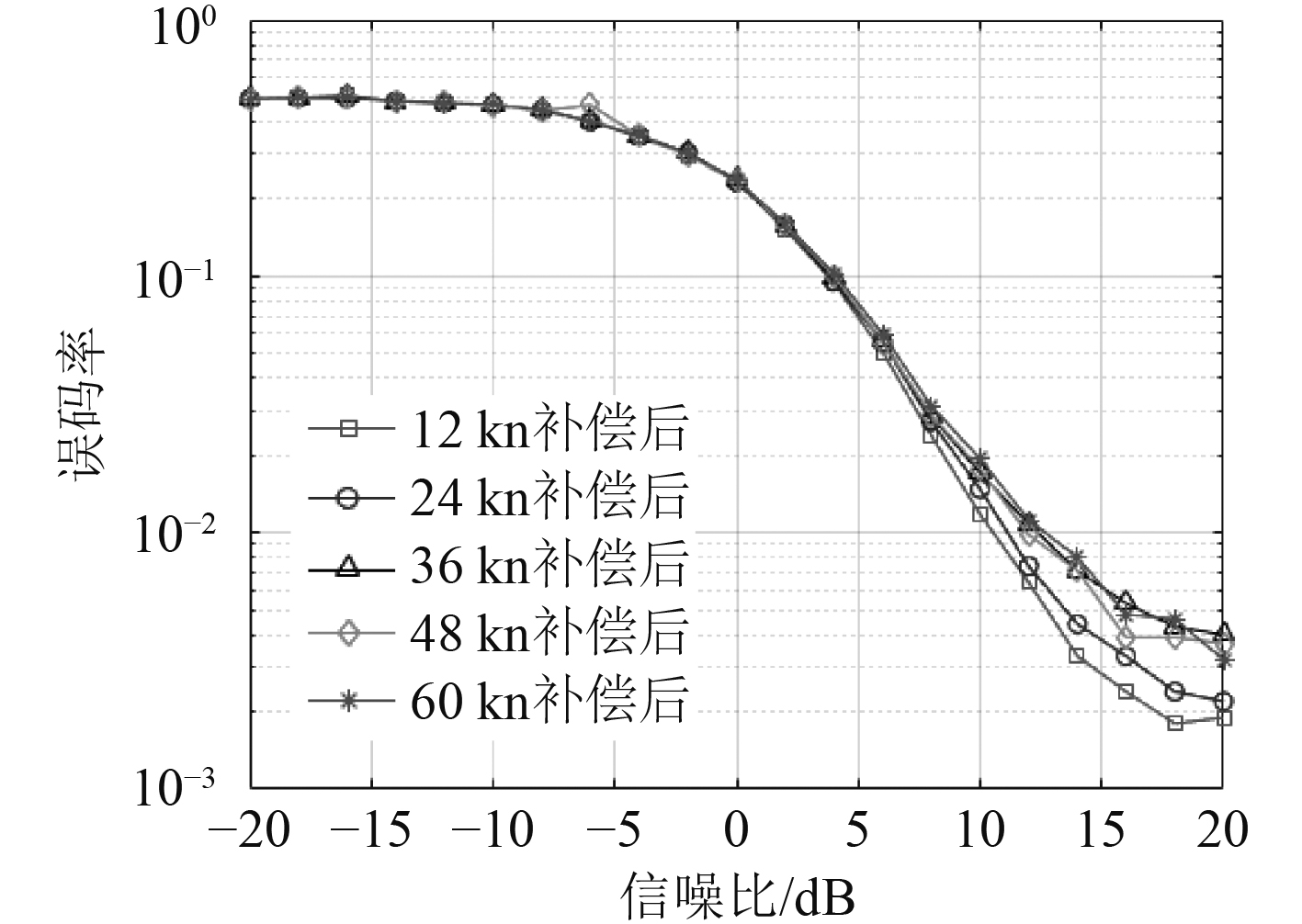
对于收发端相对运动速度分别为12 kn,24 kn,36 kn,42 kn和60 kn等不同情况,分别仿真给出采用HFM作为同步导引信号时水声通信的误码率性能,仿真结果如图12所示。
|
图 12 HFM信号的误码率 Fig. 12 Bit error ratio with HFM signal |
可知,当收发两端相对运动速度分别为12 kn,24 kn,36 kn,42 kn和60 kn的不同条件时,采用HFM信号作为同步导引信号可以获得较一致的通信误码率性能。
5 结 语对于水下高速移动平台的通信系统,水声通信信号的多普勒估计与补偿不可或缺。本文分析多普勒效应对水声通信信号影响,同时分析HFM信号特性,利用其对多普勒频移的不敏感程度,提出了一种基于时域叠加上扫频和下扫频HFM信号作为前导同步信号进行多普勒因子与补偿的水声通信帧同步方法。
通过接收端配置2个并行相关器对接收信号进行拷贝相关处理,并根据2个相关峰之间的时延差来估计多普勒因子。在此基础上通过线性内插方法进行重采样,实现多普勒补偿。仿真分析该算法在实测水声多途信道条件下,3种多普勒估计算法的估计性能以及所提方法在不同持续时间、带宽前导同步信号和不同信噪比条件下的多普勒因子估计性能。此外,针对典型的DBPSK水声通信系统,仿真分析无多普勒补偿、利用LFM信号进行多普勒估计与补偿和利用HFM信号进行多普勒估计与补偿的通信误码率情况,并在此基础上进一步仿真分析了采用HFM信号作为帧同步信号的通信方法,对于收发两端存在不同相对运动速度条件下,通信误码率性能的一致性。
本文提出的多普勒估计与补偿方法计算复杂度低且简单实用,为水下高速移动通信帧同步提供了一种有效的解决方案。
| [1] |
岳玲, 樊书宏, 冯西安. 鱼雷协同制导对水声通信能力的需求分析[J]. 水下无人系统学报, 2018, 26(5): 427-432. YUE L, FAN S H, FENG X A. Capability requirements analysis of underwater acoustic communication for torpedo cooperative guidance[J]. Journal of Unmanned Undersea Systems, 2018, 26(5): 427-432. |
| [2] |
SHARIF B S, NEASHAM J, HINTON O R. A computationally efficient Doppler compensation system for underwater acoustic communications[J]. IEEE Journal of Oceanic Engineering, 2000, 25(1): 52-61. DOI:10.1109/48.820736 |
| [3] |
岳玲, 樊书宏, 王明洲. 高速移动水声通信中的多普勒频移估计方法研究[J]. 系统仿真学报, 2011, 23(11): 2366-2370. YUE L, FAN S H, WANG M Z, et al. Study on Doppler-shift estimation for underwater high-range-rate acoustic mobile communications[J]. Journal of System Simulation, 2011, 23(11): 2366-2370. |
| [4] |
HAN X, GE W, YIN J W, et al. Mobile underwater acoustic communication with constantly changing Doppler effect[C]//OCEANS, IEEE, 2018: 1–5.
|
| [5] |
LI Y F, WANG Y Y, GUAN X P. Joint synchronization and Doppler scale estimation using zadoff-chu sequences for underwater acoustic communications[C]//OCEANS 2017-Anchorage. IEEE, 2017: 1–5.
|
| [6] |
WANG K X, CHEN S M, LIU C Z, et al. Doppler estimation and timing synchronization of underwater acoustic communication based on hyperbolic frequency modulation signal[C]//2015 IEEE 12th International Conference on Networking, Sensing and Control. IEEE, 2015: 75–80.
|
| [7] |
KHUC B, VYLEGZHANIN E, CHILINGAROV A, et al. Preamble signals for detection timing and Doppler synchronization in underwater acoustic communications[C]//International Youth Conference on Electronics, Telecommunications and Information Technologies, 2021: 683–698.
|
| [8] |
LING Z Q, XIE L, CHEN H F. Joint doppler scale estimation and timing synchronization in underwater acoustic communications[C]//2019 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). IEEE. 2019: 1–6.
|
 2023, Vol. 45
2023, Vol. 45
